Selektionseffekte

Einleitung

Selektionseffekte können drastische Auswirkungen auf Datenanalysen haben. Sie treten auf, wenn die Stichprobe nicht repräsentativ für die Grundgesamtheit ist, da nur ein ganz bestimmter Teil beobachtbar war. Hängt die Selektion von einer Variable ab, die wir erhoben haben, so können wir diesen Effekt herausrechnen. Einer der Ersten denen dies gelang war der Ökonom James J. Heckman (Heckman, 1979; siehe auch Briggs, 2004).

Selektionsbias am Heckman Modell

Entsprechend wollen wir den Selektionsbias an dem einfachsten “Heckman”-Modell untersuchen. Dazu schauen wir uns ein Modell mit einer Prädiktorvariable an.

$$Y_i = b_0 + b_1X_i + \underbrace{e_i}_{rZ_i+\varepsilon_i}$$ $b_0$ und $b_1$ sind hier die Regressionskoeffizienten in der Population, welche es zu schätzen gilt. $X_i$ ist der Prädiktor und $e_i$ ist das Regressionsresiduum der Person/Erhebung $i$ ($i=1,\dots,n$, wobei $n$ die Gesamtstichprobengröße ist). Das allgemeine Modell wird natürlich für beliebig viele Prädiktoren formuliert. Die Idee von Heckman war nun, dass, wenn sich bspw. nur bestimmte Personen (das Ganze kann natürlich auch für den nicht-psychologischen Kontext formuliert werden) bereiterklären an der Studie teilzunehmen, dann werden die Regressionsgewichte verschätzt. Wenn nun die Selektion auf eine ganz bestimmte Weise abläuft, dann lässt sich dieser Bias wieder herausrechnen. Heckman nahm dazu an, dass die Selektion dem sogenannten Probit-Modell folgt. Das Probit-Modell ist, ähnlich wie das logistische Modell (siehe bspw. logistische Regressionssitzung in R), ein Regressionsmodell zur Modellierung dichotomer abhängiger Variablen.

Probit-Modell: der Selektionsmechanismus

Und zwar ist im Probit-Modell die Wahrscheinlichkeit selektiert zu werden (Erfolg zu haben) nicht die logistische (Ogiven)-Funktion, wie in der logistischen Regression, sondern die Verteilungsfunktion der Standardnormalverteilung $\Phi$. Dies hört sich zunächst sehr kompliziert an, ist es aber eigentlich nicht. Wir schauen uns den Selektionsmechanismus an, um dieser Sache auf den Grund zu gehen. Eine Person nimmt an der Studie teil, wenn sie sich selbst in diese hinein selektiert, da sie bspw. ein bestimmtes Mindset hat und somit eine bestimmte Variablenkonstellation aufweist, die sie mit erhöhter Wahrscheinlichkeit an der Studie teilnehmen lässt.

$$s_i = 1 \Longleftrightarrow Z_i \le \beta_0 + \beta_1X_i$$ und $$s_i=0 \text{ sonst}$$

$\Longleftrightarrow$ bedeutet “genau dann, wenn”. Ist $s_i=1$, so wird selegiert (die Person nimmt teil). $Z_i$ ist standardnormalverteilt und $\beta_0$ und $\beta_1$ sind die Regressionsgewichte der Selektion. Die Variable (hier $X$), die für die Selektion zuständig ist, ist beliebig. Sie muss nur bekannt und beobachtet sein! Wir schauen uns den (speziellen) Fall an, in welchem auch der Prädiktor aus der Regression für die Selektion zuständig ist. Dies könnte zum Beispiel der Fall sein, wenn wir den Therapieeffekt einer langwierigen Therapieform untersuchen wollen (Symptomstärke nach vollendeter Therapie = $Y$) und diese durch das Commitment ($X$) vorhersagen. Menschen, die mehr Commitment zur Therapie zeigen, ziehen die Therapie wahrscheinlicher bis zum Ende durch und werden somit mit höherer Wahrscheinlichkeit in den Pool der beobachteten Stichprobe selegiert. Der Ausdruck $Z_i \le \beta_0 + \beta_1X_i$ beschreibt diese Phänomen nochmals. Wir wissen aus früheren Semestern, dass die Standardnormalverteilung einen Mittelwert von 0 hat und eine Standardabweichung von 1. Somit ist $Z_i$ genau dann mit hoher Wahrscheinlichkeit kleiner oder gleich groß wie $\beta_0 + \beta_1X_i$ (und damit würde $s_i=1$ ausfallen), wenn dieser Ausdruck groß ist. Schauen wir uns dies einmal an: Angenommen $\beta_0 + \beta_1X_i = -1$ (kleiner Wert), dann ist $Z_i$ sehr häufig größer als $-1$.

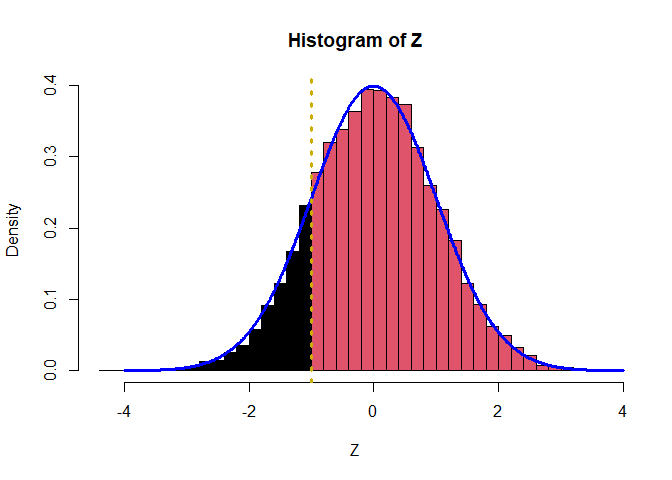
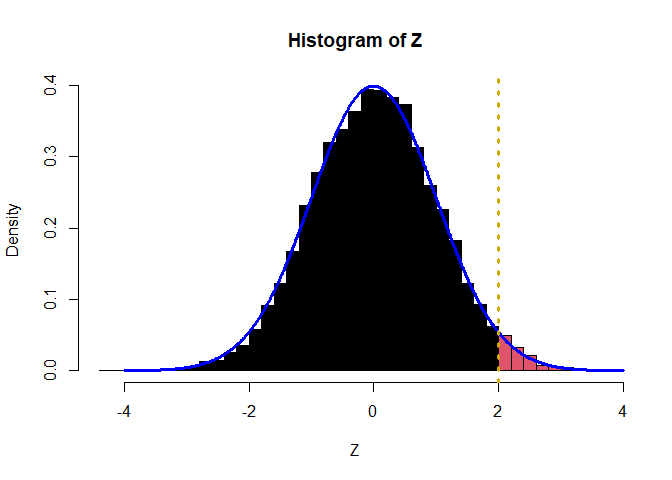
In schwarz sehen wir den Bereich, in welchem $Z_i$ kleiner als -1 ausfällt und somit selegiert werden würde. Sie erinnern sich vielleicht, dass bei einer Standardnormalverteilung gerade der Wert -1 bedeutet, dass die Variable eine Standardabweichung kleiner als der Mittelwert (0) ausfällt. In blau sehen wir außerdem die Dichte der Standardnormalverteilung. Die vertikale gestrichelte Linie repräsentiert hier den Wert -1. Nehmen wir nun an, dass $\beta_0 + \beta_1X_i = 2$ (großer Wert), dann ist $Z_i$ sehr häufig kleiner als $2$.

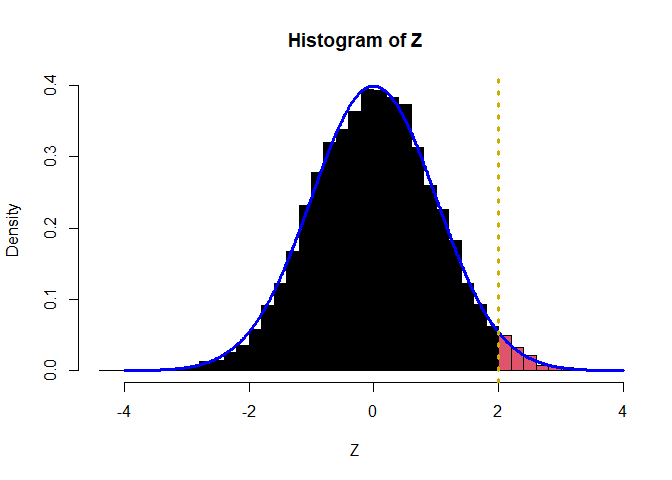
Für den Code der Grafiken, siehe in Appendix A nach. Die schwarze Fläche ist genau die Wahrscheinlichkeit, dass die Standardnormalverteilung einen Wert kleiner der oberen Grenze annimmt: also $\mathbb{P}(Z_i\le\beta_0+\beta_1X_i)=\Phi(\beta_0+\beta_1X_i)$. Diese fällt für einen Wert von 2 deutlich größer aus als für einen Wert von -1! In R lässt sich diese Wahrscheinlichkeit sehr leicht bestimmen:

set.seed(123456)                 # Vergleichbarkeit
Z <- rnorm(10000)                # 10^4 std. normalverteilte Zufallsvariablen simulieren
pnorm(q = -1, mean = 0, sd = 1)  # Theoretische Wahrscheinlichkeit, dass Z <= -1

## [1] 0.1586553

mean(Z <= -1)                    # Empirische (beoabachtete) Wahrscheinlichkeit, dass Z <= -1

## [1] 0.1544

pnorm(q = 2, mean = 0, sd = 1)   # Theoretische Wahrscheinlichkeit, dass Z <= 2

## [1] 0.9772499

mean(Z <= 2)                     # Empirische (beoabachtete) Wahrscheinlichkeit, dass Z <= 2

## [1] 0.9745

Die beobachtete Wahrscheinlichkeit, dass die generierte Variable Z kleiner oder gleich groß wie -1 bzw. wie 2 ist, liegt sehr nah an der theoretischen dran (Z <= -1 bzw. Z <= 2 wandeln den Vektor Z in TRUE und FALSE um, mit der mean Funktion wird dann die relative Häufigkeit von TRUE, was R-intern als 1 verstanden wird, bestimmt; FALSE wird R-intern als 0 verstanden; siehe auch Sitzung zur logistischen Regression um relative Häufigkeiten von 01-Folgen zu wiederholen oder in der Sitzung zu Simulationsstudien in R, in welcher dies zur Berechnung der Power etc. verwendet wurde). Analog zur logistischen Regression wählen wir $p=\mathbb{P}(s_i=1|X_i)=\mathbb{P}(Z_i\le\beta_0+\beta_1X_i)=\Phi(\beta_0+\beta_1X_i)$ und bestimmen die Gewichte mit der Maximum Likelihood Methode. Dies geschieht in der glm-Funktion, die wir in der Sitzung zur logistischen Regression behandelt haben. Hier muss lediglich das family-Argument angepasst werden: family = binomial(link = "probit"):

set.seed(1234567)
n <- 1000
Z <- rnorm(n = n, mean = 0, sd = 1)
X <- rnorm(n = n, mean = 2, sd = 5) # die Verteilung von X ist beliebig

# Selektion
beta0 <- -2
beta1 <- .5
s <- beta0 + beta1*X + Z > 0

probit_model <- glm(s ~ 1 + X, family = binomial(link = "probit"))
summary(probit_model)

## 
## Call:
## glm(formula = s ~ 1 + X, family = binomial(link = "probit"))
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -2.10216    0.13720  -15.32   <2e-16 ***
## X            0.50715    0.03248   15.61   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 1279.40  on 999  degrees of freedom
## Residual deviance:  488.79  on 998  degrees of freedom
## AIC: 492.79
## 
## Number of Fisher Scoring iterations: 7

Der Output gleicht fast vollkommen dem der logistischen Regression. Lediglich die family-Spezifikation ist eine andere. Der Output ist analog zum logistischen Modell (Logit-Modell) zu interpretieren. Wir sehen, dass die Schätzungen von $\beta_0$ und $\beta_1$ recht nah an den vorgegebenen wahren Werten -2 und 0.5 dran liegen! Dies bedeutet also, dass wir mit der Probit-Regression die Koeffizienten $\beta_0$ und $\beta_1$ schätzen können.

Die Populationsregressionsgleichung

Selegieren wir unsere Stichprobe anhand des eben vorgestellten Selektionsmechanismus, so folgt, dass das Residuum der Regressionsanalyse nicht länger unabhnängig von den Prädiktoren ist. Dies können wir in der Populationsgleichung auch explizit vermerken, indem wir $Z$ in die Gleichung mit aufnehmen. Im Endeffekt ist dies nur eine Umformulierung des Residuums, welche auf Grund der Normalverteilung der Residuuen geschieht (genaue Begründungen gehen über das nötige Wissen für diese Sitzung hinaus, aber im Grunde ist die Kovarianz zwischen $e_i$ und $X_i$ in Gruppe $s_i=1$ gegeben durch den Parameter $r$ sowie den Selektionsparameter $\beta_1$):

$$Y_i = b_0+b_1X_i +rZ_i+\varepsilon_i,$$ wobei das Residuum zuvor $e_i=rZ_i+\varepsilon_i$ war. $Z$ ist hier das $Z$ von der Selektion - diese ist auf Populationsebene allerdings eine latente (nicht beobachtbare) Variable. Wäre die Stichprobe repräsentativ, so wären $X$ und $Z$ unkorreliert und wir hätten kein Problem. Würden jedoch bspw. nur im Vergleich zu $Z$ große $X$ mit erhöhter Wahrscheinlichkeit in die Stichprobe gewählt, so resultierte eine Korrelation zwischen $X$ und $Z$, die die Parameterschätzung verzerrt. Damit kommt es zu einem Parameterbias, falls die Selektion tatsächlich von anderen Variablen (hier $X$) abhängt (hier also $\beta_1\neq0$). Um dennoch sinnvolle Schätzungen für $b_0$ und $b_1$ abgegeben zu können, müssen wir das $Z$ in der Populationsgleichung durch dessen (bedingte) Erwartung annähern. Glücklicherweise müssen wir das nicht mehr nachrechnen. Das haben andere bereits für uns erledigt. Die (bedingte) Erwartung für $Z_i$ ist gerade das Inverse von Mills-Ratio ($\lambda$), welches von $\beta_0, \beta_1$ und $X$ abhängt: $$\lambda(X)=\frac{\phi(\beta_0+\beta_1X)}{\Phi(\beta_0+\beta_1X)},$$ wobei $\phi$ die Dichte- (in R: dnorm(x = ?, mean = 0, sd = 1)) und $\Phi$ die Verteilungsfunktion (in R: pnorm(q = ?, mean = 0, sd = 1)) der Standardnormalverteilung ist.

Einfluss der Selektion

Um den Einfluss auf die Regression genauer zu erkennen, schauen wir uns ein simuliertes Beispiel in R an: Wir beginnen damit die Daten für die Populationsregression zu simulieren: b0 und b1 sind die Regressionskoeffizienten $b_0 = 0.5$ und $b_1 = 1.2$, X und Z sind $X$ und $Z$, r ist $r = 2$ in der Populationsgleichung und sigma ist die Standardabweichung (= 2) des unabhängigen Teils des Residuums $\varepsilon$.

set.seed(1234567)
n <- 1000
X <- rnorm(n = n, mean = 2, sd = 2)
Z <- rnorm(n = n, mean = 0, sd = 1)

# Populationsregression
b0 <- 0.5
b1 <- 1.2
r <- 2
sigma <- 2

eps <- rnorm(n = n, mean = 0, sd = sigma)
Y <- b0 + b1*X + r*Z + eps # Populationsregression


# Selektion
beta0 <- -2
beta1 <- .5
s <- beta0 + beta1*X + Z > 0   # Selektionsmechanismus

Y_obs <-rep(NA, length(Y))
Y_obs[s == 1] <- Y[ s== 1]     # beobachtbares Y

Nachdem wir $Y$ simuliert haben (als gäbe es keinen Selektionseffekt), fügen wir die Selektion nachträglich hinzu. Dafür erstellen wir zunächst einen leeren Vektor Y_obs mit dem reps Befehl, den wir aus der letzten Sitzung zu Simulationsstudien in R kennen. Anschließend füllen wir alle Stellen des Vektors an denen $s$ gleich 1 ist, also an dem selegiert wurde (in R: s == 1), mit den entsprechenden Werten aus $Y$ auf. Wenn wir nun eine Regression rechnen und nur die beobachteten Werte verwenden (R führt per Default listwise deletion: listenweisen Fallausschluss) durch, so erkennen wir, dass die Regressionsparameter deutlich verschätzt sind. Das Modell dazu nennen wir reg_obs für Regressionsobjekt observed. Führen wir hingegen eine Regression auf Populationsebene durch, indem wir Y anstatt Y_obs verwenden, so liegen die Regressionsschätzer hier sehr nah an den wahren Werten. Hierbei müssen wir unbedingt beachten, dass Z in beiden Gleichungen nicht auftaucht (die wahren Werte sind: $b_0 = 0.5$ und $b_1 = 1.2$):

reg_obs <- lm(Y_obs ~ X)
reg_obs

## 
## Call:
## lm(formula = Y_obs ~ X)
## 
## Coefficients:
## (Intercept)            X  
##      5.4403       0.3922

reg_pop <- lm(Y ~ X)
reg_pop

## 
## Call:
## lm(formula = Y ~ X)
## 
## Coefficients:
## (Intercept)            X  
##      0.5175       1.1619

Die Unterschiede liegen daran, dass $X$ und $Z$ korreliert sind in der selegierten Stichprobe:

cor(X[s==1], Z[s==1])

## [1] -0.6101458

Während sie es nicht sind in der repräsentativen Gesamtstichprobe:

cor(X, Z)

## [1] -0.03086995

Wir können das Ganze auch mit einen Signifikanztest untermauern:

cor.test(X[s==1], Z[s==1])

## 
## 	Pearson's product-moment correlation
## 
## data:  X[s == 1] and Z[s == 1]
## t = -11.628, df = 228, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.6854068 -0.5219864
## sample estimates:
##        cor 
## -0.6101458

cor.test(X, Z)

## 
## 	Pearson's product-moment correlation
## 
## data:  X and Z
## t = -0.97568, df = 998, p-value = 0.3295
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.09268566  0.03118280
## sample estimates:
##         cor 
## -0.03086995

Nur im repräsentativen Fall ist die Korrelation nicht signifikant von 0 verschieden!

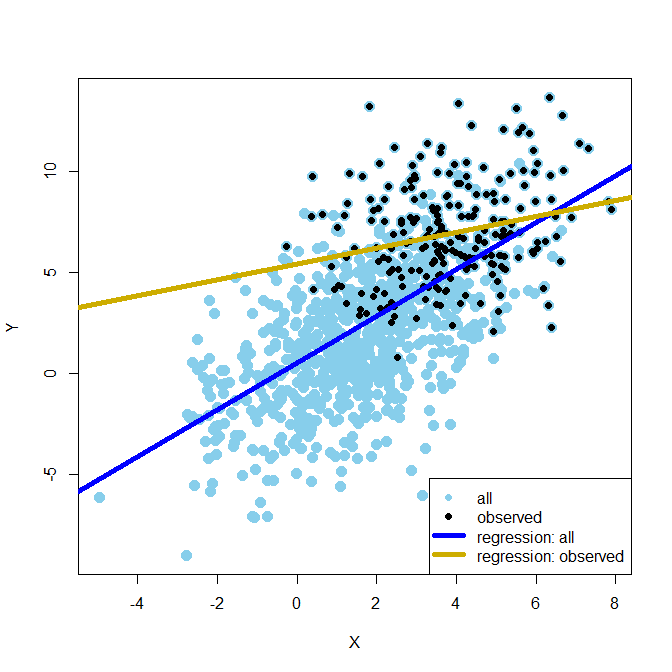
Diese Phänomen lässt sich auch sehr gut in einer Grafik veranschaulichen:

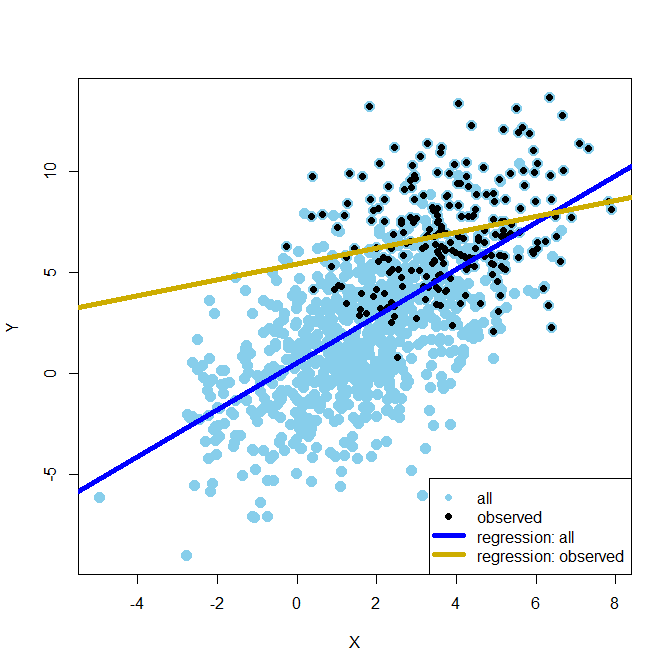
Hier repräsentieren die hellblauen Punkte die repräsentative Stichprobe. Die schwarzen Punkte hingegen stellen die selegierte/verzerrte Stichprobe (biased sample) dar. Genauso zeigt die blaue Linie die korrekte Regressionsgerade, während die goldene Linie die verzerrte darstellt (für den Code der Grafik, siehe Appendix A). Wir erkennen deutlich die Verzerrung der Ergebnisse. Sie können sich die Verzerrung wie folgt erklären: Die Regression wird unter der Annahme der Unabhängigkeit der Residuuen von den Prädiktoren in der Regressionsgleichung geschätzt. Da aber $e_i=rZ_i+\varepsilon_i$ gilt und wir weiter oben gesehen haben, dass $X$ und $Z$ in der Selektionsgruppe korreliert sind, bedeutet dies, dass das Residuum nicht länger unabhängig vom Prädiktor ist. Da dies aber eine Annahme ist und das Verfahren nur so geschätzt werden kann, werden die Parameter so verzerrt, damit die Residuen möglichst unsystematisch sind. Insbesondere der Mittelwert der Residuen muss 0 sein für jede Ausprägung von X. Es muss also gelten $\mathbb{E}[e_i|X_i]=0$. Allerdings ist dies nicht der Fall in der Selektionsgruppe:

Die Umformung und Herleitung gehen über den Stoff dieses Kurses hinaus und dienen nur zu Illustrationszwecken. Dennoch hebt dies hervor, welchen fatalen Fehler wir begehen können, wenn unsere Stichproben verzerrt sind und wie enorm wichtig es ist, dass die Daten unabhängig gezogen werden und repräsentativ sind!

Heckman Ansatz zum Schätzen der Regressionskoeffizienten in R

Nun wollen wir allerdings noch die Methode von Heckman verwenden, um doch noch zu den richtigen Regressionsparameter zu kommen. Die Idee ist hierbei, dass wir zunächst die Probit-Regression verwenden, um den Selektionseffekt zu schätzen, damit dann das Inverse von Mills-Ratio bestimmen und dieses dann in die Regression von den tatsächlich beobachteten $Y$-Werten mit aufnehmen und somit den Effekt von $Z$ herausrechnen können. Glücklicherweise müssen wir dies nicht selbst programmieren, sondern können einfach auf die Funktion heckit (abgeleitet vom Namensgeber Heckman) des sampleSelection Pakets von Toomet und Henningsen (2008) zurückgreifen (dieses muss zuvor installiert werden: install.packages("sampleSelection")). Der Funktion heckit müssen wir zwei Argumente übergeben: die Selektionsgleichung (selection = s ~ 1 + X) sowie die Regressionsgleichung (outcome = Y_obs ~ 1 + X). Wir speichern das Ganze als Objekt heckman ab und schauen uns die Summary an:

library(sampleSelection) # Paket laden
heckman <- heckit(selection = s ~ 1 + X, outcome = Y_obs ~ 1 + X)
summary(heckman)

## --------------------------------------------
## Tobit 2 model (sample selection model)
## 2-step Heckman / heckit estimation
## 1000 observations (770 censored and 230 observed)
## 7 free parameters (df = 994)
## Probit selection equation:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -1.97383    0.10924  -18.07   <2e-16 ***
## X            0.47668    0.03332   14.30   <2e-16 ***
## Outcome equation:
##             Estimate Std. Error t value Pr(>|t|)  
## (Intercept)  -1.4740     5.3634  -0.275   0.7835  
## X             1.3896     0.7893   1.761   0.0786 .
## Multiple R-Squared:0.0687,	Adjusted R-Squared:0.0605
##    Error terms:
##               Estimate Std. Error t value Pr(>|t|)
## invMillsRatio   3.2594     2.4788   1.315    0.189
## sigma           3.5439         NA      NA       NA
## rho             0.9197         NA      NA       NA
## --------------------------------------------

Die Summary sagt uns,

##  --------------------------------------------
##  Tobit 2 model (sample selection model)
##  2-step Heckman / heckit estimation
##  1000 observations (770 censored and 230 observed)
##  7 free parameters (df = 994)

dass hier das 2-Stufige Heckman-Modell angesetzt wurde (es gibt auch eine simultane Maximum-Liklihood [ML] Methode, die wir uns etwas später auch ansehen werden). Insgesamt von den 1000 Beoachtungen waren 770 zensiert (nicht beobachtet) und nur 230 konnten beobachtet werden. Insgesamt wurden 7 Parameter geschätzt ($\beta_0, \beta_1, b_0, b_1, r, \sigma$ und $\rho$, wobei $\rho$ eine Schätzung für die Korrelation zwischen den Residuen der Selektionsgleichung und der Regressionsgleichung ist - diesen Parameter haben wir bisher nicht benutzt).

##  Probit selection equation:
##              Estimate Std. Error t value Pr(>|t|)    
##  (Intercept) -1.97383    0.10924  -18.07   <2e-16 ***
##  X            0.47668    0.03332   14.30   <2e-16 ***

ist quasi das Ergebnis der Probit-Regression. Dieses Ergebnis unterscheidet sich nur geringfügig von dem Ergebnis der Schätzung mit der glm-Funktion (siehe oben).

##  Outcome equation:
##              Estimate Std. Error t value Pr(>|t|)  
##  (Intercept)  -1.4740     5.3634  -0.275   0.7835  
##  X             1.3896     0.7893   1.761   0.0786 .
##  Multiple R-Squared:0.0687,   Adjusted R-Squared:0.0605

zeigt das Regressionsergebnis. Hier ist deutlich zu sehen, dass die Standardfehler sehr groß sind und der Anteil erklärter Varianz klein. Dies kann allerdings auch sehr stark an der sehr geringen Stichprobengröße liegen. Das Heckman-Modell braucht im Vergleich zur normalen Regression deutlich größere Stichprobengrößen!

##     Error terms:
##                Estimate Std. Error t value Pr(>|t|)
##  invMillsRatio   3.2594     2.4788   1.315    0.189
##  sigma           3.5439         NA      NA       NA
##  rho             0.9197         NA      NA       NA
##  --------------------------------------------

zeigt die übrigen Parameter im Modell. invMillsRatio ist hierbei der angenäherte Einfluss von $Z$ in der Regressionsgleichung - also eine Schätzung für r. sigma ist die unabhängige Residualvarianz in der Regressionsgleichung. Für diese und für rho ist keine Signifikanzentscheidung möglich.

Wir können, wie bei fast allen geschätzten Modellen, die Parameterschätzungen auch mit dem coef Befehl erhalten. Wenden wir diesen auf die Summary an, erhalten wir hier auch die Standardfehler:

coef(summary(heckman))

##                 Estimate Std. Error     t value     Pr(>|t|)
## (Intercept)   -1.9738300 0.10924269 -18.0683023 2.542551e-63
## X              0.4766792 0.03332402  14.3043738 2.410538e-42
## (Intercept)   -1.4739783 5.36337752  -0.2748228 7.835095e-01
## X              1.3896056 0.78931666   1.7605172 7.862765e-02
## invMillsRatio  3.2593587 2.47880769   1.3148897 1.888502e-01
## sigma          3.5439299         NA          NA           NA
## rho            0.9197018         NA          NA           NA

So können die Koeffizienten auf leichte Weise weiterverwendet werden (bspw. für eine Simulationsstudie).

Ergebnisinterpretation: Insgesamt ist keiner der Parameter im Regressionsmodell des Heckman-Modells signifikant. Da wir aber das Modell vorgegeben haben, wird dies daran liegen, dass die Stichprobengröße zu klein ausgefallen ist. Wir wissen nämlich, dass es Effekte gab!

Wiederholen Sie doch einmal gleiches Modell für eine Stichprobengröße von $n=10^5$ (Achtung: unter Umständen müssen Sie hier eine Weile auf das Ergebnis warten!). Sie können auch gerne die in Appendix B zu findende Funktion nutzen, mit welcher Sie das Heckman-Modell direkt als data.frame simulieren können und anschließend mit den oben besprochenen Mitteln auswerten können.

Wenn Sie die ML-Variante verwenden wollen, in der alle Parameter simultan geschätzt werden, dann müssen Sie die selection Funktion aus dem gleichen Paket verwenden. Das interessante hier ist nun, dass auch rho und sigma eine Signifikanzentscheidung erhalten. Ansonsten sind die beiden Varianten sehr ähnlich. Die ML-Variante ist numerisch aufwendiger (der PC hat mehr zu tun). Allerdings, wenn alle Annahmen erfüllt sind, hat die ML-Variante kleiner Standardfehler. Sind die Annahmen nicht erfüllt, dann ist die zweistufige Variante etwas robuster, da nicht so viele Parameter gleichzeitig geschätzt werden müssen:

heckman_ML <- selection(selection = s ~ 1 + X, outcome = Y_obs ~ 1 + X)
summary(heckman_ML)

## --------------------------------------------
## Tobit 2 model (sample selection model)
## Maximum Likelihood estimation
## Newton-Raphson maximisation, 7 iterations
## Return code 1: gradient close to zero (gradtol)
## Log-Likelihood: -919.1355 
## 1000 observations (770 censored and 230 observed)
## 6 free parameters (df = 994)
## Probit selection equation:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  -1.9658     0.1087  -18.08   <2e-16 ***
## X             0.4739     0.0331   14.32   <2e-16 ***
## Outcome equation:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -0.04707    1.32532  -0.036    0.972    
## X            1.18706    0.21928   5.413 7.76e-08 ***
##    Error terms:
##       Estimate Std. Error t value Pr(>|t|)    
## sigma  3.16491    0.34039   9.298   <2e-16 ***
## rho    0.81232    0.09426   8.618   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## --------------------------------------------

Ganz oben in der Summary steht nun, dass es sich um die ML-Methode handelt. sigma und rho haben nun auch eine Signifikanzentscheidung. Die Ergebnisse sind allerdings so gut wie identisch zum zweistufigen Verfahren.

coef(summary(heckman_ML))

##                Estimate Std. Error      t value     Pr(>|t|)
## (Intercept) -1.96576392 0.10871837 -18.08124947 2.130815e-63
## X            0.47390677 0.03309905  14.31783549 2.053078e-42
## (Intercept) -0.04707479 1.32532398  -0.03551946 9.716727e-01
## X            1.18705607 0.21928459   5.41331268 7.756977e-08
## sigma        3.16491167 0.34038533   9.29802601 8.821179e-20
## rho          0.81231960 0.09426220   8.61766038 2.655787e-17

Wenn Sie erstmal einen vorgefertigten Datensatz untersuchen wollen, so laden Sie sich doch diesen herunter: Datensatz HeckData.rda. Sie können HeckData.rda auch analog herunterladen und direkt einladen:

load(url("https://pandar.netlify.app/post/HeckData.rda"))

In diesem Datensatz sind neben in dieser Sitzung präsentierten Parametern ($\beta_0=-2,\beta_1=0.5, b_0 = 0.5, b_1=1.2, r= 2,\sigma=2$) die Variablen $X,Y_{obs}$ und $s$ enthalten, sowie zu Demonstrationszwecken $Z$ und $Y$.

Appendix

Appendix A

Code zu R Grafiken

set.seed(123456) # Vergleichbarkeit
Z <- rnorm(10000) # 10^4 std. normalverteilte Zufallsvariablen simulieren
h <- hist(Z, breaks=50, plot=FALSE)
cuts <- cut(h$breaks, c(-4,-1,4)) # Grenzen festlegen für Färbung
plot(h, col=cuts,  freq = F)
lines(x = seq(-4,4,0.01), dnorm(seq(-4,4,0.01)), col = "blue", lwd = 3)
abline(v = -1, lwd = 3, lty = 3, col = "gold3")

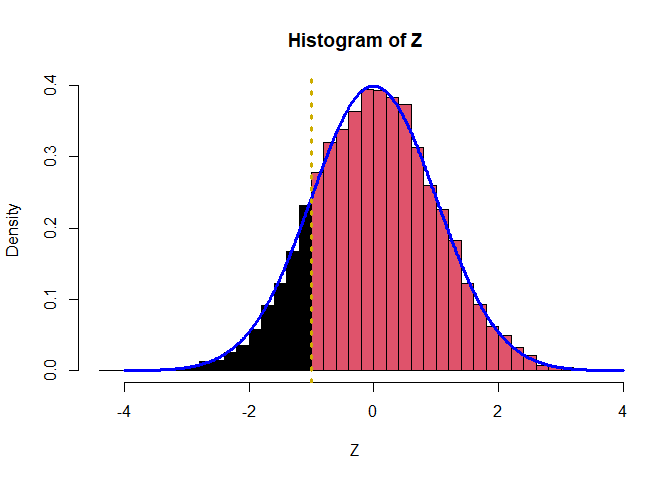
h <- hist(Z, breaks=50, plot=FALSE)
cuts <- cut(h$breaks, c(-4,2,4)) # Grenzen festlegen für Färbung
plot(h, col=cuts,  freq = F)
lines(x = seq(-4,4,0.01), dnorm(seq(-4,4,0.01)), col = "blue", lwd = 3)
abline(v = 2, lwd = 3, lty = 3, col = "gold3")

plot(X, Y, pch = 16, col = "skyblue", cex = 1.5)
points(X, Y_obs, pch = 16, col = "black")
abline(reg_pop, col = "blue", lwd = 5)
abline(reg_obs, col = "gold3", lwd = 5)
legend(x = "bottomright", legend = c("all", "observed", "regression: all", "regression: observed"), col = c("skyblue", "black", "blue", "gold3"), lwd = c(NA, NA, 5, 5), pch = c(16, 16, NA, NA))

Appendix B

simulate_heckman <- function(n, 
                             beta0, beta1,
                             b0, b1, r,
                             sigma)
{
     X <- rnorm(n = n, mean = 2, sd = 2)
     Z <- rnorm(n = n, mean = 0, sd = 1)
     
     # Populationsregression
     eps <- rnorm(n = n, mean = 0, sd = sigma)
     Y <- b0 + b1*X + r*Z + eps # Populationsregression
     
     
     # Selektion
     s <- beta0 + beta1*X + Z > 0   # Selektionsmechanismus
     
     Y_obs <-rep(NA, length(Y))
     Y_obs[s == 1] <- Y[s == 1]     # beobachtbares Y
     
     df <- data.frame("X" = X, "s" = s, "Y_obs" = Y_obs)
     return(df)
}

set.seed(404) # Vergleichbarkeit
# Daten simulieren
data_heckman <- simulate_heckman(n = 10^5, 
                                 beta0 = -2, beta1 = 0.5, 
                                 b0 = 0.5, b1 = 1.2, r = 2, sigma = 2)
head(data_heckman) # Daten ansehen

##            X     s    Y_obs
## 1  3.5472786  TRUE  8.01523
## 2  2.1193767 FALSE       NA
## 3  1.3658543 FALSE       NA
## 4  0.9815069 FALSE       NA
## 5 -0.3060732 FALSE       NA
## 6  4.1044826  TRUE 11.09013

# Heckman Modell schätzen für große n
heckman_model  <- heckit(selection = s ~ 1 + X, outcome = Y_obs ~ 1 + X, data = data_heckman)
summary(heckman_model)

##  --------------------------------------------
##  Tobit 2 model (sample selection model)
##  2-step Heckman / heckit estimation
##  100000 observations (76025 censored and 23975 observed)
##  7 free parameters (df = 99994)
##  Probit selection equation:
##               Estimate Std. Error t value Pr(>|t|)    
##  (Intercept) -2.004099   0.011093  -180.7   <2e-16 ***
##  X            0.502194   0.003425   146.6   <2e-16 ***
##  Outcome equation:
##              Estimate Std. Error t value Pr(>|t|)    
##  (Intercept)  0.41902    0.37339   1.122    0.262    
##  X            1.21045    0.05605  21.595   <2e-16 ***
##  Multiple R-Squared:0.1329,   Adjusted R-Squared:0.1328
##     Error terms:
##                Estimate Std. Error t value Pr(>|t|)    
##  invMillsRatio   2.0698     0.1747   11.85   <2e-16 ***
##  sigma           2.8613         NA      NA       NA    
##  rho             0.7234         NA      NA       NA    
##  ---
##  Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##  --------------------------------------------

Literatur

Briggs, D. C. (2004). Causal inference and the Heckman model. Journal of Educational and Behavioral Statistics, 29(4), 397–420. https://doi.org/10.3102/10769986029004397

Heckman, J. (1979). Sample selection bias as a specification error.Econometrica, 47, 153–161. https://doi.org/10.2307/1912352

Heckman, J. (1976). The common structure of statistical models of truncation, sample selection and limited dependent variables and a simple estimator for such models. Annals of Economic and Social Measurement, 5(4). http://www.nber.org/chapters/c10491

Toomet, O., & Henningsen, A. (2008). Sample selection models in R: Package sampleSelection.Journal of Statistical Software, 27(7), 1-23. https://doi.org/10.18637/jss.v027.i07