Pakete laden
# Benötigte Pakete --> Installieren, falls nicht schon vorhanden
library(psych) # Für logistische Transformationen
library(ggplot2) # Grafiken
library(gridExtra)
library(MatchIt) # Für das Propensity Score Matching
library(questionr) # Für gewichtete Tabellen
Datenbeispiel
Wir verwenden wieder unserer fiktives Datenbeispiel, in dem Patient*innen, die an einer Depression oder einer Angststörung leiden, entweder mit einer kognitiven Verhaltenstherapie (CBT) behandelt oder in einer Wartekontrollgruppe belassen wurden. Die Zuordnung konnte nicht randomisiert erfolgen, weshalb der Effekt der Behandlung nicht ohne weiteres berechenbar ist.
load(url("https://pandar.netlify.app/daten/CBTdata.rda"))
head(CBTdata)
| Age | Gender | Treatment | Disorder | BDI_pre | SWL_pre | BDI_post | SWL_post |
|---|---|---|---|---|---|---|---|
| 39 | female | CBT | ANX | 27 | 10 | 24 | 15 |
| 36 | female | CBT | ANX | 22 | 13 | 13 | 17 |
| 61 | female | CBT | ANX | 24 | 11 | 17 | 14 |
| 70 | female | CBT | ANX | 30 | 15 | 22 | 19 |
| 64 | female | CBT | DEP | 32 | 12 | 26 | 20 |
| 50 | female | CBT | ANX | 24 | 15 | 23 | 22 |
Wir wissen auch bereits, dass der Prima-Facie-Effekt (PFE) von 0.39 Punkten nicht signifikant ist. Im Folgenden werden wir auf Basis von Kovariaten einen Propensity Score schätzen und auf verschiedene Weisen verwenden, um eine adjustierte Schätzung des Treatment-Effekts vorzunehmen.
Konstruktion des Propensity Scores
Zur Bildung des Propensity Scores verwenden wir eine logistische Regression mit den Variablen, von denen wir bereits wissen, dass sich die Gruppen darin unterscheiden: Art der Störung, Prätest im BDI und Prätest im SWL:
# Vorhersage des Treatments durch Kovariaten
mod_ps1 <- glm(Treatment ~ Disorder + BDI_pre + SWL_pre,
family = "binomial", data = CBTdata)
summary(mod_ps1)
##
## Call:
## glm(formula = Treatment ~ Disorder + BDI_pre + SWL_pre, family = "binomial",
## data = CBTdata)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.89704 1.12602 -0.797 0.42565
## DisorderDEP -0.77678 0.27580 -2.816 0.00486 **
## BDI_pre 0.16953 0.03750 4.520 6.18e-06 ***
## SWL_pre -0.13763 0.03443 -3.998 6.39e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 449.86 on 325 degrees of freedom
## Residual deviance: 349.89 on 322 degrees of freedom
## AIC: 357.89
##
## Number of Fisher Scoring iterations: 4
Wir sehen, dass alle Kovariaten auch bei gemeinsamer Berücksichtigung einen signifikanten Effekt auf die Treatment-Zugehörigkeit haben. Sicherheitshalber untersuchen wir auch die Wechselwirkungen:
# Einschluss von Wechselwirkungen, hierzu zunächst Zentrierung der Prädiktoren
CBTdata$BDI_pre_c <- scale(CBTdata$BDI_pre, scale = F)
CBTdata$SWL_pre_c <- scale(CBTdata$SWL_pre, scale = F)
mod_ps2 <- glm(Treatment ~ Disorder + BDI_pre_c + SWL_pre_c +
Disorder:BDI_pre_c + Disorder:SWL_pre_c + BDI_pre_c:SWL_pre_c +
Disorder:BDI_pre_c:SWL_pre_c,
family = "binomial", data = CBTdata)
summary(mod_ps2)
##
## Call:
## glm(formula = Treatment ~ Disorder + BDI_pre_c + SWL_pre_c +
## Disorder:BDI_pre_c + Disorder:SWL_pre_c + BDI_pre_c:SWL_pre_c +
## Disorder:BDI_pre_c:SWL_pre_c, family = "binomial", data = CBTdata)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.69555 0.20390 3.411 0.000647 ***
## DisorderDEP -0.82670 0.28607 -2.890 0.003854 **
## BDI_pre_c 0.14802 0.05433 2.724 0.006446 **
## SWL_pre_c -0.13322 0.05650 -2.358 0.018378 *
## DisorderDEP:BDI_pre_c 0.05187 0.07791 0.666 0.505586
## DisorderDEP:SWL_pre_c -0.03984 0.07692 -0.518 0.604514
## BDI_pre_c:SWL_pre_c 0.01808 0.01161 1.557 0.119472
## DisorderDEP:BDI_pre_c:SWL_pre_c -0.02353 0.01893 -1.243 0.213798
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 449.86 on 325 degrees of freedom
## Residual deviance: 345.66 on 318 degrees of freedom
## AIC: 361.66
##
## Number of Fisher Scoring iterations: 4
Da keiner der Wechselwirkungs-Terme signifikant ist, verwenden wir im nächsten Schritt das einfachere Modell mod_ps1. Mit der predict-Funktion erhalten wir vorhergesagte Werte in Logit-Einheiten, mit der logistic-Funktion des psych-Paktets können wir diese in Wahrscheinlichkeiten transformieren:
CBTdata$PS_logit <- predict(mod_ps1)
CBTdata$PS_P <- logistic(CBTdata$PS_logit)
plot(CBTdata$PS_logit, CBTdata$PS_P)
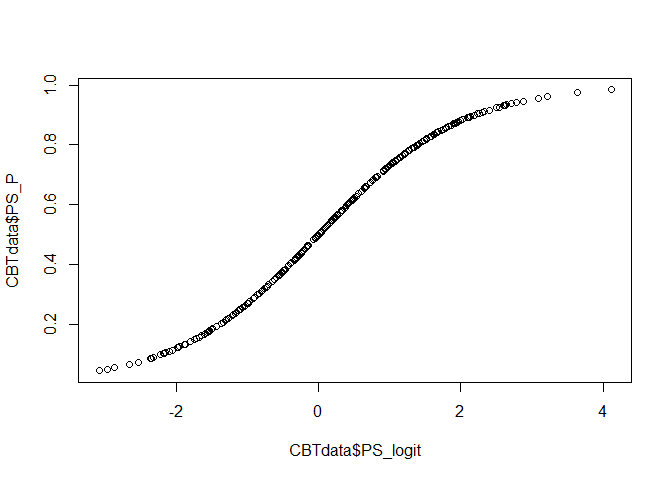
Der Plot zeigt uns nun den Zusammenhang zwischen dem vorhergesagtem Propensity Score PS_logit in der Logit-Skala und dem zugehörigen Propensity Score in der in Wahrscheinlichkeiten transformierten Skala PS_P. Wir erkennen wieder die Ogive (S-Form), die wir bereits in der Sitzung zur logistischen Regression kennengelernt haben (Sitzung zur logistischen Regression).
Prüfung des Overlap
Die Unterschiede im resultierenden Propensity Score in Logit-Einheiten können wir uns durch eine grafische Darstellung der Verteilungen in den Gruppen veranschaulichen. Die Treatment-Wahrscheinlichkeit ist in der Treatment-Gruppe deutlich höher, was z.B. durch eine Selektion nach Dringlichkeit der Fälle zustande gekommen sein kann. Durch ein Abtragen der Treatmentwahrscheinlichkeiten können wir zusätzlich veranschaulichen, wie groß die Überschneidungen der Gruppen (common support) sind. In dieser Grafik sind auch das Minimum der Wahrscheinlichkeit in der Treatment-Gruppe und das Maximum in der Kontrollgruppe eingetragen - diese definieren die Grenzen der Überschneidung zwischen den Gruppen.
## Overlap & Common Support ----
p1 <- ggplot(CBTdata, aes(x=PS_logit, fill = Treatment)) +
theme_bw() + theme(legend.position="top") +
scale_fill_manual(values=c("#E69F00", "#56B4E9")) +
geom_density(alpha=0.5)
p2 <- ggplot(CBTdata, aes(x=PS_P, fill = Treatment)) +
theme_bw() +
labs(x="P(X=1)", y="") + xlim(c(0,1)) +
scale_y_continuous(breaks=c(-1.5,1.5), # "manuelle" Achsenbeschriftungen, um die Gruppen einzutragen
labels=c("CBT", "WL")) +
geom_histogram(data = CBTdata[CBTdata$Treatment=="WL",], aes(y=..density..), # Histogramm WL
alpha=0.5, fill="#E69F00") +
geom_histogram(data = CBTdata[CBTdata$Treatment=="CBT",], aes(y=-..density..), # Histogramm CBT
alpha=0.5, fill="#56B4E9") +
# Minimum in CBT und maximum in WL einzeichnen
geom_vline(xintercept = c(min(CBTdata$PS_P[CBTdata$Treatment=="CBT"]),
max(CBTdata$PS_P[CBTdata$Treatment=="WL"])),
linetype=2) +
coord_flip()
grid.arrange(p1, p2, nrow=1) # Beide Plots nebeneinander
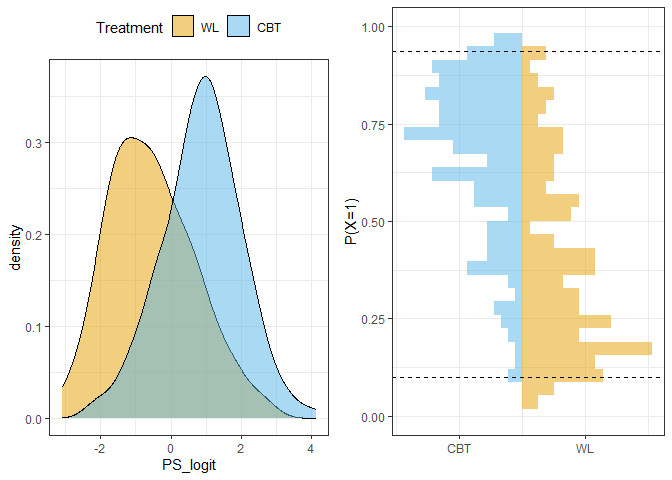
Wem die Grafiken etwas kompliziert erscheinen, kann in Appendix A nachlesen, wie eine sehr kurze 2-Zeilen (aber nicht so schöne) Variante funktioniert.
Für Fälle außerhalb der common support region können keine kausalen Effekte geschätzt werden. Für diese gibt es nämlich keine “vergleichbaren” Studienteilnehmenden. Die Fälle, um die es geht, sind gerade Personen aus der CBT-Gruppe, die eine sehr hohe Wahrscheinlichkeit aufweisen, das Treatment bekommen zu haben (was sie auch haben, aber das ist hier nicht die Frage). Um genauer zu sein: Wir wollen diejenigen Fälle aus der CBT-Gruppe identifizieren, die eine höhere Treatmentwahrscheinlichkeit und damit einen höheren Propensity-Score in der Wahrscheinlichkeits-Skala haben als alle Personen aus der WL-Gruppe. Genauso wollen wir Personen aus der WL-Gruppe identifizieren, die einen niedrigeren Propensity-Score haben als alle Personen aus der CBT-Gruppe.
Den kleinsten Wert in der CBT-Gruppe erhalten wir mit
min(subset(CBTdata, Treatment=="CBT")$PS_P)
## [1] 0.09774259
wobei mit subset ein Subdatensatz erstellt wird, für den gilt, dass Treatment == "CBT". Auf diesen Subdatensatz greifen wir mit $ zu und wählen den Propensity-Score aus. Mit min erhalten wir schließlich das Minimum.
Nun sind die Personen, die in der WL-Gruppe sind und einen PS_P-Wert kleiner als diesen minimalen Wert haben, die folgenden:
CBTdata[(CBTdata$Treatment=="WL" &
CBTdata$PS_P < min(subset(CBTdata, Treatment=="CBT")$PS_P)),]
## Age Gender Treatment Disorder BDI_pre SWL_pre BDI_post SWL_post PS_logit PS_P
## 202 41 female WL DEP 13 21 10 21 -2.360192 0.08625907
## 210 56 male WL DEP 11 23 8 26 -2.974504 0.04859106
## 264 70 female WL DEP 17 26 19 27 -2.370231 0.08547105
## 272 51 male WL DEP 10 21 10 21 -2.868773 0.05371901
## 273 48 male WL DEP 13 21 10 23 -2.360192 0.08625907
## 274 28 female WL DEP 12 22 10 24 -2.667348 0.06492778
## 285 69 male WL DEP 14 22 15 23 -2.328294 0.08880658
## 295 61 female WL DEP 16 30 9 34 -3.090276 0.04351015
## 315 35 male WL DEP 16 26 11 25 -2.539758 0.07311756
Es ist leicht zu sehen, dass die gewählten Personen alle sehr kleine Propensity Scores haben.
Analog erhalten wir die Personen aus der CBT-Gruppe, die größere Propensity-Score Werte haben als alle in der WL-Gruppe. Wir beginnen wieder mit dem Maximum:
max(subset(CBTdata, Treatment=="WL")$PS_P)
## [1] 0.9374229
Nun sind die Personen, die in der WL-Gruppe sind und einen PS_P-Wert kleiner als diesen minimalen Wert haben, die folgenden:
CBTdata[(CBTdata$Treatment=="CBT" &
CBTdata$PS_P > max(subset(CBTdata, Treatment=="WL")$PS_P)),]
## Age Gender Treatment Disorder BDI_pre SWL_pre BDI_post SWL_post PS_logit PS_P
## 63 55 male CBT ANX 30 7 25 12 3.225356 0.9617774
## 77 38 female CBT ANX 29 9 19 9 2.780570 0.9416168
## 122 44 female CBT ANX 30 4 33 6 3.638244 0.9743754
## 125 34 male CBT ANX 30 8 23 10 3.087727 0.9563836
## 132 29 male CBT ANX 32 3 24 0 4.114927 0.9839352
## 147 47 female CBT ANX 32 12 29 17 2.876263 0.9466605
## 172 67 male CBT ANX 34 12 26 12 3.215317 0.9614066
Wir schließen 16 Fälle aus, die außerhalb des Überschneidungsbereichs liegen (das ! negiert die logische Aussage, mit Hilfe derer wir die Fälle überhaupt identifizieren konnten):
### Fälle außerhalb der Überschneidung ausschließen ----
# Fälle der Kontrollgruppe entfernen, deren Wahrscheinlichkeit kleiner ist als
# die kleinste Wahrscheinlichkeit in der Treatment-Gruppe
CBTdata.red <- CBTdata[!(CBTdata$Treatment=="WL" &
CBTdata$PS_P < min(subset(CBTdata, Treatment=="CBT")$PS_P)),]
# Fälle der Treatment-Gruppe entfernen, deren Wahrscheinlichkeit größer ist als
# die größte Wahrscheinlichkeit in der Kontrollgruppe
CBTdata.red <- CBTdata.red[!(CBTdata.red$Treatment=="CBT" &
CBTdata.red$PS_P > max(subset(CBTdata, Treatment=="WL")$PS_P)),]
Nach dieser Korrektur überlappen sich die Propensity Scores beider Gruppen vollständig:
## Overlap & Common Support nach Fallausschluss ----
p1 <- ggplot(CBTdata.red, aes(x=PS_logit, fill = Treatment)) +
theme_bw() + theme(legend.position="top") +
scale_fill_manual(values=c("#E69F00", "#56B4E9")) +
geom_density(alpha=0.5)
p2 <- ggplot(CBTdata.red, aes(x=PS_P, fill = Treatment)) +
theme_bw() +
labs(x="P(X=1)", y="") + xlim(c(0,1)) +
scale_y_continuous(breaks=c(-1.5,1.5), # "manuelle" Achsenbeschriftungen, um die Gruppen einzutragen
labels=c("CBT", "WL")) +
geom_histogram(data = CBTdata.red[CBTdata.red$Treatment=="WL",], aes(y=..density..), # Histogramm WL
alpha=0.5, fill="#E69F00") +
geom_histogram(data = CBTdata.red[CBTdata.red$Treatment=="CBT",], aes(y=-..density..), # Histogramm CBT
alpha=0.5, fill="#56B4E9") +
coord_flip()
grid.arrange(p1, p2, nrow=1) # Beide Plots nebeneinander
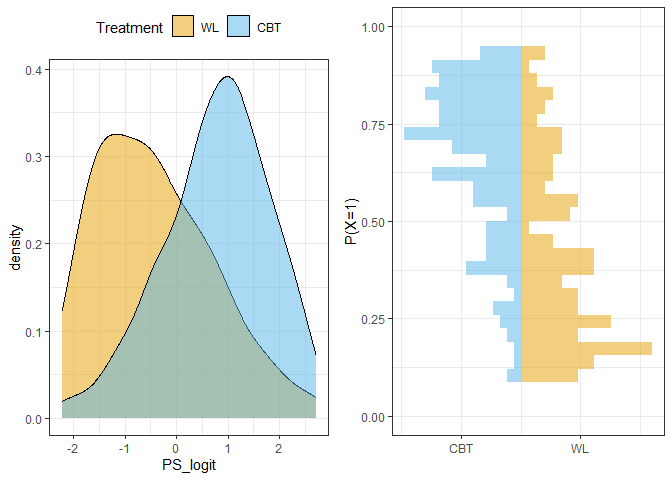
Verwendung des Propensity Score in der ANCOVA
Wir können den Treatment-Effekt schätzen, indem wir den Propensity Score anstelle der ursprünglichen Kovariaten als Kontrollvariable verwenden. Wir vergleichen hier die klassische ANCOVA mit allen Kovariaten mit einem Modell, in dem nur der Propensity Score kontrolliert wird. (Achtung, aufgrund der Reduktion des Datensatzes entsprechen die Ergebnisse des 1. Modells nicht exakt denen im ersten Teil dieses Blocks!)
Dazu stellen wir zwei ANCOVA-Modelle auf: einmal mittels Kovariatenadjustierung (BDI.adj) und einmal mittels Propensity-Score (BDI.PS) in der Logit-Skala. Zur besseren Vergleichbarkeit runden wir den Gruppenunterschiedsparameter (das ist der 2. in diesem Fall, der 1. ist das Interzept) auf 2 Nachkommastellen.
BDI.adj <- lm(BDI_post ~ Treatment + Disorder + BDI_pre + SWL_pre, data = CBTdata.red)
round(coef(BDI.adj)[2],2)
## TreatmentCBT
## -4.08
BDI.PS <- lm(BDI_post ~ Treatment + PS_logit, data = CBTdata.red)
round(coef(BDI.PS)[2],2)
## TreatmentCBT
## -4.15
Wir sehen, dass die auf beiden Wegen geschätzen Effekte praktisch identisch sind.
Propensity Score Matching
Im Folgenden führen wir ein Matching mit der Funktion matchit aus dem Paket MatchIt mit zwei verschiedenen Algorithmen durch. Optimal Pair Matching bildet “statistische Zwillinge”, Full Optimal Matching bildet unterschiedlich große Subklassen mit Gewichtung.
# Optimal Pair Matching
m.optimal <- matchit(Treatment ~ Disorder + BDI_pre + SWL_pre, method = "optimal",
data = CBTdata, distance = "glm", link = "logit")
## Warning: Fewer control units than treated units; not all treated units will get a match.
# Full Optimal Matching
m.full <- matchit(Treatment ~ Disorder + BDI_pre + SWL_pre, method = "full",
data = CBTdata, distance = "glm", link = "logit")
Die matchit-Funktion nimmt als erstes Argument die Formel Treatment ~ Disorder + BDI_pre + SWL_pre entgegen, die wir auch zur Bildung des Propensity-Scores verwendet hatten, um so die Gruppenzugehörigkeit zu untersuchen. Mit method wählen wir die Matching-Methode ("optimal" oder "full"), data ordnen wir unseren Datensatz zu. Wir nehmen hier wieder den ursprünglichen CBTdata-Datensatz, die Kürzung unseres Datensatzes aus dem Abschnitt zuvor ging also verloren. Mit den Optionen distance = "glm" und link = "logit"wird eingestellt, dass das Matching mit Propensity Scores erfolgt, die durch logistische Regression gebildet werden (das ist auch die Standardeinstellung, das könnte man also weglassen).
Für die Methode, die Zwillingspaare bildet, erhalten wir eine Warnung, da die Stichprobe weniger Kontrollpersonen als Treatmentpersonen enthält und dadurch Personen aus der Treatment-Gruppe ausgeschlossen werden. Diese Warnung ist hilfreich, da wir unseren Datensatz (und damit die Power) verringern. Das resultierende Objekt enthält noch nicht den gematchten Datensatz, sondern nur die Zuordnung der Paare und weitere Informationen.
Inspektion der Datensätze
Für beide Methoden wird der durch das Matching gebildete Datensatz mit der Funktion match.data extrahiert. Diesen sortieren wir anschließend nach Subklasse und Treatment mittels order und wenden dies auf die Zeilen (vor dem ,) an. (Es könnten auch die Spalten sortiert werden.)
# Datensätze speichern und nach Subklasse & Treatment sortieren
df.optimal <- match.data(m.optimal)
df.optimal <- df.optimal[order(df.optimal$subclass, df.optimal$Treatment),]
df.full <- match.data(m.full)
df.full <- df.full[order(df.full$subclass, df.full$Treatment),]
Das Optimal Pair Matching resultiert in einem Datensatz, in dem Paare (Variable subclass) enthalten sind, die aus je einer Person aus der Treatment- und einer Person aus der Kontrollgruppe bestehen. Die Gewichtung (Variable weights) ist für alle Personen 1. Wir sehen zudem, dass die von matchit erzeugte Distanz (distance) unserem oben erzeugten Propensity Score (PS_P) entspricht.
head(df.optimal)
| Age | Gender | Treatment | Disorder | BDI_pre | SWL_pre | BDI_post | SWL_post | PS_logit | PS_P | distance | weights | subclass | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 177 | 40 | female | WL | DEP | 19 | 21 | 15 | 25 | -1.3430306 | 0.2070121 | 0.2070121 | 1 | 1 |
| 163 | 29 | female | CBT | DEP | 15 | 13 | 16 | 15 | -0.9201030 | 0.2849369 | 0.2849369 | 1 | 1 |
| 186 | 68 | female | WL | ANX | 16 | 15 | 16 | 17 | -0.2490556 | 0.4380560 | 0.4380560 | 1 | 2 |
| 35 | 64 | female | CBT | ANX | 25 | 16 | 18 | 14 | 1.1390570 | 0.7575065 | 0.7575065 | 1 | 2 |
| 276 | 43 | female | WL | DEP | 23 | 14 | 22 | 14 | 0.2984828 | 0.5740716 | 0.5740716 | 1 | 3 |
| 17 | 30 | male | CBT | ANX | 22 | 17 | 17 | 19 | 0.4928469 | 0.6207769 | 0.6207769 | 1 | 3 |
Das Full Optimal Matching resultiert in einem Datensatz, in dem in den Subklassen unterschiedlich viele Fälle enthalten sind. Die Personen der Treatmentgruppe (CBT) erhalten ein Gewicht von 1, die Personen aus der Kontrollgruppe werden so gewichtet, dass die Häufigkeit der Subklassen derjenigen der Treatment-Gruppe entspricht. Im Auszug sind in Subklasse 5 mehr Kontroll- als Treatment-Fälle enthalten, diese werden entsprechend geringer gewichtet. In Subklasse 6 sind mehr Treatment-Fälle, hier erhält der Kontroll-Fall ein höheres Gewicht (in die Gewichte geht zusätzlich noch die Verteilung der Treatment-Fälle auf die Subklassen ein; mehr Informationen stehen in Appendix B).
df.full[df.full$subclass %in% c(5,6),]
| Age | Gender | Treatment | Disorder | BDI_pre | SWL_pre | BDI_post | SWL_post | PS_logit | PS_P | distance | weights | subclass | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 207 | 34 | male | WL | DEP | 23 | 20 | 20 | 14 | -0.5272936 | 0.3711483 | 0.3711483 | 0.8522727 | 5 |
| 102 | 56 | female | CBT | DEP | 19 | 15 | 17 | 16 | -0.5172542 | 0.3734945 | 0.3734945 | 1.0000000 | 5 |
| 208 | 44 | male | WL | ANX | 25 | 17 | 19 | 18 | 1.0014276 | 0.7313392 | 0.7313392 | 1.7045455 | 6 |
| 108 | 67 | male | CBT | DEP | 28 | 15 | 21 | 17 | 1.0084878 | 0.7327241 | 0.7327241 | 1.0000000 | 6 |
| 152 | 20 | male | CBT | ANX | 29 | 22 | 18 | 27 | 0.9913882 | 0.7293620 | 0.7293620 | 1.0000000 | 6 |
Demonstration der Gewichtung
Der Vergleich der Häufigkeiten der Subklassen in den Gruppen mit gewichteten Häufigkeiten zeigt den Effekt der Gewichtung. Die gewichteten relativen Häufigkeiten der Subklassen in der Kontrollgruppe entsprechen denjenigen der Treatment-Gruppe (die absoluten Werte sind etwas niedriger, da in der Kontrollgruppe weniger Fälle sind als in der Kontrollgruppe).
# Auszug as dem Datensatz
demo.df <- subset(df.full, as.numeric(subclass) < 10)
demo.df$subclass <- droplevels(demo.df$subclass)
# Ungewichtete Häufigkeiten
table(demo.df$Treatment, demo.df$subclass)
##
## 1 2 3 4 5 6 7 8 9
## WL 1 1 3 1 1 1 1 1 1
## CBT 7 4 1 1 1 2 3 1 1
# Gewichtete Häufigkeiten
round(wtd.table(y = demo.df$subclass,
x = demo.df$Treatment, weights = demo.df$weights), 2)
## 1 2 3 4 5 6 7 8 9
## WL 5.97 3.41 0.85 0.85 0.85 1.70 2.56 0.85 0.85
## CBT 7.00 4.00 1.00 1.00 1.00 2.00 3.00 1.00 1.00
Hier eine kurz Erklärung zum Code: Im ersten Schritt haben wir hier nur diejenigen Fälle ausgewählt, die in den Subklassen 1,…,9 sind. Anschließend werden mit droplevels diejenigen Levels (also kategorialen Ausprägungen) des factors subclass entfernt, die jetzt nicht mehr in den Daten enthalten sind. Mit Hilfe von table erhalten wir eine einfache 2x9-Häufigkeitstabelle. Die Zahlen entsprechen den absoluten Häufigkeiten der beiden Gruppen (in den Zeilen) in den jeweiligen Subklassen (in den Spalten). Mit Hilfe der wtd.table Funktion erhalten wir eine gewichtete Häufigkeitstabelle. Die funktioniert analog zu table, nur müssen wir dieses mal noch die Gewichtung dem Argument weights zuordnen. Damit das Ganze übersichtlicher wird, runden wir noch auf 2 Nachkommastellen.
Kontrolle der Balance
Die mit beiden Methoden erzielte Balance der Kovariaten lassen wir uns mit plot(summary()) anzeigen. In diesen Plots wird die absolute (“ohne Vorzeichen”) standardisierte Mittelwertsdifferenz (x-Achse) zwischen den beiden Gruppen auf den Kovariaten (y-Achse) für den vollen Datensatz (“All”) und den gematchten Datensatz (“Matched”) dargestellt. Je näher die Punkte an der Null liegen, desto besser. Die vertikalen Linien zeigen einen Bereich an, der als erstrebenswert gilt. Hier sind die Unterschiede zwischen den Gruppen nur minimal (i.d.R. nicht signifikant).
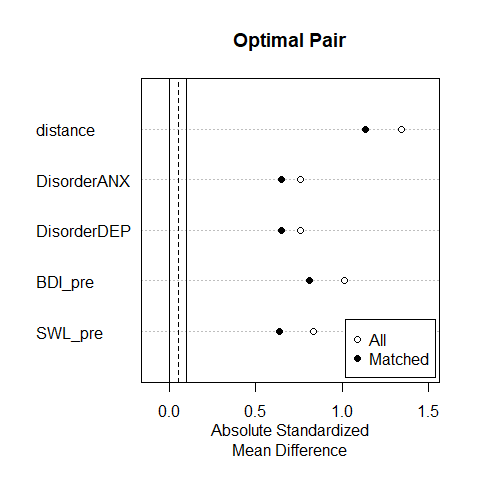
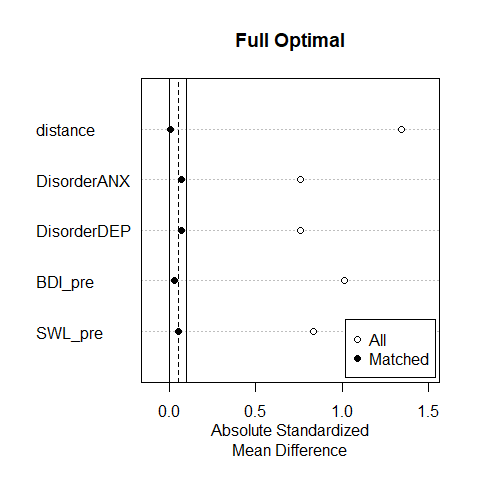
Wir sehen, dass die bestehenden Unterschiede durch das Optimal Pair Matching nur geringfügig reduziert werden. Durch das ungünstige Verhältnis von Treatment- zu Kontrollfällen sind die Möglichkeiten der Zwillingsbildung für den Datensatz sehr begrenzt. Die Reduktion der Unterschiede kommt nur durch den Ausschluss der “unpassendsten” Treatment-Fälle (!) zustande. Im Unterschied hierzu erreicht das Full Optimal Matching eine sehr gute Balance.
Effektschätzung
Für das Optimal Pair Matching kann eine Effektschätzung einfach unter Verwendung des gematchten Datensatzes erfolgen. Wir stellen dazu das Regressionsmodell auf und vergleichen unser Ergebnis mit dem PFE:
lm.PFE <- lm(BDI_post ~ Treatment, data = CBTdata)
summary(lm.PFE)
##
## Call:
## lm(formula = BDI_post ~ Treatment, data = CBTdata)
##
## Residuals:
## Min 1Q Median 3Q Max
## -12.4943 -3.4943 -0.1067 3.5057 17.8933
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 18.1067 0.4235 42.750 <2e-16 ***
## TreatmentCBT 0.3877 0.5764 0.672 0.502
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.187 on 324 degrees of freedom
## Multiple R-squared: 0.001394, Adjusted R-squared: -0.001688
## F-statistic: 0.4523 on 1 and 324 DF, p-value: 0.5017
lm.optimal <- lm(BDI_post ~ Treatment, data = df.optimal)
summary(lm.optimal)
##
## Call:
## lm(formula = BDI_post ~ Treatment, data = df.optimal)
##
## Residuals:
## Min 1Q Median 3Q Max
## -11.5400 -3.2150 -0.1067 3.4600 17.8933
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 18.1067 0.4057 44.630 <2e-16 ***
## TreatmentCBT -0.5667 0.5738 -0.988 0.324
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.969 on 298 degrees of freedom
## Multiple R-squared: 0.003263, Adjusted R-squared: -8.216e-05
## F-statistic: 0.9754 on 1 and 298 DF, p-value: 0.3241
Wir sehen, dass sich der Effekt von $\beta = -0.57$ gegenüber der Analyse mit dem Gesamtdatensatz ($\beta = 0.39$) nur geringfügig verändert hat und weiterhin nicht signifikant ist.
Bei der Analyse der mit Full Optimal Matching gebildeten Daten muss die Gewichtung verwendet werden. Dies geschieht, indem wir in der lm-Funktion dem Argument weights die bestimmten Gewichte zuordnen.
lm.full <- lm(BDI_post ~ Treatment, data = df.full, weights = weights)
summary(lm.full)
##
## Call:
## lm(formula = BDI_post ~ Treatment, data = df.full, weights = weights)
##
## Weighted Residuals:
## Min 1Q Median 3Q Max
## -13.358 -3.532 -1.494 1.506 29.797
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 22.8232 0.4314 52.900 < 2e-16 ***
## TreatmentCBT -4.3289 0.5872 -7.372 1.41e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.284 on 324 degrees of freedom
## Multiple R-squared: 0.1436, Adjusted R-squared: 0.141
## F-statistic: 54.35 on 1 and 324 DF, p-value: 1.411e-12
Hier finden wir einen starken signifikanten Effekt des Treatments ($\beta = -4.33$), der ähnlich ausfällt wie der unter Kontrolle der Kovariaten geschätzte Effekt aus dem ersten Teil dieses Themenblocks (dieser betrug $\beta = -4.06$).
Stratifizierung
Stratifizierung ist als Methode subclass in der matchit-Funktion enthalten. Wir bilden fünf Strata und extrahieren den Datensatz, der die Zugehörigkeit zu den Strata enthält (Variable subclass). Wir müssen lediglich das Argument method = "subclass" wählen. Anschließend matchen wir direkt den Datensatz und speichern diesen neu ab:
m.strat <- matchit(Treatment ~ Disorder + BDI_pre + SWL_pre, data = CBTdata,
distance = "logit", method = "subclass", subclass = 5)
df.strat <- match.data(m.strat)
Um zu sehen, wie die Zuordnung zu den Strata geklappt haben, schauen wir uns wieder die table an:
# Zugehörigkeit der Fälle zu Treatment und Stratum
table(df.strat$Treatment, df.strat$subclass)
##
## 1 2 3 4 5
## WL 101 23 12 8 6
## CBT 35 34 36 35 36
Die Kreuztabelle zeigt, dass die Strata so gebildet wurden, dass die Treatment-Gruppe gleichmäßig aufgeteilt wurde. Die Anzahl der jeweils “passenden” Kontrollgruppen-Fälle in den Strata unterscheidet sich stark.
Die folgende Grafik veranschaulicht die gebildeten Strata, als Grenzen sind jeweils die Untergrenzen (Minima in den Gruppen) eingezeichnet:
ggplot(df.strat, aes(x=distance, fill = Treatment)) +
theme_bw() + theme(text = element_text(size = 20)) +
labs(x="P(X=1)", y="") +
scale_y_continuous(breaks=c(-1.5,1.5), # "manuelle" Achsenbeschriftungen, um die Gruppen einzutragen
labels=c("CBT", "WL")) +
geom_histogram(data = df.strat[df.strat$Treatment=="WL",], aes(y=..density..), # Histogramm WL
alpha=0.5, fill="#E69F00") +
geom_histogram(data = df.strat[df.strat$Treatment=="CBT",], aes(y=-..density..), # Histogramm CBT
alpha=0.5, fill="#56B4E9") +
coord_flip() +
geom_vline(xintercept = aggregate(df.strat$distance, by=list(df.strat$subclass), FUN=min)$x[2:5],
linetype=2) +
coord_flip()
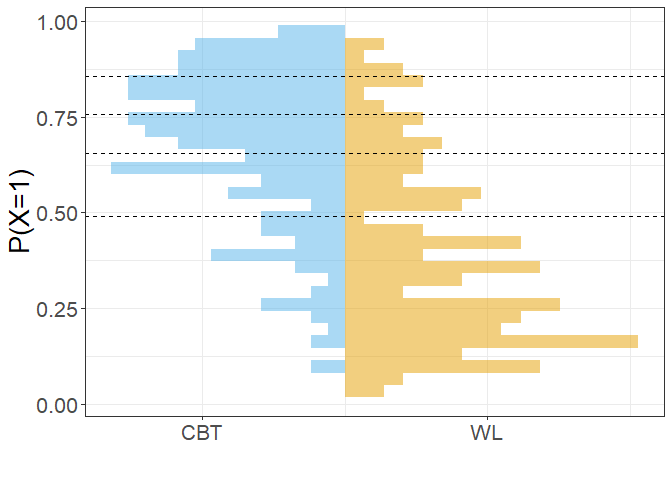
Der Effekt der bei der Stratifizierung gebildeten Gewichte lässt sich veranschaulichen, indem dieselbe Grafik mit gewichteten Häufigkeiten erzeugt wird. Die Häufigkeiten in der Treatment-Gruppe bleiben unverändert, die in der Kontrollgruppe werden der Treatmentgruppe angeglichen:
ggplot(df.strat, aes(x=distance, fill = Treatment, weights=weights)) +
theme_bw() + theme(text = element_text(size = 20)) +
labs(x="P(X=1)", y="") +
scale_y_continuous(breaks=c(-1.5,1.5), # "manuelle" Achsenbeschriftungen, um die Gruppen einzutragen
labels=c("CBT", "WL")) +
geom_histogram(data = df.strat[df.strat$Treatment=="WL",], aes(y=..density..), # Histogramm WL
alpha=0.5, fill="#E69F00") +
geom_histogram(data = df.strat[df.strat$Treatment=="CBT",], aes(y=-..density..), # Histogramm CBT
alpha=0.5, fill="#56B4E9") +
coord_flip() +
geom_vline(xintercept = aggregate(df.strat$distance, by=list(df.strat$subclass), FUN=min)$x[2:5],
linetype=2) +
coord_flip()
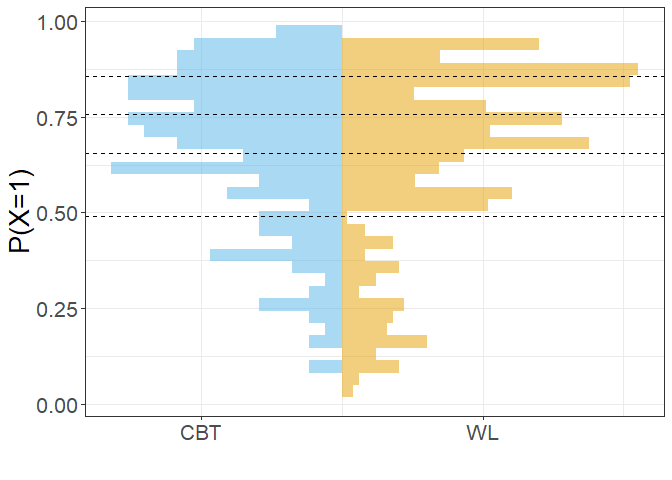
Effektschätzung
Es gibt nun mehrere Möglichkeiten bei Stratifizierung den Treatmenteffekt zu bestimmen. Entweder können wir in jedem Stratum den Effekt schätzen, indem wir die Mittelwerte in der CBT und der WL Gruppe vergleichen (siehe hierzu Appendix C) oder wir verwenden die Gewichte, die bei der Stratifizierung ebenfalls bestimmt werden und rechnen erneut eine gewichtete Regression. Da bei der ersten Variante das Bestimmen des Standardfehlers und die damit verbundene Signifikanzentscheidung recht schwierig ist, schauen wir uns jetzt, wie für das Full Optimal Matching, eine Schätzung mit dem linearen Modell unter Verwendung der Gewichte an. Der hier resultierende Effekt von $\beta = -3.89$ ist ähnlich dem beim Full Optimal Matching. Beide Methoden sind sich konzeptuell ähnlich, bei der Stratifizierung werden mit einer einfacheren Methode weniger Subklassen gebildet.
lm.strat <- lm(BDI_post ~ Treatment, data = df.strat, weights = weights)
summary(lm.strat)
##
## Call:
## lm(formula = BDI_post ~ Treatment, data = df.strat, weights = weights)
##
## Weighted Residuals:
## Min 1Q Median 3Q Max
## -15.004 -4.494 -1.494 1.506 30.792
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 22.3833 0.4458 50.206 < 2e-16 ***
## TreatmentCBT -3.8890 0.6068 -6.409 5.16e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.46 on 324 degrees of freedom
## Multiple R-squared: 0.1125, Adjusted R-squared: 0.1098
## F-statistic: 41.08 on 1 and 324 DF, p-value: 5.156e-10
Die Gewichte waren im Datensatz df.strat unter dem Argument weights verfügbar und mussten so wie zuvor beim Full Optimal Matching im lm-Befehl nur entsprechend zugeordnet werden.
Gewichtung mit dem Propensity Score
Alternativ zur Bildung von Gewichten durch Matching können wir die Gewichte direkt auf Basis des Propensity Scores $\pi$ und der Treatmentgruppenzugehörigkeit $X \in {0,1}$ konstruieren. Die Formel hierfür ist
$$\frac{X_i}{\pi_i}+\frac{1-X_i}{1-\pi_i}$$
# mit (CBTdata$Treatment=="CBT")*1 wird Treatment numerisch mit 1, Kontrollgruppe mit 0 kodiert
CBTdata$ps_w <- (CBTdata$Treatment=="CBT")*1/CBTdata$PS_P + (1 - (CBTdata$Treatment=="CBT")*1)/(1 - CBTdata$PS_P)
Diese Gewichte können in der lm-Funktion verwendet werden, um eine Schätzung mittels weighted least squares (WLS) vorzunehmen. Hierbei erhalten wir mit einem geschätzten Treatment-Effekt von -4.59 eine ähnliche Schätzung wie mit den anderen Methoden.
BDI.weighted <- lm(BDI_post ~ Treatment, data = CBTdata, weights = ps_w)
summary(BDI.weighted)
##
## Call:
## lm(formula = BDI_post ~ Treatment, data = CBTdata, weights = ps_w)
##
## Weighted Residuals:
## Min 1Q Median 3Q Max
## -25.164 -6.222 -0.731 3.931 55.347
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 21.4538 0.4603 46.611 < 2e-16 ***
## TreatmentCBT -4.5866 0.6629 -6.919 2.43e-11 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 8.515 on 324 degrees of freedom
## Multiple R-squared: 0.1287, Adjusted R-squared: 0.1261
## F-statistic: 47.88 on 1 and 324 DF, p-value: 2.435e-11
Wir sehen, dass alle Korrekturen zu ähnlichen Ergebnissen kommen. Der Treatmenteffekt ist signifikant. Nur in der Ausprägung kommt es von Methode zu Methode zu leichten Unterschieden. Diese Unterschiede kommen mitunter zu Stande, weil die Methoden unterschiedlich viele Informationen über die Daten nutzen. Bspw. hatten wir bei der Stratifizierung nur 5 Subklassen gebildet, während beim Full Matching deutlich mehr Subklassen extrahiert wurden (die Methode war aber auch etwas anders!). Wir können also, unter den (strengen) Annahmen der Methoden, vor allem Strong Ignoribility, schließen, dass es einen Treatmenteffekt gibt (mit einer Irrtumswahrscheinlichkeit von 5%).
Appendix A
Kurze Grafiken
Mit density kann man die Dichte (also die Häufigkeitsverteilung) einer Variable bestimmen. Diese kann man recht leicht plotten:
## Overlap & Common Support ----
plot(density(CBTdata$PS_P[CBTdata$Treatment == "CBT"]),
type = "l")
lines(density(CBTdata$PS_P[CBTdata$Treatment == "WL"]))
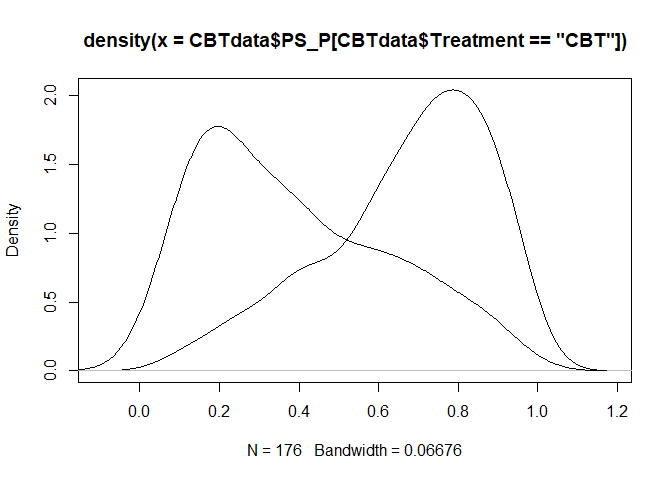
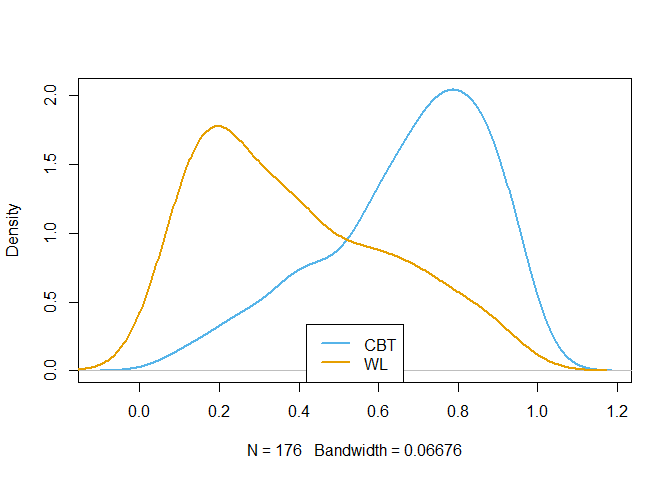
Jetzt können wir leider die Linien nicht unterscheiden, weswegen wir die Farben aus den anderen Grafiken nun auch hier verwenden. Außerdem fügen wir eine Legende hinzu, änderen die Dicke der Linien und entfernen den seltsamen Titel:
## Overlap & Common Support ----
plot(density(CBTdata$PS_P[CBTdata$Treatment == "CBT"]),
col = "#56B4E9", lwd = 2, type = "l", main = "")
lines(density(CBTdata$PS_P[CBTdata$Treatment == "WL"]),
col = "#E69F00", lwd = 2)
legend(legend = c("CBT", "WL"), lwd = 2,
col = c("#56B4E9", "#E69F00"), x = "bottom")
Appendix B
Bildung der Gewichte
Die Gewichte zur Schätzung des ATT, mit denen die relativen Häufigkeiten der Kovariaten-Subklassen der Treatment-Gruppe an die Kontrollgruppe angeglichen werden, werden wie folgt gebildet:
$$w_{Cs}=\frac{N_C}{n_{Cs}}*\frac{n_{Ts}}{N_T}$$ Hierbei sind
- $w_{Cs}$ das Gewicht für Kontrollpersonen in Subklasse $s$
- $N_C$ die Größe der Kontrollgruppe
- $N_T$ die Größe der Treatment-Gruppe
- $n_{Cs}$ die Anzahl von Kontrollpersonen in Subklasse $s$
- $n_{Ts}$ die Anzahl von Treatment-Personen in Subklasse $s$
Die Gewichte werden also umso größer, je mehr Treatment-Personen in einer Subklasse $s$ sind und umso kleiner, je mehr Kontrollpersonen in der Subklasse sind. Die Summe der Gewichte über alle Subklassen $S$ entspricht der ursprünglichen Fallzahl $N_C$:
$$\sum^S_{s=1}{w_{Cs}}=N_C$$
Appendix C
Effektschätzung bei Stratifizierung per Hand
Den Treatment-Effekt können wir “per Hand” berechnen. Die Funktion tapply wird hierbei benutzt, um die Mittelwerte von Treatment- und Kontrollgruppe in den Strata zu berechnen. tapply wendet dabei eine Funktion (hier mean) auf eine Kombination aus Gruppierungen an. Diese Mittelwerte packen wir anschließend in einen data.frame, um sie uns besser anzusehen.
Die Mittelwerte in der CBT und der WL Gruppen werden dann als Schätzer für $Y^0$ und $Y^1$ verwendet, aus ihrer Differenz ergibt sich der ATT innerhalb jedes Stratum. Für jedes Stratum wird anhand des Anteils der Fälle an der Gesamtstichprobe ein Gewichtungsfaktor berechnet.
##ATEs in den Strata berechnen und als neuen Datensatz
MWs <- tapply(df.strat$BDI_post, list(df.strat$subclass, df.strat$Treatment), mean)
MWW <- data.frame(Y0 = MWs[, 1], Y1 = MWs[, 2], ATEq = MWs[, 2]-MWs[, 1])
MWW
## Y0 Y1 ATEq
## 1 15.78218 14.71429 -1.067893
## 2 22.08696 15.47059 -6.616368
## 3 20.66667 18.52778 -2.138889
## 4 23.37500 19.80000 -3.575000
## 5 29.83333 23.72222 -6.111111
Der ATT ergibt sich dann als gewichtete Summe der Effekte innerhalb der Strata. Hierzu müssen wir zunächst kurz die Gewichte mittels table bestimmen, diese dann durch die Gesamtanzahl (nrow(df.strat)) teilen und dann die gewichtete Summe berechnen.
##Gesamt-ATE als gewichtetes Mittel über die Strata berechnen
MWW$Wq <- table(df.strat$subclass)/nrow(df.strat) # Anteil des Stratum an der Stichprobe
# Gesamteffekt als gewichtete Summe:
sum(MWW$Wq * MWW$ATEq)
## [1] -3.176149
Wir erhalten hier mit -3.18 einen geringfügig geringeren Effekt als bei anderen Methoden.
Eine Alternative zur Bildung für die Mittelwerte wäre aggregate gewesen:
aggregate(BDI_post ~ subclass + Treatment, data = df.strat, FUN = mean)
## subclass Treatment V1
## 1 1 WL 15.78218
## 2 2 WL 22.08696
## 3 3 WL 20.66667
## 4 4 WL 23.37500
## 5 5 WL 29.83333
## 6 1 CBT 14.71429
## 7 2 CBT 15.47059
## 8 3 CBT 18.52778
## 9 4 CBT 19.80000
## 10 5 CBT 23.72222
](/media/header/dusk_or_dawn.jpg)