Einführung
In der letzten Sitzung hatten wir uns angesehen, wie Mittelwerte bzw. Differenzwerte metaanalytisch zusammengefasst werden können. Falls Sie sich die vergangene Sitzung noch nicht angesehen haben, dann wird dies dringend empfohlen, da sie das Fundament für die jetztige Sitzung liefert. Wir beginnen wieder mit dem Laden des metafor-Pakets.
library(metafor)
Daten
In dieser Sitzung wollen wir einen Datensatz von Molloy et al. (2014) verwenden, der mit dem metafor-Paket mitgeliefert wird. Dieser heißt dat.molloy2014. Die Autor:innen haben den Zusammenhang zwischen der Persönlichkeitseigenschaft Gewissenhaftigkeit und dem Einnehmen von Medikamenten untersucht.
head(dat.molloy2014)
| authors | year | ni | ri | controls | design | a_measure | c_measure | meanage | quality |
|---|---|---|---|---|---|---|---|---|---|
| Axelsson et al. | 2009 | 109 | 0.187 | none | cross-sectional | self-report | other | 22.00 | 1 |
| Axelsson et al. | 2011 | 749 | 0.162 | none | cross-sectional | self-report | NEO | 53.59 | 1 |
| Bruce et al. | 2010 | 55 | 0.340 | none | prospective | other | NEO | 43.36 | 2 |
| Christensen et al. | 1999 | 107 | 0.320 | none | cross-sectional | self-report | other | 41.70 | 1 |
| Christensen & Smith | 1995 | 72 | 0.270 | none | prospective | other | NEO | 46.39 | 2 |
| Cohen et al. | 2004 | 65 | 0.000 | none | prospective | other | NEO | 41.20 | 2 |
In authors steht die verwendete Studie, year zeigt das Jahr an, ni ist die Stichprobengröße, ri ist die Korrelation, controls gibt an, ob Kontrollvariablen in der Analyse verwendet wurden. design gibt an, welches Studiendesign verwendet wurde, a_measure gibt an, wie die Medikamenteneinnahme untersucht wurde. c_measure gibt an, wie die Gewissenhaftigkeit gemessen wurde (meistens Versionen des NEO), meanage ist das Durchschnittsalter der Stichprobe, quality ist ein Qualitätsindex der Studie (für mehr Informationen dazu siehe Molloy et al., 2014).
Fragestellungen
Insgesamt wollen wir nun untersuchen,
- ob es einen Zusammenhang zwischen Gewissenhaftigkeit und Medikamenteneinnahme gibt
- ob Heterogenität in der linearen Beziehung durch Moderatoren erklärt werden kann
Überblick über die Daten
Wir schauen uns zunächst einmal die Korrelationen an:
summary(dat.molloy2014$ri)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -0.0900 0.0325 0.1685 0.1552 0.2625 0.3700
Die Korrelationskoeffizienten liegen also zwischen -0.09 und 0.37. Auch ein Mittelwert wird uns bereits ausgegeben: 0.155. Dies gibt uns ein erstes Gefühl dafür, wo der tatsächlich gepoolte mittlere Korrelationskoeffizient, der die Beziehung zwischen der Gewissenhaftigkeit und dem Einnehmen von Medikamenten quantifiziert, liegen könnte. Jedoch wurden in diesem Mittelwert etwaige Unterschiede zwischen Studien (Größe, Streuung, Qualität, Kovariaten, etc.) nicht berücksichtigt.
Grafische Veranschaulichung der Beziehung zwischen der Medikamenteneinnahme und der Gewissenhaftigkeit
Wir wollen uns die Daten zunächst noch etwas genauer ansehen. Plotten wir erst einmal die Korrelationskoeffizienten.
boxplot(dat.molloy2014$ri)
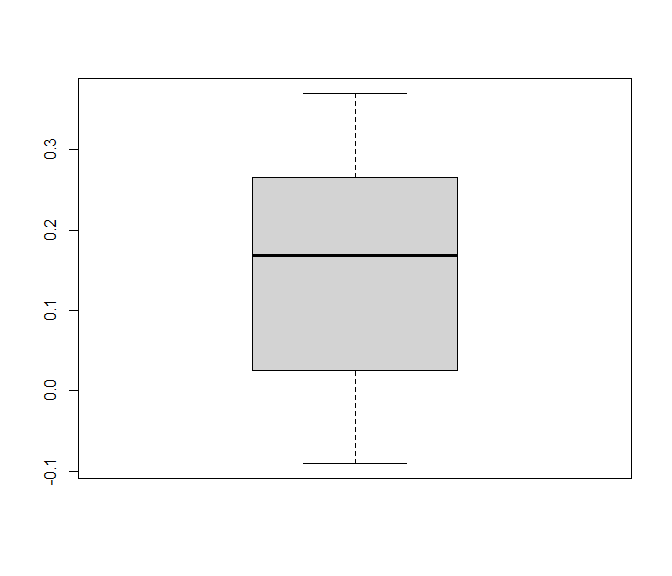
Wir sehen, dass die meisten Korrelationen zwischen -0.09 und 0.37 liegen. 50% der Korrelationen liegen allerdings zwischen 0.025 und 0.265, also im positiven Bereich; der Median liegt bei 0.1685. Bei Metaanalysen wird sehr häufig das sogenannte
$80\%$-Credibility-Interval (
$80\%$-CRI) angegeben. Es gibt Auskunft darüber, zwischen welchen Werten die mittleren
$80\%$ der Daten liegen. Wir erhalten es, indem wir den Prozentrang 10 (
$10\%$) und den Prozentrang 90 (
$90\%$) über die quantile-Funktion anfordern:
quantile(dat.molloy2014$ri, probs = c(0.1, 0.9))
## 10% 90%
## 0.00 0.33
Das $80\%$-CRI erstreckt sich also von 0 bis 0.33.
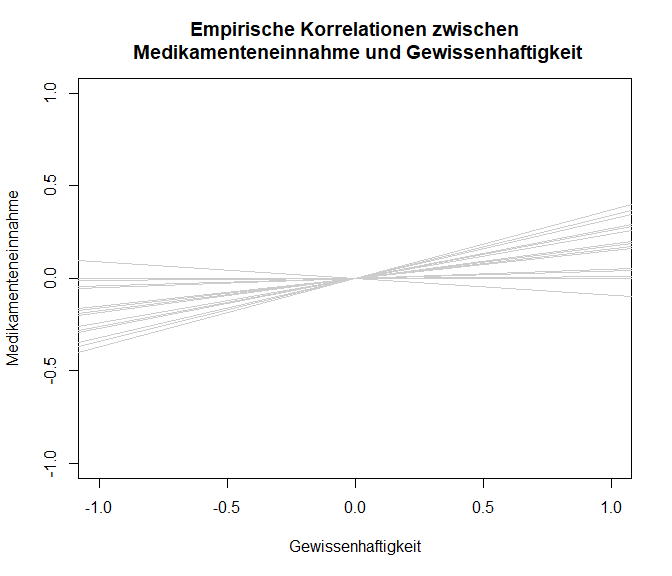
Wir wollen uns außerdem die Unterschiedlichkeit der Korrelationskoeffizienten als Darstellung der verschiedenen Einfach-Regressionen von Gewissenhaftigkeit und Medikamenteneinnahme ansehen. Hierzu plotten wir quasi eine standardisierte Regressionsgerade ($\beta_0=0$ und $\beta_1=r_i$, wobei $r_i:=$ Korrelationskoeffizient von Studie $i$) pro Studie. Um den zugrundeliegenden Code anzusehen, können Sie Appendix A nachschlagen.
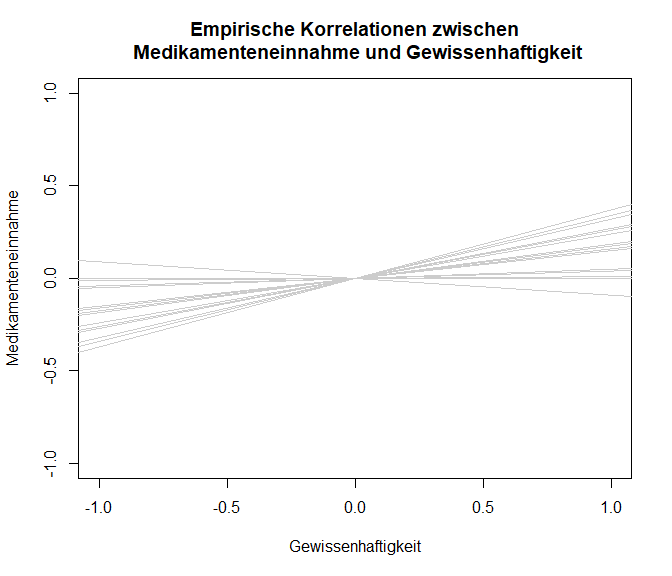
Die Beziehungen zwischen den beiden Variablen erscheint nicht sonderlich stark. Trotzdem würden wir gerne eine durchschnittliche Regressionsgerade in diese Grafik hineinlegen.
Fisher’s $z$-Transformation
Für eine durchschnittliche Regressionsgerade können wir allerdings nicht einfach alle Korrelationskoeffizienten mitteln. Die Korrelation ist ein besonderer Koeffizient, da er nur Werte zwischen -1 und 1 annehmen kann. Er ist dem $\Delta$-Maß gleichzusetzen (Döring & Bortz, 2016). Somit ist hier einfaches Mitteln der Korrelationskoeffizienten nicht ohne Weiteres möglich (es ist jedoch zu beachten, dass diese Meinung nicht überall verbreitet ist, weswegen dies ein Thema für sich ist, welches zur Diskussion steht!). Aus diesem Grund werden Korrelationskoeffizienten häufig mit Hilfe von Fisher’s $z$-Transformation in $z$-Werte übertragen. Dies haben Sie vielleicht im ersten Bachelor-Semester schon einmal kennengelernt, als Sie Korrelationskoeffizienten mitteln wollten. Der zugehörige $z$-Wert zu einer Korrelation $r_i$ lässt sich wie folgt bestimmen:
$$Z_i:=\frac{1}{2}\log\left(\frac{1+r_i}{1-r_i}\right)$$.
Das Schöne an den transformierten Daten (den $z$-Werten) ist, dass wir nun die Varianzen (bzw. die Standardfehler) der Korrelationskoeffizienten kennen. Es gilt nämlich:
$$\mathbb{V}ar[Z_i]:=\frac{1}{n_i-3},$$
wobei $n_i$ die Stichprobengröße der Studie $i$ ist. Der Standardfehler (SE) wäre $\sqrt{\frac{1}{n_i-3}}=\frac{1}{\sqrt{n_i-3}}$. Wir sehen, dass die Variation der Korrelationskoeffizienten unabhängig von ihrer Höhe ist. Im Idealfall kennen wir die Stichprobengrößen der Studien, sodass sich die SE nach Transformation leicht ermitteln lassen. Das macht es uns leicht, da wir nicht, wie bspw. beim Mittelwert, noch die Standardabweichungen aus den Studien kennen müssen. Wir müssen diese Transformation selbstverständlich nicht per Hand durchführen, sondern können uns einfach der Funktion escalc aus dem metafor-Paket bedienen. Diese Funktion hatten wir bereits beim Bestimmen der standardisierten Mittelwertsdifferenz kennengelernt (siehe dazu vergangene Sitzung).
Um diese Funktion zu verwenden und somit die Daten zu $z$-transformieren, müssen wir folgende Argumente an die Funktion übergeben: measure = "ZCOR" bewirkt, dass auch tatsächlich die $r$-to-$z$-Transformation (Fisher’s $z$-Transformation) durchgeführt wird. Das Argument ri nimmt die beobachteten Korrelationskoeffizienten entgegen (diese heißen hier auch ri), ni nimmt die Stichprobengrößen der Studien entgegen (diese heißen hier auch ni). Das Argument data nimmt, wie der Namen schon verrät, den Datensatz entgegen, in dem die Studien zusammengefasst sind (hier dat.molloy2014). Die Funktion erzeugt einen neuen Datensatz, welcher um die $z$-Werte sowie deren Varianzen erweitert wurde. Diesen wollen wir unter einem neuen Namen abspeichern. Als Beweis meines Einfallsreichtums nennen wir diesen Datensatz einfach data_transformed. Auch die Namen, der neu zu erstellenden Variablen lassen sich in der Funktion festlegen. Dies ergibt insbesondere dann Sinn, wenn wir mehrere Analysen an einem Datensatz durchführen. Das geht mit dem var.names-Argument, welchem wir einen Vektor mit zwei Einträgen übergeben müssen: dem Namen der $z$-Werte und dem Namen der Varianzen. Wir wollen sie z_ri und v_ri nennen: var.names = c("z_ri", "v_ri"). Der fertige Code sieht folglich so aus (mit head schauen wir uns wieder die ersten 6 Zeilen an):
data_transformed <- escalc(measure="ZCOR", ri=ri, ni=ni,
data=dat.molloy2014,
var.names = c("z_ri", "v_ri"))
head(data_transformed)
##
## authors year ni ri controls design a_measure c_measure meanage quality
## 1 Axelsson et al. 2009 109 0.187 none cross-sectional self-report other 22.00 1
## 2 Axelsson et al. 2011 749 0.162 none cross-sectional self-report NEO 53.59 1
## 3 Bruce et al. 2010 55 0.340 none prospective other NEO 43.36 2
## 4 Christensen et al. 1999 107 0.320 none cross-sectional self-report other 41.70 1
## 5 Christensen & Smith 1995 72 0.270 none prospective other NEO 46.39 2
## 6 Cohen et al. 2004 65 0.000 none prospective other NEO 41.20 2
## z_ri v_ri
## 1 0.1892 0.0094
## 2 0.1634 0.0013
## 3 0.3541 0.0192
## 4 0.3316 0.0096
## 5 0.2769 0.0145
## 6 0.0000 0.0161
Wenn wir den Namen des Datensatzes nicht an die Funktion übergeben, und stattdessen nur die beobachteten Korrelationen und die Stichprobengrößen angeben, werden im erzeugten Datensatz nur die $z$-Werte und die Varianzen gespeichert; die Werte werden nicht an den bestehenden Datensatz angehängt (was für spätere Analysen weniger sinnvoll erscheint).
data_transformed_2 <- escalc(measure="ZCOR", ri=dat.molloy2014$ri,
ni=dat.molloy2014$ni,
var.names = c("z_ri", "v_ri"))
head(data_transformed_2)
##
## z_ri v_ri
## 1 0.1892 0.0094
## 2 0.1634 0.0013
## 3 0.3541 0.0192
## 4 0.3316 0.0096
## 5 0.2769 0.0145
## 6 0.0000 0.0161
Wir entnehmen dem Output, dass die Benennung geklappt hat und das hier nur ein Datensatz mit den $z$-Werten und den Varianzen entstanden ist.
Aus unserem neuen Datensatz data_transformed können wir nun wieder die entsprechenden Werte herausziehen. Wir können bspw. die Berechnung der Streuung der $z$-Werte überprüfen. Mithilfe von eckigen Klammern können die bezeichneten Einträge eines Vektors indiziert werden. Mit data_transformed$v_ri[1:4] werden entsprechend die ersten 4 Elemente im Vektor bezeichnet. Somit können wir uns mit [1:4] die ersten 4 Einträge der beiden Vektoren anschauen, um diese zu vergleichen:
data_transformed$v_ri[1:4]
## [1] 0.009433962 0.001340483 0.019230769 0.009615385
1/(dat.molloy2014$ni - 3)[1:4]
## [1] 0.009433962 0.001340483 0.019230769 0.009615385
Wir sehen, dass unsere Berechnung per Hand $\left(\frac{1}{n_i-3}\right)$ zum gleichen Ergebnis kommt, wie die Berechnung mit escalc, was daran liegt, dass die Funktion escalc mit den oben gewählten Zusatzargumenten genau das gemacht hat! Was genau hat nun die Transformation bewirkt?
plot(x = data_transformed$ri, y = data_transformed$z_ri,
xlab = "r", ylab = "z",
main = "Fisher's z-Transformation")
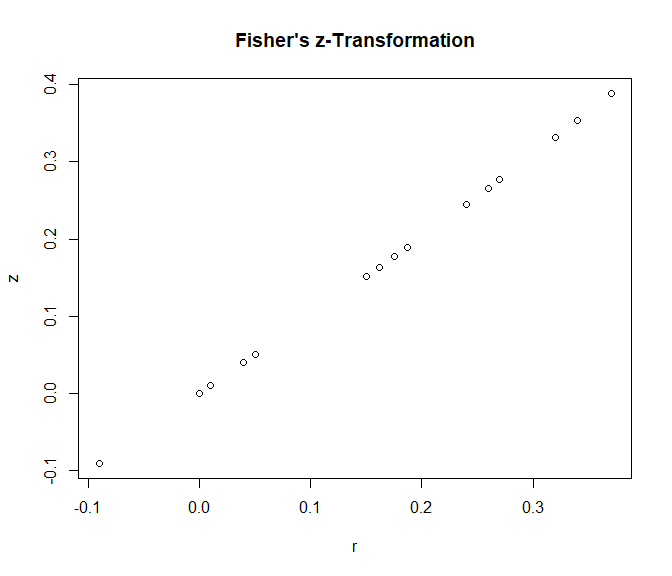
Der Grafik sollte zu entnehmen sein, dass nach Transformation Korrelationswerte nahe 1 stärker gewichtet werden (sie haben größere $z$-Ausprägungen). Dies war das Ziel, da es deutlich unwahrscheinlicher ist, in einer Studie einen Korrelationskoeffizient von .90 zu finden als einen von .20 und die Korrelation von .90 somit stärker ins Gewicht fallen sollte. Vor allem wenn wir den mittleren Korrelationskoeffizienten gegen 0 testen wollen, sollte berücksichtigt werden, dass einige Korrelationskoeffizienten nahe 1 lagen. Falls diese Werte aufgrund zufälliger Schwankungen gefunden worden sind, so sollte dies daran liegen, dass der Standardfehler groß, also die Stichprobengröße klein ist, da der Standardfehler der Korrelation antiproportional zur Stichprobengröße ist (da $=\left(\frac{1}{\sqrt{n_i-3}}\right)$). Somit können wir auch solche Stichproben weniger stark gewichten, die zwar einen hohen Korrelationskoeffizienten aufweisen, aber eine sehr kleine Stichprobe haben, da in solchen Fällen eine hohe Korrelation auch mal durch Zufall auftreten kann! Allerdings waren alle Korrelationen recht gering, sodass wir hier kaum Unterschiede in der Gewichtung erkennen können.
Nach unseren Berechnungen können wir die Transformation natürlich auch wieder ganz leicht rückgängig machen (auch hier gibt es wieder eine Funktion, die dies für uns übernimmt, welche wir uns anschauen, wenn es soweit ist): $$r_i = \frac{e^{2z_i}-1}{e^{2z_i}+1}$$
Random Effects Modell
Wir überspringen hier das Fixed Effects Modell (siehe dazu vergangene Sitzung). Wir beginnen also mit einem Random Effects Modell, da es sinnig ist, dass es Heterogenität zwischen den Studien gibt (allein schon deswegen, weil unterschiedliche Krankheiten untersucht wurden). Das Modell sah so aus:
$$Y_i = \theta + \vartheta_i + \varepsilon_i,$$
Für eine Wiederholung siehe hier. Das Modell schätzen wir so:
REM <- rma(yi = z_ri, vi = v_ri, data=data_transformed)
summary(REM)
##
## Random-Effects Model (k = 16; tau^2 estimator: REML)
##
## logLik deviance AIC BIC AICc
## 8.6096 -17.2191 -13.2191 -11.8030 -12.2191
##
## tau^2 (estimated amount of total heterogeneity): 0.0081 (SE = 0.0055)
## tau (square root of estimated tau^2 value): 0.0901
## I^2 (total heterogeneity / total variability): 61.73%
## H^2 (total variability / sampling variability): 2.61
##
## Test for Heterogeneity:
## Q(df = 15) = 38.1595, p-val = 0.0009
##
## Model Results:
##
## estimate se zval pval ci.lb ci.ub
## 0.1499 0.0316 4.7501 <.0001 0.0881 0.2118 ***
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Der Output ist vom Aufbau her komplett identisch zum Output bei Mittelwertsvergleichen. Der einzige Unterschied findet sich darin, dass hier alle Koeffizienten bzgl. der $z$-transformierten Werte angegeben sind. Der mittlere Wert muss also retransformiert werden. Zur Wiederholung wird der Output nochmals durchgesprochen:
Als Überschrift lesen wir Random-Effects Model, wobei k die Anzahl der Studien angibt (hier k=16). Außerdem wird uns das Schätzverfahren für die Heterogenitätsvarianz $\tau^2$ angegeben unter tau^2 estimator: (hier REML).
In den darunterliegenden Zeilen können wir die Heterogenitätsvarianz ablesen, welche bei 0.0081 liegt. Der Standardfehler (SE = 0.0055) gibt uns an, dass diese Heterogenitätsvarianz wahrscheinlich nicht signifikant von 0 verschieden ist. In der Zeile von I^2 wird die $I^2$-Statistik ausgegeben, welche ein Maß für die Heterogenität in den Daten sein soll. Diese liegt hier bei
$61.73\%$ und deutet somit auf Heterogenität der Korrelationskoeffizienten hin.
Auch wird die Heterogenitätsvarianz mit einem Signifikanztest auf Verschiedenheit von 0 geprüft. Die Ergebnisse hierzu entnehmen wir Test for Heterogeneity. Hier zeigt der p-Wert ein signifikantes ($p<0.05$) Ergebnis an: Die Heterogenitätsvarianz unterscheidet sich (mit einer Irrtumswahrscheinlichkeit von
$5\%$) von 0, es liegt also Heterogenität/ systematische Unterschiedlichkeit in den Korrelationen über die Studien hinweg vor.
Unter Model Results können wir nun (endlich) die Schätzergebnisse unseres REM ablesen. estimate steht hierbei für die gepoolte $z$-transformierte Korrelation, se ist der Standardfehler, zval der zugehörige z-Wert $\left(\frac{Est}{SE}\right)$, pval der p-Wert und ci.lb und ci.ub geben die untere und die obere Grenze eines
$95\%$-igen Konfidenzintervall an. Hier ist zu erkennen, dass die mittlere Korrelation wohl von 0 verschieden ist, da der $z$-transformierte Wert statistisch bedeutsam ist. Wir können nun schon sagen, dass “wir für die Population folglich die Nullhypothese, dass es im Mittel keine Beziehung zwischen Gewissenhaftigkeit und Medikamenteneinnahme gibt, verwerfen”. Den exakten vorhergesagten Wert kennen wir allerdings noch nicht; hierzu müssen wir den $z$-Wert erst wieder in eine Korrelation retransformieren. Selbstverständlich können wir auf das Objekt REM mit $ zugreifen und dadurch noch zahlreiche weitere Informationen erhalten. Welche dies genau sind, erfahren wir wieder mit names:
names(REM)
## [1] "b" "beta" "se" "zval" "pval" "ci.lb"
## [7] "ci.ub" "vb" "tau2" "se.tau2" "tau2.fix" "tau2.f"
## [13] "I2" "H2" "R2" "vt" "QE" "QEp"
## [19] "QM" "QMdf" "QMp" "k" "k.f" "k.eff"
## [25] "k.all" "p" "p.eff" "parms" "int.only" "int.incl"
## [31] "intercept" "allvipos" "coef.na" "yi" "vi" "X"
## [37] "weights" "yi.f" "vi.f" "X.f" "weights.f" "M"
## [43] "outdat.f" "ni" "ni.f" "ids" "not.na" "subset"
## [49] "slab" "slab.null" "measure" "method" "model" "weighted"
## [55] "test" "dfs" "ddf" "s2w" "btt" "m"
## [61] "digits" "level" "control" "verbose" "add" "to"
## [67] "drop00" "fit.stats" "data" "formula.yi" "formula.mods" "version"
## [73] "call" "time"
Beispielsweise können wir dem Objekt so auch die mittlere Schätzung ($b) oder $\tau^2$ ($tau2) entlocken.
REM$b
## [,1]
## intrcpt 0.149918
REM$tau2
## [1] 0.008110504
Diese Ergebnisse können wir mithilfe der R-internen predict-Funktion unter Angabe des Zusatzarguments transf=transf.ztor (transformiere $z_i$ zu $r_i$) retransformieren.
predict(REM, transf=transf.ztor)
##
## pred ci.lb ci.ub pi.lb pi.ub
## 0.1488 0.0878 0.2087 -0.0371 0.3248
Das Konfidenzintervall (CI) reicht von ci.lb (confidence interval lower boundary) bis ci.ub (confidence interval upper boundary). Die Aussage, die wir treffen können ist, dass wenn wir diese Metaanalyse an unabhängigen Stichproben unendlich häufig wiederholen könnten, dieses Intervall, welches sich in dieser Metaanalyse von 0.0878 bis 0.2087 erstreckt (und welches von Metaanalyse zu Metaanalyse von unabhängigen Ansammlungen von Stichproben unterscheiden würde), den wahren mittleren Populationsmittelwert ($\theta$) in
$95\%$ der Fälle enthalten würde. Auf Basis dieses Konfidenzintervalls würden wir die Nullhypothese, dass es keine Beziehung zwischen Gewissenhaftigkeit und Medikamenteneinnahme gibt, auf dem
$5\%$-igen Alpha-Fehler-Niveau verwerfen. Des Weiteren wird uns das Predictive Interval (PI; pi.lb = predictive interval lower bound, pi.ub = predictive interval upper bound) ausgegeben. Dieses Intervall ist wieder ein Konfidenzintervall, welches diesmal allerdings die Heterogenität zwischen Studien miteinbezieht. Im REM ist es ja so, dass der wahre mittlere Wert pro Studie $i$ gegeben ist durch $\theta_i = \theta + \vartheta_i$, wobei $\vartheta_i$ die systematische Abweichung der Studie (und damit Subpopulation) $i$ ausdrückt. Im Grunde berücksichtigt das Predictive Interval die Heterogenitätsvarianz $\tau^2$ zusätzlich zur Sampling-Variance $\sigma^2$. Schließt das PI die 0 mit ein, bedeutet dies, dass es (durch das Modell vorhergesagte) Studien gibt, in denen der wahre subpopulationsspezifische mittlere Wert gleich 0 (oder kleiner in diesem Beispiel) sein kann, der mittlere Wert über alle Subpopulationen hinweg ist allerdings $\neq 0$, was wir am CI abgelesen hatten. Wir erkennen, welchen Effekt die Heterogenität in den Daten hat: Sie vergrößert die Unsicherheit in der Vorhersage, wenn wir eine spezifische Vorhersage für eine bestimmte Studie machen wollen. So kann es Subpopulationen geben, für welche es keine Beziehung zwischen Gewissenhaftigkeit und Medikamenteneinnahme gibt. Werfen wir alle Subpopulationen in einen Pott und ignorieren die Heterogenität für einen Moment, dann schlussfolgern wir, dass es einen Effekt gibt zwischen Gewissenhaftigkeit und Medikamenteneinnahme.
Auch der Output dieses Befehls lässt sich erneut als Objekt abspeichern und wir können dann auf dieses zugreifen:
pred_REM <- predict(REM, transf=transf.ztor)
names(pred_REM)
## [1] "pred" "se" "ci.lb" "ci.ub" "pi.lb" "pi.ub" "cr.lb" "cr.ub"
## [9] "slab" "digits" "method" "transf" "pred.type"
pred_REM$pred # retransformierter gepoolter Korrelationskoeffizient
## [1] 0.1488048
Wir sehen, dass der mittlere $z$-Wert sich kaum vom mittleren Korrelationskoeffizienten unterscheidet. Dies ist im Allgemeinen auch so: $z$-Wert und $r$-Wert sind für betraglich kleine Korrelationen annähernd identisch, also für $-.25<r_i<.25$: hier liegt die betragliche Differenz bei $|r_i-Z_i|<.005$.
Finales Ergebnis des Random Effects Modells
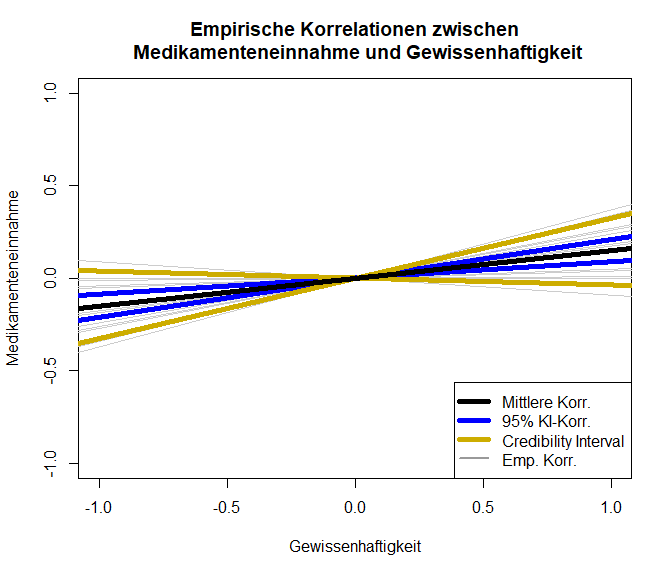
Schauen wir uns die Ergebnisse nun grafisch an:
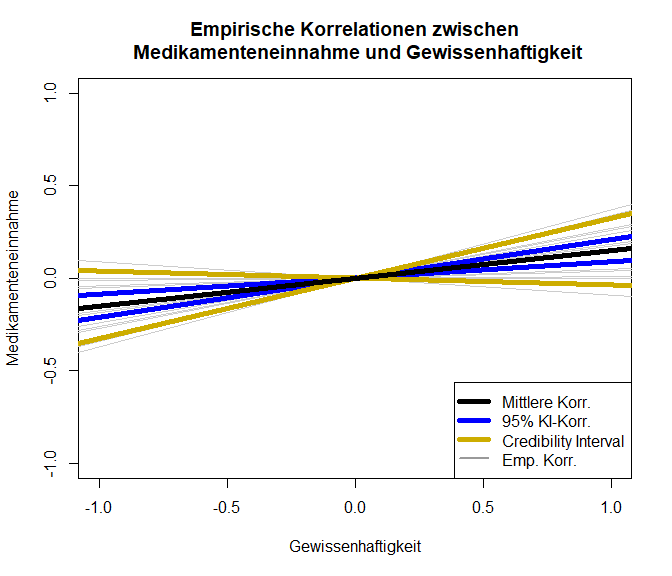
Es scheint wohl eine Beziehung zwischen Gewissenhaftigkeit und Medikamenteneinnahme zu geben. Allerdings ist diese Beziehung mit einer Korrelation von 0.1488 nicht sehr stark; lediglich $2.21\%$ der Variation an der Medikamenteneinnahme können durch die Gewissenhaftigkeit erklärt werden. Das Credibility-Intervall zeigt an, in welchem Bereich ca. $80\%$ der beobachteten Werte liegen.
Analyse Plots
Das metafor Paket bietet außerdem noch einige grafische Veranschaulichungen der Daten. Beispielsweise lässt sich ganz leicht ein Funnel-Plot erstellen mit der funnel-Funktion, welche lediglich unser Metaanalyse-Objekt REM entgegennehmen muss. Diese Plots haben wir in der vergangenen Sitzung bereits kennengelernt. Sie sind deshalb nur in Appendix B aufgeführt.
Insgesamt zeigen uns die Plots, dass von einem stabilen Effekt ausgegangen werden kann. Der Funnel-Plot ist viel regelmäßiger als der Funnel-Plot der vergangenen Sitzung.
Mixed Effects Modelle
Da die Heterogenitätsvarianz signifikant von 0 verschieden war, wäre es sinnvoll zu versuchen, diese Variation in den Korrelationskoeffizienten zwischen den Studien mithilfe von Moderatoren zu erklären. Dies überlassen wir Ihnen als Übung (Tipp: interessante Moderatoren sind die Studienqualität und die Involvierung von Kontrollvariablen).
Weitere Moderatoren und Psychometrische Metaanalysen
Das Ziel einer psychometrischen Metaanalyse nach Hunter und Schmidt (2004) ist es, so viele Varianzeinflüsse wie möglich zu kontrollieren/korrigieren. So ist es nach diesem Ansatz üblich, dass Korrelationen um deren Reliabilität korrigiert werden. Auch Range-Restrictions (also Einschränkungen im Wertebereich) können berücksichtigt werden. Da das Korrigieren der Korrelationen ein häufiges Vorgehen ist, schauen wir uns dieses noch genauer an. Die Korrektur wird mithilfe der Information über die Reliabilität der Skalen mittels der Minderungskorrektur durchgeführt:
$$r_{xy\text{,corrected}} = \frac{r_{xy}}{\sqrt{r_{xx}r_{yy}}},$$ wobei $r_{xy}$ die Korrelation der Variablen $X$ und $Y$ ist (hier ist $Y$ wieder eine Variable und kein Koeffizient, wie es bei Metaanalysen üblich ist), $r_{xx}$ und $r_{yy}$ sind jeweils die Reliablitäten der Skalen, die zur Messung von $X$ und $Y$ verwendet wurden. Je geringer die Reliabilität ausfällt, desto größer ist der Korrekturterm (da durch die Reliabilität geteilt wird). Um keine verzerrten Ergebnisse zu erhalten, ist es also konservativer, größere Reliabilitäten zu verwenden, wenn bspw. nur eine Range für eine Reliabilität in einem Artikel angegeben wird. Liegen keine Informationen für die Reliabilität vor oder ist eine Variable direkt beobachtbar, wird die Reliabilität als 1 angenommen. Angenommen wir haben einen Datensatz mit vier Studien und den folgenden Koeffizienten:
df <- data.frame(r = c(0.3, 0.3, 0.5, 0.4),
RelX = c(0.6, 0.8, 1, 1),
RelY = c(0.5, 0.7, 0.8, 1),
n = c(65, 65, 34, 46))
head(df)
## r RelX RelY n
## 1 0.3 0.6 0.5 65
## 2 0.3 0.8 0.7 65
## 3 0.5 1.0 0.8 34
## 4 0.4 1.0 1.0 46
Dann reichen diese Informationen aus, um die Korrelationen um deren Reliabilität zu korrigieren. Hierbei hat die Variable $X$ zweimal eine Reliabilität von 1, was wie eben erwähnt daran liegen kann, dass keine Informationen vorlagen oder dass diese Merkmale direkt beobachtbar waren (bspw. das Gehalt oder Berufserfahrung in Jahren, etc. haben keine Unsicherheit). Nun führen wir die Minderungskorrektur durch und fügen die korrigierten Korrelationen direkt unserem Datensatz hinzu:
df$r_correct <- df$r/sqrt(df$RelX*df$RelY)
head(df)
## r RelX RelY n r_correct
## 1 0.3 0.6 0.5 65 0.5477226
## 2 0.3 0.8 0.7 65 0.4008919
## 3 0.5 1.0 0.8 34 0.5590170
## 4 0.4 1.0 1.0 46 0.4000000
Wir sehen, dass in der ersten Studie die Korrelation am stärksten angestiegen ist. Das liegt daran, dass hier beide Relibilitäten am geringsten ausgefallen sind. In der zweiten Studie wurden beide Merkmale etwas reliabler erfasst, sodass hier die Korrektur wesentlich geringer ausgefallen ist. In der letzten Studie wurden nur direkt beobachtbare Variablen verwendet (manifeste Variablen) oder es lagen nicht genug Informationen über die Reliablitäten vor, sodass hier keinerlei Korrektur vorgenommen wurde.
Die psychometrische Metaanalyse von Irmer, Kern, Schermelleh-Engel, Semmer und Zapf (2019) wurde mit diesem R-Paket durchgeführt. Sie behandelt die Validierung des Instrument zur stressbezogenen Tätigkeitsanalyse (ISTA) von Semmer, Zapf und Dunckel (1995, 1999), indem die linearen Beziehungen der Skalen des Instruments untereinander sowie mit Kriteriumsvariablen untersucht wurden. Außerdem wurden die Mittelwerte und die Standardabweichungen (metaanalytisch) gemittelt. Alle Koeffizienten (Mittelwerte, Standardabweichungen und [reliabilitätskorrigierte] Korrelationen) wurden hinsichtlich systematischer Unterschiede über das Geschlecht (% Frauen), den Publikationsstatus (publiziert vs. nicht publiziert), die ISTA-Version sowie die Branche (des Arbeitsplatzes) untersucht. Das genaue metaanalytische Vorgehen ist dem Appendix des Artikels zu entnehmen.
Appendix A
Codes
In diesem Appendix finden Sie die Codes, die zum Erstellen der Grafiken verwendet wurden.
plot(NA, xlim = c(-1,1), ylim = c(-1,1), xlab = "Gewissenhaftigkeit", ylab = "Medikamenteneinnahme",
main = "Empirische Korrelationen zwischen\n Medikamenteneinnahme und Gewissenhaftigkeit")
for(i in 1:length(dat.molloy2014$ri))
{
abline(a = 0, b = dat.molloy2014$ri[i], col = "grey80")
}
plot(NA, xlim = c(-1,1), ylim = c(-1,1), xlab = "Gewissenhaftigkeit", ylab = "Medikamenteneinnahme",
main = "Empirische Korrelationen zwischen\n Medikamenteneinnahme und Gewissenhaftigkeit")
for(i in 1:length(dat.molloy2014$ri))
{
abline(a = 0, b = dat.molloy2014$ri[i], col = "grey80")
}
abline(a = 0, b = pred_REM$ci.lb, col = "blue", lwd = 5)
abline(a = 0, b = pred_REM$ci.ub, col = "blue", lwd = 5)
abline(a = 0, b = pred_REM$cr.lb, col = "gold3", lwd = 5)
abline(a = 0, b = pred_REM$cr.ub, col = "gold3", lwd = 5)
abline(a = 0, b = pred_REM$pred, col = "black", lwd = 5)
legend(x = "bottomright", col = c("black", "blue", "gold3", "grey60"), pch = NA, lwd = c(5,5,5,2),
legend = c("Mittlere Korr.", "95% KI-Korr.", "Credibility Interval", "Emp. Korr."))
Appendix B
Analyse Plots
In diesem Appendix finden Sie Analyse-Plots, die in der vergangenen Sitzung bereits besprochen wurden.
Funnel Plot und Trim-and-Fill Methode
Der Funnel-Plot wird verwendet, um das bekannte Problem des Publication-Bias zu untersuchen. Hier wird der gefundene Effekt (hier $z$-transformierte Korrelation zwischen Gewissenhaftigkeit und Medikamenteneinnahme) gegen den Standardfehler jeder Studie geplottet. Es wird die Annahme zugrunde gelegt, dass alle Studien in der Metaanalyse eine gewisse zufällige Schwankung um den wahren Effekt haben, und dabei diese zufällige Schwankung größer ist, je größer der Standardfehler in einer Studie ist und je kleiner die Stichprobe war. Sofern eine Studie unabhängig von der Effektgröße sowie der Streuung (und damit auch der Signifikanz) publiziert wurde, sollte so das typische symmetrische Dreieck (Funnel = Trichter) entstehen.
# funnel plot
funnel(REM)
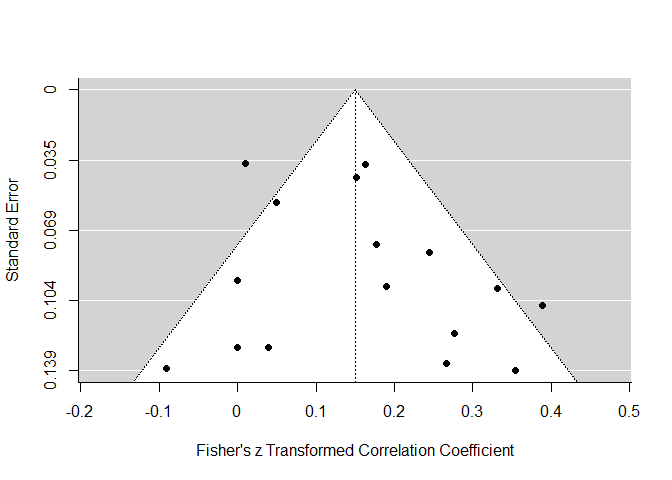
Der Grafik ist zu entnehmen, dass sich die meisten Effektstärken im positiven Bereich tummeln. Je kleiner der Effekt (je näher an der Null), desto präziser die Schätzung (desto kleiner der SE - höher dargestellt im Funnel-Plot). Der Plot erscheint insgesamt recht symmetrisch und unverzerrt. Allein vom Funnel-Plot zu urteilen scheint es keinen Publication-Bias gegeben zu haben.
Die Trim-and-Fill Methode wird verwendet, um zu bestimmen, wie viele Studien hinzugenommen (fill) oder entfernt (trim) werden müssten, damit der Funnel-Plot symmetrisch ist. Die Methode kann auch zur Schätzung eines (um einen möglichen Publication-Bias) bereinigten Effekt verwendet werden.
trimfill(REM, estimator = "R0")
##
## Estimated number of missing studies on the left side: 0 (SE = 1.4142)
## Test of H0: no missing studies on the left side: p-val = 0.5000
##
## Random-Effects Model (k = 16; tau^2 estimator: REML)
##
## tau^2 (estimated amount of total heterogeneity): 0.0081 (SE = 0.0055)
## tau (square root of estimated tau^2 value): 0.0901
## I^2 (total heterogeneity / total variability): 61.73%
## H^2 (total variability / sampling variability): 2.61
##
## Test for Heterogeneity:
## Q(df = 15) = 38.1595, p-val = 0.0009
##
## Model Results:
##
## estimate se zval pval ci.lb ci.ub
## 0.1499 0.0316 4.7501 <.0001 0.0881 0.2118 ***
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Die Funktion bestimmt selbst, auf welcher Seite mögliche fehlende (nicht publizierte) Werte ergänzt werden sollten. Der Output sieht dem REM sehr ähnlich. In der ersten Zeile steht, dass 0 Studien auf der linken Seite des geschätzten durchschnittlichen Effekts ergänzt wurden. Der Output hat sich somit nicht verändert. Der mittlere Effekt ist identisch zu unserer Analyse zuvor (0.15 vs 0.15). Wenn wir nun wieder die funnel-Funktion darauf anwenden, sehen wir auch, dass keine Studien hinzugefügt wurden:
funnel(trimfill(REM, estimator = "R0"))
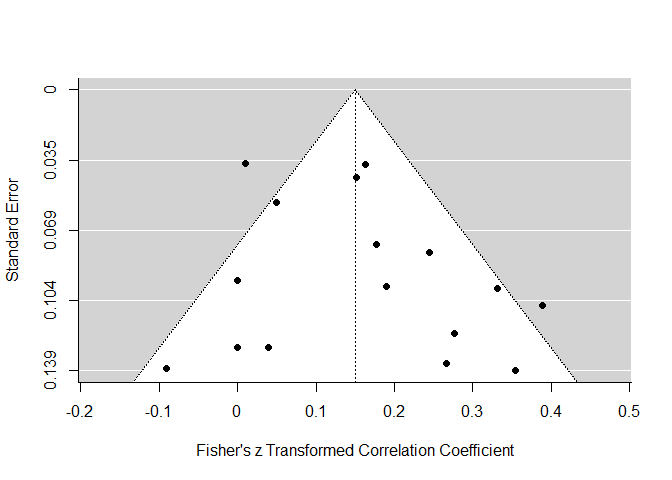
Wir gehen somit insgesamt davon aus, dass kein Publication Bias vorliegt und verwerfen die eben betrachteten Trim-and-Fill-Ergebnisse.
Forest-Plot
Auch Forest-Plots funktionieren auf die gleiche Weise mit der forest-Funktion. Der Forest-Plot stellt die unterschiedlichen Studien hinsichtlich ihrer Parameterschätzungen (Effektstärken) und die zugehörige Streuung grafisch dar. So können beispielsweise Studien identifiziert werden, welche besonders hohe oder niedrige Werte aufweisen oder solche, die eine besonders große oder kleine Streuung zeigen.
# forest plot
forest(REM)
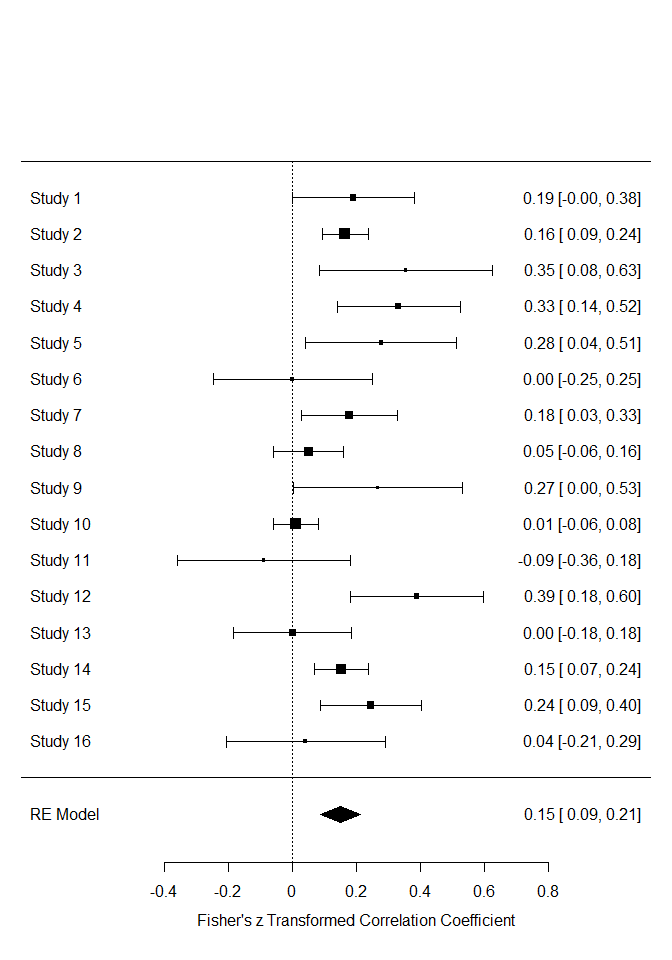
Wir sehen, dass einige Studien Konfidenzintervalle aufweisen, die die Null einschließen, also nicht signifikante Ergebnisse berichtet haben. Außerdem wird im Plot selbst schon angezeigt, dass es sich um $z$-transformierte Werte handelt. Auch ein kumulativer Forest-Plot wäre möglich. Dazu müssen wir auf unser REM-Objekt noch die Funktion cumul.rma.uni anwenden:
# kumulativer Forest Plot
forest(cumul.rma.uni(REM))
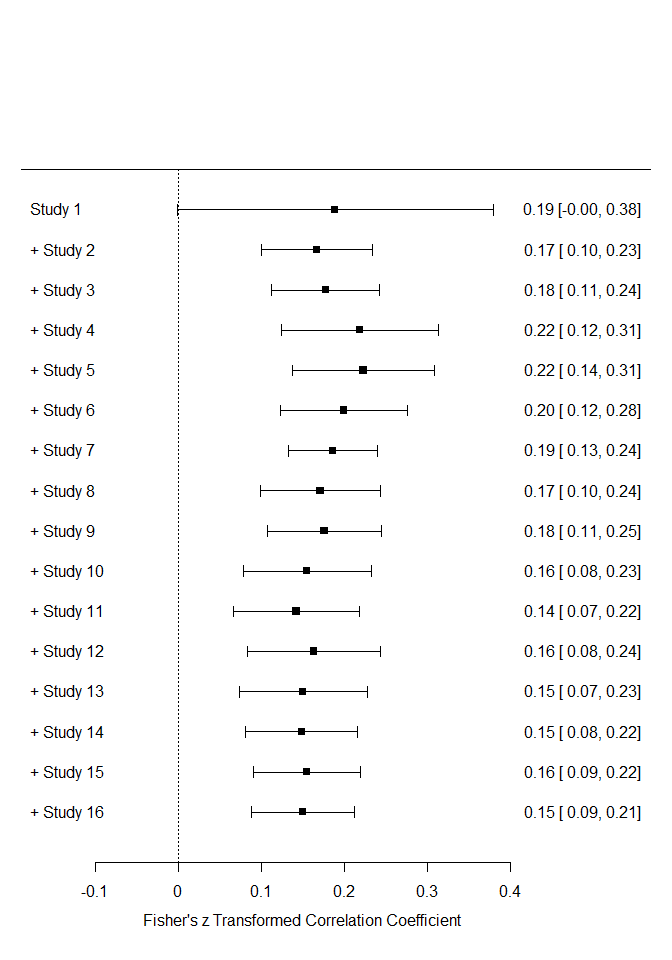
Die Funktion cumul.rma.uni führt sukzessive immer wieder eine Metaanalyse durch, wobei nach und nach eine Studie hinzugefügt wird. Anders als beim ersten Forest-Plot wird immer das Ergebnis der jeweiligen Metaanalyse dargestellt und nicht jede Studie einzeln. Wir sehen, dass sich sowohl die mittlere Effektstärke als auch die Streuung von oben nach unten einpendeln. Das finale Ergebnis ist identisch mit unserer Metaanalyse. Die gestrichelte Linie der Forest-Plots symbolisiert die 0, da in den meisten Fällen gegen 0 getestet wird und es daher von Interesse ist, wie viele Studien sich von 0 unterscheiden und ob sich der mittlere Effekt von 0 unterscheidet.
Literatur
Döring, N., & Bortz, J. (2016). Meta-Analyse. In Forschungsmethoden und Evaluation in den Sozial- und Humanwissenschaften (pp. 893-943). Springer, Berlin, Heidelberg.
Hunter, J. E., & Schmidt, F. L. (2004). Methods of meta-analysis: Correcting error and bias in research findings. Sage.
Irmer, J. P., Kern, M., Schermelleh-Engel, K., Semmer, N. K., & Zapf, D. (2019). The instrument for stress oriented job analysis (ISTA) – a meta-analysis. Zeitschrift für Arbeits- & Organisationspsychologie – German Journal of Work and Organizational Psychology, 63(4), 217-237. https://doi.org/10.1026/0932-4089/a000312
Molloy, G. J., O’Carroll, R. E., & Ferguson, E. (2014). Conscientiousness and medication adherence: A meta-analysis. Annals of Behavioral Medicine, 47(1), 92–101. https://doi.org/10.1007/s12160-013-9524-4
Semmer, N. K., Zapf, D., & Dunckel, H. (1995). Assessing stress at work: A framework and an instrument. In O. Svane, & C. Johansen (Eds.), Work and health – scientific basis of progress in the working environment, (pp. 105 – 113). Luxembourg, Luxembourg: Office for Official Publications of the European Communities.
Semmer, N. K., Zapf, D., & Dunckel, H. (1999). Instrument zur Stressbezogenen Tätigkeitsanalyse (ISTA) [Instrument for stress-oriented task analysis (ISTA)]. In H. Dunkel (Ed.), Handbuch psychologischer Arbeitsanalyseverfahren (pp. 179 – 204). Zürich, Switzerland: vdf Hochschulverlag an der ETH.
Viechtbauer, W. (2010). Conducting meta-analyses in R with the metafor package. Journal of Statistical Software, 36(3), 1–48. https://www.jstatsoft.org/v036/i03.
- Blau hinterlegte Autor:innenangaben führen Sie direkt zur universitätsinternen Ressource.
](/media/header/meds_and_ampules.jpg)