Inhaltsverzeichnis
Einleitung
Die ANalysis of COVAriance hatten wir bereits im 2. Semester der Bachelorstudiengangs behandelt und dabei schon vorausahnen lassen, dass wir uns das Ganze im Rahmen des KliPPs-Masters noch einmal detaillierter angucken werden. Dieser Spannungsbogen soll nun hier abgeschlossen werden.
Im Allgemeinenen wird die ANCOVA in der Psychotherapieforschung immer dann genutzt, wenn wir Interventionsgruppen betrachten werden, die sich zum ersten Zeitpunkt hinsichtlich des Outcomes oder beliebiger Kovariaten unterscheiden können. Hierbei ist besonders wichtig zu unterscheiden, ob es sich um randomisierte Studien (üblicherweise “Randomized Controlled Trial”, kurz RCT, genannt) handelt oder nicht. Üblicherweise sollten sich die Gruppen im ersten Fall nicht systematisch unterscheiden, aber wir werden im Abschnitt zum Dropout noch genauer darauf eingehen, wie so etwas trotzdem entstehen kann. Darüber hinaus werden wir einige kritische Entscheidungen und Abgrenzungen besprechen, z.B. wann es empfehlenswert ist als abhängige Variable die Differenz aus den zwei Messzeitpunkten (also den Indikator der Veränderung) statt des Messwerts zum 2. Zeitpunkt zu nutzen.
Interventionsstudie zur Depression während der COVID Pandemie
Auch wenn dieser Beitrag etwas theorielastiger wird, als die vergangenen Abschnitte, werden wir uns auch dieses mal hauptsächlich an einer spezifische klinischen Studie orientieren. Die Basis für unsere Auswertungen liefert eine Studie von Schleider et al. (2022). Anders als bei den bisherigen Beiträgen muss ich allerdings von vornherein zugeben, dass wir die Ergebnisse nicht exakt reproduzieren werden - und das hier auch nicht direkt anpeilen werden - weil in der Studie mitunter etwas aufwändigere Datenauf- und -vorbereitungsschritte durchgeführt wurden, die uns hier etwas zu weit vom eigentlichen Thema ablenken würden.
Wie immer können Sie die Originaldaten direkt aus dem OSF Repo beziehen. Die relevante Auswahl aus dem sehr großen Datensatz habe ich schon einmal vorbereitet und hier hinterlegt:
source('https://pandar.netlify.app/daten/Data_Processing_cope.R')
Im Datensatz sind insgesamt 51 Variablen enthalten, von denen zwar nicht alle zentral für die ANCOVA sind, aber zumindest in den Tabellen der Studie aufbereitet werden. Im Artikel werden die Ergebnisse einer großen Interventionsstudie vorgestellt, in der die Effektivität von zwei selbst-administrierten single-session interventions (SSI) mit Hinblick auf die Reduktion von depressiven Symptomen bei Jugendlichen während der COVID-19 Pandemie untersucht wurde. Die Studie ist im Journal Nature Human Behavior, erschienen und gehört mit seinen 126 Zitationen zum 1% der am häufigst zitierten psychologischen Publikationen des Jahres 2022.
Variablenübersicht
| Variable | Beschreibung | Ausprägungen |
|---|---|---|
condition | Experimentalbedingung | Placebo Control, Project Personality, Project ABC |
race_... | Verschiedene Angaben zur Ethnizität | 0 = identifiziert sich nicht als, 1 = identifiziert sich als |
gender_... | Verschiedene Angaben zum Geschlecht | 0 = identifiziert sich nicht als, 1 = identifiziert sich als |
sex | Geburtsgeschlecht | Female, Male, Other, Prefer not to say |
orientation | Sexuelle Orientierung | Asexual, Bisexual, Gay/Lesbian/Homosexual, Heterosexual/Straight, I do not use a label, I do not want to respond, Other/Not listed (please specify), Pansexual, Queer, Unsure/Questioning |
age | Alter | Alter in Jahren |
CDI1 | Children’s Depression Inventory, Baseline | Skalenmittelwert, 0-2 |
CDI3 | Children’s Depression Inventory, Follow-up | Skalenmittelwert, 0-2 |
CTS1 | COVID Trauma Symptoms, Baseline | Skalenmittelwert, 1-4 |
CTS3 | COVID Trauma Symptoms, Follow-up | Skalenmittelwert, 1-4 |
GAD1 | Generalized Anxiety Disorder, Baseline | Skalenmittelwert, 1-4 |
GAD3 | Generalized Anxiety Disorder, Follow-up | Skalenmittelwert, 1-4 |
SHS1 | State Hope Scale, Perceived Agency Subscale, Baseline | Skalenmittelwert, 1-8 |
SHS2 | State Hope Scale, Perceived Agency Subscale, Post-Intervention | Skalenmittelwert, 1-8 |
SHS3 | State Hope Scale, Perceived Agency Subscale, Follow-up | Skalenmittelwert, 1-8 |
BHS1 | Beck Hopelessness Scale, Baseline | Skalenmittelwert, 0-3 |
BHS2 | Beck Hopelessness Scale, Post-Intervention | Skalenmittelwert, 0-3 |
BHS3 | Beck Hopelessness Scale, Follow-up | Skalenmittelwert, 0-3 |
DRS1 | Dietary Restriction Screener, Baseline | Skalenmittelwert, 0-1 |
DRS3 | Dietary Restriction Screener, Follow-up | Skalenmittelwert, 0-1 |
pfs_1 | Program Feedback Scale, “Enjoyed” | 1-5 |
pfs_2 | Program Feedback Scale, “Understood” | 1-5 |
pfs_3 | Program Feedback Scale, “Easy to Use” | 1-5 |
pfs_4 | Program Feedback Scale, “Tried My Hardest” | 1-5 |
pfs_5 | Program Feedback Scale, “Helpful to Other Kids” | 1-5 |
pfs_6 | Program Feedback Scale, “Would Recommend to a Friend” | 1-5 |
pfs_7 | Program Feedback Scale, “Agree with Message” | 1-5 |
dropout1 | Abbruch der Teilnahme, Post-Intervention | 0 = nicht abgebrochen, 1 = abgebrochen |
dropout2 | Abbruch der Teilnahme, Follow-Up | 0 = nicht abgebrochen, 1 = abgebrochen |
Deskriptivstatistik
Wie schon in den anderen Beiträgen, können wir zunächst checken, ob unsere Daten mit denen aus dem Artikel übereinstimmen, indem wir die deskriptivstatistischen Tabellen nachvollziehen. Tabelle 1 (S. 260) gibt dabei eine sehr detaillierte Übersicht über die die Verteilung der demografischen Variablen Ethnizität, Geschlecht und sexueller Orientierung. Diese Ergebnisse sind mit dem bereitgestellten Datensatz soweit reproduzierbar - allerdings aufgrund der fehlenden Exklusivität der Kategorien nicht so einfach zu erstellen, wie in den vergangenen beiden Beiträgen:
# Ethnizität
ethnicity <- aggregate(cope[, grep('race_', names(cope))], by = list(cope$condition), FUN = sum)
names(ethnicity) <- c('condition', 'Native', 'Asian', 'Hispanic', 'Pacific Islander', 'White', 'Black', 'Other', 'Prefer not to say')
ethnicity
## condition Native Asian Hispanic Pacific Islander White Black Other Prefer not to say
## 1 Placebo Control 36 101 159 14 546 85 19 9
## 2 Project Personality 29 100 148 14 550 88 11 10
## 3 Project ABC 27 109 164 11 536 84 17 5
# Geschlecht
gender <- aggregate(cope[, grep('gender_', names(cope))], by = list(cope$condition), FUN = sum)
names(gender) <- c('condition', 'agender', 'not sure', 'other', 'androgynous', 'nonbinary', 'two spirited', 'Trangender female to male', 'trans female', 'trans male', 'Gender expansive', 'Third gender', 'Genderqueer', 'Transgender male to female', 'Man', 'Woman')
gender
## condition agender not sure other androgynous nonbinary two spirited Trangender female to male
## 1 Placebo Control 19 71 32 50 128 5 59
## 2 Project Personality 23 65 28 55 129 6 62
## 3 Project ABC 12 60 27 52 127 5 59
## trans female trans male Gender expansive Third gender Genderqueer Transgender male to female Man Woman
## 1 7 67 7 2 46 6 122 70
## 2 9 64 9 3 49 6 126 58
## 3 9 65 11 1 45 3 115 58
## NA
## 1 514
## 2 516
## 3 514
Für das biologische Geschlecht und die sexuelle Orientierung können wir die Ergebnisse mittels einfacher Häufigkeitstabeller erzeugen:
# Biologisches Geschlecht
table(cope$sex, cope$condition)
##
## Placebo Control Project Personality Project ABC
## Female 723 719 718
## Male 87 78 86
## Other 2 7 12
## Prefer not to say 6 9 5
# Sexuelle Orientierung
table(cope$orientation, cope$condition)
##
## Placebo Control Project Personality Project ABC
## Asexual 39 38 46
## Bisexual 228 220 230
## Gay/Lesbian/Homosexual 86 91 76
## Heterosexual/Straight 172 165 161
## I do not use a label 52 47 41
## I do not want to respond 3 2 5
## Other/Not listed (please specify) 32 38 23
## Pansexual 87 79 98
## Queer 49 51 47
## Unsure/Questioning 70 82 94
Und zu guter Letzt noch die mittlere Ausprägung des Primäroutcomes (Depressive Symptomatik) getrennt nach Interventionsgruppe zur Baseline. Dabei ist zu bedenken, dass die Variable im Datensatz als Mittelwert vorliegt (und auch in späteren Berechnungen so verwendet wird), in dieser Tabelle allerdings als Summenscore angegeben wird. Daher müssen wir den Mittelwert wieder mit der Anzahl der Items (12) multipliuieren:
# Baseline CDI
psych::describeBy(cope$CDI1*12, cope$condition)
##
## Descriptive statistics by group
## group: Placebo Control
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 818 14.31 4.12 14.5 14.42 5.19 1 24 23 -0.25 -0.46 0.14
## ---------------------------------------------------------------------------------
## group: Project Personality
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 813 14.22 4.13 14 14.35 4.45 3 24 21 -0.28 -0.28 0.15
## ---------------------------------------------------------------------------------
## group: Project ABC
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 821 14.15 4.06 14 14.25 4.45 0 24 24 -0.25 -0.27 0.14
Im Artikel präsentieren Schleider et al. (2022) in Tabelle 2 außerdem die Akzeptanz bzw. Zufriedenheit mit der jeweiligen Intervention, die wir ebenfalls sehr leicht rekonstruieren können:
# Akzeptanz
pfs <- subset(cope, select = c('condition', grep('pfs_', names(cope), value = TRUE))) |> na.omit()
psych::describeBy(pfs, pfs$condition)
##
## Descriptive statistics by group
## group: Placebo Control
## vars n mean sd median trimmed mad min max range skew kurtosis se
## condition* 1 630 1.00 0.00 1 1.00 0.00 1 1 0 NaN NaN 0.00
## pfs_1 2 630 3.80 0.79 4 3.83 0.00 1 5 4 -0.57 0.71 0.03
## pfs_2 3 630 4.54 0.56 5 4.59 0.00 2 5 3 -0.86 0.66 0.02
## pfs_3 4 630 4.46 0.64 5 4.53 0.00 2 5 3 -0.97 0.87 0.03
## pfs_4 5 630 4.45 0.65 5 4.53 0.00 1 5 4 -0.97 0.91 0.03
## pfs_5 6 630 4.24 0.81 4 4.34 1.48 1 5 4 -0.96 0.83 0.03
## pfs_6 7 630 3.97 0.95 4 4.07 1.48 1 5 4 -0.67 -0.18 0.04
## pfs_7 8 630 4.50 0.62 5 4.58 0.00 2 5 3 -0.98 0.49 0.02
## ---------------------------------------------------------------------------------
## group: Project Personality
## vars n mean sd median trimmed mad min max range skew kurtosis se
## condition* 1 653 2.00 0.00 2 2.00 0.00 2 2 0 NaN NaN 0.00
## pfs_1 2 653 3.83 0.77 4 3.84 0.00 1 5 4 -0.41 0.36 0.03
## pfs_2 3 653 4.48 0.64 5 4.55 0.00 1 5 4 -1.18 2.02 0.02
## pfs_3 4 653 4.39 0.68 4 4.49 1.48 2 5 3 -0.94 0.73 0.03
## pfs_4 5 653 4.45 0.67 5 4.55 0.00 1 5 4 -1.20 1.83 0.03
## pfs_5 6 653 4.20 0.83 4 4.31 1.48 1 5 4 -1.09 1.50 0.03
## pfs_6 7 653 3.93 1.00 4 4.05 1.48 1 5 4 -0.72 -0.07 0.04
## pfs_7 8 653 4.47 0.70 5 4.59 0.00 1 5 4 -1.40 2.37 0.03
## ---------------------------------------------------------------------------------
## group: Project ABC
## vars n mean sd median trimmed mad min max range skew kurtosis se
## condition* 1 729 3.00 0.00 3 3.00 0.00 3 3 0 NaN NaN 0.00
## pfs_1 2 729 3.93 0.73 4 3.95 0.00 1 5 4 -0.35 0.07 0.03
## pfs_2 3 729 4.46 0.59 5 4.50 0.00 2 5 3 -0.64 -0.11 0.02
## pfs_3 4 729 4.42 0.64 4 4.50 1.48 2 5 3 -0.81 0.32 0.02
## pfs_4 5 729 4.42 0.69 5 4.52 0.00 1 5 4 -1.01 0.85 0.03
## pfs_5 6 729 4.30 0.76 4 4.41 1.48 1 5 4 -0.92 0.52 0.03
## pfs_6 7 729 4.12 0.89 4 4.22 1.48 1 5 4 -0.84 0.26 0.03
## pfs_7 8 729 4.54 0.57 5 4.59 0.00 3 5 2 -0.76 -0.43 0.02
Dropout
Schwieriger als im letzten Abschnitt wird es, wenn wir versuchen die Werte in Tabelle 3 des Artikels zu reproduzieren. Das liegt an folgendem Vorgehen, das auf S. 266 von Schleider et al. (2022) beschrieben wird:
We imputed participant-level missing data using the expectation-maximization and bootstrapping algorithm implemented with Amelia II in R, allowing more conservative intent-to-treat analyses than other approaches
Was hier beschrieben wird, ist der Umgang mit einem zentralen Problem in jeder Form längsschnittlicher Datenerhebung, das aber in der Psychotherapieforschung besonders relevant ist: dem Studienabbruch von Teilnehemden. Generell können wir niemals davon ausgehen, dass alle Personen, die zum ersten Zeitpunkt an einer Studie teilnehmen, dieser auch langfristig erhalten bleiben. Insbesondere, wenn die Studienteilnahme mit Anstrengungen oder Zeitaufwand verbunden ist (was quasi unumgänglich ist) oder wir z.B. Personen mit psychischen Störungen untersuchen, ist die Rate an Studienabbrüchen oft sehr hoch. Cooper und Conklin (2015) zeigen in einer Meta-Analyse eine Drop-Out Rate von 17,5% bis 20% (wobei einzelne Studien von 0% bis 50% reichen) in klinischen RCT Studien. Generell ist es natürlich “schade” wenn Personen zu späteren Zeitpunkten nicht mehr an der Studie teilnehmen, weil wir so für Veränderungshypothesen weniger Power haben, aber das eigentliche Problem stellt sogenannter differentieller Dropout dar. Damit ist gemeint, dass Personen aus unterschiedlichen Experimentalgruppen in unterschiedlichem Umfang und aus unterschiedlichen Gründen die Teilnahme an der Studie abbrechen. Das kann dazu führen, dass die Gruppen sich in ihrer Zusammensetzung verändern und damit die schönen Gruppeneigenschaften, für die wir uns extra ein Randomisierungsschema ausgedacht haben, wieder verloren gehen. So kann es passieren, dass Gruppen, die zwar zur Baseline noch direkt vergleichbar waren, im Verlauf der Zeit immer unterschiedlicher werden.
Der erste logische Schritt mit diesem Problem umzugehen ist es, festzustellen in welchem Ausmaß der Dropout über die Gruppen hinweg unterschiedlich ist. Im Artikel von Schleider et al. (2022) wird auf S. 259 genau das getan. Um Häufigkeitsverteilung zwischen mehreren Gruppen zu vergleichen, wird üblicherweise der $\chi^2$ herangezogen:
dropouts <- table(cope$condition, cope$dropout1)
dropouts
##
## remain dropout
## Placebo Control 631 187
## Project Personality 653 160
## Project ABC 730 91
prop.table(dropouts, margin = 1)
##
## remain dropout
## Placebo Control 0.7713936 0.2286064
## Project Personality 0.8031980 0.1968020
## Project ABC 0.8891596 0.1108404
chisq.test(dropouts)
##
## Pearson's Chi-squared test
##
## data: dropouts
## X-squared = 41.469, df = 2, p-value = 9.888e-10
Wir sehen hier die Ergebnisse, die auch von Schleider et al. (2022) berichtet werden: es gibt einen statistisch bedeutsamen Unterschied in den Häufigkeiten des Teilnahmeabbruchs über die Gruppen hinweg ($\chi^2 = 41.47$, $df = 2$, $p < .001$) und zwar in der Form, dass im Project ABC deutlich seltener abgebrochen wird, als in den anderen beiden Gruppen. Diese unterschiedliche Quote des Abbruchs kann kausale Schlüsse hinsichtlich der Interventionen gefährden. Nähere Informationen dazu, wie wir bessere kausale Effektschätzer ermitteln können und was wir dabei bedenken müssen, finden Sie unter anderem in den beiden Beiträgen zur Kausaleffektschätzung mit EffectLite bzw. Propensity-Scores.
Bevor wir untersuchen, ob die Tendenz zum Dropout auch mit anderen relevanten Variablen zusammenhängt, an dieser Stelle ein extrem kurzer Überblick über die drei Kategorien, anhand derer fehlende Werte statistisch unterschieden werden:
| Typ | Abkürzung | Implikation |
|---|---|---|
| Missing Completely at Random | MCAR | Fehlende Werte sind unabhängig von den beobachteten und nicht beobachteten Werten |
| Missing at Random | MAR | Fehlende Werte sind abhängig von den beobachteten Werten, aber nicht von den nicht beobachteten Werten |
| Missing Not at Random | MNAR | Fehlende Werte sind abhängig von den nicht beobachteten Werten |
Was mit der Abhängigkeit von beobachteten bzw. nicht-beobachteten Werten gemeint ist, wir am besten mit ein paar Beispielen deutlich. MCAR sind üblicherweise fehlende Werte, die durch den Versuchsaufbau gezielt herbei geführt werden. Wenn wir zum Beispiel an extrem vielen Konstrukten interessiert sind, aber unsere Studienteilnehmenden nicht alle durch eine 4-stündige Erhebung quälen wollen, können wir die Personen randomisiert in Gruppen zuweisen, die jeweils unterschiedliche Kombinationen von Fragebögen in der Erhebung durchlaufen müssen. In diesem Fall hängt das Fehlen der Werte ausschließlich von dieser zufälligen Einteilung ab. Wenn wir zum Beispiel eine Erhebung mit Kindern in einer Schulstunde durchführen und die Befragung ziemlich genau auf die 45 Minuten angelegt ist, kann es vorkommen, dass einige Kinder aufgrund einer Dyslexie die Fragebögen sehr viel langsamer bearbeiten und so deren Werte auf den letzten Skalen fehlen. In diesem Fall liegt das Fehlen der Werte an der Dyslexie, also einer anderen Variablen, die wir (idealerweise) bereits zuvor irgendwo erfasst haben. Solche Fälle bezeichnet man als MAR (missing at random), weil sie nach der Kontrolle auf diese Störvariablen zufällig fehlen. Missing not at random (MNAR) sind Werte dann, wenn sie fehlen, weil Personen auf der spezifische Variable eine besondere Ausprägung haben. So kann es sein, dass Personen sich weigern Fragen zu ihrem Alkoholkonsum zu beantworten, wenn sie diesen selbst bereits als problematisch wahrnehmen und daher versuchen, ihn zu verbergen. Da in diesen Fällen das Fehlen von Werten von den Werten abhängt, die wir nicht beobachten konnten, ist es hier sehr viel schwieriger das Problem fehlender Werte nach der Erhebung mit statistischen Modellen zu lösen. Gerade in der Psychotherapieforschung ist es aber nicht unwahrscheinlich, dass Personen die Studienteilnahme abbrechen, weil sie die Intervention nicht als wirksam erleben oder z.B. eine so schwere Episode erleiden, dass sie stationär behandelt werden müssen und somit nicht mehr an der Erhebung in der Ambulanz teilnehmen können.
Prädiktoren des Dropouts
Wie Sie aus diesem (etwas zu lang geratenen) Absatz vermutlich ableiten können, sollten Entscheidungen zur Behandlung fehlender Werte vor allem auf inhaltlichen Überlegungen fußen. Statistisch können wir zumindest prüfen, ob die Variablen, die wir zum 1. Messzeitpunkt erhoben haben, prädiktiv für einen Teilnahmeabbruch sind und demzufolge die inhaltlichen und kausalen Schlussfolgerungen hinsichtlich der Interventionseffektivität gefährden würden. Dazu können wir im einfachsten Fall die logistische Regression, die wir im letzten Beitrag erarbeiteten hatten, nutzen, um das Fehlen von Werten vorherzusagen.
Für den Dropout während der Intervention gibt es die Variable dropout1 als Indikator. Auf dieser Variable ist kodiert, ob Teilnehmende die 1. Frage des Fragebogen direkt nach Abschluss der Intervention ausgefüllt haben. In logistischer Regression können wir diese also relativ einfach durch die Baselinevariablen vorhersagen, um zu sehen, ob es spezifische Prädiktoren für den Abbruch gibt. Damit ich die Namen der Prädiktoren nicht alle einzeln hinschreiben muss, erzeuge ich mir erst einen Datensatz, der nur die relevanten Variablen enthält und nutze dann alle darin enthaltenen Variablen als Prädiktoren.
# Datenauswahl zur Dropout-Vorhersage
drop_dat <- cope[, c('dropout1', grep('^gender', names(cope), value = TRUE),
grep('^race', names(cope), value = TRUE),
'age', 'CDI1', 'CTS1', 'GAD1', 'SHS1', 'BHS1', 'DRS1')]
# Vorhersage von Dropout mit logistischer Regression
drop_mod <- glm(dropout1 ~ ., drop_dat, family = 'binomial')
Die etwas lange Ergebnistabelle
summary(drop_mod)
##
## Call:
## glm(formula = dropout1 ~ ., family = "binomial", data = drop_dat)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1.1265595 0.9556823 -1.179 0.2385
## gender_agender 0.3519673 0.3396431 1.036 0.3001
## gender_not_sure 0.3402405 0.1911349 1.780 0.0751 .
## gender_other_please_specify -0.2544671 0.3329464 -0.764 0.4447
## gender_androgynous 0.1737942 0.2319843 0.749 0.4538
## gender_nonbinary -0.0975538 0.1828862 -0.533 0.5937
## gender_two_spirited -0.2538865 0.6957078 -0.365 0.7152
## gender_female_to_male_transgender_ftm -0.1902710 0.3378816 -0.563 0.5733
## gender_trans_female_trans_feminine -0.3975158 0.6297381 -0.631 0.5279
## gender_trans_male_trans_masculine 0.0045856 0.3441799 0.013 0.9894
## gender_gender_expansive -0.4966064 0.5822746 -0.853 0.3937
## gender_third_gender 0.5610380 0.9150772 0.613 0.5398
## gender_genderqueer 0.1308056 0.2427265 0.539 0.5900
## gender_male_to_female_transgender_mtf 0.5355085 0.6830419 0.784 0.4330
## gender_man_boy -0.0676839 0.2185922 -0.310 0.7568
## gender_transgender 0.1316265 0.3060697 0.430 0.6672
## gender_woman_girl -0.0771633 0.1724972 -0.447 0.6546
## race_american_indian_or_alaska_native 0.5570829 0.2467266 2.258 0.0240 *
## race_asian_including_asian_desi 0.1100817 0.1935428 0.569 0.5695
## race_hispanic_latinx 0.1191387 0.1677376 0.710 0.4775
## race_native_hawaiian_or_other_pacific_islander -0.3416961 0.4929787 -0.693 0.4882
## race_white_caucasian_non_hispanic_includes_middle_eastern 0.2468457 0.1657302 1.489 0.1364
## race_black_african_american -0.0415952 0.2034652 -0.204 0.8380
## race_other_specify 0.3813399 0.3768827 1.012 0.3116
## race_prefer_not_to_answer -0.6705623 0.7603591 -0.882 0.3778
## age -0.0476536 0.0567854 -0.839 0.4014
## CDI1 -0.1423414 0.2471832 -0.576 0.5647
## CTS1 0.0017235 0.0985556 0.017 0.9860
## GAD1 -0.0507514 0.0924135 -0.549 0.5829
## SHS1 0.0174072 0.0499594 0.348 0.7275
## BHS1 0.2132303 0.1010266 2.111 0.0348 *
## DRS1 0.0002739 0.1357147 0.002 0.9984
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 2290.4 on 2446 degrees of freedom
## Residual deviance: 2262.4 on 2415 degrees of freedom
## (5 Beobachtungen als fehlend gelöscht)
## AIC: 2326.4
##
## Number of Fisher Scoring iterations: 4
Von den 32 Tests der Regressionsgewichte sind insgesamt 2 statistisch bedeutsam, was zunächst nicht vielsagend wirkt (wenn man die 5% Irrtumswahrscheinlichkeit bedenkt). Oder etwas wissenschaftlicher ausgedrückt: nach Bonferroni-Holm Adjustierung liegt der niedrigste $p$-Wert der Regressionsgewichte bei 0.766. Auch die Confusion-Matrix, die wir im letzten Beitrag genutzt hatten, um die Güte des Modells genauer zu beurteilen, deutet darauf hin, dass wir nicht besonders gut in der Lage sind, den Dropout anhand der Baselinevariablen vorherzusagen (weil wir für beinahe alle Personen vorhersagen, dass sie zum 2. Zeitpunkt teilnehmen):
# Vorgesagte Werte
cope$dropout_pred <- predict(drop_mod, cope, type = 'response') > .5
cope$dropout_pred <- factor(cope$dropout_pred, labels = c('remain', 'dropout'))
# Confusion Matrix
caret::confusionMatrix(cope$dropout_pred, cope$dropout1)
## Confusion Matrix and Statistics
##
## Reference
## Prediction remain dropout
## remain 2012 434
## dropout 0 1
##
## Accuracy : 0.8226
## 95% CI : (0.8069, 0.8376)
## No Information Rate : 0.8222
## P-Value [Acc > NIR] : 0.4917
##
## Kappa : 0.0038
##
## Mcnemar's Test P-Value : <2e-16
##
## Sensitivity : 1.000000
## Specificity : 0.002299
## Pos Pred Value : 0.822567
## Neg Pred Value : 1.000000
## Prevalence : 0.822231
## Detection Rate : 0.822231
## Detection Prevalence : 0.999591
## Balanced Accuracy : 0.501149
##
## 'Positive' Class : remain
##
Umgang mit Dropouts
Dass sich Abbrecher*innen hinsichtlich ihrer Baselineeigenschaften kaum von Personen unterscheiden, die zum 2. Zeitpunkt teilgenommen haben, bietet jedoch keine Sicherheit, dass die Dropouts tatsächlich MCAR sind. Genausogut könnten die fehlenden Werte davon abhängen, dass die Personen die Intervention nicht gut fanden (und dementsprechend andere Effekte der Interventionen für sie gelten) oder durch andere Baseline-Kovariaten gesteuert sein, die einfach nicht erhoben wurden (z.B. Gewissenhaftigkeit). Üblicherweise werden daher in der Psychotherapieforschung mehrere Schätzer der Effekte bestimmt, welche eine Einengung des tatsächlichen Effekts erlauben sollen. Als “Obergrenze” wird dabei die Schätzung angesehen, die aus der Analyse der vollständigen Beobachtungen (sogenannte Complete Case Analysis, CCA) hervorgeht. Die Annahme ist dabei, dass Personen deren Outcomes besonders gut sind, dem Treatment treu bleiben. Dem gegenüber kann als “Untergrenze” die Analyse aller Personen angesehen werden, die mit dem Treatment begonnen haben (sogennantes Intent-to-Treat, ITT). Dabei stellt sich natürlich die Frage, welche Werte genutzt werden sollen, um die fehlenden Werte zu ersetzen. Eine der klassischen Methoden ist es, die zuletzt gemachte Beobachtung zu kopieren und somit für die Personen, die abgebrochen haben, anzunehmen, dass sie sich nicht verändert hätten. In der Psychotherapieforschung wird diese Methode oft als Last Observation Carried Forward (LOCF) bezeichnet. Neben diesen eher klassischen Methoden gibt es außerdem eine Vielzahl von modernen statistischen Verfahren, welche verwendet werden können, um bessere Schätzungen dieser fehlenden Werte zu erhalten. Im Artikel von Schleider et al. (2022) wird die multiple Imputation verwendet, die in R zum Beispiel im Paket Amelia oder mice implementiert ist. Andere Methoden sind zum Beispiel die Nutzung von Propensity scores (wie sie im dazugehörigen Beitrag vorgestellt werden) oder generalized estimating equations.
Hier werden wir uns erst einmal auf die klassischen Methoden beschränken und CCA und LOCF nutzen, um eine grobe Vorstellung von den Interventionseffekten zu bekommen. Die Umsetzung mit Amelia, die im Artikel von Schleider et al. (2022) durchgeführt wurde ist aber im entsprechenden Skript im OSF-Repo zu finden. Um LOCF auch umsetzen zu können, müssen wir einen Datensatz erstellen, in dem alle fehlenden Werte durch den vorangegangenen Wert ersetzt sind:
locf <- cope
# LOCF, post-intervention
locf$SHS2 <- ifelse(is.na(locf$SHS2), locf$SHS1, locf$SHS2)
locf$BHS2 <- ifelse(is.na(locf$BHS2), locf$BHS1, locf$BHS2)
# LOCF, follow-up
locf$CDI3 <- ifelse(is.na(locf$CDI3), locf$CDI1, locf$CDI3)
locf$CTS3 <- ifelse(is.na(locf$CTS3), locf$CTS1, locf$CTS3)
locf$GAD3 <- ifelse(is.na(locf$GAD3), locf$GAD1, locf$GAD3)
locf$SHS3 <- ifelse(is.na(locf$SHS3), locf$SHS2, locf$SHS3)
locf$BHS3 <- ifelse(is.na(locf$BHS3), locf$BHS2, locf$BHS3)
locf$DRS3 <- ifelse(is.na(locf$DRS3), locf$DRS1, locf$DRS3)
Hier nutzen wir ifelse, um zu prüfen, ob auf einer Variable ein fehlender Wert vorliegt. Wenn dem so ist (zweites Argument) wird der Wert durch den Wert der vorherigen Messung ersetzt, ansonsten durch den beobachteten Werte (drittes Argument).
ANCOVA
Nachdem wir uns nun ausführlich mit dem Problem des Dropouts beschäftigt haben, kommen wir zum eigentlich Punkt dieses Beitrags zurück. Mit der ANCOVA können wir Gruppenunterschiede testen, während wir gleichzeitig auf Kovariaten kontrollieren. Häufig ist dabei der Wert des Outcomes zur Baseline die zentrale Kovariate, aber letztlich ist jede Kovariate dabei denkbar. Im Artikel von Schleider et al. (2022) werden anhand verschiedener ANCOVAs die Effekt der Intervention auf dem Primär- und allen Sekundäroutcomes überprüft. Die Ergebnisse werden allerdings nicht im Artikel selbst, sondern in der Supplementary Information berichtet.
Wir können uns hier zunächst auf das Primäroutcome konzentrieren und werden dabei auch ein wenig vom Vorgehen von Schleider et al. (2022) abweichen. Zum Einen haben wir nicht mit der Multiple Imputation gearbeitet, zum Anderen werden wir auch noch die generalisierte ANCOVA nutzen, um zu untersuchen, ob die unterschiedlichen Interventionen differentielle Effekte aufweisen. Zunächst aber die klassische ANCOVA.
Im Artikel wird die ANCOVA genutzt, um sicherzustellen, dass die Unterschiede zwischen den Gruppen bedingt auf die Werte zum ersten Zeitpunkt interpretiert werden können. Gucken wir uns am besten genauer an, was ich damit meine:
# ANOVA model
mod1 <- lm(CDI3 ~ condition, cope)
# Ergebniszusammenfassung
summary(mod1)
##
## Call:
## lm(formula = CDI3 ~ condition, data = cope)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.02153 -0.28108 -0.01913 0.31180 1.06420
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.02153 0.01858 54.967 < 2e-16 ***
## conditionProject Personality -0.06424 0.02662 -2.413 0.01594 *
## conditionProject ABC -0.08573 0.02619 -3.273 0.00109 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4185 on 1500 degrees of freedom
## (949 Beobachtungen als fehlend gelöscht)
## Multiple R-squared: 0.007637, Adjusted R-squared: 0.006314
## F-statistic: 5.772 on 2 and 1500 DF, p-value: 0.003183
Im klassischen ANOVA-Modell als Prädiktor genutzt, um die abhängige Variable vorherzusagen. Die jeweilige Regressionsgewichte sind also die mittleren Gruppenunterschiede (zur Äquivalenz von ANOVA und Regression gibt es hier noch einen expliziten Beitrag). Das heißt, wenn wir die Gruppenmittelwerte des CDI zur Baseline betrachten:
# Gruppenmittelwerte zur Baseline
tapply(cope$CDI1, cope$condition, mean)
## Placebo Control Project Personality Project ABC
## 1.192274 1.184912 1.178755
dass wir Personen aus der Kontrollgruppe nutzen, die einen CDI1-Wert von $1.19$ hatten, wärend die Personen aus Project ABC einen Wert von $1.18$ hatten. Dieser Unterschied mag numerisch klein wirken, aber wir vergleichen eben (aufgrund des Dropouts) leicht unterschiedliche Personen miteinander. In der ANCOVA ziehen wir zusätzlich den CDI-Wert aus der Baselinebefragung als Prädiktor heran:
# Einfache ANCOVA
mod2 <- lm(CDI3 ~ CDI1 + condition, cope)
# Ergebniszusammenfassung
summary(mod2)
##
## Call:
## lm(formula = CDI3 ~ CDI1 + condition, data = cope)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.1849 -0.2145 0.0147 0.2341 1.0395
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.28877 0.03473 8.314 < 2e-16 ***
## CDI1 0.63254 0.02668 23.712 < 2e-16 ***
## conditionProject Personality -0.07184 0.02271 -3.163 0.001592 **
## conditionProject ABC -0.08561 0.02234 -3.831 0.000133 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.357 on 1499 degrees of freedom
## (949 Beobachtungen als fehlend gelöscht)
## Multiple R-squared: 0.2783, Adjusted R-squared: 0.2769
## F-statistic: 192.7 on 3 and 1499 DF, p-value: < 2.2e-16
Der deutliche Sprung im $R^2$ weist darauf hin, dass die Depressionsymptomatik über die Zeit deutlich korreliert ist. Wie immer in der multiplen Regression ist der Effekt der Prädiktoren jetzt unter der Bedingungen zu interpretieren, dass die Werte auf den anderen Prädiktoren konstant sind. Heißt in unserem Fall, dass wir hier nun im Regressionsgewicht von Project Personality den Unterschied zwischen Personen aus den beiden Gruppen sehen, die mit dem gleichen BDI zur Baseline gestartet sind. Als Bild ausgedrückt:

CDI1 der Gleiche - wir können den Abstand der Linien an jeden Punkt bestimmen und es sind immer die Regressionsgewichte aus mod2. In der ANOVA hingegen haben wir konkret die drei eingezeichneten Punkte verglichen, die sich nicht nur deswegen unterscheiden, weil die Linien (die bedingten Gruppenmittelwerte) um $b_2$ bzw. $b_3$ versetzt sind, sondern auch, weil wir an unterschiedlichen Stellen der x-Achse nachgucken. In diesem Fall ist der Unterschied zwischen beiden zwar minimal (weil es sich um einen immens großen RCT handelt), aber prinzipiell könnten wir so auf diese Unterschiede kontrollieren.
Im Abgleich der Wege die fehlenden Werte zu behandeln, können wir die ANCOVA auch noch einmal für den locf Datensatz durchführen:
# Modell mit Last-Observation-Carried-Forward
mod2_locf <- lm(CDI3 ~ CDI1 + condition, locf)
# Ergebniszusammenfassung
summary(mod2_locf)
##
## Call:
## lm(formula = CDI3 ~ CDI1 + condition, data = locf)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.30808 -0.13580 0.07954 0.17221 1.05887
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.16312 0.02383 6.846 9.55e-12 ***
## CDI1 0.79201 0.01790 44.249 < 2e-16 ***
## conditionProject Personality -0.04305 0.01501 -2.869 0.004159 **
## conditionProject ABC -0.05722 0.01497 -3.821 0.000136 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3031 on 2448 degrees of freedom
## Multiple R-squared: 0.4471, Adjusted R-squared: 0.4465
## F-statistic: 660 on 3 and 2448 DF, p-value: < 2.2e-16
Oder für die optischeren unter uns:

CDI1 und CDI3 deutlich größer wird. Das überrascht wenig, wenn man bedenkt, dass wir für einige Personen den Werte aus der ersten einfach in die zweite Variable kopiert haben. Eine Überschätzung der Stabilität liegt also in der Natur der Sache. Es wird außerdem deutlich, dass der Effekt der Interventionen deutlich kleiner geworden ist, weil wir für die fehlenden Personen eine Veränderung von 0 angenommen haben. Die Schlussfolgerungen bleiben dennoch erhalten: beide Interventionen haben einen statistisch bedeutsamen Effekt über die Plazebo-Kontrollbedingung hinaus.
Change-Modelle
Eine naheliegende Alternative zu den ANCOVA Modellen ist es, statt des zweiten Zeitpunkts die Veränderung zwischen den Zeitpunkten $Y_2 - Y_1$ durch Kovariaten vorherzusagen. Mit dem Vergleich dieser, sogenannten “Change-Modelle” mit der ANCOVA haben sich diverse Studien und methodische Arbeiten befasst. Ein klassisches Argument gegen die ANCOVA ist Lord’s Paradox, in dem es zu unterschiedlichen Ergebnissen kommt, je nachdem ob man eine Veränderung mit einer ANCOVA oder einem Veränderungsmodell analysiert, wenn die Gruppen sich zum 1. Messzeitpunkt unterscheiden.
Lord's Paradox
Im ursprünglichen Kommentar von Lord (1967) wird eine Situation beschrieben, in der eine Universität ihr Mensa-Essen evaluieren möchte. Dazu wird das Gewicht von Männern und Frauen zu Beginn des Wintersemesters und zum Ende des folgenden Sommersemesters erhoben. Nehmen wir als extremes Beispiel, dass beide Gruppen im Mittel 5kg zugelegt hätten:
# Seed festlegen
set.seed(123)
# Werte Frauen
y1f <- rnorm(100, 70, 10)
y2f <- 5 + .5*y1f + rnorm(100, 35, sqrt(75))
# Werte Männer
y1m <- rnorm(100, 80, 10)
y2m <- 5 + .5*y1m + rnorm(100, 40, sqrt(75))
# Datensatz
d <- data.frame(y1 = c(y1f, y1m), y2 = c(y2f, y2m),
g = rep(c('f', 'm'), each = 100))
In den Termini des bisherigen Beitrags ist das Geschlecht die Gruppen-Zuweisung. Wenn wir also untersuchen wollen, ob es einen Effekt der Variable Geschlecht gibt und dabei eventuelle Unterschiede in der Baseline berücksichtigen wollen (die es ja gibt), finden wir einen signifikanten Effekt:
# ANCOVA
lord_ancova <- lm(y2 ~ y1 + g, d)
summary(lord_ancova)
##
## Call:
## lm(formula = y2 ~ y1 + g, data = d)
##
## Residuals:
## Min 1Q Median 3Q Max
## -21.144 -5.735 -0.255 5.707 28.513
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 42.1819 4.7876 8.811 6.48e-16 ***
## y1 0.4561 0.0664 6.869 8.26e-11 ***
## gm 6.0700 1.4081 4.311 2.57e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 8.703 on 197 degrees of freedom
## Multiple R-squared: 0.3858, Adjusted R-squared: 0.3795
## F-statistic: 61.86 on 2 and 197 DF, p-value: < 2.2e-16
Die ANCOVA würde uns also zurückmelden, dass das Geschlecht selbst nach Kontrolle auf die Baselineunterschiede einen signifikanten Effekt auf die Gewichtszunahme hat. Wenn wir aber die Veränderung zwischen den Zeitpunkten betrachten, finden wir keinen signifikanten Effekt:
# Change-Modell
lord_change <- lm(y2 - y1 ~ g, d)
summary(lord_change)
##
## Call:
## lm(formula = y2 - y1 ~ g, data = d)
##
## Residuals:
## Min 1Q Median 3Q Max
## -23.779 -6.559 0.180 6.187 34.545
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.6166 1.0052 3.598 0.000405 ***
## gm 0.4674 1.4215 0.329 0.742656
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 10.05 on 198 degrees of freedom
## Multiple R-squared: 0.0005457, Adjusted R-squared: -0.004502
## F-statistic: 0.1081 on 1 and 198 DF, p-value: 0.7427
Frauen verändern sich bedeutsam (im Intercept dargestellt) und die Veränderung der Männer unterscheidet sich nicht bedeutsam (im Regressionsgewicht dargestellt). Dieses Artefakt wird seither als Lord’s Paradox bezeichnet.
Wenn wir einen Change-Ansatz nutzen möchten, um die Effekte der Interventionen auf das primäre Outcome (den CDI Depressionsscore) zu untersuchen, sieht das relativ einfach so aus:
# Change-Modell
mod3 <- lm(CDI3 - CDI1 ~ condition, cope)
# Ergebniszusammenfassung
summary(mod3)
##
## Call:
## lm(formula = CDI3 - CDI1 ~ condition, data = cope)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.28683 -0.19642 0.04651 0.22245 1.22025
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.13692 0.01682 -8.139 8.26e-16 ***
## conditionProject Personality -0.07626 0.02410 -3.165 0.001583 **
## conditionProject ABC -0.08554 0.02371 -3.608 0.000319 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3788 on 1500 degrees of freedom
## (949 Beobachtungen als fehlend gelöscht)
## Multiple R-squared: 0.01025, Adjusted R-squared: 0.008929
## F-statistic: 7.766 on 2 and 1500 DF, p-value: 0.0004412
Numerisch sind die Effekte der beiden Gruppen beinahe identisch. Allerdings ist die inhaltliche Interpretation ein wenig unterschiedlich: in der ANCOVA war die Bedeutung des Regressionsgewichts von Project Personality, dass es den Unterschied zwischen Personen aus der Kontrollgruppe und dieser Gruppe zum zweiten Zeitpunkt beschreibt, wenn sie zum ersten Zeitpunkt den gleichen CDI Wert hatten. Im Change-Modell beschreibt das Regressionsgewicht hingegen den Unterschied zwischen zwei Personen aus den beiden Gruppen hinsichtlich ihrer Veränderung zwischen dem 1. und dem 2. Messzeitpunkt. Wenn wir dieses Modell jetzt in eine ANOVA überführen:
# Change zur ANOVA
anova(mod3)
## Analysis of Variance Table
##
## Response: CDI3 - CDI1
## Df Sum Sq Mean Sq F value Pr(>F)
## condition 2 2.228 1.11414 7.766 0.0004412 ***
## Residuals 1500 215.195 0.14346
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Entspricht der Test der condition genau dem Test, den wir für den Interaktionseffekt in der Messwiederholten ANOVA erhalten hätten. (Probieren Sie es gerne mit der Messwiederholten ANOVA aus!) Letztlich ist die Entscheidung zwischen Change-Model oder ANCOVA also die gleiche wie die zwischen Messwiederholter ANOVA und ANCOVA.
Wenn Sie eine Interventionsstudie durchführen, für welchen der beiden Ansätze sollten Sie sich jetzt also Entscheiden? Generell gibt es ein paar handfeste Empfehlungen: van Breukelen (2013) konnte zeigen, dass beide Ansätze zu den gleichen Ergebnissen führen, wenn die Gruppen randomisiert zugewiesen werden, in solchen Fällen aber die ANCOVA mehr Power hat. Wenn “natürliche” Gruppen verglichen werden, die sich in der Variable vor der Intervention unterscheiden können und die Kovariaten mit Messfehler behaftet sind, wird generell empfohlen den Change-Ansatz zu verwenden. Lüdtke und Robitzsch (2023) zeigen darüber hinaus, dass der Change-Ansatz dann genutzt werden sollte, wenn nicht alle potentiellen Kovariaten erhoben wurden, weil es in diesem Ansatz (unter der Annahme, dass die Konfundierung zu allen Zeitpunkten identisch ist) durch die Bildung der Differenz nicht notwendig ist, alle Kovariaten in das Modell aufzunehmen. Allerdings wird dabei Vorausgesetzt, dass das Outcome zum 1. Messzeipunkt keine Auswirkung auf die Gruppenzuordnung hat. In Fällen, in denen vorab eine sinnvolle und stichhaltige Erhebung potentieller Störvariablen geplant wurde, ist die Nutzung der ANCOVA empfehlenswert, sofern sie nicht aufgrund von Baselineunterschieden in Variablen mit fehlenden Werte zu potentiellen Problemen des Lord’s Paradox führt.
Generalisierte ANCOVA
Die oben vorgestellte ANCOVA lässt sich nach Belieben um mehr Kovariaten erweitern. Das sollte (wie gerade besprochen) auch passieren, da sie besonders dann gut geeignet ist, wenn auf viele relevante Störvariablen kontrolliert werden kann. Dabei gehen wir bereits etwas über die ursprüngliche Auswertung von Schleider et al. (2022) hinaus, die nur die Baselinevariable als Kovariate genutzt hatten. Das Besondere an der ANCOVA ist darüber hinaus aber, dass wir sie in den Fall der generalisierten ANCOVA erweitern können.
Im vorherigen Abschnitt zur ANCOVA hatten wir angenommen, dass Kovariaten den Effekt eventuell verzerren könnten und sie daher aufgenommen, um einen “bereinigten” Effektschätzer der Intervention zu erhalten. Dabei wird allerdings (wie an den parallelen Linien zu sehen war) davon ausgegangen, dass der Interventionseffekt bei allen Ausprägungen der Kovariate der Gleiche ist. Diese Annahme lässt sich prüfen, indem wir einen Interaktionseffekt in die ANCOVA aufnehmen. Dafür gilt, wie schon im Beitrag zur moderierten Regression, dass wir kontinuierliche Variablen unbedingt zentrieren sollten. Das hilft zum Einen bei der Interpretaion, aber kann auch Multikollinearität verringern.
# Zenrierung der Kovariate
cope$CDI1_c <- scale(cope$CDI1, scale = FALSE)
# Generalisierte ANCOVA
mod4 <- lm(CDI3 ~ CDI1_c * condition, cope)
# Ergebniszusammenfassung
summary(mod4)
##
## Call:
## lm(formula = CDI3 ~ CDI1_c * condition, data = cope)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.18191 -0.21888 0.01634 0.23083 1.03391
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.03821 0.01591 65.270 < 2e-16 ***
## CDI1_c 0.62109 0.04581 13.557 < 2e-16 ***
## conditionProject Personality -0.07191 0.02276 -3.160 0.001612 **
## conditionProject ABC -0.08427 0.02242 -3.759 0.000178 ***
## CDI1_c:conditionProject Personality -0.01406 0.06499 -0.216 0.828708
## CDI1_c:conditionProject ABC 0.04964 0.06546 0.758 0.448373
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3571 on 1497 degrees of freedom
## (949 Beobachtungen als fehlend gelöscht)
## Multiple R-squared: 0.2788, Adjusted R-squared: 0.2764
## F-statistic: 115.8 on 5 and 1497 DF, p-value: < 2.2e-16
Die Ergebnisse zeigen keine bedeutsamen Interaktionseffekte. Das bedeutet also, dass die Interventionen in ihrer Wirksamkeit nicht statistisch bedeutsam davon abhängen, mit welchem Depressionsscore die Personen die Studie gestartet haben.
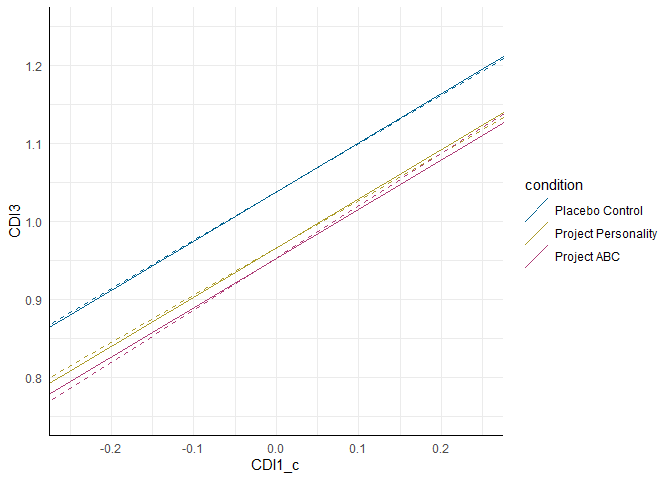
Erneut sind sowohl optisch als auch numerisch die Unterschiede zwischen den Interventionsansätzen minimal. Dennoch sehen wir, dass im Bereich der unterdurchschnittlichen CDI1-Werte Teilnehmende des Project ABC niedrigere Depressionswerte zum Follow-Up aufweisen, während sich dieser Effekt bei überdurchschnittlichen Werten zugunsten von Project Personality verschiebt. Um diese Effekte zu testen, können wir in unserem Modell die CDI1-Variable so transformieren, dass die Gruppenunterschiede sich auf andere Ausprägungen dieser Variable beziehen. Z.B.:
# Effekt bei überdurchschnittlicher Kovariate
cope$CDI1_above <- cope$CDI1_c + sd(cope$CDI1_c)
mod4b <- lm(CDI3 ~ CDI1_above * condition, cope)
summary(mod4b)
##
## Call:
## lm(formula = CDI3 ~ CDI1_above * condition, data = cope)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.18191 -0.21888 0.01634 0.23083 1.03391
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.82577 0.02145 38.502 < 2e-16 ***
## CDI1_above 0.62109 0.04581 13.557 < 2e-16 ***
## conditionProject Personality -0.06710 0.03086 -2.175 0.029809 *
## conditionProject ABC -0.10125 0.03041 -3.329 0.000893 ***
## CDI1_above:conditionProject Personality -0.01406 0.06499 -0.216 0.828708
## CDI1_above:conditionProject ABC 0.04964 0.06546 0.758 0.448373
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3571 on 1497 degrees of freedom
## (949 Beobachtungen als fehlend gelöscht)
## Multiple R-squared: 0.2788, Adjusted R-squared: 0.2764
## F-statistic: 115.8 on 5 and 1497 DF, p-value: < 2.2e-16
# Effekt bei unterdurchschnittlicher Kovariate
cope$CDI1_below <- cope$CDI1_c - sd(cope$CDI1_c)
mod4c <- lm(CDI3 ~ CDI1_below * condition, cope)
summary(mod4c)
##
## Call:
## lm(formula = CDI3 ~ CDI1_below * condition, data = cope)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.18191 -0.21888 0.01634 0.23083 1.03391
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.25065 0.02318 53.964 <2e-16 ***
## CDI1_below 0.62109 0.04581 13.557 <2e-16 ***
## conditionProject Personality -0.07672 0.03275 -2.343 0.0193 *
## conditionProject ABC -0.06729 0.03291 -2.045 0.0411 *
## CDI1_below:conditionProject Personality -0.01406 0.06499 -0.216 0.8287
## CDI1_below:conditionProject ABC 0.04964 0.06546 0.758 0.4484
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3571 on 1497 degrees of freedom
## (949 Beobachtungen als fehlend gelöscht)
## Multiple R-squared: 0.2788, Adjusted R-squared: 0.2764
## F-statistic: 115.8 on 5 and 1497 DF, p-value: < 2.2e-16
In Fällen, in denen solche Effekte deutlicher ausfallen, könnten wir diese Ergebnisse heranziehen, um z.B. für Patient*innen mit hoher Belastung eine Intervention zu empfehlen, für Patient*innen mit niedrigerer Belastung aber eine Andere.
Literatur
Lord, F. M. (1967). A Paradox in the Interpretation of Group Comparisons. Psychological Bulletin 68(5), 304-305. https://doi.org/10.1037/h0025105.
Lüdtke, O. & Robitzsch, A. (2023). ANCOVA versus Change Score for the Analysis of Two-Wave Data. The Journal of Experimental Education, 1–33. https://doi.org/10.1080/00220973.2023.2246187
Schleider, J.L., Mullarkey, M.C., Fox, K.R., Dobias, M. L., Shroff, A., Hart, E. A. & Roulston, C. A. (2022). A randomized trial of online single-session interventions for adolescent depression during COVID-19. Nature Human Behavior, 6, 258–268. https://doi.org/10.1038/s41562-021-01235-0
van Breukelen, G. J. P. (2013). ANCOVA Versus CHANGE From Baseline in Nonrandomized Studies: The Difference. Multivariate Behavioral Research, 48(6), 895–922. https://doi.org/10.1080/00273171.2013.831743
](/media/header/canceled.jpg)