Einleitung
In dieser Sitzung schauen wir uns die Unterschiede und Gemeinsamkeiten von ANOVA und Regression an. Vielleicht ist es Ihnen auch schon einmal untergekommen, dass Ihnen gesagt wurde: ANOVA und Regression ist doch alles dasselbe — alles nur das allgemeine lineare Modell (ALM). Diese Aussage ist im Grunde auch richtig und wir schauen uns diesen Sachverhalt im Folgenden genauer an.
Diese Sitzung basiert auf Literatur aus Eid et al. (2017) Kapitel 11 und 13 sowie Kapitel 16 bis 19.
Daten laden
Im Gegensatz zu den vorherigen Sitzungen wollen wir einen Datensatz direkt aus dem Open Science Framwork (OSF) laden. Dort werden Unterlagen im Sinne der Open-Sience-Initiative abgelegt. In diesem Fall nutzen wir einen Datensatz von Schaeuffele et al. (2020), die den Effekt des Unified Protocol (UP) als Internetintervention für bestimmte psychische Störungen durchgeführt haben. Die OSF-Daten finden wir hier. Wenn wir dort zum Datensatz navigieren, können wir das “csv”-File direkt in R einbinden, ohne es auf unserem Rechner ablegen zu müssen — wie als würde der Datensatz auf PandaR liegen. Der nötige Befehl lautet read.csv, mit dem wir auch ein lokales “csv”-File einlesen können. Wir müssen der Funktion lediglich den Link zum downloadbaren “csv”-File übergeben. Der Vollständigkeit halber sagen wir R dann noch, dass es sich um einen Dateipfad ins Internet handelt, indem wir die url-Funktion darauf anwenden. Wir nennen die eingelesenen Daten unglaublich einfallsreich einfach mal osf und schauen uns die Variablen des Datensatzes mit names an.
osf <- read.csv(file = url("https://osf.io/zc8ut/download"))
names(osf)
## [1] "X" "ID" "group"
## [4] "stratum" "bsi_pre" "bsi_mid"
## [7] "bsi_post" "bsi_fu" "bsi_fu2"
## [10] "panas_pa_pre" "panas_pa_mid" "panas_pa_post"
## [13] "panas_pa_fu" "panas_pa_fu2" "panas_na_pre"
## [16] "panas_na_mid" "panas_na_post" "panas_na_fu"
## [19] "panas_na_fu2" "swls_pre" "swls_mid"
## [22] "swls_post" "swls_fu" "swls_fu2"
## [25] "phq9_pre" "phq9_post" "gad7_pre"
## [28] "gad7_post" "lsas_pre" "lsas_post"
## [31] "lsas_anx_pre" "lsas_anx_post" "lsas_avo_pre"
## [34] "lsas_avo_post" "pas_pre" "pas_post"
## [37] "shai_anx_pre" "shai_anx_post" "shai_neg_pre"
## [40] "shai_neg_post" "phq15_pre" "phq15_post"
## [43] "NEQ_1_A" "NEQ_1_B" "NEQ_1_C"
## [46] "NEQ_2_A" "NEQ_2_B" "NEQ_2_C"
## [49] "NEQ_3_A" "NEQ_3_B" "NEQ_3_C"
## [52] "NEQ_4_A" "NEQ_4_B" "NEQ_4_C"
## [55] "NEQ_5_A" "NEQ_5_B" "NEQ_5_C"
## [58] "NEQ_6_A" "NEQ_6_B" "NEQ_6_C"
## [61] "NEQ_7_A" "NEQ_7_B" "NEQ_7_C"
## [64] "NEQ_8_A" "NEQ_8_B" "NEQ_8_C"
## [67] "NEQ_9_A" "NEQ_9_B" "NEQ_9_C"
## [70] "NEQ_10_A" "NEQ_10_B" "NEQ_10_C"
## [73] "NEQ_11_A" "NEQ_11_B" "NEQ_11_C"
## [76] "NEQ_12_A" "NEQ_12_B" "NEQ_12_C"
## [79] "NEQ_13_A" "NEQ_13_B" "NEQ_13_C"
## [82] "NEQ_14_A" "NEQ_14_B" "NEQ_14_C"
## [85] "NEQ_15_A" "NEQ_15_B" "NEQ_15_C"
## [88] "NEQ_16_A" "NEQ_16_B" "NEQ_16_C"
## [91] "NEQ_17_A" "NEQ_17_B" "NEQ_17_C"
## [94] "NEQ_18_A" "NEQ_18_B" "NEQ_18_C"
## [97] "NEQ_19_A" "NEQ_19_B" "NEQ_19_C"
## [100] "NEQ_20_A" "NEQ_20_B" "NEQ_20_C"
## [103] "csq8_1" "csq8_2" "csq8_3"
## [106] "csq8_4" "csq8_5" "csq8_6"
## [109] "csq8_7" "csq_8" "completed_modules"
## [112] "logins_after_allocation" "sent_messages" "received_messages"
## [115] "exercises_total" "time_spent_after_allocation_hours" "exercises_per_login"
Das sind sehr viele Variablen. Wir beschränken uns in dieser und in der folgenden Sitzung auf einige wenige Variablen, die nach dem Durchführen des Treatments erhoben wurden: ID (Teilnehmendennummer), group (Gruppenzugehörigkeit: Wartelistenkontrollgruppe vs. Treatmentgruppe), stratum (Krankheitsbild: Angststörung [ANXiety], Depression [DEPression] oder somatische Belastungsstörung [SOMatic symptom disorder]), bsi_post (Symptomschwere), swls_post (Lebenszufriedenheit [Satisfaction With Life Screening]) und pas_post (Panikstörung und Agoraphobie [Panic and Agoraphobia Screening]). Wir kürzen entsprechend den Datensatz und schauen ihn uns mit head an:
osf <- osf[, c("ID", "group", "stratum", "bsi_post", "swls_post", "pas_post")]
head(osf)
## ID group stratum bsi_post swls_post pas_post
## 1 1 Treatment DEP 2 29 1
## 2 2 Treatment ANX 11 22 7
## 3 3 Treatment ANX 22 6 1
## 4 4 Treatment DEP 2 23 3
## 5 5 Treatment ANX NA NA NA
## 6 6 Treatment ANX NA NA NA
Wir erkennen direkt, dass es einige fehlende Werte auf den Variablen gibt. Der Einfachheit halber entfernen wir diese Missings. Wir führen also den listenweisen Fallausschluss (engl. list-wise deletion) durch. Dieser darf allerdings nur gemacht werden, wenn die fehlenden Werte rein zufällig passiert sind (missing completely at random!). Allerdings sei erwähnt, dass der listenweise Fallausschluss natürlich die Stichprobengröße verringert und dadurch die Power der Analysen reduziert. Aus Illustrationszwecken wollen wir uns damit nicht weiter aufhalten.
dim(osf) # vorher
## [1] 129 6
osf <- na.omit(osf)
dim(osf) # nach Fallauschluss
## [1] 94 6
Der Befehl na.omit führt den listenweisen Fallausschluss für uns durch. Achtung: Das sollte nicht als Standardvorgehen gemacht werden. Wir sollten uns bei einer “echten” Analyse genau Gedanken machen, wie die Missings aufgetreten sein können und uns überlegen, ob es nicht Möglichkeiten gibt, alle verfügbaren Informationen zu nutzen.
Regression: Modellvergleiche
In der vorherigen Sitzung haben wir noch einmal die Regressionsanalyse wiederholt. Wenn wir beispielsweise wissen möchten, ob nach dem Treatment die Symptomschwere mit der Lebenszufriedenheit oder der Ausprägung einer möglichen Panikstörung mit oder ohne Agoraphobie zusammenhängt, wissen wir nun, wie wir dies untersuchen können:
reg <- lm(bsi_post ~ 1 + swls_post + pas_post, data = osf)
summary(reg)
##
## Call:
## lm(formula = bsi_post ~ 1 + swls_post + pas_post, data = osf)
##
## Residuals:
## Min 1Q Median 3Q Max
## -16.427 -4.201 -1.023 4.574 21.560
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 20.98937 2.44425 8.587 2.30e-13 ***
## swls_post -0.57053 0.11068 -5.155 1.47e-06 ***
## pas_post 0.53832 0.07204 7.472 4.68e-11 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 7.209 on 91 degrees of freedom
## Multiple R-squared: 0.5272, Adjusted R-squared: 0.5168
## F-statistic: 50.73 on 2 and 91 DF, p-value: 1.584e-15
Offensichtlich tragen beide Prädiktoren signifikant zur Varianzerklärung des Kriteriums bei. Damit können wir für die Population (mit einer Irrtumswahrscheinlichkeit von
$5\%$) konkludieren, dass höhere Symptomschwere mit geringerer Lebenszufriedenheit und höherer Panik- und Agoraphobiesymptomatik assoziiert ist. Dies haben wir an den Parametertests und den zugehörigen $t$-Tests abgelesen. Allerdings können wir auch Sets von Prädiktoren auf signifikante Vorhersagekraft testen. Bspw. können wir untersuchen, ob die beiden Prädiktoren gemeinsam Varianz an der Symptomschwere erklären. Dazu müssen wir quasi ein leeres Regressionsmodell aufstellen, welches nur ein Interzept enthält. Nennen wir dieses mal reg0. Anschließend können wir die beiden Modelle mit dem anova-Befehl vergleichen. Dieser führt dann den sogenannten $F$-Test durch:
reg0 <- lm(bsi_post ~ 1, data = osf)
anova(reg0, reg)
## Analysis of Variance Table
##
## Model 1: bsi_post ~ 1
## Model 2: bsi_post ~ 1 + swls_post + pas_post
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 93 10001
## 2 91 4729 2 5272.2 50.726 1.584e-15 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Der anova-Output sagt uns zunächst, welche beiden Modelle miteinander verglichen wurden. Diese werden hier Model 1 und Model 2 genannt. Anschließend erhalten wir für den Modellvergleich Informationen über die Residualfreiheitsgrade (Res.Df), die Residualquadratsumme (RSS, Residual Sum of Squares), die Freiheitsgrade des Modellvergleichs (Df; entspricht der Differenz der Res.Df zwischen Modellen!), die Differenz der Quadratsummen (Sum of Sq), den empirischen $F$-Wert (F) sowie den zugehörigen $p$-Wert (Pr(>F)). Aus den ersten vier Informationen können wir den $F$-Wert bestimmen. Die Residualfreiheitsgrade sind $n-(p+1)$, wobei $n$ die Stichprobengröße und $p$ die Anzahl an Variablen im Modell ist. Somit ist $p+1$ gerade die Anzahl an Parametern ($\beta$s), wenn es ein Interzept gibt. Die Residualquadratsumme ist die quadratische Summe der Regressionsresiduen: $RSS := \sum_{i=1}^n ( y_i - \hat{y}_i)^2$, wobei die Regressionsresiduen $\hat{e}_i:= y_i - \hat{y}_i$ sind. Die Freiheitsgrade entsprechen der Anzahl an Parametern, um welche sich die beiden Modelle unterscheiden. Da das eine Modell nur aus einem Interzept besteht und im zweiten zwei Variablen (also zwei Steigungskoeffizienten) enthalten sind, gilt Df = 2. Die Differenz der Quadratsumme entspricht der erklärten Quadratsumme, die auf das Hinzufügen der Variablen in das Modell zurückzuführen ist. Wenn Sie sich den Determinationskoeffizienten wieder ins Gedächtnis rufen, erinnern Sie sich, dass dieser dem Anteil erklärter Varianz entspricht. Der Determinationskoeffizinet lässt sich auch anders beschreiben, er ist quasi der Anteil der erklärten Quadratsumme an der totalen Quadratsumme. Wir berechnen diesen schnell per Hand, indem wir das anova-Objekt abspeichern und die entsprechenden Informationen entnehmen.
anova0 <- anova(reg0, reg)
R2 <- anova0$`Sum of Sq`[2] / anova0$RSS[1]
R2 # R^2 mit Hand
## [1] 0.5271566
summary(reg)$r.squared # R^2 aus dem lm-Objekt
## [1] 0.5271566
var(predict(reg))/var(osf$bsi_post) # über die Vorhersage von Werten mittels "predict"
## [1] 0.5271566
Mit predict erhalten wir den vorhergesagten Wert $\hat{y}_i$ für jede Erhebung (sozusagen den bedingten Erwartungswert gegeben die Prädiktoren). Wir erkennen, dass $R^2$ nichts anderes ist als der Quotient aus der Varianz der vorhergesagten Werte und der Varianz des Kriteriums ($R^2\hat{=}\frac{\mathbb{V}ar[\hat{Y}]}{\mathbb{V}ar[Y]}$).
Der $F$-Wert entsteht, indem wir $R^2$ für zwei Modelle miteinander vergleichen. Dabei sei $R^2_u$ das $R^2$ des uneingeschränkten Modells mit mehr Prädiktoren und $R^2_e$ das eingeschränkte $R^2$ mit weniger Prädiktoren. Dann ist
$$F := \frac{(R^2_u-R^2_e)/df_h}{(1-R^2_u)/df_e},$$
wobei $df_h (=p_u-p_e)$ den Hypothesenfreiheitsgraden (Df oben) und $df_e (=n-p_u-1)$ den Fehlerfreiheitsgraden (Res.Df oben) des uneingeschränkten Modells entspricht. Dabei ist $p_u$ bzw. $p_e$ die Anzahl der Prädiktoren (auch Parameter) im jeweiligen Modell. Ist das eingeschränkte Modell das Null-Modell ohne Prädiktoren, so gilt $R^2_e=0$, was die Formel nochmals vereinfacht. $1-R^2_u$ ist der Anteil unerklärter Varianz im uneingeschränkten Modell — also der Anteil der Residualvarianz an der Gesamtvarianz. Entsprechend bekommen wir den empirischen $F$-Wert (R2 von oben entspricht $R^2_u$):
F_emp <- (R2/2)/((1-R2)/91)
F_emp # empirischer F-Bruch mit Hand
## [1] 50.72637
anova0$F[2] # empirischer F-Bruch aus anova-Objekt
## [1] 50.72637
Der $F$-Wert ist genau dann groß, wenn das Varianzinkrement im Vergleich zur Fehlervarianz groß ist, also wenn der Effekt relativ zur zufälligen Streuung in den Daten groß ist.
Der Vergleich gegen das Null-Modell wird in jeder summary mit ausgegeben. Dies ist der $F$-Test, der im Output ganz am Ende ausgegeben wird. Dieser testet das multiple $R^2$ gegen 0 und ist damit ein Omnibustest für alle Prädiktoren gemeinsam im Modell.
Regression: Kategoriale Prädiktoren
Wir können in ein Regressionsmodell auch kategoriale Prädiktoren aufnehmen. Das haben wir bereits in der vergangenen Sitzung gemacht, indem wir das Geschlecht mit in die Gleichung aufgenommen haben. Der Default in R ist, dass Dummyvariablen verwendet werden, um Gruppenzugehörigkeiten auszudrücken. So kann erreicht werden, dass Abweichungen zu einer Referenzkategorie kodiert werden können. Wir sagen die Symptomschwere durch die Gruppenvariable, die die Zuweisung zum Treatment enthält, vorher. Zunächst müssen wir sichergehen, dass es sich bei dieser Variable um eine Gruppierungsvariable handelt, indem wir sie in einen factor umwandeln.
osf$group <- factor(osf$group)
reg_dummy1 <- lm(bsi_post ~ 1 + group, data = osf)
summary(reg_dummy1)
##
## Call:
## lm(formula = bsi_post ~ 1 + group, data = osf)
##
## Residuals:
## Min 1Q Median 3Q Max
## -14.889 -7.178 -0.582 6.572 35.111
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 13.275 1.463 9.073 2.03e-14 ***
## groupWaitlist 9.614 1.930 4.980 2.96e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 9.253 on 92 degrees of freedom
## Multiple R-squared: 0.2124, Adjusted R-squared: 0.2038
## F-statistic: 24.8 on 1 and 92 DF, p-value: 2.956e-06
Wir erkennen im Output, dass im Modell ein Interzept sowie ein Steigungskoeffizient für groupWaitlist geschätzt wurde. Hier ist es nun so, dass groupWaitlist uns verrät, dass es sich hier um die Variable group handelt und dass die Ausprägung Waitlist im Vergleich zur Referenzkategorie betrachtet wird. Das können wir auch herausfinden, indem wir levels auf die Variable group anwenden:
levels(osf$group)
## [1] "Treatment" "Waitlist"
"Treatment" ist hier die Referenzkategorie. Damit unterscheiden sich die beiden Gruppen hinsichtlich der Symptomschwere um 9.614. Der Mittelwert der Symptomschwere in der Treatmentgruppe liegt bei 13.275, was dem Interzept entspricht. Die Wartelistenkontrollgruppe hatte eine durchschnittliche Symptomschwere von (13.275$+$9.614$=$) 22.889. Das können wir auch mit aggregate nochmals prüfen und uns die Mittelwerte in den beiden Gruppen ausgeben lassen. Hier müssen wir lediglich sagen, welche Variable in welche Gruppen aufgeteilt werden soll (AV ~ UV) und was in den Gruppen passieren soll (FUN = mean sagt, dass Mittelwerte bestimmt werden sollen):
aggregate(bsi_post ~ group, data = osf, FUN = mean)
## group bsi_post
## 1 Treatment 13.27500
## 2 Waitlist 22.88889
Wenn wir nun wieder einen Modellvergleich vornehmen, können wir den Effekt des Treatments bestimmen:
anova(reg0, reg_dummy1)
## Analysis of Variance Table
##
## Model 1: bsi_post ~ 1
## Model 2: bsi_post ~ 1 + group
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 93 10001.2
## 2 92 7877.3 1 2123.8 24.805 2.956e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Das Treatment scheint die Symptomschwere signifikant zu verringern (mit einer Irrtumswahrscheinlichkeit von $5\%$). Wir können auch nachsehen, wie viel Variation durch die Zuteilung zur Treatment- oder Wartekontrollgruppe an der Symptomschwere erklärt wird:
summary(reg_dummy1)$r.squared
## [1] 0.2123605
Somit gehen 21.24% der Variation auf die Gruppenzugehörigkeit zurück.
Einfaktorielle ANOVA und $t$-Test
Mithilfe der ANOVA können wir unsere Daten auf Mittelwertsunterschiede über Gruppen hinweg untersuchen. Im Bachelorstudium hatten wir hier die ezANOVA Funktion kennengelernt. Diese kommt aus dem ez-Paket, welches zunächst geladen werden muss.
(Das Folgende ist zum Teil auch in der Sitzung ANOVA I aus dem Bachelor zu finden, natürlich mit einem anderen Datensatz.)
# Paket laden (ggf. vorher installieren mit install.packages)
library(ez)
Weil die Funktion für verschiedene Arten von ANOVAs geeignet ist, benötigt sie einige sehr spezifische Argumente. Für die einfaktorielle ANOVA werden vier Argumente benötigt:
data =: der genutzte Datensatzwid =: eine Personen ID-Variabledv =: die abhängige Variable (dependent variable)between =: eine Gruppierungsvariable (die zwischen Personen unterscheidet)
ID ist die ID-Variable unseres Datensatzes. Diese müssen wir nur noch in einen factor umwandeln:
osf$ID <- as.factor(osf$ID)
Jetzt kann die ANOVA mit dem ezANOVA-Befehl durchgeführt werden, indem wir einfach den oben stehenden Argumenten unsere Variablen übergeben:
ezANOVA(data = osf, wid = ID, dv = bsi_post, between = group)
## Warning: Data is unbalanced (unequal N per group). Make sure you specified a well-considered value for the type
## argument to ezANOVA().
## Coefficient covariances computed by hccm()
## $ANOVA
## Effect DFn DFd F p p<.05 ges
## 1 group 1 92 24.80471 2.955702e-06 * 0.2123605
##
## $`Levene's Test for Homogeneity of Variance`
## DFn DFd SSn SSd F p p<.05
## 1 1 92 77.62461 3059.801 2.333964 0.1300101
Zunächst werden wir mit einer ## Warning darauf hingewiesen, dass das Design unbalanciert ist: die Gruppen sind nicht alle gleich groß. Das kann Konsequenzen auf die Vertrauenswürdigkeit der Ergebnisse haben, wenn wir ANOVAs mit mehr als einem Faktor bestimmen (dazu später mehr).
Die zweite Hälfte der Ergebnisse ($Levene's Test for Homogeneity of Variance) liefert die Überprüfung der Homoskedastizitätsannahme mit dem Levene-Test. Dieser wird von ezANOVA immer automatisch mitgeliefert.
Der erste Abschnitt der Ausgabe der ezANOVA-Funktion liefert die Ergebnisse der ANOVA selbst. Dabei wird zunächst die unabhängige Variable aufgeführt (Effect), dann die Anzahl der Zählerfreiheitsgrade (DFn = $df_1$), dann die Anzahl der Nennerfreiheitsgrade (DFd = $df_2$). Darauf folgen der $F$-Wert (F = $F_{emp}$) und der resultierende $p$-Wert. Die Ergebnisse sind vollständig identisch mit den Ergebnissen aus dem Regressionsteil! Die Nullhypothese wird bei einem $\alpha$-Fehlerniveau von .05 verworfen: Die Mittelwerte der beiden Gruppen sind nicht gleich. Der * in der nächsten Spalte liefert uns diesbezüglich einen optischen Hinweis.
Die letzte Spalte liefert das generalisierte $\eta^2$ (ges = Generalized Eta-Squared), ein Effektstärkenmaß für ANOVAs. Dieses berechnet sich in diesem Fall einfach aus $\eta^2 = \frac{SS_\text{between}}{SS_{tot}}$, wobei $SS_\text{between}$ die Quadratsumme (engl. sum of squares $SS$), die durch Variation zwischen den Gruppen entsteht, und $SS_{tot}$ die totale Quadratsumme der abhängigen Variablen beschreibt. Um die Quadtratsummen (SSn = $SS_\text{between}$, SSd = $SS_\text{within}$) zu erhalten, kann mithilfe des Arguments detailed = TRUE eine detaillierte Ausgabe angefordert werden.
ezANOVA(data = osf, wid = ID, dv = bsi_post, between = group, detailed = T)
## Warning: Data is unbalanced (unequal N per group). Make sure you specified a well-considered value for the type
## argument to ezANOVA().
## Coefficient covariances computed by hccm()
## $ANOVA
## Effect DFn DFd SSn SSd F p p<.05 ges
## 1 group 1 92 2123.851 7877.308 24.80471 2.955702e-06 * 0.2123605
##
## $`Levene's Test for Homogeneity of Variance`
## DFn DFd SSn SSd F p p<.05
## 1 1 92 77.62461 3059.801 2.333964 0.1300101
Für $\eta^2$ haben sich - wie für viele Effektgrößen - Konventionen bezüglich der Interpretation etabliert. Für die Varianzanalyse wird $\eta^2 \approx .01$ als kleiner, $\eta^2 \approx .06$ als mittlerer und $\eta^2 \approx .14$ als großer Effekt interpretiert. Der Wert liegt hier bei 0.2124, was einem großem Effekt entspricht. In der Praxis ist es jedoch empfehlenswert, Effektstärken nicht (allein) anhand von Konventionen zu interpretieren, sondern etwa Effekte vergleichbarer Studien oder Behandlungsinterventionen zu Rate zu ziehen.
Die Effektstärke bedeutet, dass 21.24% der Variation auf die Gruppenzugehörigkeit zurückgehen. Dieser Wert sollte Ihnen reichlich bekannt vorkommen. Hier gilt nämlich $\eta^2=R^2$ aus der Regression! Um dies genauer zu sehen, speichern wir uns die Ergebnisse der ezANOVA ab:
ezANOVA1 <- ezANOVA(data = osf, wid = ID, dv = bsi_post, between = group, detailed = T)
## Warning: Data is unbalanced (unequal N per group). Make sure you specified a well-considered value for the type
## argument to ezANOVA().
## Coefficient covariances computed by hccm()
ezANOVA1$ANOVA$ges
## [1] 0.2123605
summary(reg_dummy1)$r.squared
## [1] 0.2123605
Auch die empirschen $F$-Werte sind identisch:
ezANOVA1$ANOVA$F
## [1] 24.80471
anova(reg0, reg_dummy1)$F
## [1] NA 24.80471
Das liegt ganz einfach daran, dass die $F$-Brüche die gleichen Ergebnisse verrechnen! Es gilt für die Quadratsummen:
$$SS_{tot} = SS_\text{between} + SS_\text{within},$$
wobei $SS_\text{within}$ der Quadratsumme innerhalb der Gruppen entspricht. Dies ist gerade die Residualquadratsumme, da die Variation innerhalb der Gruppen in der ANOVA als Fehlervariation angesehen wird. Um den $F$-Wert bestimmen zu können, brauchen wir die mittleren Quadratsummen $MS_\text{between} = \frac{SS_\text{between}}{df_\text{between}}$ und $MS_\text{within} = \frac{SS_\text{within}}{df_\text{within}}$. Hierbei sind $df_\text{between}=K-1$ die zwischen-Freiheitsgrade und $df_\text{within}=N-K$ die innerhalb-Freiheitsgrade, wobei $N$ = Anzahl aller Personen in der Stichprobe und $K$ = Anzahl Gruppen. Wir erkennen, dass für unser Beispiel $df_\text{between}=df_h$ und $df_\text{within}=df_{e}$ gilt. Nun können wir den $F$-Wert bestimmen. Dieser ergibt sich als $$F_{emp} = \frac{MS_\text{between}}{MS_\text{within}}=\frac{SS_\text{between}/df_\text{between}}{SS_\text{within}/df_\text{within}}.$$ Wir erkennen, dass hier einfach die Variation zwischen den Gruppen (Variation der Mittelwerte) relativ zur (zufälligen) Variation innerhalb der Gruppen betrachtet wird. Ist die Variation zwischen den Gruppen relativ zur zufälligen Variation groß, so gehen wir davon aus, dass dies ein nicht-zufälliger Unterschied ist: Die Mittelwerte müssen sich also bei einem großen $F$-Wert unterscheiden. Das Verhältnis der Quadratsummen folgt mit $df_\text{between} = K - 1$ und $df_\text{within} = N - K$ einer $F$-Verteilung. Daher wird der $F_{emp}$ mit dem $F_{krit}$ mit $df_1 = K - 1$ (Zählerfreiheitsgraden) und $df_2 = N - K$ (Nennerfreiheitsgraden) verglichen. Die Gleichheit kann nachvollzogen werden, indem wir den $F$-Bruch mit der totalen Quadratsumme erweitern und feststellen, dass $\eta^2=R^2=\frac{SS_\text{between}}{SS_{tot}}$ und $1-\eta^2=1-R^2=\frac{SS_\text{within}}{SS_{tot}}$ in diesem Beispiel gilt und damit:
Auch der $t$-Test kommt zum selben Ergebnis. Hier müssen wir der zugehörigen Funktion t.test allerdings noch sagen, dass wir Student’s $t$-Test (der $t$-Test, den Sie vermutlich im 1. Semester kennengelernt haben) wünschen, da nur dieser die Äquivalenz aufweist. Die Defaultvariante in R ist die robuste Variante nach Welch (Welch’s $t$-Test). Für den “Heimgebrauch” sollten sie auch immer Welch’s Variante verwenden, da diese der anderen in den meisten Fällen überlegen ist und zu weniger falsch-positiven Ergebnissen führt, wenn Voraussetzungen nicht erfüllt sind. (Interessierte finden hier eine über diesen Kurs hinausgehende Quelle die dies untersucht und diskutiert.) Wir verwenden Student’s $t$-Test hier rein aus Demonstrationszwecken. Das machen wir mit der Zusatzeinstellung var.equal = T in der Funktion t.test.
ttest1 <- t.test(bsi_post ~ group, data = osf, var.equal = T)
ttest1
##
## Two Sample t-test
##
## data: bsi_post by group
## t = -4.9804, df = 92, p-value = 2.956e-06
## alternative hypothesis: true difference in means between group Treatment and group Waitlist is not equal to 0
## 95 percent confidence interval:
## -13.447695 -5.780082
## sample estimates:
## mean in group Treatment mean in group Waitlist
## 13.27500 22.88889
Auf den ersten Blick sieht das Ergebnis anders aus als das Ergebnis der ANOVA oder der Regression. Allerdings sind die $p$-Werte in allen 3 Verfahren identisch:
ezANOVA1$ANOVA$p
## [1] 2.955702e-06
anova(reg0, reg_dummy1)$`Pr(>F)`
## [1] NA 2.955702e-06
ttest1$p.value
## [1] 2.955702e-06
Wenn Sie nun noch wissen, dass die $t(df)$-Verteilung im Quadrat der $F(1,df)$ Verteilung entspricht, dann können Sie den $t$-Wert in diesem Beispiel in den $F$-Wert transformieren:
ezANOVA1$ANOVA$F
## [1] 24.80471
anova(reg0, reg_dummy1)$F
## [1] NA 24.80471
ttest1$statistic^2
## t
## 24.80471
Mehrfaktorielle ANOVA
Die Mehrfaktorielle ANOVA ist nun etwas kniffliger. Hier hängt bei der ANOVA die Signifikanzentscheidung der Gruppenkombination nämlich von der Quadratsummenwahl ab. Diese kann unterschiedlich gewählt werden. Es gibt verschiedene R-Pakete, die dies für uns übernehmen.
In einer zweifaktoriellen ANOVA sind drei verschiedene Arten von Effekten möglich: Haupteffekt des Faktors A (erster Faktor), Haupteffekt des Faktors B (zweiter Faktor) und Interaktionseffekt (AxB). Die Wahl der Quadratsumme entscheidet nun, in welcher Reihenfolge die Prädiktoren in das Modell aufgenommen werden. In der ezANOVA-Funktion können wir die Quadratsumme ganz einfach mit dem Argument type einstellen. Es gibt drei Typen der Quadratsummen.
Zweifaktorielle ANOVA: Quadratsumme vom Typ I
Dieser Quadratsummentyp entspricht im Grunde dem stückchenweisen Aufnehmen von Prädiktoren im Regressionskontext. Dies bedeutet, dass die Signifikanzentscheidung der Faktoren von der Reihenfolge der Aufnahme der Faktoren in das Modell abhängt. Das gilt auch für kontinuierliche Prädiktoren: Je nachdem, welche Prädiktoren bereits im Modell enthalten sind, liefert der nächste Prädiktor signifikante inkrementelle Varianzaufklärung des Kriteriums oder eben nicht. Diesem Umstand geschuldet wählen Selektionsverfahren, wie etwa die Forward-Selektion, immer denjenigen Prädiktor aus, der signifikante Vorhersagekraft leistet und die größte Veränderung in $R^2$ über die bereits enthaltenen Prädiktoren liefert.
Wir können unser ANOVA-Modell um die Diagnose der Proband:innen erweitern, indem wir dem Argument between in ezANOVA einen Vektor von Variablen übergeben (between = c(group, stratum)). Bevor wir dies tun, sollten wir die Gruppierungsvariable stratum noch in einen factor umwandeln! Dann stellen wir noch den Quadratsummentype ein, speichern das Objekt als ezANOVA1 ab und erhalten:
osf$stratum <- factor(osf$stratum)
ezANOVA1 <- ezANOVA(data = osf, dv = bsi_post, between = c(group, stratum), wid = ID,
detailed = T, type = 1)
## Warning: Data is unbalanced (unequal N per group). Make sure you specified a well-considered value for the type
## argument to ezANOVA().
## Warning: Using "type==1" is highly questionable when data are unbalanced and there is more than one variable.
## Hopefully you are doing this for demonstration purposes only!
ezANOVA1
## $ANOVA
## Effect DFn DFd SSn SSd F p p<.05 ges
## 1 group 1 88 2123.85124 7662.031 24.39286833 3.706554e-06 * 0.217032172
## 2 stratum 2 88 201.48236 7662.031 1.15703320 3.191539e-01 0.025622436
## 3 group:stratum 2 88 13.79514 7662.031 0.07921999 9.239025e-01 0.001797218
Wir erhalten direkt zwei Warnungen. Einmal wird uns mitgeteilt, dass das Design nicht balanciert ist und somit nicht gleich viele Beobachtungen pro Gruppe vorliegen. Die zweite Meldung bezieht sich auf die Quadratsumme vom Typ I:
## ## Warning: Using "type==1" is highly questionable when data are unbalanced and
## ## there is more than one variable. Hopefully you are doing this for demonstration
## ## purposes only!
Hier wird uns mitgeteilt, dass die Verwendung der Quadratsumme vom Typ I keine so gute Idee ist. Zum Glück machen wir das hier tatsächlich nur zu Demonstrationszwecken! Eines der Hauptprobleme ist nämlich, dass die Reihenfolge der Prädiktoren die Signifikanzentscheidung beeinflusst. Der Effekt group entspricht dem Haupteffekt der Treatmentzuweisung, stratum entspricht dem Haupteffekt der Diagnose und group:stratum entspricht dem Interaktionseffekt. Dem Output ist zu entnehmen, dass nur die Treatmentzuweisung einen signifikanten Einfluss auf die Symptomschwere hat. Somit hätte das Treatment einen Effekt, welcher sich unabhängig von der Diagnose auf die Symptomschwere auswirkt (mit einer Irrtumswahrscheinlichkeit von
$5\%$). Das Ergebnis lässt sich auch super leicht grafisch darstellen, indem wir die ezPlot-Funktion aus dem ez-Paket verwenden. Diese nimmt dieselben Argumente wie ezANOVA entgegen. Es fehlt lediglich die Aufteilung der Effekte. x = stratum lässt die Diagnose auf der $x$-Achse erscheinen. split = group lässt unterschiedliche Linien für Treatment und Wartekontrollgruppe erscheinen:
ezPlot(data = osf, dv = bsi_post, between = c(group, stratum), wid = ID, x = stratum, split = group)
## Warning: Data is unbalanced (unequal N per group). Make sure you specified a well-considered value for the type
## argument to ezANOVA().
## Coefficient covariances computed by hccm()
## Warning in ezStats(data = data, dv = dv, wid = wid, within = within, within_full = within_full, : Unbalanced
## groups. Mean N will be used in computation of FLSD
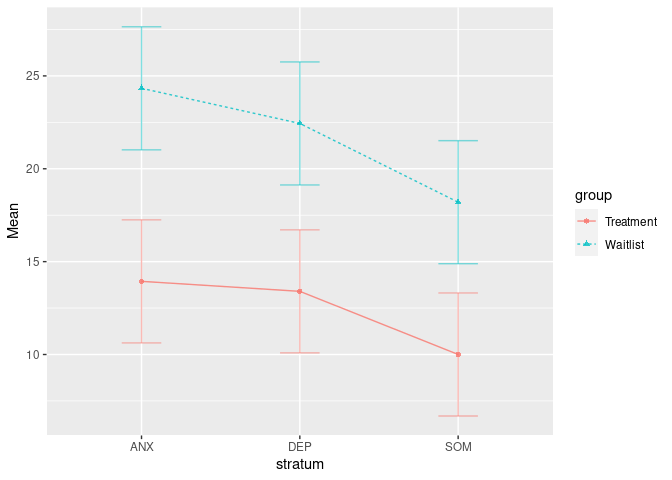
Die Fisher’s Least Significant Distance (FLSD) ist eine Schätzung für die minimale Distanz zwischen Mittelwerten in Gruppen, die signifikant wäre. Damit gibt dieser Plot erste Anzeichen über mögliche signifikante Mittelwertsunterschiede.
Wenn wir dieselbe Analyse nun wiederholen und zuerst die Diagnose in das Modell aufnehmen, erhalten wir andere Ergebnisse:
ezANOVA(data = osf, dv = bsi_post, between = c(stratum, group), wid = ID,
detailed = T, type = 1)
## Warning: Data is unbalanced (unequal N per group). Make sure you specified a well-considered value for the type
## argument to ezANOVA().
## Warning: Using "type==1" is highly questionable when data are unbalanced and there is more than one variable.
## Hopefully you are doing this for demonstration purposes only!
## $ANOVA
## Effect DFn DFd SSn SSd F p p<.05 ges
## 1 stratum 2 88 244.18457 7662.031 1.40225503 2.514844e-01 0.030885141
## 2 group 1 88 2081.14903 7662.031 23.90242466 4.525815e-06 * 0.213600597
## 3 stratum:group 2 88 13.79514 7662.031 0.07921999 9.239025e-01 0.001797218
Das spielt natürlich eine immer größere Rolle, je mehr Gruppierungsvariablen wir haben und je überlappender die Effekte sind. In diesem spezifischen Beispiel sind die Unterschiede gar nicht so groß und auch die Signifikanzentscheidung ist am Ende des Tages dieselbe. Allerdings erkennen wir, dass der F-Wert der beiden Haupteffekte leicht unterschiedlich ist. Der F-Wert und die Signifikanzentscheidung der Interaktion ist in beiden Fällen gleich.
Um nun dieselben Ergebnisse wie in ezANOVA1 mit der Regressionsanalyse zu erhalten, müssen wir das entsprechende Modell aufstellen. Um den Modellvergleich besser nachvollziehen zu können, stellen wir gleich eine Reihe von Modellen auf. Hierbei kann die Interaktion mit : in das Modell aufgenommen werden:
reg0 <- lm(bsi_post ~ 1, data = osf) # Null-Modell (leeres Modell)
reg_g <- lm(bsi_post ~ group, data = osf) # Modell mit Haupteffekt des Treatments
reg_s <- lm(bsi_post ~ stratum, data = osf) # Modell mit Haupteffekt der Diagnose
reg_gs <- lm(bsi_post ~ group + stratum, data = osf) # Modell mit beiden Haupteffekten
reg_gsi <- lm(bsi_post ~ group + stratum + group:stratum, data = osf) # Modell mit beiden Haupteffekten und Interaktion
Insgesamt erhalten wir also fünf Modelle. Um das inkrementelle Aufnehmen der Faktoren abzubilden, müssen wir diejenigen Modelle auswählen, die auseinander hervorgehen. Wir wollen zuerst den Effekt der Gruppierungsvariable (group) untersuchen. Anschließend wird dann die Diagnose (stratum) in das Modell aufgenommen. Als letztes fügen wir noch die Interaktion in das Modell hinzu. Somit benötigen wir das Modell reg_s, welches nur die Diagnose (stratum) enthält, in diesen Modellvergleichen nicht.
Wir wollen nun diese Modelle inkrementell gegeneinander vergleichen. Dafür verwenden wir die anova-Funktion, welcher wir einfach alle Modelle (in der richtigen Reihenfolge!!) übergeben. Wenn wir nun vier geschachtelte Modelle gegeneinander testen, erhalten wir jeweils paarweise Vergleiche. Wir beginnen mit dem Null-Modell und ergänzen dann das Treatment. Dann wird die Diagnose dem Modell hinzugefügt und zum Schluss die Interaktion:
anova(reg0, reg_g, reg_gs, reg_gsi)
## Analysis of Variance Table
##
## Model 1: bsi_post ~ 1
## Model 2: bsi_post ~ group
## Model 3: bsi_post ~ group + stratum
## Model 4: bsi_post ~ group + stratum + group:stratum
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 93 10001.2
## 2 92 7877.3 1 2123.85 24.3929 3.707e-06 ***
## 3 90 7675.8 2 201.48 1.1570 0.3192
## 4 88 7662.0 2 13.80 0.0792 0.9239
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Die Effekte sind komplett identisch zum ezANOVA1-Output. Wir erkennen, dass Quadratsummen vom Typ I also einem schrittweisen Aufnehmen der Prädiktoren entspricht, wobei die Reihenfolge entscheidend ist. Im Übrigen hätten wir uns das Erstellen der Modelle sparen können und einfach anova auf reg_gsi anwenden können:
anova(reg_gsi)
## Analysis of Variance Table
##
## Response: bsi_post
## Df Sum Sq Mean Sq F value Pr(>F)
## group 1 2123.9 2123.85 24.3929 3.707e-06 ***
## stratum 2 201.5 100.74 1.1570 0.3192
## group:stratum 2 13.8 6.90 0.0792 0.9239
## Residuals 88 7662.0 87.07
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Allerdings war uns an dieser Stelle wichtig, zu zeigen, wie man auf die jeweiligen Modellvergleiche kommt. Die anderen Quadratsummentypen sollen nun unabhängig von der Reihenfolge jeweils Signifikanzentscheidungen für die Haupteffekte ausgeben können.
Zweifaktorielle ANOVA: Quadratsumme vom Typ II
Quadratsummen vom Typ II sind häufig der Default in Programmen, die nicht das schrittweise Vorgehen wählen wollen. Dieser Typ sollte verwendet werden, wenn es keine Interaktion zwischen den Faktoren gibt. Dann können die Haupteffekte sinnvoll interpretiert werden. Die Effekte werden hier als Partialeffekte bestimmt. Es spielt also keine Rolle, in welcher Reihenfolge die Faktoren aufgenommen werden. Wir rechnen zunächst wieder eine zweifaktorielle ANOVA mit dem ezANOVA-Befehl mit Quadratsummen vom zweiten Typ. Um den Output etwas zu verkürzen, lassen wir das Argument detailed weg:
ezANOVA2 <- ezANOVA(data = osf, dv = bsi_post, between = c(group, stratum), wid = ID,
type = 2)
## Warning: Data is unbalanced (unequal N per group). Make sure you specified a well-considered value for the type
## argument to ezANOVA().
## Coefficient covariances computed by hccm()
ezANOVA2
## $ANOVA
## Effect DFn DFd F p p<.05 ges
## 1 group 1 88 23.90242466 4.525815e-06 * 0.213600597
## 2 stratum 2 88 1.15703320 3.191539e-01 0.025622436
## 3 group:stratum 2 88 0.07921999 9.239025e-01 0.001797218
##
## $`Levene's Test for Homogeneity of Variance`
## DFn DFd SSn SSd F p p<.05
## 1 5 88 244.7046 2907.497 1.481274 0.2040363
ezANOVA(data = osf, dv = bsi_post, between = c(stratum, group), wid = ID,
type = 2)
## Warning: Data is unbalanced (unequal N per group). Make sure you specified a well-considered value for the type
## argument to ezANOVA().
## Coefficient covariances computed by hccm()
## $ANOVA
## Effect DFn DFd F p p<.05 ges
## 1 stratum 2 88 1.15703320 3.191539e-01 0.025622436
## 2 group 1 88 23.90242466 4.525815e-06 * 0.213600597
## 3 stratum:group 2 88 0.07921999 9.239025e-01 0.001797218
##
## $`Levene's Test for Homogeneity of Variance`
## DFn DFd SSn SSd F p p<.05
## 1 5 88 244.7046 2907.497 1.481274 0.2040363
Zusätzlich zu den Tests auf Haupt- und Interaktionseffekte, wird uns auch noch der $Levene's Test for Homogeneity of Variance ausgegeben. Wie der Namen schon sagt, wird hier auf Varianzhomogenität geprüft. Es wird also die wichtige Annahme der ANOVA untersucht, dass die Varianzen in allen Gruppen gleich groß sind. Da der Test nicht signifikant ist, wird an dieser Annahme hier nicht gezweifelt. Wie Sie sehen, spielt die Reihenfolge nun keine Rolle mehr. Die Tests auf Haupt- und Interaktionseffekte kommen zu identischen Ergebnissen — nur die Reihenfolge im Output ändert sich. Es ist sehr schwierig, mithilfe von Modellvergleichen diese Tests anhand der Regression zu replizieren. Wir können aber bspw. die Anova-Funktion aus dem car-Paket verwenden, um Quadratsummen vom Typ II aus einem lm-Objekt zu bekommen. Das Regressionsmodell mit zwei Faktoren inklusive Interaktion hieß reg_gsi:
library(car)
Anova(reg_gsi, type = 2)
## Anova Table (Type II tests)
##
## Response: bsi_post
## Sum Sq Df F value Pr(>F)
## group 2081.1 1 23.9024 4.526e-06 ***
## stratum 201.5 2 1.1570 0.3192
## group:stratum 13.8 2 0.0792 0.9239
## Residuals 7662.0 88
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Auch diese kommt zum selben Ergebnis. Die Interaktion ist nicht signifikant, also können wir die Haupteffekte interpretieren. Von diesen ist nur der Haupteffekt des Treatments signifikant. Wenn wir konzeptionell verstehen wollen, was genau hier passiert, können wir uns mal die Effekte ohne den Interaktionseffekt ansehen, der sowieso nicht signifikant war. Dazu wenden wir die Anova-Funktion aus dem car-Paket auf das zweifaktorielle Modell ohne Interaktion an (dieses hieß reg_gs). Wenn wir dieses Ergebnis nun mit den Modellvergleichen von oben vergleichen, fallen uns Ähnlichkeiten auf. Um das genauer zu zeigen, führen wir nun den inkrementellen Test der Haupteffekte jeweils über den anderen Haupteffekt hinaus durch. Wir testen also das Inkrement erklärter Varianz des Treatments über die Diagnose hinaus, sowie das Inkrement erklärter Varianz der Diagnose über das Treatment hinaus:
Anova(reg_gs, type = 2) # simulatane Inkrementsprüfung
## Anova Table (Type II tests)
##
## Response: bsi_post
## Sum Sq Df F value Pr(>F)
## group 2081.1 1 24.4017 3.586e-06 ***
## stratum 201.5 2 1.1812 0.3116
## Residuals 7675.8 90
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
anova(reg_s, reg_gs) # Inkrement des Treatments
## Analysis of Variance Table
##
## Model 1: bsi_post ~ stratum
## Model 2: bsi_post ~ group + stratum
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 91 9757.0
## 2 90 7675.8 1 2081.2 24.402 3.586e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
anova(reg_g, reg_gs) # Inkrement der Diagnose
## Analysis of Variance Table
##
## Model 1: bsi_post ~ group
## Model 2: bsi_post ~ group + stratum
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 92 7877.3
## 2 90 7675.8 2 201.48 1.1812 0.3116
Wir erkennen, dass die Tests der Inkremente jeweils der Haupteffektsprüfung mit Quadratsummen vom Typ II entsprechen. Es ist also so, dass die unterschiedlichen Quadratsummen keine neue Methode darstellen, sondern einfach bestimmten Hypothesen entsprechen. Diesen Hypothesen sollten wir uns bewusst sein, bevor wir die Ergebnisse interpretieren.
Zweifaktorielle ANOVA: Quadratsumme vom Typ III
Ist der Interaktionseffekt signifikant, so sollten die Quadratsummen vom Typ III verwendet werden. Diese erhalten wir entweder mit der ezANOVA-Funktion aus dem ez-Paket oder der Anova-Funktion aus dem car-Paket.
Mit ezANOVA:
ezANOVA(data = osf, dv = bsi_post, between = c(group, stratum), wid = ID,
type = 3)
## Warning: Data is unbalanced (unequal N per group). Make sure you specified a well-considered value for the type
## argument to ezANOVA().
## Coefficient covariances computed by hccm()
## $ANOVA
## Effect DFn DFd F p p<.05 ges
## 2 group 1 88 13.61713235 0.0003877831 * 0.134004297
## 3 stratum 2 88 1.06050567 0.3506639157 0.023535148
## 4 group:stratum 2 88 0.07921999 0.9239024794 0.001797218
##
## $`Levene's Test for Homogeneity of Variance`
## DFn DFd SSn SSd F p p<.05
## 1 5 88 244.7046 2907.497 1.481274 0.2040363
Nutzen wir Anova, so müssen wir für Quadratsummen vom Typ III die Art der Kontrastbildung in R verändern. Der Default lautet:
options("contrasts")
## $contrasts
## unordered ordered
## "contr.treatment" "contr.poly"
Hier sehen wir , dass es immer Treatment-Kontraste sind (contr.treatment), also dass immer eine Referenzkategorie gebildet wird. Wir brauchen hier Summen-Kontraste (contr.sum). Die Umstellung kann entweder innerhalb options geschehen, allerdings ändert sich dann die Einstellung für die gesamte R-Sitzung, oder wir ergänzen den lm-Befehl um das Argument contrasts. Wir entscheiden uns hier für die 2. Variante. Damit wird auch ersichtlich, dass die Modelle nochmals geschätzt werden müssen! Wir nennen das Objekt auch nochmal um, um den Unterschied der Kodierung klar zu machen:
reg_gsi_contr.sum <- lm(bsi_post ~ group + stratum + group:stratum, data = osf,
contrasts = list("group" = contr.sum, "stratum" = contr.sum)) # contr.sum-Kodierung
Anova(reg_gsi_contr.sum, type = 3)
## Anova Table (Type III tests)
##
## Response: bsi_post
## Sum Sq Df F value Pr(>F)
## (Intercept) 16249.7 1 186.6310 < 2.2e-16 ***
## group 1185.6 1 13.6171 0.0003878 ***
## stratum 184.7 2 1.0605 0.3506639
## group:stratum 13.8 2 0.0792 0.9239025
## Residuals 7662.0 88
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Die beiden Analysen kommen zum selben Ergebnis. Der Intercept-Output fehlt hier bei ezANOVA. Dieser ist allerdings auch nicht relevant für unsere Hypothesen.
Bei Quadratsummen vom Typ III werden die Haupteffekte nicht nur gegeben der anderen Haupteffekte bestimmt, sondern es wird auch der Interaktionseffekt herausgerechnet. Da der Interaktionseffekt nicht signifikant ist, sollten wir allerdings besser das Ergebnis aus den Analysen mit Quadratsummen vom Typ II interpretieren.
Fazit aus allen Analysen
Insgesamt kamen alle Analysen zum selben Ergebnis: Die Intervention zeigt einen Effekt auf die Symptomschwere unabhängig von der vorliegenden Diagnose (mit einer Irrtumswahrscheinlichkeit von $5\%$). Wir haben in dieser Sitzung gesehen, dass Regression und ANOVA zum selben Ergebnis kommen, wenn dieselben Hypothesen geprüft werden. Die Wahl der Quadratsumme hängt von der Art der Hypothese, die geprüft werden soll, ab!
Literatur
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden (5. Auflage, 1. Auflage: 2010). Weinheim: Beltz.
Datensatzliteratur
Schaeuffele, C., Homeyer, S. L., Perea, L., Scharf, L., Schulz, A., Knaevelsrud, C., … Boettcher, J. (2020, December 16). The Unified Protocol as an Internet-based Intervention for Emotional Disorders: Randomized Controlled Trial. https://doi.org/10.31234/osf.io/528tw
- Blau hinterlegte Autor:innenangaben führen Sie direkt zur universitätsinternen Ressource.
](/media/header/daily_report_color.jpg)