Die Lösungen sind exemplarische Möglichkeiten. In R gibt es immer viele Wege, die zum Ziel führen. Wenn Sie einen anderen mit dem korrekten Ergebnis gewählt haben, kann dieser genauso richtig sein wie die hier präsentierten Ansätze.
Vorbereitung
Laden Sie die Daten aus
fb23.rdaoder direkt von der Website über die gelernten Befehle. Die Bedeutung der einzelnen Variablen und ihre Antwortkategorien können Sie dem Dokument Variablenübersicht entnehmen.
Lösung
Daten laden:
load(url('https://pandar.netlify.app/daten/fb23.rda'))
Überblick über den Datensatz verschaffen:
dim(fb23)
## [1] 179 40
str(fb23)
## 'data.frame': 179 obs. of 40 variables:
## $ mdbf1_pre : int 4 2 4 NA 3 3 2 3 3 2 ...
## $ mdbf2_pre : int 2 2 3 3 3 2 3 2 2 1 ...
## $ mdbf3_pre : int 3 4 2 2 2 3 3 1 2 2 ...
## $ mdbf4_pre : int 2 2 1 2 1 1 3 2 3 3 ...
## $ mdbf5_pre : int 3 2 3 2 2 1 3 3 2 4 ...
## $ mdbf6_pre : int 2 1 2 2 2 2 2 3 2 2 ...
## $ mdbf7_pre : int 4 3 3 1 1 2 2 3 3 3 ...
## $ mdbf8_pre : int 3 2 3 2 3 3 2 3 3 2 ...
## $ mdbf9_pre : int 2 4 1 2 3 3 4 2 2 3 ...
## $ mdbf10_pre : int 3 2 3 3 2 4 2 2 2 2 ...
## $ mdbf11_pre : int 3 2 1 2 2 1 3 1 2 4 ...
## $ mdbf12_pre : int 1 1 2 3 2 2 2 3 3 2 ...
## $ lz : num 5.4 3.4 4.4 4.4 6.4 5.6 5.4 5 4.8 6 ...
## $ extra : num 3.5 3 4 3 4 4.5 3.5 3.5 2.5 3 ...
## $ vertr : num 1.5 3 3.5 4 4 4.5 4 4 3 3.5 ...
## $ gewis : num 4.5 4 5 3.5 3.5 4 4.5 2.5 3.5 4 ...
## $ neuro : num 5 5 2 4 3.5 4.5 3 2.5 4.5 4 ...
## $ offen : num 5 5 4.5 3.5 4 4 5 4.5 4 3 ...
## $ prok : num 1.8 3.1 1.5 1.6 2.7 3.3 2.2 3.4 2.4 3.1 ...
## $ nerd : num 4.17 3 2.33 2.83 3.83 ...
## $ grund : chr "Berufsziel" "Interesse am Menschen" "Interesse und Berufsaussichten" "Wissenschaftliche Ergänzung zu meinen bisherigen Tätigkeiten (Arbeit in der psychiatrischen Akutpflege, Gestalt"| __truncated__ ...
## $ fach : num 4 4 4 4 4 4 NA 4 4 NA ...
## $ ziel : num 2 2 2 2 2 2 NA 4 2 2 ...
## $ wissen : int 5 4 5 4 2 3 NA 4 3 3 ...
## $ therap : int 5 5 5 5 4 5 NA 3 5 5 ...
## $ lerntyp : num 3 3 1 3 3 1 NA 1 3 3 ...
## $ hand : int 2 2 2 2 2 2 NA 2 1 2 ...
## $ job : int 1 1 1 1 2 2 NA 2 1 2 ...
## $ ort : int 2 1 1 1 1 2 NA 1 1 2 ...
## $ ort12 : int 2 1 2 2 2 1 NA 2 2 1 ...
## $ wohnen : num 4 1 1 1 1 2 NA 3 3 2 ...
## $ uni1 : num 0 1 0 1 0 0 0 0 0 0 ...
## $ uni2 : num 1 1 1 1 1 1 0 1 1 1 ...
## $ uni3 : num 0 1 0 0 1 0 0 1 1 0 ...
## $ uni4 : num 0 1 0 1 0 0 0 0 0 0 ...
## $ attent_pre : int 6 6 6 6 6 6 NA 4 5 5 ...
## $ gs_post : num 3 2.75 4 2.5 3.75 NA 4 2.75 3.75 2.5 ...
## $ wm_post : num 2 1 3.75 2.75 3 NA 3.25 2 3.25 2 ...
## $ ru_post : num 2.25 1.5 3.75 3.5 3 NA 3.5 2.75 2.75 2.75 ...
## $ attent_post: int 6 5 6 6 6 NA 6 4 5 3 ...
Der Datensatz besteht aus 179 Zeilen (Beobachtungen) und 40 Spalten (Variablen).
Aufgabe 1
Untersuchen Sie, welche Arbeitsbranche Sie und Ihre Kommiliton:innen nach dem Studium anstreben!
- Vergeben Sie zunächst die korrekten Wertelabels an die Ausprägungen der Variable.
- Lassen Sie sich absolute und relative Häufigkeiten ausgeben.
- Untersuchen Sie mit den geeigneten Maßen die zentrale Tendenz und Dispersion dieser Variable.
Lösung
Faktor erstellen
fb23$ziel <- factor(fb23$ziel,
levels = 1:4,
labels = c("Wirtschaft", "Therapie", "Forschung", "Andere"))
levels(fb23$ziel)
## [1] "Wirtschaft" "Therapie" "Forschung" "Andere"
Absolute und relative Häufigkeiten anfordern
table(fb23$ziel) # absolut
##
## Wirtschaft Therapie Forschung Andere
## 15 106 29 19
prop.table(table(fb23$ziel)) # relativ
##
## Wirtschaft Therapie Forschung Andere
## 0.0887574 0.6272189 0.1715976 0.1124260
Zentrale Tendenz und Dispersion für nominalskalierte Variablen: Modus, relativer Informationsgehalt
# Modus
which.max(table(fb23$ziel))
## Therapie
## 2
#relativer Informationsgehalt
hj <- prop.table(table(fb23$ziel)) # hj erstellen
ln_hj <- log(hj) # Logarithmus bestimmen
summand <- ln_hj * hj # Berechnung fuer jede Kategorie
summe <- sum(summand) # Gesamtsumme
k <- length(hj) # Anzahl Kategorien bestimmen
relInf <- -1/log(k) * summe # Relativer Informationsgehalt
relInf
## [1] 0.7615196
Der Modus der Variable lautet Therapie - die meisten Ihres Jahrgangs (n = 106 bzw. 62.72%) streben einen Job in diesem Bereich an. Der relative Informationsgehalt der Variable beträgt 0.76. Sie sehen hier, dass wir im Code einen kleinen Unterschied zum Tutorial eingebaut haben. Die Anzahl der Kategorien wird nicht mehr durch dim(tab) sondern durch length(hj) bestimmt. Das Resultat ist nicht verschieden - die Anzahl der Kategorien wird gezählt. Wir wollen somit aber nochmal deutlich machen, dass es in R immer sehr viele Wege zu einem Ziel geben kann.
Aufgabe 2
Die Variable therap enthält die Angaben über das Ausmaß, in dem sich Sie und Ihre Kommilitonen:innen für anwendungsbezogene Aspekte interessieren.
- Bestimmen Sie für diese Variable den Modus.
- Untersuchen Sie die Streuung für diese Variable optisch, indem Sie einen Boxplot erstellen.
- Bestimmen Sie die Quartile, den Interquartilsbereich (IQB) und den Interquartilsabstand auch als Zahlen.
Lösung
Modus
which.max(table(fb23$therap))
## 5
## 4
Häufigkeiten
table(fb23$therap)
##
## 2 3 4 5
## 3 11 65 97
prop.table(table(fb23$therap))
##
## 2 3 4 5
## 0.01704545 0.06250000 0.36931818 0.55113636
Der Modus der Variable therap beträgt 4, d.h. diese Antwortkategorie wurde am häufigsten genannt (n = 97 bzw. 55.11%).
Boxplot
boxplot(fb23$therap)

Quartile
quantile(fb23$therap, c(.25,.5,.75), na.rm=T)
## 25% 50% 75%
## 4 5 5
Der Median beträgt 5. Das 1. und 3. Quartil betragen 4 bzw. 5. Folglich sind die Grenzen des Interquartilsbereich (IQB) 4 und 5. Der Interquartilsabstand (IQA) beträgt 1.
Aufgabe 3
Erstellen Sie für die Variable wohnen eine geeignete Abbildung.
- Stellen Sie sicher, dass die einzelnen Ausprägungen der Variable in der Darstellung interpretierbar benannt sind!
- Dekorieren Sie diese Abbildung nach eigenen Wünschen (z.B. mit einer Farbpalette und Achsenbeschriftungen).
- Speichern Sie die Grafik per Syntax als .jpg-Datei mit dem Namen “Befragung-fb23.jpg” ab.
Lösung
Faktor erstellen
fb23$wohnen <- factor(fb23$wohnen,
levels = 1:4,
labels = c("WG", "bei Eltern", "alleine", "sonstiges"))
Default Darstellung und überarbeitete Grafik
Um die Vergleichbarkeit zu erhöhen, wird im folgenden Code ein kleiner Trick angewendet. Die beiden Histogramme sollten am besten gleichzeitig unter Plots angezeigt werden. Durch die verwendete Funktion par() kann man verschiedene Plots gemeinsam in einem Fenster zeichnen. Das Argument bestimmt dabei, dass es eine Zeile und zwei Spalten für die Plots gibt.
par(mfrow=c(1,2))
# Default
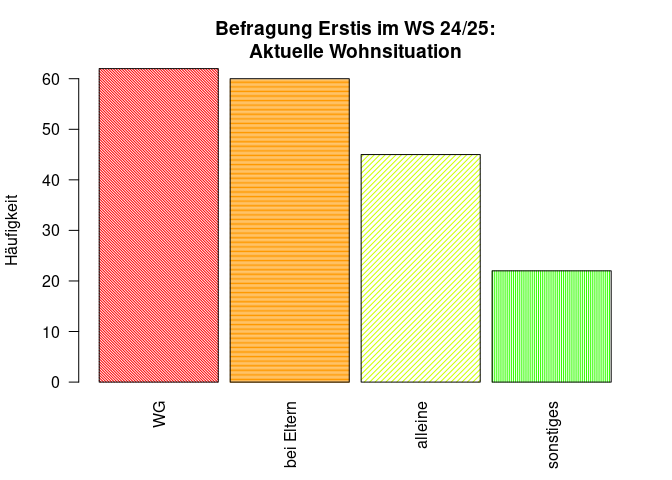
barplot(table(fb23$wohnen))
# Überarbeitet
barplot(
# wichtig: Funktion auf Häufigkeitstabelle, nicht die Variable selbst anwenden:
table(fb23$wohnen),
# aussagekräftiger Titel, inkl. Zeilenumbruch ("\n")
main = "Befragung Erstis im WS 23/24:\nAktuelle Wohnsituation",
# y-Achsen-Beschriftung:
ylab = "Häufigkeit",
# Farben aus einer Farbpalette:
col = rainbow(10),
# Platz zwischen Balken minimieren:
space = 0.1,
# graue Umrandungen der Balken:
border = "grey2",
# Unterscheidlich dichte Schattierungen (statt Füllung) für die vier Balken:
density = c(50, 75, 25, 50),
# Richtung, in dem die Schattierung in den vier Balken verläuft
angle = c(-45, 0, 45, 90),
# Schriftausrichtung der Achsen horizontal:
las=2,
#y-Achse erweitern, sodass mehr Platz zum Titel bleibt:
ylim = c(0,60))
Speichern (per Syntax)
jpeg("Befragung-fb23.jpg", width=20, height=10, units="cm", res=200)
barplot(
table(fb23$wohnen),
main = "Befragung Erstis im WS 23/24:\nAktuelle Wohnsituation",
ylab = "Häufigkeit",
col = rainbow(10),
space = 0.1,
border = "grey2",
density = c(50,75,25,50),
angle = c(-45,0,45,90),
las=2,
ylim = c(0,60))
dev.off()
Im Arbeitsverzeichnis sollte die Datei nun vorliegen.
](/media/header/frogs_on_phones.jpg)