Deskriptivstatistik für Nominal- und Ordinalskalen

Wiederholung aus der Vorlesung: Skalenniveaus

Vorbereitende Schritte

Nachdem wir in der letzten Sitzung die Arbeit mit dem CSV Format kennen gelernt haben, nutzen wir jetzt die Datei im RDA Format für das Einlesen des Datensatzes. Den Datensatz fb25 können Sie im RDA Format hier herunterladen. Außerdem ist es prinzipiell ratsam, zu Beginn wieder das Arbeitsverzeichnis mit Hilfe von setwd() zu bestimmen. Dies stellt sicher, dass wenn Sie später Daten speichern (z.B. Datensätze oder Grafiken), diese auch am gewünschten Ort auf Ihrem Computer abgelegt werden.

Eine alternative Variante ist, den Datensatz direkt mit dem folgenden Befehl aus dem Internet einzuladen. Dies ist immer dann möglich, wenn der Datensatz auch über eine URL aufrufbar ist.

load(url('https://pandar.netlify.app/daten/fb25.rda'))   # Daten laden
names(fb25)        # Namen der Variablen

##  [1] "mdbf1"       "mdbf2"       "mdbf3"       "mdbf4"       "mdbf5"       "mdbf6"       "mdbf7"       "mdbf8"       "mdbf9"      
## [10] "mdbf10"      "mdbf11"      "mdbf12"      "time_pre"    "lz"          "extra"       "vertr"       "gewis"       "neuro"      
## [19] "offen"       "prok"        "trust"       "uni1"        "uni2"        "uni3"        "uni4"        "sicher"      "angst"      
## [28] "fach"        "ziel"        "wissen"      "therap"      "lerntyp"     "hand"        "job"         "ort"         "ort12"      
## [37] "wohnen"      "attent_pre"  "gs_post"     "wm_post"     "ru_post"     "time_post"   "attent_post"

dim(fb25)          # Anzahl Zeile und Spalten

## [1] 211  43

In der letzten Sitzung haben wir schon einige Befehle für das Screening eines Datensatzes kennen gelernt. Dabei zeigt names() alle Variablennamen an, während dim() uns Zeilen und Spalten ausgibt. Der Datensatz hat also 211 Beobachtungen auf 43 Variablen.

Nominalskalierte Variablen

Typische Beispiele für nominalskalierte Variablen in der Psychologie sind das bspw. natürlich vorkommende Gruppierungen (z.B. das Geschlecht) oder die Experimentalbedingungen (z.B. “Experimentalgruppe” und “Kontrollgruppe”). Nominalskalierte Variablen sollten in R als Faktoren hinterlegt werden. Faktoren in R sind Vektoren mit einer vorab definierten Menge an vorgegebenen möglichen Ausprägungsmöglichkeiten. Sowohl numerische als auch character-Variablen können als Faktor kodiert werden, was mit jeweiligen Vorteilen einhergeht:

• für numerische Variablen: es können (aussagekräftige) Labels zugewiesen (“hinterlegt”) werden. Diese werden dann für Tabellen und Grafiken übernommen
• Für character-Variablen: Faktoren können für Analysen verwendet werden (z.B. als Prädiktoren in einer Regression), was für character-Variablen nicht möglich gewesen wäre

Jeder numerischen Faktorstufe (level) kann ein Label zugewiesen werden. Faktorstufe und –label bestehen auch dann, wenn die entsprechende Ausprägung empirisch nicht auftritt.

Beispiel 1: Die (numerische) Variable hand als Faktor aufbereiten

str(fb25$hand)

##  int [1:211] 2 2 2 2 2 2 2 2 1 2 ...

fb25$hand

##   [1]  2  2  2  2  2  2  2  2  1  2  2  2  2  2  1  2  2  1  2  2  2  2  2 NA  1  2  2  2  2  2  2 NA  2  2  2  2  2  2  2  2  2  2
##  [43]  1  2  2  1  2  1  2  2  1  2  2  2  2  2  2  2  2  2  2  2  2  2  2  1  2  2 NA  2  2  2  2  2 NA  2  2  2  2  2  1  2  2  2
##  [85]  2  2  2  2  2  2  2  2 NA  2  2  2  2  2  1  2  2  2  2  2  2  2  2  2 NA  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2 NA  2
## [127]  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2  1  2  2  2  2  2  1  2  2  2  1  2  2  2  2  1  2  2  2  2  2  2  2  2  2
## [169]  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2  2  1  2  2  2  2  2  1  2  2  2  2  2  2  2  1  2  2
## [211]  2

Die Variable hand liegt numerisch vor, es treten die Werte 1 und 2 empirisch auf. Anhand des Kodierschemas ( Variablenübersicht) kann den vorkommenden Zahlen eine inhaltliche Bedeutung zugewiesen werden. Beispielsweise bedeutet der Wert 1 “links”. Diese Label werden nun im Faktor hinterlegt.

Außerdem ist erkennbar, dass manche Einträge als NA ausgegeben werden.NA ist kurz für “not available” und kennzeichnet, dass der Wert an dieser Stelle fehlt (z.B., weil jemand dieses Item im Fragebogen nicht beantwortet hat). Wie genau damit umgehen soll, wird später erläutert.

Vorgehensweise:

• Erstellung einer neuen Variable im Datensatz per Objektzuweisung: datensatz$neueVariable <- factor(...)
• Faktor erstellen mit der Funktion factor(Ausgangsvariable, levels = Stufen, labels = Label)
• Spezifikation der Faktorstufen im Argument levels, also der numerischen Ausprägungen auf der Ursprungsvariable (hier: 1 und 2)
• Spezifikation des Arguments labels, also die Label für die in levels hinterlegten numerischen Stufen (hier: “links”, “rechts”; unbedingt auf gleiche Reihenfolge achten!)

fb25$hand_factor <- factor(fb25$hand,                       # Ausgangsvariable
                           levels = 1:2,                  # Faktorstufen
                           labels = c("links", "rechts")) # Label für Faktorstufen
str(fb25$hand_factor)

##  Factor w/ 2 levels "links","rechts": 2 2 2 2 2 2 2 2 1 2 ...

head(fb25$hand_factor)

## [1] rechts rechts rechts rechts rechts rechts
## Levels: links rechts

Beispiel 2: Lieblingsfach (numerisch) als Faktor aufbereiten

Analog dazu wird nachfolgend die ebenfalls numerische Variable fach in einen Faktor umgewandelt. Sie wurde wie folgt erhoben:

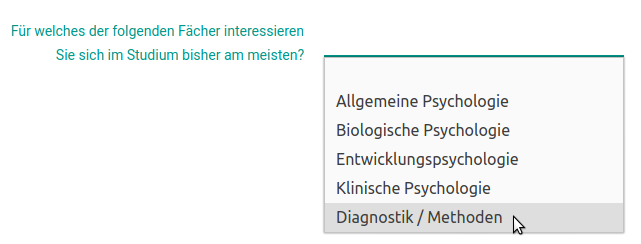
fb25$fach

##   [1]  4  4  4  4  4  4  4  2  2  2  5  4  3  2  3  4  3  4  5  5  4  3  4  4  4  5  4  3  3  4  2 NA  4  4  4  1  4  2  3  4  4  2
##  [43]  2  1  3  2  4  3  3  5  3  4  4  4  2  4  2  4  4  1  1  2  5  1  4  3  4  4 NA  3  1  1  4  1  4  5  3  3  4  3  4  4 NA  4
##  [85]  1  4  4  4  4  3  1  4 NA  1  4  3  3  3  4  4  3  1  4  4  3  4  4  3 NA  1  4  3  4  3  1  3  3  4  1  1  1  4  1  4  4  4
## [127]  4  3  4  4  4  1  4  1  4  2  2  3  4  2  4  5  4  1  1  4  2  1  1  1  5  2  4  4  4  4  2  4  4  3  5  5  3  4  2  1  4  1
## [169]  4  4  4  2  4  1  2  4  1  5  4  3  2  4  2  2  4  2  4  4  3  4  3  5  3  4  3  4  1  4  3  2  4  1  1  4  4  5  5  3  3  5
## [211]  4

Es treten die Ausprägungen 1 bis 5 empirisch auf. Auch hier werden die Label aus dem Kodierschema zugewiesen.

fb25$fach <- factor(fb25$fach,
                    levels = 1:5,
                    labels = c('Allgemeine', 'Biologische', 'Entwicklung', 
                               'Klinische', 'Diag./Meth.'))
str(fb25$fach)

##  Factor w/ 5 levels "Allgemeine","Biologische",..: 4 4 4 4 4 4 4 2 2 2 ...

Ein wichtiger Hinweis: In Beispiel 2 wurde die Ursprungsvariable mit dem Faktor überschrieben. D.h., die alte numerische Version dieser Variablen ist nun verschwunden, der Datensatz enthält nur noch den Faktor. Wenn Sie sich für diese Variante entscheiden, einen Faktor zu erstellen, ist es sehr wichtig, dass Sie den Befehl nur einmal ausführen und nicht versehentlich ein zweites Mal. Sonst kann es zu unerwünschtem Verhalten kommen (z.B., dass plötzlich alle Werte auf dieser Variablen als NA erscheinen).

Wir haben nun also gelernt, dass Faktoren auf verschiedene Weisen erstellt werden können. Wir benutzen nun die Funktion factor(), wenn unsere Variable zunächst nur numerisch vorlag (Beispiele 1 und 2) und wir eine Bedeutung zuordnen wollen.

In der Intro-Sitzung haben Sie bereits gesehen, dass Sie character-Variablen, deren Ausprägungen im Originaldatensatz im Textformat (statt wie in unserem Beispielen 1 und 2 als Zahlen) vorliegen, auch mit dem Befehl as.factor() in einen Faktor umwandeln konnten. Bei as.factor() handelt es sich um eine für solche Fälle geschaffene, etwas einfachere und schnellere Version des factor()-Befehls (das nennt man bei R eine “Wrapper”-Funktion), die keine zusätzlichen Argumente benötigt. factor() ist aber für eine größere Bandbreite von Fällen anwendbar, weshalb wir uns an ihn gewöhnen werden.

Hinweise zu den Levels und Labels

Die Reihenfolge von Levels und Labels ergibt sich während der Faktorerstellung:

• bei numerischen Variablen: entspricht den Ausprägungen der numerischen Ursprungsvariable
• bei character-Variablen: entspricht der alphabetischen Reihenfolge der Ausprägungen auf der Ursprungsvariable

Die Labels eines Faktors können mit der Funktion levels() abgerufen werden. Die Reihenfolge kann mithilfe der relevel()-Funktion geändert werden. Dafür muss dasjenige Label angesprochen werden, das die erste Position einnehmen soll (hier: ‘Diag./Meth.’).

levels(fb25$fach)         # Abruf

## [1] "Allgemeine"  "Biologische" "Entwicklung" "Klinische"   "Diag./Meth."

fb25$fach <- relevel(
  fb25$fach,              # Bezugskategorie wechseln
  'Diag./Meth.')          # Neue Bezugskategorie

Häufigkeitstabellen

Eine deskriptivstatistische Möglichkeit zur Darstellung diskreter (zählbarer) nominalskalierter Variablen sind Häufigkeitstabellen. Diese können in R mit der Funktion table() angefordert werden.

Absolute Häufigkeiten

table(fb25$fach)

## 
## Diag./Meth.  Allgemeine Biologische Entwicklung   Klinische 
##          16          32          26          39          93

Bei näherer Betrachtung fällt auf, dass an dieser Tabelle etwas nicht stimmt. Summiert man alle darin vorkommenden Werte auf…

table(fb25$fach) |> sum()

## [1] 206

… sieht man, dass nur 206 von allen 211 Beobachtungen darin Eingang gefunden haben. Das liegt daran, dass der table-Befehl ohne zusätzliche Argumente alle NAs einfach ignoriert. Um zu sehen, wieviele fehlende Werte wir insgesamt auf dieser Variable haben, müssen wir das Argument useNA spezifizieren. "ifany" bedeutet, dass fehlende Werte nur mitgezählt werden, falls es welche gibt.

table(fb25$fach, useNA = "ifany")

## 
## Diag./Meth.  Allgemeine Biologische Entwicklung   Klinische        <NA> 
##          16          32          26          39          93           5

Häufig sind relative Häufigkeiten informativer. Nachfolgend werden zwei Möglichkeiten zur Erstellung von relativen Häufigkeitstabellen in R gezeigt.

Relative Häufigkeiten (manuell)

Relative Häufigkeiten können aus absoluten Häufigkeiten abgeleitet werden: $h_j = \frac{n_j}{n}$.

Diese einfache Rechenvorschrift (Kategorienhäufigkeit geteilt durch Gesamthäufigkeit) kann auf das gesamte Tabellenobjekt angewendet werden. So wird jede einzelne absolute Kategorienhäufigkeit am Gesamtwert relativiert, es resultiert eine Tabelle der relativen Häufigkeiten.

tab <- table(fb25$fach, useNA = "ifany") # Absolute Haeufigkeiten
sum(tab)         # Gesamtzahl

## [1] 211

tab / sum(tab)   # Relative Haeufigkeiten

## 
## Diag./Meth.  Allgemeine Biologische Entwicklung   Klinische        <NA> 
##  0.07582938  0.15165877  0.12322275  0.18483412  0.44075829  0.02369668

Relative Häufigkeiten (per Funktion)

Alternativ kann die Funktion prop.table() (steht für proportions) auf das Tabellenobjekt mit den absoluten Häufigkeiten angewendet werden.

tab <- table(fb25$fach, useNA = "ifany")  # Absolute
prop.table(tab)                           # Relative

## 
## Diag./Meth.  Allgemeine Biologische Entwicklung   Klinische        <NA> 
##  0.07582938  0.15165877  0.12322275  0.18483412  0.44075829  0.02369668

Ungefähr 7.58% Ihres Jahrgangs geben als Lieblingsfach “Diagnostik/Methoden” an! Vielleicht können wir ja noch mehr von Ihnen mit dem nächsten Thema begeistern. :-)

Grafiken in R

Die Darstellung als Tabelle wirkt häufig langweilig, und zu viele Tabellen in einem Bericht / einer Arbeit schecken Leser*innen meist ab. Im Folgenden zeigen wir Ihnen mehrere mögliche grafische Darstellungsformen für diskrete nominalskalierte Variablen. Hierfür haben Sie in der Vorlesung die Optionen eines Balken- bzw. Säulendiagramms und eines Tortendiagramms kennengelernt.

Säulen- oder Balkendiagramm

Die Erstellung ist mit der Funktion barplot() möglich. Diese braucht zunächst nur ein Tabellenobjekt als Input, dass die absoluten Häufigkeiten für die verschiedenen Kategorien einer Variable enthält. Um uns das Leben etwas einfacher zu machen, ziehen wir für diese Abbildung nur eine Tabelle ohne fehlende Werte (ohne NAs) heran.

tab <- table(fb25$fach)
barplot(tab)

Die Grafik erscheint in der RStudio-Standardansicht “unten rechts” im Reiter “Plots”:

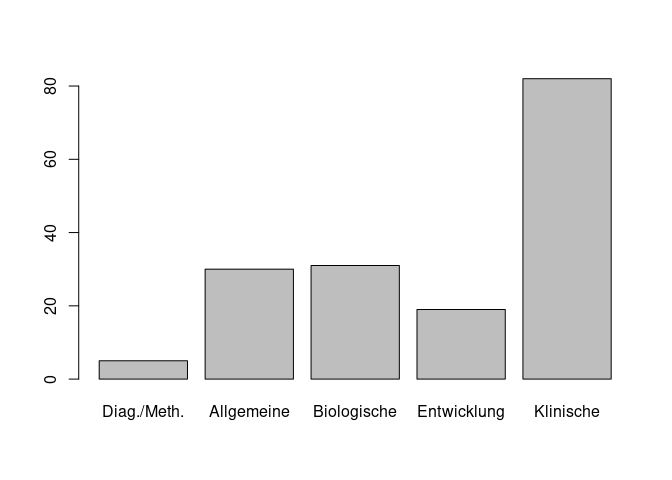
Tortendiagramm

Die Erstellug eines Tortendiagramms ist ebenfalls leicht zu erreichen. Die Funktion heißt pie() und braucht denselben Input wie barplot.

# Tortendiagramm
pie(tab)

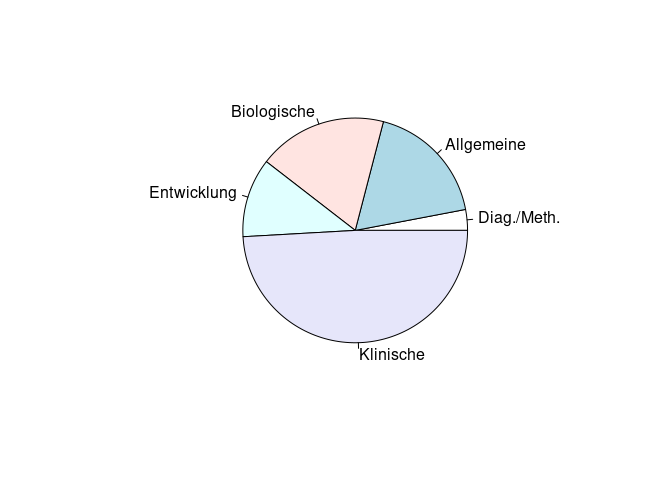
In der Vorlesung haben Sie bereits gelernt, dass diese Form der Darstellung aber nicht für detaillierte Analysen zu empfehlen ist, weil Erkenntnisse daraus viel schwerer zu ziehen sind. Bei den Zusatzargumenten werden wir uns also nur mit der Funktion barplot() beschäftigen.

Zusatzargumente für Plots

Die Funktionen zur Erstellung sehr simpler Grafiken sind also denkbar einfach - die Grafiken selbst aber zunächst nicht unbedingt hübsch. R bietet diverse Zusatzargumente zur Anpassung der Optik von Grafiken.

Farben in R

R kennt eine ganze Reihe vordefinierter Farben ($N = $ 657) mit teilweise sehr poetischen Namen. Diese können mit der Funktion colors() (ohne Argument) abgerufen werden. Hier sind die ersten 20 Treffer:

colors()[1:20]

##  [1] "white"         "aliceblue"     "antiquewhite"  "antiquewhite1" "antiquewhite2" "antiquewhite3" "antiquewhite4" "aquamarine"   
##  [9] "aquamarine1"   "aquamarine2"   "aquamarine3"   "aquamarine4"   "azure"         "azure1"        "azure2"        "azure3"       
## [17] "azure4"        "beige"         "bisque"        "bisque1"

Die Farben aus der Liste können als Zahl (Index) oder per Name angesprochen werden. Eine vollständige Liste der Farben findet sich zum Beispiel unter https://r-charts.com/colors. Farben können aber auch per RGB-Vektor (Funktion rgb()) oder HEX-Wert angesprochen werden.

Zusätzlich können Farbpaletten verwendet werden. Sie bestehen aus einem Farbverlauf, aus dem einzelne Farben “herausgezogen” werden, wodurch ein zusammengehöriges Farbthema in einer Abbildung entsteht. R liefert einige dieser Paletten: rainbow(...), heat.colors(...), topo.colors(...), … Die Farbpalette wird ebenfalls per col-Argugment spezifiziert. Technisch handelt es sich um eine Funktion, für die als Argument die Anzahl der Farben spezifiziert werden muss, die aus der Palette “gezogen” werden sollen. Es wäre also so, als würden wir diese 5 Farben per Hand eingeben, nur dass wir die Person entscheiden lassen, die eine Palette programmiert hat Beispielsweise werden mit col = rainbow(5) fünf Farben aus der rainbow-Palette gezogen. Der Output würde so aussehen.

rainbow(5)

## [1] "#FF0000" "#CCFF00" "#00FF66" "#0066FF" "#CC00FF"

Die Farben werden hier nicht direkt mit ihrem Namen, sondern mit dem Hex-Code ausgegeben. #FF0000 steht dabei beispielsweise für ein rot.

Beispiel für angepasste Abbildung

barplot(tab,
        col = rainbow(5),                        # Farbe
        ylab = 'Anzahl Studierende',             # y-Achse Bezeichnung
        main = 'Lieblingsfach im 1. Semester',   # Überschrift der Grafik
        las = 2,                                 # Ausrichtung der Labels
        cex.names = 0.8)                         # Schriftgröße der Labels

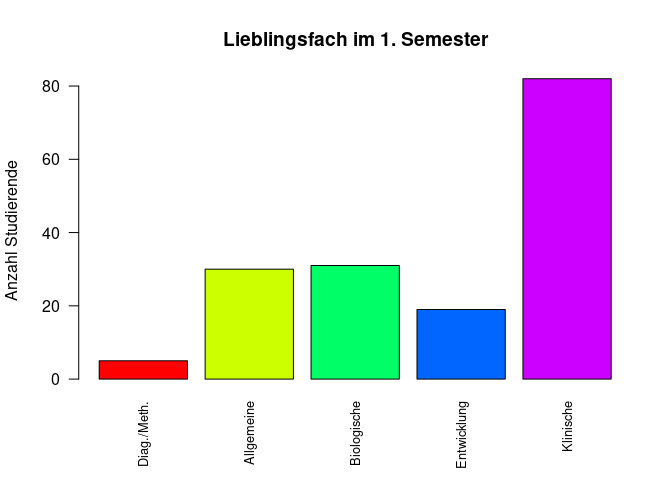
Alle verwendeten Argumente (bis auf eines) sind bereits in der Tabelle oben beschrieben. Wir fügen einen Titel zur y-Achse mittels ylab hinzu. main ist verantwortlich für den Titel der Grafik, während las (kurz für “label axis style”) die Beschriftung der Säulen dreht. Das bisher nicht genannte Argument cex.names (kurz für “character expansion”) verändert die Schriftgröße für die Beschriftung der Balken. Wenn wir diese nicht anpassen würden, würde die Schrift den Rahmen der Standardeinstellungen für Grafen in R sprengen und damit teilweise außerhalb des Bildes stehen.

Hinweis: Es gibt natürlich noch viele weitere Argumente, mit denen Sie Bestandteile des Diagramms anpassen können. Falls Sie sich beispielsweise fragen, wie sie aus dem Säulendiagramm ein Balkendiagramm machen können, könnten Sie das mit dem Argument horiz erreichen. Wenn Sie also die horizontale Ausrichtung der Grafik auf TRUE setzen, erhalten Sie horizontale Balken anstatt vertikale Säulen.

Grafiken speichern

Es gibt zwei Möglichkeiten, um in R erzeugte Grafiken als Bilddatei zu speichern: manuell und per Funktion.

Möglichkeit 1: Manuelles Speichern

Klicken Sie auf die Schaltfläche “Export” und dann auf “Save as Image”…

…und spezifizieren Sie dann Dateiname (ggf. Pfad) und Größe/Größenverhältnis.

Wenn kein Pfad spezifiziert wird, erscheint die Datei in Ihrem aktuellen Arbeitsverzeichnis.

Möglichkeit 2: Speichern mit der Funktion jpeg("Dateiname.jpg")

Auch ohne die grafische Oberfläche von RStudio ist die Erstellung und das Speichern einer Grafik mittels R möglich. Zunächst wird das für Euch keinen großen Einfluss haben, da wir nicht nur in der Konsole arbeiten. Wenn jemand sich doch in die Richtung vertieft, ist die Interaktion mit Servern auf Grundlage einer Konsole selten zu vermeiden. Dann könnte auch die folgende Erstellung eine Rolle spielen.

Wir starten die Erstellung einer Grafik mittels Code mit der jpeg()-Funktion. Hierin machen wir sozusagen eine grafische Umgebung auf. In dieser legen wir bereits einige Paramter der Bilddatei fest (wie Höhe, Breite und auch Auflösung). Als nächstes kommt der Code für die Grafik. Diesen haben wir bereits gesehen. Der entstehende Plot wird jetzt in die zuvor erzeugte grafische Umgebung “abgelegt”. Mit der Funktion dev.off() wird die Erstellung beendet. Die grafische Umgebung (und damit die Entwicklung unserer Bild-Datei) wird damit “geschlossen”.

jpeg("Mein-Barplot.jpg", width=15, height=10, units="cm", res=150) # Eröffnung Bilderstellung
barplot(tab,
 col = rainbow(5),
 ylab = 'Anzahl Studierende',
 main = 'Lieblingsfach im 1. Semester',
 las = 2,
 cex.names = 0.8)
dev.off()                                                         # Abschluss Bilderstellung

Auch hier gilt: Wenn kein Pfad spezifiziert wurde, liegt die Datei in Ihrem Arbeitsverzeichnis. In der Funktion jpeg() kann mit den Argumenten units angegeben werden, in welcher Einheit die anderen Argumente zu verstehen sind.

Deskriptivstatistische Kennwerte auf Nominalskalenniveau

Modus

Der Modus (Mo) ist ein Maß der zentralen Tendenz, das die häufigste Ausprägung einer Variable anzeigt. Die Häufigkeiten sind ja schon in der Häufigkeitstabelle enthalten. Man könnte den Modus also einfach ablesen. Das gleiche lässt sich allerdings auch anhand von Funktionen tun:

tab            # Tabelle ausgeben

## 
## Diag./Meth.  Allgemeine Biologische Entwicklung   Klinische 
##          16          32          26          39          93

max(tab)       # Größte Häufigkeit

## [1] 93

which.max(tab) # Modus

## Klinische 
##         5

Der Modus der Variable fach lautet also Klinische, die Ausprägung trat 93 mal auf.

Relativer Informationsgehalt

Der relative Informationsgehalt ist ein Dispersionsmaß, das schon auf Nominalskalenniveau funktioniert. Dafür gibt es in R allerdings keine Funktion! Aus Lehreinheit 1 wissen Sie jedoch, dass R als Taschenrechner genutzt werden kann, folglich können beliebig komplexe Gleichungen in R umgesetzt werden. Die Formel zur Berechnung des relativen Informationsgehalts $H$ lautet:

$$H = -\frac{1}{\ln(k)} \sum_{j=1}^k{h_j * \ln h_j} $$

Wir benötigen also $h_j$, was die relativen Häufigkeiten der einzelnen Kategorien bezeichnet. Hier haben wir schon gelernt, dass wir diese durch anwenden der Funktion prop.table auf unser Objekt tab erhalten können. Anschließend muss noch mit der Funktion log gearbeitet werden, die den natürlichen Logarithmus als Standardeinstellung berechnet. $k$ ist in diesem Fall die maximale Nummer einer unserer Kategorien - also die Kategorienanzahl 5. Falls wir diese nicht selbst zählen möchten, kann dim uns die Anzahl an Spalten in tab verraten. Der Rest ist dann nur einfache Multiplikation, Addition und Division.

hj <- prop.table(tab)       # hj erstellen
ln_hj <- log(hj)            # Logarithmus bestimmen
ln_hj                       # Ergebnisse für jede Kategorie

## 
## Diag./Meth.  Allgemeine Biologische Entwicklung   Klinische 
##  -2.5552874  -1.8621403  -2.0697796  -1.6643145  -0.7952767

summand <- ln_hj * hj       # Berechnung für jede Kategorie
summe <- sum(summand)       # Gesamtsumme
k <- dim(tab)               # Anzahl Kategorien
relinf <- -1/log(k) * summe # Relativer Informationsgehalt
relinf

## [1] 0.884215

Eine kleine Abkürzung durch Einsparen der Schritte am Ende könnte hier folgendermaßen mittels Pipe erreicht werden:

relinf <- (ln_hj * hj) |> sum() * (-1/log(k))  # Relativer Informationsgehalt
relinf

## [1] 0.884215

Eine alternative Schreibweise, die ohne Zwischenschritte auskommt, dafür aber in Form von vielen Klammern stark verschachtelt ist, lautet:

- 1/log(dim(table(fb25$fach))) * sum(prop.table(table(fb25$fach)) * log(prop.table(table(fb25$fach))))

## [1] 0.884215

Wie man hier sieht, stößt die Schachtelung ohne das Speichern von Zwischenergebnissen oder das nutzen der Pipe schnell an die Grenzen der Übersichtlichkeit.

In allen drei Varianten kommen wir aber zum gleichen Schluss: der relative Informationsgehalt der Variable fach beträgt 0.884. Da der mögliche Wertebereich zwischen 0 (für alle Personen selbe Kategorie) und 1 (für alle Kategorien gleich viele Personen) variiert, kann hier von einer starken Verteilung der Personen ausgegangen werden.

Ordinalskalierte Variablen

In diesem Abschnitt lernen Sie deskriptivstatistische Kennwerte für ordinalskalierte Variablen kennen. Aus der Vorlesung wissen Sie schon, dass Median und Interquartilsabstand (IQA) nur für die Klasse der geordneten Kategorien (auch “Rangklassen”) sinnvoll sind, nicht für singuläre Daten (“Rangwerte”).

Zunächst aber eine Wiederholung: Wie Sie aus der Vorlesung wissen, können die in der Tabelle am Anfang dieses Dokuments aufgeführten statistischen Kennwerte (Zentrale Lage, Dispersion) auch für Skalenniveaus genutzt werden, die “weiter unten” in der Tabelle stehen. Für ordinalskalierte Variablen (Rangklassen) kann also auch der Modus berechnet werden.

Nachfolgend soll mit dem Item zur Sicherheit in der Studienwahl gearbeitet werden. Auf dem Screenshot ist das Item (obere) nochmal abgebildet.

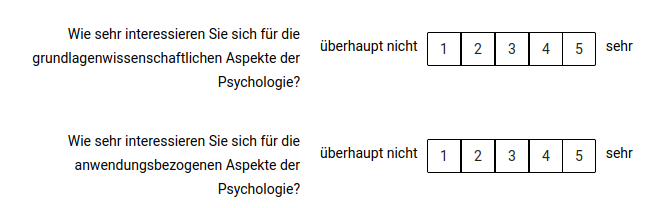
Es treten die Werte 1 bis 4 empirisch auf, außerdem gibt es 5 fehlende Werte (dargestellt als NA):

fb25$sicher

##   [1]  3  4  4  4  4  3 NA  3  4  3  4  4  4  4  3  3  4  4  4  4  3  4  4  4  4  4  3  4  3  3  3 NA  3  3  4  4  4  4  4  3  4  4
##  [43]  2  3  3  3  3  4  4  3  4  3  3  4  4  3  4  3  3  3  4  4  4  4  4  4  3  4 NA  3  4  3  1  3  4  1  4  4  4  4  4  2  3  4
##  [85]  4  3  3  3  4  4  3  4 NA  4  3  3  4  4  4  4  3  4  3  3  4  4  4  4 NA  4  3  3  4  4  3  2  4  3  3  4  4  3  4  4  4  3
## [127]  3  3  3  4  4  4  2  3  4  3  4  3  3  3  4  3  4  3  3  4  2  3  3  4  4  4  3  4  4  4  3  3  3  3  3  4  4  4  3  3  3  4
## [169]  4  4  4  3  3  3  4  4  3  3  3  4  3  4  3  3  4  3  3  3  4  3  3  4  3  3  3  4  2  3  3  4  2  4  3  3  4  4  3  4  4  4
## [211]  4

Wiederholung:

table(fb25$sicher, useNA = "ifany")              # Absolute Haeufigkeiten (ohne NA)

## 
##    1    2    3    4 <NA> 
##    2    7   90  107    5

prop.table(table(fb25$sicher, useNA = "ifany"))  # Relative Haeufigkeiten

## 
##           1           2           3           4        <NA> 
## 0.009478673 0.033175355 0.426540284 0.507109005 0.023696682

which.max(table(fb25$sicher))                    # Modus

## 4 
## 4

Fehlende Werte

Fehlende Werte (dargestellt als NA) in empirischen Untersuchungen können aus vielen Gründen auftreten:

• Fragen überlesen / nicht gesehen
• Antwort verweigert
• Unzulässige Angaben gemacht (im Papierformat)
• Unleserliche Schrift (im Papierformat)
• …

Für statistische Analysen sind fehlende Werte ein Problem, weil sie außerhalb der zulässigen Antworten liegen.

Wir haben bereits gesehen, dass wir in der table-Funktion mit Argumenten festlegen können, ob NAs in der Zusammenfassung angezeigt werden oder nicht. Aber wie geht man bei statistischen Berechnungen damit um? In R kann man solche Fälle auf zwei unterschiedlichen Ebenen berücksichtigen:

• Global: na.omit(datensatz)
  • Entfernt alle Beobachtungen, die auf irgendeiner Variable einen fehlenden Wert haben
  • Häufig auch “listenweiser Fallausschluss” genannt
• Lokal: na.rm = TRUE
  • Das Argument na.rm ist in vielen Funktionen für univariate Statistiken enthalten
  • Per Voreinstellung wird NA als Ergebnis produziert, wenn fehlende Werte vorliegen
  • Fehlende Werte werden nur für diese eine Analyse ausgeschlossen, wenn sie auf der darin untersuchten Variable keinen Wert haben - Datensatz bleibt erhalten

Fehlende Werte sind ein ganz eigenes Forschungsgebiet der Methodik und man könnte eine ganze Veranstaltung nur zu diesem Thema halten. Hierfür haben wir leider keine Zeit, weshalb wir uns der sehr einfachen Methode bedienen, dass wir fehlende Werte von der Analyse ausschließen. Dies ist kein empfohlenes Vorgehen für empirische Arbeiten im fortgeschrittenen Verlauf des Studium!

Deskriptivstatistische Kennwerte ab Ordinalskalenniveau

Median

Wir können uns den Einfluss fehlender Werte auf die Arbeit mit R mit der Betrachtung der Funktion für den Median, die praktischerweise median() heißt, veranschaulichen, indem wir einmal ein extra Argument benennen.

median(fb25$sicher)                 # Ohne Argument für NA: funktioniert nicht

## [1] NA

median(fb25$sicher, na.rm = TRUE)   # Expliziter Ausschluss: funktioniert

## [1] 4

Ohne Argument für die Behandlung der fehlenden Werte wird NA auch als Ergebnis ausgegeben. Mit passendem Argument erhalten wir ein numerisches Ergebnis: Der Median für die Variable sicher beträgt also 4.

Quantile, IQB und IQA

Für eine Beschreibung der Dispersion wird häufig der Interquartilsbereich (IQB) genutzt. IQB ist der Bereich zwischen dem 1. und dem 3. Quartil.

Um die Quartile oder jedes beliebige andere Quantil einer Verteilung zu erhalten, kann die Funktion quantile() verwendet werden. Beispielsweise können wir die Grenzen des IQB und den Median mit folgender Eingabe gleichzeitig abfragen.

quantile(fb25$sicher,
         c(.25, .5, .75),                   # Quartile anfordern
         na.rm = TRUE)

## 25% 50% 75% 
##   3   4   4

Der Interquartilsbereich liegt also zwischen 3 und 4.

Den Interquartilsabstand (IQA) können wir nun bestimmen, indem wir das Ergebnis für das dritte und das erste Quartil subtrahieren.

$$IQA = Q_3 - Q_1$$

Mit quantile() ist die Umsetzung in R etwas umständlich, da wir die Funktion zwei Mal aufrufen und die Differenz daraus bilden müssen.

quantile(fb25$sicher, .75, na.rm=TRUE) - quantile(fb25$sicher, .25, na.rm=TRUE)

## 75% 
##   1

Dabei ist in der Ausgabe besonders die Überschrift verwirrend (75%), die hier nichts mit der Bedeutung des Wertes zu tun hat. Der IQA der Variable sicher beträgt 1. Für die Berechnung des IQA gibt es auch die direkte Funktion IQR(), die uns das ganze einfacher macht.

IQR(fb25$sicher, na.rm = TRUE)

## [1] 1

Boxplots

Eine geeignete grafische Darstellungsform für (mindestens) ordinalskalierte Daten ist der Boxplot. In der Theorie wird dieser Plot meist in der Idealform vorgestellt.

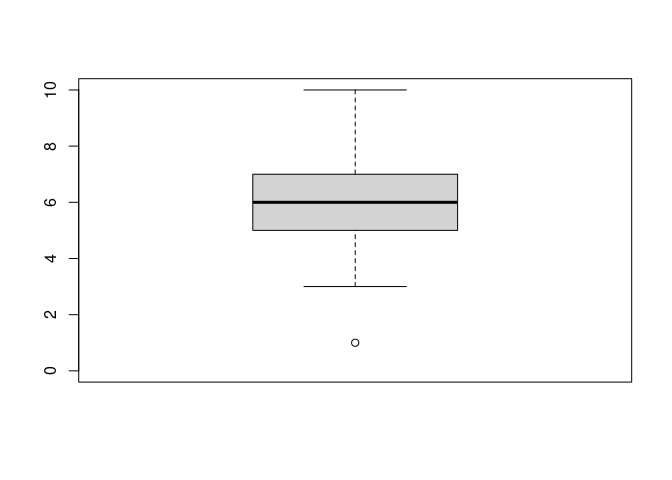
Die Box liegt zwischen dem ersten (5) und dritten Quartil (7). Der dicke schwarze Balken stellt den Median (6) dar. Die Whisker entsprechen dem jeweils extremstem empirischem Wert im Bereich Q3 + 1.5*IQA für das Maximum bzw. Q1 - 1.5*IQA für das Minimum. Der IQA beträgt in unserem Beispiel 2. Das bedeutet, dass die maximalen Whisker-Grenzen 2 und 10 sind. Wir sehen in der Abbildung, dass der obere Whisker seine maximale Grenze von 10 erreicht, während der untere nur bis zum Wert 3 geht. Das zeigt uns, dass es empirisch keine Werte gab, die kleiner als 3 aber größer gleich 2 waren. 3 ist also der kleinste empirische Wert innerhalb der Grenzen für den Whisker. Noch extremere Werte werden als Punkte dargestellt wie wir auf der Grafik sehen können.

In der Praxis wird diese Idealform aber nicht immer erreicht. Wir wollen für unsere Variable sicher diesen Plot erstellen. Er kann über die Funktion boxplot() angefordert werden:

boxplot(fb25$sicher)

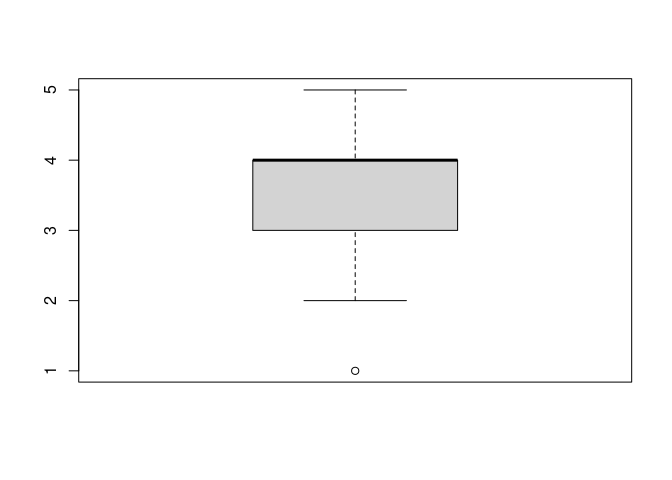
In diesem Beispiel betragen Median, Q3 sowie der obere Whisker jeweils 4, sodass sich die entsprechenden Linien überlagern.

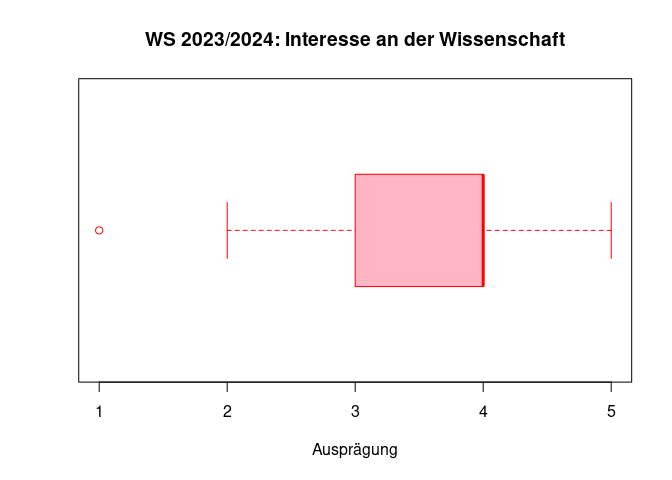
Auch ein Boxplot kann grafisch angepasst werden. Nachfolgend sehen Sie ein Beispiel, in dem möglichst viel verändert wurde, um die verschiedenen Möglichkeiten aufzuzeigen. Nicht alle Veränderungen sind unbedingt sinnvoll in diesem Fall.

boxplot(fb25$sicher,
        horizontal = TRUE,                # Ausrichtung des Boxplots
        main = "WS 2025/26: Sicherheit in der Studienwahl",  # Überschrift der Grafik
        xlab = "Ausprägung",              # x-Achse Bezeichnung 
        las = 1,                          # Ausrichtung der Labels
        border = "red",                   # Farbe der Linien im Boxplot
        col = "pink1",                    # Farbe der Fläche innerhalb der Box
        xaxt = "n")                       # x-Achsenbeschriftung unterdrücken
axis(1, at = 1:4)                         # Bessere x-Achsenbeschriftung