Tests für unabhängige Stichproben

Vorbereitende Schritte

Den Datensatz fb24 haben wir bereits über diesen Link heruntergeladen und können ihn über den lokalen Speicherort einladen oder Sie können Ihn direkt mittels des folgenden Befehls aus dem Internet in das Environment bekommen. In den vorherigen Tutorials und den dazugehörigen Aufgaben haben wir bereits Änderungen am Datensatz durchgeführt, die hier nochmal aufgeführt sind, um den Datensatz auf dem aktuellen Stand zu haben:

#### Was bisher geschah: ----

# Daten laden
load(url('https://pandar.netlify.app/daten/fb24.rda'))

# Nominalskalierte Variablen in Faktoren verwandeln
fb24$hand_factor <- factor(fb24$hand,
                             levels = 1:2,
                             labels = c("links", "rechts"))
fb24$fach <- factor(fb24$fach,
                    levels = 1:5,
                    labels = c('Allgemeine', 'Biologische', 'Entwicklung', 'Klinische', 'Diag./Meth.'))
fb24$ziel <- factor(fb24$ziel,
                        levels = 1:4,
                        labels = c("Wirtschaft", "Therapie", "Forschung", "Andere"))
fb24$wohnen <- factor(fb24$wohnen, 
                      levels = 1:4, 
                      labels = c("WG", "bei Eltern", "alleine", "sonstiges"))

# Rekodierung invertierter Items
fb24$mdbf4_r <- -1 * (fb24$mdbf4 - 5)
fb24$mdbf11_r <- -1 * (fb24$mdbf4 - 5)
fb24$mdbf3_r <- -1 * (fb24$mdbf4 - 5)
fb24$mdbf9_r <- -1 * (fb24$mdbf4 - 5)

# Berechnung von Skalenwerten
fb24$gs_pre  <- fb24[, c('mdbf1', 'mdbf4_r', 
                        'mdbf8', 'mdbf11_r')] |> rowMeans()
fb24$ru_pre <-  fb24[, c("mdbf3_r", "mdbf6", 
                         "mdbf9_r", "mdbf12")] |> rowMeans()

# z-Standardisierung
fb24$ru_pre_zstd <- scale(fb24$ru_pre, center = TRUE, scale = TRUE)

Was erwartet Sie?

Nachdem wir uns zuletzt mit der Frage auseinandergesetzt haben, ob unsere Stichprobe aus einer Population mit bekanntem Mittelwert ($\mu_0$) stammt oder aus einer davon abweichenden Grundgesamtheit, fokussieren wir uns nun auf Unterschiede zwischen Stichproben aus zwei Gruppen. Hierbei muss zwischen unabhängigen und abhängigen Stichproben unterschieden werden - um den ersten Fall geht es uns hier, den Zweiten gucken wir uns in der nächsten Sitzung an.

In dieser Sitzung geht es uns um primär um zwei Vergleiche:

1. Unterscheiden sich Studierende, die primäre an klinischen Inhalten interessiert sind in ihrer Lebenszufriedenheit von denen, die ihre Interessen eher in anderen Bereichen der Psychologie sehen? (t-Test und Cohen’s d für unabhängige Stichproben)
2. Sind klinisch interessierte Studierende zu Beginn der allerersten Sitzung eines Statistik Kurs im Psychologiestudium im Mittel schlechter gelaunt, als Studierende mit anderen Interessenslagen? (Wilcoxon-Test für unabhängige Stichproben)

Außerdem finden Sie im Anhang auch noch eine weitere Frage:

3. Haben Studierende mit Wohnort in Uninähe (Frankfurt) mit gleicher Wahrscheinlichkeit einen Nebenjob wie Studierende, deren Wohnort außerhalb von Frankfurt liegt? (Vierfelder-$\chi^2$-Test)

Mittelwertsvergleich

Wie oben bereits vorgestellt, geht es uns in diesem Abschnitt darum, dass wir untersuchen wollen, ob Studierende, die sich für die klinische Psychologie interessieren, im Mittel das gleiche Ausmaß an Lebenszufriedenheit aufweisen wie Studierende, deren Hauptinteresse in einem der vielen und spannenden anderen Bereiche der Psychologie liegt (zum Beispiel der Methodenlehre!). Hinsichtlich der Richtung der Hypothese können wir uns nicht genau festlegen, weil wir für beides hinreichend gute Argumente gefunden haben. Haben Personen, die sich für die klinische Psychologie interessieren eine stärkere Tendenz dazu, sich mit Problemen und Krankheiten zu befassen und sind deswegen weniger zufrieden mit ihrem Leben ($H_1: \mu_1 < \mu_2$)? Oder freuen sich Studierende, die sich für klinische Inhalte interessieren mehr darüber nun, im Psychologiestudium, dieser Faszination endlich stärker nachgehen zu können ($H_1: \mu_1 > \mu_2$)? Weil wir diese und sehr viele andere Möglichkeiten nicht ausreichend gut gegeneinander abwägen können, legen wir ein ungerichtetes Hypothesenpaar fest: $H_0 : \mu_1 = \mu_2$ und $H_1: \mu_1 \neq \mu_2$.

Vorbereitende Schritte

Die Gruppierungsvariable in unserer Fragestellung muss für die Nutzung der Funktionen in R als Faktor vorliegen. Bei uns soll es um das Interesse am Fach klinischer Psychologie gehen (ja vs. nein). Die entsprechende (nominalskalierte) Variable liegt noch nicht im Datensatz vor, kann aber einfach erstellt werden, indem die nichtklinischen Interessen in eine Kategorie zusammengefasst werden. Dies erfolgt per logischer Abfrage (fb24$fach == "Klinische") und anschließender Transformation des Ergebnisses in eine Faktorvariable:

fb24$fach_klin <- factor(as.numeric(fb24$fach == "Klinische"),
                         levels = 0:1,
                         labels = c("nicht klinisch", "klinisch"))

Wir können mit is.factor() überprüfen, ob die Variable fach_klin im Datensatz tatsächlich ein Faktor ist.

is.factor(fb24$fach_klin)

## [1] TRUE

Diese Funktion gibt uns einen boolschen Wert (TRUE oder FALSE) und beantwortet damit unsere Frage, ob das klinische Interesse ein factor ist oder nicht. Wir sehen aufgrund der Antwort als TRUE, dass die Variable fach_klin als Faktor vorliegt.

Auch die levels können wir bestimmen

levels(fb24$fach_klin)

## [1] "nicht klinisch" "klinisch"

Der Faktor hat also 2 Stufen.

Deskriptivstatistik

Im ersten Schritt wollen wir uns die Daten deskriptiv anschauen. Dazu können wir die Daten entweder visuell oder durch statistische Kennwerte aufbereiten. Wir werfen zunächst vorbereitend einen tabellarischen Blick auf die Variable klinisches Interesse:

table(fb24$fach_klin)

## 
## nicht klinisch       klinisch 
##             99             88

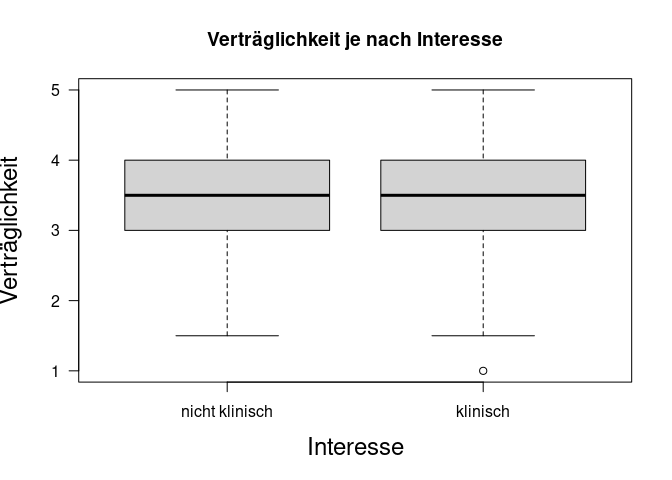
Mithilfe eines Boxplots, bzw. mithilfe von Histogrammen, lassen sich Unterschiede zwischen Gruppen gut untersuchen. Wir verwenden hier einige Zusatzeinstellungen, um die Grafiken übersichtlicher und auch ein wenig ansprechender zu gestalten.

# Gruppierter Boxplot :
boxplot(fb24$lz ~ fb24$fach_klin, 
        xlab="Interesse", ylab="Lebenszufriedenheit", 
        las=1, cex.lab=1.5, 
        main="Lebenszufriedenheit je nach Interesse")

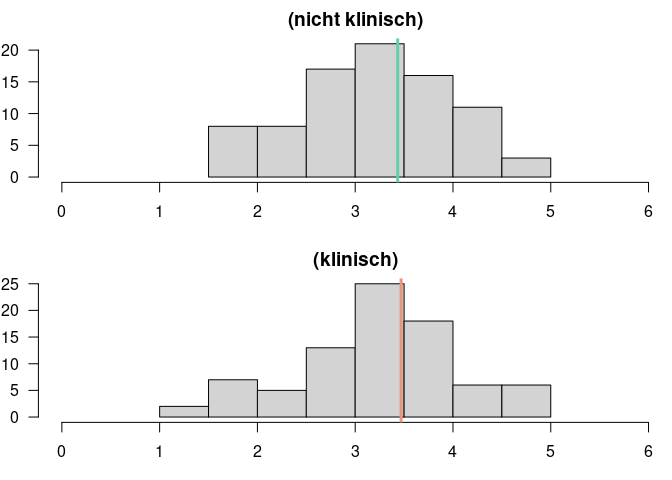
# Je ein Histogramm pro Gruppe, untereinander dargestellt, vertikale Linie für den jeweiligen Mittelwert
par(mfrow=c(2,1), mar=c(3,2,2,0))
hist(fb24[(fb24$fach_klin=="nicht klinisch"), "lz"], main="(nicht klinisch)", 
     xlim=c(1,7), xlab="", ylab="", las=1)
abline(v=mean(fb24[(fb24$fach_klin=="nicht klinisch"), "lz"], na.rm=T), col="aquamarine3", lwd=3)
hist(fb24[(fb24$fach_klin=="klinisch"), "lz"], main="(klinisch)", 
     xlim=c(1,7), xlab="", ylab="", las=1)
abline(v=mean(fb24[(fb24$fach_klin=="klinisch"), "lz"], na.rm=T), col="darksalmon", lwd=3)

fb24$lz ~ fb24$fach_klin ist die Formelnotation in R, welche Sie im Rahmen der Regression noch genauer kennenlernen werden. Links von der ~ (Tilde) steht die abhängige Variable (hier der Wert in der Lebenszufriedenheit), deren Mittelwertsunterschiede durch die unabhängige Variable (hier Interesse) rechts der ~ “erklärt” werden soll. Der Befehl par(mfrow=c(2,1), mar=c(3,2,2,0)) bewirkt, dass 2 Grafiken untereinander dargestellt werden - und zwar im selben Plot. Das Argument mfrow definiert ein Plot-Array mit der angegebenen Anzahl von Zeilen und Spalten (wobei mit mfrow die Plots zeilenweise verteilt werden; alternativ mit mfcol). Mit dem Argument mar werden für unten, links, oben und rechts die Randabstände spezifiziert. Spielen Sie doch einmal selbst an den Einstellungen herum und schauen nach, was die Argumente jeweils bewirken!

Damit von nun an nicht immer zwei Grafiken in einem Plot dargestellt werden, können wir die Einstellungen zurücksetzen, indem wir den klassischen IT Trick des “Ausschalten und wieder Einschalten” nutzen:

dev.off()

## null device 
##           1

Wir können uns auch Deskriptivstatistiken ansehen. Bspw. könnten wir uns die Mittelwerte oder die SDs etc. ausgeben lassen. Dazu nehmen wir entweder die summary() und wählen die entsprechenden Fälle aus oder wir machen uns das psych-Paket zunutze. Wir hatten im letzen Beitrag detaillierter besprochen, was Pakete sind und wie sie funktionieren. Um psych nutzen zu können, muss es installiert sein (install.packages()). Falls dem so ist, kann das Paket mit library() eingeladen werden. Die Funktion, die uns interessiert, heißt describeBy(), welche die Gruppenaufteilung bereits für uns übernimmt.

library(psych)
describeBy(x = fb24$lz, group = fb24$fach_klin)        # beide Gruppen im Vergleich 

## 
##  Descriptive statistics by group 
## group: nicht klinisch
##    vars  n mean   sd median trimmed  mad min max range  skew kurtosis   se
## X1    1 99 5.07 1.15    5.2    5.15 1.19   2   7     5 -0.57    -0.22 0.12
## --------------------------------------------------------------- 
## group: klinisch
##    vars  n mean   sd median trimmed  mad min max range skew kurtosis   se
## X1    1 88 4.76 1.14    4.8     4.8 1.19   2   7     5 -0.3    -0.51 0.12

Achtung, bei den hier berichteten sd handelt es sich nicht um die Stichprobenkennwerte $s$, sondern um die Populationsschätzer $\hat{\sigma}$. Daher berechnen wir die Standardabweichung auch nochmals per Hand:

vertr_nichtKlinisch <- fb24$vertr[fb24$fach_klin=="nicht klinisch"]
sigma_nichtKlinisch <- sd(vertr_nichtKlinisch, na.rm = T)
n_nichtKlinisch <- length(vertr_nichtKlinisch[!is.na(vertr_nichtKlinisch)])
sd_nichtKlinisch <- sigma_nichtKlinisch * sqrt((n_nichtKlinisch-1) / n_nichtKlinisch)
sd_nichtKlinisch

## [1] 0.761505

vertr_klinisch <- fb24$vertr[fb24$fach_klin=="klinisch"]
sigma_klinisch <- sd(vertr_klinisch, na.rm = T)
n_klinisch <- length(vertr_klinisch[!is.na(vertr_klinisch)])
sd_klinisch <- sigma_klinisch * sqrt((n_klinisch-1) / n_klinisch)
sd_klinisch

## [1] 0.854448

Voraussetzungen

Damit wir den Ergebnissen des t-Tests trauen können, müssen dessen Voraussetzungen erfüllt sein. Diese sind:

1. zwei unabhängige Stichproben $\rightarrow$ ok
2. die einzelnen Messwerte innerhalb der Gruppen sind voneinander unabhängig (Messwert einer Vpn hat keinen Einfluss auf den Messwert einer anderen) $\rightarrow$ ok
3. das untersuchte Merkmal ist in den Grundgesamtheiten der beiden Gruppen normalverteilt $\rightarrow$ (ggf.) optische Prüfung
4. Homoskedastizität: Varianzen der Variablen innerhalb der beiden Populationen sind gleich $\rightarrow$ Levene-Test

Wenn das Merkmal, das wir untersuchen, in der Population normalverteilt ist (Voraussetzung 3), können wir den $t$-Test nutzen. Allerdings haben wir in den meisten Fällen keine zusätzliche Information über die Verteilung in der Population als die, die wir aus unserer Stichprobe ziehen können. Daher ist es üblich, die Annahme optisch zu prüfen. Das werden wir im Folgenden auch tun, nur vorab der Zusatz, dass in vielen Studien aufgrund der Stichprobengröße auf die Prüfung der Normalverteilungsannahme verzichtet wird. In Fällen, in denen die Stichprobe ausreichend groß ist, folgt die Stichprobenkennwerteverteilung wegen des zentralen Grenzwertsatzes auch unabhängig von der Verteilung in der Population der $t$-Verteilung. Dabei ist es Auslegungssache was genau “ausreichend groß” bedeutet. Häufig wird die Daumenregel von $n > 30$ in jeder Gruppe genutzt. Bei solch kleinen Stichproben greift der Effekt allerdings nur dann, wenn das Merkmal zumindest symmetrisch verteilt ist. Andere Empfehlungen gehen besonders bei sehr schiefen Verteilungen in Richtung von $n > 80$ pro Gruppe.

Um die Verteilung optisch zu prüfen, haben wir zwei Möglichkeiten:

• Möglichkeit 1: die bei Normalverteilung erwartete Dichtefunktion über das Histogramm legen und so die Übereinstimmung beurteilen
• Möglichkeit 2: QQ-Plot (quantile-quantile): es wird die beobachtete Position eines Messwerts gegen diejenige Position, die unter Gültigkeit der Normalverteilung zu erwarten wäre, abgetragen. Bei Normalverteilung liegen die Punkte (in etwa) auf einer Geraden.

Für den QQ-Plot gibt es in der Basis-Funktionalität von R zwar einen integrierten Befehl (qqnorm()), aber die Funktion qqPlot() aus dem Paket car liefert uns noch einige bequeme Zusatzinformationen. Wie immer muss das Paket vorher installiert werden (install.packages("car")).

library(car)

## Loading required package: carData

## 
## Attaching package: 'car'

## The following object is masked from 'package:psych':
## 
##     logit

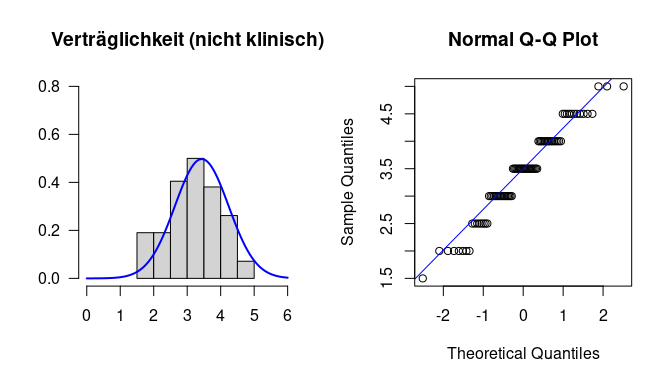
# Gruppe 1 (nichtKlinisch) 
par(mfrow=c(1,2))

lz_nichtKlinisch <- fb24[(fb24$fach_klin=="nicht klinisch"), "lz"]

hist(lz_nichtKlinisch, 
     xlim=c(1,7), ylim=c(0,.8), 
     main="Lebenszufriedenheit (nicht klinisch)", 
     xlab="", ylab="", 
     las=1, probability=T)
curve(dnorm(x, 
            mean = mean(lz_nichtKlinisch, na.rm=T), 
            sd = sd(lz_nichtKlinisch, na.rm=T)), 
      col="blue", lwd=2, add=T)

qqPlot(lz_nichtKlinisch)

## [1] 97 77

dev.off()

## null device 
##           1

Mithilfe von curve() kann eine Linie in eine Grafik eingezeichnet werden. Hierbei bezeichnet x die x-Koordinate. dnorm() hatten wir bereits kennen gelernt. Diese Funktion beschreibt die Dichte der Normalverteilung. Die Normalverteilung ist eindeutig durch ihren Mittelwert und durch ihre Standardabweichung definiert. Wir müssen dnorm() also jeweils den empirischen Mittelwert sowie die empirische Standardabweichung übergeben. Wenn man es sehr genau nehmen will, müsste man hier also eine Verrechnung der von R erzeugten Standardabweichung vornehmen. Wie im letzten Tutorial beschrieben nutzen wir aber einfach das Ergebnis von sd(). Dies wird auch in allen weiteren Tutorials ohne zusätzlichen Hinweis gemacht. Das Argument add = T ist nötig, da sonst ein neuer Plot für die Kurve erstellt wird. Durch add = T wird sie dem Histogramm hinzugefügt. Damit die Dichte sichtbar ist, muss im Histogramm zuvor das Argument probability = T gewählt werden. Ansonsten würden absolute Häufigkeiten anstatt der relativen Häufigkeiten abgetragen werden. Der qqPlot()-Befehl erzeugt uns den QQ-Plot samt Konfidenzband, um so eine leichtere Einschätzung hinsichtlich des Ausmaß der Abweichung von der Normalverteilung zu ermöglichen.

Hier scheinen sowohl das Histogramm als auch der QQ-Plot keinen Anlass zu geben, die Normalverteilungsannahme zu verwerfen. Die Ausprägungen scheinen zwar vom Scheitelpunkt der Skala etwas in Richtung der höheren Ausprägungen versetzt, aber eine starke Linksschiefe, wie man sie aus anderen Studien zur Lebenszufriedenheit kennt, scheint hier nicht vorzuliegen.

Wir wiederholen die Befehle auch für die zweite Gruppe:

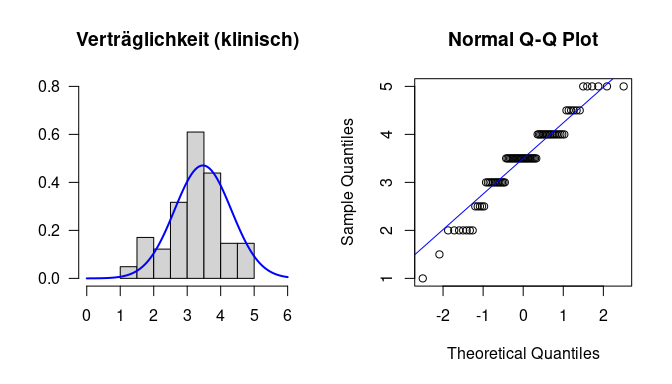
# Gruppe 2 (klinisch) 
par(mfrow=c(1,2))

lz_klinisch <- fb24[(fb24$fach_klin=="klinisch"), "lz"]
hist(lz_klinisch, 
     xlim=c(1,7), ylim=c(0,.8), 
     main="Lebenszufriedenheit (klinisch)", 
     xlab="", ylab="", las=1, probability=T)
curve(dnorm(x, 
            mean = mean(lz_klinisch, na.rm=T),
            sd = sd(lz_klinisch, na.rm=T)), 
      col="blue", lwd=2, add=T)

qqPlot(lz_klinisch)

## [1]  6 54

dev.off()

## null device 
##           1

In dieser Gruppe sehen wir, dass die Verteilung etwas in die Mitte gerückt ist (ein erster Hinweise bezüglich unserer ursprünglichen Hypothese), aber auch hier spricht wenig gegen die Normalverteilungsannahme.

Die vierte Annahme (Homoskedastizität - also die Varianzgleichheit in beiden Populationen) wird typischerweise mit einem inferenzstatistischen Verfahren geprüft, weil Varianzen meist weniger leicht optisch einzuschätzen sind. Wie in der Vorlesung besprochen, kann dafür der Levene-Test genutzt werden. Das Hypothesenpaar, das er prüft sieht so aus:

• $H_0$: $\sigma_1 = \sigma_2$ (Homoskedastizität ist gegeben)
• $H_1$: $\sigma_1 \neq \sigma_2$ (Homoskedastizität ist nicht gegeben)

Ein nicht-signifikantes Ergebnis (p > .05) deutet also darauf hin, dass wir nicht ausreichend Grundlage haben, um die Homoskedastizitätsannahme zu verwerfen. Auch der Levene-Test ist im car-Paket implementiert und die dazugehörige Funktion heißt praktischerweise leveneTest(). Sie nimmt eine Formel entgegen, die die Punktzahl ihrer jeweiligen Gruppe zuweist. Links von der ~ (Tilde) steht die abhängige Variable (hier die Lebenszufriedenheit), deren Varianzunterschied durch die unabhängige Variable (hier Interesse) rechts der ~ erklärt werden soll. Wir merken uns also, dass die Gruppenzugehörigkeit rechts der ~ stehen muss.

leveneTest(fb24$lz ~ fb24$fach_klin)

## Levene's Test for Homogeneity of Variance (center = median)
##        Df F value Pr(>F)
## group   1  0.0058 0.9395
##       185

Das Testergebnis zeigt mit einem $p$-Wert von 0.94, dass die Nullhypothese beibehalten wird, wir also weiterhin von der Gültigkeit der Homoskedastizitätsannahme ausgehen können. Für den Fall, dass die Annahme nicht hält, gibt es die Welch-Korrektur für den $t$-Test. Diese ist in R sogar die Voreinstellung.

Durchführung des $t$-Test

Zur Erinnerung - unsere Fragestellung für diesen Test war:

Unterscheiden sich Studierende, die primäre an klinischen Inhalten interessiert sind in ihrer Lebenszufriedenheit von denen, die ihre Interessen eher in anderen Bereichen der Psychologie sehen?

Weil die Fragestellung ungerichtet ist, brauchen wir auch eine ungerichtete Hypothese. Konkret ist unsere Hypothese also eine ungerichtete Unterschiedshypothese. Inhaltlich lässt sich das Paar aus $H_0$ und $H_1$ so formulieren:

• $H_0$: Klinisch und nicht klinisch interessierte Studierende unterscheiden sich nicht in ihrer Lebenszufriedenheit.
• $H_1$: Klinisch und nicht klinisch interessierte Studierende unterscheiden sich in ihrere Lebenszufriedenheit.

Etwas formaler ausgedrückt:

• $H_0$: $\mu_\text{nicht klinisch} = \mu_\text{klinisch}$ bzw. $\mu_\text{nicht klinisch} - \mu_\text{klinisch} = 0$
• $H_1$: $\mu_\text{nicht klinisch} \ne \mu_\text{klinisch}$ bzw. $\mu_\text{nicht klinisch} - \mu_\text{klinisch} \ne 0$

Wie so häufig gehen wir von einem $\alpha$-Fehlerniveau von 5% aus.

Wir hatten im Rahmen des Einstichproben-t-Tests bereits die Funktion t.test() kennengelernt. Diese nutzen wir wieder. Wir übergeben dieser wieder die Formel, die wir bereits im Boxplot und im Levene-Test verwendet haben. Außerdem wählen wir einige Zusatzargumente, die dann zum Zweistichproben-t-Test für unabhängige Stichproben führen:

t.test(fb24$lz ~ fb24$fach_klin,     # abhängige Variable ~ unabhängige Variable
      #paired = FALSE,                  # Stichproben sind unabhängig (Default) 
      alternative = "two.sided",        # zweiseitige Testung (Default)
      var.equal = TRUE,                 # Homoskedastizität liegt vor (-> Levene-Test)
      conf.level = .95)                 # alpha = .05 (Default)

## 
## 	Two Sample t-test
## 
## data:  fb24$lz by fb24$fach_klin
## t = 1.8347, df = 185, p-value = 0.06815
## alternative hypothesis: true difference in means between group nicht klinisch and group klinisch is not equal to 0
## 95 percent confidence interval:
##  -0.02312308  0.63726450
## sample estimates:
## mean in group nicht klinisch       mean in group klinisch 
##                     5.070707                     4.763636

Anhand der Ergebnisse können wir folgende Aussage treffen: Studierende, die sich für klinische Inhalte interessieren unterscheiden sich in ihrer Lebenszufriedenheit nicht bedeutsam von Studierenden, die sich primär für andere Inhalte interessieren ($t = 185, df = 1.835$, $p = 0.068$). In Fällen wie diesem ist es wichtig, sich nicht von dem kleinen $p$-Wert dazu verleiten zu lassen, Dinge wie “knapp” oder “marginal” in seine Interpretation aufzunehmen. Das NHST, welches wir hier betreiben, gibt eine klare Entscheidungsgrenze vor, welche wir vorab definiert haben. Wenn wir uns entscheiden, ein Alpha-Fehlerniveau von 5% festzulegen, müssen wir uns strikt daran halten.

Berechnung der Effektstärke Cohen’s $d$

Obwohl wir hier zunächst keinen statistisch bedeutsamen Unterschied entdeckt haben, wollen wir zur Eindordnung des Ergebnisses die Effektstärke ermitteln: Cohen’s $d$ gibt den standardisierten Mittelwertsunterschied zwischen zwei Gruppen an. “Standardisiert” bedeutet, dass wir uns nicht mehr auf der Originalmetrik befinden (hier auf der Skala von 1 bis 7), sondern mit Standardabweichungen arbeiten. Ein Wert von 1 zeigt also an, dass sich die Gruppenmittelwerte um eine Standardabweichung voneinander unterscheiden. Die Effektstärke berechnet sich wie folgt:

wobei

Cohen (1988) hat folgende Konventionen zur Beurteilung der Effektstärke $d$ vorgeschlagen, die man heranziehen kann, um den Effekt “bei kompletter Ahnungslosigkeit” einschätzen zu können (wissen wir mehr über den Sachverhalt, so sollten Effektstärken lieber im Bezug zu anderen Studienergebnissen interpretiert werden):

Wir führen die Berechnung von Cohen’s $d$ zunächst von Hand durch. Dafür speichern wir uns die nötigen Größen ab und wenden dann die präsentierte Formel an:

lz_nichtKlinisch <- fb24[(fb24$fach_klin=="nicht klinisch"), "lz"]
mw_nichtKlinisch <- mean(lz_nichtKlinisch, na.rm=T)
n_nichtKlinisch <- sum(!is.na(lz_nichtKlinisch))
sigma_qu_nichtKlinisch <- var(lz_nichtKlinisch, na.rm=T) 

lz_klinisch <- fb24[(fb24$fach_klin=="klinisch"), "lz"]
mw_klinisch <- mean(lz_klinisch, na.rm=T)
n_klinisch <- sum(!is.na(lz_klinisch))
sigma_qu_klinisch <- var(lz_klinisch, na.rm=T) 

sigma_inn <- sqrt((sigma_qu_nichtKlinisch* (n_nichtKlinisch - 1) + sigma_qu_klinisch* (n_klinisch - 1)) / (n_nichtKlinisch-1 + n_klinisch-1))

d1 <- (mw_nichtKlinisch - mw_klinisch) / sigma_inn
d1

## [1] 0.2688003

Natürlich gibt es in R auch eine angenehmere Alternative:

# install.packages("effsize")
library("effsize")

## 
## Attaching package: 'effsize'

## The following object is masked from 'package:psych':
## 
##     cohen.d

d2 <- cohen.d(fb24$lz, fb24$fach_klin, na.rm=T)
d2

## 
## Cohen's d
## 
## d estimate: 0.2688003 (small)
## 95 percent confidence interval:
##       lower       upper 
## -0.02153908  0.55913976

Der Vorteil der Funktion cohen.d ist, dass wir zusätzlich zur Effektstärke direkt auch ein Konfidenzintervall erhalten. Der Wert sollte aber natürlich der Gleiche sein, wie der, den wir gerade per Hand berechnet hatten.Fällt der Wert negativ aus, interpretieren wir den Betrag.

Ergebnisinterpretation

Wir haben untersucht, ob sich klinisch und nicht klinisch interessierte Studierende im Wert Ihrer Verträglichkeit unterscheiden. Tatsächlich findet sich deskriptiv ein nur geringer Unterschied: Nicht klinisch interessierte Studierende weisen einen durchschnittlichen Wert von 5.071 (SD = 0.762) auf, während klinisch interessierte Studierende einen Wert von 4.764 (SD = 0.854) aufweisen. Dies entspricht nach Cohens Konvention (1988) einem sehr kleinen Effekt ($d$= 0.269).

Zur Beantwortung der Fragestellung haben wir - nachdem wir sowohl die Normalverteilungsannahme als auch die Homoskedastizitätsannahme gepüft haben - einen $t$-Test durchgeführt. Der Gruppenunterschied ist nicht bedeutsam ($t_{df = 185} = 1.835$, $p = 0.068$) - wir behalten die Nullhypothese also bei. Klinisch und nicht klinisch interessierte Studierende unterscheiden sich im Testwert für Verträglichkeit nicht bedeutsam.

Medianvergleich

Wir widmen uns nun der 2. Fragestellung. Dazu prüfen wir, ob klinisch interessierte Studierende in der ersten Sitzung des Statistikseminars weniger gut gelaunt sind, als Studierende, die sich primär für andere Inhalte interessieren. Hierbei handelt es sich also um eine gerichtete Hypothese. Da die aktuelle Stimmung sehr häufig nicht der Normalverteilung folgt, entscheiden wir uns statt der Mittelwerte die weniger anfälligen Mediane zu vergleichen. Also nutzen wir hier den Wilcoxon-Test.

Deskriptivstatistik

Wir beginnen damit uns, wie oben, erst einmal grafisch anzusehen, wie die Lebenszufriedenheit lz in beiden Gruppen aussieht. Dafür beginnen wir dieses mal mit einem Boxplot:

# Gruppierter Boxplot:
boxplot(fb24$gs_pre ~ fb24$fach_klin, 
        xlab="Interesse", ylab="Gute Stimmung", 
        las=1, cex.lab=1.5, 
        main="Gute Stimmung nach Interesse")

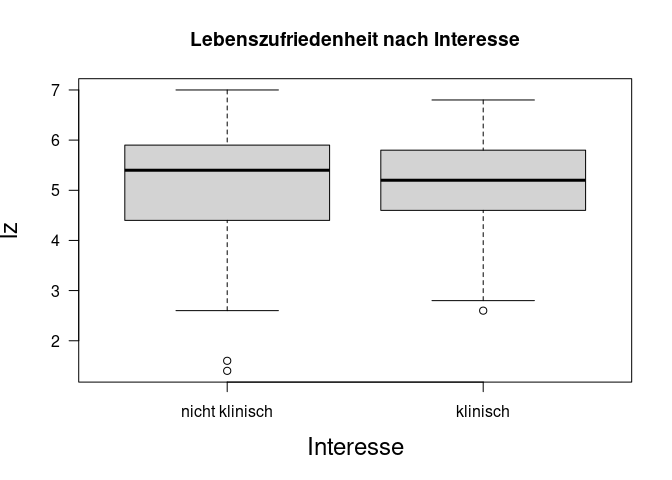
Hier können wir direkt (als dicke Linie eingezeichnet) die beiden Gruppenmediane sehen. Erst einmal sieht es so aus, als seien die beiden Mediane unterschiedlich. Für etwas mehr Details, nutzen wir die Deskriptivstatistik aus der describeBy Funktion:

describeBy(fb24$gs_pre, fb24$fach_klin) # beide Gruppen im Vergleich

## 
##  Descriptive statistics by group 
## group: nicht klinisch
##    vars  n mean   sd median trimmed  mad min max range skew kurtosis   se
## X1    1 99 3.34 0.59    3.5    3.42 0.74   1   4     3 -1.2     1.54 0.06
## --------------------------------------------------------------- 
## group: klinisch
##    vars  n mean   sd median trimmed  mad min max range  skew kurtosis   se
## X1    1 88 3.14 0.65   3.25    3.19 0.74   1   4     3 -0.71    -0.06 0.07

Auch hier sehen wir wieder, dass die Gruppe der nicht klinisch interessierten Studierenden einen etwas gößeren Median aufweist als die Gruppe der klinisch interessierten Studierenden.

Voraussetzungsprüfung

Wie schon der $t$-Test, hat auch der Wilcoxon-Test vier Voraussetzungen. Die ersten beiden bleiben gleich, nur die letzten beiden Unterscheiden sich leicht:

1. zwei unabhängige Stichproben $\rightarrow$ ok
2. die einzelnen Messwerte sind innerhalb der beiden Gruppen voneinander unabhängig (Messwert einer Vpn hat keinen Einfluss auf den Messwert einer anderen) $\rightarrow$ ok
3. das untersuchte Merkmal ist stetig (mindestens singulär-ordinal skaliert)
4. das Merkmal folgt in beiden Gruppen der gleichen Verteilung

Stetige Variablen haben theoretisch unendlich viele mögliche Ausprägungen. Dabei sind die Konsequenzen dieser Annahme jedoch nicht binär. Je mehr Ausprägungen eine Variable hat, desto besser funktioniert der Test. In unserem Fall ist die Variable lz ein Skalenwert, der sich als der Mittelwert von fünf Items mit jeweils sieben Antwortkategorien ergibt. Insgesamt sind das also 29 mögliche Abstufungen. Wir beschließen an dieser Stelle, dass 29 nah genug an unendlich dran ist, um von einer stetigen Variable zu sprechen.

Um die Verteilung in beiden Gruppen zu untersuchen, gucken wir uns wieder die Histogramme und die QQ-Plots an:

# Gruppe 1 (nicht klinisch) 
par(mfrow=c(1,2))
gs_nichtKlinisch <- fb24[(fb24$fach_klin=="nicht klinisch"), "gs_pre"]
hist(gs_nichtKlinisch, xlim=c(1,4), ylim=c(0,.8), main="Gute Sitmmung (nicht klin.)", xlab="", ylab="", las=1, probability=T)
curve(dnorm(x, mean=mean(gs_nichtKlinisch, na.rm=T), sd=sd(gs_nichtKlinisch, na.rm=T)), col="blue", lwd=2, add=T)
qqPlot(gs_nichtKlinisch)

## [1] 29  4

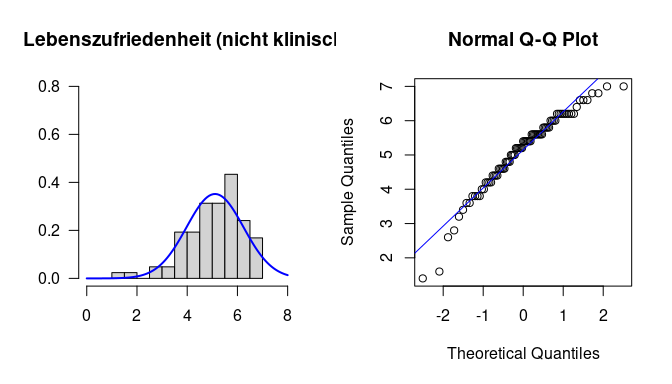
# Gruppe 2 (klinisch) 
par(mfrow=c(1,2))
gs_klinisch <- fb24[(fb24$fach_klin=="klinisch"), "gs_pre"]
hist(gs_klinisch, xlim=c(1,4), ylim=c(0,.8), main="Gute Stimmung (klin.)", xlab="", ylab="", las=1, probability=T)
curve(dnorm(x, mean=mean(gs_klinisch, na.rm=T), sd=sd(gs_klinisch, na.rm=T)), col="blue", lwd=2, add=T)
qqPlot(gs_klinisch)

## [1] 80 11

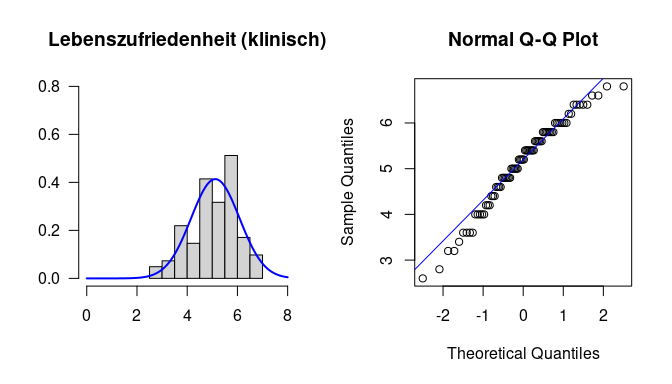Wir sehen hier die vermutete Schiefe der Verteilung in beiden Gruppen, auch wenn in der zweiten Gruppe nur sehr leicht ausfällt. Es sei an dieser Stelle gesagt, dass unter diesen Voraussetzungen ein $t$-Test auch funktionieren würde, weil die beiden Verteilungen nicht dramatisch von der Normalität abweichen und die beiden Stichproben jeweils relativ groß sind. Dennoch wollen wir hier den Wilcoxon-Test nutzen, weil wir nicht Mittelwerte, sondern Mediane vergleichen möchten. Die Verteilungen sehen in den beiden Gruppen sehr ähnlich aus. Wie man ganze Verteilungen auf Gleichheit prüft, werden wir im kommenden Semester noch näher betrachten, aber wenn zwei Verteilungen gleich sind, impliziert dies auch, dass die Streuung in beiden Populationen gleich sein muss. Um diese Annahme zu prüfen, können wir auch hier den Levene-Test nutzen:

leveneTest(fb24$gs_pre ~ fb24$fach_klin)

## Levene's Test for Homogeneity of Variance (center = median)
##        Df F value Pr(>F)
## group   1  2.0776 0.1512
##       185

Auch hier sehen wir ein nicht bedeutsames Ergebnis ($F_{1, 185} = 2.08$, $p = 0.151$), sodass wir die Nullhypothese beibehalten und die Annahme der Homoskedastizität nicht verwerfen müssen. An dieser Stelle sei noch einmal auf das generelle Problem der Prüfung von Voraussetzungen mittels inferenzstatistischen Tests hingewiesen: generell prüfen wir in solchen Tests Nullhypothesen. Für diese können wir lediglich feststellen, dass wir sie verwerfen, wenn das empirische Ergebnis ausreichend unwahrscheinlich ist. Dabei ist die Prüfung zusätzlich (aus Gewohnheit) sehr zugunsten des Beibehaltens der Nullhypothese ausgelegt. Wenn wir die Nullyhpothese nicht verwerfen, ist das also kein Beweis für die Korrektheit der Annahme. Wir haben lediglich nicht ausreichend viel oder ausreichend extreme Information gefunden, um die Annahme (hier die Homoskedastizität) zu verwerfen.

Inferenzstatistik mit dem Wilcoxon-Test

Zur Erinnerung, hier die Fragestellung, die wir untersuchen wollten:

Sind klinisch interessierte Studierende zu Beginn der allerersten Sitzung eines Statistik Kurs im Psychologiestudium im Mittel schlechter gelaunt, als Studierende mit anderen Interessenslagen?

Wir müssen aus dieser Fragestellung also eine gerichtete Hypothese ableiten:

• $H_0$: Nicht klinisch interessierte Studierende erreichen sind im Mittel schlechter oder genauso gut gelaunt wie klinisch interessierte Studierende.
• $H_1$: Nicht klinisch interessierte Studierende erreichen sind im Mittel besser gelaunt als klinisch interessierte Studierende.

Wieder etwas formaler ausgedrückt:

• $H_0$: $\eta_\text{nicht klinisch} \leq \eta_\text{klinisch}$ bzw. $\eta_\text{nicht klinisch} - \eta_\text{klinisch} \leq 0$
• $H_1$: $\eta_\text{nicht klinisch} \gt \eta_\text{klinisch}$ bzw. $\eta_\text{nicht klinisch} - \eta_\text{klinisch} \gt 0$

Wie so häufig, nehmen wir auch hier ein $\alpha$-Fehlerniveau von 5% an.

Die Funktion wilcox.test() nimmt im Grunde die gleichen Argumente entgegen wie die Funktion t.test(). Damit wir die gerichtete Hypothese in die richtige Richtung aufstellen können, müssen wir wissen, welches das erste Level des Faktors ist:

levels(fb24$fach_klin) # wichtig zu wissen: die erste der beiden Faktorstufen ist "nicht klinisch" 

## [1] "nicht klinisch" "klinisch"

Da die erste Faktorstufe “nicht klinisch” ist, wissen wir, dass die gerichtete Hypothese “>” lauten muss. In R wird mit dem Argument alternative immer Bezug genommen auf die Formulierung der Alternativhypothese. In unseren Fall ist diese, dass die erste Gruppe (nicht klinisch) einen höheren Median hat, als die zweite Gruppe (klinisch), also müssen wir alternative = 'greater' angeben:

wilcox.test(fb24$gs_pre ~ fb24$fach_klin,     # abhängige Variable ~ unabhängige Variable
            #paired = FALSE,              # Stichproben sind unabhängig (Default)
            alternative = "greater",      # einseitige Testung
            conf.level = .95)             # alpha = .05

## 
## 	Wilcoxon rank sum test with continuity correction
## 
## data:  fb24$gs_pre by fb24$fach_klin
## W = 5175, p-value = 0.01232
## alternative hypothesis: true location shift is greater than 0

Per Voreinstellung wird in R der exakte $p$-Wert bestimmt, wenn die Stichprobe insgesamt weniger als 50 Personen umfasst und keine Rangbindungen vorliegen. Bei größeren Stichproben folgt die Rangsumme aufgrund des zentralen Grenzwertsatzes ausreichend gut der Normalverteilung und es wird ein $z$-Test der Rangsumme durchgeführt. Weil die Rangsumme allerdings nur ganze Zahlen annehmen kann ist diese Approximation ein wenig ungenau (insbesondere dann, wenn die Stichprobe noch relativ klein ist). Per Voreinstellung wird daher in R eine Kontinuitätskorrektur durchgeführt (mit dem Argument correct = TRUE), sodass Sie nicht den gleichen Wert erhalten, den Sie bekommen, wenn Sie den Test händisch durchführen würden. Wenn Sie diese Korrektur ausschalten (correct = FALSE) erhalten Sie den gleichen Wert.

Ergebnisinterpretation

Wir haben untersucht, ob nicht klinisch interessierte Studierende im Mittel höhere Werte in der aktuellen Stimmung erreichen als klinisch interessierte Studierende. Deskriptiv besteht ein Unterschied: Beide Gruppen unterscheiden sich etwas im Median in der erwarteten Richtung: $Md_\text{nicht klinisch}$ = 3.5 und $Md_\text{klinisch}$ = 3.25. Zur Überprüfung der Hypothese wurde ein Wilcoxon-Test durchgeführt. Der Gruppenunterschied ist demnach statistisch bedeutsam ($W = 5175$, $p = 0.012$). Somit wird die Nullhypothese verworfen: Nicht klinisch interessierte Studierende erreichen zu Beginn ihres ersten Statistik Seminars höheren Werte in der aktuellen guten Stimmung als klinisch interessierte Studierende.

In diesem Beitrag haben wir gesehen, wie wir die zentrale Tendenz (Mittelwert oder Median) bei zwei unabhängigen Stichproben untersuchen können. Im nächsten Beitrag sehen wir dann, wie das Ganze funktioniert, wenn wir zwei Gruppen betrachten, zwischen denen eine Abhängigkeit besteht (z.B. weil wir wiederholt die gleichen Personen untersucht haben). Im Anhang finden Sie außerdem noch einen Test, mit dem Sie untersuchen können, ob sich die Häufigkeitsverteilungen in zwei unabhängigen Stichproben unterscheiden. Dieser Test bietet also die Möglichkeit auch nominalskalierte abhängige Variablen über zwei Gruppen zu vergleichen.

Appendix

is.factor(fb24$ort)

## [1] FALSE

is.factor(fb24$job)

## [1] FALSE

# Achtung, nur einmal durchführen (ansonsten Datensatz neu einladen und Code erneut durchlaufen lassen!)
fb24$ort <- factor(fb24$ort, levels=c(1,2), labels=c("FFM", "anderer"))

fb24$job <- factor(fb24$job, levels=c(1,2), labels=c("nein", "ja"))

tab <- table(fb24$ort, fb24$job)
tab

##          
##           nein ja
##   FFM       68 43
##   anderer   53 24

tab_mar <- addmargins(tab) # Randsummen zu Tabelle hinzufügen
tab_mar

##          
##           nein  ja Sum
##   FFM       68  43 111
##   anderer   53  24  77
##   Sum      121  67 188

expected <- data.frame(nein=c((tab_mar[1,3]*tab_mar[3,1])/tab_mar[3,3],
                              (tab_mar[2,3]*tab_mar[3,1])/tab_mar[3,3]),
                       ja=c((tab_mar[1,3]*tab_mar[3,2])/tab_mar[3,3],
                            (tab_mar[2,3]*tab_mar[3,2])/tab_mar[3,3]))
expected

##       nein       ja
## 1 71.44149 39.55851
## 2 49.55851 27.44149

chi_quadrat_Wert <- (tab[1,1]-expected[1,1])^2/expected[1,1]+
                    (tab[1,2]-expected[1,2])^2/expected[1,2]+
                    (tab[2,1]-expected[2,1])^2/expected[2,1]+
                    (tab[2,2]-expected[2,2])^2/expected[2,2]
chi_quadrat_Wert

## [1] 1.135776

qchisq(.95, 1) # kritischer Wert

## [1] 3.841459

pchisq(chi_quadrat_Wert, 1, lower.tail = FALSE) # p-Wert

## [1] 0.2865467

chisq.test(tab,        # Kreuztabelle
           correct=F)  # keine Kontinuinitätskorrektur nach Yates

## 
## 	Pearson's Chi-squared test
## 
## data:  tab
## X-squared = 1.1358, df = 1, p-value = 0.2865

effekt_YulesQ <- (tab[1,1]*tab[2,2]-tab[1,2]*tab[2,1])/
                 (tab[1,1]*tab[2,2]+tab[1,2]*tab[2,1])
effekt_YulesQ

## [1] -0.1654308

effekt_phi <- (tab[1,1]*tab[2,2]-tab[1,2]*tab[2,1])/
  sqrt((tab[1,1]+tab[1,2])*(tab[1,1]+tab[2,1])*(tab[1,2]+tab[2,2])*(tab[2,1]+tab[2,2]))
effekt_phi

## [1] -0.07772618

# alternativ mit psych Paket
library(psych)
phi(tab, digits = 8)

## [1] -0.07772618

Yule(tab)

## [1] -0.1654308

# Äquivalentes Ergebnis mittels Pearson-Korrelation (kommt in den nächsten Sitzungen)
# (dichotome Variablen)
ort_num <- as.numeric(fb24$ort)
job_num <- as.numeric(fb24$job)
cor(ort_num, job_num, use="pairwise")

## [1] -0.07772618