Aufgabe 1
Lineare Beziehungen zwischen Variablen: Korrelationstest unter $H_1$
Wir wollen uns ebenfalls die Power für den Korrelationstest ansehen. Dazu müssen wir allerdings korrelierte Variablen generieren. Um das hinzubekommen, müssen wir einige Eigenschaften der Normalverteilung ausnutzen: bspw. dass die Summe zweier normalverteilter Zufallsvariablen wieder normalverteilt ist. Für zwei unabhängige (unkorrelierte) standardnormalverteilte Zufallsvariablen $X$ und $Z$, ist die Zufallsvariable $Y$, die folgendermaßen gebildet wird:
$$Y:= \rho X + \sqrt{1-\rho^2}Z,$$
wieder standardnormalverteilt und um den Korrelationskoeffizienten $\rho$ korreliert mit $X$. Wir können also relativ einfach zwei korrelierte Variablen generieren. Wie in der Sitzung verwenden wir $N=20$:
N <- 20
set.seed(12345)
X <- rnorm(N)
Z <- rnorm(N)
Y <- 0.5*X + sqrt(1 - 0.5^2)*Z
cor(X, Y) # empirische Korrelation
## [1] 0.579799
sd(X)
## [1] 0.8339354
sd(Y)
## [1] 1.232089
Falls Sie die oben genutzte Formel zur Generierung korrelierter Zufallsvariablen überprüfen wollen, dann setzen Sie doch einmal N = 10^6 (also eine Stichprobe von 1 Mio). Dann sollte die empirische Korrelation sehr nah an der theoretischen liegen. Auch sollten dann die empirischen Standardabweichungen sehr nah an der 1 liegen.
Verwenden Sie für diese Aufgabe stets den Seed 12345 (set.seed(12345)).
- Betrachten Sie das Modell für eine Stichprobe von
N = 10^6. Berichten Sie die empirische Korrelation sowie die empirischen Standardabweichungen.
Lösung
N <- 10^6
set.seed(12345)
X <- rnorm(N)
Z <- rnorm(N)
Y <- 0.5*X + sqrt(1 - 0.5^2)*Z
cor(X, Y) # empirische Korrelation
## [1] 0.4994574
sd(X)
## [1] 1.001315
sd(Y)
## [1] 0.9994427
Die Korrelation liegt bei $\hat{\rho}_{XY}=$0.4995 und liegt damit sehr nah an der theoretischen (wahren) 0.5. Die beiden Standardabweichungen liegen bei $\hat{\sigma}_X=$ 1.0013 und $\hat{\sigma}_Y=$ 0.9994 und damit beide sehr nah an der theoretischen (wahren) 1.
- Untersuchen Sie die Power des Korrelationstests für eine Korrelation von $\rho=0.5$ und $N = 20$. Führen Sie eine Simulationsstudie durch. Wie groß ist die Power?
Lösung
N <- 20
set.seed(12345)
pcor_H1 <- replicate(n = 10000, expr = {X <- rnorm(N)
Z <- rnorm(N)
Y <- 0.5*X + sqrt(1 - 0.5^2)*Z
cortestH1 <- cor.test(X, Y)
cortestH1$p.value})
mean(pcor_H1 < 0.05) # empirische Power
## [1] 0.6385
Die Power des Korrelationstests für eine Korrelation von 0.5 für $N=20$ liegt bei 63.85%.
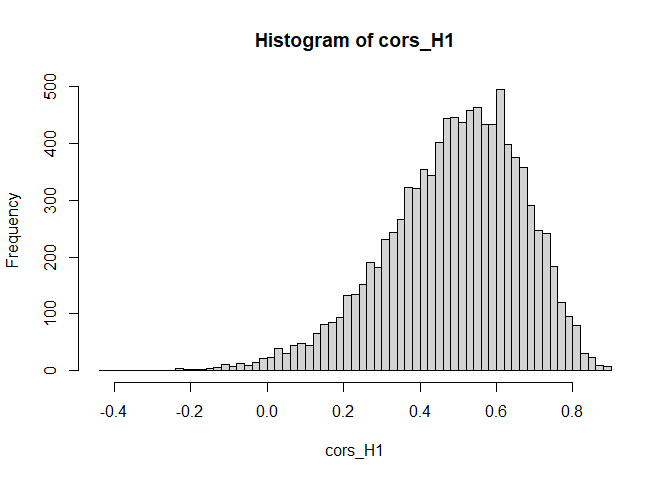
- Stellen Sie die Verteilung der empirischen Korrelationen (für $\rho=0.5$ und $N=20$) unter der $H_1$ dar.
Lösung
set.seed(12345)
cors_H1 <- replicate(n = 10000, expr = {X <- rnorm(N)
Z <- rnorm(N)
Y <- 0.5*X + sqrt(1 - 0.5^2)*Z
cor(X, Y)})
summary(cors_H1)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -0.4293 0.3791 0.5080 0.4889 0.6177 0.8997
hist(cors_H1, breaks = 50)
Aufgabe 2
Lineare Beziehungen zwischen Variablen: Korrelationstest unter $H_1$ für ungleiche Varianzen
Wiederholen Sie die Analyse. Verändern Sie diesmal die Varianz der beiden Variablen Xund Y. X soll eine Varianz von 9 haben (multiplizieren Sie dazu X mit 3, nachdem Sie Y mithilfe von X und Z generiert haben), und Y soll eine Varianz von 0.25 haben (multiplizieren Sie dazu Y mit 0.5, nachdem Sie Y mit Hilfe von X und Z generiert haben).
- Betrachten Sie das Modell für eine Stichprobe von
N = 10^6. Berichten Sie die empirische Korrelation sowie die empirischen Standardabweichungen.
Lösung
N <- 10^6
set.seed(12345)
X <- rnorm(N)
Z <- rnorm(N)
Y <- 0.5*X + sqrt(1 - 0.5^2)*Z
X_new <- 3*X
Y_new <- 0.5*Y
cor(X_new, Y_new) # empirische Korrelation
## [1] 0.4994574
sd(X_new)
## [1] 3.003945
sd(Y_new)
## [1] 0.4997214
Die Korrelation liegt bei $\hat{\rho}{X\text{new}Y_\text{new}}=$0.4995 und liegt damit sehr nah an der theoretischen (wahren) 0.5. Insbesondere ist diese Korrelation gleich der Korrelation zwischen X und Y von oben! Das liegt daran, dass die Varianz die Korrelation nicht beeinflusst. Die beiden Standardabweichungen liegen bei $\hat{\sigma}{X\text{new}}=$ 3.0039 und $\hat{\sigma}{Y\text{new}}=$ 0.4997 und damit beide sehr nah an der theoretischen (wahren) dran. Diese entsprechen gerade den Vorfaktoren, die wir daran multipliziert haben. Also 3 für $X_\text{new}$ und 0.5 für $Y_\text{new}$.
- Führen Sie eine Simulationsstudie durch (für $\rho=0.5$ und $N=20$). Wie verändert sich die Power des Tests durch die veränderten Varianzen?
Lösung
N <- 20
set.seed(12345)
pcor_H1_new <- replicate(n = 10000, expr = {X <- rnorm(N)
Z <- rnorm(N)
Y <- 0.5*X + sqrt(1 - 0.5^2)*Z
X_new <- 3*X
Y_new <- 0.5*Y
cortestH1 <- cor.test(X_new, Y_new)
cortestH1$p.value})
mean(pcor_H1_new < 0.05) # empirische Power
## [1] 0.6385
Die Power des Korrelationstests für eine Korrelation von 0.5 für $N=20$ und Variablen mit Varianzen von 9 und 0.25 liegt bei 63.85%. Diese Power ist identisch zur Power zuvor. Das zeigt uns, dass die Power des Korrelationstests unter Voraussetzung der Normalverteilung nur von der Korrelationsgröße, aber nicht von der Varianz der Variablen, abhängt. (Natürlich dürfen wir nicht eine Variable mit 0 multiplizieren, da das zu einer Konstanten führt, die immer eine Korrelation von 0 mit allen anderen Zufallsvariablen hat.)
Aufgabe 3
Sensitivitätsanalyse für die Korrelation
In den Inhalten zu dieser Sitzung haben Sie neben der Poweranalyse auch die Sensitivitätsanalyse für den $t$-Test kennengelernt. Diese lässt sich mithilfe des Pakets WebPower auch für die Korrelation durchführen.
- Laden Sie zunächst das Paket
WebPowerund schauen Sie sich die Funktion für die Poweranalyse bei einer Korrelation an.
Lösung
library(WebPower)
## Warning: Paket 'WebPower' wurde unter R Version 4.3.1 erstellt
## Lade nötiges Paket: MASS
##
## Attache Paket: 'MASS'
## Das folgende Objekt ist maskiert 'package:dplyr':
##
## select
## Lade nötiges Paket: lme4
## Lade nötiges Paket: Matrix
## Warning: Paket 'Matrix' wurde unter R Version 4.3.2 erstellt
## Lade nötiges Paket: lavaan
## Warning: Paket 'lavaan' wurde unter R Version 4.3.1 erstellt
## This is lavaan 0.6-16
## lavaan is FREE software! Please report any bugs.
##
## Attache Paket: 'lavaan'
## Das folgende Objekt ist maskiert 'package:psych':
##
## cor2cov
## Lade nötiges Paket: parallel
## Lade nötiges Paket: PearsonDS
## Warning: Paket 'PearsonDS' wurde unter R Version 4.3.1 erstellt
?wp.correlation
- Nehmen Sie an, dass Sie eine Gruppe von $N=50$ Personen untersucht haben. Sie möchten nun wissen, wie groß der Korrelationskoeffizient theoretisch sein müsste, damit eine Power von $95\%$ erreicht werden kann. Das $\alpha$-Fehleriveau soll dabei bei $0.05$ liegen.
Lösung
Für die Sensitivitätsanalyse legen wir in der Funktion wp.correlation die Stichprobengröße ($N$), die Power für die wir uns interessieren sowie das $\alpha$-Fehlerniveau fest. Den Korrelationskoeffizienten r lassen wir hingegen leer:
wp.correlation(n = 50, r = NULL, power = 0.95, alpha = 0.05, alternative = c("two.sided"))
## Power for correlation
##
## n r alpha power
## 50 0.4780569 0.05 0.95
##
## URL: http://psychstat.org/correlation
Es müsste also eine Korrelation von 0.4780569 vorliegen, damit wir mit unserer Stichprobe eine Power von $95\%$ erreichen.
Aufgabe 4
Type I-Error und Power zu einem $\alpha$-Niveau von $0.1%$ des $t$-Test
Wir wollen nun die Power des $t$-Tests für ein anderes $\alpha$-Fehlerniveau bestimmen. Wiederholen Sie also die Poweranalysen aus der Sitzung für den $\alpha$-Fehler und die Power für ein $\alpha$-Fehlerniveau von $0.1%$.
Nutzen Sie den Seed 12345 (set.seed(12345)).
- Führen Sie eine Simulation durch, um das empirische $\alpha$-Niveau des $t$-Tests zu bestimmen für $N=20$. Vergleichen Sie das Ergebnis mit dem Ergebnis aus der Sitzung.
Lösung
N <- 20
set.seed(12345)
pt_H0 <- replicate(n = 10000, expr = {X <- rnorm(N)
Y <- rnorm(N)
ttestH1 <- t.test(X, Y, var.equal = TRUE)
ttestH1$p.value})
mean(pt_H0 < 0.001) # empirischer Alpha-Fehler
## [1] 0.0011
Der empirische $\alpha$-Fehler liegt bei 0.11% und liegt damit sehr nah an dem vorgegebenem Niveau von $\alpha = 0.1%$. In der Sitzung hatten wir einen empirischen $\alpha$-Fehler, der sehr nah an den theoretischen $5%$ lag. Der Unterschied ist zu erwarten, da wir das vorgegebene $\alpha$-Fehlerniveau verändert haben!
- Führen Sie eine Simulation durch, um die empirische Power des $t$-Tests zu bestimmen für $N=20$, $d = 0.5$ und $\alpha = 0.1%$. Vergleichen Sie das Ergebnis mit dem Ergebnis aus der Sitzung. Was bedeutet dies für die Wahl der Irrtumswahrscheinlichkeit?
Lösung
set.seed(12345)
pt_H1 <- replicate(n = 10000, expr = {X <- rnorm(N)
Y <- rnorm(N) + 0.5
ttestH1 <- t.test(X, Y, var.equal = TRUE)
ttestH1$p.value})
mean(pt_H1 < 0.001) # empirische Power
## [1] 0.0362
Die empirische Power liegt bei 3.62%. Dieser Wert fällt nun deutlich geringer aus, als die 33.5%, die wir in der Sitzung beobachtet hatten. Dies zeigt nochmal deutlich auf, dass wenn wir unsere Irrtumswahrscheinlichkeit drastisch reduzieren wollen, wir in Kauf nehmen, dass die Power einen Effekt zu finden, wenn dieser da ist, deutlich eingeschränkt wird!
Sie können sich die Power auch für andere Irrtumswahrscheinlichkeiten anschauen, indem Sie die 0.001 ersetzen durch Ihre gewünschte Irrtumswahrscheinlichkeit!
Aufgabe 5
Power-Plots für den $t$-Test
Wir wollen nun die Power des $t$-Tests für unterschiedliche Effektgrößen untersuchen. In den beiden Gruppen soll jeweils eine Varianz von 1 herrschen. Verändern Sie also den Code der Sitzung nur hinsichtlich der Effektgröße. Das $\alpha$-Fehlerniveau soll wieder bei $0.05$ liegen.
Nutzen Sie den Seed 12345 (set.seed(12345)).
- Erstellen Sie einen Power-Plot für die folgenden Effekte $d = 0, 0.25, 0.5, 0.75, 1,$ und $1.25$ bei einer Stichprobengröße von $N = 20$. Stellen Sie die Effektgröße auf der x-Achse dar.
Lösung
set.seed(12345)
pt_H1_0 <- replicate(n = 10000, expr = {X <- rnorm(20)
Y <- rnorm(20)
ttestH1 <- t.test(X, Y, var.equal = TRUE)
ttestH1$p.value})
pt_H1_0.25 <- replicate(n = 10000, expr = {X <- rnorm(20)
Y <- rnorm(20) + 0.25
ttestH1 <- t.test(X, Y, var.equal = TRUE)
ttestH1$p.value})
pt_H1_0.5 <- replicate(n = 10000, expr = {X <- rnorm(20)
Y <- rnorm(20) + 0.5
ttestH1 <- t.test(X, Y, var.equal = TRUE)
ttestH1$p.value})
pt_H1_0.75 <- replicate(n = 10000, expr = {X <- rnorm(20)
Y <- rnorm(20) + 0.75
ttestH1 <- t.test(X, Y, var.equal = TRUE)
ttestH1$p.value})
pt_H1_1 <- replicate(n = 10000, expr = {X <- rnorm(20)
Y <- rnorm(20) + 1
ttestH1 <- t.test(X, Y, var.equal = TRUE)
ttestH1$p.value})
pt_H1_1.25 <- replicate(n = 10000, expr = {X <- rnorm(20)
Y <- rnorm(20) + 1.25
ttestH1 <- t.test(X, Y, var.equal = TRUE)
ttestH1$p.value})
t_power_d <- c(mean(pt_H1_0 < 0.05),
mean(pt_H1_0.25 < 0.05),
mean(pt_H1_0.5 < 0.05),
mean(pt_H1_0.75 < 0.05),
mean(pt_H1_1 < 0.05),
mean(pt_H1_1.25 < 0.05))
Ds <- seq(0, 1.25, 0.25)
plot(x = Ds, y = t_power_d, type = "b", main = "Power vs. d")
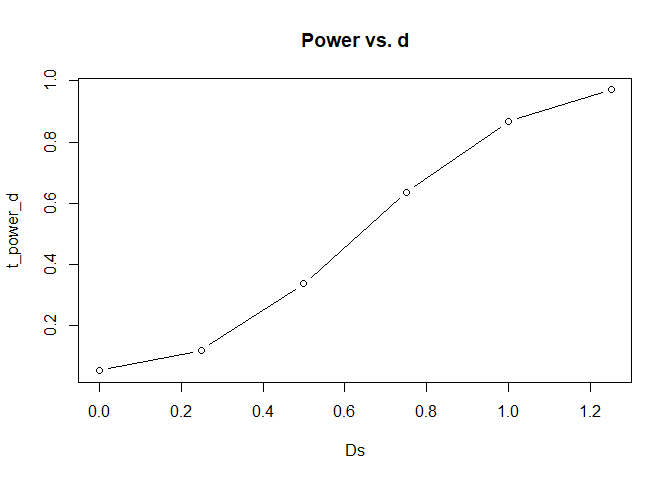
Dem Plot ist zu entnehmen, dass die Power mit steigender Effektgröße ansteigt.
- Welcher Effekt muss mindestens bestehen, damit die Power bei $80%$ liegt?
Lösung
Diesem Plot ist nun zu entnehmen, dass eine Mittelwertsdifferenz von größer 0.8 nötig ist, damit die Power hinreichend groß ist. Außerdem wird in diesem Plot auch ersichtlich, dass wenn die Mittelwertsdifferenz 0 ist, dann sind wir gerade im Fall der $H_0$ gelandet. Die Power sollte hier dann nur bei $5%$ liegen. Falls wir negative Mittelwertsdifferenzen gewählt hätten, dann wäre der Plot identisch, nur an der x-Achse gespiegelt.
Aufgabe 6
Powervergleich: $t$-Test vs. Wilcoxon-Test
Wir wollen nun die Power des $t$-Tests mit der Power des Wilcoxon-Test vergleichen. Der Wilcoxon-Test ist flexibler anzuwenden, da er weniger Annahmen aufweist. Untersuchen Sie, wie sich dies auf die Power auswirkt. Das $\alpha$-Fehlerniveau soll wieder bei $5%$ liegen.
Nutzen Sie den Seed 12345 (set.seed(12345)).
- Verwenden Sie das gleiche Setting wie aus der Sitzung und bestimmen Sie die Power des Wilcoxon-Tests für $N=20$, $d = 0.5$ und $\alpha = 5%$. Vergleichen Sie das Ergebnis mit dem Ergebnis aus der Sitzung.
Lösung
N <- 20
set.seed(12345)
pt_H1_t <- replicate(n = 10000, expr = {X <- rnorm(N)
Y <- rnorm(N) + 0.5
ttestH1 <- t.test(X, Y, var.equal = TRUE)
ttestH1$p.value})
mean(pt_H1_t < 0.05) # empirische Power des t-Tests
## [1] 0.335
set.seed(12345)
pt_H1_W <- replicate(n = 10000, expr = {X <- rnorm(N)
Y <- rnorm(N) + 0.5
wilcoxonH1 <- wilcox.test(X, Y)
wilcoxonH1$p.value})
mean(pt_H1_W < 0.05) # empirische Power des Wilcoxon-Tests
## [1] 0.3198
Die empirische Power des $t$-Tests liegt bei 33.5%. Die empirische Power des Wilcoxon-Tests liegt bei 31.98%. Damit fällt die Power des Wilcoxon-Test marginal geringer aus, als die des $t$-Tests. Dies lässt sich dadurch erklären, dass die Intervallskala mehr statistische Informationen trägt. Allerdings ist der $t$-Test anfälliger gegen Verstöße von Modellannahmen!
Bspw. mit solchen Fragen beschäftigen sich Methodiker:innen aus verschiedensten Disziplinen. Wenn Sie sich dafür interessieren, fragen Sie doch gerne in einer der beiden Abteilungen nach!
](/media/header/windmills_but_fancy.jpg)