Vorbereitende Schritte

Den Datensatz fb23 haben wir bereits unter diesem Link heruntergeladen und können ihn über den lokalen Speicherort einladen oder Sie können Ihn direkt mittels des folgenden Befehls aus dem Internet in das Environment bekommen. In den vorherigen Tutorials und den dazugehörigen Aufgaben haben wir bereits Änderungen am Datensatz durchgeführt, die hier nochmal aufgeführt sind, um den Datensatz auf dem aktuellen Stand zu haben:

#### Was bisher geschah: ----

# Daten laden
load(url('https://pandar.netlify.app/daten/fb23.rda'))

# Nominalskalierte Variablen in Faktoren verwandeln
fb23$hand_factor <- factor(fb23$hand,
                             levels = 1:2,
                             labels = c("links", "rechts"))
fb23$fach <- factor(fb23$fach,
                    levels = 1:5,
                    labels = c('Allgemeine', 'Biologische', 'Entwicklung', 'Klinische', 'Diag./Meth.'))
fb23$ziel <- factor(fb23$ziel,
                        levels = 1:4,
                        labels = c("Wirtschaft", "Therapie", "Forschung", "Andere"))
fb23$wohnen <- factor(fb23$wohnen, 
                      levels = 1:4, 
                      labels = c("WG", "bei Eltern", "alleine", "sonstiges"))

# Rekodierung invertierter Items
fb23$mdbf4_pre_r <- -1 * (fb23$mdbf4_pre - 4 - 1)
fb23$mdbf11_pre_r <- -1 * (fb23$mdbf11_pre - 4 - 1)
fb23$mdbf3_pre_r <-  -1 * (fb23$mdbf3_pre - 4 - 1)
fb23$mdbf9_pre_r <-  -1 * (fb23$mdbf9_pre - 4 - 1)

# Berechnung von Skalenwerten
fb23$gs_pre  <- fb23[, c('mdbf1_pre', 'mdbf4_pre_r', 
                        'mdbf8_pre', 'mdbf11_pre_r')] |> rowMeans()
fb23$ru_pre <-  fb23[, c("mdbf3_pre_r", "mdbf6_pre", 
                         "mdbf9_pre_r", "mdbf12_pre")] |> rowMeans()

# z-Standardisierung
fb23$ru_pre_zstd <- scale(fb23$ru_pre, center = TRUE, scale = TRUE)

Was erwartet Sie heute?

Nachdem wir uns die letzten Wochen mit Deskriptivstatistik und Verteilungen beschäftigt haben, werden wir heute in die Inferenzstatistik starten. Diese wird auch als prüfende Statistik bezeichnet – wir wollen also nicht nur Daten beschreiben sondern auch unsere Hypothesen überprüfen. Der Einstieg soll mit einem möglichst einfachen Fall dargestellt haben. Dafür nutzen wir Tests, die nur mit einer Stichprobe arbeiten.

Einstichproben-z-Test

Für die Einstichprobentests ist es essentiell, dass gewisse Populationsinformationen vorliegen, da wir unsere Stichprobe mit dieser vergleichen wollen. Das Vorliegen von Informationen kann beispielsweise bei genormten Tests (wie IQ-Tests) gegeben sein. Stellen wir uns also vor, dass es für den Fragebogen zur Nerdiness (nerd) aus der fb23 Umfrage Normwerte gibt. Der imaginierte Mittelwert der Population liegt bei $\mu_0 = 2.5$, während die Standardabweichung der Population bei $\sigma = 3.1$ liegt. Wir wollen nun im folgenden untersuchen, ob sich unsere Stichprobe in fb23 (also die Studierenden des ersten Semesters) von diesem Wert unterscheiden.

Im Endeffekt befinden wir also bei einem ähnlichen Setting wie im vorhergehenden Tutorial zu Verteilungen. Die Population kann hier durch die Kurve dargestellt werden, während der Mittelwert unserer Stichprobe mit einem roten Strich eingezeichnet ist. Wir haben gelernt, dass man für den spezifischen Wert einer gezogenen Person aus dieser Population nun sagen könnte, wie viel Prozent der Verteilung kleiner (und auch größer) als dieser Wert sind.

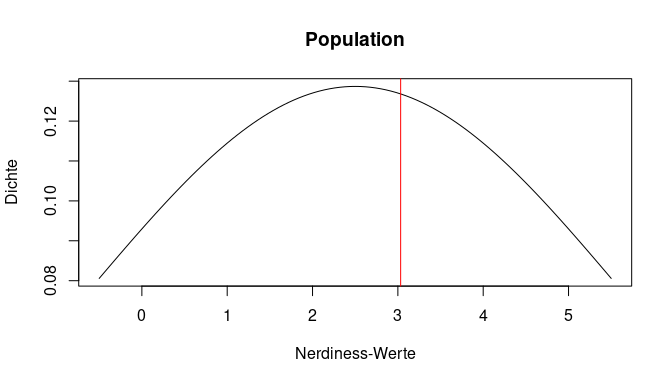
Dies wäre hier jedoch nicht angebracht, da unsere Stichprobe mehr als eine Person umfasst. Schließlich ist es viel unwahrscheinlicher, zwei Personen mit einem Mittelwert von in unserem Beispiel 5 zu ziehen, als nur eine Person. Auch die Streuung der Population spielt eine Rolle. Wir müssen also die Wahrscheinlichkeit an einer anderen Verteilung ablesen. Hier kommt die Stichprobenkennwerteverteilung der Mittelwerte ins Spiel, die wir uns gleich anschauen werden. Zunächst gehen wir auf die Grundlagen des zugehörigen Tests ein.

Für den Einstichproben-z-Test (auch Einstichproben-Gauß-Test genannt) benötigen wir neben dem Mittelwert der Stichprobe auch den Mittelwert der Population und (im Unterschied zu dem später betrachteten Einstichproben-t-Test) auch die Populationsstandardabweichung. Da wir diese drei Informationen haben, ist er die richtige Wahl. Bevor wir mit einer inferenzstatistischen Testung starten, sollten allerdings Hypothesen vorliegen. Diese leitet man in der Praxis aus der Literatur ab. Wir gehen hier jetzt erstmal davon aus, dass wir den Mittelwert der Stichprobe auf einen Unterschied zum Mittelwert der Population testen wollen, ohne eine Richtung anzunehmen.

Dafür können wir nun ein Hypothesenpaar bestehend aus $H_0$ und $H_1$ aufstellen. Aus Übungszwecken machen wir das einmal inhaltlich und einmal durch eine statistische Schreibweise.

Inhaltlich

$H_0$: Der Mittelwert unserer Stichprobe auf der Variable Nerdiness unterscheidet sich nicht von der Population.

$H_1$: Der Mittelwert unserer Stichprobe auf der Variable Nerdiness unterscheidet sich von der Population.

Statistisch

$$H_0: \mu_0 = \mu_1$$

$$H_1: \mu_0 \neq \mu_1$$

Außerdem sollten wir eine Irrtumswahrscheinlichkeit $\alpha$ festlegen, die wir auch später nochmal genauer besprechen werden. Wir entscheiden uns hier für den in der Psychologie häufig verwendeten Wert von 5%.

Nach diesen Festlegungen wird bei inferenzstatistischen Testungen häufig eine deskriptive Betrachtung im Rahmen der Hypothesen vollzogen. Für den vorliegenden Test würde es hier Sinn machen, dass der Mittelwert unserer Stichprobe auf der Variable Nerdiness nerd bestimmt wird. Den Code dafür haben wir bereits kennengelernt. Um vor der Durchführung zu testen, ob es auf der Variable fehlende Werte gibt, die die Berechnung beeinflussen würden, können wir die Funktion anyNA() verwenden.

anyNA(fb23$nerd)

## [1] FALSE

Dabei gibt es auf der Variable keine fehlenden Werte. Also können wir die mean() Funktion ohne weiteres Argument verwenden.

mean(fb23$nerd)

## [1] 3.032588

Wir sehen hier bereits, dass ich der Wert der Stichprobe von dem der Population rein deskriptiv unterscheidet. Doch reicht dieses deskriptive Ergebnis, um daraus Schlussfolgerungen für die Hypothesen zu ziehen?

Nein. Erst mit Hilfe der Inferenzstatistik kann herausgefunden werden, wie (un)wahrscheinlich die beobachtete Diskrepanz unter Annahme der $H_0$ (also dass es eigentlich keinen Unterschied gibt) ist.

Der Einstichproben-z-Test setzt voraus, dass das Merkmal in der Population, auf die sich die Nullhypothese ($H_0$) bezieht, normalverteilt ist und (wie bereits erwähnt) der Mittelwert sowie die Standardabweichung der Population bekannt sind. Des Weiteren verwendet der Einstichproben-z-Test grundsätzlich die Standardnormalverteilung als Stichprobenkennwerteverteilung (SKV), weswegen er für kleine Stichproben nicht gut geeignet ist.

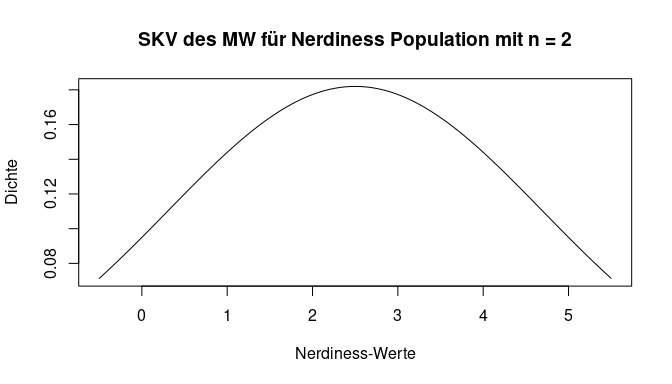
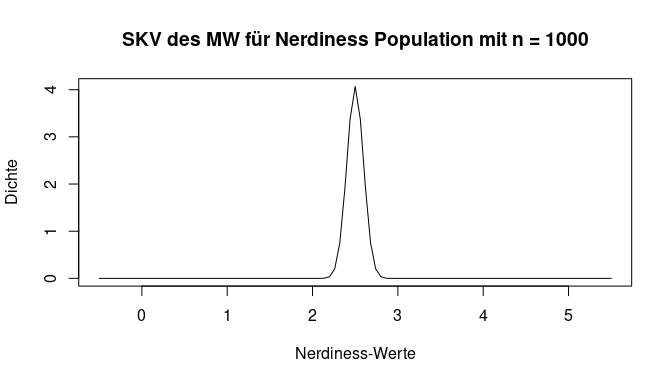
Der Einstichproben-z-Test prüft anhand des arithmetischen Mittels einer Stichprobe, ob der Erwartungswert der zugehörigen Grundgesamtheit ungleich (bzw. kleiner oder größer) als ein vorgegebener Wert ist. Wir müssen also bestimmen, wie wahrscheinlich der empirisch gefundene Mittelwert unter der Voraussetzung ist, dass er aus der Population mit ihrem Mittelwert und dessen Standardabweichung stammt. Zu Beginn haben wir bereits überlegt, dass sowohl die Standardabweichung als auch die Stichprobengröße einen Einfluss auf die Wahrscheinlichkeit von verschiedenen Mittelwerten haben sollten. Wir stellen hier den Einfluss der Stichprobengröße nochmal bildlich da. Gehen wir davon aus, dass wir nur 2 Personen aus der Populaion erheben, dann ist das Auffinden eines Wertes der weit vom eigentlichen Mittelwert der Population entfernt ist leichter möglich. Im Gegensatz dazu sollte sich bei 1000 Personen in einer Stichprobe auch der Mittelwert der Population widerfinden und Abweichungen seltener sein. Die Gegenüberstellung ist in den nächsten 2 Plots nochmal dargestellt. Bei beiden wurde unendlich oft aus unserer Population der Nerdiness eine Stichprobe gezogen. Jeweils wird ein Mittelwert berechnet, in der Grafik abgetragen und dadurch eine Übersicht über die Häufigkeit erstellt. Bei der ersten Grafik werden pro Wiederholung jeweils nur 2 Personen, während es bei der zweiten 1000 sind. Diese Verteilungen ist nun Stichprobenkennwerteverteilung des Mittelwerts. Unsere Annahmen zeigen sich bestätigt - die Mittelwerte streuen stärker mit weniger Personen.

In unserer Stichproben haben wir nicht so einen extremen Fall - die Stichprobengröße beträgt $n = $179. Der rote Strich symbolisiert weiterhin den von uns gefundenen Mittelwert in der Stichprobe. Wie wahrscheinlich ist dieser nun, wenn wir davon ausgehen, dass er aus der beschriebenen Population der Nerdiness stammt? Dafür müssen wir die Verteilung wieder als Fläche betrachten und die exakte Wahrscheinlichkeit bestimmen. Doch schon hier in der Abbildung deutlich, dass der gefundene Wert sehr viel Fläche nach links abschneidet – also ein sehr unwahrscheinlicher Fall vorliegt.

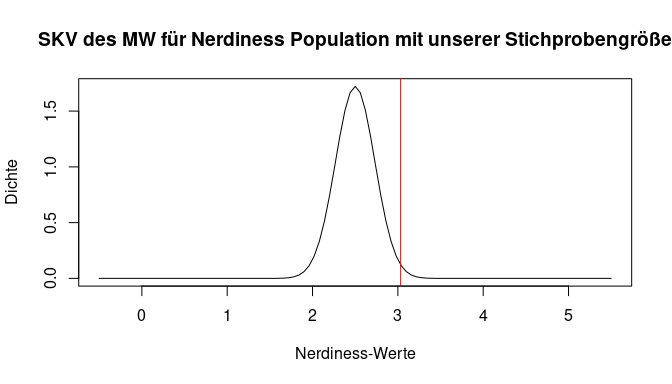
Nochmal soll hier erwähnt sein, dass die Streuung der SKV des Mittelwerts (neben der Stichprobengröße) auch positiv von der Populationsvarianz abhängt, jedoch wollen wir nun zum praktischen Teil übergehen.

Um die theoretischen Überlegungen mathematisch umzusetzen, werden wir zuerst den empirischen z-Wert bestimmen – also den Wert auf der x-Achse auf dem Bild. Zu diesem können wir dann bestimmen, wie unwahrscheinlich er ist.

Die Formel für den empirischen z-Wert $z_{emp}$ ist:

$$z_{emp} = \frac{\bar{x} - {\mu}}{\sigma_{\bar{x}}}$$ wobei sich der Standardfehler (SE) des Mittelwerts wie folgt berechnet:

$$\sigma_{\bar{x}} = {\frac{{\sigma}}{\sqrt{n}}}$$

Wie bereits besprochen wird der Standardfehler des Mittelwerts (also die Streuung der SKV) kleiner, wenn wir mehr Personen untersuchen und größer, wenn die Varianz in der Population größer ist. Zunächst legen wir alle für den z-Wert relevanten Informationen in unser Environment ab, die wir entweder per Hand eingeben müssen (Populationsinformationen) oder mit einer einfachen Funktion bestimmen können.

pop_mean_nerd <- 2.5                 # Mittelwert Grundgesamtheit
pop_sd_nerd <- 3.1                 # SD der Grundgesamtheit
sample_mean_nerd <- mean(fb23$nerd)  # Stichprobenmittelwert
sample_size <- nrow(fb23)            # Stichprobengröße (da keine NA)

Als nächstes müssen wir den Standardfehler des Mittelwerts ($\sigma_{\bar{x}}$) berechnen.

se_nerd <- pop_sd_nerd/sqrt(sample_size) # Standardfehler des Mittelwerts

Der empirische z-Wert $z_{emp}$ zeigt nun einfach auf, wie viele Standardfehler (also Standardabweichungen in der SKV) der gefundene Mittelwert von dem Populationsmittelwert abweicht. Er wird wie folgt berechnet:

z_emp <- (sample_mean_nerd - pop_mean_nerd)/ se_nerd
z_emp

## [1] 2.298564

Der beobachtete Stichprobenmittelwert weicht demnach um $z_{emp}$ = 2.3 SE (nach oben) vom Mittelwert der Grundgesamtheit ab.
Um entscheiden zu können, ob es sich um eine signifikante Abweichung handelt, muss nun bestimmt werden wie wahrscheinlich ein solcher oder noch extremerer Unterschied ist. Dafür können wir den p-Wert bestimmen. Dieser ist im Endeffekt eine Aussage über die Fläche der Verteilung, die außerhalb unseres gefunden Werts liegt.

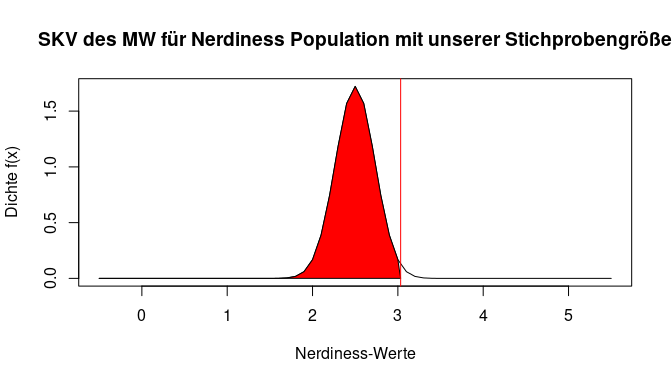
In Rot ist die Fläche für kleinere Werte als unseren eingzeichnet. Es wird bereits deutlich, dass die Fläche in unserem Fall sehr groß sein sollte. Umgekehrt muss der Anteil der Fläche, der für größere Werte als unseren in der Verteilung vorliegt (also der weiße Anteil), sehr gering sein. Mit pnorm() und lower.tail = FALSE können wir direkt bestimmen, wie viel Prozent der Fläche der Verteilung noch für Werte größer als den unseren übrig ist.

pnorm(z_emp, lower.tail = FALSE)

## [1] 0.01076486

Ungefähr 1.08% der Werte sind also größer als unserer.

Achtung: Dieser Wert ist hier noch nicht unser p-Wert, da wir eine zweiseitige Testung haben. Wir haben nur die Fläche für den Fall “größer” bestimmt und nicht für “extremer”. Wir können uns aber die Symmetrie der Verteilung zu nutze machen und den gefundenen Wert mit 2 multiplizieren.

2*pnorm(z_emp, lower.tail = FALSE) #verdoppeln, da zweiseitig

## [1] 0.02152972

Insgesamt 2.15% der Werte extremer als unserer. Wir erkennen, dass der Wert kleiner als .05 (5%) ist. Demnach ist die Wahrscheinlichkeit, diesen Wert (oder einen noch extremeren Wert) per Zufall erhalten zu haben, sehr gering, wenn die $H_0$ gilt. Wir würden uns für die $H_1$ entscheiden.

Weitere Möglichkeit: Vergleich mit kritischem Wert

Neben der Verwendung des p-Werts, ist in der Literatur auch noch häufig die Sprache von einem **kritischen z-Werts $z_{krit}$. Hier wird das Herangehen etwas modifiziert. Statt den p-Wert für unser $z_{emp}$ zu bestimmen, wird sich im Vorhinein überlegt, welcher z-Wert 5% der Verteilung abschneiden würde. Wir können diese Frage mit dem Wissen aus dem Tutorial zu Verteilungen beantworten, indem wir qnorm() benutzen. In unserem Fall suchen wir aufgrund der zweitseitigen Hypothese nach der Hälfte der akzeptierten Irrtumswahrscheinlichkeit.

z_krit <- qnorm(1-.05/2) # Bestimmung des kritischen Wertes
z_krit

## [1] 1.959964

Insgesamt 5% der Verteilung werden also durch -1.96 nach links und 1.96 nach rechts abgetrennt. Der kritische z-Wert beträgt demnach $z_{krit}$ = 1.96. Damit das Ergebnis als signifikant gewertet wird, muss der empirische z-Wert extremer als der kritische Wert sein z-Wert ($|z_{emp}|$ > $|z_{krit}|$). Hierfür können wir auch eine logische Abfrage nutzen. Für die Verwendung der Beträge gibt es die Funktion abs().

abs(z_emp) > abs(z_krit)

## [1] TRUE

Das Ergebnis TRUE zeigt uns, dass unser Wert extremer ist und es sich um einen signifikanten Unterschied handelt. Mit einer Irrtumswahrscheinlichkeit von 5% kann die $H_0$ verworfen werden. Die durschnittliche Nerdiness der Stichprobe unterscheidet sich von der durchschnittlichen Nerdiness der Grundgesamtheit.

Konfidenzintervalle

Alternativ (oder auch ergänzend) können wir ein Konfidenzintervall bestimmen, um unsere Hypothese zu testen. In der Literatur wird häufig folgende Definition benutzt: Das (1 − α)-Konfidenzintervall bezeichnet den Bereich um einen geschätzten Populationsparameter (also den Wert aus der Stichprobe), für den gilt, dass er mit einer Wahrscheinlichkeit von 1 − α den Populationsparameter (bei Mittelwerten $\mu$) überdeckt. Eine etwas technischere Formulierung wäre: Die Wahl von 5% Irrtumswahrscheinlichkeit bei der Bildung eines Konfidenzintervalles heißt, dass das Intervall mit 5%-iger Wahrscheinlichkeit zu den Intervallen gehört, die den Populationsparameter (bei Mittelwerten $\mu$) nicht enthalten.

Die Idee für die Absicherung bleibt bei beiden Definitionen dieselbe - einfach gesagt: Wir legen einen Bereich um unserern Stichprobenwert, dessen Breite wir anhand einer Irrtumswahrscheinlichkeit bestimmen. Wenn der uns bekannte Populationsparameter (bei Mittelwerten $\mu$) nun nicht in diesem Bereich liegt, gehen wir davon aus, dass unsere Stichprobe nicht zu dieser Population gehört. Denn wir sind uns ja zu (1- $\alpha$ )% sicher, dass unser Konfidenzintervall den Populationswert, der zu unserer Stichprobe gehört, überdecken sollte. Damit würden wir im Fall von Mittelwerten vermuten, dass $\mu_0 \neq \mu_1$, was genau der $H_1$ Hypothese unserer vorangegangen Testung entspricht.

Für die Berechnung des Konfidenzintervalls brauchen wir Parameter, die uns bereits bekannt sind. Folgendes wird berechnet.

$$\bar{x} \pm z_{1-\frac{\alpha}{2}} * \sigma_{\bar{x}} = \bar{x} \pm z_{1-\frac{\alpha}{2}}*\frac{\sigma}{\sqrt{n}}$$

Die Gleichtung enthält den Standardfehler ($\sigma_\bar{x}$) des Mittelwerts, der weiterhin aus der Standardabweichung ($\sigma$) der Population und der Wurzel aus der Stichprobengröße ($n$) bestimmt werden kann. Wenn wir ein 95%-Konfidenzintervall bestimmen wollen, brauchen wir das zugehörige Quantil aus der Standardnormalverteilung - also den z-Wert für $1-\frac{\alpha}{2}$. Wir müssen das $\alpha$-Niveau halbieren, da wir wie besprochen eine zweiseitige Testung durchführen.

Wir haben bereits gesehen, dass man Quantile aus der Normalverteilung mit der Funktion qnorm() erhalten kann. Die Standardnormalverteilung mit Mittelwert von 0 und Standardabweichung von 1 ist dabei der Default, aber wir geben die Argumente zur Übung trotzdem selbst an.

z_quantil_zweiseitig <- qnorm(p = 1-(.05/2), mean = 0, sd = 1)
z_quantil_zweiseitig

## [1] 1.959964

Dieser Wert kommt uns bekannt vor – er entspricht dem bereits bestimmten $z_{krit}$. Dies ist auch kein Zufall, da wir jeweils danach gesucht haben, welcher Wert die extremsten 5% (2.5% jeweils unten und oben) von der Verteilung abtrennt. Nun haben wir alle wichtigen Informationen, um ein zweiseitiges Konfidenzintervall um unseren Mittelwert der Stichprobe zu legen.

up_conf_nerd <- sample_mean_nerd+((z_quantil_zweiseitig*pop_sd_nerd)/sqrt(sample_size))

lo_conf_nerd <- sample_mean_nerd-((z_quantil_zweiseitig*pop_sd_nerd)/sqrt(sample_size))

up_conf_nerd

## [1] 3.486722

lo_conf_nerd

## [1] 2.578455

In diesem Fall würde man den wahren Mittelwert der Grundgesamtheit, aus der die Stichprobe gezogen wurde, zwischen 2.58 und 3.49 vermuten. Mit einer Wahrscheinlichkeit von 95% enthält unser Konfidenzintervall zwischen 2.58 und 3.49 den wahren Wert der zugehörigen Population.

Optisch ansprechender können wir das Ergebnis natürlich ausgeben, indem wir unsere beiden Werte in einen gemeinsamen Vektor ablegen.

conf_nerd <- c(lo_conf_nerd, up_conf_nerd)
conf_nerd

## [1] 2.578455 3.486722

Das Konfidenzintervall kann nun dafür genutzt werden, unsere Hypothesen zu überprüfen. Wir sind uns dabei zu 95% sicher, dass unser Konfidenzintervall den wahren Wert der Population, aus dem unsere Stichprobe stammt enthält. Das Konfidenzintervall überdeckt allerdings nicht den vorgegebenen Populationswert von $\mu_0 = 2.5$. Daher würden wir davon ausgehen, dass sich der Mittelwert der Population, aus der unsere Stichprobe stammt, von diesem unterscheidet $\mu_0 \neq \mu_1$. Die Hypothese $H_0$ wird damit verworfen und die $H_1$ angenommen.

t-Test

Die Bekanntheit des Populationsmittelwertes und der Populationsvarianz ist jedoch ein seltener Fall in der Praxis. Zunächst machen wir eine Erweiterung auf den Fall, dass die Populationsvarianz nicht bekannt ist. Trotzdem soll weiterhin ein Stichprobenmittelwert mit einem bekannten Populationsmittelwert verglichen werden. Wir werden sehen, dass dies zwar ein paar Veränderungen im Vorgehen und den Gleichungen mit sich bringt, das Prinzip aber erhalten bleibt. Bezeichnet wird das Vorgehen nun als t-Test, den wir im Einstichproben-Fall hier durchführen möchten.

Für dieses statistische Verfahren stellen wir uns die Frage, ob der Neurotizismus Wert der Psychologie-Studierenden in unserer Stichprobe größer ist als der Populationsmittelwert aller Studierenden. Nehmen wir dafür an, dass der mittlere Neurotizismuswert in der Population der Studierenden bei $\mu = 3.1$ liegt, aber die Populationsstandardabweichung nicht bekannt ist. Zunächst sollten wir wieder Hypothesen aufstellen, was wir wieder inhaltlich und statistisch machen.

Inhaltlich

In der Fragestellung fällt direkt ein Unterschied auf. Wir haben hier eine Richtung in unserer Fragestellung – nehmen wir an, dass wir diese aus der Literatur ableiten konnten. Also haben wir keine ungerichteten sondern gerichtete Hypothesen. Dies muss sich natürlich auch in unserer Formulierung wiederspiegeln. Unsere Vermutung (Stichprobenmittelwert ist größer als Populationsmittelwert) nehmen wir als $H_1$ auf, während in der $H_0$ alle gegenteiligen Fälle (kleiner oder gleich) aufgeführt sind.

$H_0$: Der mittlere Neurotizismuswert unserer Stichprobe ist gleich oder niedriger als der mittlere Neurotizismuswert der Studierenden-Population.

$H_1$: Der mittlere Neurotizismuswert unserer Stichprobe ist höher als der mittlere Neurotizismuswert der Studierenden-Population.

Statistisch

Auch in der statistischen Hypothesennotation bildet sich die Richtung der Hypothesen natürlich ab.

$$H_0: \mu_0 \geq \mu_1$$

$$H_1: \mu_0 < \mu_1$$ Um eine weitere Modifikation unseres Vorgehens im Vergleich zum letzten Test zu haben, ändern wir auch unser Signifikanzniveau. Wir wollen diesmal auf der sehr sicheren Seite sein und wählen daher im weiteren Vorgehen $\alpha = 1$%.

Bevor wir in die inferenzstatistische Analyse einsteigen, ist es immer gut, sich einen Überblick über die deskriptiven Werte zu verschaffen. Wir können nun natürlich einfach die bereits gelernten Funktionen zu Mittelwert, Varianz, Minimum, etc. nutzen. Doch gibt es einen schnelleren Weg? Die Basisinstallation von R bietet uns keine Alternative. Jedoch gibt es zusätzliche Pakete, die den Pool an möglichen Funktionen erweitern. Die Logik wird im Folgenden erläutert.

Wie können andere Funktionen in R genutzt werden? - Library und Pakete

R ist in einer Pakete-Logik aufgebaut. Das liegt daran, dass es immer mehr Funktionen in R gibt, die aber nie jemand alle gleichzeitig brauchen wird. Zur Schonung der Kapazität sind diese Funktionalitäten also in Pakete aufgeteilt. In Basispaketen, die standardmäßig geladen werden (also vorinstalliert sind und aktiviert werden beim Öffnen von R / RStudio), sind grundlegende Befehle und Analysen implementiert. Beispiele für solche Basispakete sind base, stats und graphics, aus denen wir unwissentlich schon einige Funktionen verwendet haben - bspw. mean(), median() und barplot().

Für spezifischere Analysen (also weitere Funktionen) müssen Zusatzpakete teilweise erst installiert, zumindest aber immer per Hand geladen werden (Beispiele sind psych, car oder ggplot2). Nur die Funktionen von erst installierten und dann geladenen Paketen können in einem Skript benutzt werden.

Unter dem Reiter Packages wird die Library angezeigt. Hier sind alle Pakete enthalten, die einmal installiert wurden. Pakete müssen ab und zu (per Hand) aktualisiert werden.

Sobald Sie eigene Pakete installiert haben, gibt es in dem Reiter Packages die Einteilung in die System Library (also standardmäßig installierte Pakete) und die User Library (von Ihnen installierte Pakete).

Die folgenden Bilder verdeutlichen nochmal das Prinzip vom Installieren und Laden. Bei der Installation von R werden die Basispakete automatisch in die Library installiert. Zusatzpakete müssen mit der Funktion install.packages() mit dem Paketnamen als Argument installiert werden. Hierzu ist meist eine Internetverbindung nötig.

Beim Start von R werden die Basispakete automatisch geladen. Zusatzpakete müssen hingegen mit der Funktion library() mit dem Paketnamen als Argument geladen werden.

Gehen wir das Prinzip an dem Beispielpaket psych durch, das verschiedene Operationen enthält, die in der psychologischen Forschung häufig benötigt werden. Die Installation muss dem Laden des Paketes logischerweise vorausgestellt sein. Wenn R einmal geschlossen wird, müssen alle Zusatzpakete neu geladen, jedoch nicht neu installiert werden.

install.packages('psych')          # installieren

library(psych)                     # laden

Wir erhalten hier als Warning Message den Hinweis, unter welcher Version das Paket erstellt wurde. Eine kleine Suche nach Hilfe zu Pakete kann man mit ?? erhalten.

??psych                          # Hilfe

Da das Paket psych nun geladen ist, können wir Funktionen aus diesem nutzen. Für unsere Übersicht über deskriptive Maße der Variable neuro gibt es die Funktion describe().

describe(fb23$neuro)

##    vars   n mean   sd median trimmed  mad min max range  skew kurtosis   se
## X1    1 179 3.35 0.98    3.5    3.37 0.74   1   5     4 -0.19    -0.68 0.07

Wir bekommen auf einen Schlag sehr viele relevante Informationen über unsere Variable. Der Mittelwert unserer Stichprobe liegt beispielsweise bei 3.35. Beachten Sie, dass auch bei describe() unter sd die geschätzte Populationsstandardabweichung angegeben wird (wie bei der Basis-Funktion sd()). Man müsste sie also umrechnen, um eine Angabe über die Stichprobe machen zu können.

Zurück zu unserer inhatlichen Fragestellung: Der Mittelwert von unserer Stichprobe ist deskriptiv größer als der Populationsmittelwert aller Studierenden. Dies reicht natürlich noch nicht, um eine inferenzstatistische Aussage zu treffen – dafür muss im Folgenden der Test durchgeführt werden. Bei gerichteten Hypothesen gibt es jedoch manchmal den Effekt, dass man bei der deskriptiven Überprüfung schon stoppen kann. Wenn sich bspw. deskriptiv gezeigt hätte, dass der Mittelwert unserer Stichprobe kleiner ist als der Populationsmittelwert, kann man die Testung abbrechen. Die $H_1$ Hypothese wird hier direkt abgelehnt und die $H_0$ weiter angenommen. Da dieser Fall hier aber nicht aufgetreten ist, machen wir mit der Testung weiter.

Voraussetzungsprüfung

Inferenzstatistische Tests haben für ihre Durchführung immer Voraussetzungen. Diese können in Anzahl und Art variieren. Verletzungen von Voraussetzungen verzerren verschiedene Aspekte der Testung. Für manche Verletzungen gibt es Korrekturen, andere führen dazu, dass man ein anderes Verfahren wählen muss. Wir werden uns im Laufe des Semesters mit vielen Voraussetzungen beschäftigen. Für den Einstichproben-t-Test ist die Liste der Voraussetzungen nicht sehr lange:

1. mindestens intervallskalierte abhängige Variable
2. Bei n < 30 : Normalverteilung der abhängigen Variable in der Population.

Die erste Voraussetzung lässt sich nicht mathematisch sondern theoretisch prüfen. Sie ist natürlich essentiell, da wir hier mit Mittelwerten und Varianzen rechnen und wir bereits gelernt haben, dass diese erst ab dem Intervallskalenniveau genutzt werden sollten. Wir haben außerdem gelernt, dass Skalenwerte häufig als intervallskaliert angenommen werden. Da wir in fb23$neuro solche Skalenwerte haben, können wir diese Voraussetzung als gegeben annehmen.

Kommen wir zu der zweiten Voraussetzung. Für die inferenzstatistische Testung bestimmen wir die Position unseres empirischen Mittelwerts in der Stichprobenkennwerteverteilung der Mittelwerte. Für diese nehmen wir eine spezifische Form an - sie soll der $t$-Verteilung (übergehend bei $n \rightarrow \infty$ in eine $z$-Verteilung) folgen. Für diese Annahme ist die Normalverteilung der Variablen in unserer Stichprobe eine hinreichende Voraussetzung. Das heißt, wenn diese gegeben ist, folgt die Stichprobenkennwerteverteilung der von uns angenommenen Form. Wie wir später besprechen werden, ist die Normalverteilung aber keine notwendige Voraussetzung. In diesem Tutorial lernen wir zunächst die optische Prüfung der Normalverteilung kennen – im weiteren Verlauf des Studiums werden auch inferenzstatistische Testungen dazu kommen. Die einfachste optische Prüfung ist das Zeichnen eines Histogramms. Wir haben bereits gelernt, dass das mit dem Befehl hist() erreicht werden kann. Statt absoluten Häufigkeiten sollen hier die Dichten angezeigt werden, was wir durch die Eingabe von freq = FALSE bestimmen.

hist(fb23$neuro, xlim=c(0,6), main = "Histogramm",
     xlab = "Score", ylab= "Dichte", freq = FALSE)

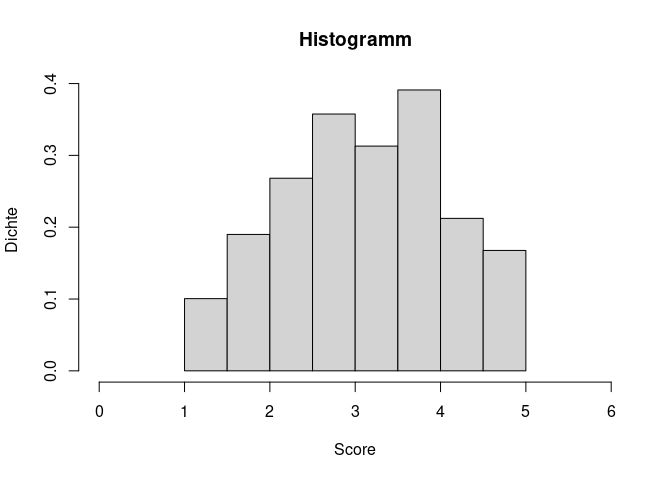
Wir sehen bereits, dass der Gipfel unserer empirischen Werte für eine Normalverteilung fehlt. Das Abflachen zu den Seiten sieht aber relativ Glockenförmig und symmetrisch aus. Für eine bessere Einordnung wäre es hilfreich, die theoretisch angenommene Normalverteilung noch zusätzlich zu unseren empirischen Werten einzuzeichnen. Hiefür nutzen wir die curve() Funktion. Da wir bereits einen Plot (das Histogramm) gezeichnet haben, können wir mit dem Argument add dafür sorgen, dass die Kurve in das bestehende Bild integriert wird. Daher müssen wir keine Angaben für from, to und Ähnliches machen. Lediglich die Form der Verteilung als Dichtefunktion der theoretischen Normalverteilung dnorm() und die dazu gehörigen beschreibenden Maße Mittelwert und Standardabweichung (hervorgehend aus unserer Nerdiness Variable) werden benötigt. Genau genommen sollte man hier die empirische Standardabweichung nutzen, weil im Histogramm ja auch die Werte aus der Stichprobe dargestellt werden. Da bei einer steigenden Stichprobengröße aber die empirische Varianz und das Ergebnis von sd() sehr ähnlich sind und wir hier nur eine optische Einordnung vornehmen, nutzen wir einfach die Funktion, damit der Code nicht zu unübersichtlich wird.

curve(dnorm(x, mean = mean(fb23$neuro), sd = sd(fb23$neuro)), add = T)

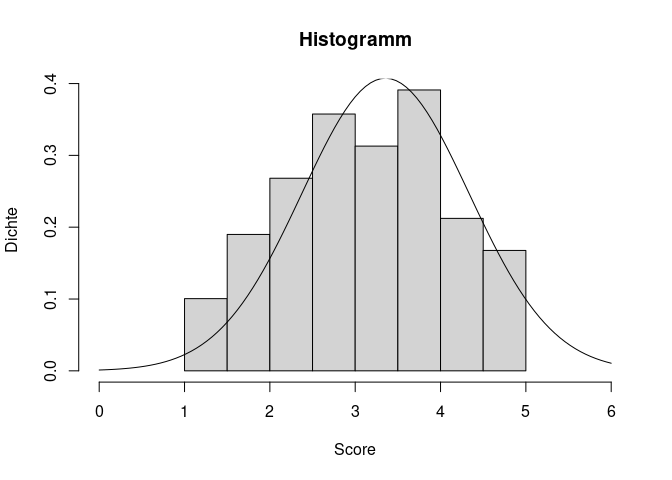
Im Plot sieht man recht gut, dass es kleine Abweichungen der wirklichen empirischen Verteilung von der theoretische, perfekten Form der Normalverteilung gibt. Kleinere Abweichungen sind jedoch zu erwarten und sollten nicht zu hoch eingestuft werden. Leider wird es bei der optischen Prüfung keine perfekt objektive Lösung geben, doch je mehr Plots man im Laufe der Forschungskarriere betrachtet, umso besser kann man auch diese Verläufe einordnen.

Eine zweite Möglichkeit ist das Erstellen eines sogenannten QQ-Plots (steht für quantile-quantile). Auf der x-Achse sind diejenige Positionen notiert, die unter Gültigkeit der theoretischen Form der Normalverteilung zu erwarten wären. Auf der y-Achse wird die beobachtete Position eines Messwerts abgetragen. Damit die Werte die gleiche Skalierung haben und damit einfacher interpretierbar sind, standardisieren wir zunächst unsere Variable neuro. Hierfür erstellen wir eine neue Variable neuro_std in unserem Datensatz. Codetechnisch ist ein QQ-Plot dann schnell erstellt. Mit qqnorm() zeichnet man die Punkte, während qqline() als Unterstützung nochmal die Linien durch die Mitte zeichnet.

fb23$neuro_std <- scale(fb23$neuro, center = T, scale = T)
qqnorm(fb23$neuro_std)
qqline(fb23$neuro_std)

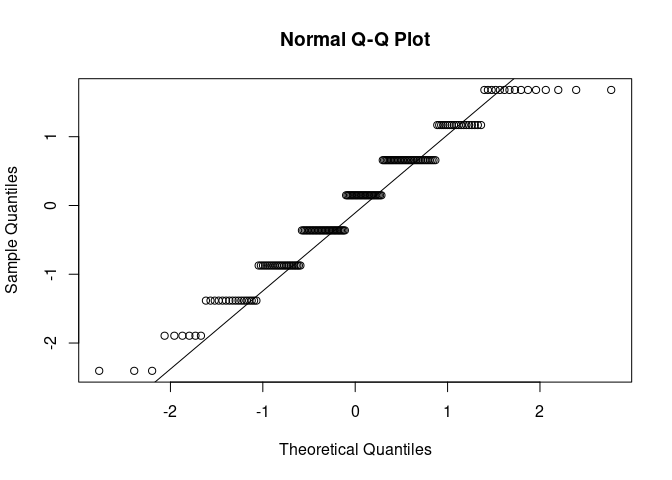
Entspricht nun unsere empirische Datenmenge der angenommenen Normalverteilung perfekt, würden alle Punkte auf der Geraden in der Mitte liegen. Auch hier gilt natürlich, dass die Bewertung letztlich eine gewisse Subjektivität hat. Die Punkte sollten nicht zu weit von der Geraden entfernt liegen.

Nach dem Plot zu urteilen könnte eine Verletzung der Normalverteilungsannahme hier vorliegen. Allerdings können wir uns behelfen und den Test trotzdem durchführen. Die Normalverteilungsannahme darf nämlich verletzt sein, wenn die Stichprobe mindestens 30 Personen umfasst. In diesen Fällen wird das inferenzstatistische Ergebnis nicht verzerrt. Dann gilt der zentrale Grenzwertsatz: Die Stichprobenkennwertverteilung der Mittelwerte nähert sich einer Normalverteilung an, unabhängig davon wie das Merkmal selbst in der Population verteilt ist. Die Stichprobengröße von 30 ist allerdings nur eine Daumenregel - bei starken Verletzungen sollte man sich auch überlegen, ob der Mittelwert der beste Repräsentant für die mittlere Ausprägung der Variable darstellt.

Signifikanz bestimmen

Nun wollen wir inferenzstatistisch prüfen, ob die Vermutung der Forschungsgruppe bestätigt werden kann. Als ersten Schritt berechnen wir den Mittelwert in unserer Stichprobe. Dabei sollten wir auch auf fehlende Werte achten, die aber nicht vorliegen.

anyNA(fb23$neuro)

## [1] FALSE

sample_mean_neuro <- mean(fb23$neuro)
pop_mean_neuro <- 3.1

Der t-Test basiert auf folgender Formel:

$$t_{emp} = \frac{\bar{x} - {\mu}}{\hat\sigma_{\bar{x}}}$$ wobei sich der Standardfehler (SE) des Mittelwerts wie folgt zusammensetzt:

$$\hat\sigma_{\bar{x}} = {\frac{{\hat\sigma}}{\sqrt{n}}}$$

Da die Standardabweichung in der Population nicht bekannt ist, muss diese mittels Nutzung der Standardabweichung der Stichprobe geschätzt werden. Dies funktioniert über die Funktion sd().

sample_sd_neuro <- sd(fb23$neuro)
sample_sd_neuro

## [1] 0.979347

Der Standardfehler des Mittelwerts wird anschließend auf der Basis dieses geschätzten Wertes selber geschätzt und nicht wie im z-Test bestimmt. Formeltechnisch wird die Schätzung durch das Dach über den Buchstaben gekennzeichnet. Für die Schätzung des Standardfehlers des Mittelwerts brauchen wir als zusätzliche Information noch die Stichprobengröße, die wir beispielsweise über nrow() unseres Datensatzes bestimmen können, da wir keine fehlenden Werte haben.

sample_size <- nrow(fb23)
se_neuro <- sample_sd_neuro/sqrt(sample_size)

Nun haben wir alle Informationen gegeben, um den empirischen *t-*Wert $t_{emp}$ zu bestimmen:

t_emp <- (sample_mean_neuro - pop_mean_neuro) / se_neuro
t_emp

## [1] 3.48018

Die Bezeichnung der empirischen Prüfgröße (wie auch der Name des Tests) weist bereits darauf hin, dass wir uns bei der Hypothesenprüfung nicht mehr im Rahmen der Standardnormalverteilung bewegen. Dies liegt daran, dass sich durch das Schätzen der Populationsvarianz keine exakte Standardnormalverteilung mehr ergibt. Stattdessen wird mit einer t-Verteilung gearbeitet, deren genaue Form von der Anzahl der Freiheitsgraden abhängt. Die Unterscheidung zwischen Standardnormalverteilung und der t-Verteilung liegt besonders in den Extrembereichen. Da genau diese jedoch für die inferenzstatistische Testung von Interesse sind, ist die Nutzung der richtigen Verteilung wichtig.

Wenn wir den $p$-Wert in einer t-Verteilung bestimmen wollen, nutzen wir pt() statt pnorm(). Als zusätzliches Argument neben dem empirischen Wert und lower.tail benötigen wir hier noch die Anzahl der Freiheitsgrade. Im Rahmen des t-Testes im Einstichproben-Fall bestimmen sich die Freiheitsgrade mittels $n - 1$.

pt(t_emp, df = sample_size - 1, lower.tail = F) #einseitige Testung

## [1] 0.0003150813

Der p-Wert ist kleiner .01 ($p < \alpha$). Der Erwartungswert für den Mittelwert unserer Sichprobe $\mu_1$ ist demnach größer als der bekannte Populationsmittelwert $\mu_0$. Demnach würden wir die $H_0$ verwerfen und die $H_1$ annehmen.

Weitere Möglichkeit: Vergleich mit kritischem Wert

Auch bei diesem Test kann statt des p-Werts der kritische t-Wert $t_{krit}$ bestimmt werden. Statt qnorm() nutzen wir hier dann natürlich qt() und geben wieder die Freiheitsgrade an.

t_krit <- qt(0.01, df = sample_size-1, lower.tail = FALSE)
t_krit

## [1] 2.347479

Der kritische *t-*Wert ($t_{krit}$) wird hier so bestimmt, dass er das den Wert sucht, der die unteren 99% abtrennt. Dies entspricht dann 1% der Verteilung nach oben und damit genau unserem $\alpha$-Niveau. Zur Entscheidung bezüglich der Hypothesen müssen wir nun den empirischen und kritischen $t$-Wert vergleichen.

t_emp > t_krit

## [1] TRUE

Der empirische t-Wert ist größer als der kritische ($t_{emp} > t_{krit}$), wodurch wir die $H_0$ verwerfen und die $H_1$ annehmen. Dies sollte uns aber nicht überraschen, da natürlich dasselbe Ergebnis rauskommen muss wie bei der Testung über den $p$-Wert.

Einseitiges Konfidenzintervall für den Einstichproben-t-Test

Auch für den Einstichproben-t-Test kann ein äquivalentes Konfidenzintervall bestimmt werden. Dies funktioniert sehr ähnlich zu dem vorherigen Vorgehen beim Einstichproben-z-Test, jedoch brauchen wir aufgrund unserer Hypothesen ein einseitiges Konfidenzintervall. Gleichzeitig müssen wir das $\alpha$-Niveau anpassen.

Die Gleichung für ein zweiseitiges Konfidenzintervall beim Einstichproben-t-Test sieht erstmal sehr ähnlich. Statt eines Wertes auf der z-Verteilung wird nun ein Wert aus der t-Verteilung abgelesen und für die Bestimmung der Grenzen verwendet. Außerdem wird der Standardfehler des Mittelwerts bzw. die Populationsvarianz hier nur geschätzt, da wir diese Informationen nicht gegeben haben.

Wenn wir nun einseitige Hypothesen haben brauchen wir nur eine der beiden Grenzen bestimmen. Wir gehen davon aus, dass unser Stichprobenmittelwert größer ist als der Populationsmittelwert. Wir legen das Konfidenzintervall um unseren Stichprobenmittelwert und können es daher nach oben offen lassen (größerer Populationsmittelwert würde sowieso immer die $H_0$ nach sich ziehen – hier brauchen wir keine Grenze). Es muss also nur eine untere Grenze bestimmt werden und die obere kann als unendlich ($\infty$) angenommen werden. Die untere Grenze kann mit dem gesamten $\alpha$-Niveau bestimmt werden. Wir müssen dieses nicht mehr auf beide Bereiche aufteilen.

Kleine Anmerkung: Natürlich könnten wir auch beim Einstichproben-z-Test ein einseitiges Konfidenzintervall berechnen, was äquivalent funktionieren würde.

Kommen wir zur Umsetzung. Den zugehörigen t-Wert können wir wieder mit der Funktion qt() bestimmen.

t_quantil_einseitig <- qt(0.01, df = sample_size-1, lower.tail = FALSE)
t_quantil_einseitig

## [1] 2.347479

Anschließend kann die untere Grenze des Intervalls sehr simpel bestimmt werden.

sample_mean_neuro - t_quantil_einseitig *(sample_sd_neuro / sqrt(sample_size))

## [1] 3.182913

Der Populationsmittelwert liegt nicht in dem Konfidenzintervall für den Erwartungswert unserer Stichprobe, sondern ist kleiner als die untere Grenze. Daher würden wir die $H_0$ in diesem Fall verwerfen. Auch beim Einstichproben-t-Test – egal ob mit einseitiger oder zweiseitiger Hypothese – gilt: Die Durchführung des inferenzstatistischen Test kommt hinsichtlich der Hypothesenbeurteilung zur selben Schlusffolgerung wie die Berechnung des äquivalenten Konfidenzintervalls.

t-test mit t.test() Funktion

Statt der händischen Berechnung gibt es auch noch die Funktion t.test(), die uns die Ergebnisse direkt ausgeben kann. Trotzdem wollten wir erstmal uns das Prinzip anschauen, weil empirische, kritische und p-Werte sowie Konfidenzintervalle sehr zentrale Konzepte der Statistik sind und uns im weiteren Verlauf immer wieder begegnen werden. Die Funktion braucht im Einstichprobenfall neben den Werten der Stichprobe noch das Argument mu, in dem der Populationsmittelwert festgehalten wird. alternative gibt an, ob wir in unseren Hypothesen eine Richtung haben (two.sided für ungerichtete Hypothesen, less oder greater für gerichtete Hypothesen). Da unsere Hypothese $H_1$ den Stichprobenmittelwert als größer als den Populationsmittelwert annimmt, wählen wir in diesem Fall greater. In conf.level geben wir $1 - \alpha$ an – mit Hilfe dieses Arguments bestimmt R das Konfidenzintervall.

t.test(x = fb23$neuro, mu = 3.1, alternative = "greater", conf.level=0.99) #gerichtet, Stichprobenmittelwert höher

## 
## 	One Sample t-test
## 
## data:  fb23$neuro
## t = 3.4802, df = 178, p-value = 0.0003151
## alternative hypothesis: true mean is greater than 3.1
## 99 percent confidence interval:
##  3.182913      Inf
## sample estimates:
## mean of x 
##  3.354749

Im Output sind bereits die wichtigsten Informationen enthalten. Wir erhalten den empirischen t-Wert $t_{emp}$ = 3.48. Der kritische Wert wird hier nicht ausgegeben, sondern stattdessen der p-Wert. Auch die Freiheitsgrade df werden mit berichtet.

Die Ergebnisse entsprechen (erfreulicherweise) genau denen, die wir auch per Hand bestimmt haben. Demnach wird die $H_0$ verworfen und die $H_0$ angenommen.

Das 99%ige Konfidenzintervall wird uns ebenfalls ausgegeben. Beachten Sie, dass es sich aufgrund unserer Hypothese um ein einseitiges Intervall handelt (nach oben offen). Dies wird in R durch Inf gekennzeichnet, was für unendlich auf Englisch (infinity) steht).

Effektgröße

Kommen wir zum letzten Thema dieses Beitrags. Neben der inferenzstatistischen Absicherung der Hypothesen sollte auch die Stärke des gefundenen Effekts untersucht werden. Bei vielen Testungen wäre es durch die reine Hinzunahme an Personen möglich, ein signifikantes Ergebnis zu erhalten. Dies bedeutet aber nur, dass ein Effekt auf die Population übertragbar ist. Die Bedeutsamkeit (in diesem Fall: wie stark unterscheiden sich die Mittelwerte) wird dadurch nicht deutlich. Die Bedeutsamkeit wird durch eine Effektgröße angegeben, wobei bei Mittelwertsunterschiede meist Cohen’s d verwendet wird.

Betrachten wir zunächst die Formel für die Berechnung beim Einstichproben-z-Test. Die Bestandteile kommen uns bekannt vor – im Zähler wird die Differenz der Mittelwerte aus Stichprobe und Population gebildet. Die Differenz wird durch die Populationsstandardabweichlung standardisiert.

$$d = |\frac{\bar{x} - {\mu}}{\sigma}|$$ Die Umsetzung in R ist aufgrund der einfachen Formel auch recht schnell. In unserem Einstichproben-z-Test haben wir die Nerdiness Werte aus unserer Stichprobe analysiert. Die funktion abs() bestimmt den Betrag einer Zahl und wird daher hier verwendet.

dz <- abs((sample_mean_nerd - pop_mean_nerd)/ pop_sd_nerd) 
dz

## [1] 0.1718027

Effektgrößen beschreiben die Relevanz von signifikanten Ergebnissen. Zudem kann es verwendet werden, um den Effekt über verschiedene Studien hinweg zu vergleichen. Normalerweise sollte die Einordnung der Größe anhand vergleichbarer Studien aus dem selben Bereich durchgeführt werden. Bei völliger Ahnungslosigkeit über relevante Größen gibt es eine Übersicht zur Orientierung. Es gilt nach Cohen (1988):

d = 0.2 -> kleiner Effekt

d = 0.5 -> mittlerer Effekt

d = 0.8 -> großer Effekt

Die Effektgröße beträgt in diesem Fall 0.17. Da wir keine Vergleichsstudien haben spricht dies für einen kleinen Effekt.

Im Fall des Einstichproben-t-Tests verwenden wir die geschätzte Populationsstandardabweichung. Ansonsten ändert sich die Berechnung nicht.

$$d = |\frac{\bar{x} - {\mu}}{\hat{\sigma}}|$$

Auch hier ist die Umsetzung in R sehr leicht – in unserer Anwendung haben wir beim Einstichproben-t-Test die Variable neuro aus unserem Datensatz verwendet.

dt <- abs((sample_mean_neuro - pop_mean_neuro)/ sample_sd_neuro)
dt

## [1] 0.2601209

Die Effektgröße beträgt 0.26, womit wir uns auch hier im Bereich eines kleinen Effektes befinden.

Literatur

Cohen, J. (1988). Statistical power analysis for the Behavioral Sciences. Routledge.