Freiwillige Übungsaufgaben - Lösungen
Hier finden Sie die Lösungen zu den Zusatzaufgaben!
Zunächst wollen wir nochmal Übungen mit einem kleinen, ausgedachten Datensatz durchführen. Stellen Sie sich dafür vor, dass Sie im Rahmen Ihres Studiums eine Untersuchung mit 10 Studierenden durchgeführt haben. Dabei haben Sie das Alter (in ganzen Zahlen), das Geschlecht (weiblich, männlich, divers), die deutsche Lieblingsstadt (Berlin, Hamburg, München, Frankfurt, Dresden) sowie die generelle Lebenszufriedenheit, gemessen mit 5 Items, erhoben.
Aufgabe 1
Laden Sie die folgenden 3 Vektoren und den Datensatz in Ihr Environment.
- Welche Klasse haben die Vektoren?
- Wie lauten die Dimensionen des Datensatzes?
#demographische Daten:
geschlecht <- c(1, 2, 2, 1, 1, 1, 3, 2, 1, 2)
alter <- c(20, 21, 19, 19, 20, 23, 22, 21, 19, 25)
stadt <- c(2, 1, 1, 4, 3, 2, 5, 4, 1, 3)
#Lebenszufriedenheit:
lz_items <- data.frame(lz1 = c(3, 4, 4, 2, 1, 4, 3, 5, 4, 3), lz2 = c(2, 2, 3, 2, 4, 1, 2, 3, 2, 2), lz3 = c(5, 3, 4, 4, 3, 5, 2, 4, 3, 4), lz4 = c(2, 1, 3, 2, 2, 3, 2, 4, 2, 1), lz5 = c(4, 4, 3, 3, 1, 4, 3, 4, 5, 3))
Lösung
An dieser Stelle zunächst eine generelle Anmerkung: Für einige der nachfolgenden Aufgaben wird es - wie eigentlich fast immer in R - mehrere Lösungswege geben. Die hier gezeigten Wege sind also exemplarische Vorlagen.
class(geschlecht)
## [1] "numeric"
class(alter)
## [1] "numeric"
class(stadt)
## [1] "numeric"
dim(lz_items)
## [1] 10 5
Die einzelnen Vektoren gehören alle zur Klasse numeric, da sie nur Zahlen beinhalten. Die Dimensionen des Datensatzes zu den lz_items betragen 10 Zeilen und 5 Spalten (in dem Fall die Anzahl der Lebenszufriedenheites-Items).
- Führen Sie die Vektoren und den Datensatz zusammen zu einem gemeinsamen Datensatz mit dem Namen
data. Wie viele Variablen hat der neue Datensatz, wieviele Proband:innen liegen vor?
Lösung
data <- data.frame(geschlecht, alter, stadt, lz_items)
dim(data)
## [1] 10 8
In dim wäre die Anzahl der Proband:innen, also die Anzahl der Zeilen, der erste Wert. Es liegen also 10 Proband:innen vor. Der zweite Wert beschreibt die Anzahl der Variablen. Hier haben wir demnach 8 Variablen.
- Wandeln Sie die Variable
geschlechtund die Variablestadtin Faktoren um. Dabei sind die Zahlen in der Reihenfolge im Beschreibungstext zugeordnet (Beispiel:1bei Geschlecht wäreweiblich). Überschreiben Sie die alten Variablen und überprüfen Sie die Umwandlung.
Lösung
data$geschlecht <- factor(data$geschlecht, levels = 1:3, labels = c("weiblich", "männlich", "divers"))
str(data$geschlecht)
## Factor w/ 3 levels "weiblich","männlich",..: 1 2 2 1 1 1 3 2 1 2
data$stadt <- factor(data$stadt, levels = 1:5, labels = c("Berlin", "Hamburg", "München", "Frankfurt", "Dresden"))
str(data$stadt)
## Factor w/ 5 levels "Berlin","Hamburg",..: 2 1 1 4 3 2 5 4 1 3
Aufgabe 2
Nun wollen wir die Extraktion von bestimmten Datenpunkten nochmal üben.
- Welche deutsche Lieblingsstadt hat Person 4 angegeben?
- Welches Geschlecht haben Person 7 und 8 angekreuzt?
- Wie lauten die Lebenszufriedenheits-Werte von Person 2 und 3 auf allen Items?
Lösung
data[4, "stadt"]
## [1] Frankfurt
## Levels: Berlin Hamburg München Frankfurt Dresden
data[c(7, 8), "geschlecht"]
## [1] divers männlich
## Levels: weiblich männlich divers
data[c(2, 3), c(4:8)]
## lz1 lz2 lz3 lz4 lz5
## 2 4 2 3 1 4
## 3 4 3 4 3 3
- Wir sehen, dass Person 4 die Stadt Frankfurt angegeben hat.
- Person 7 hat das Geschlecht divers angegeben und Person 8 männlich.
- In der ausgegebenen Tabelle werden die Lebenszufriedenheits-Werte von Person 2 und 3 auf allen Items ausgegeben.
Aufgabe 3
Im Folgenden soll nicht nur extrahiert, sondern auch ersetzt werden.
- Ihnen fällt auf, dass die Angabe der 3. Person in Item
lz2undlz4nicht korrekt sind. Die korrekten Werte betragen 2 (fürlz2) und 1 (fürlz4). Wandeln Sie die Angaben im Datensatz entsprechend um.
Lösung
data[3, "lz2"] <- 2
data[3, "lz4"] <- 1
- Person 6 hat zudem ein falsches Alter angegeben (eigentlich 24). Welches Alter steht noch im Datensatz? Korrigieren Sie es entsprechend.
Lösung
data[6, "alter"]
## [1] 23
Im Datensatz steht, dass das Alter der Person 6 23 beträgt. Hier muss also das richtige Alter (24 Jahre) zugeordnet werden.
data[6, "alter"] <- 24
Aufgabe 4
Bei Item lz2 und lz4 handelt es sich um invertierte Items. Wandeln Sie die Items entsprechend um, sodass einheitlich eine hohe Ausprägung für eine hohe Lebenszufriedenheit steht. Überschreiben Sie dabei die Ursprungsvariablen. Die Variablen hatten 5 mögliche Antwortkategorien.
Lösung
data$lz2 <- -1 * (data$lz2 - 6)
data$lz4 <- -1 * (data$lz4 - 6)
Aufgabe 5
Datenextraktion kann auch mit logischer Überprüfung kombiniert werden. Bearbeiten Sie dafür folgende Fragestellungen
- Haben Person 1 und Person 5 dasselbe Alter und Geschlecht?
- Haben Person 2 und Person 10 dasselbe Geschlecht und dieselbe Lieblingsstadt angegeben?
Lösung
data[1, c("alter", "geschlecht")] == data[5, c("alter", "geschlecht")]
## alter geschlecht
## 1 TRUE TRUE
data[2, c("geschlecht", "stadt")] == data[10, c("geschlecht", "stadt")]
## geschlecht stadt
## 2 TRUE FALSE
Natürlich könnte man die Vergleiche auch jeweils einzeln durchführen, doch mit diesem Code geht es etwas schneller. Wenn man das “und” als verbindendes Element verstehen will (beide Werte müssen gleich sein), könnte man es folgendermaßen lösen.
data[1, "alter"] == data[5,"alter"] & data[1, "geschlecht"] == data[5, "geschlecht"]
## [1] TRUE
data[2, "geschlecht"] == data[10, "geschlecht"] & data[2, "stadt"] == data[10, "stadt"]
## [1] FALSE
Dabei wird nur dann TRUE als Resultat ausgegeben, wenn beide durch & verbundenen Aussagen als TRUE gewertet werden. Da, wie wir bereits gesehen haben, die Angabe in stadt nicht gleich ist beim zweiten Vergleich, erhalten wir hier ein FALSE.
Aufabe 6
Der Datensatz enthält noch nicht die vollständige Menge an erhobenen Informationen. Sie hatten zusätzlich die Lieblingsfarbe der Versuchspersonen erhoben:
farbe <- c(1, 2, 1, 1, 3, 4, 2, 2, 1, 4) #1 = blau, 2 = rot, 3 = grün, 4 = schwarz
- Diese Angaben fehlen jedoch in
data. Fügen Sie diese neue Spalte mit den entsprechenden Labels dem Datensatz hinzu.
Lösung
data$farbe <- farbe
data$farbe <- factor(data$farbe, levels = 1:4, labels = c("blau", "rot", "grün", "schwarz"))
str(data$farbe)
## Factor w/ 4 levels "blau","rot","grün",..: 1 2 1 1 3 4 2 2 1 4
Aufgabe 7
Nach einiger Zeit können Sie noch 3 weitere Proband:innen von der Teilnahme überzeugen. Fügen Sie diese zusätzlich an den Datensatz an. Die aufgeführten Zeilen wurden bereits invertiert.
c("weiblich", 21, "Frankfurt", 4, 4, 3, 4, 4, "blau")
c("männlich", 19, "Dresden", 2, 5, 2, 4, 3, "schwarz")
c("weiblich", 20, "Berlin", 1, 5, 1, 5, 1, "blau")
Lösung
data[11, ] <- c("weiblich", 21, "Frankfurt", 4, 4, 3, 4, 4, "blau")
data[12, ] <- c("männlich", 19, "Dresden", 2, 5, 2, 4, 3, "schwarz")
data[13, ] <- c("weiblich", 20, "Berlin", 1, 5, 1, 5, 1, "blau")
Hier sollte es am einfachsten sein, die neuen Personen manuell an den Datensatz anzufügen. Dabei starten wir natürlich mit der nächsten Zeile nach der vorherigen Anzahl. In diesem Fall hatten wir schon 10 Personen erhoben, starten also mit 11.
Aufgabe 8
Schauen Sie sich die Struktur Ihres Datensatzes an. Was fällt Ihnen auf? Passen Sie den Datensatz ggf. wieder an seine ursprüngliche Struktur an.
Lösung
str(data)
## 'data.frame': 13 obs. of 9 variables:
## $ geschlecht: Factor w/ 3 levels "weiblich","männlich",..: 1 2 2 1 1 1 3 2 1 2 ...
## $ alter : chr "20" "21" "19" "19" ...
## $ stadt : Factor w/ 5 levels "Berlin","Hamburg",..: 2 1 1 4 3 2 5 4 1 3 ...
## $ lz1 : chr "3" "4" "4" "2" ...
## $ lz2 : chr "4" "4" "4" "4" ...
## $ lz3 : chr "5" "3" "4" "4" ...
## $ lz4 : chr "4" "5" "5" "4" ...
## $ lz5 : chr "4" "4" "3" "3" ...
## $ farbe : Factor w/ 4 levels "blau","rot","grün",..: 1 2 1 1 3 4 2 2 1 4 ...
Es fällt auf, dass unsere numeric Variablen jetzt als chr angezeigt werden. Sie sollten also zurücktransformiert werden.
data$alter <- as.numeric(data$alter)
data$lz1 <- as.numeric(data$lz1)
data$lz2 <- as.numeric(data$lz2)
data$lz3 <- as.numeric(data$lz3)
data$lz4 <- as.numeric(data$lz4)
data$lz5 <- as.numeric(data$lz5)
Aufgabe 9
Erstellen Sie eine neue Variable lz_ges im Datensatz data, die die Antworten auf den lz-Items bestmöglich zusammenfasst.
Lösung
data$lz_ges <- rowMeans(data[, 4:8])
data$lz_ges
## [1] 4.0 4.0 4.0 3.4 2.2 4.2 3.2 3.6 4.0 3.8 3.8 3.2 2.6
Aufgabe 10
Speichern Sie den Datensatz als RDA-Datei unter dem Namen Data_lz lokal in Ihrem Praktikums-Ordner ab. Lassen Sie sich erst den Pfad des aktuellen Working Directory ausgeben und ändern Sie diesen gegebenenfalls.
Lösung
getwd()
setwd("...")
save(data, file = "Data_lz.rda")
Aufgabe 11
Nachdem nun der Datensatz auf dem finalen Niveau ist, sollen Sie erste deskriptivstatistische Werte bestimmen.
- Wieviele Proband:innen haben die Farbe “schwarz” als Lieblingsfarbe ausgewählt?
- Was ist der Modus der Variable
farbe? Wie hoch ist die Häufigkeit?
Lösung
table(data$farbe) # Häufigkeiten
##
## blau rot grün schwarz
## 6 3 1 3
which.max(table(data$farbe)) # Modus
## blau
## 1
max(table(data$farbe)) # Ausprägung
## [1] 6
- 3 Proband:innen haben die Farbe “schwarz” als Lieblingsfarbe ausgewählt.
- Der Modus der Variable
farbeist blau und kommt 6 mal vor.
Aufgabe 12
Betrachten wir statt der Variable farbe nun die Variable geschlecht.
- Lassen Sie sich die absolute Häufigkeit in der für Menschen ungünstigeren grafischen Darstellungsform ausgeben.
- Wie hoch ist der relative Anteil der Versuchspersonen, die “männlich” angegeben haben?
Lösung
pie(table(data$geschlecht))
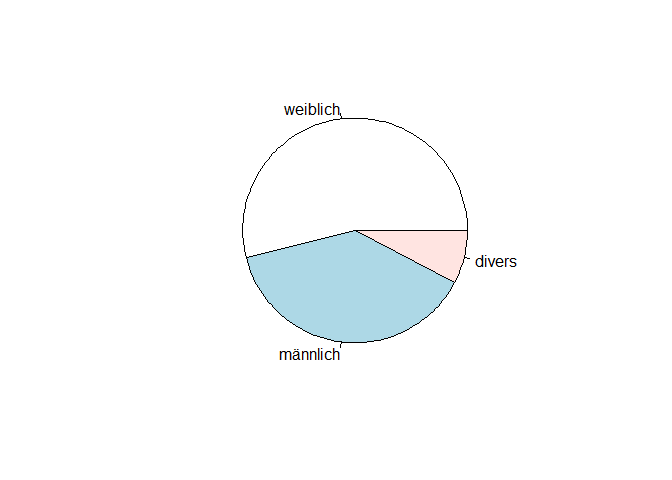
prop.table(table(data$geschlecht))
##
## weiblich männlich divers
## 0.53846154 0.38461538 0.07692308
Der relative Anteil der Versuchspersonen, die “männlich” angegeben haben, beträgt 0.385.
Aufgabe 13
Berechnen Sie den relativen Informationsgehalt für die Variable stadt. Was bedeutet das Ergebnis?
Lösung
bruch <- -(1/log(5))
hj <- prop.table(table(data$stadt))
summe <- sum(hj * log(hj))
bruch * summe
## [1] 0.9723626
Das Maximum des relativen Informationsgehaltes ist bei 1. Dieses steht für eine Gleichverteilung auf alle möglichen Ausprägungen, also alle Kategorien. Daher ist unser Ergebnis ein Hinweise auf eine recht gleichmäßige Verteilung der Lieblingsstädte in Deutschland, denn für die Variable stadt ergibt sich ein relativer Informationsgehalt von 0.972.
Aufgabe 14
Betrachten wir nun ein einzelnes Item (lz3) aus dem Fragebogen zur Lebenszufriedenheit.
- Berechnen Sie ein geeignetes Maß der zentralen Tendenz.
- Geben Sie den Interquartilsbereich an.
- Überprüfen Sie Ihre Angabe, indem Sie sich einen Boxplot ausgeben lassen.
- Berechnen Sie zudem den Interquartilsabstand.
Lösung
median(data$lz3)
## [1] 3
quantile(data$lz3, c(.25, .75))
## 25% 75%
## 3 4
boxplot(data$lz3)
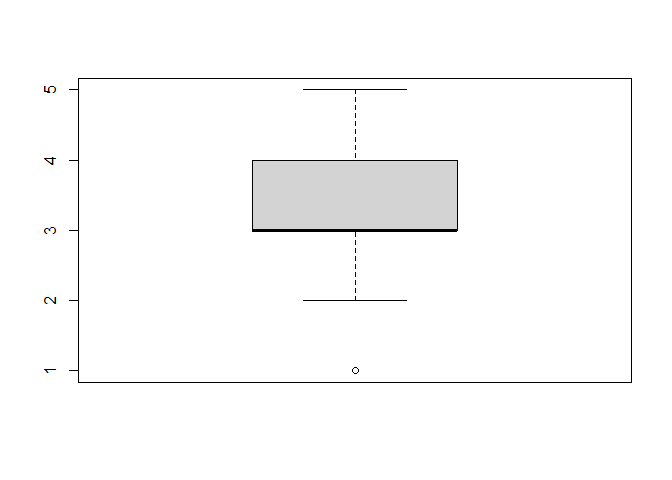
quantile(data$lz3, .75) - quantile(data$lz3, .25)
## 75%
## 1
- Der Median für
lz3beträgt 3. - Der Interquartilsbereich erstreckt sich vom Wert 3 bis zum Wert 4.
- Der Interquartilsabstand beträgt 1.
Aufgabe 15
Anstatt nur einer Variable soll nun der gesamte Skalenwert lz_ges betrachtet werden.
- Berechnen Sie ein sinnvolles Maß der zentralen Tendenz.
- Bestimmen Sie ein passendes Streuungsmaß.
Lösung
mean(data$lz_ges)
## [1] 3.538462
#Varianz (beide Wege)
var(data$lz_ges) * (12 / 13)
## [1] 0.3346746
sum((data$lz_ges - mean(data$lz_ges))^2) / 13
## [1] 0.3346746
- Das arithmetische Mittel beträgt 3.538.
- Die Varianz beträgt 0.335.
Aufgabe 16
Legen wir die ausgedachten Werte nun beiseite. Die restlichen Zusatzaufgaben beschäftigen mit dem Datensatz des letzten Jahrgangs. Löschen Sie die Inhalte Ihres Environments und laden Sie sich den Datensatz fb22 in das Environment. Dies können sie lokal von ihrem PC, aber auch mittels der URL von der PandaR-Website machen. Der Datensatz sollte 159 Versuchspersonen enthalten.
rm(list = ls())
load(url('https://pandar.netlify.app/daten/fb22.rda'))
Wandeln Sie zum Start die Variable lerntyp in einen Faktor um. Die Labels lauten in dieser Reihenfolge: c(alleine, Gruppe, Mischtyp). Erstellen Sie dafür keine neuen Spalten, sondern überschreiben Sie die bereits bestehenden. Überprüfen Sie im Nachhinein die Umwandlung.
Lösung
fb22$lerntyp <- factor(fb22$lerntyp, levels = 1:3, labels = c("alleine", "Gruppe", "Mischtyp"))
str(fb22$lerntyp)
## Factor w/ 3 levels "alleine","Gruppe",..: 1 1 1 1 1 NA 3 2 3 1 ...
Aufgabe 17
Erstellen Sie ein Balkendiagramm mit der Variable lerntyp. Geben Sie der Grafik einen Titel, eine Achsenbeschriftung, sowie ein fesches, hippes farbliches Design.
Lösung
colours <- c("#CFB1B3", "#BC7B7D", "#DAB457") #HEX-Werte (Paletten auf Pinterest)
colours2 <- c("#B7C5D5", "#D6EDEC", "#E7E8ED")
table_lerntyp <- table(fb22$lerntyp)
barplot(table_lerntyp, main = "Lerntypen Jahrgang 2022", ylab = "Anzahl Studierende", col = colours)
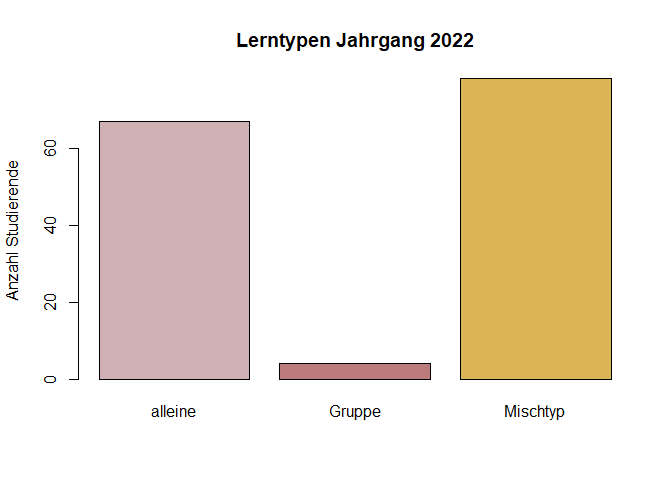
barplot(table_lerntyp, main = "Lerntypen Jahrgang 2022", ylab = "Anzahl Studierende", col = colours2)
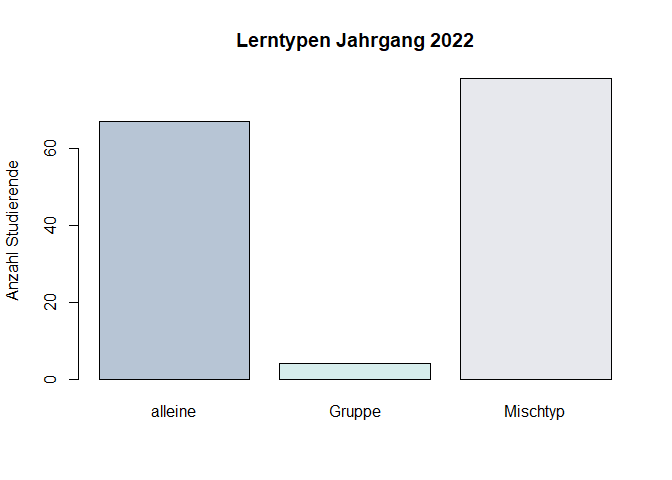
Aufgabe 18
Betrachten Sie die Variablen prok4 und prok10. Liegen NAs vor? Wenn ja, wieviele? Überprüfen Sie dies mit Ihnen bekannten Befehlen.
Lösung
sum(is.na(fb22$prok4))
## [1] 2
sum(is.na(fb22$prok10))
## [1] 0
- Die Variable
prok4enthält 2 fehlende Werte. - Die Variable
prok10enthält 0 fehlende Werte.
Aufgabe 19
Die beiden Variablen sollen weiter betrachtet werden. Entfernen Sie bei Analysen (falls nötig) die fehlenden Werte.
- Bestimmen Sie das Maß der zentralen Tendenz für die beiden Variablen. Ist es für
prok4undprok5dieselbe Kategorie, die die Proband:innen-Angaben in zwei gleich große Hälften teilt? - In welchem Bereich liegen die mittleren 50% der Angaben in den beiden Variablen
prok4undprok10? - Lassen Sie sich dies zusätzlich grafisch ausgeben.
Lösung
Da wir gefunden haben, dass in prok10 keine fehlenden Werte vorliegen, können wir die Befehle ohne die Ergänzung na.rm = T durchführen.
median(fb22$prok4, na.rm = T)
## [1] 3
median(fb22$prok10)
## [1] 3
quantile(fb22$prok4, c(.25, .75), na.rm = T)
## 25% 75%
## 2 3
quantile(fb22$prok10, c(.25, .75))
## 25% 75%
## 2 4
- Der Median von
prok4liegt bei 3, beiprok10liegt er bei 3. Es ist also für die beiden Variablen dieselbe Kategorie, die die Angaben der Proband:innen in zwei gleich große Hälften teilt. - Die mittleren 50% der Angaben in der Variable
prok4reichen vom Wert 2 bis zum Wert 3, bei der Variableprok10reichen sie von 2 bis 4.
boxplot(fb22$prok4)
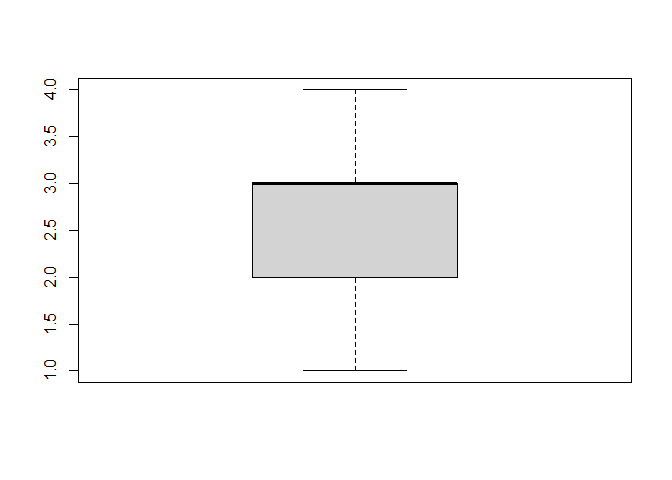
boxplot(fb22$prok10)
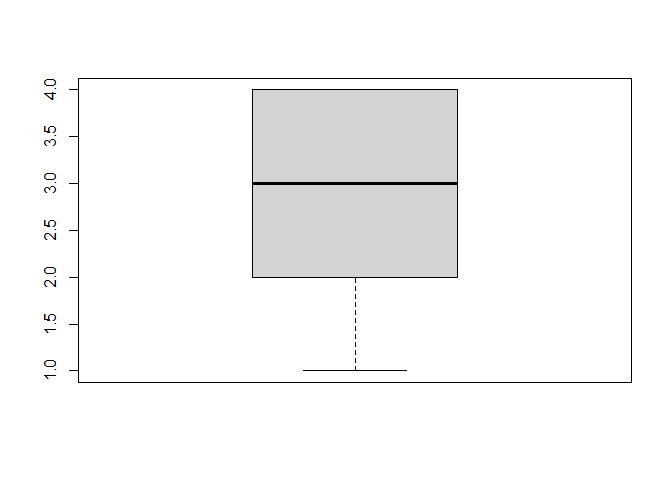
Aufgabe 20
Nun betrachten wir den Skalenwert, der unter gewis abgelegt ist. Dieser steht für die Persönlichkeitseigenschaft Gewissenhaftigkeit.
- Was ist der niedrigste, was ist der höchste Wert der Variable?
- Wie hoch ist die mittlere Ausprägung?
Lösung
range(fb22$gewis)
## [1] 2 5
mean(fb22$gewis)
## [1] 3.883648
- Der niedrigste Gewissenhaftigskeitswert liegt bei 2, der höchste bei 5.
- Die mittlere Ausprägung der Gewissenhaftigkeit liegt bei 3.884.
Aufgabe 21
Erzielt der Jahrgang 22 im Mittel, rein deskriptiv betrachtet, höhere Werte in Gewissenhaftigkeit (gewis) als in Extraversion (extra) oder liegt genau der umgekehrte Fall vor? In welcher der beiden Variablen variieren die Angaben stärker? Gehen Sie für die Beantwortung davon aus, dass die Skalen gleich genormt sind.
Lösung
Zunächst sollten wir überprüfen, ob es fehlende Werte auf den Skalen gibt.sum(is.na(fb22$gewis))
## [1] 0
sum(is.na(fb22$extra))
## [1] 0
Das ist offensichtlich nicht der Fall. Daher können wir die Befehle auch ohne den ergänzenden Teil durchführen.
mean(fb22$gewis)
## [1] 3.883648
mean(fb22$extra)
## [1] 3.378931
var(fb22$gewis) * (158/159)
## [1] 0.4361477
var(fb22$extra) * (158/159)
## [1] 0.4951693
Der Mittelwert von gewis liegt bei 3.884, der von extra bei 3.379. Unter den getroffenen Annahmen ist dieser Jahrgang stärker gewissenhaft als extravertiert. Auch die Streuung ist deskriptiv bei der Extraversion größer. Hier liegt sie bei 0.495, während sie bei der Gewissenheit bei 0.436 liegt.
Aufgabe 22
Verträglichkeit ist in vertr abgelegt.
- Lassen Sie sich das Histogramm ausgeben.
- Zentrieren Sie die Variable
vertr. Legen Sie dafür eine neue Spalte infb22mit dem Namenvertr_zan und lassen Sie sich erneut ein Histogramm ausgeben. Was hat sich verändert? - Standardisieren Sie die Variable
vertrund speichern Sie diese ebenfalls unter einer neuen Spalte mit dem Namenvertr_stab. Was ist nun anders beim Histogramm?
Lösung
hist(fb22$vertr)
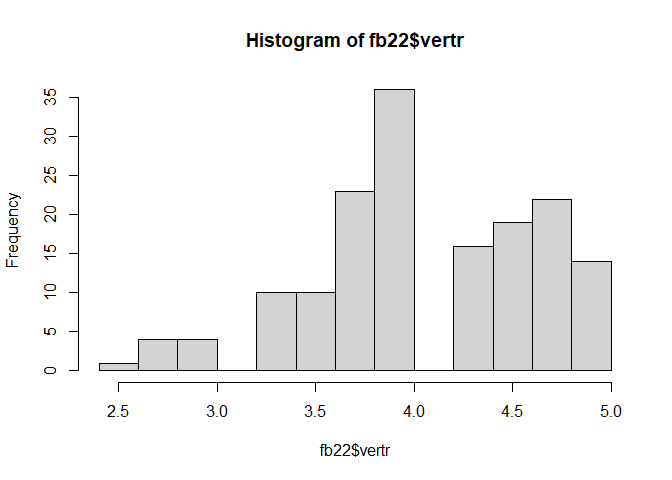
Dieses Histogramm soll erstmal zum Vergleich dienen. Wir sehen die ursprünglichen Skalenwerte.
fb22$vertr_z <- scale(fb22$vertr, scale = F)
hist(fb22$vertr_z)
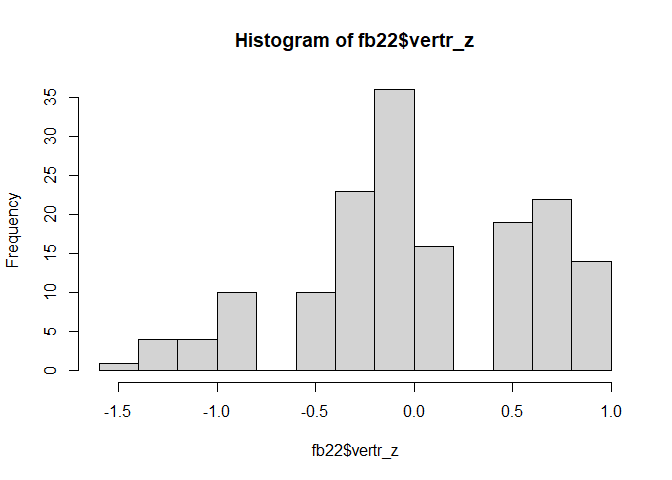
Durch die Zentrierung verändert sich die Form erstmal nicht. Der Mittelwert der Werte wird auf 0 gesetzt. Optisch äußert sich das dadurch, dass die Werte auf der x-Achse nun andere sind.
fb22$vertr_st <- scale(fb22$vertr, scale = T)
hist(fb22$vertr_st)
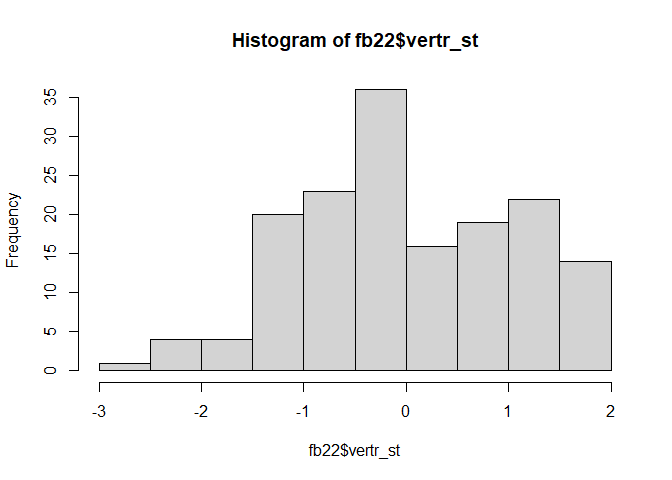
Die Standardisierung setzt die Standardabweichung auf 1. Aufgrund der neuen Wertestruktur wird natürlich auch die Kategorienanzahl geändert.
Aufgabe 23
Vergleichen Sie deskriptiv das Maß der zentralen Tendenz in der Variable extra zwischen den Teilnehmenden, die alleine, und denjenigen, die Gruppen in der bevorzugten Lernform angegeben haben. Welche der beiden Gruppen hat die höhere Ausprägung? Welche der beiden Gruppen ist im Mittel nerdier (nerd)?
Lösung
Da wir zwei Analysen durchführen wollen, wäre es eine gute Möglichkeit, die Personen in reduzierten Datensätzen abzulegen. Dies kann mittels der Funktion subset gelöst werden.
fb22_alleine <- subset(fb22, subset = lerntyp == "alleine")
fb22_gruppe <- subset(fb22, subset = lerntyp == "Gruppe")
Über das Argument subset geben wir an, in welcher Variable (lerntyp) die Auswahl stattfindet und anschließend legen wir die Auswahl der einzelnen Gruppen über das bereits bekannte == fest.
Eine andere Möglichkeit wäre die Verwendung der logischen Auswahl anhand eckiger Klammern.
fb22_alleine <- fb22[fb22$lerntyp == "alleine",]
fb22_gruppe <- fb22[fb22$lerntyp == "Gruppe",]
Nun können Mittelwerte für die beiden Gruppen bestimmt werden. Beachten Sie, dass die Ergänzung von na.rm = T nur auf dem zweiten demonstrierten Weg wichtig ist. Dort können Personen, die keinen Eintrag in der Auswahl-Variable haben, nicht richtig zugeordnet werden und sind daher in den beiden Datensätzen erhalten - allerdings nicht mit ihren richtigen Werten, stattdessen steht bei ihnen in jeder Spalte NA. Die Funktion subset nimmt diese Fälle hingegen nicht mit auf.
mean(fb22_alleine$extra, na.rm = T)
## [1] 3.085821
mean(fb22_gruppe$extra, na.rm = T)
## [1] 4.125
mean(fb22_alleine$nerd, na.rm = T)
## [1] 3.226368
mean(fb22_gruppe$nerd, na.rm = T)
## [1] 2.75
Personen, die angaben gerne in Gruppen zu lernen, weisen einen Mittelwert von 4.125 auf. Sie sind rein deskriptiv extravertierter als Personen, die angaben lieber alleine zu lernen. Diese haben hier einen Mittelwert von 3.086. Umgekehrtes gilt in unserer Stichprobe hingegen für die Nerdiness. Hier haben Personen, die in Gruppen lernen, einen Wert von 2.75 und Personen, die lieber alleine lernen, einen Wert von 3.226.
Aufgabe 24
Etwa 75% Prozent der Psychologiestudierenden in Deutschland sind weiblich. Sie treffen zufällig auf 15 Psychologiestudierende.
- Wie wahrscheinlich ist es, dass genau 9 dieser Personen weiblich sind?
Lösung
dbinom(9, 15, 0.75)
## [1] 0.09174777
Die Wahrscheinlichkeit beträgt 9.17%.
- Wie wahrscheinlich ist es, dass mindestens 11 der Personen weiblich sind?
Lösung
1- pbinom(10, 15, 0.75)
## [1] 0.6864859
#Alternativ:
pbinom(10, 15, 0.75, lower.tail = F)
## [1] 0.6864859
Die Wahrscheinlichkeit beträgt 68.65%.
- Stellen Sie die Verteilungsfunktion der kummulierten Wahrscheinlichkeit aller Werte in einem Plot dar.
Lösung
X <- 0:15
wk <- pbinom(X, 15, 0.75)
plot(x = X, y = wk, typ = "h", xlab = "Anzahl Frauen", ylab = "kummulierte Wahrscheinlichkeit")
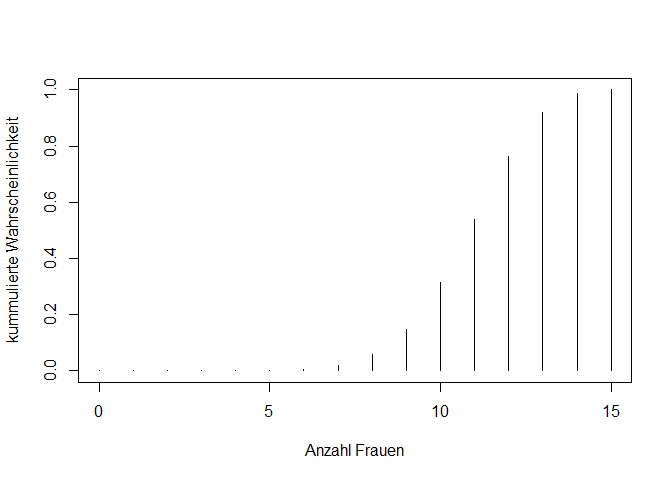
Aufgabe 25
In Deutschland liegt die Gewissenhaftigkeit (gewis) bei Frauen im Mittel bei µ = 3.73.
- Sind Frauen, die Psychologie studieren, im Mittel gewissenhafter als Frauen in der Allgemeinbevölkerung? Stellen Sie die Hypothesen ($H_0$ und $H_1$) auf und führen Sie einen geeigneten Test durch.
- Geben Sie zudem das $99\%$-ige Konfidenzintervall und die Effektgröße an.
Lösung
Hypothesen
$H_0$: Die durchschnittliche Gewissenhaftigkeit der Frauen, die Psychologie studieren, ist gleich oder geringer als die der Frauen in der Allgemeinbevölkerung.
$H_0$: $\mu_0$ $\geq$ $\mu_1$
$H_1$: Die durchschnittliche Gewissenhaftigkeit der Frauen, die Psychologie studieren, ist höher als die der Frauen in der Allgemeinbevölkerung.
$H_1$: $\mu_0$ $<$ $\mu_1$
Wir testen zuerst ob unsere Variable Geschlecht bereits als Faktor vorliegt. Wenn nicht, wandeln wir sie in einen Faktor um.
load(url('https://pandar.netlify.app/daten/fb22.rda'))
is.factor(fb22$geschl)
## [1] FALSE
fb22$geschl <- factor(fb22$geschl,
levels = 1:3,
labels = c("weiblich", "männlich", "anderes"))
Nun erstellen wir ein subset, indem nur die weiblichen Teilnehmenden des fb22 Datensatzes enthalten sind.
fb22_frauen <- subset(fb22, geschl == "weiblich")
t-Test
Da wir einen Stichprobenmittelwert mit einem Populationsmittelwert vergleichen wollen und die Varianz in der Population nicht vorliegt, führen wir einen Einstichproben-t-Test durch.
t.test(fb22_frauen$gewis, mu = 3.73, alternative = "greater", conf.level = .99)
##
## One Sample t-test
##
## data: fb22_frauen$gewis
## t = 4.7902, df = 124, p-value = 2.333e-06
## alternative hypothesis: true mean is greater than 3.73
## 99 percent confidence interval:
## 3.858015 Inf
## sample estimates:
## mean of x
## 3.982
Mit einer Irrtumswahrscheinlichkeit von $5\%$ kann die $H_0$ verworfen und die $H_1$ angenommen werden. Die weiblichen Psychologiestudierenden haben verglichen mit der Gesamtbevölkerung der Frauen höhere Gewissenhaftswerte. Das $99\%$-ige Konfidenzintervall liegt zwischen 3.86 und $\infty$ (außerhalb des definierten Wertebereichs). Das bedeutet, dass in $99\%$% der Fälle in einer wiederholten Ziehung aus der Grundgesamtheit die mittleren Verträglichkeitswerte zwischen 3.86 und $\infty$ (außerhalb des definierten Wertebereichs) liegen.
Effektgröße
Für das Effektgrößemaß berechnen wir Cohen’s d.
mean_gewis_frauen <- mean(fb22_frauen$gewis, na.rm = T)
sd_gewis_frauen <- sd(fb22_frauen$gewis, na.rm = T)
mean_gewis_population <- 3.73
d <- abs((mean_gewis_frauen - mean_gewis_population)/sd_gewis_frauen)
Die Effektgröße ist mit 0.43 als groß einzustufen.
Aufgabe 26
Unterscheiden sich Personen, die gerne alleine lernen, in ihrer Extraversion (extra) von Personen, die es bevorzugen in Gruppen zu lernen oder ein Mischtyp sind (lerntyp)? Schauen Sich sich die Daten graphisch an und führen sie nach Voraussetzungsprüfung einen geeigneten Test durch.
Lösung
Zuerst schauen wir uns an, ob die Variable Lerntyp bereits als Faktor vorliegt und wandeln sie gegebenenfalls um.
is.factor(fb22$lerntyp)
## [1] FALSE
fb22$lerntyp <- factor(fb22$lerntyp,
levels = 1:3,
labels = c("alleine", "Gruppe", "Mischtyp"))
Nun wollen wir eine neue Variable erstellen, in der die Personen, die gerne in der Gruppe lernen oder ein Mischtyp sind, zusammengefasst werden.
fb22$lerntyp_neu <- fb22$lerntyp == "alleine"
fb22$lerntyp_neu <- as.numeric(fb22$lerntyp_neu) #Umwandlung in Numeric, da der Variablen Typ nun Logical ist
fb22$lerntyp_neu <- factor(fb22$lerntyp_neu,
levels = 0:1,
labels = c("Gruppe oder Mischtyp", "alleine"))
Jetzt können wir uns die Extraversion der Gruppen deskriptiv in einem Boxplot darstellen lassen.
boxplot(fb22$extra ~ fb22$lerntyp_neu, xlab = "Lerntyp", ylab = "Extraversion")
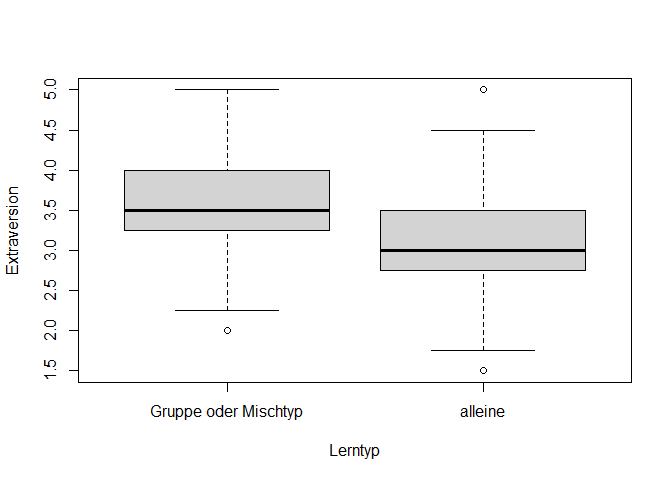
Deskriptiv lässt sich ein Mittelwertsunterschied feststellen. Diesen wollen wir aber nun noch inferenzstatistisch überprüfen. Dafür überprüfen wir die Voraussetzungen eines t-Tests für unabhängige Stichproben. Wir können annehmen, dass die abhängige Variable intervallskaliert ist und dass die einzelnen Messwerte voneinander unabhängig sind. Wir müssen nun noch die Normalverteilung der Extraversion in den Gruppen und die Homoskedastizität überprüfen.
Prüfung der Normalverteilung
Wir nutzen dafür die qqPlot-Funktion aus dem car-Paket.
library(car)
qqPlot(fb22$extra[fb22$lerntyp_neu == "alleine"])
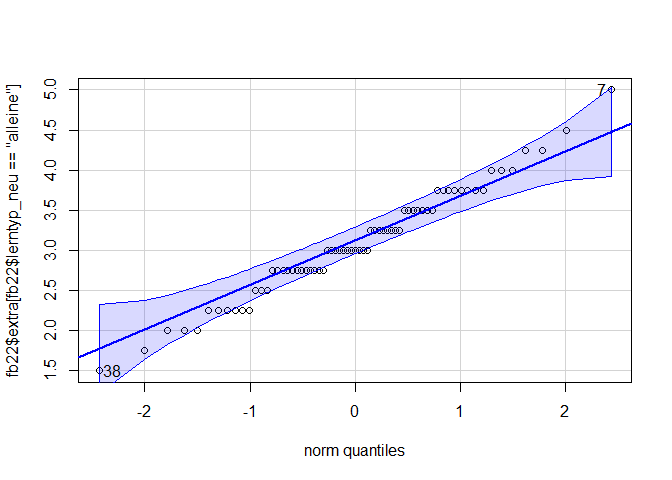
## [1] 7 38
qqPlot(fb22$extra[fb22$lerntyp_neu == "Gruppe oder Mischtyp"])
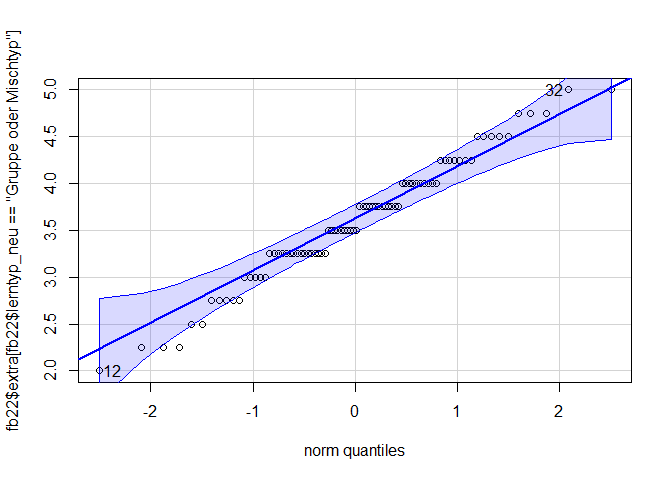
## [1] 12 32
Die Abweichungen sind nicht zu weit. Trotzdem führen wir zur weiteren Absicherung noch den Shapiro-Test durch.
shapiro.test(fb22$extra[fb22$lerntyp_neu == "alleine"])
##
## Shapiro-Wilk normality test
##
## data: fb22$extra[fb22$lerntyp_neu == "alleine"]
## W = 0.98369, p-value = 0.5273
shapiro.test(fb22$extra[fb22$lerntyp_neu == "Gruppe oder Mischtyp"])
##
## Shapiro-Wilk normality test
##
## data: fb22$extra[fb22$lerntyp_neu == "Gruppe oder Mischtyp"]
## W = 0.98029, p-value = 0.2395
Keiner der Tests ist signifikant, sodass wir die Normalverteilungsannahme beibehalten.
Homoskedastizität
Diese überprüfen wir mittels Levene-Test.
leveneTest(fb22$extra ~ fb22$lerntyp_neu)
## Levene's Test for Homogeneity of Variance (center = median)
## Df F value Pr(>F)
## group 1 0.0049 0.9445
## 147
Das Ergebnis ist nicht signifikant, sodass wir die $H_0$ nicht ablehnen und die Homoskedastizität der Varianzen annehmen können. Damit sind alle Voraussetzungen eines t-Tests erfüllt.
t.test(fb22$extra ~ fb22$lerntyp_neu, var.equal = T)
##
## Two Sample t-test
##
## data: fb22$extra by fb22$lerntyp_neu
## t = 4.6444, df = 147, p-value = 7.506e-06
## alternative hypothesis: true difference in means between group Gruppe oder Mischtyp and group alleine is not equal to 0
## 95 percent confidence interval:
## 0.2922374 0.7251452
## sample estimates:
## mean in group Gruppe oder Mischtyp mean in group alleine
## 3.594512 3.085821
Der deskriptive Unterschied der Mittelwerte lässt sich somit auch inferenzstatistisch feststellen, denn mit einer Irrtumswahrscheinlichkeit von $5\%$ kann die $H_0$ verworfen und die $H_1$ angenommen werden. Die Teilnehmenden, die lieber alleine lernen, unterscheiden sich von den Teilnehmenden, die lieber in der Gruppe lernen oder ein Mischtyp sind, in ihrer Extraversion ($t$(df = 147, zweis.) = 4.64, p = <.001).
Aufgabe 27
Haben Studierende, die bei ihren Eltern wohnen (wohnen), mit gleicher Wahrscheinlichkeit einen Nebenjob (job) wie Studierende, die nicht bei ihren Eltern wohnen?
- Prüfen Sie die Voraussetungen für einen Chi-Quadrat-Test.
Lösung
Als erstes müssen wir den Datensatz aufbereiten.
is.factor(fb22$wohnen)
## [1] FALSE
is.factor(fb22$job)
## [1] FALSE
fb22$wohnen <- factor(fb22$wohnen, levels = 1:4, labels = c("WG", "bei Eltern", "alleine", "sonstiges"))
fb22$job <- factor(fb22$job, levels = 1:2, labels = c("nein", "ja"))
fb22$wohnen_bei_Eltern <- fb22$wohnen == "bei Eltern" #wir erstellen eine Variable, die angibt, ob eine Personen bei den Eltern wohnt oder nicht
Die Voraussetzungen, dass die einzelnen Beobachtungen voneinander unabhängig sind und jede Person eindeutig einer Merkmalskombination zuordbar ist, ist durch das Studiendesign erfüllt. Wir müssen aber noch prüfen, ob jede Zelle mit mehr als fünf Personen gefüllt ist.
tab <- table(fb22$wohnen_bei_Eltern, fb22$job)
tab
##
## nein ja
## FALSE 62 30
## TRUE 35 21
Die Voraussetzungen für einen Chi-Quadrat-Test sind erfüllt.
- Berechnen Sie die erwarteten Häufigkeiten der Zellen und treffen Sie eine Signifikanzentscheidung.
Lösung
Für die erwarteten Häufigkeiten brauchen wir die Randsummen. Diese erhalten wir mit dem Befehl addmargins.
tab_mar <- addmargins(tab)
tab_mar
##
## nein ja Sum
## FALSE 62 30 92
## TRUE 35 21 56
## Sum 97 51 148
Die erwarteten Häufigkeiten der Zellen erhalten wir wie folgt:
n <- tab_mar[3,3]
erwartet_11 <- (tab_mar[1,3]*tab_mar[3,1])/n
erwartet_12 <- (tab_mar[1,3]*tab_mar[3,2])/n
erwartet_21 <- (tab_mar[2,3]*tab_mar[3,1])/n
erwartet_22 <- (tab_mar[2,3]*tab_mar[3,2])/n
erwartet <- data.frame(nein = c(erwartet_11, erwartet_21), ja = c(erwartet_12, erwartet_22))
erwartet
## nein ja
## 1 60.2973 31.7027
## 2 36.7027 19.2973
Für die Signifikanzentscheidung berechnen wir den empirischen Chi-Quadrat-Wert und den zugehörigen p-Wert.
chi_quadrat_Wert <- (tab[1,1]-erwartet[1,1])^2/erwartet[1,1]+
(tab[1,2]-erwartet[1,2])^2/erwartet[1,2]+
(tab[2,1]-erwartet[2,1])^2/erwartet[2,1]+
(tab[2,2]-erwartet[2,2])^2/erwartet[2,2]
chi_quadrat_Wert
## [1] 0.368761
pchisq(chi_quadrat_Wert, 1, lower.tail = F) #Freiheitsgrad beträgt 1
## [1] 0.5436804
Somit ist der Test nicht signifikant und es lässt sich feststellen, dass das Wohnen bei den Eltern nicht damit zusammen hängt, ob ein Nebenjob ausgeübt wird oder nicht.
Wir können unser Ergebnis auch noch mit dem Befehl chisq.test() überprüfen und sehen, dass dieser das gleiche Ergebnis liefert.
chisq.test(tab, correct = F)
##
## Pearson's Chi-squared test
##
## data: tab
## X-squared = 0.36876, df = 1, p-value = 0.5437
Aufgabe 28
Weichen Psychologiestudierende, die einen Nebenjob haben, in ihrem Intellekt (intel) von Psychologiestudierenden, die keinen Nebenjob haben, ab.
- Führen Sie nach Voraussetzungsprüfung einen geeigneten Test durch.
Lösung
Wir beginnen die Voraussetzungen des t-Tests für unabhängige Stichproben zu überprüfen. Die Voraussetzungen, dass die unabhängige Variable intervallskaliert ist und die einzelnen Messwerte unabhängig voneinander sind, sind per Untersuchungsdesign erfüllt. Wir wollen nun also die Normalverteilung des Merkmals in den Gruppen überprüfen.#Wir überprüfen erst wieder, ob die Variable Nebenjob als Faktor vorliegt
is.factor(fb22$job)
## [1] TRUE
library(car)
qqPlot(fb22$intel[fb22$job == "nein"])
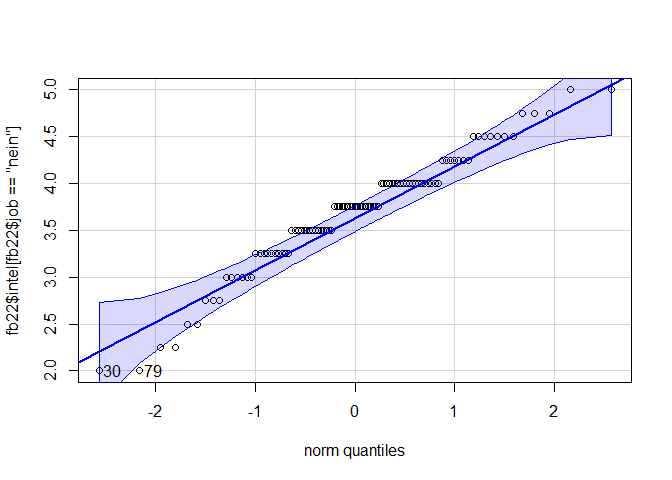
## [1] 30 79
qqPlot(fb22$intel[fb22$job == "ja"])
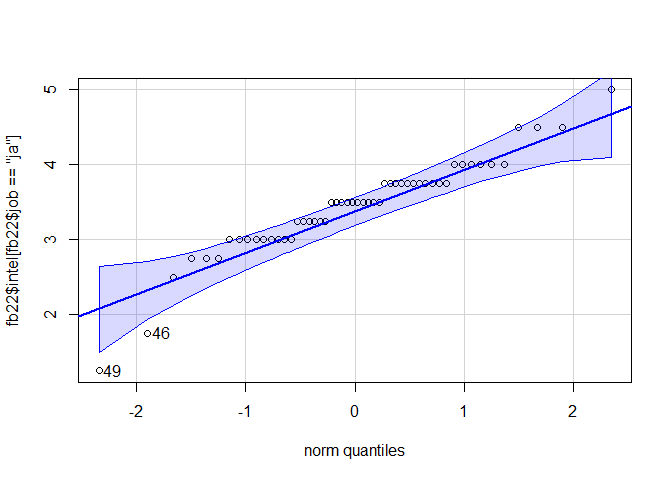
## [1] 49 46
shapiro.test(fb22$intel[fb22$job == "nein"])
##
## Shapiro-Wilk normality test
##
## data: fb22$intel[fb22$job == "nein"]
## W = 0.96409, p-value = 0.009372
shapiro.test(fb22$intel[fb22$job == "ja"])
##
## Shapiro-Wilk normality test
##
## data: fb22$intel[fb22$job == "ja"]
## W = 0.93146, p-value = 0.005113
Die Normalverteilungsannahme ist nicht erfüllt. Wir können also keinen t-Test durchführen. Wir überprüfen nun die Voraussetzungen des Wilcoxon-Tests. Wir überprüfen optisch, ob die Messwerte der beiden Gruppen ungefähr derselben Verteilung folgen.
hist(fb22$intel[fb22$job == "ja"])
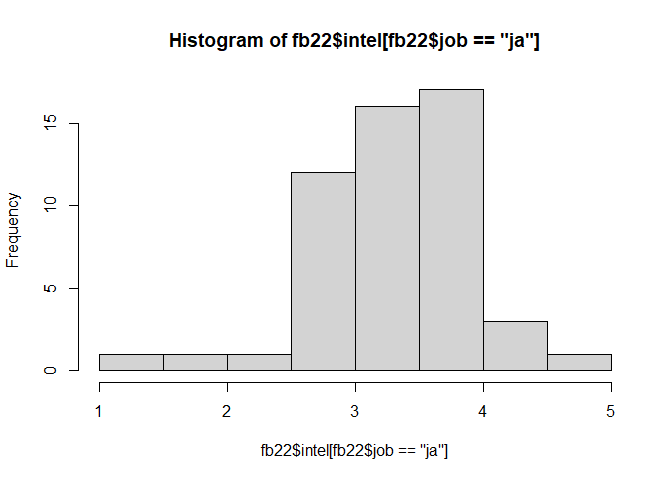
hist(fb22$intel[fb22$job == "nein"])
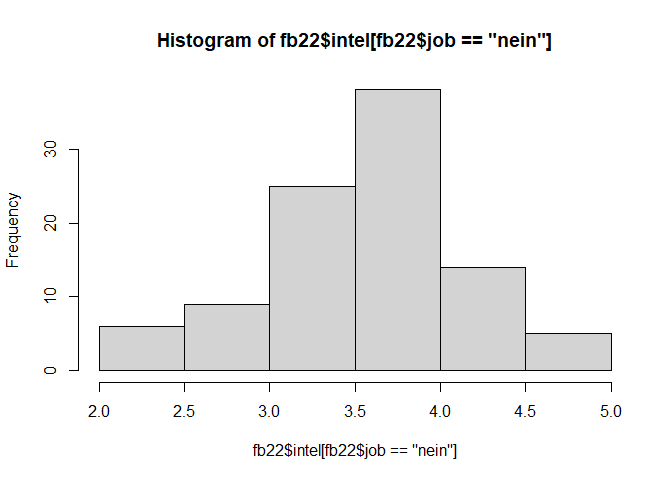
leveneTest(fb22$intel ~ fb22$job)
## Levene's Test for Homogeneity of Variance (center = median)
## Df F value Pr(>F)
## group 1 0.0088 0.9254
## 147
Wir können von Varianzhomogenität ausgehen und somit einen Wilcoxon-Test durchführen.
wilcox.test(fb22$lz ~ fb22$ort)
##
## Wilcoxon rank sum test with continuity correction
##
## data: fb22$lz by fb22$ort
## W = 2775, p-value = 0.3029
## alternative hypothesis: true location shift is not equal to 0
Das Ergebnis des zweiseitigen Wilcoxon-Tests ist nicht signifikant (W = 2775, p = 0.303 ). Die Nullhypothese konnte nicht verworfen werden und wird beibehalten. Wir gehen also davon aus, dass sich Psychologiestudierende, die einen Nebenjob haben, und Psychologiestudierende, die keinen Nebenjob haben, nicht in ihrem Intellekt unterscheiden.
Aufgabe 29
Unterscheiden sich Nerdiness (nerd) und Intellekt (intel) von Psychologiestudierenden im Durchschnitt voneinander? Gehen Sie für die Beantwortung davon aus, dass die Skalen gleich genormt sind.
- Stellen sie die Hypothesen auf.
Lösung
$H_0$: Die durchschnittliche Nerdiness von Psychologiestudierenden unterscheidet sich nicht von deren Intellekt.
$H_0$: $\mu_0$ $=$ $\mu_1$
$H_1$: Die durchschnittliche Nerdiness von Psychologoiestudierenden unterscheidet sich von deren Intellekt.
$H_1$: $\mu_0$ $≠$ $\mu_1$
- Begründen Sie weshalb Sie welchen Test benutzen wollen.
Lösung
Da die Nerdiness- und Intellekt-Werte, die verglichen werden sollen, immer von derselben Person stammen, sind die Werte voneinander abhängig. Daher wollen wir einen t-Test für abhängige Stichproben durchführen. Die Werte sind intervallskaliert, voneinander abhängig und die Differenzvariable ist normalverteilt, da wir bei einer Stichprobe von n ≥ 30 direkt davon ausgehen können. Somit sind alle Voraussetzungen für den t-Test erfüllt.
- Führen Sie den Test durch und berechnen Sie gegebenfalls eine Effektgröße.
Lösung
t.test(fb22$nerd, fb22$intel, paired = T)
##
## Paired t-test
##
## data: fb22$nerd and fb22$intel
## t = -7.0571, df = 158, p-value = 5.052e-11
## alternative hypothesis: true mean difference is not equal to 0
## 95 percent confidence interval:
## -0.5923110 -0.3332655
## sample estimates:
## mean difference
## -0.4627883
Der Gruppenunterschied ist signifikant ($t$(158) = -7.06 , p < .001), somit wird die Nullhypothese verworfen. Unter den getroffenen Annahmen weisen Psychologiestudierende unterschiedliche Werte auf der Skala Nerdiness und auf der Skala Intellekt auf.
Effektstärke:
library("effsize")
cohen.d(fb22$nerd, fb22$intel, paired = T, within = F)
##
## Cohen's d
##
## d estimate: -0.559661 (medium)
## 95 percent confidence interval:
## lower upper
## -0.7274678 -0.3918542
Der Effekt ist mit -0.56 als mittel bis groß einzuschätzen.
Aufgabe 30
Hängt die Gewissenhaftigkeit (gewis) positiv mit der Anzahl an geschriebenen Wörtern zusammen, die als Begründung (grund) für die Wahl des Psychologiestudiums angegeben wurden? Überprüfen Sie die Voraussetzungen für das gewählte Zusammenhangsmaß.
Tipp: Mit folgendem Befehl lässt sich die Anzahl an Wörtern einer Eingabe berechnen:
library(stringr) #falls noch nicht installiert: install.packages("stringr")
str_count("Wie viele Wörter hat dieser Satz?", "\\w+")
## [1] 6
Lösung
Als erstes erstellen wir eine Variable mit der Anzahl an geschriebenen Wörtern.
fb22$woerter_grund <- str_count(fb22$grund, "\\w+")
Nun schauen wir uns den Zusammenhang der Variablen in einem Scatterplot an.
plot(x = fb22$woerter_grund, y = fb22$gewis)
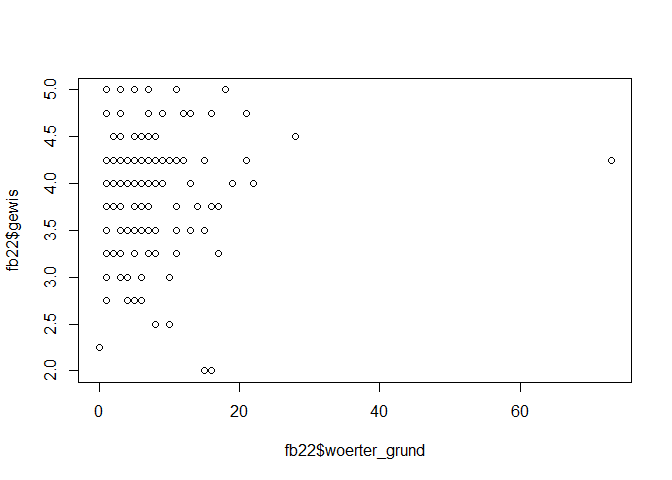
Wir schließen einen nicht linearen Zusammenhang nicht aus und überprüfen nun die Normalverteilung der Variablen.
library(car)
qqPlot(fb22$gewis)
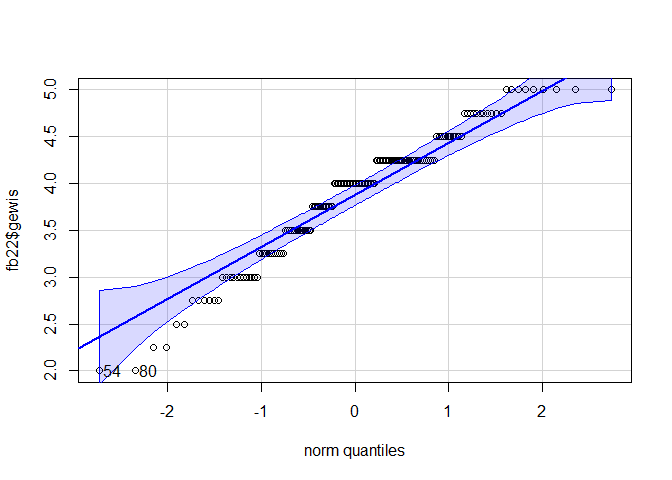
## [1] 54 80
qqPlot(fb22$woerter_grund)
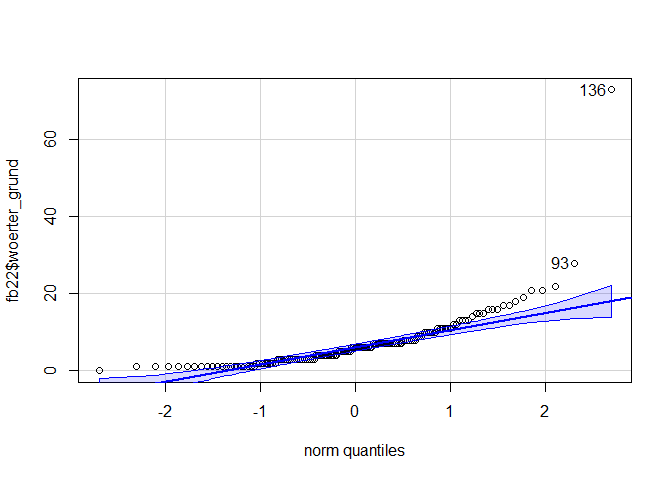
## [1] 136 93
Die Normalverteilungsannahme ist nicht erfüllt. Daher können wir keine Pearson Produkt-Moment-Korrelation ermitteln und berechnen stattdessen die Rangkorrelation nach Spearman, die nicht an die Normalverteilungsannahme gebunden ist.
cor.test(fb22$woerter_grund, fb22$gewis, method = "spearman", alternative = "greater")
## Warning in cor.test.default(fb22$woerter_grund, fb22$gewis, method = "spearman", :
## Kann exakten p-Wert bei Bindungen nicht berechnen
##
## Spearman's rank correlation rho
##
## data: fb22$woerter_grund and fb22$gewis
## S = 466277, p-value = 0.3041
## alternative hypothesis: true rho is greater than 0
## sample estimates:
## rho
## 0.0432278
Es besteht kein positiver Zusammenhang zwischen Gewissenhaftigkeit und der Anzahl an geschriebenen Wörter bei der Begründung für das Psychologiestudium.
Aufgabe 31
Lässt sich Prokrastination durch Gewissenhaftigkeit (gewis) vorhersagen?
(Falls noch nicht geschehen, berechnen sie den Skalenwert der Prokrastination.)
fb22$prok2_r <- -1 * (fb22$prok2 - 5)
fb22$prok3_r <- -1 * (fb22$prok3 - 5)
fb22$prok5_r <- -1 * (fb22$prok5 - 5)
fb22$prok7_r <- -1 * (fb22$prok7 - 5)
fb22$prok8_r <- -1 * (fb22$prok8 - 5)
fb22$prok_ges <- fb22[, c('prok1', 'prok2_r', 'prok3_r',
'prok4', 'prok5_r', 'prok6',
'prok7_r', 'prok8_r', 'prok9',
'prok10')] |> rowMeans()
- Stellen Sie die Regressionsgerade auf und prüfen sie die Voraussetzungen.
Lösung
Die einzige Voraussetzung, die wir vor der Aufstellung des Regressionsmodell prüfen können, ist der lineare Zusammenhang der Variablen mit Hilfe eines Scatterplot.
plot(fb22$gewis, fb22$prok_ges, xlab = "Gewissenhaftigkeit", ylab = "Prokrastination",
main = "Zusammenhang zwischen Gewissenhaftigkeit und Prokrastination", pch = 19)
lines(loess.smooth(fb22$gewis, fb22$prok_ges), col = 'blue')
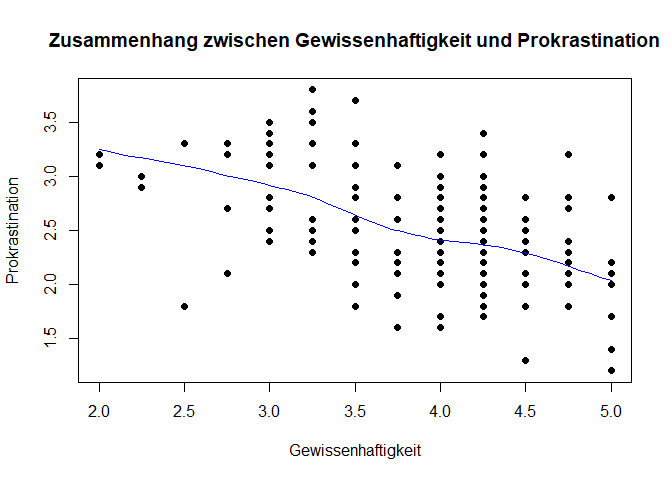
Die Voraussetzung ist erfüllt. Wir können nun also unser Regressionsmodell aufstellen.
fm <- lm(prok_ges ~ 1 + gewis, data = fb22)
Nun prüfen wir die anderen Voraussetungen.
par(mfrow = c(2, 2)) #vier Abbildungen gleichzeitig
plot(fm)
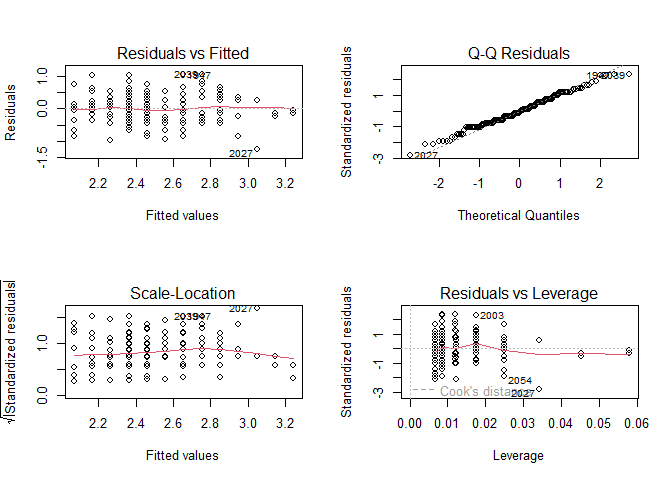
Der Q-Q-Plot oben rechts deutet auf Normalverteilung hin. Die rote Anpassungslinie des Scale-Location Plots unten links ist annähernd parallel zur x-Achse, sodass wir von Varianzhomogenität ausgehen können. Da auch der vierte Plot unten rechts nicht auf potentiell problematische, einflussreiche Datenpunkte hindeutet, sind alle Vorausetzungen erfüllt.
fm
##
## Call:
## lm(formula = prok_ges ~ 1 + gewis, data = fb22)
##
## Coefficients:
## (Intercept) gewis
## 4.0282 -0.3922
Die Regressionsgleichung lautet also $$ y_i = 4.028 - 0.392*x_i + e_i $$.
- Prüfen Sie nun mit einem $99\%$-Konfidenzintervall die Signifikanz der Koeffizienten.
Lösung
confint(fm, level = .99)
## 0.5 % 99.5 %
## (Intercept) 3.4658771 4.5906215
## gewis -0.5352757 -0.2490569
In keinem der Intervalle ist die Null enthalten, sodass wir davon ausgehen können, dass die beiden Koeffizienten tatsächlich von Null verschieden sind.
- Wie viel Prozent der Varianz von Prokrastination lassen sich durch die Gewissenhaftigkeit aufklären?
Lösung
summary(fm)
##
## Call:
## lm(formula = prok_ges ~ 1 + gewis, data = fb22)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.24783 -0.35371 -0.05175 0.33846 1.04629
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.02825 0.21564 18.680 < 2e-16 ***
## gewis -0.39217 0.05487 -7.147 3.27e-11 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4524 on 155 degrees of freedom
## (2 Beobachtungen als fehlend gelöscht)
## Multiple R-squared: 0.2478, Adjusted R-squared: 0.243
## F-statistic: 51.07 on 1 and 155 DF, p-value: 3.273e-11
summary(fm)$r.squared
## [1] 0.2478399
Durch die Gewissenhaftigkeit können $ 24.78\%$ der Varianz von Prokrastination erklärt werden.
- Eine Person hat einen Gewissenhaftswert von 3.2. Welchen Prokrastinationswert sagt das Modell für diese Person voraus?
Lösung
fm$coefficients[1] + 3.2*fm$coefficients[2]
## (Intercept)
## 2.773317
#Alternativ:
predict(fm, newdata = data.frame(gewis = 3.2))
## 1
## 2.773317
Das Modell sagt einen Prokrastinationswert von 2.77 voraus.
Aufgabe 32
In Aufgabe 29 haben wir herausgefunden, dass sich die Werte von Nerdiness und Intellekt von Psychologiestudierenden unterscheiden. Die gefundene Effektgröße betrug $d=-0.56$. Wir wollen nun eine Poweranalyse durchführen, indem wir die Studie $10^4$ mal wiederholen.
Nutzen Sie den Seed 4321 (set.seed(4321)).
- Führen Sie eine Simulation durch, um die empirische Power des t-Tests zu bestimmen.
Lösung
d <- -0.56 #Effektstärke
N <- 159 #Anzahl der Teilnehmenden von fb22
set.seed(4321)
tH1 <- replicate(n = 10^4, expr = {X <- rnorm(159)
Y <- rnorm(159) + d #Normalverteilte Stichproben mit Mittelwertsunterschied von d Standardabweichungen
ttestH1 <- t.test(X, Y, var.equal = TRUE, paired = T) #Paired = T, da es sich um einen t-Test für abhängige Stichproben handelt
ttestH1$p.value})
mean(tH1 < .05 )
## [1] 0.9989
Die Power des Tests beträgt 99.89%.
- Wie hoch ist die Wahrscheinlichkeit eines $\beta$-Fehlers?
Lösung
1 - mean(tH1 < .05 )
## [1] 0.0011
Die Wahrscheinlichkeit eines $\beta$-Fehlers beträgt 0.11%.
- Angenommen wir wollen das $\alpha$-Niveau verändern. Wie würde sich das auf die Power des Tests auswirken? Simulieren sie diesmal den empirischen t-Wert und erstellen Sie einen Powerplot, in dem $\alpha$ = 0.001, $\alpha$ = 0.01, $\alpha$ = 0.025, $\alpha$ = 0.05, $\alpha$ = 0.1 abgetragen sind.
Lösung
set.seed(4321)
tH1 <- replicate(n = 10^4, expr = {X <- rnorm(159)
Y <- rnorm(159) + d
ttestH1 <- t.test(X, Y, var.equal = TRUE, paired = T)
ttestH1$statistic})
power <- c(mean(abs(tH1) > qt(p = 1- 0.001/2, df = N)), mean(abs(tH1) > qt(p = 1- 0.01/2, df = N)), mean(abs(tH1) > qt(p = 1- 0.025/2, df = N)), mean(abs(tH1) > qt(p = 1- 0.05/2, df = N)), mean(abs(tH1) > qt(p = 1- 0.1/2, df = N)))
x <- c(.001, 0.01, 0.025, 0.05, 0.1)
plot(x = x, y = power, type = "b", main = "Power vs. Alpha")
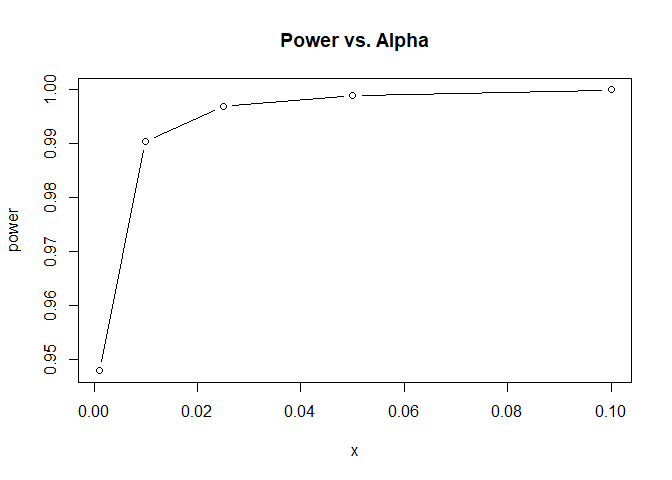
Wir sehen: Je größer das $\alpha$-Niveau ist, desto höher ist unsere Power. Mit unserer Stichprobengröße von n = 159 haben wir selbst bei einem hypothetischen $\alpha$-Niveau von 0.1% noch eine Power von knapp 95%.
](/media/header/mechanical_number_display.png)