Regressionsanalyse I

Einleitung

In der letzten Sitzung haben wir unter anderem Korrelationen zwischen zwei Variablen behandelt. Zur Wiederholung: Mithilfe einer Korrelation kann die Stärke des Zusammenhangs zwischen zwei Variablen quantifiziert werden. Dabei haben beide Variablen den gleichen Stellenwert, d.h. eigentlich ist es egal, welche Variable die x- und welche Variable die y-Variable ist. Wir haben außerdem Methoden kennengelernt, mit denen der Einfluss einer (oder mehrerer) Drittvariablen kontrolliert werden kann; die Partial- und Semipartialkorrelation. In der heutigen Sitzung wollen wir uns hingegen mit gerichteten Zusammenhängen, d.h. mit Regressionen, beschäftigen.

Lineare Regression

Das Ziel einer Regression besteht darin, eine Variable durch eine oder mehrere andere Variablen vorherzusagen (Prognose). Die vorhergesagte Variable wird als Kriterium, Regressand oder auch abhängige Variable (AV) bezeichnet und üblicherweise mit $y$ symbolisiert. Die Variablen zur Vorhersage der abhängigen Variablen werden als Prädiktoren, Regressoren oder unabhängige Variablen (UV) bezeichnet und üblicherweise mit $x$ symbolisiert. Im ersten Semester hatten wir stets nur einen Prädiktor - dies kann jedoch jetzt erweitert werden. Deshalb bekommen die Prädiktoren einen Indize $x_1$, $x_2$ usw. Die häufigste Form der Regressionsanalyse ist die lineare Regression, bei der der Zusammenhang über eine Gerade bzw. eine Ebene (bei zwei Prädiktoren) beschrieben wird. Demzufolge kann die lineare Beziehung zwischen den vorgesagten Werten und den Werten der unabhängigen Variablen mathematisch folgendermaßen beschreiben werden:

$$y_i = b_0 +b_{1}x_{i1} + … +b_{m}x_{im} + e_i$$

• $b_0$ = y-Achsenabschnitt/ Ordinatenabschnitt/ Konstante/ Interzept:

  • Der Wert von $y$ bei einer Ausprägung von 0 in allen $x$-Variablen

• $b_{1}/ b_m$ = Regressionsgewichte der Prädiktoren:

  • beziffern die Steigung der Regressionsgeraden
  • Interpretation: die Steigung der Geraden lässt erkennen, um wie viele Einheiten $y$ zunimmt, wenn $x$ um eine Einheit zunimmt

• $e_i$ = Regressionsresiduum (kurz: Residuum), Residualwert oder Fehlerwert:

  • die Differenz zwischen einem vorhergesagten ($\hat{y}$) und beobachteten ($y$) y-Wert
  • je größer die Fehlerwerte, umso größer ist die Abweichung eines beobachteten vom vorhergesagten Wert

Einfache lineare Regression

Die einfache lineare Regression hat nur einen Prädiktor. Daher entsteht eine Gerade im Modell. Das Modell folgt der uns bekannten Form:

$\hat{y_i} = b_0 +b_{1}x_{i1}$ (Regressiongerade = vorhergesagte Werte)

Grafische Darstellung einer einfachen linearen Regression

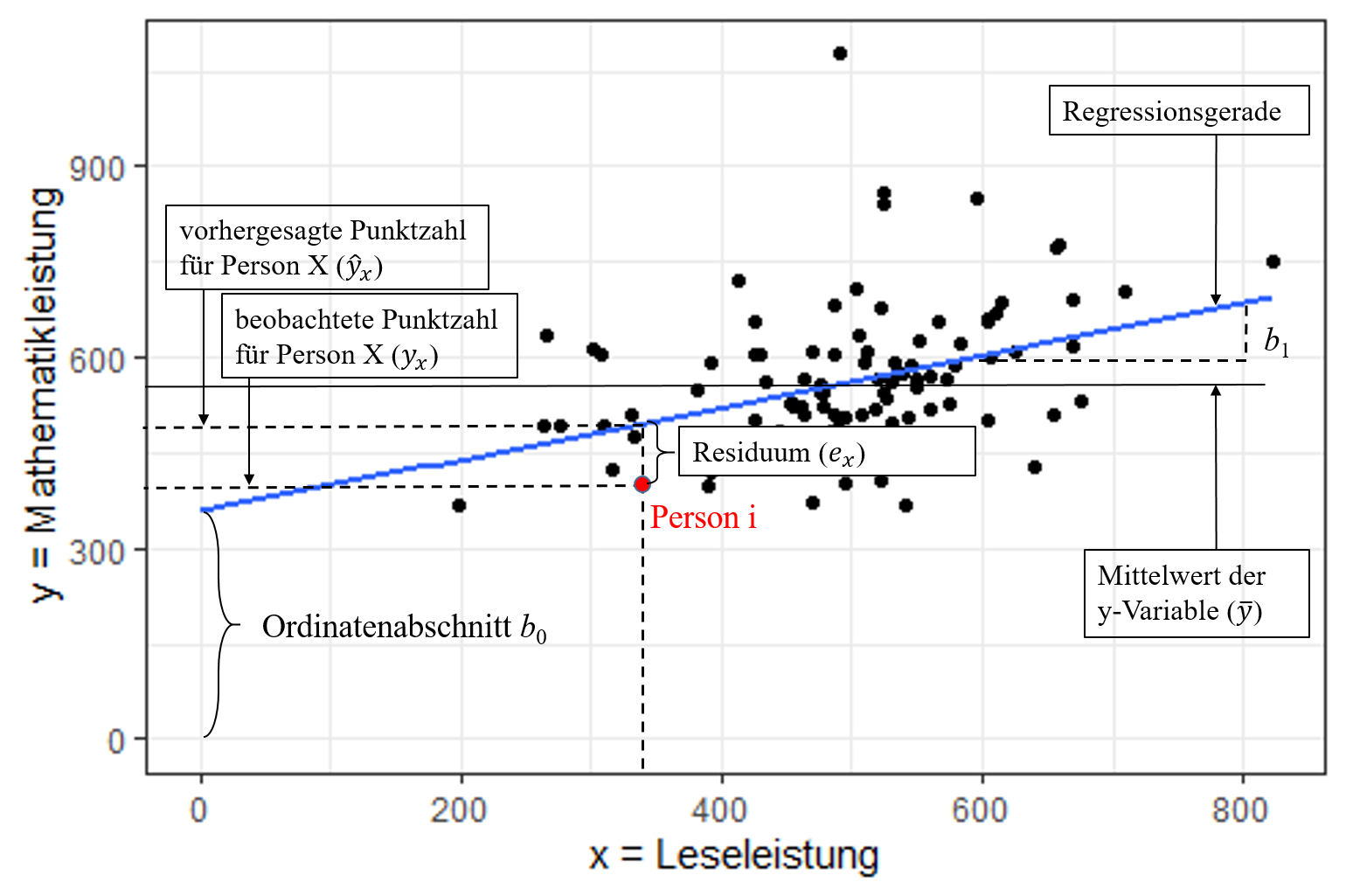
Multiple Regression (mehrere Prädiktoren)

Wenn wir nun 2 Prädiktoren haben, wird zwischen diesen und der abhängigen Variable eine Ebene aufgespannt. Die Modellgleichung lautet dabei wie bereits gezeigt:

$y_i = b_0 +b_{1}x_{i1} + b_{2}x_{i2} + e_i$

Grafische Darstellung einer multiplen Regression

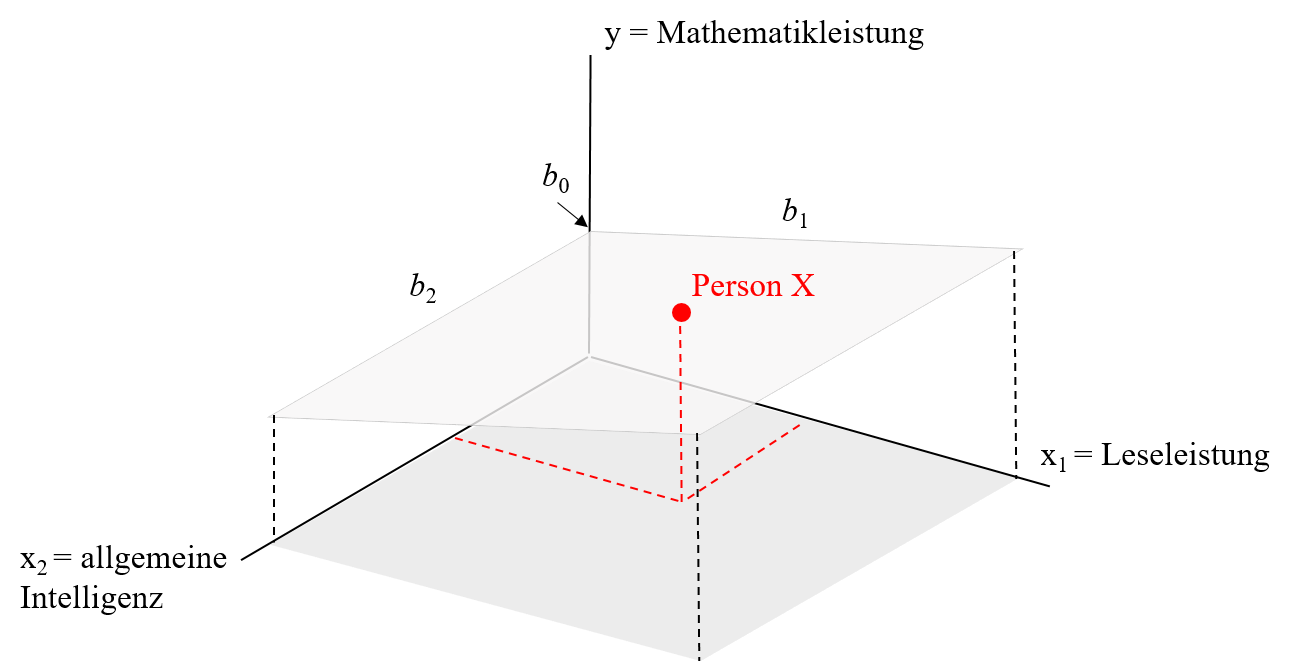
Eine Erweiterung auf mehr als zwei Prädiktoren ist mathematisch problemlos möglich, aber grafisch nicht mehr schön darstellbar. Deshalb hören wir mit Zeichnungen an dieser Stelle auf.

Berechnung der Regressionsgewichte $b_i$ mit Hilfe der händischen Formeln in R

In der Vorlesung haben Sie das Vorgehen zur Bestimmung der Regressionskoeffizienten $b_i$ kennen gelernt. Dies ist mit einem einfachen Taschenrechner, aber natürlich auch mit der Hilfe von R möglich. Diesen Einsatz wollen wir hier demonstieren.

Folgendes Anwendungsbeispiel setzen wir dabei ein: Eine Stichprobe von 100 Schüler:innen hat einen Lese- und einen Mathematiktest sowie zusätzlich einen allgemeinen Intelligenztest bearbeitet. Die Testleistungen sind untereinander alle positiv korreliert. Auch die beiden fachspezifischen Tests für Lesen (reading) und Mathematik (math) korrelieren substanziell.

Oft wird argumentiert, dass zum Lösen von mathematischen Textaufgaben auch Lesekompetenz erforderlich ist (z. B. bei Textaufgaben). Anhand des Datensatzes soll untersucht werden, wie stark sich die Mathematikleistungen durch Lesekompetenz und allgemeine Intelligenz vorhersagen lassen.

Die Formel lautet demnach:

$$y_{i,math} = b_0 +b_{reading}x_{i,reading} + b_{IQ}x_{i,IQ} + e_i$$ oder in Matrixform:

Die Daten der Schüler:innen können Sie sich direkt ins Environment einladen.

# Datensatz laden
load(url("https://pandar.netlify.app/daten/Schulleistungen.rda"))
names(Schulleistungen)

## [1] "female"  "IQ"      "reading" "math"

Zusätzlich zu den bereits beschriebenen Variablen gibt es hier noch female, wobei eine 1 für eine weibliche Person steht. Diese Variable werden wir heute allerdings nicht nutzen. Die Variable math gibt die Leistungen der Schüler:innen im Mathematik-Test wieder. Diese sollen unsere abhängige Variable darstellen, weshalb wir sie einem Objekt namens y zuordnen.

# Vektor y
y <- Schulleistungen$math
str(y)

##  num [1:100] 452 590 509 560 659 ...

Durch die Anwendung von str sehen wir, dass es sich bei dem Vektor erwartungsgemäß um einen numerischen handelt.

Als nächstes wollen wir unsere Prädiktoren vorbereiten. Diese werden gemeinsam in der Matrix X erfasst. Hierfür müssen wir die Spalten reading und IQ aus unserem Datensatz Schulleistungen auswählen.

# Matrix X vorbereiten 
X <- as.matrix(Schulleistungen[,c("reading", "IQ")])      

Anschließend wird noch eine Spalte mit Einsen benötigt, die für die Regressionskonstante eintritt. Da die Regressionskonstante für alle Personen denselben Einfluss hat, können die zugehörigen $x_0$ Werte mit 1 beschrieben werden. Wir nennen den Vektor zunächst constant. Erstellt wird er mit der Funktion rep. Diese sorgt dafür, dass 1en (erstes Argument) wiederholt werden - und dabei genau nrow(X)-mal, da die Anzahl der Zeilen von X die Anzahl der Personen beschreibt. Typischerweise steht die Regressionskonstante als erstes, weshalb der 1en-Vektor constant als erstes in cbind eingeht. Wir fügen als zweites die vorher erstellte Matrix X ein und überschreiben diese.

# Matrix X erweitern
constant <- rep(1, nrow(X))
X <- cbind(constant, X)                         
head(X)

##      constant  reading        IQ
## [1,]        1 449.5884  81.77950
## [2,]        1 544.8495 106.75898
## [3,]        1 331.3466  99.14033
## [4,]        1 531.5384 111.91499
## [5,]        1 604.3759 116.12682
## [6,]        1 308.7457 106.14127

Durch die Betrachtung der ersten 6 Zeilen mit head sehen wir, dass unsere Zusammenführung funktioniert hat. In handschriftlicher Notation würden unsere beiden erstellten Vektoren nun folgendermaßen aussehen. \begin{align}y = \begin{bmatrix}451.98 \\589.65 \\509.33\\560.43\\...\\603.18\end{bmatrix}\end{align} \begin{align}X=\begin{bmatrix}1 & 449.59 & 81.78\\1 & 544.85 & 106.76\\1 & 331.35 & 99.14\\1 & 531.54 & 111.91\\... & ... & ... \\1 & 487.22 & 106.13\end{bmatrix}\end{align}

Mit X und y in unserem Environment können wir nun in die Berechnung starten.

Vorgehen bei der Berechnung der Regressionsgewichte:

Die Regressionsgewichte in der multiplen Regression können mit folgender Formel geschätzt werden:

$$\hat{b} = (X’X)^{-1}X’y$$

Wir wollen zunächst die Gleichung in einzelne Schritte zerlegen, um die nötigen Notationen in R kennenzulernen.

1. Berechnung der Kreuzproduktsumme (X’X)
2. Berechnung der Inversen der Kreuzproduktsumme ($(X’X)^{-1}$)
3. Berechnung des Kreuzproduksummenvektors (X’y)
4. Berechnung des Einflussgewichtsvektor

1. Berechnung der Kreuzproduktsumme (X’X)

Die Kreuzproduktsumme (X’X) wird berechnet, indem die transponierte Matrix X (X’) mit der Matrix X multipliziert wird. Die transponierte Matrix X’ erhalten Sie in R durch die Befehl t(X).

t(X) # X' erhalten Sie durch t(X)

##              [,1]     [,2]      [,3]     [,4]     [,5]     [,6]      [,7]      [,8]
## constant   1.0000   1.0000   1.00000   1.0000   1.0000   1.0000   1.00000   1.00000
## reading  449.5884 544.8495 331.34664 531.5384 604.3759 308.7457 478.24576 550.18962
## IQ        81.7795 106.7590  99.14033 111.9150 116.1268 106.1413  85.44854  93.24323
##              [,9]     [,10]     [,11]    [,12]    [,13]     [,14]    [,15]    [,16]
## constant   1.0000   1.00000   1.00000   1.0000   1.0000   1.00000   1.0000   1.0000
## reading  822.0051 413.84938 655.53908 605.8732 625.3337 391.33058 709.9150 490.0105
## IQ       135.1974  89.90152  92.72073 115.9012 114.5409  83.28294 126.4167 107.2044
##              [,17]     [,18]    [,19]    [,20]     [,21]    [,22]     [,23]    [,24]
## constant   1.00000   1.00000   1.0000   1.0000   1.00000   1.0000   1.00000   1.0000
## reading  487.01641 444.92014 668.8459 502.2504 495.87525 485.7415 524.04072 461.2220
## IQ        90.03418  98.34044 117.0687 115.5514  68.11351 125.6478  93.34804 106.9365
##              [,25]     [,26]    [,27]     [,28]     [,29]     [,30]    [,31]
## constant   1.00000   1.00000   1.0000   1.00000   1.00000   1.00000   1.0000
## reading  425.66559 385.71861 521.5388 453.28591 640.76462 265.02068 539.1343
## IQ        98.78466  78.93267 113.0538  92.86905  86.44483  70.17249 111.4461
##              [,32]     [,33]     [,34]     [,35]     [,36]     [,37]     [,38]
## constant   1.00000   1.00000   1.00000   1.00000   1.00000   1.00000   1.00000
## reading  524.99381 263.22535 536.29904 469.38977 275.25090 424.78162 416.07719
## IQ        93.78654  87.54754  87.01957  69.32581  92.85801  70.56712  74.17486
##             [,39]    [,40]     [,41]    [,42]    [,43]    [,44]    [,45]     [,46]
## constant   1.0000   1.0000   1.00000   1.0000   1.0000   1.0000   1.0000   1.00000
## reading  559.0645 572.9057 549.99247 524.8635 656.9045 475.6473 430.1947 338.43936
## IQ       105.6119 110.6390  91.54624 105.7314 125.2621 101.1487 111.0958  79.99545
##              [,47]     [,48]     [,49]    [,50]     [,51]    [,52]    [,53]     [,54]
## constant   1.00000   1.00000   1.00000   1.0000   1.00000   1.0000   1.0000   1.00000
## reading  563.40059 543.48860 529.81881 668.8536 478.48482 596.3659 493.1522 333.78586
## IQ        84.45429  84.50532  96.60821 103.9056  81.03395 126.1281  89.4765  80.78064
##             [,55]    [,56]     [,57]    [,58]     [,59]     [,60]    [,61]    [,62]
## constant   1.0000   1.0000   1.00000   1.0000   1.00000   1.00000   1.0000   1.0000
## reading  476.6246 433.0946 395.12879 615.4441 674.95494 551.51318 582.4867 550.8037
## IQ       106.4885 103.5806  84.88878 115.9093  97.28407  91.60586 121.7788 110.2619
##             [,63]    [,64]    [,65]     [,66]     [,67]    [,68]    [,69]    [,70]
## constant   1.0000   1.0000   1.0000   1.00000   1.00000   1.0000   1.0000   1.0000
## reading  505.1084 579.3319 469.0869 463.25972 310.39499 494.8413 566.2383 412.3524
## IQ       100.3214 112.6516 122.8403  96.45124  75.48471  91.2755 111.8578  92.7289
##              [,71]     [,72]    [,73]     [,74]    [,75]    [,76]    [,77]    [,78]
## constant   1.00000   1.00000   1.0000   1.00000   1.0000   1.0000   1.0000   1.0000
## reading  317.15817 454.67678 518.8499 522.48525 575.6985 509.0475 603.9479 391.1594
## IQ        76.84326  92.93814 103.2558  81.15462  92.2719 106.4095  96.7028 104.0638
##             [,79]     [,80]     [,81]    [,82]    [,83]    [,84]     [,85]     [,86]
## constant   1.0000   1.00000   1.00000   1.0000   1.0000   1.0000   1.00000   1.00000
## reading  462.6678 540.62765 487.71683 519.8697 300.6192 512.1456 390.68524 380.51429
## IQ       107.9850  60.76781  94.55947 103.5597 101.8328 113.0630  76.56824  97.56684
##             [,87]    [,88]    [,89]     [,90]    [,91]    [,92]    [,93]    [,94]
## constant   1.0000   1.0000   1.0000   1.00000   1.0000   1.0000   1.0000   1.0000
## reading  559.4885 525.6131 609.9593 409.51193 604.2912 543.1018 425.8297 659.4646
## IQ       104.2866 106.0855 120.9776  82.65717 108.4118 103.3896 100.5953 122.7979
##              [,95]     [,96]     [,97]    [,98]     [,99]   [,100]
## constant   1.00000   1.00000   1.00000   1.0000   1.00000   1.0000
## reading  506.42468 454.15287 483.78242 531.9650 198.10626 487.2215
## IQ        97.91853  92.96729  77.51862 105.0199  54.05485 106.1264

\begin{align}X=\begin{bmatrix}1 & 449.59 & 81.78\\1 & 544.85 & 106.76\\1 & 331.35 & 99.14\\1 & 531.54 & 111.91\\... & ... & ... \\1 & 487.22 & 106.13\end{bmatrix}\end{align} \begin{align}X'=\begin{bmatrix} 1 & 1 & 1 & 1 & ... & 1\\449.59 & 544.85 & 331.35 & 531.54 & ... & 487.22\\81.78 & 106.76 & 99.14 & 111.91 & ... & 106.13\end{bmatrix}\end{align} Wir nennen das Kreuzprodukt an dieser Stelle X.X und nicht X'X, da dies mit der Bedeutung von ’ in der Sprache nicht funktioniert. Für das Erstellen der Kreuzproduktsumme muss das normale Zeichen für die Multiplikation * von zwei %-Zeichen umschlossen werden. An dieser Stelle würde sonst auch eine Fehlermeldung resultieren, aber bei quadratischen Matrizenist der Unterschied von Bedeutung.

# Berechnung der Kreuzproduktsumme X’X in R
X.X <- t(X) %*% X       
X.X

##           constant    reading          IQ
## constant   100.000    49606.6    9813.425
## reading  49606.605 25730126.1 4962448.077
## IQ        9813.425  4962448.1  987595.824

Die zugehörige handschriftliche Notation würde demnach so aussehen:

2. Berechnung der Inversen der Kreuzproduktsumme $(X’X)^{-1}$

Die Inverse der Kreuzproduktsumme kann in R durch den solve() Befehl berechnet werden.

# Berechnung der Inversen (mit Regel nach Sarrus) in R
solve(X.X)

##               constant       reading            IQ
## constant  0.4207610612 -1.568521e-04 -3.392822e-03
## reading  -0.0001568521  1.316437e-06 -5.056210e-06
## IQ       -0.0033928220 -5.056210e-06  6.013228e-05

3. Berechnung des Kreuzproduktsummenvektors (X’y)

Der Kreuzproduktsummenvektor (X’y) wird durch die Multiplikation der transponierten X Matrix (X’) und des Vektors y berechnet.

Die Verwendung von %*% zum Bilden des Kreuzprodukts und der Funktion t() zum Transponieren haben wir bereits kennengelernt und können hier problemlos den Code schreiben.

# Berechnung des Kreuzproduksummenvektors X`y in R
X.y <- t(X) %*% y        
X.y

##                 [,1]
## constant    56146.45
## reading  28313059.77
## IQ        5636931.00

4. Berechnung des Einflussgewichtsvektors

Die geschätzten Regressionsgewichte nach dem Kriterium der kleinsten Quadrate werden berechnet, indem die Inverse der Kreuzproduktsumme $((X’X)^{-1})$ mit dem Kreuzproduktsummenvektor (X’y) multipliziert wird.

# Berechnung des Einflussgewichtsvektor in R
b_hat <- solve(X.X) %*% X.y     # Vektor der geschätzten Regressionsgewichte
b_hat

##                 [,1]
## constant 58.17167003
## reading  -0.03584686
## IQ        5.30981976

Vorhersage der Mathematikleistung

Den Vektor mit den vorhergesagten Werten von y ($\hat{y}$) können Sie durch die Multiplikation der Matrix $X$ mit den Regressionsgewichten ($\hat{b}$) berechnen.

y_hat <- X %*% b_hat # Vorhersagewerte für jede einzelne Person 
head(y_hat)

##          [,1]
## [1,] 476.2897
## [2,] 605.5115
## [3,] 572.7112
## [4,] 633.3661
## [5,] 653.1192
## [6,] 610.6951

Berechnung der standardisierten Regressionsgewichte

Bisher wurden nur die unstandardisierten Regressionsgewichte berechnet. Diese haben den Vorteil, dass die Interpretation bei bekannten Skalen anschaulicher ausfällt. So wird das unstandardisierte Regressionsgewicht folgendermaßen interpretiert: wenn sich die unabhängige Variable um eine Einheit (bspw. der IQ um einen Punkt) verändert, verändert sich die abhängige Variable (bspw. die Note um 0.1) um den unstandardisierten Koeffizienten. Besonders bei dichotomen Prädiktoren ist die Bedeutsamkeit der unstandardisierten Regressionsgewichte viel leichter. Der Nachteil dieser unstandardisierten Regressionsgewichte ist jedoch, dass die Regressionsgewichte verschiedener Prädiktoren innerhalb eines Modells nicht vergleichbar sind. Demzufolge kann anhand der Größe der Regressionsgewichte nicht gesagt werden, welcher Regressionskoeffizient, d.h. welcher Prädiktor, eine stärkere Erklärungskraft hat.

Daher werden die Regressionsgewichte häufig standardisiert. Durch die Standardisierung sind die Regressionsgewichte nicht mehr von der ursprünglichen Skala abhängig und haben daher den Vorteil, dass sie miteinander verglichen werden können. Die Interpretation der standardisierten Regressionsgewichte lautet folgendermaßen: wenn sich die unabhängige Variable um eine Standardabweichung erhöht (und unter Kontrolle weiterer unabhängiger Variablen), so beträgt die erwartete Veränderung in der abhängigen Variable $\beta$ Standardabweichungen.

Die standardisierten Regressionsgewichte können bestimmt werden, indem zunächst alle Variablen standardisiert werden. Dafür haben wir bereits im letzten Semester den Befehl scale kennen gelernt. Wir wenden ihn auf die Werte der abhängigen Variable y und die der Prädiktoren X an.

#Berechnung der standardisierten Regressionsgewichte
y_s <- scale(y) # Standardisierung y
X_s <- scale(X) # Standardisierung X
head(X_s)

##      constant    reading          IQ
## [1,]      NaN -0.4365869 -1.03830315
## [2,]      NaN  0.4582463  0.54755176
## [3,]      NaN -1.5472873  0.06387225
## [4,]      NaN  0.3332090  0.87488817
## [5,]      NaN  1.0174054  1.14228148
## [6,]      NaN -1.7595886  0.50833564

Bei der Ansicht des standardisierten Objektes X_s sehen wir, dass alle Werte in der ersten Spalte nun NaN sind. Dies liegt daran, dass in dieser Spalte ja keine Streuung vorhanden ist und die Standardisierung somit nicht funktioniert. Wir sollten uns allerdings überlegen, ob wir den Achsenabschnitt überhaupt brauchen. Wir haben im ersten Semester gelernt, dass die Regressionsgrade immer durch den Punkt (Mittelwert unabhänige Variable / Mittelwert abhängige Variable geht). Im standardisierten Fall bedeutet dies, dass der Punkt (0/0) auf der Grade liegen musste und damit der Achsenabschnitt (an Stelle x = 0) auf jeden Fall 0 sein musste. Diese Überlegung geht auch in der multiplen Regression, wo die Regressionsebene im standardisierten Fallnun also durch den Punkt (0/0/0) geht. Wir können daher den ehemaligen Einsenvektor ignorieren und entfernen die erste Spalte aus unserem Objekt X_s.

X_s <-  X_s[,-1]     # erste Spalte entfernen   

Die bereits im unstandardisierten Fall zur Bestimmung der Regressionsgewichte könnten nun wieder einzeln durchgeführt werden. Allerdings kann man diese natürlich auch in einer Zeile Code durchführen, was hier demonstriert wird.

b_hat_s <- solve(t(X_s)%*% X_s) %*% t(X_s)%*%y_s #Regressionsgewichte aus den standardisierten Variablen
round(b_hat_s, 3)

##           [,1]
## reading -0.033
## IQ       0.716

Die Operation gibt uns für beide Prädiktoren jeweils ein Steigungsgewicht zurück. Wir erkennen, dass der Einfluss des IQs der Lesefähigkeit deskriptiv überlegen ist. Die genaue Interpretation greifen wir später nochmal auf.

Berechnung des globalen Signifikanztest

Deskriptiv haben wir nun ein Modell aufgestellt. Wie auch im letzten Semester stellt sich aber die Frage, ob wir dieses auch auf die Population übertragen können. Der Test des gesamten Modells wird auch als Omnibus-Test bezeichnet. Wir wollen im ersten Schritt betrachten, wie viel Varianz unser Modell erklären kann und es im Anschluss auf Signifikanz testen.

Determinationskoeffizient $R^2$ per Quadratsummen

Der Determinationskoeffizient $R^2$ gibt an, wieviel Varianz in der abhängigen Variable durch die unabhängigen Variablen erklärt werden kann. Dafür müssen die Quadratsummen bestimmt werden, die die Streuung der Variablen repräsentieren. Einfach gesagt, hat die abhängige Variable eine totale Quadratsumme, die in einen durch die Regression erklärten und einen nicht erklärten Teil geteilt werden kann.

$$Q_{t} = Q_d + Q_e$$

Die totale Quadratsumme wird bestimmt, indem die Abweichungen aller Fälle vom Mittelwert der Variablen bestimmt werden.

$$ Q_{t} = \sum^n_{i=1}(y_i - \bar{y})^2$$

Q_t <- sum((y - mean(y))^2)          # Totale Quadratsumme
Q_t

## [1] 1350290

Der erklärte Teil wird auch als Regressionsquadratsumme bezeichnet und mit $Q_d$ repräsentiert. Erklärt werden kann der Teil der Abweichungen vom Mittelwert, der auf der von uns berechneten Regressionsgrade liegt - also die vorhergesagten Werte für die Personen $\hat{y}_i$.

$$ Q_{d} = \sum^n_{i=1}(\hat{y}_i - \bar{y})^2$$

Q_d <- sum((y_hat - mean(y))^2)    # Regressionsquadratsumme
Q_d

## [1] 658051.7

Der nicht erklärte Anteil wird als Fehlerquadratsumme $Q_e$ bezeichnet. Hierbei wird die Abweichung unserer vorhergesagten Werte $\hat{y}_{i}$ vom wahren Wert der Personen $y$ bestimmt.

$$ Q_{e} = \sum^n_{i=1}(y_{i} - \hat{y}_i)^2$$

Q_e <- sum((y - y_hat)^2)          # Fehlerquadratsumme
Q_e

## [1] 692238.6

Die Summe aus aus der Regressionsquadratsumme und der Fehlerquadratsumme ergibt die totale Quadratsumme. Wir können also überprüfen, ob unsere bisherigen Berechnungen plausibel sind. Aufgrund der großen Zahlen kann es zu kleinen Ungenauigkeiten kommen, weshalb wir hier die Nachkommastellen durch Rundung auf zwei reduzieren.

round(Q_t,2) == round(Q_d + Q_e, 2)

## [1] TRUE

Spannender ist jedoch, dass wir durch den Quotient aus der Regressionsquadratsumme und der totalen Quadratsumme den Anteil der erklärten Varianz simpel bestimmen können.

$$R^2= \dfrac{Q_d}{Q_d + Q_e}$$

R2 <- Q_d / (Q_d + Q_e)            # Determinationskoeffizient R^2
# Alternativ Q_d / Q_t

$R^2= \dfrac{Q_d}{Q_d + Q_e} = \dfrac{658051.69}{658051.69 + 1350290.32} = 0.49$

0.49 der Varianz in der Mathematikleistung können demnach durch unser Modell erklärt werden.

Determinationskoeffizient $R^2$ per Semipartialkorrelation

An dieser Stelle können wir anstatt der Quadratsummen auch unser Wissen aus dem letzten Tutorial nutzen und die Semipartialkorrelation zur Hilfe ziehen.

In der einfachen Regression haben wir gelernt, dass sich der Determinationskoeffizient als Quadrat der Korrelation bestimmen lässt. Wenn wir nun also die Mathematikleistung zunächst nur durch Lesefähigkeit vorhersagen wollen, können wir die Funktion cor nutzen und das Ergebnis quadrieren. Beachtet, dass wir die Mathematikleistung unter y abgelegt haben. Die Lesefähigkeit, als ersten Prädiktor, finden wir in der zweiten Spalte der Matrix X. Die erste Spalte haben wir mit einem Einsenvektor belegt (also obwohl wir in der zweiten Spalte schauen, nennen wir den Prädiktor in der Notation $x_1$).

corx1y <- cor(y, X[,2])
corx1y^2 

## [1] 0.1401049

Bei multipler Regression ist der Determinationskoeffizient neben der Berechnung der Quadratsummen auch so definiert, dass für jeden weiteren Prädiktor das Quadrat einer Semipartialkorrelatin aufaddiert wird, um den multiplen Determinationskoeffizienten zu bestimmen. Dabei wird der schon aufgenommene Prädiktor aus dem neuen herauspartialisiert und der Rest dann mit dem Kriterium korreliert (also die Semipartialkorrelation bestimmt).

$R^2 = r^2_{yx_1} + r^2_{y(x_2.x_1)} + r^2_{y(x_3.x_2x_1)}$

Wie man in der Gleichung sieht, kann man diese Logik natürtlich auch auf mehr als einen Prädiktor erweitern. Die schon vorhanden Prädiktoren werden dabei stets aus dem neu aufgenommenen herauspartialisiert. In unserem Beispiel ist das nicht notwendig, da wir insgesamt nur zwei Prädiktoren haben. Wir müssen nun also eine Semipartialkorrelation bestimmen, wofür wir das Paket ppcor kennen gelernt haben. Darin gibt es die Funktion spcor.test. Als Argument benötigen wir hier in y die Werte, aus denen herauspartialisiert werden sollen. Hier müssen wir also unserer neuen Prädiktor $x_2$ allgemeine Intelligenz eintragen, der in der dritten Spalte der Matrix X zu finden ist. Im Argument z werden die Variable eingetragen, die herauspartialisert wird - also die Lesefähigkeit. Für das Kriterium Mathematikfähigkeit bleibt also nur noch das Argument x.

library(ppcor)

## Loading required package: MASS

## 
## Attaching package: 'MASS'

## The following object is masked from 'package:dplyr':
## 
##     select

spcor.test(x = y, y = X[,3], z = X[,2])

##    estimate      p.value statistic   n gp  Method
## 1 0.5892674 1.396055e-10  7.183236 100  1 pearson

Wie besprochen, kann man die Ergebnisse von Analysen auch in ein Objekt ablegen. Dies hat den Vorteil, dass man dann auf verschiedene Informationen zugreifen kann. Mit $estimate können wir uns ausschließlich den Wert der Semipartialkorrelation anzeigen lassen.

semipartial <- spcor.test(x = y, y = X[,3], z = X[,2])
semipartial$estimate

## [1] 0.5892674

Zur Bestimmung des multiplen Determinationskoeffizienten, müssen wir nun nur noch der Formel folgend aufaddieren. Zuerst nehmen wir die einfache Korrelation von Lesefähigkeit und Mathematikfähigkeit zum Quadrat. Anschließend wird noch die Semipartialkorrelation zum Quadrat hinzu addiert.

corx1y^2 + semipartial$estimate^2

## [1] 0.4873409

Wir erhalten auf diese Weise natürlich dasselbe Ergebnis, das wir auch mit den Quadratsummen bestimmen konnten. Wer mit den ganzen Buchstaben ein bisschen verwirrt wurde, kann sich dasselbe Vorgehen nochmal mit den Variablennamen in Appendix A anschauen.

F-Wert

Der F-Wert dient zur Überprüfung der Gesamtsignifikanz des Modells. Er sagt aus, ob der Determinationskoeffizient $R^2$ signifikant von 0 verschieden ist. Der empirische Testwert wird über die folgende Formel bestimmt.

$F_{omn} = \dfrac{\dfrac{R^2}{m}}{\dfrac{1-R^2}{n-m-1}}$

$R^2$ haben wir bereits im vorherigen Abschnitt bestimmt. Ergänzend müssen wir also noch $n$ und $m$ bestimmen. $n$ ist die Anzahl an Peronen oder Fällen in unserem Datensatz. Diese können wir beispielweise über die Länge length des Objekts mit den abhängigen Varibalen y bestimmen. $m$ beschreibt die Anzahl der Prädiktoren. Wenn wir dies von R automatisch bestimmen lassen wollen, können wir die Anzahl der Spalten ncol unserer Prädiktorenmatrix X bestimmen. Allerdings müssen wir bedenken, dass wir noch eine Spalten mit 1en hinzugefügt haben. Diese muss von der Zahl der Spalten also noch abgezogen werden.

n <- length(y)                     # Fallzahl (n=100)
m <- ncol(X)-1                     # Zahl der Prädiktoren (m=2)
F_omn <- (R2/m) / ((1-R2)/(n-m-1)) # empirischer F-Wert
F_omn

## [1] 46.10478

$F_{omn} = \dfrac{\dfrac{R^2}{m}}{\dfrac{1-R^2}{n-m-1}} = \dfrac{\dfrac{0.49}{2}}{\dfrac{1-0.49}{100-2-1}} = 46.1$

Der berechnete Wert entspricht einem empirischen Wert, der mit einem kritischen Wert verglichen werden muss, um die Signifikanz zu bewerten. Hierfür müssen wir in die F-Verteilung schauen. Die zugehörigen Freiheitsgrade können aus den bereits berechneten $m$ und $n$ bestimmt werden.

$df_1 = 2, df_2 = n-m-1 = 100-2-1 =97$

Zusätzlich benötigen wir natürlich noch einen $\alpha$-Fehler, der auch hier häufig auf 5% gesetzt wird. Im letzten Semester haben wir gelernt, dass wir Quantile aus Verteilungen mit dem Präfix q und dann dem Familiennamen (bspw. qnorm oder qt) ausgeben können. Wenig überraschend funktioniert an dieser Stelle also der Befehl qf.

F_krit <- qf(.95, df1=m, df2=n-m-1)  # kritischer F-Wert (alpha=5%)

$F_{krit}(\alpha=.05, df_1=2, df_2= 97)= 3.09$

Für eine Signifikanzentscheidung müssen die F-Werte nun miteinander verglichen werden.

F_krit < F_omn  # Vergleich durch logische Überprüfung

## [1] TRUE

Da der kritische Wert kleiner ist, verwerfen wir die Nullhypothese. Das Gesamtmodell wird als signifikant angesehen. Man kann anstatt des kritischen Wertes auch einfach den $p$-Wert bestimmen, der zu unserem empirischen F_omn korrespondiert. Für die Bestimmung von Wahrscheinlichkeiten in Verteilungen haben wir den Präfix p kennen gelernt. Mit Angabe der zugehörigen Freiheitsgrade können wir den $p$-Wert erhalten und mit unserem $\alpha$ vergleichen.

p <- 1-pf(F_omn, m, n-m-1)           # p-Wert
p < 0.05

## [1] TRUE

$p=8.44e-15$

Das Ergebnis ist hier natürlich das gleiche - die Nullhypothese wird verworfen.

Berechnung der Regression mit lm-Funktionen in R

Im ersten Semester haben wir bereits die einfache lineare Regression in R durchgeführt. Natürlich gibt es auch für die multiple lineare Regression eine Funktionalität. Wir werden uns zunächst den unstandardisierten und dann den standardisierten Fall anschauen und auch nochmal die Interpretation klar machen.

Unstandardisierte Regression

Für die Schätzung von Regressionsmodellen kann, wie im Fall mit einem Prädiktor, die Basis-Funktion lm verwendet werden. Verschiedene Prädiktoren werden alle hinter der Tilde ~ aufgeführt und mit dem +-Zeichen getrennt. Wir wollen hier weiterhin in unserem Datensatz Schulleistungen die Mathematikleistung (math) durch die Leseleistung (reading) und den IQ (IQ) vorhersagen. Die beiden Prädiktoren werden nach der vorangegangenen Beschreibung also mit + getrennt.

# Regressionsanalyse mit lm (nicht mehr händisch)
reg <- lm(math ~ reading + IQ, data = Schulleistungen)

Nun wollen wir überprüfen, ob die Ergebnisse den händisch berechneten entsprechen. Eine gute Übersicht über das Modell erhält man mit der Funktion summary.

summary(reg)

## 
## Call:
## lm(formula = math ~ reading + IQ, data = Schulleistungen)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -86.60 -48.89 -19.10  23.59 467.25 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 58.17167   54.79738   1.062    0.291    
## reading     -0.03585    0.09693  -0.370    0.712    
## IQ           5.30982    0.65508   8.106  1.6e-12 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 84.48 on 97 degrees of freedom
## Multiple R-squared:  0.4873,	Adjusted R-squared:  0.4768 
## F-statistic:  46.1 on 2 and 97 DF,  p-value: 8.447e-15

Die Übereinstimmung mit den händisch berechneten Regressionsgewichten wird bereits deutlich. Im nächsten Abschnitt befassen wir uns nochmal genauer mit der Interpretation.

Ergebnisinterpretation unstandardisierte Regression

• die Lesekompetenz und allgemeine Intelligenz erklären gemeinsam 48.73% der Varianz in der Mathematiktestleistung
• Dieser Varianzanteil ist signifikant von null verschieden
• Regressionsgewichte:
  • Regressionskonstante $b_0$:
    • Der Erwartungswert der Mathematikleistung für ein Individuum mit null Punkten im IQ und null Punkten in Lesekompetenz beträgt 58.17 Punkte.
  • Regressionsgewicht $b_1$:
    • bei einem Punkt mehr in der Lesekompetenz und unter Kontrolle (Konstanthaltung) des IQ beträgt die erwartete Veränderung in der Mathematikleistung -0.04 Punkte.
    • Der Einfluss von Lesekompetenz auf Mathematikleistung ist nicht signfikant von null verschieden ($p$=0.71)
  • Regressionsgewicht $b_2$:
    • unter Kontrolle (Konstanthaltung) der Lesekompetenz beträgt die erwartete Veränderung in der Mathematikleistung bei einem Punkt mehr im IQ 5.31 Punkte.
    • Der Einfluss der allgemeinen Intelligenz auf Mathematikleistung ist signfikant von null verschieden ($p$=1.6e-12)

Standardisierte Regression

Zur Durchführung der standardisierten Regression mit Hilfe von Funktionen in R könnten wir natürlich händisch alle Variablen mit scale() standardisieren und dann in lm() übergeben. Dieses Vorgehen würde aber den Achsenabschnitt mitschätzen, was wir nicht brauchen Es gibt eine bereits geschriebene Funktion lm.beta() aus dem gleichnamigen Paket lm.beta, die für uns eine zusätzliche Anzeige der standardisierten Regressionsgewichte bereit hält. Das Paket haben wir im normalen Ablauf der Tutorials noch nicht installiert, weshalb wir hier nochmal darauf verweisen. Aus diesem Grund werden oft standardisierte Regressionskoeffizienten berechnet und berichtet.

install.packages("lm.beta") #Paket installieren (wenn nötig)

Nach der (ggf. nötigen) Installation müssen wir das Paket für die Bearbeitung laden.

library(lm.beta)

lm steht hier für lineares Modell und beta für die standardisierten Koeffizienten. Anmerkung: In der Literatur werden oft auch unstandardisierte Regressionkoeffizienten als $\beta$s bezeichnet, sodass darauf stets zu achten ist, was gemeint ist.

Die Funktion lm.beta() muss auf ein Ergebnis der normalen lm-Funktion angewendet werden. Wir haben dieses Ergebnis im Objekt reg hinterlegt. Anschließend wollen wir uns für die Interpretation wieder das summary() ausgeben lassen. Natürlich kann man diese Schritte auch mit der Pipe lösen, was als Kommentar noch aufgeführt ist.

# Ergebnisausgabe einschließlich standardisierter Koeffizienten mit lm.beta
reg_s <- lm.beta(reg)
summary(reg_s)         # reg |> lm.beta() |> summary()

## 
## Call:
## lm(formula = math ~ reading + IQ, data = Schulleistungen)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -86.60 -48.89 -19.10  23.59 467.25 
## 
## Coefficients:
##             Estimate Standardized Std. Error t value Pr(>|t|)    
## (Intercept) 58.17167           NA   54.79738   1.062    0.291    
## reading     -0.03585     -0.03268    0.09693  -0.370    0.712    
## IQ           5.30982      0.71615    0.65508   8.106  1.6e-12 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 84.48 on 97 degrees of freedom
## Multiple R-squared:  0.4873,	Adjusted R-squared:  0.4768 
## F-statistic:  46.1 on 2 and 97 DF,  p-value: 8.447e-15

Wir sehen, dass die ursprüngliche Ausgabe um die Spalte standardized erweitert wurde. An der standardisierten Lösung fällt auf, dass das Interzept $\beta_0$ als NA angezeigt wird. Dies liegt wie bereits besprochen daran, dass beim Standardisieren die Mittelwerte aller Variablen (Prädiktoren und Kriterium) auf $0$ und die Standardabweichungen auf $1$ gesetzt werden. Somit muss das Interzept hier genau $0$ betragen. Weil jeder geschätzte Parameter der Regressionsgleichung einen Freiheitsgrad kostet, wird der Parameter besser einfach nicht mitgeschätzt, also als NA angegeben.

Ergebnisinterpretation standardisierte Regression

• Standardisierte Regressionsgewichte
  • Standardisiertes Regressionsgewicht $\beta_0$: Der Achsenabschnitt ist null, da die Ebene durch den Punkt der Mittelwerte aller Variablen geht (0/0/0).
  • Standardisiertes Regressionsgewicht $\beta_1$: Unter Kontrolle (Konstanthaltung) des IQ beträgt die erwartete Veränderung in der Mathematikleistung bei einer Standardabweichung mehr in Lesekompetenz 0.72 Standardabweichungen.
  • Standardisiertes Regressionsgewicht $\beta_2$: Unter Kontrolle (Konstanthaltung) der Lesekompetenz beträgt die erwartete Veränderung in der Mathematikleistung bei einer Standardabweichung mehr im IQ NA Standardabweichungen.

Verweis zu letzter Sitzung: In solch einer multiplen Regression können Suppressoreffekte gut aufgedeckt werden. Diese zeigen sich dann, wenn die $\beta$-Gewichte in der multiplen Regression dem Betrag nach größer sind, als deren korrespondierende $\beta$-Gewichte in einer einfachen Regression. Dies ist in unserem Beispiel jedoch nicht der Fall.

Appendix A

cor.mathreading <- cor(Schulleistungen$math, Schulleistungen$reading)
cor.mathreading

## [1] 0.3743059

library(ppcor)
spcor.test(x = Schulleistungen$math, 
           y = Schulleistungen$IQ, 
           z = Schulleistungen$reading)

##    estimate      p.value statistic   n gp  Method
## 1 0.5892674 1.396055e-10  7.183236 100  1 pearson

semipartial <- spcor.test(x = y, y = X[,3], z = X[,2])
semipartial$estimate

## [1] 0.5892674

cor.mathreading^2 + semipartial$estimate^2

## [1] 0.4873409