Regression V: nichtlineare Regression - exponentielles Wachstum

Bisher hatten wir mittels Regressionsanalysen lineare Beziehungen modelliert. In der Sitzung zur quadratischen und moderierte Regresssion kamen dann im Grunde quadratische Effekte mit hinzu. Wir können unser Wissen über Regressionen allerdings auch nutzen um nichtlineare Effekte zu modellieren. Wie das geht und was zu beachten ist, schauen wir uns im Folgenden an. Dazu laden wir zunächst altbekannte Pakete:

library(ggplot2) # Grafiken
library(car)     # Residuenplots
library(MASS)    # studres

Einführung: Exponentielles Wachstum

Ein sehr wichtiges Vorhersagemodell zu Zeiten der Corona-Pandemie oder in Anbetracht von starkem weltweitem Bevölkerungswachstum ist das exponentielle Wachstum. Genauso könnten wir auch die Zahl der Kaiserpinguine der Antarktis modellieren (siehe Foto oben). Um dieses genauer zu verstehen, werden einige Grundlagen im Umgang mit Exponenten benötigt. Zum Beispiel müssen wir uns überlegen, welche Rate und welche Basis ein exponentieller Verlauf hat. Beispielsweise wächst $10^x$ deutlich schneller als $2^x$ (für gleiches wachsendes $x$).

Im folgenden Exkurs haben Sie die Möglichkeit Ihr Wissen nochmal aufzufrischen und zu erweitern. Ihnen werden Quellen genannt, in welchen Sie weitere Inhalte nachlesen können. Dieser Exkurs stellt eine Wiederholung dar. Sie können ihn auch überspringen.

Exkurs

# gleiches Ergebnis:
10^3

## [1] 1000

exp(3*log(10))

## [1] 1000

# gleiches Ergebnis:
log(10^3, base = 10) # Logarithmus von 1000 zur Basis 10

## [1] 3

log(10^3)/log(10) # mit ln

## [1] 3

# gleiches Ergebnis:
log(9, base = 3) # Logarithmus von 9 zur Basis 3

## [1] 2

log(9)/log(3) # mit ln

## [1] 2

Das Modellieren von exponentiellem Wachstum

Wir betrachten nun eine allgemeine exponentielle Wachstumsfunktion $$f(x) = a\ b^{c\ x}$$ (hierbei ist $a$ ein Vorfaktor, der die Ausprägung an der Stelle $x=0$ beschreibt, $b$ ist die Basis des exponentiellen Wachstums und $c$ ist ein eigentlich redundanter Ratenparameter). Wegen der Beliebigkeit der Basis ist dies gleich $$f(x) = e^{\text{ln}(a\ b^{c\ x})}=e^{\text{ln}(a) + \text{ln}(b)cx}.$$ Nun sind $\text{ln}(a)$ und $\text{ln}(b)c$ zwei Konstanten, die wir einfach umbenennen dürfen. Wir können sie beispielsweise $\beta_0$ und $\beta_1$ nennen; also $\beta_0 := \text{ln}(a)$ und $\beta_1:=\text{ln}(b)c$. Folglich steht $$f(x) = e^{\beta_0 + \beta_1x}$$ für beliebiges exponentielle Wachstum (wir erhalten den Verlauf “$2^x$” indem wir $\beta_0 = \text{ln}(a) = 0$ und $\beta_1=\text{ln}(b)c = \text{ln}(2)$ wählen; also $a=1, b=2$ und $c=1$). Gleichzeitig bedeutet dies, dass, durch Logarithmieren, $$\text{ln}(f(x)) = \beta_0 + \beta_1x$$ eine lineare Funktion ist, welche wir ganz einfach mit einer Regressionsanalyse, also lm in R, untersuchen können! Wir können somit sagen, dass wir durch Logarithmieren von $f(x)$ in der Lage sind, das exponentielle Wachstum zu Linearisieren, also das exponentielle Wachstum in eine lineare Funktion zu transformieren, welche mit Auswertungsinstrumenten für lineare Funktionen untersucht werden können. Wahnsinn, oder? Dies bedeutet, dass wir nach Logarithmieren der abhängigen Variable in der Lage sind die gesamte Klasse der exponentiellen Funktionen/des exponentiellen Wachstums für die Modellierung unserer Daten zu verwenden. Der gleichen Logik bedienen sich auch bestimmte Kontraste, die untersuchen, ob Mittelwerte einer bestimmten Funktion (z.B. exponentiellen Verlauf) entsprechen, indem sie lienearisiert werden und anschließend auf Linearität untersucht werden. Was genau Kontraste sind, erfahren Sie in den kommenden Sitzungen zur ANOVA.

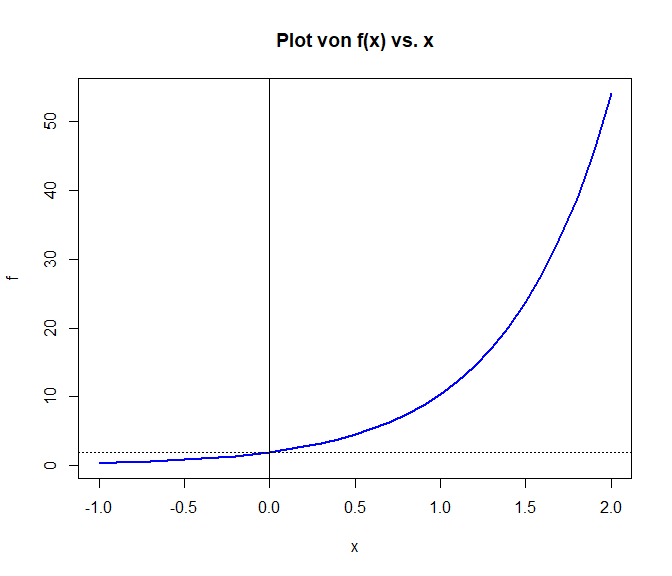
Die folgenden zwei Grafiken verdeutlichen dies (Der folgende Block ist gedacht, dass Sie diesen kopieren und die Inputparameter verändern und sich den Effekt auf die Grafiken ansehen; die horizontale gestrichelte Linien repräsentiert jeweils den Wert $a$ bzw. $\text{ln}(a)$, an welchem die Kurve $f$ bzw. $\ln(f)$ die y-Achse schneiden):

##################
#### Einstellen der Koeffizienten und berechnen von f(x)
#### 
x <- seq(-1,2,0.1) # x = Variablen (als Zahlen zwischen -1 und 2)
a <- 2   # Vorfaktor, der die Ausprägung an der Stelle x=0 beschreibt
b <- 3   #  Basis des exponentiellen Wachstums
c <- 1.5 # *eigentlich redundanter* Ratenparameter
f <- a*b^(c*x) # f(x), eine exponentiell-wachsende Funktion in x

##################
#### Plot von f(x) vs. x
#### 
plot(x = x, y = f, type = "l", col = "blue", lwd = 2, main = "Plot von f(x) vs. x") # plotte f(x) gegen x
abline(v = 0, lwd = 0.7) # y-Achse, v = 0 zeichnet eine vertikale Linie bei x = 0
abline(h = a, lty = 3) # im Punkt a schneidet f (das exponentielle Wachstum) die y-Achse (x=0), h = a zeichnet zu y = a eine horizontale Linie

##################
#### Plot von ln(f(x)) vs. x
#### 
plot(x = x, y = log(f), type = "l", col = "blue", lwd = 2, main = "Plot von ln(f(x)) vs. x") # plotte ln(f(x)) gegen x
abline(v = 0, lwd = 0.7) # y-Achse, v = 0 zeichnet eine vertikale Linie bei x = 0
abline(h = log(a), lty = 3)  # im Punkt log(a) schneidet log(f) (das linearisierte exponentielle Wachstum) die y-Achse (x=0), h =llog(a) zeichnet zu y = log(a) eine horizontale Linie

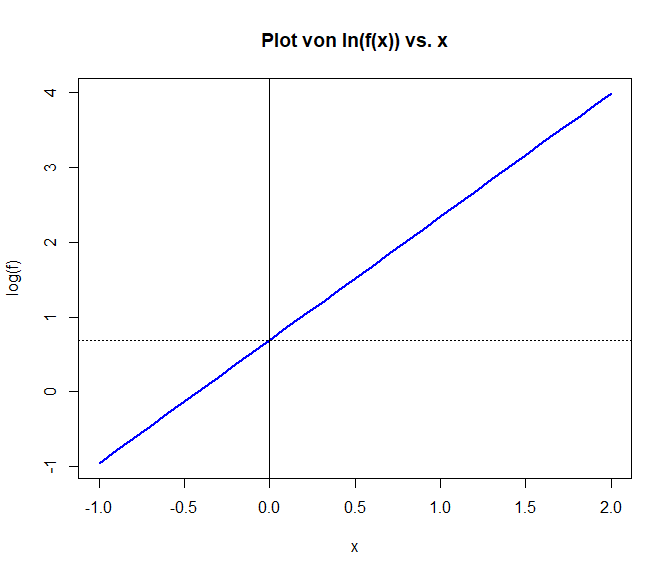
All dies bedeutet nun, dass wir durch eine sehr simple Transformation der Daten, Schlüsse über exponientielles Wachstum treffen können. Dies schauen wir uns nun an einem inhaltlichen Beispiel an!

Das Modellieren von exponentiellem Wachstum am Beispiel der Weltbevölkerung von 1800 bis 2020

Nun können wir beispielsweise die Entwicklung der Weltbevölkerung von 1800 bis 2020 modellieren. Dazu müssen wir zunächst die Daten laden: Die Dokumentation des Datensatzes mit Datenquellen sind hier einzusehen: gapminder.org-Dokumentationen. Sie können den im Folgenden verwendeten Datensatz “WorldPopulation.rda” hier herunterladen.

Daten laden

Wir laden zunächst die Daten: entweder lokal von Ihrem Rechner:

load("C:/Users/Musterfrau/Desktop/WorldPopulation.rda")

oder wir laden sie direkt über die Website:

load(url("https://pandar.netlify.app/daten/WorldPopulation.rda"))

Nun sollte in R-Studio oben rechts in dem Fenster unter der Rubrik “Data” unser Datensatz mit dem Namen “WorldPopulation” erscheinen.

Überblick über die Daten

Schauen wir uns die Daten an:

head(WorldPopulation)

##   Year Population
## 1 1800  982454635
## 2 1801  985895135
## 3 1802  989555435
## 4 1803  992954135
## 5 1804  995485735
## 6 1805 1000098535

In der ersten Spalte steht das Jahr; in der 2. die Weltbevölkerungsgröße. Wir wollen uns dies grafisch ansehen. Dazu verwenden wir ggplot, um die Population (Population) gegen das Jahr (Year) abzutragen und zwar als Punkte mit geom_point(). Sie können Grafiken mit ggplot2 in der zugehörigen Sitzung wiederholen.

ggplot(data = WorldPopulation, aes(x = Year, y = Population))+geom_point()

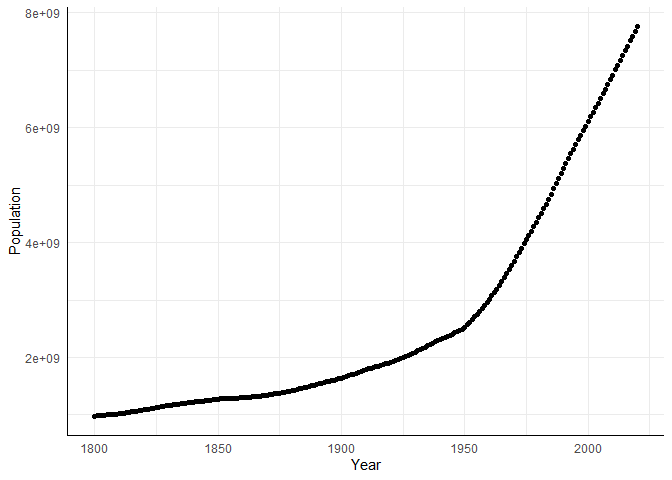
Das Diagramm lässt deutlich einen nichtlinearen Anstieg der Weltbevölkerung von 1800 bis 2020 vermuten. Auffällig ist auch der leichte Knick, der um 1950 zu vermuten ist und ab welchem die Bevölkerung, deskriptiv gesehen, noch stärker wächst. Dieser Knick ist zum Teil durch das Ende des Krieges, aber auch durch modernere Landwirtschaft und das Aufkommen von neuen Medikamenten (z.B. Penicilline) zu erklären.

Lineares Modell für das Bevölkerungswachstum

Wir wollen uns naiverweise ein lineares Regressionmodell, also einen linearen Verlauf, der Weltbevölkerung vorhergesagt durch das Jahr, ansehen.

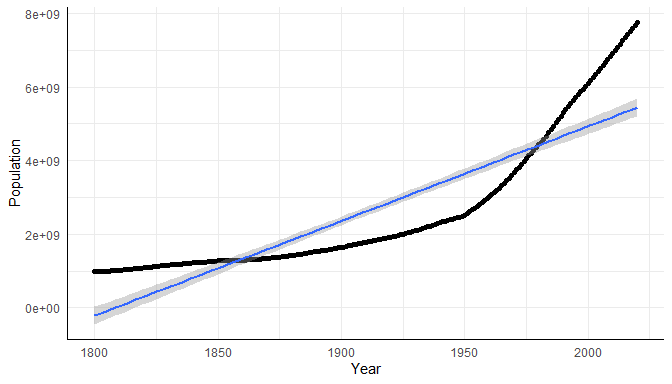
ggplot(data = WorldPopulation, aes(x = Year, y = Population))+
     geom_point()+geom_smooth(method="lm", formula = "y~x")         # plotte linearen Verlauf 

m_l <- lm(Population ~ Year, data = WorldPopulation) # linearer Verlauf
summary(m_l)  

## 
## Call:
## lm(formula = Population ~ Year, data = WorldPopulation)
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -1.128e+09 -7.964e+08 -1.629e+08  6.811e+08  2.313e+09 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -4.646e+10  1.801e+09  -25.79   <2e-16 ***
## Year         2.569e+07  9.426e+05   27.26   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 8.94e+08 on 219 degrees of freedom
## Multiple R-squared:  0.7723,	Adjusted R-squared:  0.7713 
## F-statistic: 742.9 on 1 and 219 DF,  p-value: < 2.2e-16

#########
### Normalverteilung der Residuen?
##
res <- studres(m_l) # Studentisierte Residuen als Objekt speichern
df_res <- data.frame(res) # als Data.Frame für ggplot
# Grafisch: Histogramm mit Normalverteilungskurve
ggplot(data = df_res, aes(x = res)) + 
     geom_histogram(aes(y =..density..),
                    bins = 10,                    # Wie viele Balken sollen gezeichnet werden?
                    colour = "blue",              # Welche Farbe sollen die Linien der Balken haben?
                    fill = "skyblue") +           # Wie sollen die Balken gefüllt sein?
     stat_function(fun = dnorm, args = list(mean = mean(res), sd = sd(res)), col = "darkblue") + # Füge die Normalverteilungsdiche "dnorm" hinzu und nutze den empirischen Mittelwert und die empirische Standardabweichung "args = list(mean = mean(res), sd = sd(res))", wähle dunkelblau als Linienfarbe
     labs(title = "Histogramm der Residuen mit Normalverteilungsdichte\n für das lineare Modell", x = "Residuen") # Füge eigenen Titel und Achsenbeschriftung hinzu

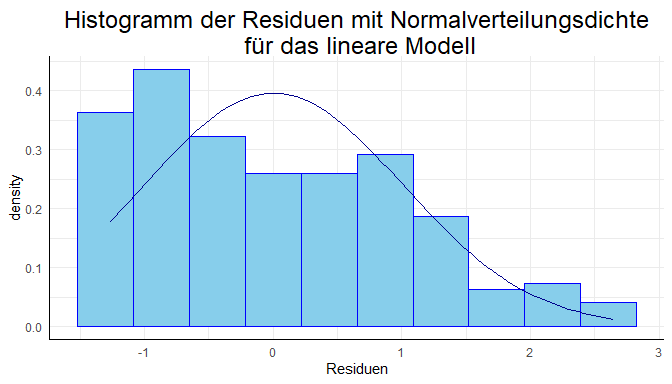
Durch + geom_smooth(method="lm", formula = "y~x"), kann mit ggplot ein linearer Trend inklusive Konfidenzintervall hinzugefügt werden. Obwohl ein linearer Verlauf sehr unwahrscheinlich erscheint, können mit dem linearen Modell bereits 77.23% der Variation der Bevölkerungsdichte durch die Jahreszahl erklärt werden (entnommen aus der Summary des linearen Modells unter Multiple R-squared: 0.7723). Wie der Grafik deutlich zu entnehmen ist, sind die Residuen in dieser Regressionsanalyse stark abhängig von der Jahreszahl (negatives Residuum von ca. 1860-1970 und positive Residuen sonst; Wiederholung: $\varepsilon_i=Y_i-\hat{Y}_i$, wobei $\hat{Y}_i$ der vorhergesagte Wert ist, das Vorzeichen erhalten wir also, indem wir uns überlegen, wann die Daten oberhalb oder unterhalb der vorhergesagten Geraden liegen). Auch wenn wir uns das zugehörige Histogramm der Residuen ansehen, widerspricht dieses der Annahme auf Normalverteilung. In Appendix A ist auch ein quadratische Trend hinzugefügt, da wir ja in der vergangenen Sitzung zu quadratischer oder moderierter Regression gesehen hatten, dass durch das Hinzufügen von quadratischen Effekten die Vorhersage des Kriteriums verbessert werden kann. Wir interessieren uns jetzt aber erstmal für das exponentielle Wachstum!

Exponentielles Modell für das Bevölkerungswachstum

Nun wollen wir prüfen, ob ein exponentieller Verlauf die Daten besser beschreibt. Dazu müssen wir zunächst die Weltpopulation logarithmieren und können anschließend ein lineares Modell verwenden. Wir transformieren hierzu die Variablen und speichern diese als weitere Spalte in unserem Datensatz mit dem Namen log_Population ab:

WorldPopulation$log_Population <- log(WorldPopulation$Population) # Logarithmus der Weltbevölkerung

Wir wollen anschließend ein einfaches Regressionsmodell schätzen, in welchem die logarithmierte Bevölkerungszahl die abhängige Variable darstellt. Das lm Objekt speichern wir hierzu unter dem Namen m_log ab und schauen uns die summary für m_log an.

m_log <- lm(log_Population ~ Year, data = WorldPopulation) # lineares Modell mit log(y) als AV (logarithmische Skala)
summary(m_log)

## 
## Call:
## lm(formula = log_Population ~ Year, data = WorldPopulation)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.20453 -0.16471 -0.02055  0.15678  0.27406 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 3.781382   0.328712   11.50   <2e-16 ***
## Year        0.009265   0.000172   53.87   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.1631 on 219 degrees of freedom
## Multiple R-squared:  0.9298,	Adjusted R-squared:  0.9295 
## F-statistic:  2902 on 1 and 219 DF,  p-value: < 2.2e-16

Es wäre auch möglich gewesen, die Daten nicht vorher zu transformieren, sondern einfach, wie in der letzten Sitzung erwähnt, I(log(...)) auf die abhängige Variable anzuwenden:

m_log2 <- lm(I(log(Population)) ~ Year, data = WorldPopulation) # lineares Modell mit log(y) als AV (logarithmische Skala)
summary(m_log2)

## 
## Call:
## lm(formula = I(log(Population)) ~ Year, data = WorldPopulation)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.20453 -0.16471 -0.02055  0.15678  0.27406 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 3.781382   0.328712   11.50   <2e-16 ***
## Year        0.009265   0.000172   53.87   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.1631 on 219 degrees of freedom
## Multiple R-squared:  0.9298,	Adjusted R-squared:  0.9295 
## F-statistic:  2902 on 1 and 219 DF,  p-value: < 2.2e-16

Das lineare Modell für die logarithmierte Bevölkerungsdichte scheint gut zu den Daten zu passen. Insgesamt können 92.98 % der Variation in den Daten durch den Zeitverlauf erklärt werden — deutlich mehr, als durch den linearen Verlauf! Die zugehörige Grafik des logarithmierten Modells sieht so aus:

ggplot(data = WorldPopulation, aes(x = Year, y = log_Population))+
     geom_point()+geom_smooth(method="lm", formula = "y~x", col = "red")+
  labs(title = "Logarithmierte Weltbevölkerung vs. Jahr")

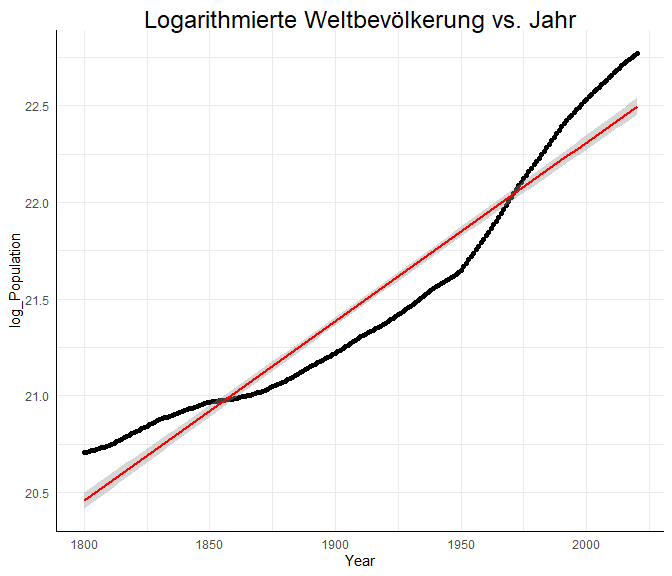
So sind die Ergebnisse aber sehr schwer mit dem linearen Trend zu vergleichen. Wir wollen die Vorhersage auch retransformiert plotten, um sie mit dem linearen Verlauf grafisch vergleichen zu können. Dazu müssen wir die vorhergesagten Werte unseres logarithmischen Modells verwenden und mit mit der Umkehrfunktion des Logarithmus retransformieren. Diese können wir einem lm-Objekt mit predict entlocken. predict berechnet die vorhergesagten Kriteriumswerte via $\hat{Y}_i=\hat{\beta}_0+\hat{\beta}_1X_i$, wobei für unser Beispiel $Y_i=$ ln(Bevölkerung) im $i$-ten Jahr und $X_i=$ $i$-tes Jahr gilt. Da wir zuvor logarithmiert hatten, müssen wir nun die Exponentialfunktion auf unsere vorhergesagten Werte anwenden: also quasi: $e^{\hat{Y}_i}$, bzw. $e^{\hat{\beta}_0+\hat{\beta}_1X_i}$. Wir nennen die neue Variable pred_Pop_exp, wobei pred für predicted und Pop_exp für exponentielles Populationswachstum steht:

WorldPopulation$pred_Pop_exp <- exp(predict(m_log)) # Abspeichern der retransformierten vorhergesagten Werten (wieder auf der Skala der Weltbevölkerung)
head(WorldPopulation)

##   Year Population log_Population pred_Pop_exp
## 1 1800  982454635       20.70556    768019076
## 2 1801  985895135       20.70906    775168245
## 3 1802  989555435       20.71277    782383962
## 4 1803  992954135       20.71620    789666848
## 5 1804  995485735       20.71874    797017526
## 6 1805 1000098535       20.72336    804436629

Dem Datensatz haben wir nun eine neue Spalte hinzugefügt, welche die vorhergesagten Populationswerte enthält (retransformiert; nicht mehr in Log-Skala). Nun schauen wir uns den exponentiellen sowie den linearen Trend für die Bevölkerungszahl an:

ggplot(data = WorldPopulation, aes(x = Year, y = Population))+
     geom_point()+geom_smooth(method="lm", formula = "y~x")+         # plotte linearen Verlauf 
     geom_line(aes(x = Year, y = pred_Pop_exp), col = "red", lwd = 1.5)

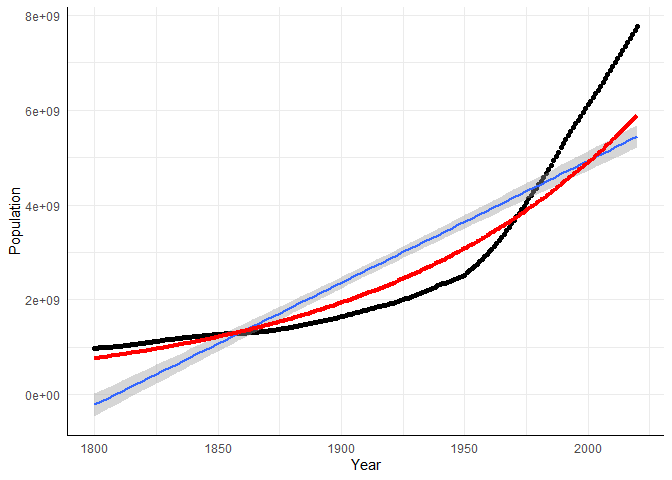
Das Diagramm der retransformierten vorhergesagten Werten signalisiert, dass ein exponentielles Wachstumsmodell die Daten gut beschreibt. Wir können die Parameter des logarithmischen Modells auch in die Bevölkerungsskala (weg von der log-Skala) übersetzen. Dazu nutzen wir wieder eine Logarithmus/Exponentenregel: $e^{a+b}=e^ae^b$. Also ist $e^{\hat{\beta_0}}$ die Bevölkerung zum Jahr 0 und $e^{\hat{\beta}_1}$ die Veränderung der Bevölkerung (multiplikativ), wenn die Jahreszahl um eine Einheit erhöht wird. Wir können dies leicht wie folgt umsetzen:

exp(coef(m_log))

## (Intercept)        Year 
##   43.876618    1.009309

Hier entlocken wir zunächst dem Objekt m_log die Koeffizienten unseres Modells und wenden anschließend die Exponentialfunktion darauf an. Die Bevölkerung im Jahre 0 lag laut Modell bei 44 Personen und wächst jede Jahr (multiplikativ) um den Faktor 1.0093. Wir erkennen, dass das Modell nicht sehr realistische Vorhersagen für das Jahr 0 treffen kann. Das ist also zu ignorieren, da das Jahr 0 1800 Jahre vom Beobachtungszeitraum entfernt liegt. Schauen wir uns lieber die Veränderung von Jahr zu Jahr an. Der multiplikative Veränderungsfaktor von 1.0093 zeigt uns, dass die Bevölkerung laut Modell jedes Jahr (die Interpretation für Regressionen bleibt gleich, wir erhöhen den Prädiktor um 1 und schauen, wie sich das Kriterium verändert!) um 9.3‰ (Achtung, hier steht Promille, das sind 0.93%) steigt (das haben wir am positiven Vorzeichen von $\hat{\beta}_1$ erkannt, bzw. das erkennen wir auch daran, dass $e^{\hat{\beta}_1}>1$ gilt). Das erscheint zunächst als super wenig, aber die Bevölkerungszahlen im tatsächlich beobachteten Zeitraum liegen zwischen knapp unterhalb einer Milliarde und 7 Milliarden. Von einer Milliarde sind 0.93% immerhin 9300000 (9.3 Millionen) und von 7 Milliarden entsprechend das 7-fache!

Diskontinuierliches Modell: Interaktion mit Dummy-Variablen

Das Modell mit exponentiellem Wachstum hat eine Varianzaufklärung von knapp 93%, was für ein Modell in der Psychologie beeindruckend wäre. Gerade für Fortpflanzungsprozesse gibt es aber meist sehr genaue mathematische Modelle, deren Varianzaufklärung bei annähernd 100% liegt - wir müssen unser Modell also noch ein bisschen verbessern.

Schon in der Abbildung ohne unsere Vorhersagen war aufgefallen, dass das Bevölkerungswachstum um das Jahr 1950 herum einen “Knick” hat und danach noch einmal schneller zuzulegen scheint. Unser Modell mit exponentiellem Wachstum war zwar gut darin, einen generellen Trend abzubilden, aber mit solchen natürlichen Unregelmäßigkeiten kommt es nicht gut zurecht.

In der Modellierung von längsschnittlichen Prozessen ist es auch in der Psychologie üblich sogenannte “diskontinuierliche Prozesse” zu untersuchen. Dabei geht es darum, den Effekt von Ereignissen adäquat abzubilden, die zu einer Veränderung des natürlichen Prozesses führen können. In der Psychologie sind das z.B. Interventionen, die den Entwicklungsverlauf von Kindern (hoffentlich positiv) beeinflussen oder auch Lebensereignisse, wie z.B. die Geburt eines Kindes, die deutliche Spuren in psychologischen Variablen hinterlassen.

Was dafür genutzt wird ist ein simpler Trick: wir erstellen eine Variable die mit 0 die Zeit “vor dem Ereignis” und mit 1 die Zeit “nach dem Ereignis” kodiert. Im Fall des Bevölkerungswachstums nehmen wir mal das Jahr 1950 als Ereginis an:

WorldPopulation$Post1950 <- as.numeric(WorldPopulation$Year > 1950)

Im Datensatz erhalten wir dann also Folgendes:

##     Year Population log_Population pred_Pop_exp Post1950
## 148 1947 2446128932       21.61777   2998437595        0
## 149 1948 2466556182       21.62609   3026348797        0
## 150 1949 2491236432       21.63604   3054519813        0
## 151 1950 2522343946       21.64845   3082953062        0
## 152 1951 2569486613       21.66697   3111650983        1
## 153 1952 2616809393       21.68522   3140616042        1
## 154 1953 2663255370       21.70282   3169850724        1

Die Idee ist jetzt, dass wir diesen Indikator $Post$ zusätzlich in die Regression aufnehmen und damit folgende Regressiongleichung erhalten:

$$ \widehat{Pop_i} = e^{\beta_0 + \beta_1 \cdot Jahr_i + \beta_2 \cdot Post_i + \beta_3 \cdot (Jahr_i \cdot Post_i)} $$

Dadurch, dass $Post$ für jedes Jahr bis 1950 den Wert 0 annimmt, entfallen die letzten beiden Terme der Gleichung für diese Jahre (weil die Multiplikation mit 0 immer 0 ergibt):

$$ \widehat{Pop_i} = e^{\beta_0 + \beta_1 \cdot Jahr_i} $$

Für alle Jahre nach 1950 hingegen, sieht die umgestellte Gleichung so aus:

$$ \widehat{Pop_i} = e^{(\beta_0 + \beta_2) + (\beta_1 + \beta_3) \cdot Jahr_i} $$ sodass wir einen neuen Interzept (verschoben um $\beta_2$) und einen neuen Effekt des Jahres (verändert um $\beta_3$) ab diesem Punkt haben. In R können wir das Ganze genauso ausdrücken, wie wir es für andere Regressionen mit Interaktionen schon gesehen hatten:

m_dis <- lm(I(log(Population)) ~ Year * Post1950, data = WorldPopulation)
summary(m_dis)

## 
## Call:
## lm(formula = I(log(Population)) ~ Year * Post1950, data = WorldPopulation)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.068476 -0.034200  0.006488  0.028597  0.090422 
## 
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    9.907e+00  1.346e-01   73.58   <2e-16 ***
## Year           5.975e-03  7.179e-05   83.23   <2e-16 ***
## Post1950      -2.024e+01  4.713e-01  -42.95   <2e-16 ***
## Year:Post1950  1.045e-02  2.385e-04   43.80   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.03845 on 217 degrees of freedom
## Multiple R-squared:  0.9961,	Adjusted R-squared:  0.9961 
## F-statistic: 1.865e+04 on 3 and 217 DF,  p-value: < 2.2e-16

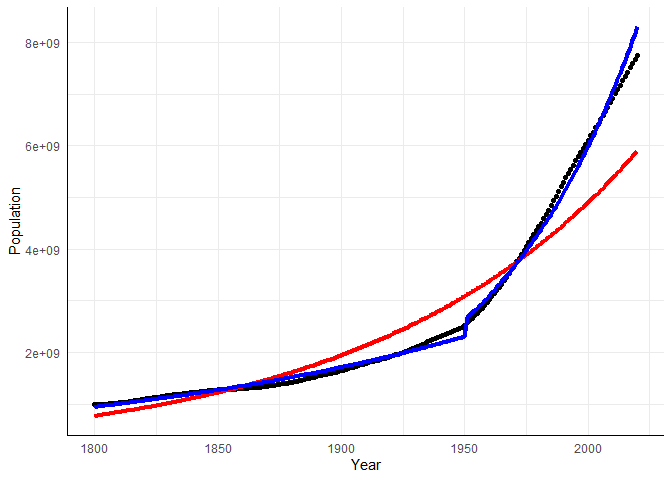
Der Effekt der Variable Post1950 enthält nun die Information über den “sofortigen Interventionseffekt” des Jahres 1950 - also den sprunghaften Anstieg der Bevölkerungszahl. Der Interaktionseffekt stellt den unterschied der beiden Wachstumsraten dar. Auch dieses Modell ist nicht perfekt, aber es ist mit 99.61 schon sehr gut. Im optischen Vergleich der beiden Modelle nähert es die tatsächliche Bevölkerungszahl besser an als das rein exponentielle Wachstum:

WorldPopulation$pred_Pop_dis <- exp(predict(m_dis))
ggplot(data = WorldPopulation, aes(x = Year, y = Population))+
  geom_point()+
  geom_line(aes(x = Year, y = pred_Pop_exp), col = "red", lwd = 1.5) +
  geom_line(aes(x = Year, y = pred_Pop_dis), col = "blue", lwd = 1.5)

Appendix A

Quadratisches Modell für das Bevölkerungswachstum

Vielleicht ist in den Daten anstatt eines exponentiellen Trends ein quadratischer Effekt versteckt? Wir möchten dem auf den Grund gehen und nutzen wieder die Funktion poly, um ein Polynom 2. Grades (eine quadratische Funktion) der Jahreszahl in unsere Analysen mit aufzunehmen.

m_q <- lm(Population ~ poly(Year,2), data = WorldPopulation) # quadratischer Verlauf
summary(m_q)

## 
## Call:
## lm(formula = Population ~ poly(Year, 2), data = WorldPopulation)
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -646432518 -267430205   89039661  288698332  475103733 
## 
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    2.617e+09  2.120e+07  123.47   <2e-16 ***
## poly(Year, 2)1 2.437e+10  3.152e+08   77.32   <2e-16 ***
## poly(Year, 2)2 1.238e+10  3.152e+08   39.30   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 315200000 on 218 degrees of freedom
## Multiple R-squared:  0.9718,	Adjusted R-squared:  0.9716 
## F-statistic:  3761 on 2 and 218 DF,  p-value: < 2.2e-16

Das Varianzinkrement im Vergleich zum linearen Verlauf beläuft sich auf:

summary(m_q)$r.squared - summary(m_l)$r.squared  # Inkrement 

## [1] 0.1995076

Da der Parameter des quadratischen Anteils signifikant ist, gehen wir davon aus, dass das Modell durch den quadratischen Verlauf verbessert wird. Wir sichern dies noch einmal mit einem Modellvergleich ab:

anova(m_l, m_q)

## Analysis of Variance Table
## 
## Model 1: Population ~ Year
## Model 2: Population ~ poly(Year, 2)
##   Res.Df        RSS Df  Sum of Sq      F    Pr(>F)    
## 1    219 1.7504e+20                                   
## 2    218 2.1652e+19  1 1.5338e+20 1544.3 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Dies ist der Modellvergleich des linearen und des quadratischen Modells. Hier sollte dem anova-Befehl immer das “kleinere” (restriktivere) Modell (mit weniger Prädiktoren und Parametern, die zu schätzen sind) zuerst übergeben werden. Hier: m_l, da sonst die df negativ sind und auch die Änderung in den Sum of Sq (Quadratsumme) negativ sind! R erkennt dies zwar und testet trotzdem die richtige Differenz auf Signifikanz, aber wir wollen uns besser vollständig korrekt aneignen!

Auch dem geom_smooth Befehl kann einfach das modifizierte Regressionsmodell übergeben werden. Stellen Sie die Weltbevölkerung sowie das lineare und das quadratische Modell dar und färben Sie die Kurve in dunkelblau (col = "darkblue").

ggplot(data = WorldPopulation, aes(x = Year, y = Population))+
     geom_point()+geom_smooth(method="lm", formula = "y~x")+         # plotte linearen Verlauf 
     geom_smooth(method="lm", formula = "y~poly(x,2)", col = "darkblue")  # plotte quadratischen Verlauf

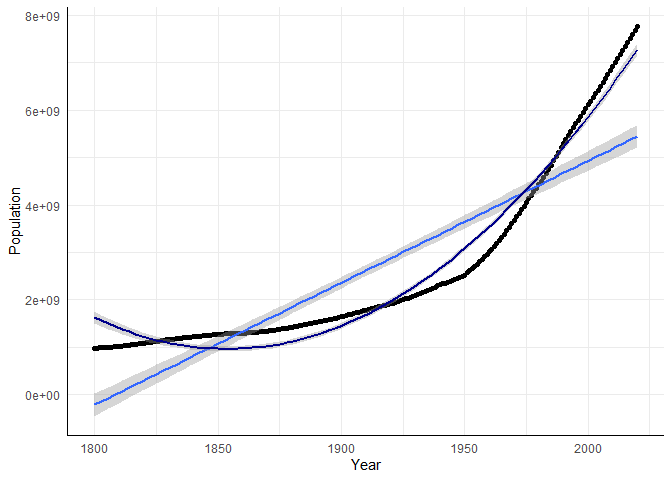
Durch den quadratischen Verlauf lassen sich 97.18% der Variation der Bevölkerungsdichte erklären, was einem signifikantem Varianzinkrement von 19.95% entspricht (mit einer Irrtumswahrscheinlichkeit von 5% ist das Inkrement in der Population nicht null. Dies ist äquivialent zu folgdender Aussage: mit einer Irrtumswahrscheinlichkeit von 5% ist der Effektparameter (der Regressionskoeffizient) des quadratischen Verlaufs in der Population nicht null; dies spricht folglich für einen quadratischen im Gegensatz zu einem linearen Verlauf). Der Grafik ist deutlich zu entnehmen, dass der quadratische Verlauf nicht weit vom empirischen entfernt liegt.

Den quadratischen Verlauf können wir, wie auch den linearen, nicht inferenzstatistisch gegen den exponentiellen Verlauf testen. Dies liegt daran, dass die Modelle nicht auseinander hervorgehen (sie sind nicht geschachtelt). Allerdings war es so, dass das lineare Modell für die logarithmierte Bevölkerungsdichte zwar gut zu den Daten zu passen schien. Insgesamt können 92.98 % der Variation in den Daten durch den Zeitverlauf erklärt werden — das war allerdings etwas weniger als durch das quadratische Wachstum, durch welches 97.18 % der Variation in den Daten durch den Zeitverlauf erklärt werden konnten.

ggplot(data = WorldPopulation, aes(x = Year, y = Population))+
     geom_point()+geom_smooth(method="lm", formula = "y~x")+         # plotte linearen Verlauf 
     geom_smooth(method="lm", formula = "y~poly(x,2)", col = "darkblue")+  # plotte quadratischen Verlauf
     geom_line(aes(x = Year, y = pred_Pop_exp), col = "red", lwd = 1.5)

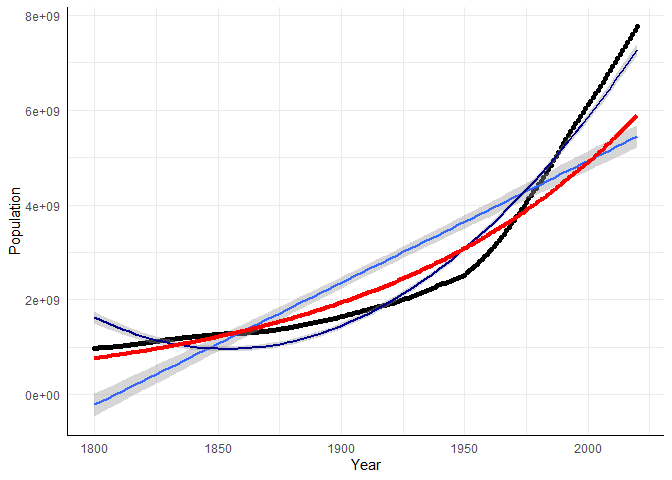
Das Diagramm der retransformierten vorhergesagten Werten signalisiert, dass ein exponentielles Wachstumsmodell die Daten gut beschreibt, allerdings scheint der quadratische Trend vor allem ab ca. 1975 die Daten besser zu beschreiben.

Appendix B

Quadratisch-exponentielles Modell für das Bevölkerungswachstum

Die Vorhersage mit dem diskontinuierlichen Modell exponentiellen Wachstums ist immer noch nicht perfekt. Insbesondere der vorhergesagte sprunghafte Anstieg von 1950 zu 1951 scheint unrealistisch. Inspizieren wir noch einmal den Residuenplot aus dem exponentiellen Modell:

residualPlot(m_log, col = "red") # Residualplot

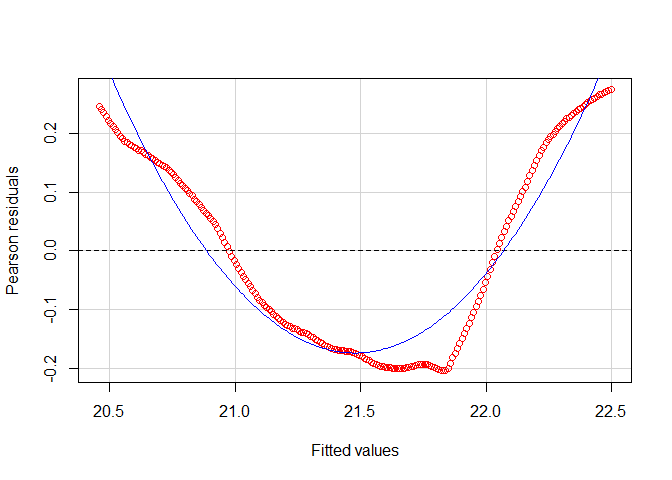
Dem Residualplot ist zu entnehmen, dass ggf. sogar ein nicht-linearer Verlauf angemessen wäre (wobei wir uns hier auf die logarithmische Skala beziehen, die Ursprungsdaten werden natürlich bereits nicht-linear, nämlich exponentiell, modelliert). Wir gehen dieser Vermutung nach, indem wir dem Log-Plot einen quadratischen Verlauf hinzufügen. Auch dem geom_smooth Befehl kann einfach das modifizierte Regressionsmodell übergeben werden. Dem Argument formula müssen wir dazu jediglich die Formel für die Regression übergeben, wobei y das Kriterium und poly(x,2) (dies hatten wir in der vergangen Sitzung zu quadratischer oder moderierter Regression kennengelernt) der Prädiktor mit linearem und quadratischen Anteil beschreibt. Mit col = "gold3" wird die neue Linie auch extra eingefärbt.

ggplot(data = WorldPopulation, aes(x = Year, y = log_Population))+
     geom_point()+geom_smooth(method="lm", formula = "y~x", col = "red")+
  geom_smooth(method="lm", formula = "y~poly(x,2)", col = "gold3")+
  labs(title = "Logarithmierte Weltbevölkerung vs. Jahr")

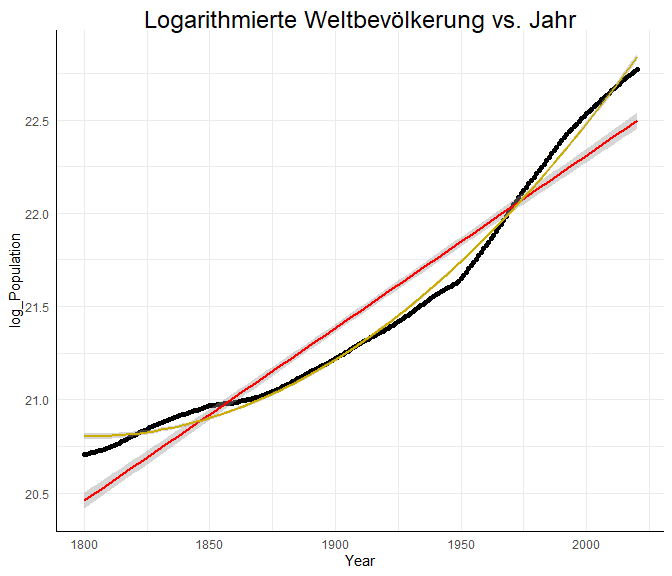
Vielleicht wächst die Bevölkerung sogar schneller als exponentiell? Die gelbe Linie im logarithmierten Plot lässt dies vermuten. Um dies genauer zu untersuchen fügen wir in das logarithmierte Modell einen quadratischen Trend der Zeit ein.

Dies wollen wir schätzen, indem wir im Regressionsmodell der logarithmierten Populationsgröße einen quadratischen Trend (poly(...,2)) für die Zeit definieren. Das Modell nennen wir, mein unbegrenztes Einfallsreichtum beweisend, m_log_quad:

m_log_quad <- lm(log_Population ~ poly(Year, 2), data = WorldPopulation) # lineares Modell mit log(y) als AV (logarithmische Skala)
summary(m_log_quad)

## 
## Call:
## lm(formula = log_Population ~ poly(Year, 2), data = WorldPopulation)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.097348 -0.037302  0.008814  0.039090  0.070984 
## 
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    21.478533   0.003111 6903.34   <2e-16 ***
## poly(Year, 2)1  8.787459   0.046253  189.99   <2e-16 ***
## poly(Year, 2)2  2.315495   0.046253   50.06   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.04625 on 218 degrees of freedom
## Multiple R-squared:  0.9944,	Adjusted R-squared:  0.9943 
## F-statistic: 1.93e+04 on 2 and 218 DF,  p-value: < 2.2e-16

Wir können dieses Modell nun gegen m_log testen und so die Modellverbesserung des quadratisch exponentiellen Verlaufs auf Signifikanz prüfen (und zwar mit dem anova-Befehl).

anova(m_log, m_log_quad)

## Analysis of Variance Table
## 
## Model 1: log_Population ~ Year
## Model 2: log_Population ~ poly(Year, 2)
##   Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
## 1    219 5.8279                                  
## 2    218 0.4664  1    5.3615 2506.1 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Durch den quadratisch-exponentiellen Verlauf (bzw. den quadratischen Verlauf in den logarithmierten Daten) lassen sich 99.44% der Variation der Bevölkerungsdichte erklären, was einem signifikantem Varianzinkrement von 6.46% im Vergleich zum reinen exponentiellen Verlaufsmodell entspricht. Interessant zu sehen ist, dass fast 100% der Variation im Datensatz erklärbar ist. Eine Übersicht über $R^2$ in den Modellen ist in Appendix C einzusehen.

Schauen wir uns den Residuenplot des quadratisch-exponentiellen Modells an (in logarithmierter Skala, in welcher das Modell auch geschätzt wurde!).

residualPlot(m_log_quad)

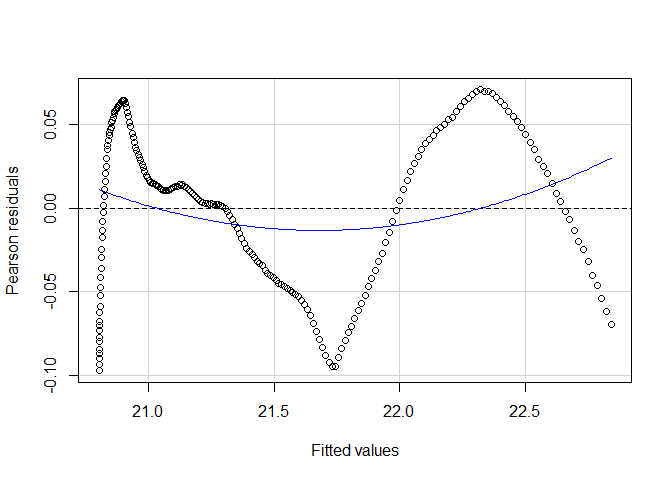
Es ist deutlich zu sehen, dass der Knick um 1950 auch im quadratisch-exponentiellen Modell noch zu sehen ist. Die Residuenplots zeigen außerdem, dass auch hier die Residuen nicht vollständig unsystematisch sind. Dennoch ist die Resiudalvarianz sehr klein. Dies erkennen wir an der y-Achse.

Stellen wir dies grafisch dar. Dazu müssen wir wieder die Vorhersage abspeichern. Diese können wir einem lm-Objekt mit predict entlocken. Wir nennen die neue Variable einfach pred_Pop_exp_quad.

WorldPopulation$pred_Pop_exp_quad <- exp(predict(m_log_quad)) # Abspeichern der retransformierten vorhergesagten Werten (wieder auf der Skala der Weltbevölkerung)
head(WorldPopulation)

##   Year Population log_Population pred_Pop_exp Post1950 pred_Pop_dis pred_Pop_exp_quad
## 1 1800  982454635       20.70556    768019076        0    940385460        1082904426
## 2 1801  985895135       20.70906    775168245        0    946020970        1082790682
## 3 1802  989555435       20.71277    782383962        0    951690251        1082769604
## 4 1803  992954135       20.71620    789666848        0    957393507        1082841189
## 5 1804  995485735       20.71874    797017526        0    963130942        1083005453
## 6 1805 1000098535       20.72336    804436629        0    968902759        1083262439

Dem Datensatz haben wir nun eine neue Spalte hinzugefügt, welche die vorhergesagten Populationswerte enthält, die durch das quadratisch-exponentielle Modell vorhergesagt werden (retransformiert; nicht mehr in Log-Skala). Im Folgenden ist die finale Grafik mit dem linearen, exponentiellen, diskontinuierlichen und dem quadratisch-exponentiellen Verlauf dargestellt. Außerdem

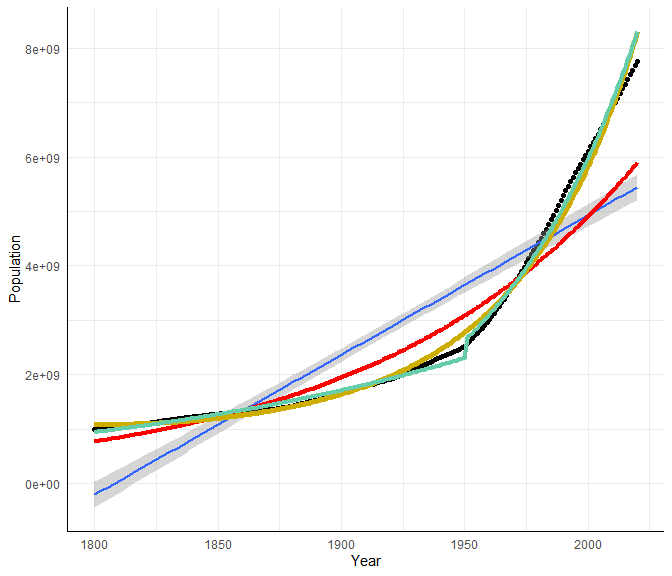
ggplot(data = WorldPopulation, aes(x = Year, y = Population))+
     geom_point()+geom_smooth(method="lm", formula = "y~x")+         # plotte linearen Verlauf 
     geom_line(aes(x = Year, y = pred_Pop_exp), col = "red", lwd = 1.5) +
     geom_line(aes(x = Year, y = pred_Pop_exp_quad), col = "gold3", lwd = 2) +
     geom_line(aes(x = Year, y = pred_Pop_dis), col = 'aquamarine3', lwd = 1.5)

# nur quadratisch-exponentiell
ggplot(data = WorldPopulation, aes(x = Year, y = Population))+
     geom_point()+
     geom_line(aes(x = Year, y = pred_Pop_exp_quad), col = "gold3", lwd = 2)+
  labs(title = "Beobachtetes und durch das quadratisch-exponentielle Modell\n vorhergesagtes Bevölkerungswachstum")

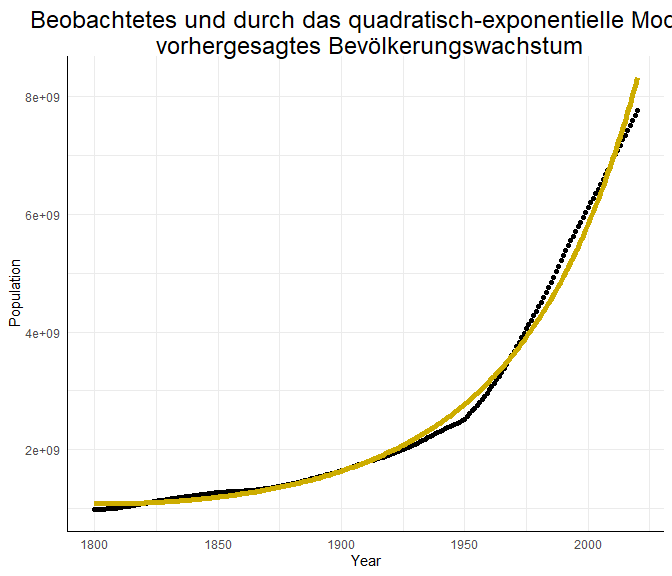
Was bedeuten nun die Parameter in unserem quadratisch-exponentiellen Modell? Der Regressionskoeffizient des linearen Trends von poly liegt bei 8.79 und der Koeffizient des quadratischen Trends bei 2.32. Dies spricht für ein beschleunigtes exponentielles Wachstum. Nach diesem Vorhersagemodell scheinen die Menschen sich schneller als exponentiell zu vermehren (zumindest von 1800 bis 2020). Eine Übersicht über die Modelle sehen Sie in Appendix D.

Wären beide Koeffizienten negativ, so würde dies für beschleunigten exponentiellen Zerfall/Abnahme sprechen. Ist der Koeffizient des quadratische Trends negativ, wird von exponentiellem Wachstum mit Dämpfung gesprochen.

Final ist zu sagen, dass die Menschheit am wahrscheinlichsten exponentiell wächst. Ein quadratisches Modell ist im Allgemeinen nicht sinnvoll (siehe Appendix A). Da wir uns in dieser Übung nur einen kleine Zeitausschnitt angesehen haben, kam es zu diesen Abweichungen. Allerdings würde das geschätzte quadratische Modell für das Jahr 0 eine Bevölkerungszahl von 7.88$*10^{11}$ vorhersagen, was absolut nicht sinnvoll ist.

Appendix C

R2 <- rbind(summary(m_l)$r.squared,
            summary(m_q)$r.squared,
            summary(m_log)$r.squared,
            summary(m_dis)$r.squared,
            summary(m_log_quad)$r.squared)
rownames(R2) <- c("linear", "quadratisch", "exponentiell (log. Modell)", "diskontinuierlich (log. Modell)", "quadratisch-exponentiell (quadratisches log. Modell)")
colnames(R2) <- "R^2"
round(R2, 4)

##                                                         R^2
## linear                                               0.7723
## quadratisch                                          0.9718
## exponentiell (log. Modell)                           0.9298
## diskontinuierlich (log. Modell)                      0.9961
## quadratisch-exponentiell (quadratisches log. Modell) 0.9944

Appendix D