Denken Sie bei allen Aufgaben daran, den Code im R-Skript sinnvoll zu gliedern und zu kommentieren.
Vorbereitung
Zunächst müssen wir das readxl, forcats und das dplyr Paket wieder aktivieren und einen Teil des Code aus dem letzten Tutorial und den letzten Aufgaben wieder durchführen.
# Paket einladen
library(readxl)
library(dplyr)
library(forcats)
# Pfad setzen
rstudioapi::getActiveDocumentContext()$path |>
dirname() |>
setwd()
# Daten einladen
data <- read_excel("Pennington_2021.xlsx", sheet = "Study_Data")
# Faktoren erstellen
data$Gender <- factor(data$Gender,
levels = c(1, 2),
labels = c("weiblich", "männlich"))
data$Year <- as.factor(data$Year)
# Faktoren Rekodieren
data$Year <- fct_recode(data$Year,
"7. Schuljahr" = "Year7",
"8. Schuljahr" = "Year8")
data$Ethnicity <- as.factor(data$Ethnicity)
# NA-Werte ersetzen
data <- data %>%
mutate(across(where(is.numeric), ~ na_if(.x, -9)))
# Skalenwerte erstellen
data <- data %>%
mutate(Total_Competence = rowMeans(data[,c("Total_Competence_Maths", "Total_Competence_English", "Total_Competence_Science")]))
data$Total_SelfConcept <- rowMeans(data[, c("Total_SelfConcept_Maths", "Total_SelfConcept_Science", "Total_SelfConcept_English")])
# Gruppierungsvariablen erstellen
data <- data %>%
mutate(Achiever = case_when(
Total_Competence_Maths >= 4 &
Total_Competence_English >= 4 &
Total_Competence_Science >= 4 ~ "High Achiever",
Total_Competence_Maths == 1 &
Total_Competence_English == 1 &
Total_Competence_Science == 1 ~ "Low Achiever",
TRUE ~ "Medium Achiever" # Alle anderen Fälle
))
data <- data %>%
mutate(Career_Recommendation = case_when(
Maths_AttainmentData > 10 |
Science_AttainmentData > 10 |
Eng_AttainmentData > 10 |
Computing_AttainmentData > 10 ~ "Empfohlen",
TRUE ~ "Nicht empfohlen"
)) # Erstellen der neuen Variable
Falls Sie nicht am Workshop teilnehmen und daher keine lokale Version des Datensatzes haben, verwenden Sie diesen Code.
# Paket einladen
library(readxl)
library(dplyr)
library(forcats)
# Daten einladen
source("https://pandar.netlify.app/workshops/fdz/fdz_data_prep.R")
# Faktoren erstellen
data$Gender <- factor(data$Gender,
levels = c(1, 2),
labels = c("weiblich", "männlich"))
data$Year <- as.factor(data$Year)
# Faktoren Rekodieren
data$Year <- fct_recode(data$Year,
"7. Schuljahr" = "Year7",
"8. Schuljahr" = "Year8")
data$Ethnicity <- as.factor(data$Ethnicity)
# NA-Werte ersetzen
data <- data %>%
mutate(across(where(is.numeric), ~ na_if(.x, -9)))
# Skalenwerte erstellen
data <- data %>%
mutate(Total_Competence = rowMeans(data[,c("Total_Competence_Maths", "Total_Competence_English", "Total_Competence_Science")]))
data$Total_SelfConcept <- rowMeans(data[, c("Total_SelfConcept_Maths", "Total_SelfConcept_Science", "Total_SelfConcept_English")])
# Gruppierungsvariablen erstellen
data <- data %>%
mutate(Achiever = case_when(
Total_Competence_Maths >= 4 &
Total_Competence_English >= 4 &
Total_Competence_Science >= 4 ~ "High Achiever",
Total_Competence_Maths == 1 &
Total_Competence_English == 1 &
Total_Competence_Science == 1 ~ "Low Achiever",
TRUE ~ "Medium Achiever" # Alle anderen Fälle
))
data <- data %>%
mutate(Career_Recommendation = case_when(
Maths_AttainmentData > 10 |
Science_AttainmentData > 10 |
Eng_AttainmentData > 10 |
Computing_AttainmentData > 10 ~ "Empfohlen",
TRUE ~ "Nicht empfohlen"
)) # Erstellen der neuen Variable
Teil 1 - Grafikerstellung
- Zeichnen Sie ein Histogramm für die Variable
Total_Mindsetund passen Sie die Grenzen der x-Achse an. Die Farbe der Umrandung der einzelnen Balekn soll Türkis sein. Finden Sie heraus, wie Sie sich alle voreingestellten Farben (wieredundblue) anzeigen lassen können und wählen Sie ein Türkis, das Ihnen gefällt.
Lösung
Um die Grenzen der x-Achse anzupassen, sollte zunächst der Bereich der Variable untersucht werden - bspw. mit der Funktion summary().
#### Aufgaben des Tutorials zu Basisfunktionen zur Grafikerstellung und linearen Modellen ----
##### Teil 1 -----
###### Aufgabe 1 ------
summary(data$Total_Mindset) # Überblick über die Variable
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 19.0 29.0 32.0 31.6 35.0 42.0 7
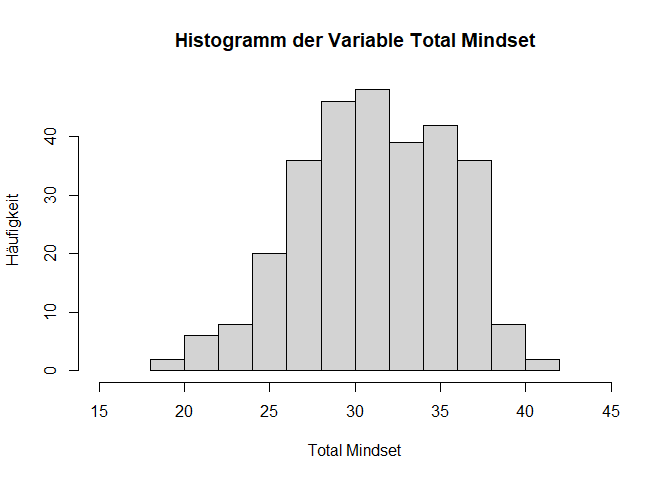
Darin sehen wir den Bereich, den wir abdecken sollten zwischen Minimum und Maximum. Die Funktion hist() wird genutzt, um ein Histogramm zu erstellen. Mit xlim() können die Grenzen der x-Achse angepasst werden.
# Histogramm mit angepasster Skalierung der x-Achse
hist(data$Total_Mindset,
main = "Histogramm der Variable Total Mindset",
xlab = "Total Mindset",
ylab = "Häufigkeit",
xlim = c(15, 45))
Die Farbe der Balken wird mit col und die Farbe der Umrandung mit border festgelegt. Um sich alle Basisfarben anzeigen zu lassen, kann die Funktion colors() genutzt werden.
colors() # Anzeigen aller Basisfarben
## [1] "white" "aliceblue" "antiquewhite"
## [4] "antiquewhite1" "antiquewhite2" "antiquewhite3"
## [7] "antiquewhite4" "aquamarine" "aquamarine1"
## [10] "aquamarine2" "aquamarine3" "aquamarine4"
## [13] "azure" "azure1" "azure2"
## [16] "azure3" "azure4" "beige"
## [19] "bisque" "bisque1" "bisque2"
## [22] "bisque3" "bisque4" "black"
## [25] "blanchedalmond" "blue" "blue1"
## [28] "blue2" "blue3" "blue4"
## [31] "blueviolet" "brown" "brown1"
## [34] "brown2" "brown3" "brown4"
## [37] "burlywood" "burlywood1" "burlywood2"
## [40] "burlywood3" "burlywood4" "cadetblue"
## [43] "cadetblue1" "cadetblue2" "cadetblue3"
## [46] "cadetblue4" "chartreuse" "chartreuse1"
## [49] "chartreuse2" "chartreuse3" "chartreuse4"
## [52] "chocolate" "chocolate1" "chocolate2"
## [55] "chocolate3" "chocolate4" "coral"
## [58] "coral1" "coral2" "coral3"
## [61] "coral4" "cornflowerblue" "cornsilk"
## [64] "cornsilk1" "cornsilk2" "cornsilk3"
## [67] "cornsilk4" "cyan" "cyan1"
## [70] "cyan2" "cyan3" "cyan4"
## [73] "darkblue" "darkcyan" "darkgoldenrod"
## [76] "darkgoldenrod1" "darkgoldenrod2" "darkgoldenrod3"
## [79] "darkgoldenrod4" "darkgray" "darkgreen"
## [82] "darkgrey" "darkkhaki" "darkmagenta"
## [85] "darkolivegreen" "darkolivegreen1" "darkolivegreen2"
## [88] "darkolivegreen3" "darkolivegreen4" "darkorange"
## [91] "darkorange1" "darkorange2" "darkorange3"
## [94] "darkorange4" "darkorchid" "darkorchid1"
## [97] "darkorchid2" "darkorchid3" "darkorchid4"
## [100] "darkred" "darksalmon" "darkseagreen"
## [103] "darkseagreen1" "darkseagreen2" "darkseagreen3"
## [106] "darkseagreen4" "darkslateblue" "darkslategray"
## [109] "darkslategray1" "darkslategray2" "darkslategray3"
## [112] "darkslategray4" "darkslategrey" "darkturquoise"
## [115] "darkviolet" "deeppink" "deeppink1"
## [118] "deeppink2" "deeppink3" "deeppink4"
## [121] "deepskyblue" "deepskyblue1" "deepskyblue2"
## [124] "deepskyblue3" "deepskyblue4" "dimgray"
## [127] "dimgrey" "dodgerblue" "dodgerblue1"
## [130] "dodgerblue2" "dodgerblue3" "dodgerblue4"
## [133] "firebrick" "firebrick1" "firebrick2"
## [136] "firebrick3" "firebrick4" "floralwhite"
## [139] "forestgreen" "gainsboro" "ghostwhite"
## [142] "gold" "gold1" "gold2"
## [145] "gold3" "gold4" "goldenrod"
## [148] "goldenrod1" "goldenrod2" "goldenrod3"
## [151] "goldenrod4" "gray" "gray0"
## [154] "gray1" "gray2" "gray3"
## [157] "gray4" "gray5" "gray6"
## [160] "gray7" "gray8" "gray9"
## [163] "gray10" "gray11" "gray12"
## [166] "gray13" "gray14" "gray15"
## [169] "gray16" "gray17" "gray18"
## [172] "gray19" "gray20" "gray21"
## [175] "gray22" "gray23" "gray24"
## [178] "gray25" "gray26" "gray27"
## [181] "gray28" "gray29" "gray30"
## [184] "gray31" "gray32" "gray33"
## [187] "gray34" "gray35" "gray36"
## [190] "gray37" "gray38" "gray39"
## [193] "gray40" "gray41" "gray42"
## [196] "gray43" "gray44" "gray45"
## [199] "gray46" "gray47" "gray48"
## [202] "gray49" "gray50" "gray51"
## [205] "gray52" "gray53" "gray54"
## [208] "gray55" "gray56" "gray57"
## [211] "gray58" "gray59" "gray60"
## [214] "gray61" "gray62" "gray63"
## [217] "gray64" "gray65" "gray66"
## [220] "gray67" "gray68" "gray69"
## [223] "gray70" "gray71" "gray72"
## [226] "gray73" "gray74" "gray75"
## [229] "gray76" "gray77" "gray78"
## [232] "gray79" "gray80" "gray81"
## [235] "gray82" "gray83" "gray84"
## [238] "gray85" "gray86" "gray87"
## [241] "gray88" "gray89" "gray90"
## [244] "gray91" "gray92" "gray93"
## [247] "gray94" "gray95" "gray96"
## [250] "gray97" "gray98" "gray99"
## [253] "gray100" "green" "green1"
## [256] "green2" "green3" "green4"
## [259] "greenyellow" "grey" "grey0"
## [262] "grey1" "grey2" "grey3"
## [265] "grey4" "grey5" "grey6"
## [268] "grey7" "grey8" "grey9"
## [271] "grey10" "grey11" "grey12"
## [274] "grey13" "grey14" "grey15"
## [277] "grey16" "grey17" "grey18"
## [280] "grey19" "grey20" "grey21"
## [283] "grey22" "grey23" "grey24"
## [286] "grey25" "grey26" "grey27"
## [289] "grey28" "grey29" "grey30"
## [292] "grey31" "grey32" "grey33"
## [295] "grey34" "grey35" "grey36"
## [298] "grey37" "grey38" "grey39"
## [301] "grey40" "grey41" "grey42"
## [304] "grey43" "grey44" "grey45"
## [307] "grey46" "grey47" "grey48"
## [310] "grey49" "grey50" "grey51"
## [313] "grey52" "grey53" "grey54"
## [316] "grey55" "grey56" "grey57"
## [319] "grey58" "grey59" "grey60"
## [322] "grey61" "grey62" "grey63"
## [325] "grey64" "grey65" "grey66"
## [328] "grey67" "grey68" "grey69"
## [331] "grey70" "grey71" "grey72"
## [334] "grey73" "grey74" "grey75"
## [337] "grey76" "grey77" "grey78"
## [340] "grey79" "grey80" "grey81"
## [343] "grey82" "grey83" "grey84"
## [346] "grey85" "grey86" "grey87"
## [349] "grey88" "grey89" "grey90"
## [352] "grey91" "grey92" "grey93"
## [355] "grey94" "grey95" "grey96"
## [358] "grey97" "grey98" "grey99"
## [361] "grey100" "honeydew" "honeydew1"
## [364] "honeydew2" "honeydew3" "honeydew4"
## [367] "hotpink" "hotpink1" "hotpink2"
## [370] "hotpink3" "hotpink4" "indianred"
## [373] "indianred1" "indianred2" "indianred3"
## [376] "indianred4" "ivory" "ivory1"
## [379] "ivory2" "ivory3" "ivory4"
## [382] "khaki" "khaki1" "khaki2"
## [385] "khaki3" "khaki4" "lavender"
## [388] "lavenderblush" "lavenderblush1" "lavenderblush2"
## [391] "lavenderblush3" "lavenderblush4" "lawngreen"
## [394] "lemonchiffon" "lemonchiffon1" "lemonchiffon2"
## [397] "lemonchiffon3" "lemonchiffon4" "lightblue"
## [400] "lightblue1" "lightblue2" "lightblue3"
## [403] "lightblue4" "lightcoral" "lightcyan"
## [406] "lightcyan1" "lightcyan2" "lightcyan3"
## [409] "lightcyan4" "lightgoldenrod" "lightgoldenrod1"
## [412] "lightgoldenrod2" "lightgoldenrod3" "lightgoldenrod4"
## [415] "lightgoldenrodyellow" "lightgray" "lightgreen"
## [418] "lightgrey" "lightpink" "lightpink1"
## [421] "lightpink2" "lightpink3" "lightpink4"
## [424] "lightsalmon" "lightsalmon1" "lightsalmon2"
## [427] "lightsalmon3" "lightsalmon4" "lightseagreen"
## [430] "lightskyblue" "lightskyblue1" "lightskyblue2"
## [433] "lightskyblue3" "lightskyblue4" "lightslateblue"
## [436] "lightslategray" "lightslategrey" "lightsteelblue"
## [439] "lightsteelblue1" "lightsteelblue2" "lightsteelblue3"
## [442] "lightsteelblue4" "lightyellow" "lightyellow1"
## [445] "lightyellow2" "lightyellow3" "lightyellow4"
## [448] "limegreen" "linen" "magenta"
## [451] "magenta1" "magenta2" "magenta3"
## [454] "magenta4" "maroon" "maroon1"
## [457] "maroon2" "maroon3" "maroon4"
## [460] "mediumaquamarine" "mediumblue" "mediumorchid"
## [463] "mediumorchid1" "mediumorchid2" "mediumorchid3"
## [466] "mediumorchid4" "mediumpurple" "mediumpurple1"
## [469] "mediumpurple2" "mediumpurple3" "mediumpurple4"
## [472] "mediumseagreen" "mediumslateblue" "mediumspringgreen"
## [475] "mediumturquoise" "mediumvioletred" "midnightblue"
## [478] "mintcream" "mistyrose" "mistyrose1"
## [481] "mistyrose2" "mistyrose3" "mistyrose4"
## [484] "moccasin" "navajowhite" "navajowhite1"
## [487] "navajowhite2" "navajowhite3" "navajowhite4"
## [490] "navy" "navyblue" "oldlace"
## [493] "olivedrab" "olivedrab1" "olivedrab2"
## [496] "olivedrab3" "olivedrab4" "orange"
## [499] "orange1" "orange2" "orange3"
## [502] "orange4" "orangered" "orangered1"
## [505] "orangered2" "orangered3" "orangered4"
## [508] "orchid" "orchid1" "orchid2"
## [511] "orchid3" "orchid4" "palegoldenrod"
## [514] "palegreen" "palegreen1" "palegreen2"
## [517] "palegreen3" "palegreen4" "paleturquoise"
## [520] "paleturquoise1" "paleturquoise2" "paleturquoise3"
## [523] "paleturquoise4" "palevioletred" "palevioletred1"
## [526] "palevioletred2" "palevioletred3" "palevioletred4"
## [529] "papayawhip" "peachpuff" "peachpuff1"
## [532] "peachpuff2" "peachpuff3" "peachpuff4"
## [535] "peru" "pink" "pink1"
## [538] "pink2" "pink3" "pink4"
## [541] "plum" "plum1" "plum2"
## [544] "plum3" "plum4" "powderblue"
## [547] "purple" "purple1" "purple2"
## [550] "purple3" "purple4" "red"
## [553] "red1" "red2" "red3"
## [556] "red4" "rosybrown" "rosybrown1"
## [559] "rosybrown2" "rosybrown3" "rosybrown4"
## [562] "royalblue" "royalblue1" "royalblue2"
## [565] "royalblue3" "royalblue4" "saddlebrown"
## [568] "salmon" "salmon1" "salmon2"
## [571] "salmon3" "salmon4" "sandybrown"
## [574] "seagreen" "seagreen1" "seagreen2"
## [577] "seagreen3" "seagreen4" "seashell"
## [580] "seashell1" "seashell2" "seashell3"
## [583] "seashell4" "sienna" "sienna1"
## [586] "sienna2" "sienna3" "sienna4"
## [589] "skyblue" "skyblue1" "skyblue2"
## [592] "skyblue3" "skyblue4" "slateblue"
## [595] "slateblue1" "slateblue2" "slateblue3"
## [598] "slateblue4" "slategray" "slategray1"
## [601] "slategray2" "slategray3" "slategray4"
## [604] "slategrey" "snow" "snow1"
## [607] "snow2" "snow3" "snow4"
## [610] "springgreen" "springgreen1" "springgreen2"
## [613] "springgreen3" "springgreen4" "steelblue"
## [616] "steelblue1" "steelblue2" "steelblue3"
## [619] "steelblue4" "tan" "tan1"
## [622] "tan2" "tan3" "tan4"
## [625] "thistle" "thistle1" "thistle2"
## [628] "thistle3" "thistle4" "tomato"
## [631] "tomato1" "tomato2" "tomato3"
## [634] "tomato4" "turquoise" "turquoise1"
## [637] "turquoise2" "turquoise3" "turquoise4"
## [640] "violet" "violetred" "violetred1"
## [643] "violetred2" "violetred3" "violetred4"
## [646] "wheat" "wheat1" "wheat2"
## [649] "wheat3" "wheat4" "whitesmoke"
## [652] "yellow" "yellow1" "yellow2"
## [655] "yellow3" "yellow4" "yellowgreen"
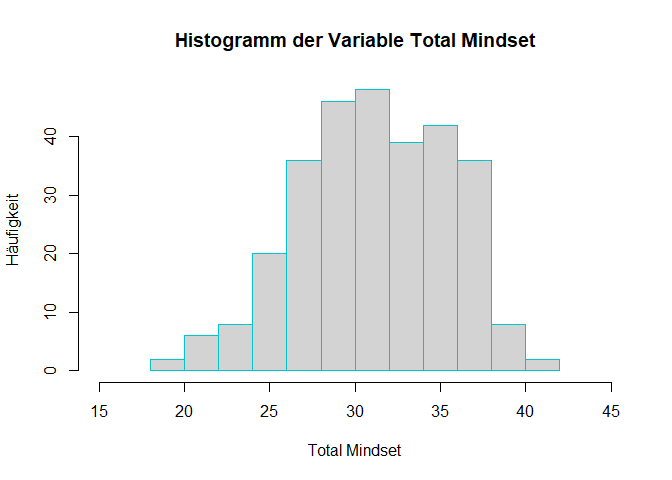
Es gibt verschiedene Versionen von Türkis. Ich entscheide mich hier an dieser Stelle für turquoise3.
# Histogramm mit angepasster Skalierung der x-Achse und Farbe der Umrandung
hist(data$Total_Mindset,
main = "Histogramm der Variable Total Mindset",
xlab = "Total Mindset",
ylab = "Häufigkeit",
xlim = c(15, 45),
border = "turquoise3")
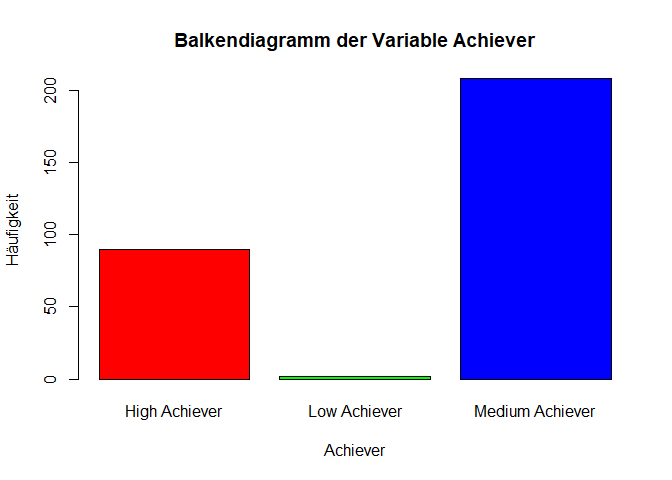
- Zeichnen Sie ein Balkendiagramm für die Variable
Achiever. Färben Sie dabei jeden Balken in einer der Regenbogenpaletterainbow().
Lösung
Zunächst einmal sollten wir uns anschauen, wie viele Kategorien die Variable Achiever hat. Dies kann mit der Funktion table() erreicht werden. Wenn man nicht selbst zählen möchte, kann man auch die Funktion length() nutzen, um die Anzahl der Kategorien zu erhalten.
###### Aufgabe 2 ------
table(data$Achiever) # Überblick über die Kategorien
##
## High Achiever Low Achiever Medium Achiever
## 90 2 208
length(table(data$Achiever)) # Anzahl der Kategorien
## [1] 3
Die Funktion barplot() wird genutzt, um ein Balkendiagramm zu erstellen. Die Farben der Balken werden mit col festgelegt. In der Funktion rainbow() wird die Anzahl der Farben angegeben, die genutzt werden sollen.
# Balkendiagramm mit Regenbogenfarben
barplot(table(data$Achiever),
main = "Balkendiagramm der Variable Achiever",
xlab = "Achiever",
ylab = "Häufigkeit",
col = rainbow(3))
- In der Funktion
boxplot()kann die Ausrichtung des Boxplots (vertikal, horizontal) und auch die Darstellung der Ausreißer verändert werden. Zeichnen Sie einen horizontalen Boxplot für die VariableTotal_Competence_Mathsund unterdrücken Sie die Darstellung der Ausreißer.
Lösung
Die passenden Argumente zur Aufgabe heißen horizontal und outline und können beide entweder auf TRUE oder FALSE gesetzt werden.
###### Aufgabe 3 ------
# Keine Darstellung der Ausreißer und horizontaler Boxplot
boxplot(data$Total_Competence_Maths,
main = "Boxplot der Variable Total Mindset",
horizontal = T,
outline = F)
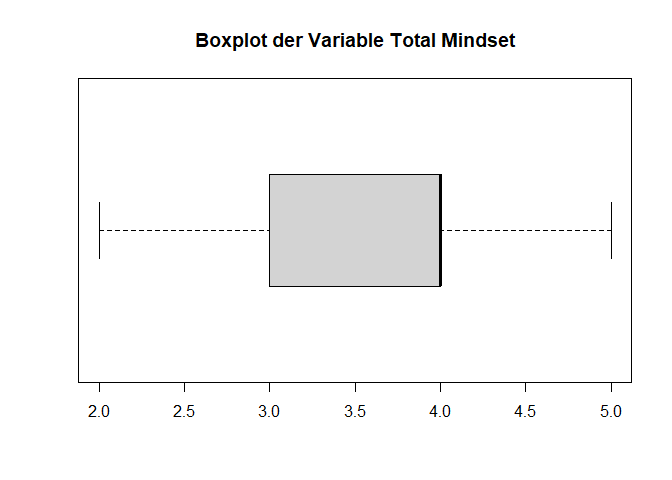
Wie wir sehen, geht der Boxplot jetzt nur von 2 bis 5 - die Zeichnung der Ausreißer mit dem Wert von 1 wurde unterdrückt.
- Zeichnen Sie einen Scatterplot für den Zusammenhang der Variablen
Total_MindsetundTotal_SelfConcept. Passen Sie die Form (Dreiecke) und Farbe der (Grün) der Punkte an.
Lösung
Die nötigen Argumente im plot() Befehl sind pch für die Form der Punkte und col für die Farbe der Punkte. Für Dreiecke muss das Argument pch auf 2 gesetzt werden. Grün ist eine der Basisfarben und kann direkt als Zeichenkette green übergeben werden.
###### Aufgabe 4 ------
# Scatterplot mit angepasster Form und Farbe der Punkte
plot(data$Total_Mindset,
data$Total_SelfConcept,
main = "Scatterplot der Variablen Total Mindset und Total SelfConcept",
xlab = "Total Mindset",
ylab = "Total SelfConcept",
pch = 2, # Form der Punkte
col = "green") # Farbe der Punkte
Teil 2 - Lineare Modelle
- In Teil 1 haben wir gelernt, dass die Funktion
boxplot()genutzt werden kann, um Boxplots zu erstellen. Erstellen Sie im Zusammenspiel mit der Syntax, die Sie in Teil 2 gelernt haben einen gruppierten Boxplot, der die Verteilung vonTotal_Competence_Mathsin den Gruppen vonGenderzeigt.
Lösung
Die Funktion boxplot() kann auch genutzt werden, um gruppierte Boxplots zu erstellen. Dazu wird die Variable, die gruppiert werden soll, als erstes Argument übergeben. Die Gruppierungsvariable wird als zweites Argument übergeben. Getrennt werden diese durch die auch in der Regression verwendeten ~.
##### Teil 2 -----
###### Aufgabe 1 ------
# Gruppierte Boxplots
boxplot(data$Total_Competence_Maths ~ data$Gender,
main = "Gruppierte Boxplots der Variable Total Competence Maths",
xlab = "Gender",
ylab = "Total Competence Maths")
- Erstellen Sie eine multiple Regression mit
Science_AttainmentDataals abhängiger Variable. Prädiktoren sollenTotal_CompetenceundTotal_Mindsetsein. Wie ist das Regressionsgewicht vonTotal_Competencein diesem Fall und welcher p-Wert wird ihm zugeschrieben?
Lösung
Die Funktion lm() wird genutzt, um ein Regressionsmodell zu erstellen. Die abhängige Variable wird als erstes Argument übergeben, die Prädiktoren als zweites Argument. Getrennt werden diese durch ~.
###### Aufgabe 2 ------
# Regressionsmodell aufstellen
mod <- lm(Total_Competence_Science ~ Total_Competence + Total_Mindset, data = data)
Um die weiteren Informationen zu erhalten, wird die Funktion summary() genutzt.
summary(mod) # Zusammenfassung des Modells
##
## Call:
## lm(formula = Total_Competence_Science ~ Total_Competence + Total_Mindset,
## data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.05869 -0.44840 -0.05825 0.46769 1.94088
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.842347 0.301379 -2.795 0.00554 **
## Total_Competence 1.166508 0.061782 18.881 < 2e-16 ***
## Total_Mindset 0.000437 0.009357 0.047 0.96278
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.6541 on 288 degrees of freedom
## (9 Beobachtungen als fehlend gelöscht)
## Multiple R-squared: 0.589, Adjusted R-squared: 0.5862
## F-statistic: 206.4 on 2 and 288 DF, p-value: < 2.2e-16
- Finden Sie mit Hilfe des Internets heraus, wie standardisierte Regressionsparameter mit Hilfe einer Funktion aus einem noch nicht verwendeten Paket ausgegeben werden können.
Lösung
Die Funktion lm.beta() aus dem Paket lm.beta kann genutzt werden, um standardisierte Regressionsparameter zu erhalten. Zuerst muss das Paket installiert werden.
###### Aufgabe 3 ------
install.packages("lm.beta") # Paket installieren
Anschließend kann das Paket aktiviert werden.
library(lm.beta) # Paket laden
## Warning: Paket 'lm.beta' wurde unter R Version 4.3.1 erstellt
Mit der Funktion lm.beta() kann das Modell analysiert werden. Am besten sollte noch die Funktion summary() genutzt werden, um die Ergebnisse übersichtlich darzustellen.
mod |> lm.beta() |> summary() # Standardisierte Regressionsparameter
##
## Call:
## lm(formula = Total_Competence_Science ~ Total_Competence + Total_Mindset,
## data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.05869 -0.44840 -0.05825 0.46769 1.94088
##
## Coefficients:
## Estimate Standardized Std. Error t value Pr(>|t|)
## (Intercept) -0.842347 NA 0.301379 -2.795 0.00554 **
## Total_Competence 1.166508 0.766795 0.061782 18.881 < 2e-16 ***
## Total_Mindset 0.000437 0.001897 0.009357 0.047 0.96278
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.6541 on 288 degrees of freedom
## (9 Beobachtungen als fehlend gelöscht)
## Multiple R-squared: 0.589, Adjusted R-squared: 0.5862
## F-statistic: 206.4 on 2 and 288 DF, p-value: < 2.2e-16
Der Output aus der Funktion summary() hat sich bei den Koeffizienten um eine Zeile erweitert.
- Diese Aufgabe ist nur zur Veranschaulichung der Syntax - keine Empfehlung für solch ein Modell: Als zuästzlicher Prädiktor soll
Total_SelfConcepthinzugefügt werden. Außerdem soll die Dreifachinteraktion der Prädiktoren aufgenommen werden, aber keine Interaktionen zwischen zwei Prädiktoren.
Lösung
Hier lohnt es sich zunächst, zentrierte Versionen der Prädiktoren zu erstellen.
###### Aufgabe 4 ------
# Zentrierte Prädiktoren erstellen
data$Total_Competence_center <- scale(data$Total_Competence, center = T, scale = F)
data$Total_Mindset_center <- scale(data$Total_Mindset, center = T, scale = F)
data$Total_SelfConcept_center <- scale(data$Total_SelfConcept, center = T, scale = F)
Die Funktion lm() wird genutzt, um das Modell zu erstellen. Wenn wir die *-Notation nutzen, werden alle Interaktionen bis zur dritten Ordnung aufgenommen.
# Modell mit Interaktionen bis zur dritten Ordnung
mod_falsch <- lm(Total_Competence_Science ~ Total_Competence_center * Total_Mindset_center * Total_SelfConcept_center, data = data)
In der Aufgabenstellung ist explizit nur die Interaktion der dritten Ordnung gewünscht. Daher sollte die :-Notation genutzt werden.
# Modell mit den spezifisch gewünschten Interaktionen
mod_korrekt <- lm(Total_Competence_Science ~ Total_Competence_center + Total_Mindset_center + Total_SelfConcept_center + Total_Competence_center:Total_Mindset_center:Total_SelfConcept_center, data = data)
Anmerkung: Es ist empfehlenswert, keine Modelle zu bestimmen, in denen Interaktionen niedrigerer Ordnung nicht drin sind. Wie gesagt war das Beispiel nur zur Veranschaulichung der Syntax.
](/media/header/rice-field.jpg)