Einleitende Worte
Der Beitrag umfasst die Inhalte des R-Workshops (Re)Start für Fortgeschrittene. Dieser wurde für angehende Psychologie und KliPPs Masterstudierende konzipiert mit dem Ziel, die im Bachelor Psychologie erworbenen Grundkenntnisse aufzufrischen und zu vertiefen. Die hierin behandelten Inhalte sind ausführlich in Statistik I und Statistik II nachzulesen.
Lernziele
In diesem Workshop wollen wir zentrale R-Kenntnisse auffrischen und vertiefen, damit ihr im Masterstudium sicher mit R arbeiten könnt. Ziel ist es, dass ihr euch in den statistischen Veranstaltungen auf die inhaltlichen Konzepte konzentrieren könnt - möglichst ohne dabei in Schwierigkeiten bei der technischen Umsetzung zu geraten.
Im Unterschied zu dem parallelen Workshop für Einsteiger*innen ohne Vorkenntnisse liegt der Fokus in diesem Beitrag auf einem vor vorneherein datenorientierten Arbeiten mit R. Wir knüpfen an euer vorhandenes Wissen and und zeigen, wie ihr R im Praxiskontext nutzen könnt, um psychologische Forschungsfragen zu beantworten. Dazu gehören zentrale Schritte wie
- Einlesen von Daten
- Datenaufbereitung
- Deskriptive Analyse
- Inferenzstatistische Analyse
- Datenvisualisierung und Kommunikation von Ergebnissen
Diese werden im Laufe des Workshops Schritt für Schritt behandelt.
Warum R?
R ist…
- kostenlos
- extrem weit verbreitet
- mit jedem teilbar
- etc.
R(-Studio) installieren oder updaten
Obwohl die “Basis” R-Software schon zur Nutzung der gleichnamigen Programmiersprache befähigt, verwenden wir aufgrund der höheren Nutzerfreundlichkeit die integrierte Entwicklungsumgebung RStudio. Beide sind kostenlos erhältlich und sollten regelmäßig aktualisiert werden. Letzteres funktioniert in beiden Fällen über eine Neuinstallation. Bei Posit findet ihr eine übersichtliche Anleitung sowie die Downloadlinks zu R und R-Studio.
Hier klicken, um zu Posit zu gelangen
Aufbau von RStudio
RStudio besteht aus vier Panels. Oben links befindet sich nach Öffnen einer neuen Skriptdatei (Strg+Shift+n (Mac OS: Cmd+Shift+n) oder über den New File Button) das Skript. Sämtlicher Code den ihr am Ende abspeichern wollt sollte hier landen. Mit Strg+Return (Mac OS: Cmd+Return) oder dem Run Button könnt ihr die Zeile in der sich euer Cursor befindet ausführen. Einer der wichtigsten Keyboard Shortcuts (dt. Tastenkürzel) in ganz R-Studio lautet Strg+Alt+B (Mac OS: Opt+Cmd+B). Hiermit führt ihr sämtlichen Code bis zu eurem Cursor aus. Die Resultate erscheinen unten links in der Konsole. Oben Rechts finden Sie das Environment. Dies sollte zu Beginn des Workshops noch leer sein und sich im Laufe des Tages mit Datensätzen und Objekten füllen. Zuguterletzt befindet sich unten rechts ein Panel mit mehreren Tabs. Unter Files könnt ihr durch Ordner Datein aufindig machen. Grafische Darstellungen erfolgen im Plots Tab. Unter Packages erhaltet ihr eine Übersicht der installierten Erweiterungen für R. Der wohl wichtigste Tab ist der Help Tab. In diesem erhaltet ihr Hilfe zu R-Funktionen und Packages.
R-Studio Settings
Mit den vielen Personalisierungsoptionen in R-Studio könnt ihr eure Arbeitsumgebung ganz nach eurem Geschmack gestalten (und nebenbei euren Code besser lesbar machen, was die Arbeit in R-Studio insgesamt angenehmer macht). Hier ein kurzer Überblick nützlicher Einstellungen und wo man diese findet:
| Einstellung | Änderung | Beschreibung |
|---|---|---|
| Font Size | Tools>Global Options>Appearance>Font Size | Anpassen der Schriftgröße |
| Theme | Tools>Global Options>Appearance>Theme | Themes beeinflussen Hintergrund- und Schriftfarbe. Idealerweise sollte ein Theme gewählt werden, welches hilft, die Syntax besser zu überblicken. |
| Rainbow Parentheses | Tools>Global Options>Code>Display>Syntax>Use Rainbow Parentheses | Zusammengehörige Klammern erhalten dieselbe Farbe. Hilft bei der Übersichtlichkeit. |
| Indentation Guidelines | Tools>Global Options>Code>Display>General>Indentation Guidelines | Die eingerückte Fläche wird farbig markiert. Hilft beim Überblick. |
Selbstverständlich gibt es noch etliche weitere Personalisierungsoptionen. Hierrein kann man sehr viel Zeit investieren. Schaut euch doch mal bei Gelegenheit um.
R Begriffserklärungen
Bevor wir nun endlich in die Daten abtauchen wollen wir ein paar Begriffe klären die die Arbeit mit R grundlegend definieren.
Funktionen
Funktionen ermöglichen es uns bestimmte Code Abläufe effizient über verschiedene Skripte wiederzuverwenden. Natürlich könnte man den Mittelwert einer Datenmenge manuell berechnen, mit der darauf ausgerichteten Funktion geht es jedoch schneller.
(34+47+23+90+23+45+89+98)/8
## [1] 56.125
mean(c(34,47,23,90,23,45,89,98))
## [1] 56.125
Dabei verwenden wir anfangs meist vordefinierte Funktionen die in R bereits enthalten sind oder wir über Pakete einladen können. Später schauen wir uns auch mal eigens definierte Funktionen an.
Objekte
Während es uns Funktionen erlauben Code Abläufe in verschiedenen Skripten wiederzuverwenden, erlauben uns Objekte Zwischenergebnisse in einem Skript abzuspeichern und wenn benötigt aufzurufen. Der Zuweisungspfeil (Alt+- (Mac OS: Opt+-)) weist dem von uns frei bennenbaren Objekt ein Ergebnis zu.
mw <- mean(c(34,47,23,90,23,45,89,98))
mw
## [1] 56.125
Operatoren
Das R wie ein Taschenrechner benutzt werden kann sollte bekannt sein. An dieser Stelle wollen wir einen besonderen Operator vorstellen und zwar die Pipe |> (Shift+Strg+M (Mac OS: Shift+Cmd+M)).
mw <- c(34,47,23,90,23,45,89,98) |> mean()
mw
## [1] 56.125
Diese erlaubt es uns komplexe Verschachtlungen von Funktionen zu umgehen und macht den Code etwas lesbarer.
Environment
Im Environment finden wir unsere erstellten Objekte wieder. Gleichzeitig werden hier, je nach Objekttyp ein paar Informationen aufgelistet. Das komplette Environment können wir uns mit ls() ausgeben lassen.
ls()
[1] "mw"
Derzeit sollte sich dort nur unser abgespeicherter Mittelwert (mw = 56.125) befinden.
Richtig praktisch wird ls() erst in Kombination mit einer weiteren Funktion. Mit
rm(list = ls())
könnt ihr das gesamte Environment leeren. Es ist empfehlenswert diesen Befehl an den Anfang jedes Skripts zu schreiben, so startet ihr jedes Skript von null und vermeidet Probleme, die entstehen können, wenn Variablen versehentlich mehrfach überschrieben werden. Ein solches Beispiel schauen wir uns später noch an.
Vor dem Schließen der Software fragt R-Studio häufig, ob man das Environment speichern will.
Dagegen spricht:
Übersichtlichkeit: es ist angenehmer mit einer leeren Umgebung zu beginnen.
Man prüft direkt ob die Ergebnisse auch für andere reproduzierbar sind. Alles Nötige sollte im Skript passieren.
Die Help Page
Bevor wir mit den Daten starten, noch ein letzter Hinweis: Die Help Page kann euch eine große Hilfe sein, insbesondere, wenn ihr euch in den Tiefen von R zurechtfinden möchtet.
Ihr erreicht sie durch:
?funktionsname()help(Funktionsname)über die Suchfunktion des Help-Tabs
F1 Drücken während der Cursor sich über der Funktion befindet
Bestandteile der Help Funktion
| Abschnitt | Inhalt |
|---|---|
| Description | Beschreibung der Funktion |
| Usage | Zeigt die Argumente an, die die Funktion entgegennimmt. Argumente auf die ein = folgt haben Standardeinstellungen und müssen nicht jedes mal aufs Neue definiert werden, Argumente ohne = jedoch schon. |
| Arguments | Liste der Argumente mit Beschreibung |
| Details | Zusatzinformationen zur Funktion |
| Values | Übersicht über die möglichen Ergebnisinhalte der Funktion |
| See also | Ähnliche Funktionen |
| Examples | Praxisbeispiel, Funktion wird angewendet |
Download der Daten
Für den Workshop nutzen wir Daten aus einer Bachelorarbeit in der Sozialpsychologie an der Goethe-Universität. Ihr könnt die Daten über die LIFOS-Plattform herunterladen. Dafür müsst ihr euch zunächst mit eurem HRZ-Account einloggen. Anschließend sollten die Daten automatisch heruntergeladen werden. Speichert die Datei am besten in einem neuen Ordner an einem geeigneten Ort auf eurem Laptop, damit ihr während und nach dem Workshop problemlos darauf zugreifen könnt.
Working Directory Einrichten
Wie ihr euch vielleicht erinnert, arbeitet R mit einem Arbeitsverzeichnis (Working Directory). Das ist der Ordner, in dem R standardmäßig Dateien speichert oder lädt. Mit folgendem Befehl könnt ihr euer aktuelles Working Directory einsehen:
getwd()
/Users/luca/Desktop
In meinem Fall liegt das Standard-Verzeichnis auf dem Desktop. Als nächstes legen wir das Working Directory auf den Ordner fest, in dem wir die Daten von LIFOS gespeichert haben:
setwd("/Users/luca/Desktop/rworkshop2025")
Bei mir befindet sich dieser Ordner rworkshop2025 auf dem Desktop. Wenn ihr mit Windows Betriebssystem arbeitet, müsst ihr den Pfad etwas anders angeben, z.B.:
setwd("C:/Users/luca/workshop2025")
Achtet darauf, normale Slashes / zu verwenden, nicht die Windows-typischen Backslashes \.
Daten einlesen
Bevor wir die Daten in R importieren, lohnt sich ein kurzer Blick auf die Rohdaten. Öffnet die CSV-Datei z. B. in einem Texteditor, um zu prüfen, wie sie aufgebaut ist. Ihr seht dort, dass die Werte durch Semikolons (;) getrennt sind und die erste Zeile die Spaltennamen enthält.
Nachdem ihr euch einen Überblick verschafft habt, könnt ihr die Daten mit der Funktion read.csv() einlesen. Wenn ihr euch unsicher seid, welche Argumente benötigt werden, hilft ein Blick in die Dokumentation – entweder mit ?read.csv oder help(read.csv).
data_raw <- read.csv(
file = "data_raw.csv", # Filename
na.strings = c("", "NA", "-9"), # -9 als fehlender Wert kodieren
header = TRUE, # Header für Spaltennamen
sep = ";" # Semikolon als Separator
)
Mit dem Argument na.strings können wir festlegen, welche Werte in den Daten als fehlende Werte interpretiert werden sollen. In unserem Fall sind das leere Zellen, “NA” und “-9” — letztere ist eine gängige Kodierung in SoSci-Survey, mit welcher die Studie erhoben wurde.
Überblick über die Daten
Um einen ersten Eindruck von unseren Daten zu bekommen, können wir verschiedene Basisfunktionen nutzen, die uns auch im weiteren Verlauf der Analyse begleiten werden:
class(data_raw) # Klasse des Objekts
## [1] "data.frame"
dim(data_raw) # Dimensionen des Datensatzes (Zeilen + Spalten)
## [1] 233 67
head(data_raw, n = 1) # ersten Zeilen ausgeben
## CASE
## 1 Interview-Nummer (fortlaufend)
## SERIAL
## 1 Personenkennung oder Teilnahmecode (sofern verwendet)
## REF
## 1 Referenz (sofern im Link angegeben)
## QUESTNNR
## 1 Fragebogen, der im Interview verwendet wurde
## MODE
## 1 Interview-Modus
## STARTED
## 1 Zeitpunkt zu dem das Interview begonnen hat (Europe/Berlin)
## DDM_AV_1
## 1 DDM-AV-AP: Ich versuche, riskante Entscheidungen zu vermeiden.
## DDM_AV_2
## 1 DDM-AV-AP: Ich \xfcberlasse riskante Entscheidungen gerne anderen.
## DDM_AV_3
## 1 DDM-AV-AP: Es ist mir unangenehm, Entscheidungen zu treffen, deren Folgen ich nicht absehen kann.
## DDM_AV_4
## 1 DDM-AV-AP: Die Unternehmensleitung sollte alle risikoreichen Entscheidungen treffen.
## DDM_AV_5
## 1 DDM-AV-AP: Ich stimme Entscheidungen grunds\xe4tzlich mit meiner F\xfchrungskraft ab.
## DDM_AP_1
## 1 DDM-AV-AP: Ich treffe riskante Entscheidungen, wenn ich das Gef\xfchl habe, dass sie richtig sind.
## DDM_AP_2
## 1 DDM-AV-AP: Ich treffe Entscheidungen, auch wenn ich nicht alle Folgen vorhersehen kann.
## DDM_AP_3
## 1 DDM-AV-AP: F\xfcr eine erfolgreiche Karriere muss man gelegentlich riskante Entscheidungen treffen.
## DDM_AP_4
## 1 DDM-AV-AP: Um innovative Ideen zu verwirklichen, ist es wichtig, Entscheidungen zu treffen, auch wenn sie mit einem gewissen Risiko verbunden sind.
## DDM_AP_5
## 1 DDM-AV-AP: Ich habe den Mut, Entscheidungen zu treffen, auch wenn sie f\xfcr mich mit einem gewissen Risiko verbunden sind.
## DDM_SI
## 1 DDM-SI: [01]
## EL_01
## 1 EL: ... \xfcbertr\xe4gt mir viel Verantwortung.
## EL_02
## 1 EL: ... macht mich f\xfcr mein eigenes Handeln verantwortlich.
## EL_03
## 1 EL: ... fragt mich um Rat, wenn Entscheidungen getroffen werden.
## EL_04
## 1 EL: ... bezieht meine Vorschl\xe4ge und Ideen bei Entscheidungen mit ein.
## EL_05
## 1 EL: ... kontrolliert viele meiner Aktivit\xe4ten.
## EL_06
## 1 EL: ... ermutigt mich, die Kontrolle \xfcber meine Arbeit zu \xfcbernehmen.
## EL_07
## 1 EL: ... erlaubt mir, meine eigenen Ziele zu setzen.
## EL_08
## 1 EL: ... ermutigt mich, eigene Ziele zu entwickeln.
## EL_09
## 1 EL: ... greift nicht ein, wenn ich Schwierigkeiten bei der Erbringung von Leistungen habe, sondern l\xe4sst mich selbstst\xe4ndig daran arbeiten.
## EL_10
## 1 EL: ... ermutigt mich, die Ursachen und L\xf6sungen meiner Probleme selbst zu finden.
## EL_11
## 1 EL: ... fordert mich dazu auf, hohe Erwartungen an mich selbst zu haben.
## EL_12
## 1 EL: ... ermutigt mich, H\xf6chstleistungen anzustreben.
## EL_13
## 1 EL: ... vertraut mir.
## EL_14
## 1 EL: ... ist \xfcberzeugt von meinen F\xe4higkeiten.
## PE_ME1
## 1 PE: Die Arbeit, die ich mache, ist mir sehr wichtig.
## PE_ME2
## 1 PE: Meine beruflichen T\xe4tigkeiten sind f\xfcr mich pers\xf6nlich bedeutsam.
## PE_ME3
## 1 PE: Die Arbeit, die ich mache, bedeutet mir viel.
## PE_CO1
## 1 PE: Ich vertraue in meine F\xe4higkeit, meine Arbeit gutzumachen.
## PE_CO2
## 1 PE: Ich f\xfchle mich selbstbewusst, wenn es darum geht, meine Arbeit zu erledigen.
## PE_CO3
## 1 PE: Ich beherrsche die f\xfcr meine Arbeit erforderlichen F\xe4higkeiten.
## PE_SD1
## 1 PE: Ich kann in hohem Ma\xdfe selbst bestimmen, wie ich meine Arbeit erledige.
## PE_SD2
## 1 PE: Ich kann selbst entscheiden, wie ich meine Aufgaben angehe.
## PE_SD3
## 1 PE: Ich verf\xfcge \xfcber ein hohes Ma\xdf an Selbstst\xe4ndigkeit und Freiraum bei der Ausf\xfchrung meiner Arbeit.
## K
## 1 PE: Bitte w\xe4hlen Sie die Antwortoption "stimme \xfcberhaupt nicht zu" aus.
## PE_IM1
## 1 PE: Mein Einfluss darauf, was in meiner Abteilung passiert, ist gro\xdf.
## PE_IM2
## 1 PE: Ich habe viel Kontrolle dar\xfcber, was in meiner Abteilung geschieht.
## PE_IM3
## 1 PE: Ich habe bedeutenden Einfluss darauf, was in meiner Abteilung passiert.
## ET
## 1 Erwerbst\xe4tig
## AZ
## 1 Dauer w\xf6chentliche Arbeit: [01]
## FK EN
## 1 Direkter Vorgesetzter Entscheidungen
## ALT WMD
## 1 Alter: Ich bin ... Jahre alt. Geschlecht
## TIME001 TIME002
## 1 Verweildauer Seite 1 Verweildauer Seite 2
## TIME003 TIME004
## 1 Verweildauer Seite 3 Verweildauer Seite 4
## TIME005 TIME006
## 1 Verweildauer Seite 5 Verweildauer Seite 6
## TIME_SUM
## 1 Verweildauer gesamt (ohne Ausrei\xdfer)
## MAILSENT
## 1 Versandzeitpunkt der Einladungsmail (nur f\xfcr nicht-anonyme Adressaten)
## LASTDATA
## 1 Zeitpunkt als der Datensatz das letzte mal ge\xe4ndert wurde
## STATUS
## 1 Status des Interviews (Markierung)
## FINISHED
## 1 Wurde die Befragung abgeschlossen (letzte Seite erreicht)?
## Q_VIEWER
## 1 Hat der Teilnehmer den Fragebogen nur angesehen, ohne die Pflichtfragen zu beantworten?
## LASTPAGE
## 1 Seite, die der Teilnehmer zuletzt bearbeitet hat
## MAXPAGE
## 1 Letzte Seite, die im Fragebogen bearbeitet wurde
## MISSING
## 1 Anteil fehlender Antworten in Prozent
## MISSREL
## 1 Anteil fehlender Antworten (gewichtet nach Relevanz)
## TIME_RSI
## 1 Ausf\xfcll-Geschwindigkeit (relativ)
tail(data_raw, n = 1) # letzten Zeilen ausgeben
## CASE SERIAL REF QUESTNNR MODE
## 233 1575 <NA> <NA> base interview
## STARTED DDM_AV_1 DDM_AV_2
## 233 2025-06-05 09:44:33 6 4
## DDM_AV_3 DDM_AV_4 DDM_AV_5 DDM_AP_1
## 233 6 5 6 5
## DDM_AP_2 DDM_AP_3 DDM_AP_4 DDM_AP_5
## 233 3 4 4 3
## DDM_SI EL_01 EL_02 EL_03 EL_04 EL_05
## 233 4 6 4 3 2 3
## EL_06 EL_07 EL_08 EL_09 EL_10 EL_11
## 233 4 6 6 6 6 4
## EL_12 EL_13 EL_14 PE_ME1 PE_ME2 PE_ME3
## 233 4 5 5 4 5 4
## PE_CO1 PE_CO2 PE_CO3 PE_SD1 PE_SD2
## 233 6 5 7 7 7
## PE_SD3 K PE_IM1 PE_IM2 PE_IM3 ET AZ FK
## 233 7 1 2 4 3 1 16 1
## EN ALT WMD TIME001 TIME002 TIME003
## 233 1 22 1 5 52 21
## TIME004 TIME005 TIME006 TIME_SUM
## 233 52 74 35 239
## MAILSENT LASTDATA STATUS
## 233 <NA> 2025-06-05 09:48:32 <NA>
## FINISHED Q_VIEWER LASTPAGE MAXPAGE
## 233 1 0 6 6
## MISSING MISSREL TIME_RSI
## 233 0 0 1,74
str(data_raw, vec.len = 2) # Struktur des Datensatzes
## 'data.frame': 233 obs. of 67 variables:
## $ CASE : chr "Interview-Nummer (fortlaufend)" "72" ...
## $ SERIAL : chr "Personenkennung oder Teilnahmecode (sofern verwendet)" NA ...
## $ REF : chr "Referenz (sofern im Link angegeben)" NA ...
## $ QUESTNNR: chr "Fragebogen, der im Interview verwendet wurde" "base" ...
## $ MODE : chr "Interview-Modus" "interview" ...
## $ STARTED : chr "Zeitpunkt zu dem das Interview begonnen hat (Europe/Berlin)" "2025-05-07 15:03:31" ...
## $ DDM_AV_1: chr "DDM-AV-AP: Ich versuche, riskante Entscheidungen zu vermeiden." "5" ...
## $ DDM_AV_2: chr "DDM-AV-AP: Ich \xfcberlasse riskante Entscheidungen gerne anderen." "5" ...
## $ DDM_AV_3: chr "DDM-AV-AP: Es ist mir unangenehm, Entscheidungen zu treffen, deren Folgen ich nicht absehen kann." "5" ...
## $ DDM_AV_4: chr "DDM-AV-AP: Die Unternehmensleitung sollte alle risikoreichen Entscheidungen treffen." "4" ...
## $ DDM_AV_5: chr "DDM-AV-AP: Ich stimme Entscheidungen grunds\xe4tzlich mit meiner F\xfchrungskraft ab." "5" ...
## $ DDM_AP_1: chr "DDM-AV-AP: Ich treffe riskante Entscheidungen, wenn ich das Gef\xfchl habe, dass sie richtig sind." "6" ...
## $ DDM_AP_2: chr "DDM-AV-AP: Ich treffe Entscheidungen, auch wenn ich nicht alle Folgen vorhersehen kann." "6" ...
## $ DDM_AP_3: chr "DDM-AV-AP: F\xfcr eine erfolgreiche Karriere muss man gelegentlich riskante Entscheidungen treffen." "6" ...
## $ DDM_AP_4: chr "DDM-AV-AP: Um innovative Ideen zu verwirklichen, ist es wichtig, Entscheidungen zu treffen, auch wenn sie mit e"| __truncated__ "6" ...
## $ DDM_AP_5: chr "DDM-AV-AP: Ich habe den Mut, Entscheidungen zu treffen, auch wenn sie f\xfcr mich mit einem gewissen Risiko verbunden sind." "6" ...
## $ DDM_SI : chr "DDM-SI: [01]" "4" ...
## $ EL_01 : chr "EL: ... \xfcbertr\xe4gt mir viel Verantwortung." "7" ...
## $ EL_02 : chr "EL: ... macht mich f\xfcr mein eigenes Handeln verantwortlich." "5" ...
## $ EL_03 : chr "EL: ... fragt mich um Rat, wenn Entscheidungen getroffen werden." "6" ...
## $ EL_04 : chr "EL: ... bezieht meine Vorschl\xe4ge und Ideen bei Entscheidungen mit ein." "7" ...
## $ EL_05 : chr "EL: ... kontrolliert viele meiner Aktivit\xe4ten." "2" ...
## $ EL_06 : chr "EL: ... ermutigt mich, die Kontrolle \xfcber meine Arbeit zu \xfcbernehmen." "7" ...
## $ EL_07 : chr "EL: ... erlaubt mir, meine eigenen Ziele zu setzen." "7" ...
## $ EL_08 : chr "EL: ... ermutigt mich, eigene Ziele zu entwickeln." "7" ...
## $ EL_09 : chr "EL: ... greift nicht ein, wenn ich Schwierigkeiten bei der Erbringung von Leistungen habe, sondern l\xe4sst mich selbstst\xe4nd "6" ...
## $ EL_10 : chr "EL: ... ermutigt mich, die Ursachen und L\xf6sungen meiner Probleme selbst zu finden." "6" ...
## $ EL_11 : chr "EL: ... fordert mich dazu auf, hohe Erwartungen an mich selbst zu haben." "6" ...
## $ EL_12 : chr "EL: ... ermutigt mich, H\xf6chstleistungen anzustreben." "6" ...
## $ EL_13 : chr "EL: ... vertraut mir." "7" ...
## $ EL_14 : chr "EL: ... ist \xfcberzeugt von meinen F\xe4higkeiten." "7" ...
## $ PE_ME1 : chr "PE: Die Arbeit, die ich mache, ist mir sehr wichtig." "7" ...
## $ PE_ME2 : chr "PE: Meine beruflichen T\xe4tigkeiten sind f\xfcr mich pers\xf6nlich bedeutsam." "6" ...
## $ PE_ME3 : chr "PE: Die Arbeit, die ich mache, bedeutet mir viel." "7" ...
## $ PE_CO1 : chr "PE: Ich vertraue in meine F\xe4higkeit, meine Arbeit gutzumachen." "7" ...
## $ PE_CO2 : chr "PE: Ich f\xfchle mich selbstbewusst, wenn es darum geht, meine Arbeit zu erledigen." "7" ...
## $ PE_CO3 : chr "PE: Ich beherrsche die f\xfcr meine Arbeit erforderlichen F\xe4higkeiten." "7" ...
## $ PE_SD1 : chr "PE: Ich kann in hohem Ma\xdfe selbst bestimmen, wie ich meine Arbeit erledige." "6" ...
## $ PE_SD2 : chr "PE: Ich kann selbst entscheiden, wie ich meine Aufgaben angehe." "7" ...
## $ PE_SD3 : chr "PE: Ich verf\xfcge \xfcber ein hohes Ma\xdf an Selbstst\xe4ndigkeit und Freiraum bei der Ausf\xfchrung meiner Arbeit." "7" ...
## $ K : chr "PE: Bitte w\xe4hlen Sie die Antwortoption \"stimme \xfcberhaupt nicht zu\" aus." "1" ...
## $ PE_IM1 : chr "PE: Mein Einfluss darauf, was in meiner Abteilung passiert, ist gro\xdf." "5" ...
## $ PE_IM2 : chr "PE: Ich habe viel Kontrolle dar\xfcber, was in meiner Abteilung geschieht." "7" ...
## $ PE_IM3 : chr "PE: Ich habe bedeutenden Einfluss darauf, was in meiner Abteilung passiert." "6" ...
## $ ET : chr "Erwerbst\xe4tig" "1" ...
## $ AZ : chr "Dauer w\xf6chentliche Arbeit: [01]" "20" ...
## $ FK : chr "Direkter Vorgesetzter" "1" ...
## $ EN : chr "Entscheidungen" "1" ...
## $ ALT : chr "Alter: Ich bin ... Jahre alt." "47" ...
## $ WMD : chr "Geschlecht" "1" ...
## $ TIME001 : chr "Verweildauer Seite 1" "57" ...
## $ TIME002 : chr "Verweildauer Seite 2" "147" ...
## $ TIME003 : chr "Verweildauer Seite 3" "47" ...
## $ TIME004 : chr "Verweildauer Seite 4" "87" ...
## $ TIME005 : chr "Verweildauer Seite 5" "69" ...
## $ TIME006 : chr "Verweildauer Seite 6" "73" ...
## $ TIME_SUM: chr "Verweildauer gesamt (ohne Ausrei\xdfer)" "480" ...
## $ MAILSENT: chr "Versandzeitpunkt der Einladungsmail (nur f\xfcr nicht-anonyme Adressaten)" NA ...
## $ LASTDATA: chr "Zeitpunkt als der Datensatz das letzte mal ge\xe4ndert wurde" "2025-05-07 15:11:31" ...
## $ STATUS : chr "Status des Interviews (Markierung)" NA ...
## $ FINISHED: chr "Wurde die Befragung abgeschlossen (letzte Seite erreicht)?" "1" ...
## $ Q_VIEWER: chr "Hat der Teilnehmer den Fragebogen nur angesehen, ohne die Pflichtfragen zu beantworten?" "0" ...
## $ LASTPAGE: chr "Seite, die der Teilnehmer zuletzt bearbeitet hat" "6" ...
## $ MAXPAGE : chr "Letzte Seite, die im Fragebogen bearbeitet wurde" "6" ...
## $ MISSING : chr "Anteil fehlender Antworten in Prozent" "0" ...
## $ MISSREL : chr "Anteil fehlender Antworten (gewichtet nach Relevanz)" "0" ...
## $ TIME_RSI: chr "Ausf\xfcll-Geschwindigkeit (relativ)" "0,76" ...
Mit dem glimpse() Befehl aus dem dplyr-Paket erhalten wir eine noch etwas übersichtlichere Darstellung der Datenstruktur als mit dem str() Befehl. Wenn ihr das Paket noch nicht installiert haben solltet, könnt ihr es mit install.packages("dplyr") herunterladen.
# install.packages("dplyr") # Nur einmalig nötig
library(dplyr)
glimpse(data_raw)
## Rows: 233
## Columns: 67
## $ CASE <chr> "Interview-Nummer (fortlau…
## $ SERIAL <chr> "Personenkennung oder Teil…
## $ REF <chr> "Referenz (sofern im Link …
## $ QUESTNNR <chr> "Fragebogen, der im Interv…
## $ MODE <chr> "Interview-Modus", "interv…
## $ STARTED <chr> "Zeitpunkt zu dem das Inte…
## $ DDM_AV_1 <chr> "DDM-AV-AP: Ich versuche, …
## $ DDM_AV_2 <chr> "DDM-AV-AP: Ich \xfcberlas…
## $ DDM_AV_3 <chr> "DDM-AV-AP: Es ist mir una…
## $ DDM_AV_4 <chr> "DDM-AV-AP: Die Unternehme…
## $ DDM_AV_5 <chr> "DDM-AV-AP: Ich stimme Ent…
## $ DDM_AP_1 <chr> "DDM-AV-AP: Ich treffe ris…
## $ DDM_AP_2 <chr> "DDM-AV-AP: Ich treffe Ent…
## $ DDM_AP_3 <chr> "DDM-AV-AP: F\xfcr eine er…
## $ DDM_AP_4 <chr> "DDM-AV-AP: Um innovative …
## $ DDM_AP_5 <chr> "DDM-AV-AP: Ich habe den M…
## $ DDM_SI <chr> "DDM-SI: [01]", "4", "0", …
## $ EL_01 <chr> "EL: ... \xfcbertr\xe4gt m…
## $ EL_02 <chr> "EL: ... macht mich f\xfcr…
## $ EL_03 <chr> "EL: ... fragt mich um Rat…
## $ EL_04 <chr> "EL: ... bezieht meine Vor…
## $ EL_05 <chr> "EL: ... kontrolliert viel…
## $ EL_06 <chr> "EL: ... ermutigt mich, di…
## $ EL_07 <chr> "EL: ... erlaubt mir, mein…
## $ EL_08 <chr> "EL: ... ermutigt mich, ei…
## $ EL_09 <chr> "EL: ... greift nicht ein,…
## $ EL_10 <chr> "EL: ... ermutigt mich, di…
## $ EL_11 <chr> "EL: ... fordert mich dazu…
## $ EL_12 <chr> "EL: ... ermutigt mich, H\…
## $ EL_13 <chr> "EL: ... vertraut mir.", "…
## $ EL_14 <chr> "EL: ... ist \xfcberzeugt …
## $ PE_ME1 <chr> "PE: Die Arbeit, die ich m…
## $ PE_ME2 <chr> "PE: Meine beruflichen T\x…
## $ PE_ME3 <chr> "PE: Die Arbeit, die ich m…
## $ PE_CO1 <chr> "PE: Ich vertraue in meine…
## $ PE_CO2 <chr> "PE: Ich f\xfchle mich sel…
## $ PE_CO3 <chr> "PE: Ich beherrsche die f\…
## $ PE_SD1 <chr> "PE: Ich kann in hohem Ma\…
## $ PE_SD2 <chr> "PE: Ich kann selbst entsc…
## $ PE_SD3 <chr> "PE: Ich verf\xfcge \xfcbe…
## $ K <chr> "PE: Bitte w\xe4hlen Sie d…
## $ PE_IM1 <chr> "PE: Mein Einfluss darauf,…
## $ PE_IM2 <chr> "PE: Ich habe viel Kontrol…
## $ PE_IM3 <chr> "PE: Ich habe bedeutenden …
## $ ET <chr> "Erwerbst\xe4tig", "1", "1…
## $ AZ <chr> "Dauer w\xf6chentliche Arb…
## $ FK <chr> "Direkter Vorgesetzter", "…
## $ EN <chr> "Entscheidungen", "1", "1"…
## $ ALT <chr> "Alter: Ich bin ... Jahre …
## $ WMD <chr> "Geschlecht", "1", "1", NA…
## $ TIME001 <chr> "Verweildauer Seite 1", "5…
## $ TIME002 <chr> "Verweildauer Seite 2", "1…
## $ TIME003 <chr> "Verweildauer Seite 3", "4…
## $ TIME004 <chr> "Verweildauer Seite 4", "8…
## $ TIME005 <chr> "Verweildauer Seite 5", "6…
## $ TIME006 <chr> "Verweildauer Seite 6", "7…
## $ TIME_SUM <chr> "Verweildauer gesamt (ohne…
## $ MAILSENT <chr> "Versandzeitpunkt der Einl…
## $ LASTDATA <chr> "Zeitpunkt als der Datensa…
## $ STATUS <chr> "Status des Interviews (Ma…
## $ FINISHED <chr> "Wurde die Befragung abges…
## $ Q_VIEWER <chr> "Hat der Teilnehmer den Fr…
## $ LASTPAGE <chr> "Seite, die der Teilnehmer…
## $ MAXPAGE <chr> "Letzte Seite, die im Frag…
## $ MISSING <chr> "Anteil fehlender Antworte…
## $ MISSREL <chr> "Anteil fehlender Antworte…
## $ TIME_RSI <chr> "Ausf\xfcll-Geschwindigkei…
An dieser Stelle sollte erwähnt werden, dass das dplyr-Paket nicht nur für eine übersichtliche Datenstruktur praktisch ist, sondern das es eines der zentralen Werkzeuge für Datenmanipulation in R ist. Es bietet eine sehr intuitive Syntax für das Filtern, Selektieren, Gruppieren oder Zusammenfassen von Daten und wird daher in der Praxis häufig verwendet. In dem Workshop konzentrieren wir uns jedoch bewusst auf Datenmanipulation mit Base R, also ohne zusätzliche Pakete. Das stärkt das Verständnis für grundlegende R-Funktionalitäten, auf denen auch dplyr und andere Pakete aufbauen. Wer sich näher mit dem Paket beschäftigen möchte, findet eine hervorragende Einführung im Buch R for Data Science von Hadley Wickham.
Mit dem colnames() Befehl können wir uns die Spaltennamen anzeigen lassen:
colnames(data_raw) # Spaltennamen des Datensatzes
## [1] "CASE" "SERIAL" "REF"
## [4] "QUESTNNR" "MODE" "STARTED"
## [7] "DDM_AV_1" "DDM_AV_2" "DDM_AV_3"
## [10] "DDM_AV_4" "DDM_AV_5" "DDM_AP_1"
## [13] "DDM_AP_2" "DDM_AP_3" "DDM_AP_4"
## [16] "DDM_AP_5" "DDM_SI" "EL_01"
## [19] "EL_02" "EL_03" "EL_04"
## [22] "EL_05" "EL_06" "EL_07"
## [25] "EL_08" "EL_09" "EL_10"
## [28] "EL_11" "EL_12" "EL_13"
## [31] "EL_14" "PE_ME1" "PE_ME2"
## [34] "PE_ME3" "PE_CO1" "PE_CO2"
## [37] "PE_CO3" "PE_SD1" "PE_SD2"
## [40] "PE_SD3" "K" "PE_IM1"
## [43] "PE_IM2" "PE_IM3" "ET"
## [46] "AZ" "FK" "EN"
## [49] "ALT" "WMD" "TIME001"
## [52] "TIME002" "TIME003" "TIME004"
## [55] "TIME005" "TIME006" "TIME_SUM"
## [58] "MAILSENT" "LASTDATA" "STATUS"
## [61] "FINISHED" "Q_VIEWER" "LASTPAGE"
## [64] "MAXPAGE" "MISSING" "MISSREL"
## [67] "TIME_RSI"
Zusätzlich ist es sinnvoll, die Daten in einem neuen Fenster zu betrachten. Das geht mit dem View() Befehl:
View(data_raw) # Datensatz in einem neuen Fenster anzeigen
Datenaufbereitung
Wie euch möglicherweise schon vielleicht aufgefallen ist, befinden sich aktuell in der ersten Zeilen unseres Datensatzes die Beschriftungen der Items, sodass wir diese Zeile entfernen müssen.
Indizierung in Objekte
In R können wir auf verschiedene Arten innerhalb eines Data Frames indizieren, also auf bestimmte Zeilen oder Spalten zugreifen.
Mit der eckigen Klammernotation [ , ] lässt sich präzise steuern, welche Zeilen und Spalten ausgewählt werden sollen:
head(data_raw[1, ]) # erste Zeile, alle Spalten
## CASE
## 1 Interview-Nummer (fortlaufend)
## SERIAL
## 1 Personenkennung oder Teilnahmecode (sofern verwendet)
## REF
## 1 Referenz (sofern im Link angegeben)
## QUESTNNR
## 1 Fragebogen, der im Interview verwendet wurde
## MODE
## 1 Interview-Modus
## STARTED
## 1 Zeitpunkt zu dem das Interview begonnen hat (Europe/Berlin)
## DDM_AV_1
## 1 DDM-AV-AP: Ich versuche, riskante Entscheidungen zu vermeiden.
## DDM_AV_2
## 1 DDM-AV-AP: Ich \xfcberlasse riskante Entscheidungen gerne anderen.
## DDM_AV_3
## 1 DDM-AV-AP: Es ist mir unangenehm, Entscheidungen zu treffen, deren Folgen ich nicht absehen kann.
## DDM_AV_4
## 1 DDM-AV-AP: Die Unternehmensleitung sollte alle risikoreichen Entscheidungen treffen.
## DDM_AV_5
## 1 DDM-AV-AP: Ich stimme Entscheidungen grunds\xe4tzlich mit meiner F\xfchrungskraft ab.
## DDM_AP_1
## 1 DDM-AV-AP: Ich treffe riskante Entscheidungen, wenn ich das Gef\xfchl habe, dass sie richtig sind.
## DDM_AP_2
## 1 DDM-AV-AP: Ich treffe Entscheidungen, auch wenn ich nicht alle Folgen vorhersehen kann.
## DDM_AP_3
## 1 DDM-AV-AP: F\xfcr eine erfolgreiche Karriere muss man gelegentlich riskante Entscheidungen treffen.
## DDM_AP_4
## 1 DDM-AV-AP: Um innovative Ideen zu verwirklichen, ist es wichtig, Entscheidungen zu treffen, auch wenn sie mit einem gewissen Risiko verbunden sind.
## DDM_AP_5
## 1 DDM-AV-AP: Ich habe den Mut, Entscheidungen zu treffen, auch wenn sie f\xfcr mich mit einem gewissen Risiko verbunden sind.
## DDM_SI
## 1 DDM-SI: [01]
## EL_01
## 1 EL: ... \xfcbertr\xe4gt mir viel Verantwortung.
## EL_02
## 1 EL: ... macht mich f\xfcr mein eigenes Handeln verantwortlich.
## EL_03
## 1 EL: ... fragt mich um Rat, wenn Entscheidungen getroffen werden.
## EL_04
## 1 EL: ... bezieht meine Vorschl\xe4ge und Ideen bei Entscheidungen mit ein.
## EL_05
## 1 EL: ... kontrolliert viele meiner Aktivit\xe4ten.
## EL_06
## 1 EL: ... ermutigt mich, die Kontrolle \xfcber meine Arbeit zu \xfcbernehmen.
## EL_07
## 1 EL: ... erlaubt mir, meine eigenen Ziele zu setzen.
## EL_08
## 1 EL: ... ermutigt mich, eigene Ziele zu entwickeln.
## EL_09
## 1 EL: ... greift nicht ein, wenn ich Schwierigkeiten bei der Erbringung von Leistungen habe, sondern l\xe4sst mich selbstst\xe4ndig daran arbeiten.
## EL_10
## 1 EL: ... ermutigt mich, die Ursachen und L\xf6sungen meiner Probleme selbst zu finden.
## EL_11
## 1 EL: ... fordert mich dazu auf, hohe Erwartungen an mich selbst zu haben.
## EL_12
## 1 EL: ... ermutigt mich, H\xf6chstleistungen anzustreben.
## EL_13
## 1 EL: ... vertraut mir.
## EL_14
## 1 EL: ... ist \xfcberzeugt von meinen F\xe4higkeiten.
## PE_ME1
## 1 PE: Die Arbeit, die ich mache, ist mir sehr wichtig.
## PE_ME2
## 1 PE: Meine beruflichen T\xe4tigkeiten sind f\xfcr mich pers\xf6nlich bedeutsam.
## PE_ME3
## 1 PE: Die Arbeit, die ich mache, bedeutet mir viel.
## PE_CO1
## 1 PE: Ich vertraue in meine F\xe4higkeit, meine Arbeit gutzumachen.
## PE_CO2
## 1 PE: Ich f\xfchle mich selbstbewusst, wenn es darum geht, meine Arbeit zu erledigen.
## PE_CO3
## 1 PE: Ich beherrsche die f\xfcr meine Arbeit erforderlichen F\xe4higkeiten.
## PE_SD1
## 1 PE: Ich kann in hohem Ma\xdfe selbst bestimmen, wie ich meine Arbeit erledige.
## PE_SD2
## 1 PE: Ich kann selbst entscheiden, wie ich meine Aufgaben angehe.
## PE_SD3
## 1 PE: Ich verf\xfcge \xfcber ein hohes Ma\xdf an Selbstst\xe4ndigkeit und Freiraum bei der Ausf\xfchrung meiner Arbeit.
## K
## 1 PE: Bitte w\xe4hlen Sie die Antwortoption "stimme \xfcberhaupt nicht zu" aus.
## PE_IM1
## 1 PE: Mein Einfluss darauf, was in meiner Abteilung passiert, ist gro\xdf.
## PE_IM2
## 1 PE: Ich habe viel Kontrolle dar\xfcber, was in meiner Abteilung geschieht.
## PE_IM3
## 1 PE: Ich habe bedeutenden Einfluss darauf, was in meiner Abteilung passiert.
## ET
## 1 Erwerbst\xe4tig
## AZ
## 1 Dauer w\xf6chentliche Arbeit: [01]
## FK EN
## 1 Direkter Vorgesetzter Entscheidungen
## ALT WMD
## 1 Alter: Ich bin ... Jahre alt. Geschlecht
## TIME001 TIME002
## 1 Verweildauer Seite 1 Verweildauer Seite 2
## TIME003 TIME004
## 1 Verweildauer Seite 3 Verweildauer Seite 4
## TIME005 TIME006
## 1 Verweildauer Seite 5 Verweildauer Seite 6
## TIME_SUM
## 1 Verweildauer gesamt (ohne Ausrei\xdfer)
## MAILSENT
## 1 Versandzeitpunkt der Einladungsmail (nur f\xfcr nicht-anonyme Adressaten)
## LASTDATA
## 1 Zeitpunkt als der Datensatz das letzte mal ge\xe4ndert wurde
## STATUS
## 1 Status des Interviews (Markierung)
## FINISHED
## 1 Wurde die Befragung abgeschlossen (letzte Seite erreicht)?
## Q_VIEWER
## 1 Hat der Teilnehmer den Fragebogen nur angesehen, ohne die Pflichtfragen zu beantworten?
## LASTPAGE
## 1 Seite, die der Teilnehmer zuletzt bearbeitet hat
## MAXPAGE
## 1 Letzte Seite, die im Fragebogen bearbeitet wurde
## MISSING
## 1 Anteil fehlender Antworten in Prozent
## MISSREL
## 1 Anteil fehlender Antworten (gewichtet nach Relevanz)
## TIME_RSI
## 1 Ausf\xfcll-Geschwindigkeit (relativ)
head(data_raw[, 1]) # alle Zeilen, erste Spalte (als Vektor)
## [1] "Interview-Nummer (fortlaufend)"
## [2] "72"
## [3] "77"
## [4] "84"
## [5] "86"
## [6] "87"
head(data_raw[, 1, drop = FALSE]) # alle Zeilen, erste Spalte (als data.frame)
## CASE
## 1 Interview-Nummer (fortlaufend)
## 2 72
## 3 77
## 4 84
## 5 86
## 6 87
head(data_raw[, "CASE", drop = FALSE]) # alle Zeilen, Spalte mit Namen "CASE" (als data.frame)
## CASE
## 1 Interview-Nummer (fortlaufend)
## 2 72
## 3 77
## 4 84
## 5 86
## 6 87
data_raw[1, 1] # erste Zeile, erste Spalte
## [1] "Interview-Nummer (fortlaufend)"
data_raw[1:5, 1:3] # erste 5 Zeilen, erste 3 Spalten
## CASE
## 1 Interview-Nummer (fortlaufend)
## 2 72
## 3 77
## 4 84
## 5 86
## SERIAL
## 1 Personenkennung oder Teilnahmecode (sofern verwendet)
## 2 <NA>
## 3 <NA>
## 4 <NA>
## 5 <NA>
## REF
## 1 Referenz (sofern im Link angegeben)
## 2 <NA>
## 3 <NA>
## 4 <NA>
## 5 <NA>
Zusätzlich gibt es Möglichkeiten, um auf Spalten per Name zuzugreifen:
head(data_raw$CASE) # Zugriff über den $-Operator (direkt als Vektor)
## [1] "Interview-Nummer (fortlaufend)"
## [2] "72"
## [3] "77"
## [4] "84"
## [5] "86"
## [6] "87"
head(data_raw[["CASE"]]) # Zugriff als Vektor, dynamisch über Spaltennamen
## [1] "Interview-Nummer (fortlaufend)"
## [2] "72"
## [3] "77"
## [4] "84"
## [5] "86"
## [6] "87"
head(data_raw[,"CASE"]) # Zugriff als Data Frame
## [1] "Interview-Nummer (fortlaufend)"
## [2] "72"
## [3] "77"
## [4] "84"
## [5] "86"
## [6] "87"
Um die erste Zeile aus unserem Datensatz zu entfernen können wir die negative Indizierung verwenden:
data_raw <- data_raw[-1, ] # erste Zeile entfernen
head(data_raw)
## CASE SERIAL REF QUESTNNR MODE
## 2 72 <NA> <NA> base interview
## 3 77 <NA> <NA> base interview
## 4 84 <NA> <NA> base interview
## 5 86 <NA> <NA> base interview
## 6 87 <NA> <NA> base interview
## 7 90 <NA> <NA> base interview
## STARTED DDM_AV_1 DDM_AV_2
## 2 2025-05-07 15:03:31 5 5
## 3 2025-05-07 15:25:18 2 1
## 4 2025-05-07 15:59:25 6 1
## 5 2025-05-07 16:05:03 6 1
## 6 2025-05-07 16:11:59 5 4
## 7 2025-05-07 16:27:34 2 2
## DDM_AV_3 DDM_AV_4 DDM_AV_5 DDM_AP_1
## 2 5 4 5 6
## 3 3 3 5 2
## 4 6 7 7 7
## 5 7 6 6 7
## 6 5 4 5 6
## 7 4 3 4 6
## DDM_AP_2 DDM_AP_3 DDM_AP_4 DDM_AP_5 DDM_SI
## 2 6 6 6 6 4
## 3 5 6 6 6 0
## 4 7 6 7 7 <NA>
## 5 7 7 7 7 10
## 6 6 5 6 5 9
## 7 7 4 6 6 5
## EL_01 EL_02 EL_03 EL_04 EL_05 EL_06 EL_07
## 2 7 5 6 7 2 7 7
## 3 7 5 6 6 1 6 6
## 4 <NA> <NA> <NA> <NA> <NA> <NA> <NA>
## 5 6 4 6 6 4 6 6
## 6 5 5 2 3 3 4 4
## 7 7 6 4 6 1 4 6
## EL_08 EL_09 EL_10 EL_11 EL_12 EL_13 EL_14
## 2 7 6 6 6 6 7 7
## 3 6 5 6 5 6 7 7
## 4 <NA> <NA> <NA> <NA> <NA> <NA> <NA>
## 5 6 2 6 4 4 6 6
## 6 4 5 4 4 4 5 5
## 7 6 4 6 4 4 6 6
## PE_ME1 PE_ME2 PE_ME3 PE_CO1 PE_CO2 PE_CO3
## 2 7 6 7 7 7 7
## 3 7 7 7 6 7 7
## 4 <NA> <NA> <NA> <NA> <NA> <NA>
## 5 7 7 7 6 7 7
## 6 4 5 3 6 6 6
## 7 7 7 7 7 7 7
## PE_SD1 PE_SD2 PE_SD3 K PE_IM1 PE_IM2
## 2 6 7 7 1 5 7
## 3 7 7 7 <NA> 7 7
## 4 <NA> <NA> <NA> <NA> <NA> <NA>
## 5 6 6 6 6 6 6
## 6 5 5 5 1 4 4
## 7 7 7 7 1 1 1
## PE_IM3 ET AZ FK EN ALT WMD
## 2 6 1 20 1 1 47 1
## 3 7 1 25 1 1 59 1
## 4 <NA> <NA> <NA> <NA> <NA> <NA> <NA>
## 5 6 1 30 2 2 47 1
## 6 4 <NA> <NA> <NA> <NA> <NA> <NA>
## 7 1 1 20 2 1 48 1
## TIME001 TIME002 TIME003 TIME004 TIME005
## 2 57 147 47 87 69
## 3 39 87 36 200 72
## 4 16 186 43 <NA> <NA>
## 5 25 71 81 136 105
## 6 9 236 80 122 79
## 7 5 78 19 116 58
## TIME006 TIME_SUM MAILSENT
## 2 73 480 <NA>
## 3 49 483 <NA>
## 4 <NA> 245 <NA>
## 5 72 490 <NA>
## 6 <NA> 526 <NA>
## 7 33 309 <NA>
## LASTDATA STATUS FINISHED
## 2 2025-05-07 15:11:31 <NA> 1
## 3 2025-05-07 15:33:21 <NA> 1
## 4 2025-05-07 16:03:30 <NA> 0
## 5 2025-05-07 16:13:13 <NA> 1
## 6 2025-05-07 16:20:45 <NA> 0
## 7 2025-05-07 16:32:43 <NA> 1
## Q_VIEWER LASTPAGE MAXPAGE MISSING MISSREL
## 2 0 6 6 0 0
## 3 0 6 6 2 2
## 4 0 3 3 9 7
## 5 0 6 6 0 0
## 6 0 5 5 0 0
## 7 0 6 6 0 0
## TIME_RSI
## 2 0,76
## 3 0,83
## 4 0,72
## 5 0,74
## 6 0,82
## 7 1,55
Diese Methode funktioniert auch für mehrere Zeilen.
nrow(data_raw)
## [1] 232
nrow(data_raw[-c(1:133), ]) # Zeilen 1 bis 113 entfernen
## [1] 99
Datenklassen Anpassen
Ein weiteres Problem ist, dass alle Spalten aktuell als Character (<chr>) eingelesen wurden. Das liegt daran, dass die erste Zeile mit den Itembeschreibungen nicht entfernt wurde, als wir die Daten eingelesen haben. Dadurch interpretiert R alle Spalten als Text.
Wir prüfen das z.B. an der Variable TIME_SUM, die die Zeit (in sek.) erfasst, die die Proband*innen für die Teilnahme an der Studie benötigt haben:
class(data_raw$TIME_SUM) # Klasse der Spalte TIME_SUM
## [1] "character"
mean(data_raw$TIME_SUM)
## Warning in mean.default(data_raw$TIME_SUM):
## Argument ist weder numerisch noch boolesch:
## gebe NA zurück
## [1] NA
Wir erhalten eine Warnung, dass wir mit einem Character-Objekt nicht rechnen können. Um das zu beheben, müssen wir die Spalte in einen numerischen Vektor umwandeln. Das geht mit der Funktion as.numeric().
data_raw$TIME_SUM <- as.numeric(data_raw$TIME_SUM)
Um diese Umwandlung nicht 67 mal für jede Spalte einzeln durchführen zu müssen und unseren Code DRY (Don’t Repeat Yourself) zu lassen, können wir uns eine Klasse von Funktionen zu Nutze machen, die die selbe Funktion wiederholt über die Spalten einer Matrix oder Dataframes anwenden — die apply() Familie.
Diese Familie umfasst Funktionen wie apply(), lapply(), sapply(), vapply() oder tapply(), die alle nach einem ähnlichen Prinzip arbeiten: Eine Funktion wird auf jedes Element einer Datenstruktur angewendet, ohne dass wir dafür explizite Schleifen (Loops) schreiben müssen.
Für wiederholte Operationen in Data Frames über Spalten ist die lapply() Funktion besonders nützlich, da sie eine Funktion automatisch auf jede Spalte anwendet und die Ergebnisse als Liste (deswegen lapply()) zurückliefert. Da Data Frames gleichzeitig auch Listen sind (deren Elemente alle die gleiche Länge haben), können wir die Ergebnisse von lapply() direkt wieder als Data Frame speichern, z.B.:
colnames(data_raw)
## [1] "CASE" "SERIAL" "REF"
## [4] "QUESTNNR" "MODE" "STARTED"
## [7] "DDM_AV_1" "DDM_AV_2" "DDM_AV_3"
## [10] "DDM_AV_4" "DDM_AV_5" "DDM_AP_1"
## [13] "DDM_AP_2" "DDM_AP_3" "DDM_AP_4"
## [16] "DDM_AP_5" "DDM_SI" "EL_01"
## [19] "EL_02" "EL_03" "EL_04"
## [22] "EL_05" "EL_06" "EL_07"
## [25] "EL_08" "EL_09" "EL_10"
## [28] "EL_11" "EL_12" "EL_13"
## [31] "EL_14" "PE_ME1" "PE_ME2"
## [34] "PE_ME3" "PE_CO1" "PE_CO2"
## [37] "PE_CO3" "PE_SD1" "PE_SD2"
## [40] "PE_SD3" "K" "PE_IM1"
## [43] "PE_IM2" "PE_IM3" "ET"
## [46] "AZ" "FK" "EN"
## [49] "ALT" "WMD" "TIME001"
## [52] "TIME002" "TIME003" "TIME004"
## [55] "TIME005" "TIME006" "TIME_SUM"
## [58] "MAILSENT" "LASTDATA" "STATUS"
## [61] "FINISHED" "Q_VIEWER" "LASTPAGE"
## [64] "MAXPAGE" "MISSING" "MISSREL"
## [67] "TIME_RSI"
vec_chr <- c("QUESTNNR", "MODE", "STARTED", "LASTDATA")
data_raw[, -match(vec_chr, colnames(data_raw))] <- lapply(
X = data_raw[, -match(vec_chr, colnames(data_raw))],
FUN = as.numeric
)
## Warning in lapply(X = data_raw[,
## -match(vec_chr, colnames(data_raw))], FUN =
## as.numeric): NAs durch Umwandlung erzeugt
Der match()-Befehl sucht dabei die Position(en) eines Wertes oder mehrerer Werte in einem Vektor. Hier wird also die Position der Spaltennamen, die in vec_chr enthalten sind, im Vektor der Spaltennamen von data_raw gesucht. Das Ergebnis wird dann negiert (-), um alle Spalten auszuwählen, die nicht in vec_chr enthalten sind. So werden nur die Spalten in numerische Werte umgewandelt, die tatsächlich numerische Daten enthalten sollten.
Für Zeitvariablen wie STARTED und LASTDATA können wir die Datums- und Zeitinformation anschließend in ein passendes Format (POSIXct) umwandeln:
head(data_raw$STARTED)
## [1] "2025-05-07 15:03:31"
## [2] "2025-05-07 15:25:18"
## [3] "2025-05-07 15:59:25"
## [4] "2025-05-07 16:05:03"
## [5] "2025-05-07 16:11:59"
## [6] "2025-05-07 16:27:34"
data_raw[, c("STARTED", "LASTDATA")] <- lapply(
X = data_raw[, c("STARTED", "LASTDATA")],
FUN = as.POSIXct
)
class(data_raw$STARTED)
## [1] "POSIXct" "POSIXt"
head(data_raw$STARTED)
## [1] "2025-05-07 15:03:31 CEST"
## [2] "2025-05-07 15:25:18 CEST"
## [3] "2025-05-07 15:59:25 CEST"
## [4] "2025-05-07 16:05:03 CEST"
## [5] "2025-05-07 16:11:59 CEST"
## [6] "2025-05-07 16:27:34 CEST"
Umwandlung von Variablen in Faktoren
Kategoriale Variablen wie Geschlecht, Entscheidungsverhalten oder Zustimmung sollten in Faktoren umgewandelt werden, damit R sie korrekt als kategorial interpretiert und in Analysen entsprechend behandelt. Dafür können wir die factor() Funktion nutzen.
# Geschlecht (Männlich = 1, Weiblich = 2, Divers = 3)
head(data_raw$WMD, n = 10)
## [1] 1 1 NA 1 NA 1 2 1 NA 2
data_raw$WMD <- factor(
x = data_raw$WMD,
levels = c(1, 2, 3),
labels = c("w", "m", "d")
)
Das gleiche machen wir für die Variablen ET und FK:
# ET: Entscheidung (1 = ja, 2 = nein)
# FK: Direkter Vorgesetzter (1 = ja, 2 = nein)
data_raw$EN <- factor(
x = data_raw$EN,
levels = c(1, 2),
labels = c("ja", "nein")
)
data_raw$FK <- factor(
x = data_raw$FK,
levels = c(1, 2),
labels = c("ja", "nein")
)
Erstellung eines Subdatensatzes
Um die Analyse übersichtlicher zu gestalten, können wir einen Subdatensatz erstellen, der nur die für unsere Analyse relevanten Variablen enthält. Mit der eckigen Klammernotation [ , ] lassen sich die gewünschten Spalten auswählen:
vec_nms <- c(
"CASE", "STARTED",
paste0("DDM_AV_", 1:5), paste0("DDM_AP_", 1:5), "DDM_SI",
sprintf("EL_%02d", 1:14), paste0("PE_ME", 1:3), paste0("PE_CO", 1:3),
paste0("PE_SD", 1:3), "K", paste0("PE_IM", 1:3),
"ET", "AZ", "EN", "FK", "ALT", "WMD", "LASTDATA", "TIME_SUM"
)
data_sub <- data_raw[, match(vec_nms, colnames(data_raw)) ]
Die paste0() Funktion fügt dabei Zeichenketten zusammen, ohne ein Trennzeichen zu verwenden. Die sprintf() Funktion lässt komplexere Zeichenketten generieren, in dem wir Platzhalter verwenden (%02d). In unserem Fall steht %d für eine ganze Zahl und %02d für eine zweistellige Zahl mit führender Null.
Alternativ kann auch der subset() Befehl genutzt werden, der das Argument select = c(...) für die Spaltenauswahl verwendet (s.h. ?subset für mehr Informationen):
data_sub <- subset(data_raw, select = vec_nms)
dim(data_raw)
## [1] 232 67
dim(data_sub)
## [1] 232 48
Umbenennung von Variablen
Um die Interpretation zu erleichtern, ist es sinnvoll, Variablen aussagekräftiger zu benennen. Mit colnames() können die Spaltennamen eines Data Frames abgefragt und überschrieben werden.
Zusätzlich ist es sinnvoll, die Variablennamen in ein einheitliches Format zu bringen. In unserem Rohdatensatz sind alle Variablen in Großbuchstaben benannt, was in R typischerweise Konstanten kennzeichnet. Deswegen wollen wir alle Variablen in Kleinschreibung umwandeln, was wir mit dem tolower() Befehl für alle Variablen gleichzeitig machen umsetzen können.
colnames(data_sub) <- tolower(colnames(data_sub))
colnames(data_sub)[c(37, 41:46)]
## [1] "k" "et" "az" "en" "fk" "alt" "wmd"
names(data_sub)[c(37, 41:46)] <- c("kontroll", "erwerb", "arbeit_std", "vorgesetzt", "entscheidung", "alter", "geschlecht")
colnames(data_sub)
## [1] "case" "started"
## [3] "ddm_av_1" "ddm_av_2"
## [5] "ddm_av_3" "ddm_av_4"
## [7] "ddm_av_5" "ddm_ap_1"
## [9] "ddm_ap_2" "ddm_ap_3"
## [11] "ddm_ap_4" "ddm_ap_5"
## [13] "ddm_si" "el_01"
## [15] "el_02" "el_03"
## [17] "el_04" "el_05"
## [19] "el_06" "el_07"
## [21] "el_08" "el_09"
## [23] "el_10" "el_11"
## [25] "el_12" "el_13"
## [27] "el_14" "pe_me1"
## [29] "pe_me2" "pe_me3"
## [31] "pe_co1" "pe_co2"
## [33] "pe_co3" "pe_sd1"
## [35] "pe_sd2" "pe_sd3"
## [37] "kontroll" "pe_im1"
## [39] "pe_im2" "pe_im3"
## [41] "erwerb" "arbeit_std"
## [43] "vorgesetzt" "entscheidung"
## [45] "alter" "geschlecht"
## [47] "lastdata" "time_sum"
So entsteht ein übersichtlicher Subdatensatz mit einheitlicher, gut interpretierbarer Namenskonvention.
Filtern des Datensatzes
In der Präregistrierung der Bachelorarbeit, aus der die Daten stammen, wurden verschiedene Ausschlusskriterien festgelegt, um die Datenqualität zu sichern und eine Stichprobe zu erhalten, die für die Forschungsfragen geeignet ist. Zusätzlich legen wir als Kriterium für unsere Analysen fest, dass Teilnehmende mit einer Bearbeitungszeit unter 60 Sekunden ausgeschlossen werden, da hier von unaufmerksamer Teilnahme auszugehen ist. Die vollständigen Kriterien lauten:
- Ausschluss von Teilnehmenden mit einer Bearbeitungszeit von unter 60 Sekunden.
- Ausschluss von Teilnehmenden, die die Kontrollfrage falsch beantwortet haben.
- Ausschluss von Teilnehmenden, die nicht erwerbstätig sind.
- Ausschluss von Teilnehmenden, die nicht volljährig sind.
- Ausschluss von Teilnehmenden, ohne direkte Führungskraft als vorgesetzte Person.
In der Umsetzung in R müssen wir also Zeilen aus dem Datensatz entfernen, denen diese Kriterien nicht entsprechen. Dafür nutzen wir logische Operatoren. Eine Übersicht dieser, von denen wir nur ein paar nutzen, findet ihr hier:
Table: Übersicht der logischen Operatoren in R
| Operator | Bedeutung | Beispiel | Ergebnis |
|---|---|---|---|
| & | Elementweises UND | c(TRUE,FALSE,TRUE) & c(TRUE,TRUE,FALSE) | TRUE FALSE FALSE |
| | | Elementweises ODER | c(TRUE,FALSE,TRUE) | c(FALSE,TRUE,FALSE) | TRUE TRUE TRUE |
| ! | Negation / NICHT | !c(TRUE,FALSE) | FALSE TRUE |
| && | Kurzes UND (erstes Element) | TRUE && FALSE | FALSE |
| || | Kurzes ODER (erstes Element) | TRUE || FALSE | TRUE |
| == | Gleich | 5 == 5 | TRUE |
| != | Ungleich | 5 != 3 | TRUE |
| < | Kleiner | 3 < 5 | TRUE |
| <= | Kleiner oder gleich | 3 <= 3 | TRUE |
| > | Größer | 5 > 3 | TRUE |
| >= | Größer oder gleich | 5 >= 5 | TRUE |
Bearbeitungszeit
Für die Umsetzung des ersten Kriteriums nutzen wir die Variable time_sum. Mit der table() Funktion erhalten wir eine Übersicht, wie viele Teilnehmende eine Bearbeitungszeit von 60 Sekunden oder weniger (als logischer Operator time_sum <= 60) hatten:
with(data_sub, table(time_sum < 60))
##
## FALSE TRUE
## 229 3
Drei Personen müssen demnach ausgeschlossen werden. Dafür können wir erneut die subset() Funktion nutzen und dieses mal das Argument subset = ... verwenden.
data_sub1 <- subset(data_sub, subset = time_sum >= 60)
Das subset Argument lässt dabei alle Zeilen in dem Datensatz, die dier Kondition time_sum => 60 erfüllen (TRUE). Mit nrow() können wir die Anzahl der Zeilen im neuen Datensatz überprüfen und vergleichen:
nrow(data_sub)
## [1] 232
nrow(data_sub1)
## [1] 229
Kontrollfrage richtig beantwortet
Mit dem zweiten Kriterium wollen wir alle Teilnehmenden ausschließen, die die Kontrollfrage falsch beantwortet haben. Die Variable kontroll kodiert die Antwort auf die Kontrollfrage, welche mit “Stimme überhaupt nicht zu” (kodiert als 1) beantwortet werden sollte. Wir können uns erneut mit table() anzeigen lassen, wie viele Teilnehmende welche Antwort gegeben haben:
table(data_sub1$kontroll, useNA = "always")
##
## 1 2 3 4 5 6 7 <NA>
## 166 1 2 8 2 3 5 42
Das Argument useNA = "always" sorgt dafür, dass auch fehlende Werte in der Tabelle angezeigt werden. Alle Werte außer 1 müssen ausgeschlossen werden.
sum(data_sub1$kontroll != 1, na.rm = TRUE) # 21 Personen müssen ausgeschlossen werden
## [1] 21
Dafür nutzen wir wieder die subset() Funktion mit dem logischen Operator kontroll != 1:
data_sub2 <- subset(data_sub1, subset = (kontroll == 1))
nrow(data_sub1)
## [1] 229
nrow(data_sub2)
## [1] 166
Erwerbstätigkeit
Als drittes Kriterium wollen wir alle Teilnehmenden ausschließen, die aktuell nicht erwerbstätig sind. Die Variable erwerb kodiert hierbei die Erwerbstätigkeit.
Aufgabe 1 (Übung)
- Wandelt die Variable
erwerbin einen Faktor um. - Verwendet dabei die Labels:
"ja","nein_teilzeit","nein". - Prüft, wie viele Teilnehmende welche Antwort gegeben haben (inkl. NAs).
- Schließt anschließend alle Teilnehmenden aus, die nicht erwerbstätig sind.
Lösung
Ihr erstellt zunächst den Faktor wie folgt:
labels_erwerb <- c("ja", "nein_teilzeit", "nein")
data_sub2$erwerb <- factor(data_sub2$erwerb, levels = c(1, 2, 3), labels = labels_erwerb)
Anschließend könnt ihr mit table() überprüfen, wie viele Teilnehmende welche Antwort gegeben haben:
table(data_sub2$erwerb, useNA = "always")
##
## ja nein_teilzeit nein
## 148 12 1
## <NA>
## 5
Um alle Teilnehmenden auszuschließen, die nicht erwerbstätig sind, könnt ihr wieder die subset() Funktion nutzen:
data_sub3 <- subset(data_sub2, subset = erwerb == "ja")
Volljährigkeit
Als letztes Kriterium wollen wir alle Teilnehmenden ausschließen, die nicht volljährig sind. Die Variable alter gibt das Alter der Teilnehmenden in Jahren an. Dafür können wir mit der min() Funktion die jüngste Person in unserem Datensatz bestimmen
min(data_sub3$alter, na.rm = TRUE)
## [1] 18
any(data_sub3$alter < 18) # Alternative
## [1] FALSE
Da keine Person jünger als 18 Jahre ist, müssen wir hier niemanden ausschließen.
Führungskraft als vorgesetzte Person
Als letztes Kriterium wollen wir alle Teilnehmenden ausschließen, die keine direkte Führungskraft als vorgesetzte Person haben. Die Variable vorgesetzt kodiert dies mit 1 = ja und 2 = nein.
table(data_sub3$vorgesetzt, useNA = "always")
##
## ja nein <NA>
## 136 12 0
data_sub4 <- subset(data_sub3, subset = vorgesetzt == "ja")
nrow(data_raw)
## [1] 232
nrow(data_sub4)
## [1] 136
Bestimmung von Skalenwerten
In unserem Datensatz gibt es mehrere Skalen, die aus mehreren Items bestehen. Um diese Skalen in der Analyse verwenden zu können, müssen wir zunächst die Skalenwerte berechnen. Dafür können wir den Mittelwert der einzelnen Items berechnen.
Schritt 1: Rekodieren von Variablen
Zunächst müssen jedoch einige Items rekodiert werden, da sie invertiert kodiert sind. Wir ziehen die Ausprägungen auf der Likert-Skala von dem maximalen Ausprägungswert ab. Neue Variablen können wir einfach mit dem $ Operator erstellen.
max_value <- 7
data_sub4$el_05i <- (max_value + 1) - data_sub4$el_05
Zusätzlich müssen wir eine gesamte Subskala des Konstrukts Defensive Decision Making (DDM) rekodieren. Dies machen wir, weil die beiden Subskalen der Konstrukts invers zueinander formuliert sind, wir jedoch einen gemeinsamen Summenscores für DDM erstellen wollen.
data_sub4$ddm_ap_1i <- (max_value + 1) - data_sub4$ddm_ap_1
data_sub4$ddm_ap_2i <- (max_value + 1) - data_sub4$ddm_ap_2
data_sub4$ddm_ap_3i <- (max_value + 1) - data_sub4$ddm_ap_3
data_sub4$ddm_ap_4i <- (max_value + 1) - data_sub4$ddm_ap_4
data_sub4$ddm_ap_5i <- (max_value + 1) - data_sub4$ddm_ap_5
Wenn wir uns wieder Zeit sparen wollen und effektiver in R arbeiten wollen, können wir auch hier wieder die lapply() Funktion nutzen, um alle Items gleichzeitig zu rekodieren:
inv_item <- c("el_05", "ddm_ap_1", "ddm_ap_2", "ddm_ap_3", "ddm_ap_4", "ddm_ap_5")
paste0(inv_item, "i")
data_sub4[paste0(inv_item, "i")] <- lapply(X = data_sub4[inv_item], FUN = function(x) max_value - x)
Hierbei ist die Funktion paste0() nützlich, um die neuen Variablennamen automatisch zu generieren, indem wir “_i” an die ursprünglichen Itemnamen anhängen.
Schritt 2: Berechnung von Skalenwerten
Nun können wir die Skalenwerte berechnen, indem wir den Mittelwert der entsprechenden Items für jede Person berechnen. In R können wir dies mit der Funktion rowMeans() tun. Wenn wir statt Mittelwerten Summenscores verwenden würden, könnten wir den analogen Befehl rowSums() nutzen.
Wir machen uns dafür wieder die sprintf() Funktion zu nutzen, um effizienter zu arbeiten.
# Empowering Leadership (el)
c(sprintf("el_%02d", 1:4), "el_05i", sprintf("el_%02d", 6:14))
## [1] "el_01" "el_02" "el_03" "el_04"
## [5] "el_05i" "el_06" "el_07" "el_08"
## [9] "el_09" "el_10" "el_11" "el_12"
## [13] "el_13" "el_14"
data_sub4$el <- rowMeans(data_sub4[, c(sprintf("el_%02d", 1:4), "el_05i", sprintf("el_%02d", 6:14))])
head(data_sub4$el)
## [1] 6.428571 5.428571 5.285714 6.714286
## [5] 6.642857 6.214286
Für die Berechnung des Skalenwerts des Konstrukts Psychological Empowerment (pe) könnten wir genau wie vorher mit dem sprintf() Befehl arbeiten um, Variablennamen zu generieren. Da wir aber die Vielfalt von R kennenlernen wollen, nutzen wir diesmal die grep() Funktion, um alle Variablen zu finden, die mit “pe” beginnen. Die Funktion grep() sucht in Character Vektoren (Argument x) nach einem Muster (Argument pattern). Das Argument value = TRUE sorgt dafür, dass die tatsächlichen Spaltennamen zurückgegeben werden, anstatt ihrer Indizes. Der Operator ^ spezifiziert dabei den Anfang des Vektors. Demnach muss der Vektor mit “pe” anfangen. Die Muster nach denen man im Argument pattern sucht, nennt man auch Regular Expressions (auch kurz Regex).
grep(pattern = "^pe", x = names(data_sub4), value = TRUE)
## [1] "pe_me1" "pe_me2" "pe_me3" "pe_co1"
## [5] "pe_co2" "pe_co3" "pe_sd1" "pe_sd2"
## [9] "pe_sd3" "pe_im1" "pe_im2" "pe_im3"
data_sub4$pe <- rowMeans(data_sub4[, grep("^pe", names(data_sub4), value = TRUE)])
head(data_sub4$pe)
## [1] 6.583333 5.500000 5.666667 6.000000
## [5] 6.833333 5.833333
Für die Berechnung des Skalenwerts des Konstrukts Defensive Decision Making (ddm) verwenden wir alle Variablen, die mit ddm_av beginnen oder mit ddm_ap beginnen und auf ein „i“ enden (also die rekodierten invertierten Items). Dafür können wir wieder die paste0()-Funktion verwenden:
c(paste0("ddm_av_", 1:5), paste0("ddm_ap_", 1:5, "i"))
## [1] "ddm_av_1" "ddm_av_2" "ddm_av_3"
## [4] "ddm_av_4" "ddm_av_5" "ddm_ap_1i"
## [7] "ddm_ap_2i" "ddm_ap_3i" "ddm_ap_4i"
## [10] "ddm_ap_5i"
data_sub4$ddm <- rowMeans(data_sub4[, c(paste0("ddm_av_", 1:5), paste0("ddm_ap_", 1:5, "i"))])
head(data_sub4$ddm)
## [1] 3.4 2.6 2.8 3.3 3.5 3.5
So sind alle Skalenwerte berechnet und können direkt in Analysen verwendet werden. Als letztes überschreiben wir noch das Objekt data_sub4 in data_analysis, damit deutlich wird, dass wir mit der Aufbereitung der Daten abgeschlossen haben.
data_analysis <- data_sub4
row.names(data_analysis) <- NULL #Zeilennummern zurücksetzen da diese nicht durchgängig sind nachdem wir welche entfernt haben
Deskriptivstatistik
Wir wollen nun einen ersten Überblick über unsere Daten gewinnen, indem wir deskriptive Statistiken berechnen.
Deskriptive Analyse für numerische Variablen
Wir können uns beispielsweise wichtige Kennwerte des Alters der Teilnehmenden anschauen. Hierfür verwenden wir wieder den describe() Befehl aus dem psych-Paket. Dieser ist sehr praktisch, da er uns Kennwerte wie Mittelwert, Standardabweichung, Median, Min, Max und weitere Statistiken auf einen Blick liefert.
# install.packages("psych")
library(psych)
psych::describe(data_analysis["alter"])
## vars n mean sd median trimmed
## alter 1 136 36.73 12.69 36 36.12
## mad min max range skew kurtosis se
## alter 17.05 18 64 46 0.25 -1.14 1.09
Wenn wir mehrere numerische Variablen deskriptiv statistisch analysieren wollen, können wir der Funktion auch einen Data Frame als Input geben. Hier wollen wir uns die Kennwerte für die Skalenwerte für Empowering Leadership (el), Psychological Empowerment (pe) und Defensive Decision Making (ddm) anschauen:
psych::describe(data_analysis[c("el", "pe", "ddm")])
## vars n mean sd median trimmed mad
## el 1 136 5.21 0.89 5.29 5.25 0.85
## pe 2 136 5.69 0.93 5.92 5.79 0.86
## ddm 3 136 3.50 0.94 3.50 3.49 0.89
## min max range skew kurtosis se
## el 2.86 6.79 3.93 -0.42 -0.38 0.08
## pe 2.42 7.00 4.58 -1.02 0.70 0.08
## ddm 1.40 5.80 4.40 0.09 -0.23 0.08
Wenn wir nach einer kategoriellen Variable gruppiert numerische Variablen deskriptivstatistisch analysieren wollen, können wir die describeBy() Funktion aus dem psych-Paket verwenden. Wir können beispielsweise unsere drei Skalenwerte zu den Konstrukten Empowering Leadership (el), Psychological Empowerment (pe) und Defensive Decision Making (ddm) getrennt nach Geschlecht anschauen:
scales_by_gender <- psych::describeBy(data_analysis[c("el", "pe", "ddm")], group = data_analysis$geschlecht)
print(scales_by_gender, digits = 2)
##
## Descriptive statistics by group
## group: w
## vars n mean sd median trimmed mad
## el 1 82 5.26 0.91 5.43 5.33 0.74
## pe 2 82 5.65 0.91 5.83 5.73 0.86
## ddm 3 82 3.72 0.90 3.70 3.71 0.89
## min max range skew kurtosis se
## el 2.86 6.79 3.93 -0.70 0.03 0.1
## pe 3.08 7.00 3.92 -0.78 0.05 0.1
## ddm 1.70 5.80 4.10 0.10 -0.46 0.1
## ---------------------------------
## group: m
## vars n mean sd median trimmed mad
## el 1 54 5.12 0.86 5.11 5.12 0.90
## pe 2 54 5.75 0.96 6.08 5.87 0.74
## ddm 3 54 3.17 0.91 3.30 3.16 0.89
## min max range skew kurtosis se
## el 3.57 6.71 3.14 0.04 -0.97 0.12
## pe 2.42 7.00 4.58 -1.32 1.48 0.13
## ddm 1.40 5.70 4.30 0.15 0.01 0.12
## ---------------------------------
## group: d
## NULL
Alternativ können wir auch eine Formelschreibweise nutzen, wie ihr möglicherweise noch aus der Regression kennt.
describeBy(alter ~ geschlecht, data = data_analysis)
Mit dem cor() Befehl können wir die Korrelationsmatrix für numerische Variablen berechnen. Hierfür können wir wieder den Data Frame mit den drei Skalenwerten als Input verwenden:
round(cor(data_analysis[c("el", "pe", "ddm")]), 3)
## el pe ddm
## el 1.000 0.664 -0.20
## pe 0.664 1.000 -0.34
## ddm -0.200 -0.340 1.00
Mit dem method Argument können wir die Art der Korrelation festlegen. Standardmäßig wird die Pearson-Korrelation berechnet. Alternativ können wir auch die Spearman- oder Kendall-Korrelation berechnen lassen:
round(cor(data_analysis[c("el", "pe", "ddm")], method = "spearman"), 3)
## el pe ddm
## el 1.000 0.622 -0.186
## pe 0.622 1.000 -0.388
## ddm -0.186 -0.388 1.000
Deskriptive Analyse für kategoriale Variablen
Um kategoriale Variablen zu analysieren, können wir die table() Funktion verwenden, um Häufigkeitstabellen zu erstellen. Wir können uns beispielsweise die Verteilung des Geschlechts in unserem Datensatz anschauen:
table(data_analysis$geschlecht)
##
## w m d
## 82 54 0
Mit der Funktion prop.table() können wir die relativen Häufigkeiten berechnen:
prop.table(table(data_analysis$geschlecht))
##
## w m d
## 0.6029412 0.3970588 0.0000000
Die Table Funktion kann auch für Kreuztabellen verwendet werden, um die Verteilung zweier kategorialer Variablen zu analysieren. Wir können uns beispielsweise die Verteilung des Geschlechts im Zusammenhang, ob bei der Arbeit Entscheidungen getroffen werden anschauen.
with(data_analysis, table(geschlecht, entscheidung))
## entscheidung
## geschlecht ja nein
## w 58 24
## m 50 4
## d 0 0
Funktionen Schreiben
Wie ihr euch möglicherweise erinnert, können wir in R nicht nur auf bereits bestehende Funktionen zurückgreifen, sondern auch eigene Funktionen schreiben. Das ist besonders nützlich, wenn wir eine bestimmte Analyse oder Berechnung mehrfach durchführen wollen, oder die Funktion so noch nicht in R oder einem Paket implementiert ist.
Im Kontext der deskriptiven Analyse könnten wir uns zum Beispiel für den Variationskoeffizient interessieren. Der Variationskoeffizient ist ein relatives Maß der Streuung und wird berechnet als das Verhältnis der Standardabweichung zum Mittelwert:
$$ CV = \frac{\sigma}{\mu} \quad \text{bzw.} \quad CV = \frac{s}{\bar{x}} $$
Ein guter Workflow beim Schreiben eigener Funktionen in R ist es, zunächst den Funktionskörper (“Body”) auszuformulieren – also den Teil, der beschreibt, was die Funktion tun soll – und diesen Schritt für Schritt zu einer vollständigen Funktion zusammenzusetzen.
Schauen wir uns dies zum Beispiel die Variable Defensive Decision Making (ddm) an. Zunächst könnten wir einfach den Variationskoeffizienten direkt berechnen, indem wir Mittelwert und Standardabweichung berechnen und dann beide dividieren.
x <- data_analysis$ddm
std <- sd(x)
m <- mean(x)
cv <- std / m
Damit haben wir die wesentlichen Berechnungsschritte definiert. Allerdings wollen wir unsere Funktion flexibler gestalten, sodass sie auch mit fehlenden Werten umgehen kann. Dafür können wir ein Argument na.rm ergänzen, das standardmäßig auf FALSE gesetzt sein soll, aber bei Bedarf auf TRUE gestellt werden kann.
na.rm <- FALSE
Nun können wir alle Bestandteile zu einer eigenen Funktion zusammenfügen:
calc_cv <- function(x, na.rm = FALSE) {
std <- sd(x, na.rm = na.rm)
m <- mean(x, na.rm = na.rm)
cv <- std / m
return(cv)
}
Mit dem return Befehl geben wir an, welches Ergebnis die Funktion an den User ausgeben soll.
Aufgabe 2 (Übung)
Schreibt eine Funktion mean_ci() in R, die für eine numerische Variable das Konfidenzintervall für den Mittelwert berechnet. Die Funktion soll folgende Eigenschaften haben:
Ein Argument
xfür die numerische Variable.Ein Argument
conf(Standardwert: 0.95) für das Konfidenzniveau.Ein Argument
na.rm(Standardwert: FALSE), um fehlende Werte zu ignorieren.Optional: Ein Argument
digits(Standardwert: 2), um die Ausgabe auf eine gewünschte Anzahl von Nachkommastellen zu runden.
Die Funktion soll den Mittelwert, das untere und obere Konfidenzintervall zurückgeben.
Tipp
Verwende die Formel:
$$ \text{CI} = \bar{x} \pm t_{\alpha/2, df} \times \frac{\hat{\sigma}}{\sqrt{n}} $$
und die Funktion qt() für den kritischen t-Wert.
Lösung
mean_ci <- function(x, conf = 0.95, na.rm = FALSE, digits = 2) {
if (na.rm) x <- x[!is.na(x)]
n <- length(x)
m <- mean(x)
s <- sd(x)
se <- s / sqrt(n)
alpha <- 1 - conf
t_crit <- qt(1 - alpha / 2, df = n - 1)
lower <- m - t_crit * se
upper <- m + t_crit * se
# Rundung auf gewünschte Anzahl Nachkommastellen
result <- round(c(lower = lower, mean = m, upper = upper), digits = digits)
return(result)
}
# Beispielaufruf
mean_ci(data_analysis$ddm)
## lower mean upper
## 3.34 3.50 3.66
Einfache Lineare Regression
Nachdem wir unsere Daten vollständig aufbereitet und sie bereits teilweise deskriptiv betrachtet haben, sind wir nun bereit, unsere Hypothesen zu testen. Wie eingangs erwähnt, stammt der Datensatz aus einer Bachelorarbeit, die ihr hier auf LIFOS finden könnt. Wir orientieren uns zunächst einmal an den Hypothesen die wir in der Präregistrierung finden können.
*$H_1$: Empowering Leadership steht in negativem Zusammenhang mit Defensive Decision Making *$H_2$: Empowering Leadership steht in positivem Zusammenhang mit Psychological Empowerment *$H_3$: Psychological Empowerment steht in negativem Zusammenhang mit Defensive Decision Making *$H_4$: Psychological Empowerment mediiert den Zusammenhang zwischen Empowering Leadership und Defensive Decision Making

Widmen wir uns der ersten Hypothese und erstellen das lineare Regressionsmodell, welches die Hypothese abbildet. Dafür nutzen wir zunächst die lm()-Funktion zur Erstellung des Modells und erhalten mit der summary()-Funktion eine ausführliche Darstellung der Ergebnisse.
# Hypothese 1 - Pfad C
modC <- lm(ddm ~ el, data_analysis)
summary(modC)
##
## Call:
## lm(formula = ddm ~ el, data = data_analysis)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.14413 -0.66742 -0.01469 0.49325 2.31265
##
## Coefficients:
## Estimate Std. Error t value
## (Intercept) 4.60510 0.47327 9.730
## el -0.21147 0.08958 -2.361
## Pr(>|t|)
## (Intercept) <2e-16 ***
## el 0.0197 *
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.9246 on 134 degrees of freedom
## Multiple R-squared: 0.03993, Adjusted R-squared: 0.03276
## F-statistic: 5.573 on 1 and 134 DF, p-value: 0.01969
Wir sehen sowohl das Regressionsgewicht $b_1$ = -0.21 und dementsprechend auch der Anteil erklärter Varianz $R^2$ = 0.04 fallen signifikant aus. Somit ist bereits eine wichtige Annahme unserer vorhergesagten Mediation erfüllt, denn diese könnte gar nicht vorliegen wenn es keinen Zusammenhang zwischen der unabhängigen Variable (el) und dem Outcome (ddm) gibt.
Nochmal zur Wiederholung die Interpretation der Regressionskoeffizienten: *$b_0$ (Intercept, y-Achsenabschnitt): Für eine Person die im Mittel den Wert 0 auf der Empowering Leadership (EL) Skala aufweist sagen wir einen Wert von 4.61 auf der Defensive Decision Making (ddm) Skala voraus. *$b_1$ (Slope, Regressionsgewicht): Wir sagen vorher, dass sich der ddm-Wert einer Person, die auf der el-Skala um 1 Punkt höher liegt als eine andere, um -0.21 unterscheidet.
Tag 02
(ab hier beginnen die Inhalte die für den zweiten Tag vorgesehen sind)
Voraussetzungen
Aufmerksamen Leser*innen wird aufgefallen sein, dass wir parametrische Tests verwendet haben, ohne zuvor deren Voraussetzungen überprüft zu haben. Für die lineare Regression sind dies die folgenden:
- Messfehlerfreiheit der unabhängigen Variable(n)
- Unabhängigkeit der Residuen
- Homoskedastizität der Residuen
- Normalverteilung der Residuen
- Korrekte Spezifikation des Modells (z.B Linearität)
Die ersten beiden Voraussetzungen werden wir an dieser Stelle nicht näher betrachten, da sie in erster Linie durch das passende Studiendesign als gegeben angesehen werden können. Ausführliche Erklärungen findet ihr hierzu im Beitrag zu Multipler Regression oder im Beitrag zu Regressionsdiagnostik.
Homoskedastizität
Die Voraussetzung der Varianzgleichheit in der linearen Regression bezieht sich auf die Varianz der Residuen über die Ausprägungen der vorhergesagten Werte hinweg.
Diese prüfen wir meist visuell anhand eines Residuenplots. Ergänzend kann ein inferenzstatistischer Test, wie etwa der Breusch-Pagan-Test, durchgeführt werden.
Den Residuenplot können wir in R ganz leicht abrufen indem wir die plot()-Funktion auf unser bereits erstelltes Regressionsmodell anwenden. Dabei erstellt die lm()-Funktion direkt vier Plots von denen wir zunächst mal mit which = 1 den ersten betrachten wollen.
plot(modC, which = 1)
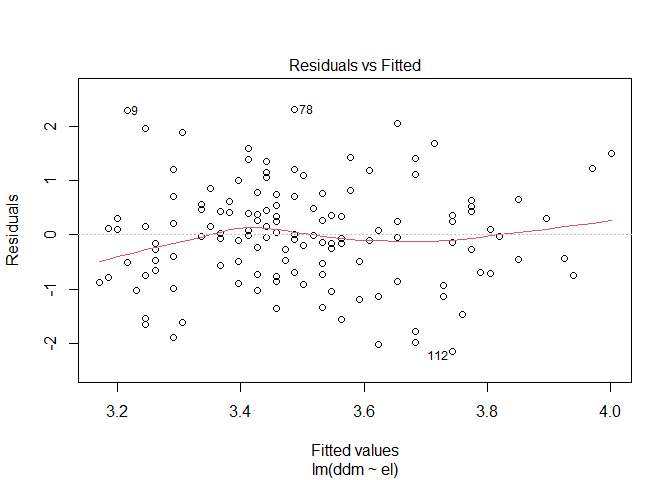
Auf der x-Achse sind die vorhergesagten Werte abgebildet und auf der y-Achse die dazugehörigen Residuen. Wenn wir davon ausgehen das sie über alle vorhergesagten werde ungefähr die gleiche Varianz aufweisen sollte die rote Linie in etwa horizontal verlaufen. Wichtig ist das wir keinen anderen Trend erkennen können. Da Residualplots manchmal etwas unübersichtlich sein können gibt uns R als dritten Plot auch den dazugehörigen Scale-Location-Plot aus.
plot(modC, which = 3)
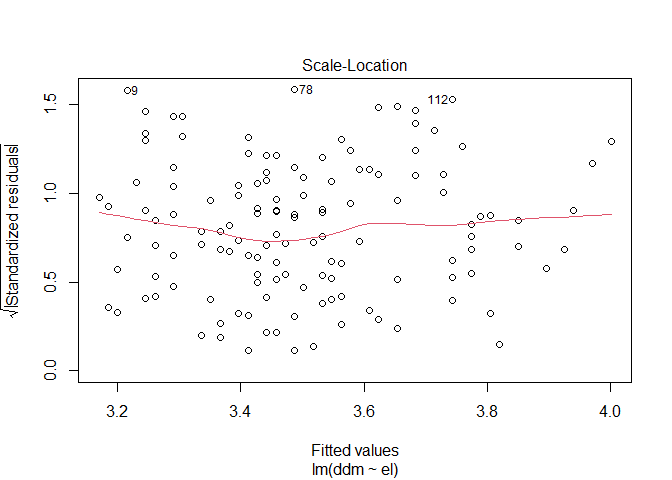
Hier wurden die Residuen transformiert und auch hier erkennen wir wie bereits im ersten Plot einen in etwa horizontalen Verlauf.
Der bereits erwähnte Breusch-Pagan-Test ist im car-Paket als ncvTest()-Funktion implementiert.
# install.packages("car")
library(car)
car::ncvTest(modC)
## Non-constant Variance Score Test
## Variance formula: ~ fitted.values
## Chisquare = 0.01971678, Df = 1, p = 0.88833
Auch dieser kommt zu einem nicht signifikanten Ergebnis weswegen wir schlussendlich die Voraussetzung als gegeben ansehen können. Hinweis: Der Breusch-Pagan-Test testet nur einen linearen Verlauf der Residuen! Natürlich kann die Homoskedastizitäts-Annahme auch verletzt sein, wenn die Residuen einem anderen Trend (z.B logarithmisch) folgen.
Normalverteilung
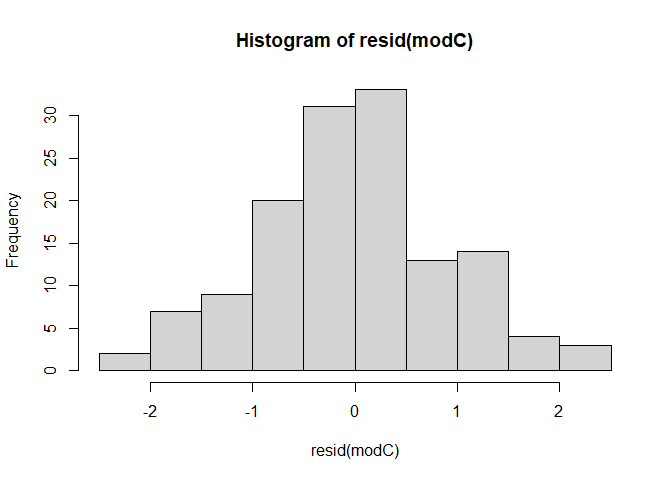
Die Annahme das Daten normalverteilt sind finden wir immer wieder in der Statistik. Bei der Regression bezieht sich diese Annahme auf die Verteilung der Residuen. Wie sie vielleicht noch aus dem Bachelor wissen, können wir uns Verteilungen in Form von Histogrammen anschauen. Glücklicherweise können wir die Residuen direkt unserem Modell entnehmen und an die hist()-Funktion übergeben.
resid(modC) |> hist()
Beliebter zur visuellen Überprüfung ist ein qq-Plot diesen können wir uns mit der gleichnamigen Funktion aus dem car-Paket ausgeben lassen.
car::qqPlot(modC)
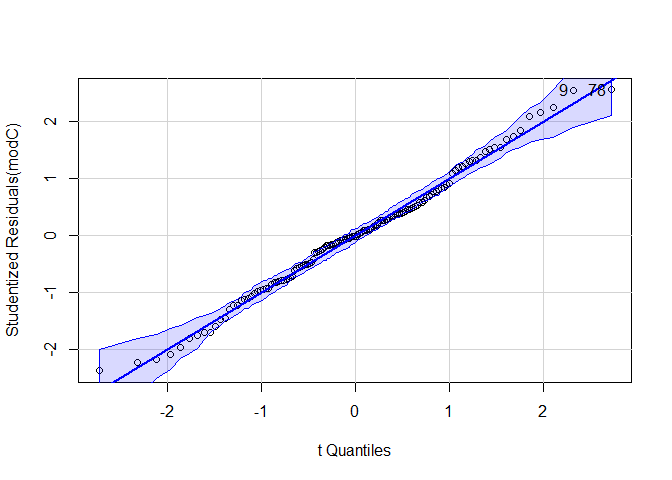
## [1] 9 78
Auch hier können wir keine besonderen Auffälligkeiten erkennen. Hinweis: Zusätzlich könnte man auch hier einen inferenzstatistischen Test durchführen z.B den Shapiro-Wilk-Test, die visuelle Überprüfung ist jedoch zu bevorzugen.
resid(modC) |> shapiro.test() # nicht signifikant
##
## Shapiro-Wilk normality test
##
## data: resid(modC)
## W = 0.99135, p-value = 0.5694
Linearität
Die korrekte Spezifikation ist eine sehr vielseitige Voraussetzung, die eher konzeptueller und weniger statischer Natur ist. Generell wird davon ausgegangen, dass in unserem Regressionmodell alle relevanten Prädiktoren aufgenommen wurden und dass die funktionale Form des Zusammenhangs korrekt abgebildet ist. Bei der linearen Regression eben, dass ein linearer Zusammenhang zwischen den Prädiktoren und dem Outcome besteht.
Ob ein linearer Zusammenhang zwischen unserem Prädiktor (el) und Outcome (ddm) besteht können wir uns z.B in einem Scatterplot anschauen.
car::scatterplot(ddm ~ el, data_analysis)
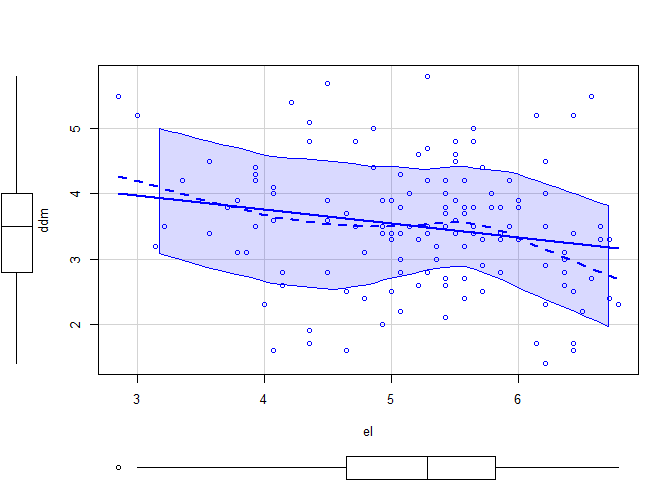
Des weiteren können wir auch hier die Residuenplots betrachten. Dafür bietet sich die residualPlots()-Funktion aus dem car-Paket an, da diese bereits einen möglichen quadratischen Trend einzeichnet.
car::residualPlots(modC)
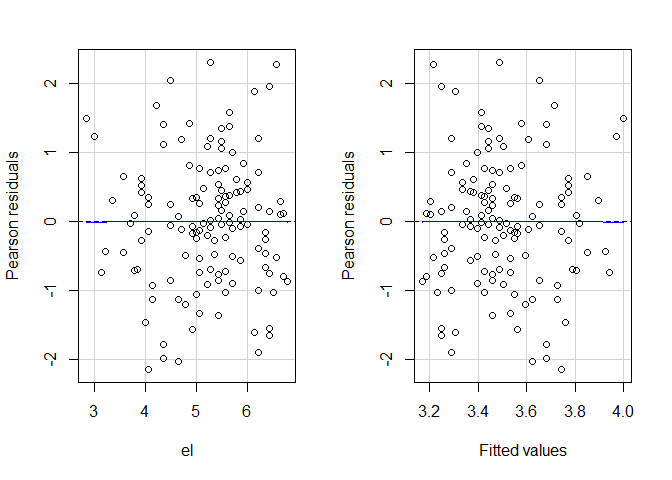
## Test stat Pr(>|Test stat|)
## el -0.0142 0.9887
## Tukey test -0.0142 0.9887
In der Console erscheint zusätzlich die inferenzstatistische Testung des quadratischen Trends. Insgesamt können wir keine nennenswerte Abweichung von der Linearität erkennen.
Ausreißer
Die Plausibilität unserer Daten ist enorm wichtig. Aus diesem Grund sollten Ausreißer oder einflussreiche Datenpunkte analysiert werden. Diese können bspw. durch Eingabefehler entstehen oder es sind seltene Fälle, welche so in natürlicher Weise (aber mit sehr geringer Häufigkeit) auftreten können. Es muss dann entschieden werden, ob Ausreißer die Repräsentativität der Stichprobe gefährden und ob diese besser ausgeschlossen werden sollten. Im Folgenden wollen wir zwei Maße betrachten die uns helfen Ausreißer zu identifizieren.
Der Hebelwert einer Person gibt an wie weit diese vom Mittelwert entfernt liegt und somit einen starken Einfluss auf das Regressionsgewicht haben könnte. Für die Beurteilung ob ein Hebelwert bedeutsam ist werden verschiedene Kriterien vorgeschlagen. So wird von Eid et al. (2017) für große Stichproben die Grenze $2 \cdot k/n$ und für kleine Stichproben $3 \cdot k/n$ vorgeschlagen.
Cook’s Distanz gibt eine Schätzung, wie stark sich die Regressionsgewichte verändern, wenn eine Person aus dem Datensatz entfernt wird. Fälle, deren Elimination zu einer deutlichen Veränderung der Ergebnisse führen würden, sollten kritisch geprüft werden. Als einfache Daumenregel gilt, dass ein Wert $> 1$ auf einen einflussreichen Datenpunkt hinweist.
Die influencePlot()-Funktion des car-Pakets berechnet uns beide für unser Modell und erstellt gleichzeitig ein Blasendiagramm. Schauen wir uns letzteres gemeinsam an. Auf der x-Achse sind die studentisierten Residuen abgetragen, auf der y-Achse die Hebelwerte. Die Größe und Einfärbung der Blasen ist Cook’s Distanz.
Fälle, die nach einem der Kriterien als Ausreißer identifiziert werden, werden im Streudiagramm durch ihre Zeilennummer gekennzeichnet. Diese Zeilennummern können verwendet werden, um sich die Daten der auffälligen Fälle anzeigen zu lassen. Diese sind im Objekt hinterlegt und wir können uns mit as.numeric(row.names(InfPlotC)) darauf zugreifen.
InfPlotC <- influencePlot(modC)
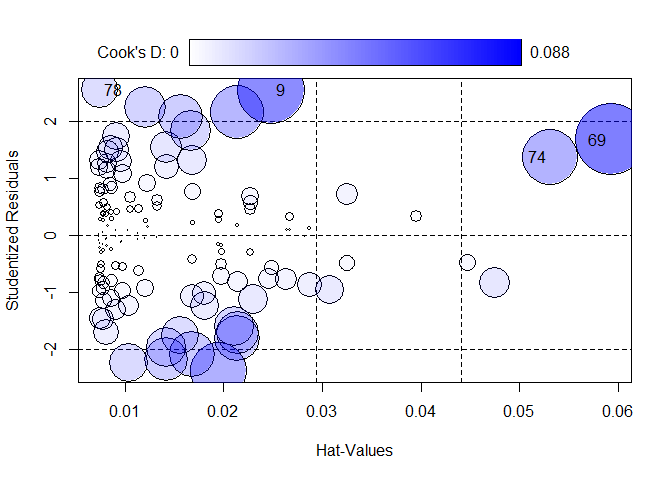
# Die Zeilennummer der auffälligen Personen abspeichern
IDsC <- as.numeric(row.names(InfPlotC))
Schauen wir uns die möglichen Ausreißer mal an.
data_analysis[IDsC, c(sprintf("el_%02d", 1:4), "el_05i", sprintf("el_%02d", 6:14), paste0("ddm_av_", 1:5), paste0("ddm_ap_", 1:5, "i"), "erwerb", "arbeit_std", "vorgesetzt", "entscheidung", "alter", "geschlecht", "time_sum")]
## el_01 el_02 el_03 el_04 el_05i el_06
## 9 7 7 7 7 5 7
## 69 6 7 1 1 1 1
## 74 2 6 1 1 2 3
## 78 7 7 1 7 7 7
## el_07 el_08 el_09 el_10 el_11 el_12 el_13
## 9 6 7 7 6 5 7 7
## 69 1 1 4 3 6 6 1
## 74 5 1 3 2 4 2 5
## 78 7 7 1 1 1 7 7
## el_14 ddm_av_1 ddm_av_2 ddm_av_3 ddm_av_4
## 9 7 7 7 7 6
## 69 1 7 7 7 7
## 74 5 6 7 7 7
## 78 7 7 7 7 7
## ddm_av_5 ddm_ap_1i ddm_ap_2i ddm_ap_3i
## 9 7 3 6 5
## 69 7 3 5 5
## 74 6 3 3 4
## 78 7 7 7 1
## ddm_ap_4i ddm_ap_5i erwerb arbeit_std
## 9 2 5 ja 20
## 69 2 5 ja 40
## 74 4 5 ja 20
## 78 1 7 ja 30
## vorgesetzt entscheidung alter geschlecht
## 9 ja ja 59 w
## 69 ja ja 36 w
## 74 ja ja 19 w
## 78 ja ja 54 w
## time_sum
## 9 421
## 69 418
## 74 302
## 78 323
- Fall 9 hat häufig mit dem maximalen Wert geantwortet jedoch vereinzelt auch recht niedrig. Dementsprechend weißt die Person zwar ein interessantes Antwortverhalten auf jedoch sehen wir keine Anzeichen das dies nicht der Realität entsprechen könnte.
- Fall 69 weißt einen geringen Empowering Leadership Wert auf. Das Antwortmuster der Person ist jedoch unauffällig.
- Fall 74 fällt durch ein großes Residuum auf. Die Person hat ausschließlich mit den extremsten Werten geantwortet. Auch das kann dem realen Antwortverhalten entsprechen gerade da dir Person eine durchschnittliche Bearbeitungszeit aufweißt.
- Fall 78 fällt durch eine unterdurchschnittliche Bearbeitungszeit auf. Die Person hat häufig mit extremen Werte geantwortet jedoch nicht immer.
- Fall NA fällt durch seinen niedrigen Empowering Leadership und Defensive Decision Making Wert auf. Das Antwortverhalten ist unauffällig.
Die Entscheidung, ob Ausreißer oder auffällige Datenpunkte aus Analysen ausgeschlossen werden, ist schwierig und kann nicht pauschal beantwortet werden. Im vorliegenden Fall gibt es keine eindeutigen Fälle die wir problemlos ausschließen könnten. Wenn Unschlüssigkeit über den Ausschluss von Datenpunkten bestehen, bietet es sich an, die Ergebnisse einmal mit und einmal ohne die Ausreißer zu berechnen und zu vergleichen. Sollte sich ein robustes Effektmuster zeigen, ist die Entscheidung eines Ausschlusses nicht essenziell.
Nun haben wir in aller Ausführlichkeit das Regressionsmodell für unseren c-Pfad erstellt. Wir erinnern uns nochmal an unser Mediationsmodell.

Nun seid ihr dran!
Aufgabe 3 (Übung)
- Erstellt das passende Regressionsmodell für den a-Pfad
Lösung
modA <- lm(pe ~ el, data_analysis)
summary(modA)
##
## Call:
## lm(formula = pe ~ el, data = data_analysis)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.28955 -0.39370 0.03077 0.40577 1.72868
##
## Coefficients:
## Estimate Std. Error t value
## (Intercept) 2.08383 0.35630 5.849
## el 0.69270 0.06744 10.271
## Pr(>|t|)
## (Intercept) 3.6e-08 ***
## el < 2e-16 ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.696 on 134 degrees of freedom
## Multiple R-squared: 0.4405, Adjusted R-squared: 0.4363
## F-statistic: 105.5 on 1 and 134 DF, p-value: < 2.2e-16
Auch hier wollen wir die Voraussetzungen testen. Dabei können wir uns an dem Code bedienen den wir für den c-Pfad geschrieben haben.
Homoskedastizität
plot(modA, which = 1)
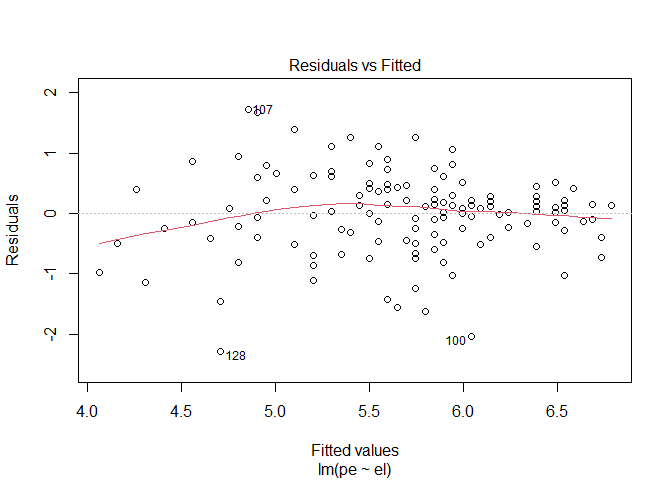
Die rote Linie ist sichtlich nicht horizontal. Betrachten wir dies nochmal im Scale-Location-Plot.
plot(modA, which = 3)
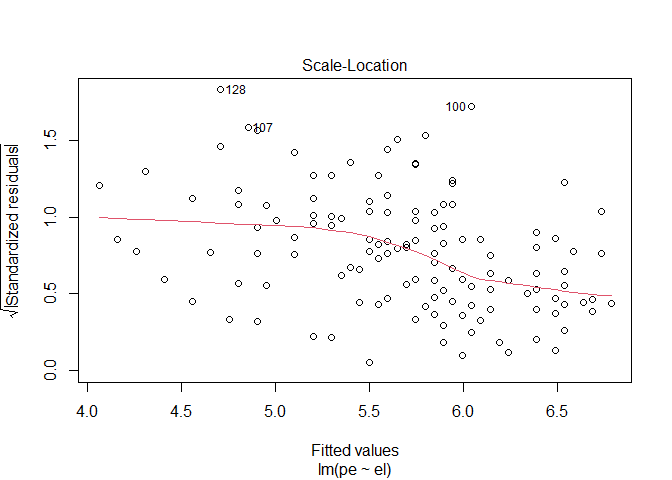
Hier erkennen wir eine deutliche Verletzung der Varianzgleichheit, die uns auch der inferenzstatistische Test bestätigt.
car::ncvTest(modA)
## Non-constant Variance Score Test
## Variance formula: ~ fitted.values
## Chisquare = 17.59425, Df = 1, p = 2.7341e-05
Umgang mit Heteroskedastizität
Wenn unsere Datenlage eine Voraussetzung für einen statistischen Test nicht erfüllt, ist die wichtigste anschließende Frage “warum?”. Eine pauschale Lösung, wie mit der Verletzung einer Annahme umgegangen werden soll, wird es nicht geben, weil - etwas dramatisch ausgedrückt - ein Symptom ein Indikator für verschiedene Krankheiten sein kann. Daher möchten wir uns an dieser Stelle erstmal nur der Frage widmen wie wir mit der Verletzung umgehen.
Bei der Verletzung der Homoskedastizitäts-Annahme haben wir folgende Möglichkeiten:
- Nutzen von weighted-least-squares (WLS) Regression
- Transformation der abhängigen Variable
- Bestimmen von robusten, korrigierten Standardfehlern
- Bootstrapping
Die gewichtete Regression wird bei starker Heteroskedastizität empfohlen. Da diese jedoch recht aufwändig ist und die Alternativen meist ausreichen behandeln wir diese. Auch auf die Transformation der anhängigen Variable werden wir im folgenden nicht näher eingehen, da diese die unschöne Nebenwirkung mit sich zieht das Ergebnisse schwieriger bis unmöglich zu interpretieren sind. Auf Bootstrapping gehen wir noch später ein.
Robuste Standardfehler
Heteroskedastizität führt vor allem zu einer Verzerrung der Standardfehler und damit zu Fehlern in der Inferenzstatistik.
Etabliert hat sich der sogennante HC3 (heteroskedasticitiy consistent) Ansatz den wir mit Hilfe des sandwich-Pakets nutzen können um die korrigierten Standardfehler zu berechnen.
# install.packages("sandwich")
library(sandwich)
se_corrected <- sandwich::vcovHC(modA)
Um diese nun bei der Berechnung unseres Regressionsmodells zu berücksichtigen brauchen wir leider ein weiteres Paket.
# install.packages("lmtest")
library(lmtest)
lmtest::coeftest(modA, vcov. = se_corrected)
##
## t test of coefficients:
##
## Estimate Std. Error t value
## (Intercept) 2.08383 0.41167 5.0618
## el 0.69271 0.07275 9.5217
## Pr(>|t|)
## (Intercept) 1.343e-06 ***
## el < 2.2e-16 ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Wie zu erwarten, die Regressionsgewichte haben sich nicht verändert jedoch die Standardfehler. Inhaltlich ändert sich in diesem Fall nichts.
Normalverteilung
resid(modA) |> hist()
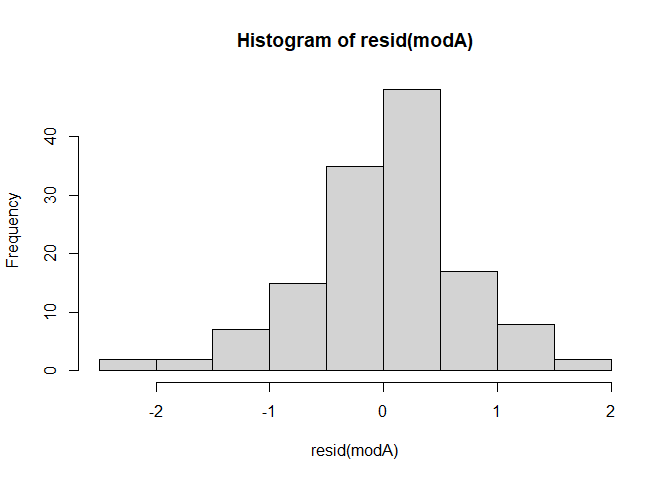
car::qqPlot(modA)
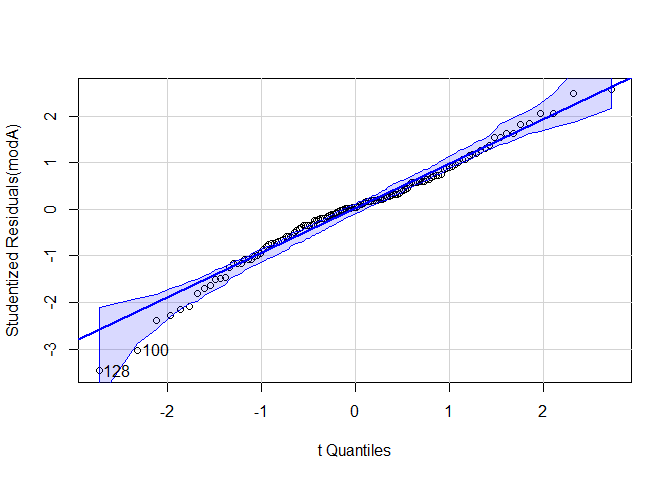
## [1] 100 128
Beide Plots lassen eine Normalverteilung erkennen.
Linearität
scatterplot(pe ~ el, data_analysis)
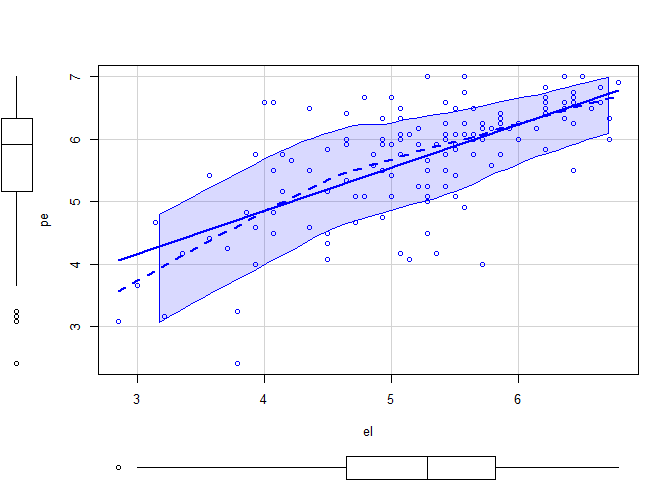
residualPlots(modA)
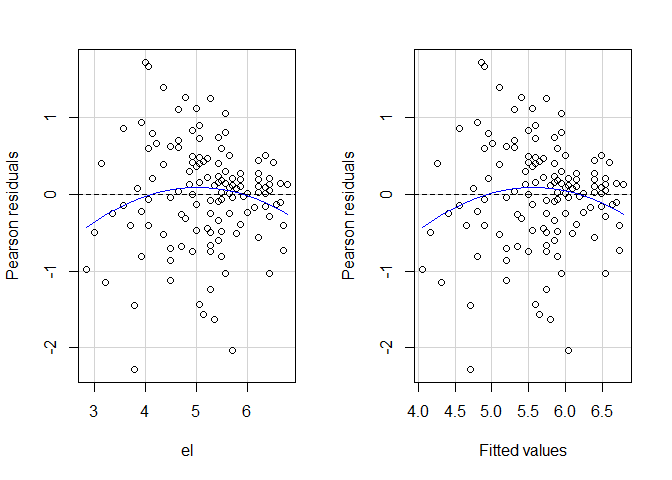
## Test stat Pr(>|Test stat|)
## el -1.8059 0.07319 .
## Tukey test -1.8059 0.07093 .
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Auch die Annahme der Linearität ist gegeben.
Ausreißer
An dieser Stelle ersparen wir uns die Überprüfung der Ausreißer. Jedoch könnt ihr das anhand des Codes für das erste Modell mal selber machen!
Nun widmen wir uns dem b-Pfad. Traditionell wird dieser in einem Modell mit Prädiktor und Mediator ermittelt (multiple Regression!). Wir wollen uns jedoch zunächst den univariaten Zusammenhang zwischen Psychological Empowerment und Defensive Decision Making anschauen.
Aufgabe 4
- Erstellt das passende Regressionsmodell für den univariaten Zusammenhang zwischen Psychological Empowerment und Defensive Decision Making
- Testet die relevanten Voraussetzungen
- Bonus: Versucht euch am Umgang mit verletzten Voraussetzungen
Lösung
# Modell aufstellen
mod_pe_ddm <- lm(ddm ~ pe, data_analysis)
summary(mod_pe_ddm)
##
## Call:
## lm(formula = ddm ~ pe, data = data_analysis)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.7099 -0.6245 -0.0261 0.4673 2.7476
##
## Coefficients:
## Estimate Std. Error t value
## (Intercept) 5.46725 0.47498 11.510
## pe -0.34498 0.08237 -4.188
## Pr(>|t|)
## (Intercept) < 2e-16 ***
## pe 5.07e-05 ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.8873 on 134 degrees of freedom
## Multiple R-squared: 0.1157, Adjusted R-squared: 0.1091
## F-statistic: 17.54 on 1 and 134 DF, p-value: 5.067e-05
# Homoskedastizität
plot(mod_pe_ddm, which = 1) # lässt eine Verletzung vermuten
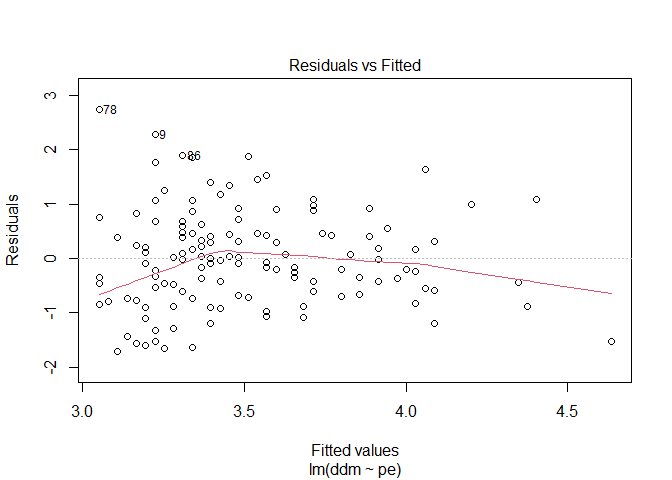
plot(mod_pe_ddm, which = 3) # rote Linie nicht wirklich horizontal
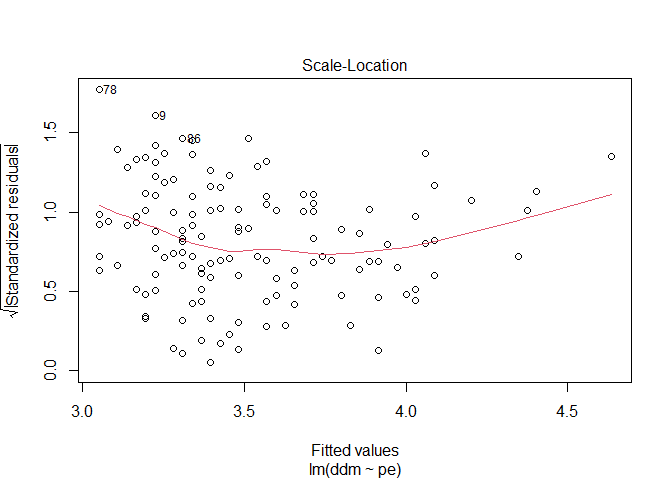
car::ncvTest(mod_pe_ddm) # bestätigt die Vermutung das eine Verletzung vorliegt
## Non-constant Variance Score Test
## Variance formula: ~ fitted.values
## Chisquare = 3.381059, Df = 1, p = 0.06595
# Normalverteilung
resid(mod_pe_ddm) |> hist()
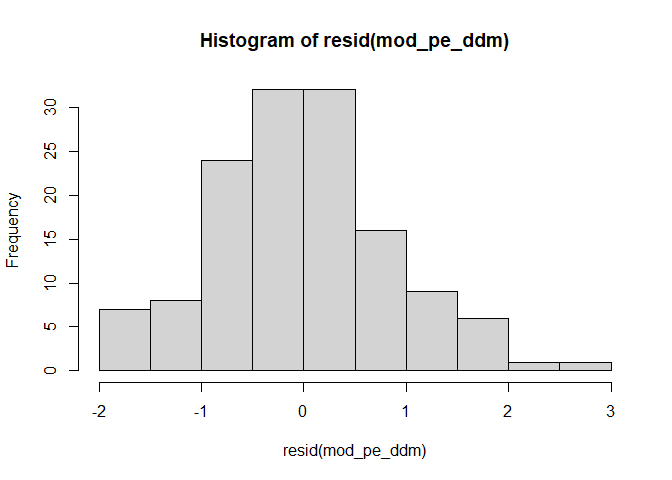
car::qqPlot(mod_pe_ddm) # sieht ok aus
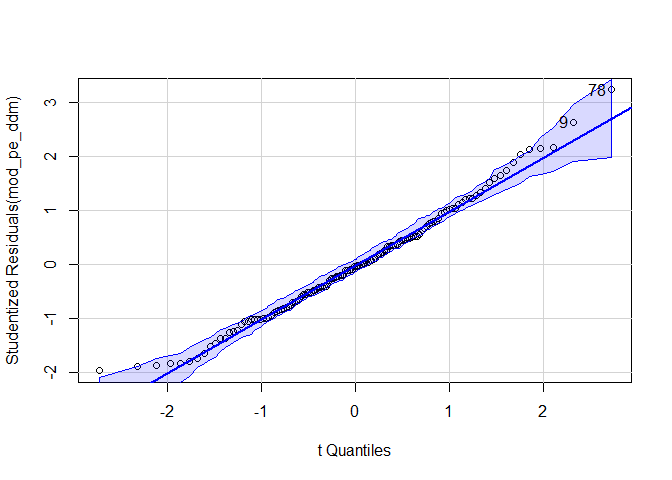
## [1] 9 78
# Bonus: Modell mit robusten Standardfehlern (HC3) rechnen
lmtest::coeftest(mod_pe_ddm, vcov. = sandwich::vcovHC(mod_pe_ddm))
##
## t test of coefficients:
##
## Estimate Std. Error t value
## (Intercept) 5.467251 0.538470 10.1533
## pe -0.344984 0.095968 -3.5948
## Pr(>|t|)
## (Intercept) < 2.2e-16 ***
## pe 0.0004551 ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Bootstrapping
Eine weitere Möglichkeit im Umgang mit verletzten Voraussetzungen ist Bootstrapping. Die Idee basiert auf dem Konzept der Stichprobenkennwerteverteilung. Diese würden wir erzeugen indem wir unsere Studie sehr häufig durchführen. Die Schwankung zwischen den Stichproben würde zu leichten Unterschieden in den Regressionsgewichten führen. Diese Schwankung wird traditionellerweise als Standardfehler bezeichnet und - unter bestimmten Annahmen - mit Formeln berechnet, auch dann, wenn wir nur eine Studie durchgeführt haben. Weil diese “bestimmten Annahmen” in unserem Fall nicht halten, könnten wir mehrere Studien durchführen und die Verteilung wirklich ermitteln. Die Grundidee beim Bootstrap ist: wenn die Beobachtungen in der Stichprobe eine Zufallsziehung sind, können wir aus dieser Stichprobe auch erneut zufällig ziehen, um eine andere Zufallsstichprobe zu erzeugen. Für diese können wir das Regressionsgewicht berechnen und dann wiederholen wir das Ganze - so lange, bis wir die Stichprobenkennwerteverteilung ausreichend genau erzeugt haben. Der Clou ist dabei, dass diese Ziehung mit Zurücklegen erfolgt, sodass jede Stichprobe im Bootstrap aus genauso vielen Beobachtungen besteht, wie unsere eigentliche Stichprobe.
Bootstrapping kann somit nicht nur bei Heteroskedastizität helfen sondern befreit uns außerdem von der Normalverteilungsannahme.
Nun zur Implementation des Ganzen. Für unseren Fall, die Regression die den univariaten Zusammenhang zwischen Psychological Empowerment und Defensive Decision Making modelliert, benötigen wir folgende X Schritte.
- Boot Stichprobe mit Zurücklegen aus der vorhandenen Stichprobe ziehen
- Regressionsmodell auf Basis der gebooteten Daten schätzen
- Regressionsgewicht extrahieren
- Sehr häufig (1000-Mal) Schritte 1.-3. wiederholen und für jede Replikation das Regressionsgewicht abspeichern
- Über alle Schätzungen des Regressionsgewichts mitteln und den Standardfehler bestimmen
- Mit Hilfe des Standardfehlers das Konfidenzintervall bestimmen und die Signifikanzentscheidung treffen
# Schritt 1
boot_data <- data_analysis[sample(1:nrow(data_analysis), nrow(data_analysis), replace = TRUE), ]
# Schritt 2
boot_mod <- lm(ddm ~ pe, boot_data)
# Schritt 3
coef(boot_mod)["pe"]
## pe
## -0.3472811
Um diese drei Schritte zu wiederholen bietet sich die replicate()-Funktion an. Diese nimmt als Input eine Funktion entgegen die sie dann so häufig wiederholt wie wir es möchten. Wie sie bereits gelernt haben ist eine Funktion auch nur Code der mehrere Zeilen Code zusammenfasst.
booting <- function(data){
# Schritt 1
boot_data <- data_analysis[sample(1:nrow(data), size =
nrow(data), replace =
TRUE), ]
# Schritt 2
boot_mod <- lm(ddm ~ pe, boot_data)
# Schritt 3
return(coef(boot_mod)["pe"])
}
Wie ihr seht mussten wir dafür nicht viel Code verändern. Unsere Funktion booting() nimmt einen Datensatz entgegen (Argument data) und gibt uns das Regressionsgewicht unseres Prädiktors mit return() aus.
# Schritt 4
set.seed(12345) # damit wir alle das gleiche Ergebnis produzieren
boot_beta_pe <- replicate(n = 1000, booting(data_analysis))
# Schritt 5
mean(boot_beta_pe)
## [1] -0.3505717
Um nun den Standardfehler zu ermitteln, erinnern wir uns daran, dass dieser die Standardabweichung der Stichprobenkennwerteverteilung ist – genau die, die wir durch das Bootstrapping simuliert haben. Dementsprechend entspricht der Standardfehler hier der Standardabweichung unserer Verteilung der Regressionsgewichte.
# Schritt 6
sd(boot_beta_pe)
## [1] 0.09074113
Da wir nun den Standardfehler bestimmt haben, kommen wir zum letzten Schritt: der Berechnung des Konfidenzintervalls. Auch hier müssen wir nicht auf die klassische Formel zurückgreifen, die wir gestern verwendet haben, da wir ja die Stichprobenkennwerteverteilung simuliert haben. Das Konfidenzintervall ergibt sich daher ganz einfach als Bereich zwischen dem 2,5%- und dem 97,5%-Quantil der Bootstrap-Verteilung:
quantile(boot_beta_pe, c(0.025, 0.975))
## 2.5% 97.5%
## -0.5367742 -0.1794189
Da das Konfidenzintervall die Null nicht umfasst, ist das Regressionsgewicht auch nach dem Bootstrapping signifikant. Bootstrapping ist ein ziemlich mächtiges Verfahren – wir haben es hier einmal Schritt für Schritt von Hand durchgeführt. In der Praxis ist es aber in vielen Paketen bereits implementiert, was uns eine Menge Arbeit abnimmt.
Kommen wir nun zurück zur eigentlichen Fragestellung der Mediation. Wie bereits weiter oben erwähnt, berechnen wir für den b-Pfad eine multiple Regression, da wir prüfen möchten, ob der Mediator den Zusammenhang zwischen Prädiktor und Outcome erklärt.
Aufgabe 5
- Erstellen sie das multiple Regressionsmodell
Lösung
modBC <- lm(ddm ~ pe + el, data_analysis)
summary(modBC)
##
## Call:
## lm(formula = ddm ~ pe + el, data = data_analysis)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.72362 -0.60717 -0.02596 0.48115 2.78474
##
## Coefficients:
## Estimate Std. Error t value
## (Intercept) 5.38914 0.51044 10.558
## pe -0.37625 0.11046 -3.406
## el 0.04916 0.11529 0.426
## Pr(>|t|)
## (Intercept) < 2e-16 ***
## pe 0.000872 ***
## el 0.670498
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.89 on 133 degrees of freedom
## Multiple R-squared: 0.117, Adjusted R-squared: 0.1037
## F-statistic: 8.807 on 2 and 133 DF, p-value: 0.0002558
Das Regressionsgewicht der unabhängigen Variable ist nun nicht mehr signifikant, während das des Mediators weiterhin signifikant bleibt. In diesem Fall sprechen wir von einer vollständigen Mediation.
Auch hier sollten wir natürlich die Voraussetzungen überprüfen. Machen wir dies kurz mal im Schnelldurchgang.
# Homoskedastizität
plot(modBC, which = 3) # starke Abweichungen zu erkennen
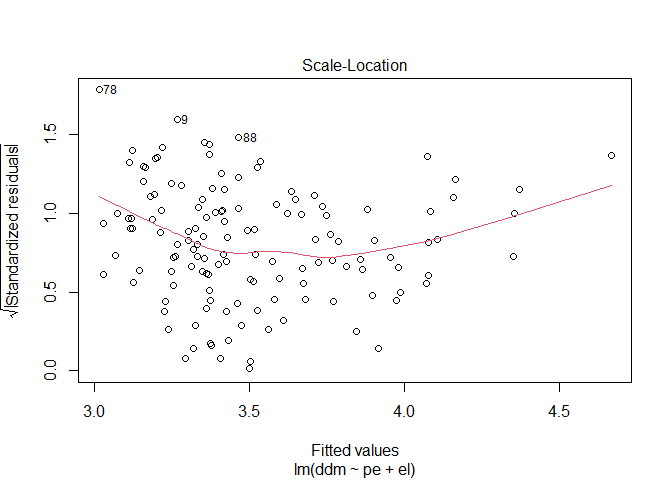
car::ncvTest(modBC) # signifikant --> Voraussetzung verletzt
## Non-constant Variance Score Test
## Variance formula: ~ fitted.values
## Chisquare = 3.154361, Df = 1, p = 0.075724
# Normalverteilung
resid(modBC) |> hist()
car::qqPlot(modBC) # unproblematisch
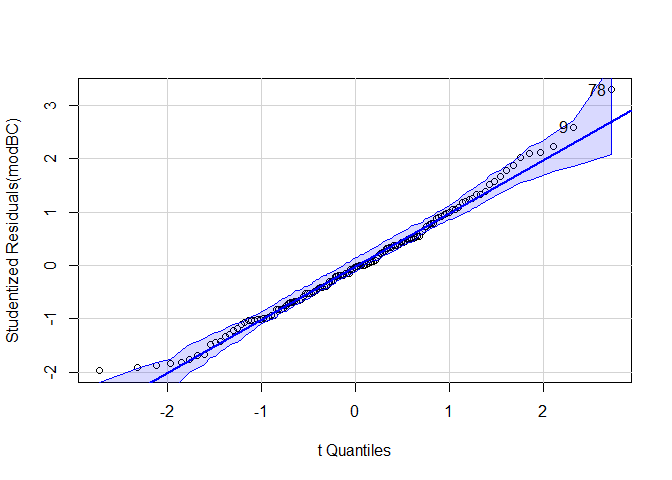
## [1] 9 78
# Linearität
car::residualPlots(modBC) # pe geht in Richtung eines quadratischen Effekts jedoch nicht signifikant
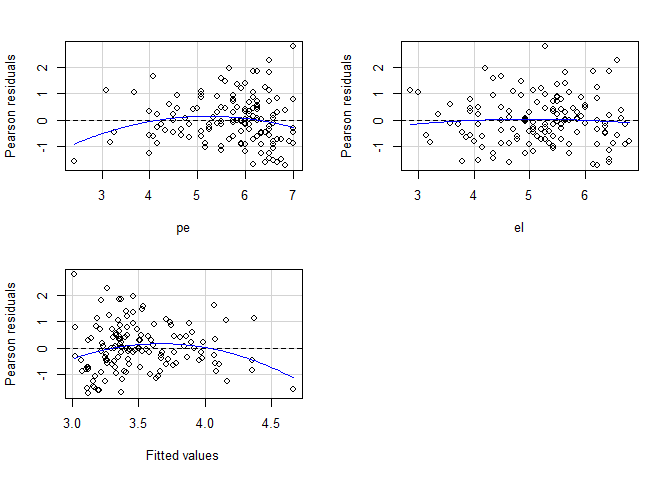
## Test stat Pr(>|Test stat|)
## pe -1.9655 0.05145 .
## el -0.5469 0.58535
## Tukey test -2.3452 0.01902 *
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Und wie nach unserer vorherigen univariaten Betrachtung kaum überraschend, ist die Homoskedastizität auch im multiplen Modell verletzt. Wir entscheiden uns auch hier zu bootstrappen und bestimmen im gleichen Atemzug den indirekten Effekt (ab).
Dafür nutzen wir die Funktion mediate() aus dem psych-Paket. In dieser Funktion stellen wir zunächst unser Modell auf, die Syntax erinnert dabei stark an die der lm()-Funktion, nur das wir einen der Prädiktoren durch die Klammern als Mediator kennzeichnen. Per default wird ein bootstrap mitberechnet.
set.seed(12345)
psych::mediate(ddm ~ el + (pe), data = data_analysis) |> summary()
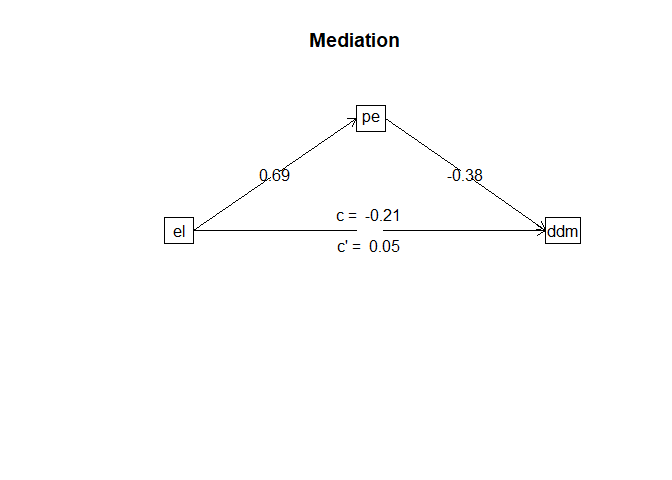
## Call: psych::mediate(y = ddm ~ el + (pe), data = data_analysis)
##
## Direct effect estimates (traditional regression) (c') X + M on Y
## ddm se t df Prob
## Intercept 5.39 0.51 10.56 133 2.66e-19
## el 0.05 0.12 0.43 133 6.70e-01
## pe -0.38 0.11 -3.41 133 8.72e-04
##
## R = 0.34 R2 = 0.12 F = 8.81 on 2 and 133 DF p-value: 0.000256
##
## Total effect estimates (c) (X on Y)
## ddm se t df Prob
## Intercept 4.61 0.47 9.73 134 2.97e-17
## el -0.21 0.09 -2.36 134 1.97e-02
##
## 'a' effect estimates (X on M)
## pe se t df Prob
## Intercept 2.08 0.36 5.85 134 3.6e-08
## el 0.69 0.07 10.27 134 1.3e-18
##
## 'b' effect estimates (M on Y controlling for X)
## ddm se t df Prob
## pe -0.38 0.11 -3.41 133 0.000872
##
## 'ab' effect estimates (through all mediators)
## ddm boot sd lower upper
## el -0.26 -0.26 0.09 -0.44 -0.08
Die Funktion gibt uns außerdem eine Abbildung aus, in der die Regressionsgewichte direkt an den entsprechenden Pfaden dargestellt sind. Voilà – wir haben unsere Mediation berechnet!
](/media/header/syntax.jpg)