](/media/header/syntax.jpg)
Lösungen zur Übung
Übung 1 - Datenhandling
Aufgabe 1
Laden Sie den Datensatz edu_exp in ihr enviroment. Die URL lautet: https://pandar.netlify.app/daten/edu_exp.rda
**Lösung anzeigen**
load(url('https://pandar.netlify.app/daten/edu_exp.rda'))
Aufgabe 2
Machen Sie einen Faktor aus der Variable Wealth und ordnen sie die Levels so, dass die höchste Wohlstandsstufe Level 1 erhält.
**Lösung anzeigen**
edu_exp$Wealth_factor <- as.factor(edu_exp$Wealth)
levels(edu_exp$Wealth_factor) #high_income ist bereits Level 1
## [1] "" "high_income" "low_income"
## [4] "lower_middle_income" "upper_middle_income"
Aufgabe 3
Entfernen Sie die Beobachtungen, die NA’s auf der Variable Income haben.
**Lösung anzeigen**
edu_exp <- edu_exp[!is.na(edu_exp$Income), ]
Aufgabe 4
Bauen sie ein data.frame aus country + primary + secondary + tertiary
EXTRA: nur Länder mit Primary > 30
**Lösung anzeigen**
edu_neu <- data.frame(country = edu_exp$Country, Primary = edu_exp$Primary, Secondary = edu_exp$Secondary , Tertiary = edu_exp$Tertiary)
# oder mit der Subset-Funktion
edu_neu2 <- subset(edu_exp, select = c(Country, Primary, Secondary, Tertiary))
# EXTRA
edu_neu3 <- subset(edu_exp, subset = Primary > 30, select = c(Country, Primary, Secondary, Tertiary))
Aufgabe 5
Welche Fuktion nutzt man um data.frames zusammenzuführen?
**Lösung anzeigen**
rbind() oder cbind()
Übung 2 - t-Tests
Aufgabe 1
Testen Sie folgende Hypothesen auf statistische Signifikanz. Die Hypothesen und Variablen sind frei erfunden. Schreibe Sie die korrekte R-Syntax für diese fiktiven Beispiele.
$H_1$: Personen mit akademischem Abschluss (edu) zeigen im Mittel eine höhere Umweltsensibilität (sens) als Personen ohne akademischen Abschluss.
Normalverteilung: gegeben
Homoskedastizität: gegeben
**Lösung anzeigen**
#t.test(sens ~ edu,
# alternative = "greater",
# paired = FALSE,
# var.equal = TRUE)
$H_1$: Nicht-Führungskräfte (lead) weisen eine geringere Stressresistenz (stress) auf als Führungskräfte.
Normalverteilung: gegeben
Homoskedastizität: gegeben
**Lösung anzeigen**
#t.test(stress ~ lead,
# alternative = "less",
# paired = FALSE,
# var.equal = TRUE)
$H_1$: Personen, die Haustiere besitzen (pet), berichten von einer höheren emotionalen Bindung (emo) zu ihren Mitmenschen als Personen ohne Haustiere.
Normalverteilung: gegeben
Homoskedastizität: nicht gegeben
**Lösung anzeigen**
#t.test(emo ~ pet,
# alternative = "greater",
# paired = FALSE,
# var.equal = FALSE)
$H_1$: Es besteht ein Unterschied in den Reaktionszeiten (react) zwischen Personen, die regelmäßig Videospiele spielen (game), und Personen, die keine Videospiele spielen.
Normalverteilung: nicht gegeben
Homoskedastizität: gegeben
**Lösung anzeigen**
#wilcox.test(react ~ game,
# alternative = "two.sided",
# paired = FALSE)
$H_1$: Ältere Geschwister (respons_old) zeigen im Durchschnitt eine höhere Verantwortungsübernahme als jüngere Geschwister (respons_young).
Normalverteilung: gegeben
Homoskedastizität: gegeben
**Lösung anzeigen**
#t.test(respons_old, respons_young,
# alternative = "greater",
# paired = TRUE)
$H_1$: Nichtraucher und Raucher (smoke) unterscheiden sich in ihrer sportlichen Leistungsfähigkeit (athl).
Normalverteilung: gegeben
Homoskedastizität: nicht gegeben
**Lösung anzeigen**
#t.test(athl ~ smoke,
# alternative = "two.sided",
# paired = FALSE,
# var.equal = FALSE)
$H_1$: Die Stressbelastung (stress) unterscheidet sich zwischen vor und nach einer Sporteinheit (time).
Normalverteilung: nicht gegeben
Homoskedastizität: nicht gegeben
**Lösung anzeigen**
#wilcox.test(stress ~ time,
# alternative = "two.sided",
# paired = TRUE)
$H_1$: Extravertierte Personen (int_extra) haben im Schnitt mehr tägliche soziale Interaktionen als introvertierte Personen (int_intro).
Normalverteilung: nicht gegeben
Homoskedastizität: nicht gegeben
**Lösung anzeigen**
#wilcox.test(int_extra, int_intro,
# alternative = "greater",
# paired = FALSE)
Aufgabe 2
Laden Sie den Datensatz distort ein, wenn noch nicht geschehen. Informationen zu den Variablen finden Sie hier.
**Tipp**
source("https://pandar.netlify.app/daten/Data_Processing_distort.R")
Testen Sie folgende Hypothese auf statistische Signifikanz. Vergessen Sie nicht zuvor die Voraussetzungen zu überprüfen.
$H_1$: Männer und Frauen unterscheiden sich in ihrer wahrgenommenen Marginalisierung.
**Lösung anzeigen**
# sex auf die relevanten Ausprägungen reduzieren
distort2 <- subset(distort, subset = sex %in% c("female", "male"))
# Normalverteilung
library(car)
car::qqPlot(distort2$marginal)
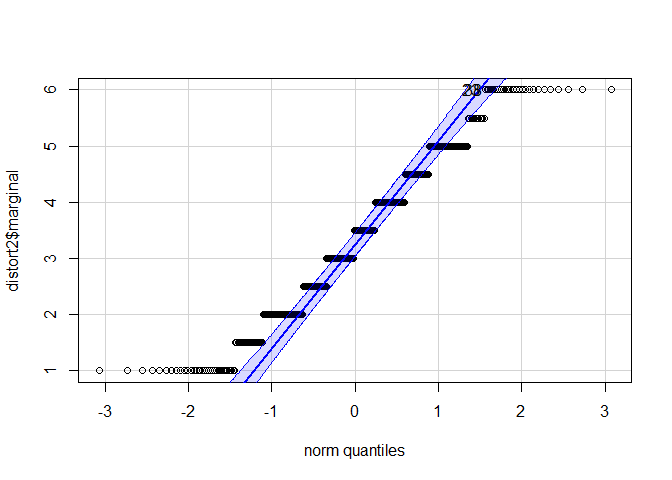
## [1] 23 38
shapiro.test(distort2$marginal)
##
## Shapiro-Wilk normality test
##
## data: distort2$marginal
## W = 0.96067, p-value = 7.166e-10
# zentraler Grenzwertsatz --> Normalverteilung kann angenommen werden
# Homoskedastizität
car::leveneTest(distort2$marginal ~ distort2$sex)
## Levene's Test for Homogeneity of Variance (center = median)
## Df F value Pr(>F)
## group 1 0.1302 0.7184
## 467
# nicht signifikant --> Homoskedastizität kann angenommen werden
# Test
t.test(distort2$marginal ~ distort2$sex,
var.equal = TRUE)
##
## Two Sample t-test
##
## data: distort2$marginal by distort2$sex
## t = -1.6061, df = 467, p-value = 0.1089
## alternative hypothesis: true difference in means between group female and group male is not equal to 0
## 95 percent confidence interval:
## -0.45928717 0.04616602
## sample estimates:
## mean in group female mean in group male
## 3.24187 3.44843
Übung 3 - Abschlussaufgabe
Vorbereitungen:
Zuerst laden wir den Datensatz “Bullyingprävention bei Jugendlichen (fairplayer)” ein:
load(url("https://pandar.netlify.app/daten/fairplayer.rda"))
Der Datensatz stammt aus einer Studie von Bull, Schultze & Scheithauer (2009), in der die Effektivität eines Interventionsprogramms zur Bullyingprävention bei Jugendlichen untersucht wurde. Das Codebook können sie dem folgenden Link entnehmen: https://pandar.netlify.app/daten/datensaetze/
1.) Beschreibung des Datensatzes a) Wie viele Beobachtungen auf wie vielen Variablen gibt es? b) Existieren fehlende Daten? c) Wie viele Beobachtungen verlieren Sie, wenn sie alle Beobachtungen mit fehlenden Werten herauswerfen?
**Lösung anzeigen**
# Aufgabe 1:
## a)
dim(fairplayer)
## [1] 155 31
## b)
sum(is.na(fairplayer))
## [1] 830
## c)
fairplayer_NA <- na.omit(fairplayer)
dim(fairplayer_NA)
## [1] 106 31
2.) Datenaufbereitung
a) Entfernen Sie den Messzeitpunkt T3.
**Lösung anzeigen**
fairplayer_T1u2 <- fairplayer_NA[, !names(fairplayer_NA) %in% c("ra1t3", "ra2t3", "ra3t3", "em1t3", "em2t3", "em3t3", "si1t3", "si2t3", "si3t3")]
b) Passen Sie die Reihennamen an: ID, Klassenstufe, Interventiosgruppe, Geschlecht. Die Items können gleich benannt bleiben.
**Tipp**
Befehl colnames()
**Lösung anzeigen**
colnames(fairplayer_T1u2)[1:4] <- c("ID", "Klassenstufe", "Interventionsgruppe", "Geschlecht")
c) Fassen Sie die Items der Skalen Relationale Angst, Empathie und Soziale Intelligenz. Achten Sie dabei darauf immer nur Items der gleichen Messzeitpunkte zusammenzufassen.
**Tipp**
Befehl rowSums()
**Lösung anzeigen**
fairplayer_T1u2$rat1 <- rowSums(fairplayer_T1u2[, c("ra1t1", "ra2t1", "ra3t1")])
fairplayer_T1u2$rat2 <- rowSums(fairplayer_T1u2[, c("ra1t2", "ra2t2", "ra3t2")])
fairplayer_T1u2$emt1 <- rowSums(fairplayer_T1u2[, c("em1t1", "em2t1", "em3t1")])
fairplayer_T1u2$emt2 <- rowSums(fairplayer_T1u2[, c("em1t2", "em2t2", "em3t2")])
fairplayer_T1u2$sit1 <- rowSums(fairplayer_T1u2[, c("si1t1", "si2t1", "si3t1")])
fairplayer_T1u2$sit2 <- rowSums(fairplayer_T1u2[, c("si1t2", "si2t2", "si3t2")])
3.) Deskriptivstatistik:
a) Erstellen Sie eine Tabelle, die die statistischen Kennwerte der Skalen relationale Angst, Empathie und Soziale Intelligenz zu T1 und T2 enthalten.
**Lösung anzeigen**
library(psych)
describe(fairplayer_T1u2[ , c("rat1", "rat2", "emt1", "emt2", "sit1", "sit2")])
## vars n mean sd median trimmed mad min max range skew kurtosis
## rat1 1 106 4.10 1.59 3.0 3.80 0.00 3 11 8 1.81 3.62
## rat2 2 106 4.04 1.66 3.0 3.69 0.00 3 11 8 2.19 5.35
## emt1 3 106 11.50 2.22 11.5 11.60 2.22 4 15 11 -0.62 0.66
## emt2 4 106 11.47 2.38 12.0 11.64 2.97 3 15 12 -0.78 0.75
## sit1 5 106 8.21 2.80 8.0 8.08 2.97 3 15 12 0.40 -0.61
## sit2 6 106 8.82 2.91 9.0 8.77 2.97 3 15 12 0.16 -0.25
## se
## rat1 0.15
## rat2 0.16
## emt1 0.22
## emt2 0.23
## sit1 0.27
## sit2 0.28
4.) T-Test:
a) Gibt es signifikante Gruppenunterschiede in der Skala soziale Intelligenz zu T1 zwischen Mädchen und Jungen? (Homoskedastizität gegeben; ohne Voraussetzungsprüfung)
**Lösung anzeigen**
t.test(fairplayer_T1u2$sit1 ~ fairplayer_T1u2$Geschlecht, # abhängige Variable ~ unabhängige Variable
alternative = "two.sided", # beidseitig
var.equal = TRUE, # Homoskedastizität liegt vor
conf.level = 0.95) # alpha = 5%
##
## Two Sample t-test
##
## data: fairplayer_T1u2$sit1 by fairplayer_T1u2$Geschlecht
## t = 0.55296, df = 104, p-value = 0.5815
## alternative hypothesis: true difference in means between group female and group male is not equal to 0
## 95 percent confidence interval:
## -0.7840392 1.3903610
## sample estimates:
## mean in group female mean in group male
## 8.344828 8.041667
b) Wie groß ist die Effektstärke dieses Unterschieds?
**Lösung anzeigen**
effsize::cohen.d(fairplayer_T1u2$sit1 ~ fairplayer_T1u2$Geschlecht,
conf.level = 0.95)
##
## Cohen's d
##
## d estimate: 0.1078979 (negligible)
## 95 percent confidence interval:
## lower upper
## -0.2793261 0.4951219
c) Erstellen Sie GGPlots, die die Gruppenunterschiede verbildlichen.
**Lösung anzeigen**
library(ggplot2)
## Most basic Plot:
ggplot(data = fairplayer_T1u2,
mapping = aes(x = sit1,
y = Geschlecht)
) +
geom_boxplot()
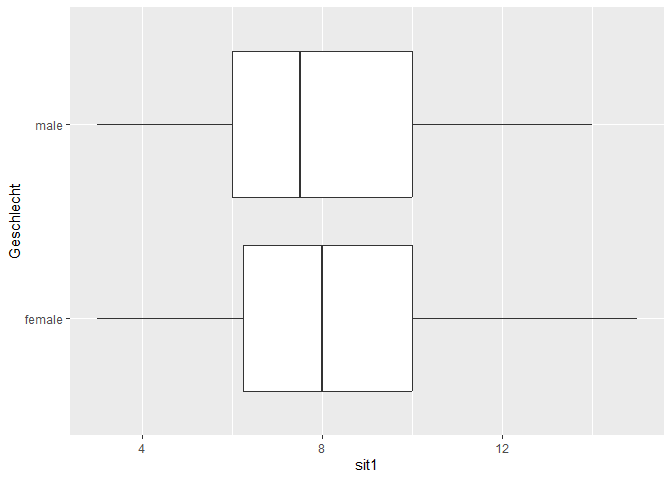
5.) Regression:
a) Sagen die Prädiktoren Geschlecht, Interventionsgruppe, Wert zu T1 (Relationale Angst) und Klassenstufe den Wert im Bereich relationale Angst zu T2 voraus? Erstellen Sie ein entsprechendes Regressionsmodell und interpretieren Sie den R-Output.
**Lösung anzeigen**
reg_mod <- lm(rat2 ~ Geschlecht + Interventionsgruppe + rat1 + Klassenstufe, data = fairplayer_T1u2)
summary(reg_mod)
##
## Call:
## lm(formula = rat2 ~ Geschlecht + Interventionsgruppe + rat1 +
## Klassenstufe, data = fairplayer_T1u2)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.9795 -0.7636 -0.4128 0.6004 6.8951
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.82898 0.70483 2.595 0.010884 *
## Geschlechtmale 0.56819 0.30776 1.846 0.067817 .
## InterventionsgruppeIGS 0.02166 0.44333 0.049 0.961134
## InterventionsgruppeIGL 0.39149 0.44619 0.877 0.382362
## rat1 0.35084 0.09715 3.611 0.000478 ***
## Klassenstufe 0.07280 0.07088 1.027 0.306880
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.561 on 100 degrees of freedom
## Multiple R-squared: 0.1535, Adjusted R-squared: 0.1111
## F-statistic: 3.625 on 5 and 100 DF, p-value: 0.004685
6.) GGPlot:
a) Erstellen Sie einen Plot, der den Zusammenhang zwischen relationaler Angst und sozialer Intelligenz zu T1 darstellt. Fügen Sie eine lineare Trendlinie hinzu und berichten sie die Korrelation und ihre Signifikant.
**Lösung anzeigen**
## Most basic Plot:
scatterplot <- ggplot(fairplayer_T1u2,
aes(x = rat1,
y = sit1)) +
geom_point()
scatterplot +
geom_smooth(method=lm , color="red", se=T)
## `geom_smooth()` using formula = 'y ~ x'
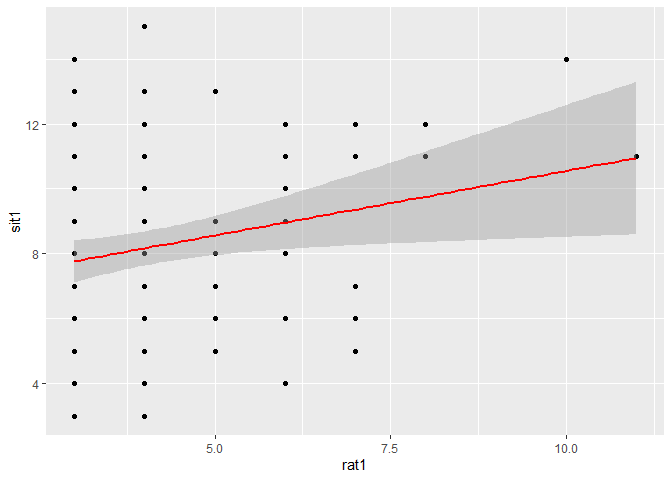
## Korrelationstest
cor.test(fairplayer_T1u2$rat1, fairplayer_T1u2$sit1)
##
## Pearson's product-moment correlation
##
## data: fairplayer_T1u2$rat1 and fairplayer_T1u2$sit1
## t = 2.3654, df = 104, p-value = 0.01987
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.03677587 0.39948371
## sample estimates:
## cor
## 0.2259462