Einleitung
In dieser Sitzung wollen wir mehrere Variablen gleichzeitig hinsichtlich Gruppenunterschiede mit Hilfe der mutlivariaten Varianzanalyse (engl. Multivariate ANalysis Of VAriance, MANOVA, vgl. bspw. Eid, Gollwitzer & Schmitt, 2017, Kapitel 15, sowie Wiederholungskapitel zur ANOVA und Mittelwertsvergleichen Kapitel 10-14, insbesondere 13-14, und Pituch und Stevens, 2016, Kapitel 4-6) untersuchen. Die MANOVA hat vor allem dann Vorteile, wenn die abhängigen Variablen, die wir bzgl. Gruppenunterschieden verrechnen wollen, korreliert sind! Wir wollen uns ein fiktives Datenbeispiel (Datensatz Therapy aus dem gleichnamigen .rda File Therapy.rda) ansehen, in welchem der Therapieerfolg auf mehreren abhängigen Variablen untersucht werden sollen. Sie können den Datensatz “Therapy.rda” hier herunterladen.
Daten laden
Wir laden zunächst die Daten: entweder lokal von Ihrem Rechner:
load("C:/Users/Musterfrau/Desktop/Therapy.rda")
oder wir laden sie direkt über die Website:
load(url("https://pandar.netlify.app/daten/Therapy.rda"))
Nun sollte in R-Studio oben rechts in dem Fenster unter der Rubrik “Data” unser Datensatz mit dem Namen “Therapy” erscheinen.
Übersicht über die Daten
Wir wollen uns einen Überblick über die Daten verschaffen:
head(Therapy)
## Lebenszufriedenheit Arbeitsbeanspruchung Depressivitaet Arbeitszufriedenheit Intervention Geschlecht
## 1 7 4 7 5 Kontrollgruppe 0
## 2 5 5 8 3 Kontrollgruppe 1
## 3 8 7 6 6 Kontrollgruppe 0
## 4 6 4 5 5 Kontrollgruppe 1
## 5 6 9 8 5 Kontrollgruppe 1
## 6 8 7 8 6 Kontrollgruppe 1
levels(Therapy$Intervention)
## [1] "Kontrollgruppe" "VT Coaching" "VT Coaching + Gruppenuebung"
levels(Therapy$Geschlecht)
## [1] "0" "1"
Die abhängigen Variablen sind Lebenszufriedenheit, Arbeitsbeanspruchung, Depressivitaet und Arbeitszufriedenheit. Die Variable Intervention hat drei Stufen: eine Kontrollgruppe, ein verhaltenstherapiebasiertes Coaching, sowie das verhaltenstherapiebasierte Coaching inklusive einer Gruppenübung. Das Geschlecht ist 0-1 kodiert, wobei 0 für männlich und 1 für weiblich steht. Insgesamt sind die Variablennamen der AVs recht lang. Wir wollen diese kürzen:
colnames(Therapy) # Spaltennamen ansehen
## [1] "Lebenszufriedenheit" "Arbeitsbeanspruchung" "Depressivitaet" "Arbeitszufriedenheit"
## [5] "Intervention" "Geschlecht"
colnames(Therapy) <- c("LZ", "AB", "Dep", "AZ", "Intervention", "Geschlecht") # Spaltennamen neu zuordnen
head(Therapy)
## LZ AB Dep AZ Intervention Geschlecht
## 1 7 4 7 5 Kontrollgruppe 0
## 2 5 5 8 3 Kontrollgruppe 1
## 3 8 7 6 6 Kontrollgruppe 0
## 4 6 4 5 5 Kontrollgruppe 1
## 5 6 9 8 5 Kontrollgruppe 1
## 6 8 7 8 6 Kontrollgruppe 1
So - schon viel übersichtlicher!
Hypothesen
Wir wollen untersuchen, ob es einen Therapieerfolg gibt, also die Therapieformen Einfluss auf die abhängigen Variablen haben. Des Weiteren wäre es interessant zu prüfen, ob sich auch die beiden Therapieformen unterscheiden. Zusätzlich wollen wir uns Geschlechtseffekte ansehen:
- Die Therapieformen sowie die Kontrollgruppe unterscheiden sich auf mindestens einer AV
- Die Therapieformen unterscheiden sich untereinander
- Das Geschlecht nimmt über die Therapieformen hinaus Einfluss auf die AVs
Pakete laden
Nachdem wir neue Pakete installiert haben (install.packages), laden wir diese:
library(heplots) # für Box-M Test für Kovarianzhomogenität
## Warning: Paket 'heplots' wurde unter R Version 4.3.2 erstellt
library(car)
Modellspezifikation
Die MANOVA ist die multivariate Erweiterung der ANOVA. Glücklicherweise ist der R-Code, den wir verwenden, um eine MANOVA zur Datenanalyse heranzuziehen, sehr ähnlich den Befehlen zu einer Regressionsanalyse oder einer ANOVA. Die Idee ist diesmal, dass wir mehrere AVs als Spalten einer Matrix links der ~ (Tilde) haben, die die AVs von den UVs trennt. Auf der rechten Seite müssen Faktoren/Gruppenzugehörigkeiten abgetragen werden. Eine multifaktorielle MANOVA führen wir durch, indem wir mehrere Faktoren durch + verknüpfen (das geht also ganz einfach!). Die MANOVA hat als Voraussetzung, dass die Kovarianzmatrizen (der Residuen) über alle Gruppen hinweg homogen sind (Kovarianzhomogenität) sowie, dass die Residuen (bzw. die Variablen) der abhängigen Variablen multivariat normalverteilt sind. Hier wird sich explizit auf die Residuen bezogen, da diese immer einen Mittelwert von 0 haben, egal wie viele Gruppierungen es in einer Analyse gibt. Außerdem wird wie in den meisten statistischen Analysen angenommen, dass die Beobachtungen aus einer independent and identically distributed ($i.i.d.$, deutsch: unabhängig und identisch verteilt) Population (dies bedeutet, dass alle Beobachtungen unabhängig sind und den gleichen Verteilungs- und Modellannahmen unterliegen) stammen. Dies bleibt allerdings eine Annahme, die nur über die sinnvolle Wahl des Designs (Randomisierung etc.) angenommen werden kann. Wir wollen die testbaren Voraussetzungen im Laufe dieser Sitzung prüfen.
Untersuchen der Hypothesen
Wir beginnen mit dem Prüfen der Hypothesen.
Hypothese 1
Bevor wir mit der Analyse der ersten Hypothese anfangen, prüfen wir noch schnell die Annahme der Kovarianzhomogenität der Residuen. Dies geschieht mit Box M-Test. Dazu verwenden wir die Funktion boxM aus dem heplots-Paket. Wir müssen der boxM Funktion eine formula ähnlich der der lm-Funktion für die Regression übergeben. Diese hat dieses mal allerdings eine Matrix mit den AVs als Spalten, welche wir mit cbind erstellen. Anschließend müssen wir sagen, durch welche Gruppierung die AVs vorhergesagt werden sollen, damit intern die Residuen bestimmt werden können, bzw. sodass die Gruppierung der Kovarianzmatrix vorgenommen werden kann. Dies machen wir ganz einfach wie in anderen (generalisierten) linearen Modellen mit der ~, die die AVs von den UVs (hier Gruppenzugehörigkeit) trennen. Als letztes Argument übergeben wir data noch den Datensatz.
boxM(cbind(LZ, AB, Dep, AZ) ~ Intervention, data = Therapy)
##
## Box's M-test for Homogeneity of Covariance Matrices
##
## data: Y
## Chi-Sq (approx.) = 19.626, df = 20, p-value = 0.4815
Der Test ist nicht statistisch signifikant, was wir an dem relativ kleinen $\chi^2$-Wert relativ zu den Freiheitsgraden $df$ sehen. Der $p$-Wert liegt bei 0.48. Folglich wird die Nullhypothese auf Kovarianzmatrixhomogenität nicht verworfen und wir nehmen diese weiterhin an (Achtung: die $H_0$ kann nicht bestätigt werden…). Schauen wir uns spaßeshalber die Kovarianzmatrizen der AVs in den 3 Gruppen an. Dazu wählen wir aus den Daten Therapy nur diejenigen Zeilen aus, für welche bspw. Therapy$Intervention == "Kontrollgruppe", also für die die Erhebung aus der Kontrollgruppe stammt. Wir wählen dann noch die 1. bis 4. Spalte via 1:4 und erhalten somit den Datensatz, der nur Personen aus der Kontrollgruppe enthält. Wenn wir nun die cov Funktion darauf anwenden, erhalten wir die Kovarianzmatrix in der Kontrollgruppe. Diese runden wir noch fix auf 2 Nachkomma stellen mit round. Probieren Sie doch selbst einmal diese Funktionen von innen nach außen aus, um zu prüfen was passiert!
round(cov(Therapy[Therapy$Intervention == "Kontrollgruppe", 1:4]), digits = 2)
## LZ AB Dep AZ
## LZ 1.44 0.14 -0.34 0.63
## AB 0.14 2.10 1.00 0.37
## Dep -0.34 1.00 1.64 -0.60
## AZ 0.63 0.37 -0.60 1.22
round(cov(Therapy[Therapy$Intervention == "VT Coaching", 1:4]), digits = 2)
## LZ AB Dep AZ
## LZ 2.41 -0.25 -1.44 1.92
## AB -0.25 1.94 1.08 -0.44
## Dep -1.44 1.08 2.82 -2.33
## AZ 1.92 -0.44 -2.33 2.83
Oder mal mit der Pipe (hier passier das Gleiche wie zuvor, nur mit anderem R-Code, der ggf. die Klammerungen erleichtert):
Therapy[Therapy$Intervention == "VT Coaching + Gruppenuebung", 1:4] |> cov() |> round(digits = 2)
## LZ AB Dep AZ
## LZ 2.09 -0.48 -0.89 1.34
## AB -0.48 1.46 0.90 -0.09
## Dep -0.89 0.90 1.70 -1.26
## AZ 1.34 -0.09 -1.26 1.91
Die Kovarianzmatrizen wirken nicht gleich, aber auch nicht drastisch unterschiedlich. Der Box-M Test hat uns diese augenscheinlich Prüfung abgenommen und uns gezeigt, dass diese Abweichung aller Voraussicht nach durch Zufall passiert sind (da nicht signifikantes Ergebnis). Wir können also getrost eine MANOVA durchführen. Diese sollten wir auch durchführen, da die AVs deutlich korreliert sind!
Der Befehl dafür heißt ganz einfach manova. Ihm übergeben wir die gleichen Informationen, wie auch der BoxM Funktion. Wir nennen dieses Objekt manova1. Da dieses Objekt noch sehr unübersichtliche Informationen enthält und wir besonders an Signifikanzentschiedungen interessiert sind, könnten wir wieder die summary auf das manova1-Objekt anwenden. Allerdings wollen wir später auch eine mehrfaktorielle MANOVA betrachten, wo wir genau mit der Quadratsummenzerlegung aufpassen müssen — dazu später mehr. Aus diesem Grund verwenden wir auch jetzt schon nicht direkt die summary, sondern wenden erst noch die Manova-Funktion aus dem car-Paket auf das manova1-Objekt an. Diese stellt den zweiten Quadratsummentyp per Default ein, welcher bei mehrfaktorielle MANOVAs immer dem Typ I, der sonst der Default ist, zu bevorzugen ist. Dieses Objekt nennen wir dann M1.
manova1 <- manova(cbind(LZ, AB, Dep, AZ) ~ Intervention,
data = Therapy)
M1 <- Manova(manova1)
summary(M1)
##
## Type II MANOVA Tests:
##
## Sum of squares and products for error:
## LZ AB Dep AZ
## LZ 172.40000 -17.266667 -77.26667 112.933333
## AB -17.26667 159.433333 86.30000 -4.466667
## Dep -77.26667 86.300000 178.70000 -121.700000
## AZ 112.93333 -4.466667 -121.70000 173.133333
##
## ------------------------------------------
##
## Term: Intervention
##
## Sum of squares and products for the hypothesis:
## LZ AB Dep AZ
## LZ 39.20000 10.266667 -37.333333 42.466667
## AB 10.26667 3.288889 -3.577778 6.022222
## Dep -37.33333 -3.577778 99.622222 -93.144444
## AZ 42.46667 6.022222 -93.144444 89.355556
##
## Multivariate Tests: Intervention
## Df test stat approx F num Df den Df Pr(>F)
## Pillai 2 0.6261275 9.684457 8 170 4.9977e-11 ***
## Wilks 2 0.4536733 10.177959 8 168 1.5202e-11 ***
## Hotelling-Lawley 2 1.0283300 10.668924 8 166 4.7746e-12 ***
## Roy 2 0.8115981 17.246459 4 85 2.1591e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Die Summary zeigt zunächst, dass Quadratsummen vom Typ II verwendet wurden. Dann werden uns die Sum of Squares and Products for error, also die Quadrat- und Kreuzproduktsummen für die Fehler. Das ist also gerade Matrix $W$, die die Within-Variation symbolisiert. Darunter stehen die Quadrat und Kreuzproduktsummen für unseren Gruppenvergleich Term: Intervention, also die Between-Variationsmatrix $B$. In Multivariate Tests: Intervention werden uns alle multivariaten Teststatistiken angezeigt und deren Signifikanzentscheidung. Es gibt hier insgesamt 4: Teststatistiken nach Pillai, Wilks, Hotelling-Lawley und Roy. Außerdem werden uns die Hypothesenfreiheitsgrade Df ausgegeben, welche die Freiheitsgrade der Mittelwertsvergleiche anzeigt. Da es insgesamt 3 Gruppen sind, liegt dieser bei 2 (und zwar für alle Teststatistiken). Bspw. zeigt Wilks den Wilks-$\Lambda$-Wert und approx F den zugehörigen $F$-Wert, in welchen $\Lambda$ (approx.) transformiert wurde. Außerdem werden die entsprechenden Zähler- (num Df, num = numerator) und Nennerfreiheitsgrade (den Df, den = denominator) von $F$ sowie der zugehörige $p$-Wert (Pr(>F) ) angezeigt. Diese können sich über die Teststatistiken unterscheiden. Wem das zu unübersichtlich ist, kann in der summary auch mit test = "Wilks" nur Wilks-$\Lambda$ abrufen.
Wir erkennen einen Wilks-$\Lambda$-Wert von 0.454. Dieser wird mit Hilfe der $F$-Statistik auf Signifikanz geprüft, indem er transformiert wird. Der zugehörige $F$-Wert liegt bei $F(8, 168)=$ 10.178, $p<0.001$. Wir können dem Summary-Objekt auch die Within und Between Kreuzproduktsummen-Matrizen entlocken, die zur Bestimmen von $\Lambda$ essentiell sind. Dazu speichern wir die Summmary in sum_manova1 ab.
sum_manova1 <- summary(M1)
Die Informationen, die wir suchen verbergen sich hinter $multivaraite.tests. Hier bekommen wir also die gewünschten Informationen, Anhand derer wir $\Lambda$ auch zu Fuß bestimmen können - nämlich via
$$\Lambda:=\frac{|W|}{|W+B|},$$
wobei $W$ für die Within-Kreuzproduktsummen (also die Variation der Residuen, “Sum of Squares and Products for Error” [SSPE]) und $B$ für die Between-Kreuzprodukt (also die Variation zwischen den Gruppen, “Sum of Squares and Products for Hypothesis” [SSPH]) summen steht.
W <- sum_manova1$multivariate.tests$Intervention$SSPE # W-Matrix (E steht für errors)
B <- sum_manova1$multivariate.tests$Intervention$SSPH # B-Matrix (H steht für Hypothesis)
det(W)/(det(B + W)) # Wilks Lambda
## [1] 0.4536733
Der Befehl für die Determinante war det. Wir erkennen, dass der zu Fuß berechnete $\Lambda$_Wert, der exakt gleiche Wert ist, wie wir ihn in der Summary oben erhalten haben. $\Lambda$ ist ein inverses Maß, was bedeutet, dass kleine Werte gegen die Nullhypothese (also Mittelwertgleichheit) sprechen. Da wir die Null-Hypothese verworfen haben, bedeutet dies, dass mindestens ein Mittelwertsvektorpaar in der Population nicht gleich ist. Gleichzeitig ist dies der Fall sobald ein Mittelwertspaar innerhalb eines Mittelwertsvektorpaar über zwei Gruppen unterschiedlich ist.
In Eid et al. (2017) wird auch Pillai’s Spur empfohlen für die Signifikanztestung einer MANOVA. Allerdings kommen alle 4 Teststatistiken hier zum identischen Ergebnis. Da dieser Test gleiche Hypothesenfreiheitsgrade bei einem etwas kleineren $F$-Wert aufweist, zeigt uns dies, dass Pillai’s Spur ggf. etwas konservativer ist.
Wie sehen die Mittelwerte aus?
Wir wissen nun, dass es Unterschiede gibt. Allerdings wissen wir noch nicht auf welchen Variablen und zwischen welchen Gruppen diese vorliegen. Um eine Idee zu erhalten, schauen wir uns das ganze einmal grafisch an (der Code zur Grafik findet sich in Appendix A). In dieser Grafik werden die SEs der Mittelwerte pro Variable dargestellt (nicht die Konfidenzintervalle). Die Fehlerbalken können also ein Indiz für mögliche signifikante Unterschiede liefern, allerdings können diese nicht die Signifikanzentscheidung ersetzen:
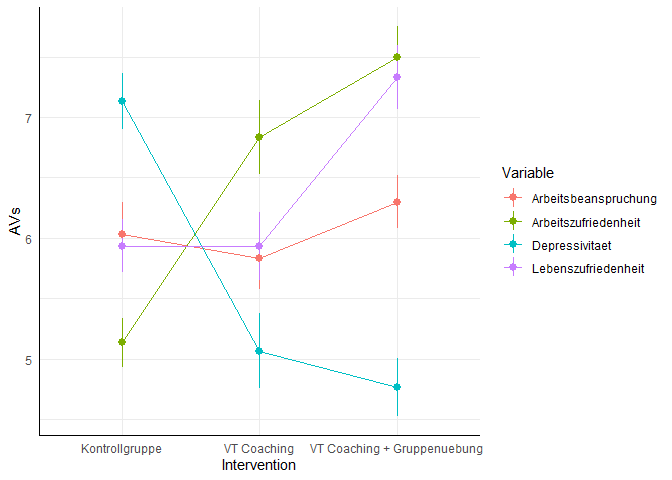
Auch können wir mit aggregate Mittelwerte (und andere Deskriptivstatistiken) sehr leicht für verschiedene Gruppen bestimmen: sie nimmt bspw. die gleiche Modellgleichung entgegen wie manova - wir müssen lediglich das Argument FUN ergänzen, welchen wir die Funktion, die pro Gruppe angewandt weden soll, übergeben müssen. Auch andere Funktionen wären hier möglich (wie etwa sd, min, median oder max).
aggregate(cbind(LZ, AB, Dep, AZ) ~ Intervention,
data = Therapy,
FUN = mean)
## Intervention LZ AB Dep AZ
## 1 Kontrollgruppe 5.933333 6.033333 7.133333 5.133333
## 2 VT Coaching 5.933333 5.833333 5.066667 6.833333
## 3 VT Coaching + Gruppenuebung 7.333333 6.300000 4.766667 7.500000
Es scheint, dass es nicht auf allen Variablen Unterschiede zwischen allen Gruppen gibt. Wir könnten bspw. vermuten, dass es auf der Variable Lebenszufriedenheit keine Unterschiede zwischen der Kontrollgruppe und dem VT-Coaching gibt. Allerdings lassen sich Unterschiede zwischen diesen beiden und der VT-Coaching plus Gruppenübung Bedingung erwarten. Wir gehen dem Ganzen auf den Grund, indem wir Post-Hoc ANOVAs durchführen.
Hypothese 2
Ist der Omnibustest signifikant, so können wir weitere Post-Hoc-Analysen durchführen, mit welchen wir herausfinden können, wo die Unterschiede zwischen den Gruppen liegen und auf welchen Variablen. Wäre die MANOVA nicht signifikant, sollten auch keine weiteren Analysen durchgeführt werden!
Post-Hoc ANOVA lassen sich super leicht durchführen. Dazu müssen wir lediglich die Funktion summary.aov auf das MANOVA-Objekt manova1 anwenden (Das auf M1 anzuwenden, funktioniert leider nicht…). Uns werden dann vier verschiedene Outputs von ANOVAs ausgegeben - nämlich jeweils eine für jede AV:
summary.aov(manova1) # post hoc anovas
## Response LZ :
## Df Sum Sq Mean Sq F value Pr(>F)
## Intervention 2 39.2 19.6000 9.891 0.0001347 ***
## Residuals 87 172.4 1.9816
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Response AB :
## Df Sum Sq Mean Sq F value Pr(>F)
## Intervention 2 3.289 1.6444 0.8973 0.4114
## Residuals 87 159.433 1.8326
##
## Response Dep :
## Df Sum Sq Mean Sq F value Pr(>F)
## Intervention 2 99.622 49.811 24.25 4.262e-09 ***
## Residuals 87 178.700 2.054
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Response AZ :
## Df Sum Sq Mean Sq F value Pr(>F)
## Intervention 2 89.356 44.678 22.451 1.375e-08 ***
## Residuals 87 173.133 1.990
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Der Output enthält folgende Informationen:
## Response LZ :
gibt an, um welche AV es sich handelt: hier Lebenszufriedenheit (LZ).
##
## Df Sum Sq Mean Sq F value Pr(>F)
## Intervention 2 39.2 19.6000 9.891 0.0001347 ***
## Residuals 87 172.4 1.9816
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Dies ist der eigentliche Output der ANOVA für die Lebenszufriedenheit. Wir erkennen beim Effekt der Intervention, dass es sich erneut um 2 Hypothesen-Df handelt. Außerdem werden uns noch die Sum Sq, also die “Sum of Squares” und die Mean Sq also die “Mean Sum of Squares” ausgegeben und zwar sowohl für die Unterschiede zwischen den Gruppen (Intervention) und innerhalb der Gruppen (Residuals). Mean Sq ist gerade einfach Sum Sq geteilt durch Df. Der $F$-Wert, der unter F value vermerkt ist, ergibt sich dann als Quotient der beiden Mean Sq $F=\frac{MQS_{zw}}{MQS_{in}}$, wobei $MQS_{zw}$ und $MQS_{in}$ jeweils die mittlere Quadratsumme zwischen und innerhalb der Gruppen beschreibt. Der zugehörige $p$-Wert zeigt uns, dass es auf der Variable Lebenszufriedenheit Unterschiede zwischen den Gruppen auch in der Population gibt (mit einer Irrtumswahrscheinlichkeit von 5%): $F(2,87)=$ 9.891, $p<0.001$. Signif. codes wird nur mit ausgegeben, sofern das Ergebnis statistisch signifikant war. Die Freiheitsgrade sind logischerweise für alle AVs gleich: Insgesamt gibt es Gruppenunterschiede bei der Lebenszufriedenheit ($F(2,87)=$ 9.891, $p<0.001$), der Depression ($F(2,87)=$ 24.25, $p<0.001$) und der Arbeitszufriedenheit ($F(2,87)=$ 22.45, $p<0.001$) (mit einer Irrtumswahrscheinlichkeit von 5%), keine aber bzgl. der Arbeitsbelastung ($F(2,87)=$ 0.41, $p>0.05$). Somit scheinen die Interventionen keinen Einfluss auf die Arbeitsbelastung zu haben. Wir haben hier keine Korrektur für die $p$-Werte durchgeführt (z.B. Bonferroni), da die MANOVA bereits signifikant war.
Wir können auch einzelne ANOVAs gezielt durchführen, indem wir bspw. nur den aov-Befehl anwenden und anschließend, wie im MANOVA Befehl, nur eben diesmal für eine Variable, das Modell spezifizieren:
anovaLZ <- aov(LZ ~ Intervention, data = Therapy)
summary(anovaLZ)
## Df Sum Sq Mean Sq F value Pr(>F)
## Intervention 2 39.2 19.600 9.891 0.000135 ***
## Residuals 87 172.4 1.982
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Wir erkennen, dass die Summary komplett identisch ist, zu der ersten ANOVA im zuvor generierten summary.aov-Objekt - nämlich der Post-Hoc ANOVA der Lebenszufriedenheit (LZ). Weitere Informationen zu ANOVAs können Sie in den Unterlagen aus dem Bachelor finden.
Um nun noch genauer zu erfahren, welche Gruppen sich unterscheiden, führen wir paar-weise $t$-Tests durch - jedoch nur für diejenigen AVs, deren ANOVA signifikant war. Der Befehl hierzu heißt pairwise.t.test. Ihr übergeben wir die Variable x, die Gruppierung g und den Umgang mit den $p$-Werten p.adjust.method = "none" (hier wählen wir keine, da die MANOVAs und die ANOVAs bereits signifikant waren). Insgesamt schauen wir uns paar-weise $t$-Tests für Lebenszufriedenheit, Depression und Arbeitszufriedenheit an.
pairwise.t.test(x = Therapy$LZ, g = Therapy$Intervention, p.adjust.method = "none")
##
## Pairwise comparisons using t tests with pooled SD
##
## data: Therapy$LZ and Therapy$Intervention
##
## Kontrollgruppe VT Coaching
## VT Coaching 1.00000 -
## VT Coaching + Gruppenuebung 0.00022 0.00022
##
## P value adjustment method: none
pairwise.t.test(x = Therapy$Dep, g = Therapy$Intervention, p.adjust.method = "none")
##
## Pairwise comparisons using t tests with pooled SD
##
## data: Therapy$Dep and Therapy$Intervention
##
## Kontrollgruppe VT Coaching
## VT Coaching 2.6e-07 -
## VT Coaching + Gruppenuebung 7.7e-09 0.42
##
## P value adjustment method: none
pairwise.t.test(x = Therapy$AZ, g = Therapy$Intervention, p.adjust.method = "none")
##
## Pairwise comparisons using t tests with pooled SD
##
## data: Therapy$AZ and Therapy$Intervention
##
## Kontrollgruppe VT Coaching
## VT Coaching 1.1e-05 -
## VT Coaching + Gruppenuebung 4.9e-09 0.071
##
## P value adjustment method: none
Der Output zeigt jeweils den $p$-Wert des jeweiligen Mittelwertvergleichs in Matrixform. Die Zeilen heißen VT Coaching und VT Coaching + Gruppenuebung, während die Spalten Kontrollgruppe und VT Coaching heißen. Somit ist der Eintrag [1,1] gerade der Mittelwertsvergleich zwischen VT Coaching und Kontrollgruppe und bspw. der Eintrag [2,2] der Mittelwertsvergleich zwischen VT Coaching + Gruppenuebung und VT Coaching.
Wollen wir die $p$-Werte weiter korrigieren bzw. kontrollieren, so können wir entweder bei der p.adjust.method bspw. "bonferroni" eingeben oder wir führen einen Post-Hoc Test durch, der das $\alpha$-Niveau über alle Tests pro ANOVA unter Kontrolle hält: Tukey’s Honest Signficance Distance (HSD). Die Funktion in R heißt hierzu tukeyHSD und muss auf ein ANOVA (aov) Objekt angewandt werden, welches wir eben kennengelernt haben. Die Ergebnisse lassen sich auch grafisch veranschaulichen, indem wir die plot-Funktion auf das Objekt anwenden (las = 1 lässt Achsenbeschriftungen horizontal erscheinen):
TukeyHSD(aov(LZ ~ Intervention, data = Therapy)) # Tukey HSD für LZ
## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = LZ ~ Intervention, data = Therapy)
##
## $Intervention
## diff lwr upr p adj
## VT Coaching-Kontrollgruppe -8.881784e-16 -0.8666764 0.8666764 1.0000000
## VT Coaching + Gruppenuebung-Kontrollgruppe 1.400000e+00 0.5333236 2.2666764 0.0006493
## VT Coaching + Gruppenuebung-VT Coaching 1.400000e+00 0.5333236 2.2666764 0.0006493
# als Plot
tukeyLZ <- TukeyHSD(aov(LZ ~ Intervention, data = Therapy))
plot(tukeyLZ, las = 1)
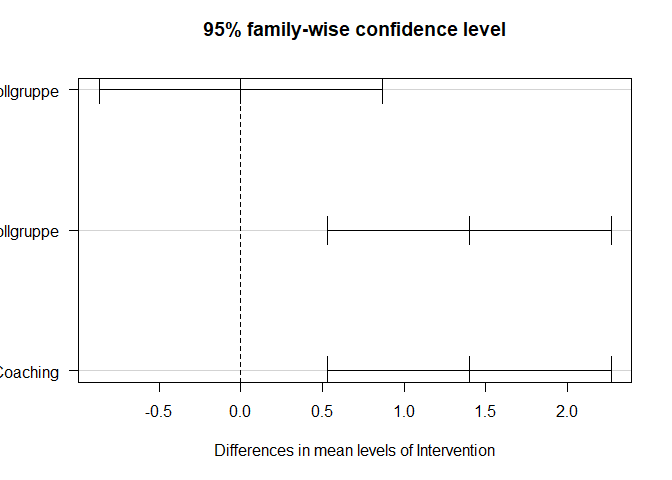
TukeyHSD(aov(Dep ~ Intervention, data = Therapy)) # Tukey HSD für Dep
## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = Dep ~ Intervention, data = Therapy)
##
## $Intervention
## diff lwr upr p adj
## VT Coaching-Kontrollgruppe -2.066667 -2.949036 -1.1842969 0.0000008
## VT Coaching + Gruppenuebung-Kontrollgruppe -2.366667 -3.249036 -1.4842969 0.0000000
## VT Coaching + Gruppenuebung-VT Coaching -0.300000 -1.182370 0.5823698 0.6974279
plot(TukeyHSD(aov(Dep ~ Intervention, data = Therapy)), las = 1) # Tukey HSD-Plot für Dep
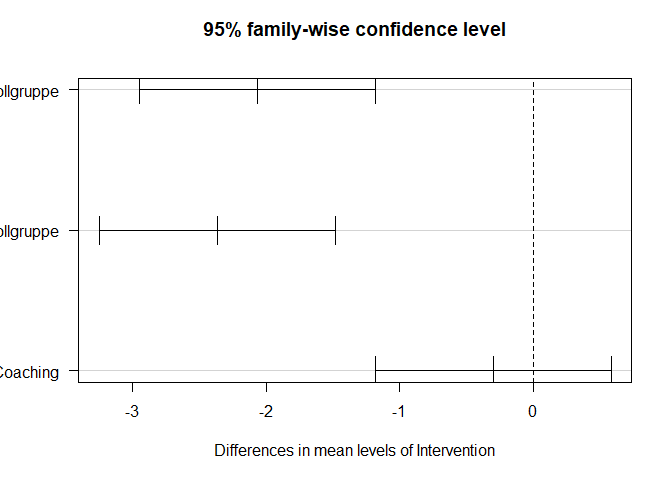
TukeyHSD(aov(AZ ~ Intervention, data = Therapy)) # Tukey HSD für AZ
## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = AZ ~ Intervention, data = Therapy)
##
## $Intervention
## diff lwr upr p adj
## VT Coaching-Kontrollgruppe 1.7000000 0.8314822 2.568518 0.0000325
## VT Coaching + Gruppenuebung-Kontrollgruppe 2.3666667 1.4981489 3.235184 0.0000000
## VT Coaching + Gruppenuebung-VT Coaching 0.6666667 -0.2018511 1.535184 0.1657892
plot(TukeyHSD(aov(AZ ~ Intervention, data = Therapy)), las = 1) # Tukey HSD-Plot für AZ
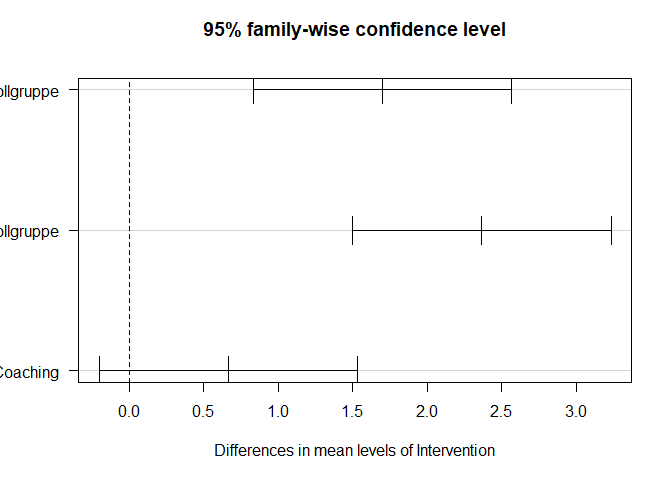
Schließen die HSD (Intervalle) die Null (vertikale gestrichelte Linie) nicht ein, so ist der Mittel in den beiden Gruppen unterschiedlich (mit einer Irrtumswahrscheinlichkeit von 5%). Wir können die Achsenbeschriftungen leider nicht sehr gut erkennen, allerdings können wir dem Output der TukeyHSD-Funktion entnehmen, welche Mittelwerte verglichen wurden: somit wissen wir, dass das erste Paar VT Coaching und Kontrollgruppe, das zweite Paar VT Coaching + Gruppenuebung und die Kontrollgruppe und das 3. Paar die beiden VT-Gruppen vergleicht.
Die Ergebnisse der $t$-Tests und der Tukey’s HSD stimmen überein und lassen sich wie folgt zusammenfassen:
| AV | Kontrollgruppe vs VT-Coaching | Kontrollgruppe vs VT-Coaching + Gruppenübung | VT-Coaching vs VT-Coaching + Gruppenübung | |
|---|---|---|---|---|
| Lebenszufriedenheit | ns | signifikant | signifikant | |
| Depression | signifikant | signifikant | ns | |
| Arbeitszufriedenheit | signifikant | signifikant | ns |
Somit ist ersichtlich, dass die Interventionen sich nicht gleich auf die AVs auswirken. VT-Coaching inklusive Gruppenübungen führte zu einer Verbesserung der Lebenszufriedenheit (da gestiegen), Depressionssymptomatik (da gesunken) und Arbeitszufriedenheit (da gestiegen) im Vergleich zur Kontrollgruppe (die Richtung konnten wir den Mittelwerten und der Grafik entnehmen). Keine Unterschiede zwischen Kontrollgruppe und VT-Coaching ließen sich bzgl. der Lebenszufriedenheit finden, bzgl. der Depressionssymptomatik und der Arbeitszufriedenheit jedoch schon. Die zusätzliche Gruppenübung hat nur eine positive Auswirkung auf die Lebenszufriedenheit, negative Stimmung (Dep) oder Arbeitszufriedenheit profitiert davon nicht. Alle Aussagen sind statistischer Natur, unterliegen somit also einer Irrtumswahrscheinlichkeit! Keinen Einfluss hatten die Interventionen auf die Arbeitsbelastung.
Interpretation
Den Ergebnissen ist zu entnehmen, dass das zusätzliche Gruppentraining nur Einfluss auf die Lebenszufriedenheit nimmt. Vielleicht wurden ja in diesem Gruppentraining spezifische Aspekte dazu vermittelt? Diese Frage können wir leider nicht beantworten, da es sich hierbei um simulierte Daten handelt… Außerdem schien das Coaching insgesamt Depressionssymptomatiken zu verbessern sowie die Arbeitszufriedenheit zu erhöhen. Eine tatsächlich Reduktion der empfundenen Arbeitsbelastungen konnte nicht erreicht werden. Folglich wurde vermutlich an der Denkweise, nicht aber an der Arbeitsweise gearbeitet! Insgesamt wird Hypothese 3 teilweise gestützt, da es Unterschiede der Interventionsgruppen bzgl. der Lebenszufriedenheit gab. Allerdings müsste weiter diskutiert werden (falls es sich hierbei um echte Daten gehandelt hätte), ob ein Effekt auf nur einer Variable ausreichen würde die Gruppenübungen zusätzlich durchzuführen (wir nehmen hier einmal an, dass das ein Mehraufwand wäre!).
Normalverteilung der Residuen
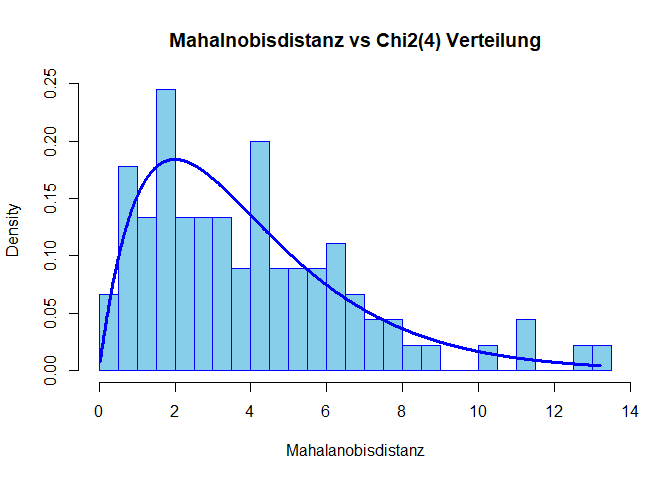
Die Annahme der Normalverteilung der Residuen können wir wieder mit Hilfe der Mahalnobisdistanz prüfen. Dafür bestimmen wir zunächst die Residuen unsere Analyse mit resid(manova1) und führen anschließend die Modellierung der Mahalanobisdistanz mit der $\chi^2(4)$-Verteilung und einem Histogramm (auch Q-Q-Plot wäre möglich) durch, wie wir es in der Sitzung zur Regression gelernt haben (mal mit Beschriftung und anderer Farbe):
MD <- mahalanobis(resid(manova1), center = colMeans(resid(manova1)), cov = cov(resid(manova1)))
hist(MD, breaks = 20, col = "skyblue", border = "blue", freq = F, main = "Mahalnobisdistanz vs Chi2(4) Verteilung",
xlab = "Mahalanobisdistanz")
xWerte <- seq(from = min(MD), to = max(MD), by = 0.01)
lines(x = xWerte, y = dchisq(x = xWerte, df = 4), lwd = 3, col = "blue")
Noch besser sieht man es vielleicht mit einem Q-Q-Plot. Wir verwenden hier wieder die Funktion aus dem car-Paket, wie in der Sitzung zur Regression.
qqPlot(MD, distribution = "chisq", df = 4)
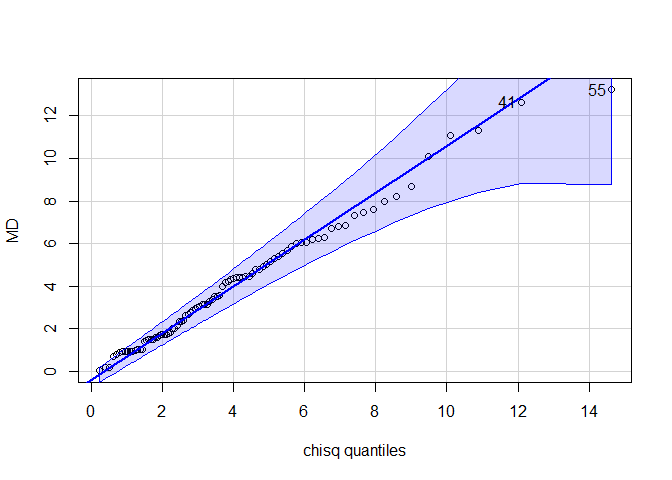
## [1] 55 41
Insgesamt scheinen die Residuen einigermaßen $\chi^2(4)$-verteilt. Somit gibt es keinen Grund an der Annahme der multivariaten Normalverteilung zu zweifeln. Folglich können wir weiterhin den Ergebnissen vertrauen. Wir hatten hier $df=4$ für die $\chi^2$-Verteilung verwendet, da es insgesamt 4 Variablen waren, die wir auf multivariate Normalität untersucht hatten.
Hypothese 3
Um unsere 3. Hypothese zu prüfen, müssen wir sowohl de Einfluss der Therapie als auch des Geschlechts mit in das Modell aufnehmen. Wir können eine mehrfaktorielle MANOVA durchführen, indem wir einfach das Geschlecht a la lm-Manier als weiteren Prädiktor in die MANOVA-Gleichung aufnehmen. Allerdings gibt es bei solchen mehrfaktoriellen Gruppenvergleichen das Problem mit den Quadratsummen. Effekte werden signifikant je nach dem, wie sie kodiert sind. Um diesem Problem aus dem Weg zu gehen, verwenden wir die Manova-Funktion aus dem car-Paket. Diese stellt nämlich die Quadratsummen vom Typ II ein, während in der Basisfunktion die Quadratsumme vom Typ I implementiert ist. Die Quadratsummen haben erst einen Einfluss auf die Berechnungen, wenn mindestens 2 Faktoren in die Analyse aufgenommen werden! Hierbei gilt, dass bei Typ I schrittweise die Faktoren in das Modell aufgenommen werden und es daher auf die Reihenfolge der Faktoren ankommt. Dies ist natürlich nicht gewünscht, denn wir wollen einfach nur wissen, ob es Unterschiede gibt und ob diese eher auf das Geschlecht oder auf die Therapieform zurückzuführen sind.Bei Typ II spielt die Reihenfolge keine Rolle. Allerdings sollte Typ II nur dann interpretiert werden, wenn die Interaktion nicht signifikant ist.
manova3 <- manova(cbind(LZ, AB, Dep, AZ) ~ Intervention + Geschlecht,
data = Therapy)
M3 <- Manova(manova3, test = "Wilks")
summary(M3)
##
## Type II MANOVA Tests:
##
## Sum of squares and products for error:
## LZ AB Dep AZ
## LZ 168.13219 -16.374624 -63.51871 102.753548
## AB -16.37462 159.246882 83.42645 -2.338925
## Dep -63.51871 83.426452 134.41355 -88.907742
## AZ 102.75355 -2.338925 -88.90774 148.852043
##
## ------------------------------------------
##
## Term: Intervention
##
## Sum of squares and products for the hypothesis:
## LZ AB Dep AZ
## LZ 25.475157 9.3241392 -4.9687967 13.490715
## AB 9.324139 3.4751989 -0.5748453 3.784616
## Dep -4.968797 -0.5748453 25.7292359 -25.586394
## AZ 13.490715 3.7846157 -25.5863937 28.425876
##
## Multivariate Tests: Intervention
## Df test stat approx F num Df den Df Pr(>F)
## Pillai 2 0.4229323 5.631703 8 168 2.4669e-06 ***
## Wilks 2 0.6196029 5.610969 8 166 2.6634e-06 ***
## Hotelling-Lawley 2 0.5452877 5.589199 8 164 2.8840e-06 ***
## Roy 2 0.3480463 7.308973 4 84 4.2256e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## ------------------------------------------
##
## Term: Geschlecht
##
## Sum of squares and products for the hypothesis:
## LZ AB Dep AZ
## LZ 4.267814 -0.8920430 -13.747957 10.179785
## AB -0.892043 0.1864516 2.873548 -2.127742
## Dep -13.747957 2.8735484 44.286452 -32.792258
## AZ 10.179785 -2.1277419 -32.792258 24.281290
##
## Multivariate Tests: Geschlecht
## Df test stat approx F num Df den Df Pr(>F)
## Pillai 1 0.3292746 10.18666 4 83 9.2872e-07 ***
## Wilks 1 0.6707254 10.18666 4 83 9.2872e-07 ***
## Hotelling-Lawley 1 0.4909232 10.18666 4 83 9.2872e-07 ***
## Roy 1 0.4909232 10.18666 4 83 9.2872e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Der Output wird um den zusätzlichen Effekt des Geschlechts auf die vier AVs erweitert. Ansonsten ist der Output völlig analog zu oben zu lesen. Sowohl die Intervention als auch das Geschlecht scheinen einen Haupteffekt zu haben. Somit scheint es Unterschiede auf mindestens einer AV zwischen mindestens 2 Gruppen zu geben. Wir erhalten die Mittelwerte pro Gruppe wieder ganz leicht mit aggregate:
aggregate(cbind(LZ, AB, Dep, AZ) ~ Intervention + Geschlecht,
data = Therapy,
FUN = mean)
| Intervention | Geschlecht | LZ | AB | Dep | AZ |
|---|---|---|---|---|---|
| Kontrollgruppe | 0 | 6.285714 | 5.571429 | 5.714286 | 5.714286 |
| VT Coaching | 0 | 6.100000 | 5.850000 | 4.450000 | 7.350000 |
| VT Coaching + Gruppenuebung | 0 | 7.423077 | 6.346154 | 4.615385 | 7.692308 |
| Kontrollgruppe | 1 | 5.826087 | 6.173913 | 7.565217 | 4.956522 |
| VT Coaching | 1 | 5.600000 | 5.800000 | 6.300000 | 5.800000 |
| VT Coaching + Gruppenuebung | 1 | 6.750000 | 6.000000 | 5.750000 | 6.250000 |
Wenn Sie sich an Ihr Bachelor-Statistikwissen zurückerinnern, so wissen Sie vielleicht noch, dass bei einer zweifaktoriellen ANOVA auch eine Interaktion zwischen den Faktoren möglich war. Dies geht selbstverständlich auch mit der MANOVA. In R lässt sich dies, wie in der Multi-Level-Sitzung diskutiert, mit * oder präziser mit : umsetzen:
manova3b <- manova(cbind(LZ, AB, Dep, AZ) ~ Intervention + Geschlecht + Intervention:Geschlecht,
data = Therapy)
M3b <- Manova(manova3b)
summary(M3b)
##
## Type II MANOVA Tests:
##
## Sum of squares and products for error:
## LZ AB Dep AZ
## LZ 168.02907 -16.754897 -63.88693 102.532131
## AB -16.75490 157.053249 82.29353 -4.263999
## Dep -63.88693 82.293526 133.03459 -89.383134
## AZ 102.53213 -4.263999 -89.38313 146.823555
##
## ------------------------------------------
##
## Term: Intervention
##
## Sum of squares and products for the hypothesis:
## LZ AB Dep AZ
## LZ 25.475157 9.3241392 -4.9687967 13.490715
## AB 9.324139 3.4751989 -0.5748453 3.784616
## Dep -4.968797 -0.5748453 25.7292359 -25.586394
## AZ 13.490715 3.7846157 -25.5863937 28.425876
##
## Multivariate Tests: Intervention
## Df test stat approx F num Df den Df Pr(>F)
## Pillai 2 0.4254341 5.538923 8 164 3.3111e-06 ***
## Wilks 2 0.6175244 5.519025 8 162 3.5664e-06 ***
## Hotelling-Lawley 2 0.5498037 5.498037 8 160 3.8533e-06 ***
## Roy 2 0.3523964 7.224126 4 82 4.9239e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## ------------------------------------------
##
## Term: Geschlecht
##
## Sum of squares and products for the hypothesis:
## LZ AB Dep AZ
## LZ 4.267814 -0.8920430 -13.747957 10.179785
## AB -0.892043 0.1864516 2.873548 -2.127742
## Dep -13.747957 2.8735484 44.286452 -32.792258
## AZ 10.179785 -2.1277419 -32.792258 24.281290
##
## Multivariate Tests: Geschlecht
## Df test stat approx F num Df den Df Pr(>F)
## Pillai 1 0.3320049 10.0646 4 81 1.1563e-06 ***
## Wilks 1 0.6679951 10.0646 4 81 1.1563e-06 ***
## Hotelling-Lawley 1 0.4970170 10.0646 4 81 1.1563e-06 ***
## Roy 1 0.4970170 10.0646 4 81 1.1563e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## ------------------------------------------
##
## Term: Intervention:Geschlecht
##
## Sum of squares and products for the hypothesis:
## LZ AB Dep AZ
## LZ 0.1031133 0.3802736 0.3682230 0.2214175
## AB 0.3802736 2.1936328 1.1329256 1.9250743
## Dep 0.3682230 1.1329256 1.3789569 0.4753923
## AZ 0.2214175 1.9250743 0.4753923 2.0284883
##
## Multivariate Tests: Intervention:Geschlecht
## Df test stat approx F num Df den Df Pr(>F)
## Pillai 2 0.0572802 0.6044334 8 164 0.77326
## Wilks 2 0.9432833 0.5998989 8 162 0.77701
## Hotelling-Lawley 2 0.0595295 0.5952947 8 160 0.78079
## Roy 2 0.0467506 0.9583868 4 82 0.43490
Die Analysen für die Interaktione erkennen wir unter dem Block Term: Intervention:Geschlecht. Hier stehen die Teststatistiken, die den Interaktionseffekt untersuchen. Auch eine Quadrat-und-Produktsumme wird dort ausgegeben.
Die Interaktion ist nicht signifikant. Somit hängt der Therapieeffekt nicht vom Geschlecht der jeweiligen Person ab. Dies ist somit eine gute Nachricht, da nicht geschlechterspezifisch vorgegangen werden müsste, falls es sich hierbei um echte Daten gehandelt hätte! Es ist aber durchaus gegeben, dass sich die Ausprägungen über die Geschlechter im Mittel unterscheiden.
Auch Post-Hoc multifaktorielle ANOVAs sind möglich. Hier erweitert sich der Output entsprechend. Da die Interaktion nicht statistisch bedeutsam war, schauen wir uns die Post-Hoc ANOVAs für manova3 an:
summary.aov(manova3)
## Response LZ :
## Df Sum Sq Mean Sq F value Pr(>F)
## Intervention 2 39.200 19.6000 10.025 0.000122 ***
## Geschlecht 1 4.268 4.2678 2.183 0.143195
## Residuals 86 168.132 1.9550
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Response AB :
## Df Sum Sq Mean Sq F value Pr(>F)
## Intervention 2 3.289 1.64444 0.8881 0.4152
## Geschlecht 1 0.186 0.18645 0.1007 0.7518
## Residuals 86 159.247 1.85171
##
## Response Dep :
## Df Sum Sq Mean Sq F value Pr(>F)
## Intervention 2 99.622 49.811 31.870 4.405e-11 ***
## Geschlecht 1 44.286 44.286 28.335 8.020e-07 ***
## Residuals 86 134.414 1.563
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Response AZ :
## Df Sum Sq Mean Sq F value Pr(>F)
## Intervention 2 89.356 44.678 25.813 1.657e-09 ***
## Geschlecht 1 24.281 24.281 14.029 0.0003249 ***
## Residuals 86 148.852 1.731
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Bzgl. der Lebenszufriedenheit gab es nur einen Haupteffekt der Intervention ($F(2,86)=$ 10.025, $p<0.001$), nicht aber bzgl. des Geschlechts ($F(1,86)=$ 2.183, $p>0.05$). Die Arbeitsbelastung unterschied sich weder über die Interventionsgruppen noch über das Geschlecht. Sowohl die Depression als auch die Arbeitszufriedenheit zeigten signifikante Haupteffekte sowohl der Intervention (Dep: $F(2,86)=$ 31.870, $p<0.001$, AZ: $F(2,86)=$ 25.813, $p<0.001$) als auch des Geschlechts (Dep: $F(1,86)=$ 28.335, $p<0.001$, AZ: $F(1,86)=$ 14.029, $p<0.001$). Insgesamt wird Hypothese 3 durch die Daten gestützt.
In Appendix B wird eine MANOVA und eine ANOVA mit Messwiederholung vorgestellt. Außerdem wird kurz die MANCOVA (multivariate Kovarianzanalyse) und die ANCOVA (Kovarianzanalyse) erwähnt. Alles beide ist in R sehr leicht umzusetzen, unterliegt allerdings weiteren Annahmen.
Die nächste Sitzung zeigt eine Diskriminanzanalyse zu diesem Datensatz. Diese ist deshalb interessant, da sie die Fragestellung der MANOVA umdreht und nicht nach Gruppenunterschiede im Mittel fragt sondern modelliert in wieweit die Gruppenzugehörigkeit durch die AVs vorhergesagt werden kann. Da es sich bei dieser Sitzung um einen (freiwiligen) Zusatz handelt, wird diese nicht so intensiv behandelt.
Appendix
Appendix A
R-Code zu den Grafiken
#### Appendix A ----
library(ggplot2)
Therapy_long <- reshape(data = Therapy, varying = names(Therapy)[1:4],idvar = names(Therapy)[5:6],
direction = "long", v.names = "AVs", timevar = "Variable", new.row.names = 1:360)
Therapy_long$Variable[Therapy_long$Variable == 1] <- "Lebenszufriedenheit"
Therapy_long$Variable[Therapy_long$Variable == 2] <- "Arbeitsbeanspruchung"
Therapy_long$Variable[Therapy_long$Variable == 3] <- "Depressivitaet"
Therapy_long$Variable[Therapy_long$Variable == 4] <- "Arbeitszufriedenheit"
ggplot(Therapy_long, aes(x = Intervention, y = AVs, group = Variable, col = Variable))+ stat_summary(fun.data = mean_se)+stat_summary(fun.data = mean_se, geom = c("line"))
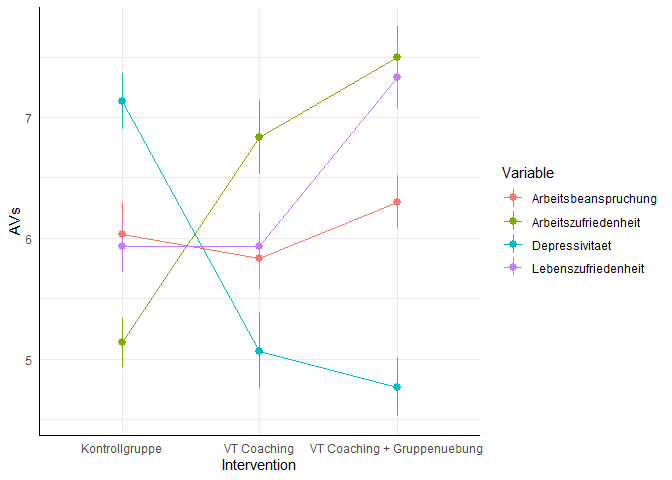
reshape transformiert den Datensatz vom Wide in das Long-Format (weites Format vs. langes Format): data nimmt den Datensatz entgegen, varying die Variablen, die wiederholt gemessen wurden (in diesem Fall unsere AVs), v.names nimmt die Namen unter dem die Variablen zusammengefasst werden sollen entgegen, timevar zeigt die Variable, die Wiederholung kennzeichnen soll, idvar sind Variablen, die sich über die Wiederholungen nicht verändern (die also Mehrfach in den Datensatz integriert werden) und direction nimmt entgegen, ob von Wide zu Long ("long") oder von Long zu Wide ("wide") transformiert werden soll. Dem Code ist ersichtlich, dass dies insbesondere für Messwiederholungen verwendet wird. Wir können hier allerdings die Variablen als Messwiederholungen auf unterschiedlichen Variablen ansehen. Das Long-Format ist insbesondere für das Darstellen mehrerer Gruppen in ggplot interessant. Hier lassen sich über die Gruppierungsvariable (hier Variable - den Namen, den wir timevar übergeben hatten) ganz leicht mehrere Linien einzeichnen. Die Fehlerbalken sind hierbei ganz einfach der SE des Mittelwerts pro Variable und Gruppe. Die Daten werden mit stat_summary und dem Zusatzargument fun.data = mean_se in Mittelwert und SE des Mittelwerts zusammengefasst. Eine detaillierte Erläuterung finden Sie in Grafiken mit ggplot2 von Prof. Dr. Martin Schultze.
Appendix B
MANOVA (und ANOVA) mit Messwiederholung
Dieser Exkurs soll zusätzliche Analysen mit Messwiederholung beschreiben. Das Ganze ist nicht sonderlich komplex, geht aber über diese Veranstaltung hinaus (da bspw. weitere Annahmen von Nöten sind) – könnte jedoch für Sie beim Schreiben Ihrer Masterarbeit relevant sein.
Sowohl bei MANOVAs als auch bei ANOVAs besteht die Möglichkeit die Messwiederholung, bspw. von Probanden, mit zu berücksichtigen. So hätte auch der gesamte Verlauf der Studie und somit der Verlauf der Merkmale über die Zeit (z.B. Prä, Post und ein Follow-Up einige Wochen nach Beendigung der Therapie) abgebildet werden können. In einem solchen Datensatz würde es eine Variable geben müssen, welche anzeigt, welche Messungen alle zum selben Objekt (bspw. zur selben Person) gehören - ganz ähnlich wie die Cluster-Variable in der hierarchischen Regression. Außerdem würde dann die Möglichkeit bestehen auch within-Effekte zu modellieren, also Prädiktoren könnten untersucht werden, die den Verlauf über die Zeit einer Person weiter erklären. Hier könnte bspw. der Messzeitpunkt als Prädiktor mit in das Modell aufgenommen werden – dann würde man untersuchen können, ob es Unterschiede über die Messzeitpunkte als Gruppierungsvariable gibt (auch kontinuierliche Variablen sind hier möglich - dann handelt es sich allerdings um eine MANCOVA, also eine multivariate Kovarianzanalyse bzw. ANCOVA also eine Kovarianzanalyse – Würden wir dann den Messzeitpunkt als 1, 2, 3,… modellieren, so würde die multivariate Kovarianzanalyse für den Messzeitpunkt eine lineare Veränderung annehmen, was für das vorgeschlagene Design wenig sinnvoll erscheint - in diesem ist es sinnvoller den Messzeitpunkt als Faktor mit aufzunehmen, um jegliche Unterschiede zwischen diesen abzubilden!). Der Output erweitert sich um eine Between und eine Within Ebene und Effekte werden auf beiden geprüft. Angenommen, wir hätten Daten, die an mehreren Tagen gemessen wurden und würden unsere Analysen “mit Messwiederholung” wiederholen. Dann könnte der Datensatz bspw. so aussehen:
| LZ | AB | Dep | AZ | Intervention | Sex | ID | day |
|---|---|---|---|---|---|---|---|
| 6.673546 | 4.483643 | 6.464371 | 6.895281 | 1 | 1 | 1 | 1 |
| 7.929508 | 3.779532 | 8.087429 | 6.338325 | 1 | 1 | 1 | 2 |
| 8.475781 | 4.594612 | 9.411781 | 6.289843 | 1 | 1 | 1 | 3 |
| 4.678759 | 3.085300 | 9.424931 | 3.255066 | 1 | 2 | 2 | 1 |
| 5.583810 | 6.543836 | 9.421221 | 4.193901 | 1 | 2 | 2 | 2 |
| 6.818977 | 6.682136 | 8.974565 | 1.910648 | 1 | 2 | 2 | 3 |
Es müssten zunächst weitere Annahmen an die Daten gestellt werden, die wir hier nicht prüfen wollen (z.B. Sphärizität der Kovarianzmatrizen).
Um eine repeated-measures MANOVA durchzuführen, müssen wir die Daten zunächst in das richtige Format bringen. Die Daten liegen gerade im Longformat vor. Wir brauchen sie allerdings im Wideformat. Die Transformation nimmt uns reshape ab:
Therapy_repeated_wide <- reshape(data = Therapy_repeated, direction = "wide",
v.names = c("LZ", "AB", "Dep", "AZ"),
timevar = "day",
idvar = "ID")
| Intervention | Sex | ID | LZ.1 | AB.1 | Dep.1 | AZ.1 | LZ.2 | AB.2 | Dep.2 | AZ.2 | LZ.3 | AB.3 | Dep.3 | AZ.3 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 6.673546 | 4.483643 | 6.464371 | 6.895281 | 7.929508 | 3.779532 | 8.087429 | 6.338325 | 8.475781 | 4.594612 | 9.411781 | 6.289843 |
| 4 | 1 | 2 | 2 | 4.678759 | 3.085300 | 9.424931 | 3.255066 | 5.583810 | 6.543836 | 9.421221 | 4.193901 | 6.818977 | 6.682136 | 8.974565 | 1.910648 |
| 7 | 1 | 1 | 3 | 8.919826 | 7.243871 | 6.144204 | 4.829248 | 8.121850 | 8.017942 | 7.958680 | 6.497212 | 9.287672 | 7.846195 | 5.522940 | 6.485005 |
| 10 | 1 | 2 | 4 | 5.905710 | 4.240687 | 6.400025 | 6.063176 | 6.435476 | 4.346638 | 6.296963 | 6.156663 | 6.211244 | 4.192505 | 6.264582 | 6.668533 |
| 13 | 1 | 2 | 5 | 6.187654 | 10.181108 | 8.698106 | 4.687974 | 6.941120 | 8.470637 | 10.033024 | 7.580400 | 6.532779 | 8.855865 | 9.469720 | 5.764945 |
| 16 | 1 | 2 | 6 | 10.701618 | 7.260760 | 8.989739 | 6.328002 | 7.856727 | 7.788792 | 6.795041 | 8.065555 | 9.053253 | 10.072612 | 9.375509 | 6.190054 |
Jetzt haben wir also jeweils 3 Variablen für LZ, nämlich LZ.1, LZ.2 und LZ.3. Gleiches gilt für AB, Dep und AZ. Als nächstes erstellen wir eine Variable, die die Zugehörigkeit zum Tag innehat. Wir wollen die Daten anschließend wie folgt zusammenschreiben: cbind(LZ.1, LZ.2, LZ.3, AB.1, AB.2, AB.3, Dep.1, Dep.2, Dep.3, AZ.1, AZ.2, AZ.3). Hier ist ersichtlich, dass die ersten 3 Spalten zu einer Variable gehören, nämlich zu LZ und dass es sich um den 1., 2. und 3. Tag handelt. Wir brauchen nun eine zweite Datenmatrix, die genau diese Information enthält:
days <- factor(rep(1:3, 4))
rep_data <- data.frame("day" = days)
head(rep_data)
## day
## 1 1
## 2 2
## 3 3
## 4 1
## 5 2
## 6 3
Mit Hilfe dieses Datensatzes transformieren wir quasi die Analyse innerhalb des Manova-Befehls wieder ins Longformat, also sagen, dass es sich um Messwiederholung handelt:
repeated_manova <- manova(cbind(LZ.1, LZ.2, LZ.3, AB.1, AB.2, AB.3, Dep.1, Dep.2, Dep.3, AZ.1, AZ.2, AZ.3) ~ Intervention*Sex, data = Therapy_repeated_wide)
Manova(repeated_manova, idata = rep_data, idesign =~ day, type = 3, test = "Wilks")
##
## Type III Repeated Measures MANOVA Tests: Wilks test statistic
## Df test stat approx F num Df den Df Pr(>F)
## (Intercept) 1 0.13325 546.38 1 84 < 2.2e-16 ***
## Intervention 2 0.89361 5.00 2 84 0.008875 **
## Sex 1 0.99435 0.48 1 84 0.491378
## Intervention:Sex 2 0.97328 1.15 2 84 0.320555
## day 1 0.88353 5.47 2 83 0.005864 **
## Intervention:day 2 0.96708 0.70 4 166 0.592622
## Sex:day 1 0.98979 0.43 2 83 0.653256
## Intervention:Sex:day 2 0.93490 1.42 4 166 0.229353
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Manova(repeated_manova, idata = rep_data, idesign =~ day, type = 3, test = "Pillai")
##
## Type III Repeated Measures MANOVA Tests: Pillai test statistic
## Df test stat approx F num Df den Df Pr(>F)
## (Intercept) 1 0.86675 546.38 1 84 < 2.2e-16 ***
## Intervention 2 0.10639 5.00 2 84 0.008875 **
## Sex 1 0.00565 0.48 1 84 0.491378
## Intervention:Sex 2 0.02672 1.15 2 84 0.320555
## day 1 0.11647 5.47 2 83 0.005864 **
## Intervention:day 2 0.03302 0.71 4 168 0.589471
## Sex:day 1 0.01021 0.43 2 83 0.653256
## Intervention:Sex:day 2 0.06539 1.42 4 168 0.229618
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Wir verwenden hier Quadratsummen vom Typ 3, damit die Interaktionen zwischen Messzeitpunkt und Faktoren sinnvoll untersuchbar sind. Nur die Intervention zeigt einen Effekt (Between Effekt). Innerhalb der Individuen (Within-Effekt) gibt es Unterschiede bzgl. des Messzeitpunktes (mit einer Irrtumswahrscheinlichkeit von 5%). Das können wir anhand des signifikanten Effekts von day ablesen. Das Ausmaß der AVs verändert sich also über die Zeit. Der Zeitpunkt wurde hier als Faktor mitmodelliert, da wir keine lineare Beziehen annehmen wollten (dies wäre dann eine MANCOVA) gewesen, wenn wir hier für day eine intervallskalierte Variable verwenden würden. Dies geht hier über den Stoff deutlich hinaus und verlangt auch noch weitere Überlegungen und ggf. andere Funktionen.
Das Ganze ginge auch mit der Basisfunktion. Allerdings müssten dann wieder die Gruppen bestimmt kodiert werden, um nicht das Problem mit den Quadratsummen zu bekommen. Der Code für Quadratsummen vom Typ I (die nicht sinnvoll sind, bzw. einer spezifischen Reihenfolge von Hypothesen entsprechen), sähen so aus:
repeated_manova <- manova(cbind(LZ, AB, Dep, AZ) ~ Intervention*Sex + factor(day) + Error(ID),
data = Therapy_repeated)
summary(repeated_manova, test = "Wilks")
Error(ID) zeigt an, dass diese Variable Mehrfachmessung kodiert. Das schöne an dieser Herangehensweise ist, dass wir die Daten im Longformat verwenden können. Für weitere Informationen zu den Quadratsumme, siehe Appendix der Sitzung zur zweifaktoriellen ANOVA aus dem Bachelorstudium.
Literatur
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden (5. Auflage, 1. Auflage: 2010). Weinheim: Beltz.
Pituch, K. A. & Stevens, J. P. (2016). Applied Multivariate Statistics for the Social Sciences (6th ed.). New York: Taylor & Francis.
- Blau hinterlegte Autor:innenangaben führen Sie direkt zur universitätsinternen Ressource.
](/media/header/beach.jpg)