Dynamische Netzwerkanalyse

Einführung

Nachdem wir letzte Woche in die Netzwerkanalyse eingestiegen sind, bei welcher wir querschnittliche Daten verarbeitet haben, geht es heute um das Setting einer Längsschnittuntersuchung. Übergeordnet werden Netzwerke mit Zeitverlaufsmessung als dynamische Netzwerke bezeichnet. Wir wollen uns im Rahmen dieses Tutorials mit einer Unterform davon auseinandersetzen - den idiographischen Netzwerken. Idiographische Netzwerke beziehen sich, wie der Name schon sagt, auf einzelne Personen. In der Praxis besteht dabei ein großes Bedürfnis nach Methoden, die die datengetriebene Personalisierung von Psychotherapie auf einzelne Patient:innen (personalized psychotherapy) ermöglichen, da die meisten sonst angewendeten Methoden sich auf Erkenntnisse auf dem Gruppen-Level fokussieren. Probleme auf individueller Ebene werden demnach mit Modellen analysiert, die auf Gruppenebene entworfen wurden. Allerdings müssen Ergebnisse, die über viele Personen gemittelt werden, nicht unbedingt auf ein Individuum zutreffen. Ganz grundsätzlich zeigt sich hier ein Problem dabei, Zusammenhänge von Variablen zwischen Personen auf den Zusammenhang innerhalb einer Person zu übertragen. Aus der Literatur (Hamaker, 2012) gibt es hier das prägnante Beispiel der Tippgeschwindigkeit (auch wenn das jetzt nicht direkt ein klinisches Beispiel ist): Erhebt man Daten zur Tippgeschwindigkeit und zu Rechtschreibfehlern über viele Personen hinweg, findet sich ein negativer Zusammenhang - wer schneller tippt, tippt auch akkurater. Würde man deswegen Einzelpersonen empfehlen, einfach schneller zu tippen, wenn sie weniger Fehler machen wollen? Nein, denn innerhalb einer Person ist der gleiche Zusammenhang positiv - wenn ich im Vergleich zu meiner typischen Geschwindigkeit schneller schreibe, mache ich auch mehr Fehler. Dieses Problem lässt sich auf verschiedene andere Zusammenhänge übertragen.

Bei psychischen Störungen, die mit einem Cut-Off über die Anzahl bzw. Stärke von Symptomen diagnostiziert werden, kommt noch hinzu, dass im Hintergrund eine große Menge an verschiedenen Kombinationen dieser Symptome bestehen kann. Diese Problematik könnte auch teilweise erklären, warum Therapiemethoden bei unterschiedlichen Personen teils sehr unterschiedlich gut wirken oder etwa auch, warum keine eindeutigen biologischen Marker/Entsprechungen für die sehr heterogenen Störungskategorien in Gehirnregionen gefunden werden. Es sollte also bei der Erforschung eines Störungsbildes nicht nur die Intensität der Störung betrachtet werden, sondern auch die individuelle Zusammensetzung und das Zusammenspiel der Symptome.

Die idiographischen Netzwerke bieten nun den Vorteil, dass sie eine individuelle Betrachtung für Einzelpersonen ermöglichen. Sie sind dabei sogar theoretisch in die Therapie einbindbar, da die einfache und sehr anschauliche Visualisierung auch für die Patient:innen verständlich sein kann. Patient:innen werden dabei aktiv integriert, da sie natürlich die zugehörigen Daten durch Beantwortung von Fragebögen erzeugen müssen. Ein erhoffter Benefit ist dabei, dass durch die gemeinsame Diskussion der Ergebnisse eine Selbstwirksamkeit oder bessere Selbstwahrnehmung in den Patient:innen erzeugt werden könnte. Mögliche Verwendungszwecke bieten dabei die Erhebung zu Beginn und gegen Ende der Therapie, um den Erfolg aufzuzeigen, oder auch die Inspektion der Netzwerkstruktur nach spezifischen Ansatzpunkten für die Therapie.

Daten

Da es sich bei den idiographischen Netzwerken wie beschrieben um dynamische Netzwerke (auf Basis von längsschnittlichen Daten dieser einzelnen Person) handelt, reicht ein einmaliges Ausfüllen von Fragebögen der Proband:innen nicht aus. Der Selbstbericht wird hier also häufig wiederholt, in der Regel mehrere Male pro Tag über ein bis mehrere Wochen. Die Integration solcher Methoden in die Forschung ist natürlich erst durch neuere technische Gegebenheiten wie internetfähige Handys weit verbreitet worden. Proband:innen werden dabei durch Push-Nachrichten einer App oder SMS an das Ausfüllen der Fragebögen in vorher festgelegten Timeslots erinnert, wobei oftmals eher kurze Fragebögen verwendet werden, um den Zeitaufwand pro Erhebung kurz zu halten. Der Zeitplan der Erfassung pro Tag kann aufgrund des personalisierbaren Settings auf den Alltag optimiert werden. Das Vorgehen wird allgemein auch als Experience Sampling Method bezeichnet und hat das Ziel, psychologische Variablen im Alltag und in verschiedenen Kontexten zu erheben, um ein möglichst akkurates Bild vom Innenleben der Teilnehmenden zu erhalten.

Für die R-Abschnitte der heutigen Sitzung beschäftigen wir uns mit einem Datensatz, der auch in der als Grundlage angegebenen Literatur (Epskamp et al., 2018a) zu einer Einführung in die idiografischen Netzwerke genutzt wird. Wie gewohnt kann der Datensatz direkt aus dem OSF in unser Environment eingeladen werden.

data <- read.csv(url("https://osf.io/g6ya4/download"))

Lassen wir uns an dieser Stelle einmal die Variablennamen im Datensatz anzeigen.

names(data)

## [1] "relaxed"           "sad"               "nervous"           "concentration"     "tired"            
## [6] "rumination"        "bodily.discomfort" "time"

Die eingeladenen Daten befassen sich mit einer einzelnen Person. Dabei handelt es sich laut der Autor:innen um eine Person, die sich nach einer Major Depression-Diagnose schon in der Behandlung befand. Die Fragen wurden von der teilnehmenden Person 5 Mal am Tag über 14 Tage hinweg ausgefüllt. Dies wird uns auch angezeigt, wenn wir uns die Spalte time ausgeben lassen.

data$time

##  [1] "2014-04-25 10:15:00" "2014-04-25 13:15:00" "2014-04-25 16:15:00" "2014-04-25 19:15:00"
##  [5] "2014-04-25 22:15:00" "2014-04-26 10:15:00" "2014-04-26 13:15:00" "2014-04-26 16:15:00"
##  [9] "2014-04-26 19:15:00" "2014-04-26 22:15:00" "2014-04-27 10:15:00" "2014-04-27 13:15:00"
## [13] "2014-04-27 16:15:00" "2014-04-27 19:15:00" "2014-04-27 22:15:00" "2014-04-28 10:15:00"
## [17] "2014-04-28 13:15:00" "2014-04-28 16:15:00" "2014-04-28 19:15:00" "2014-04-28 22:15:00"
## [21] "2014-04-29 10:15:00" "2014-04-29 13:15:00" "2014-04-29 16:15:00" "2014-04-29 19:15:00"
## [25] "2014-04-29 22:15:00" "2014-04-30 10:15:00" "2014-04-30 13:15:00" "2014-04-30 16:15:00"
## [29] "2014-04-30 19:15:00" "2014-04-30 22:15:00" "2014-05-01 10:15:00" "2014-05-01 13:15:00"
## [33] "2014-05-01 16:15:00" "2014-05-01 19:15:00" "2014-05-01 22:15:00" "2014-05-02 10:15:00"
## [37] "2014-05-02 13:15:00" "2014-05-02 16:15:00" "2014-05-02 19:15:00" "2014-05-02 22:15:00"
## [41] "2014-05-03 10:15:00" "2014-05-03 13:15:00" "2014-05-03 16:15:00" "2014-05-03 19:15:00"
## [45] "2014-05-03 22:15:00" "2014-05-04 10:15:00" "2014-05-04 13:15:00" "2014-05-04 16:15:00"
## [49] "2014-05-04 19:15:00" "2014-05-04 22:15:00" "2014-05-05 10:15:00" "2014-05-05 13:15:00"
## [53] "2014-05-05 16:15:00" "2014-05-05 19:15:00" "2014-05-05 22:15:00" "2014-05-06 10:15:00"
## [57] "2014-05-06 13:15:00" "2014-05-06 16:15:00" "2014-05-06 19:15:00" "2014-05-06 22:15:00"
## [61] "2014-05-07 10:15:00" "2014-05-07 13:15:00" "2014-05-07 16:15:00" "2014-05-07 19:15:00"
## [65] "2014-05-07 22:15:00" "2014-05-08 10:15:00" "2014-05-08 13:15:00" "2014-05-08 16:15:00"
## [69] "2014-05-08 19:15:00" "2014-05-08 22:15:00"

Die Zieluhrzeiten des Ausfüllens blieben über die 14 Tage hinweg konstant. Dabei wurde ein dreistündlicher Rhythmus vom Morgen bis zum späten Abend gewählt. Leider ist das Format für eine Datumsvariable in einer CSV-Datei und einem Datensatz in R verschieden. Es gibt jedoch einen einfachen Weg, die Transformation zwischen den Formaten durchzuführen mittels der Funktion as.POSIXct. Unter dem Argument tz kann dabei noch die passende Zeitzone ausgewählt werden - in diesem Fall wurde die Studie in den Niederlanden durchgeführt. Wenn wir uns dann einen kleinen Ausschnitt der überschriebenen Variable anzeigen lassen, merken wir zwar, dass sich nicht viel verändert hat, jedoch ist es für R ein großer Unterschied.

data$time <- as.POSIXct(data$time, tz = "Europe/Amsterdam")
data$time[1:8]

## [1] "2014-04-25 10:15:00 CEST" "2014-04-25 13:15:00 CEST" "2014-04-25 16:15:00 CEST" "2014-04-25 19:15:00 CEST"
## [5] "2014-04-25 22:15:00 CEST" "2014-04-26 10:15:00 CEST" "2014-04-26 13:15:00 CEST" "2014-04-26 16:15:00 CEST"

Modell

Das in diesem Tutorial beschriebene Modell zur Repräsentation personenbezogener Längsschnittdaten und damit verbundener Schätzung dynamischer Netzwerke setzt sich aus zwei Bestandteilen zusammen. An dieser Stelle ist es - wie auch im Tutorial letzte Woche - wichtig zu erwähnen, dass die hier vorgestellten Modelle noch der wissenschaftlichen Diskussion in der Methodenforschung unterliegen. Wir stellen damit einen noch recht jungen Ansatz vor, der zwar bereits in verschiedenen Situationen zum Einsatz kommt, aber natürlich innerhalb der Psychologie nicht mit der langen Historie wie bspw. einer Hierarchischen Regression versehen ist. Später werden wir einige Kritikpunkte auch noch konkreter besprechen

Den ersten Teil der Modellierung stellt ein sogenanntes Vektorautoregressives Modell dar, in welchem die Daten eines Messzeitpunkts auf die Daten eines vorherigen Messzeitpunktes regressiert werden. Dieser Teil der Modellierung wird deshalb auch als temporal bezeichnet. Die Ausprägung auf einer Variable hängt dabei von vergangenen Ausprägungen dieser Variable und aller anderen Variablen im Modell ab, wobei der sogenannte lag ausdrückt, wie viele Messzeitpunkt man in die Vergangenheit schaut. Ein Lag 1 würde also etwa bedeuten, dass man den vorherigen Messzeitpunkt zur Modellierung verwendet. Dies stellt auch das aktuelle Standardvorgehen in der Psychologie dar, wobei auch größere Lags modelliert werden könnten. Wenn wir lediglich einen Lag 1 modellieren, gehen wir davon aus, dass sich alle Zusammenhänge zwischen den Variablen in diesem Zeitraum abspielen, bzw. andere Zusammenhänge stets durch dieses Zusammenspiel erklärt werden können. Andere (größere) Zeiträume werden also in der Modellierung in der Psychologie meist außer Acht gelassen. Der Bezug einer Variable auf sich selbst vom letzten Messzeitpunkt wird auch auto-regressiv genannt. Dadurch entstehen in der optischen Repräsentation des Netzwerks self-loops. Doch auch die anderen Variablen vom vorherigen Messzeitpunkt werden im Modell verwendet, woher auch der Name vektorautoregressiv stammt, da statt einer Variable ein ganzer Vektor von Variablen verwendet wird, um zeitliche Zusammenhänge zu modellieren. Der Zusammenhang einer Variable mit einer anderen wird als cross-lagged bezeichnet. Dadurch, dass alle Variablen wie in einer normalen multiplen Regression simultan in die Schätzung aufgenommen werden, repräsentiert ein gefundenes Gewicht zwischen zwei Knoten einen Einfluss, der über den Einfluss aller anderen Knoten hinaus existiert.

Diese Methode, zeitliche Zusammenhänge zwischen Variablen darzustellen, existiert schon sehr lange. Es lässt sich jedoch feststellen, dass (wie in jedem statistischen Modell) Residuen bei dieser Modellierung zurückbleiben, die noch weitere Informationen liefern können (Epskamp et al., 2018a). Eine potentiell sehr wichtige Information fehlt uns nämlich noch: Wie hängen die Variablen an einem bestimmten Messzeitpunkt gleichzeitig zusammen? Da zu jedem einzelnen Zeitpunkt Residuen auf jeder Variable existent bleiben, können diese zur Bestimmung von Partialkorrelationen verwendet werden. Diese zeigen an, wie stark die Ausprägung von zwei Knoten zu einem gleichzeitigen Messzeitpunkt zusammenhängt. Dieser Teil der Modellierung wird auch als contemporaneous (also gleichzeitiges Netzwerk) bezeichnet. Die Idee der Modellierung sollte uns durch das Tutorial zu den querschnittlichen Netzwerken sehr bekannt vorkommen. Die Logik und Berechnung ist dabei auch sehr ähnlich, jedoch wird in dem vorliegenden Fall nur auf Grundlage der Residuen die Struktur des Netzwerks bestimmt, wodurch für den Einfluss des Messzeitpunkts davor kontrolliert werden kann. Eine Trennung von Effekten über Zeitfenster hinweg und innerhalb eines Zeitfensters wird damit ermöglicht.

Die Kombination der beiden Modelle wird von Epskamp et al. (2018a) als graphicalVAR bezeichnet und ist auch im bereits verwendeten Paket unter diesem Namen ansprechbar. Um die Schätzung mit einem Lag von 1 nochmal zusammenzufassen: Jeder Knoten wird zum Zeitpunkt t` mittels Maximum-Likelihood-Schätzung auf sich selbst und alle anderen Knoten zum Zeitpunkt t-1 regressiert. Bei dieser Schätzung entstehen nicht nur Zusammenhangsgewichte, sondern auch Residuen, also Anteile, die nicht durch die Knoten am Zeitpunkt t-1 erklärt werden können. Die Kovarianz dieser Residuen über alle Messungen hinweg dient dann dazu, den gleichzeitigen Zusammenhang zu t darzustellen. Wie auch bei den querschnittlichen Netzwerken lässt sich hier sowohl bei den temporalen, als auch bei den gleichzeitigen Netzwerken der lasso benutzen, um die Schätzungen zu regularisieren und falsch-positive Kanten zu vermeiden. Die resultierenden Zusammenhänge werden dann in der Regel in eine Partialkorrelationsmatrix umgewandelt, welche letztendlich zur Visualisierung der Netzwerke verwendet wird. Es werden dabei sowohl für die temporalen als auch die gleichzeitigen Aspekte Bestrafungsparameter genutzt. Aus den vielen resultierenden Netzwerken wird wieder das Informationskriteriuem BIC bzw. EBIC (bei einem Hyperparameter größer als 0) zur Selektion der besten Modellierung verwendet.

Stationarität

Bevor wir die bereits eingeladenen Daten aber für eine Schätzung verwenden können, müssen wir uns noch mit wichtigen Annahmen im Rahmen der Modellierung beschäftigen. Für den temporalen Aspekt sollten die Messungen in gleichmäßigen Abständen vorgenommen werden. Dafür wurde bereits beschrieben, dass ein Erhebungsplan am besten auf eine Person angepasst werden sollte, wobei Erinnerungen durch Apps das Ausfüllen zusätzlich absichern können. Da die Personen aber natürlich trotzdem normal schlafen sollen, ist der Abstand zwischen der letzten Messung an einem und der ersten Messung am nächsten Tag nicht entsprechend der Abstände zwischen den anderen Messungen. Dies kann als einer der Gründe dafür angesehen werden, dass tagesübergreifende Messungen bei der Modellierung nicht in einen Zusammenhang gestellt werden. Stationarität fordert dabei im Modell, dass die Netzwerkstruktur über die Zeit hinweg konstant ist. Anders formuliert sollten Modellparameter (also Kovarianzen/Mittelwerte/Varianzen) von der Zeit unabhängig sein. In der psychologischen Forschung ist anzunehmen, dass diese Voraussetzung nicht unbedingt gilt. So lässt sich etwa leicht vorstellen, dass sich sowohl Mittelwerte als auch Zusammenhänge zwischen Symptomen während einer Psychotherapie verändern. Vor der Modellschätzung wird daher empfohlen, den linearen Trend aus den Daten zu bereinigen. Wir versuchen uns an dieser Stelle mal damit, solch ein Detrending selbst vorzunehmen.

Im Endeffekt geht es beim Detrending um eine Überprüfung des Zeiteffekts auf die Variablen im Netzwerk. Nehmen wir mal als Beispiel tired. Wenn der Effekt der Zeit (Spalte time) erkundet werden soll, geht das im einfachsten Fall natürlich mit einer linearen Regression.

lm_tired <- lm(tired ~ time, data = data)

Um zu überprüfen, ob ein Detrending nötig ist, würden wir jetzt überprüfen, ob die Zeit ein signifikanter Prädiktor ist. Das können wir uns beispielsweise mit der Funktion summary anzeigen lassen. Wir sehen, dass die Zeit einen deutlichen Effekt hatte.

summary(lm_tired)

## 
## Call:
## lm(formula = tired ~ time, data = data)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.36927 -0.32883 -0.01885  0.32075  2.50944 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -1.741e+03  4.062e+02  -4.286 6.34e-05 ***
## time         1.248e-06  2.904e-07   4.298 6.10e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.7846 on 63 degrees of freedom
##   (5 observations deleted due to missingness)
## Multiple R-squared:  0.2267,	Adjusted R-squared:  0.2144 
## F-statistic: 18.47 on 1 and 63 DF,  p-value: 6.1e-05

Es ist ein signifikanter Effekt zu erkennen, weshalb die Variable detrendet werden sollte. Hier können wir uns der Logik der Regression bedienen. Wenn der Einfluss der Zeit herausgerechnet werden soll, können einfach die Residuen des linearen Modells mit der Zeit als Prädiktor genommen werden. Schließlich können diese nicht durch die Zeit erklärt werden. Die Variable im Datensatz wird also durch die Residuen (ansprechbar im Objekt lm_tired durch die Funktion residuals) ersetzt. Wichtig ist hier, dass die fehlenden Werte nicht in die Berechnung der Regression mit eingehen und es damit auch kein Residuum dafür gibt. Wenn wir die Daten ersetzen, müssen wir also sicher stellen, dass die Zeilen mit fehlenden Werten nicht beachtet werden. Wir wählen in unserem Datensatz also alle Zeilen, für die gilt, dass sie in tired nicht (!) fehlend (is.na) sind und ersetzen sie durch die Residuen.

data[!is.na(data["tired"]),"tired"] <- residuals(lm_tired) 

Man will natürlich nicht für jede Variable diese Schritte händisch durchführen. Für das vorliegende Netzwerk mit wenigen Variablen wird das noch gehen, aber 18 Mal wird es schon anstrengender, weshalb die Arbeit mit for empfohlen wird. Der Code ist jedoch nicht sehr simpel und kann für das komplette Durchdringen etwas Zeit brauchen. Das Verständnis ist also vor allem an die besonders Interessierten gerichtet, die Ausführung ist aber auch für die kommenden Befehle wichtig.

Zunächst einmal werden alle Variablen (rel_vars) festgehalten, die Teile des Netzwerkes sein sollen. Anschließend wird ein for-Loop mit dem Laufzeichen v gestartet, der einmal für alle Zahlen zwischen 1 und der gesamten Variablenanzahl (repräsentiert durch length) die folgenden Befehle in den geschweiften Klammern {} durchführt, indem sie für v eingesetzt werden. Zuerst wird die Formel für eine lineare Regression erstellt. Dabei wird zunächst der Variablennamen aus rel_vars ausgelesen und mit der Vorhersage durch die Zeit ~ time mit paste0 zusammengesetzt. Daraus entsteht bspw. dass Entspannung durch Zeit vorhergesagt wird: relaxed ~ time. Mit as.formula wird dafür gesorgt, dass diese Buchstaben nicht nur als character, sondern wirklich als Formel in lm_form abgelegt werden. Im zweiten Schritt wird nun die lineare Regression zu der zugehörigen Formel mit lm bestimmt und direkt die summary von ihr als Objekt angelegt. In der summary einer einfachen linearen Regression ist der p-Wert für den Steigungskoeffizienten unter $coefficients[,4][2] abgelegt. Wenn der Steigungskoeffizient nicht signifikant ist, muss nichts weiter gemacht werden. Eine Aktion ist nur erforderlich, wenn der p-Wert kleiner als der festgelegte $\alpha$-Fehler ist, was hier mit 0.05 repräsentiert wird. Daher ist hier eine if-Bedingung aufgeführt, die nur aktiviert wird, wenn die Signifikanz gegeben ist. In den {} wird nun festgehalten, dass zunächst eine Nachricht in die Konsole geschrieben wird, die uns Bescheid gibt, dass ein Detrending bei einer spezifischen Variable nötig ist. Anschließend wir die Variable durch das Residuum aus der linearen Modellierung ersetzt, wie wir es auch im händischen Code gemacht haben. v wird dabei natürlich verwendet, damit auch die richtige Variable ersetzt wird.

rel_vars <- c("relaxed","sad","nervous","concentration","tired","rumination","bodily.discomfort")


for (v in 1:length(rel_vars)){
  # Respektive Variable auf die Zeit regressieren
  lm_form <- as.formula(paste0(rel_vars[v], "~ time"))
  # lineares Modell rechnen
  lm_res <- summary(lm(lm_form, data = data))
  # wenn der Zeittrend signifikant ist, detrenden wir mit den Residuen
  # [,4] greift auf die Spalte der p-Werte zu
  # [2] auf den p-Wert des Regressionsgewichts des Datums
  if(lm_res$coefficients[,4][2] < 0.05){
    print(paste0("Detrende Variable: ", rel_vars[v]))
    data[!is.na(data[rel_vars[v]]),rel_vars[v]] <- residuals(lm_res)
  }
}

## [1] "Detrende Variable: rumination"

Modellschätzung in R

Nachdem wir Stationarität in den Daten erstellt haben, können wir nun ein Modell schätzen lassen. Dafür brauchen wir auch wie bei den querschnittlichen Netzwerken das bootnet-Paket. Für den Zeitablauf haben wir ja bereits gesehen, dass es die Variable time gibt. Die verwendete Funktion benötigt aber eine Variable, die die Messungen nach Tagen aufteilt und dann eine, die die einzelnen Messungen innerhalb eines Tages nochmal nummeriert. So kann sicher gestellt werden, dass - wie bereits beschrieben - die erste Messung eines Tages nicht auf den Vortag regressiert wird. Eine Variable, in der nur der Tag erhalten ist, ist sehr schnell erstellt. Mit as.Date kann unsere Zeitangabe auf die Tage reduziert werden. Wir ordnen das einer neuen Variable im Datensatz date zu.

data$date <- as.Date(data$time, tz = "Europe/Amsterdam")

Aus der Struktur unserer Datenerhebung wissen wir, dass wir 14 Mal 5 Messungen durchgeführt haben. Außerdem wissen wir durch die erste Betrachtung, dass die Messungen in den Zeilen nach zeitlicher Abfolge aufgeführt sind. Um die Nummerierung zu erstellen, können wir daher einfach 14 Mal 1 bis 5 in die Spalte beep einfügen. Dies ist durch die rep Funktion möglich. Bei dieser Funktion wird zuerst die Angabe gebraucht, was wiederholt wird, als zweites Argument wird die Häufigkeit der Wiederholung aufgeführt.

data$beep <- rep(1:5, 14)

Falls eine so geordnete Datenstruktur unglücklicherweise nicht vorliegt, braucht man für die Nummerierung der einzelnen Antworten innerhalb eines Tages wieder einen etwas komplizierteren Code, um eine automatische Durchführung zu erreichen. Deshalb wird hier wieder ein Stück Code beschrieben, der besonders für interessierte Personen gedacht ist. Die Durchführung ist an diesem Punkt auch nicht nötig, da wieder die bereits erstellte data$beep-Variable behandelt wird.

Hier wird wieder ein for-Loop erstellt, weil die Nummerierung für die beep-Variable an jedem Datum getrennt durchgeführt werden soll. Durch die Funktion unique werden alle einzigartigen Daten einmal durchlaufen. Wenn wir diesen Teil weglassen würden, würde der Loop manche Tage auch häufiger betrachten, was die Durchführung verlangsamt. Anschließend weisen wir alle Zeilen, die einem bestimmten Tag i entsprechen, einem kleineren Datensatz zu, den wir hier set nennen. Dieser Schritt ist nicht unbedingt nötigt, aber ohne ihn würde der Code noch komplizierter werden. Wichtig ist, dass die Reihenfolge der Zeilen nicht verändert wird. Die Zeile eines Datums, die bei data als erste von oben steht, macht das nun auch bei set. Daher können wir auch auf die Ordnung der Zeit time in unserem neuen kleineren Datensatz set zugreifen. Mit order wird jedem Wert seine Größe in der Gesamtreihenfolge zugeordnet - in unserem Beispiel also die Werte von 1 bis 4. Diese wollen wir aber nicht nur im kleinen Datensatz belassen, sondern in data der (neuen) Variable beep zuordnen. Dabei müssen wir data auf die Zeilen reduzieren, die dem Datum i entsprechen, das gerade behandelt wird. Hier ist es also entscheidend, dass in beiden Datensätzen dieselbe Zeile eines Datums an erster, zweiter, … Stelle steht, damit die Zahlen der Größenreihenfolge korrekt zugeordnet werden.

# Starte Loop für einzigartige Daten
for (i in unique(data$date)){
  
  # Schreibe alle Messungen eines Tages einen getrennten Datensatz
  set <- data[data$date == i,]
  
  # Schaue in diesem Datensatz die Ordnung der Zeit-Variable an
  # Schreib die zugehörige Zahl in der Reihenfolge in den Original-Datensatz
  data$beep[data$date==i] <- order(set$time)
}

Nachdem diese Vorbereitung getroffen ist, kann nun mit der Schätzung gestartet werden. Diese wird weiterhin mit dem Paket bootnet und der dazugehörigen Funktion durchgeführt. Vieles wird uns also bekannt vorkommen. An dieser Stelle muss noch angemerkt werden, dass bootnet für die Durchführung auf ein anderes Paket graphcialVAR zugreift. Dieses müsste daher eigentlich bei der Installation direkt dabei sein. Jedoch tritt das nicht (immer) auf, weshalb wir hier nochmal darauf hinweisen, dass das Paket auch selbst installiert werden kann.

install.packages("graphicalVAR")

Nun also zu der Funktion estimateNetwork. Zunächst muss im default wieder die passende Methode gewählt werden, was in unserem Fall nun graphicalVAR (wie das Paket) ist. Die Anzahl der Bestrafungsparameter nlambda wird für das gleichzeitige und temporale Netzwerk gemeinsam festgelegt. Jeweils werden 25 Parameter in unserem Code verwendet. Per Voreinstellung sollten es 100 sein, aber aus Zeitgründen reduzieren wir das an dieser Stelle. Der Tuning-Parameter kann auch wieder festgelegt werden. In der idiografischen Netzwerkanalyse wird hier meist 0 gewählt, damit die Sensitivität etwas erhöht wird und die Netzwerke nicht komplett leer ausgegeben werden. Nun zu den uns unbekannten Argumenten: In vars kann angegeben werden, wenn nicht alle Variablen aus einem Datensatz auch als Knoten im Netzwerk auftreten sollen. Das ist bei uns der Fall. Glücklicherweise haben wir bereits ein Objekt, in dem die Namen aller relevanten Variablen enthalten sind (rel_vars). In dayvar kann festgelegt werden, welche Variable im Datensatz den Tag anzeigt. beepvar gibt an, der wievielte Alarm es jeweils an einem Tag war. So kann die Funktion die Reihenfolge und auch die Tagesübergänge erkennen. Die beiden Variablen in dayvar und beepvar müssen natürlich nur im ursprünglichen Datensatz (data) enthalten sein und kein Knoten im Netzwerk (rel_vars) werden!

library(qgraph)
library(bootnet)

res <- estimateNetwork(data = data,
                                default = "graphicalVAR",   # verwendetes Package
                                vars = rel_vars,            # Variablennamen
                                dayvar = "date",            # Tagesvariable
                                beepvar = "beep",           # Notifikation
                                tuning = 0,                 # EBIC Tuningparameter
                                nLambda  = 25)              # Anzahl getesteter LASSO Tuningparameter 

## Estimating Network. Using package::function:
##   - graphicalVAR::graphicalVAR for model estimation

Die beiden ausgewählten Teilnetzwerke sind in res$graph abgelegt.

res$graph

## $contemporaneous
##                       relaxed          sad     nervous concentration      tired  rumination bodily.discomfort
## relaxed            0.00000000 -0.126105027 -0.04342341    0.13282464 -0.1277847 0.000000000       -0.21395865
## sad               -0.12610503  0.000000000  0.00000000   -0.01188015  0.3044483 0.005695221        0.07501887
## nervous           -0.04342341  0.000000000  0.00000000    0.00000000  0.0000000 0.000000000        0.00000000
## concentration      0.13282464 -0.011880150  0.00000000    0.00000000  0.0000000 0.000000000       -0.08499385
## tired             -0.12778465  0.304448284  0.00000000    0.00000000  0.0000000 0.000000000        0.00000000
## rumination         0.00000000  0.005695221  0.00000000    0.00000000  0.0000000 0.000000000        0.11110291
## bodily.discomfort -0.21395865  0.075018873  0.00000000   -0.08499385  0.0000000 0.111102907        0.00000000
## 
## $temporal
##                   relaxed sad   nervous concentration     tired rumination bodily.discomfort
## relaxed                 0   0 0.0000000             0 0.0000000 0.00000000        0.00000000
## sad                     0   0 0.0000000             0 0.0000000 0.00000000        0.00000000
## nervous                 0   0 0.0000000             0 0.0000000 0.00000000        0.00000000
## concentration           0   0 0.0000000             0 0.0000000 0.00000000        0.00000000
## tired                   0   0 0.0000000             0 0.2261836 0.00000000        0.00000000
## rumination              0   0 0.0000000             0 0.0000000 0.21562737        0.08979839
## bodily.discomfort       0   0 0.2541923             0 0.0000000 0.07305415        0.00000000

Wenn man sich nur eins anzeigen lassen möchte, kann man dies mit einem weiteren $-Zeichen in Kombination mit dem Namen durchführen (res$graph$temporal oder res$graph$contemporaneous). Ansonsten ist die Struktur des Ergebnis-Objektes sehr ähnlich zu dem der querschnittlichen Netzwerkanalyse. Man kann wieder tiefer in einzelne Berechnungsschritte einsteigen, sofern man das möchte. Wir gehen an dieser Stelle zum nächsten Schritt über.

Die optische Darstellung bleibt einer der großen Vorteile der Netzwerkanalyse. An diesem Punkt haben wir zwei Strukturen, die in der Darstellung aber zusammen wahrgenommen werden sollten. Dafür wäre es zunächst wichtig, ein gemeinsames Layout zu erschaffen, da sonst die Knoten an anderen Orten aufgezeigt werden würden. Dabei wird empfohlen, zunächst ein durchschnittliches Layout mit der Funktion averageLayout aus dem qgraph Paket zu bestimmen.

Layout <- averageLayout(res$graph$temporal, 
                        res$graph$contemporaneous)

Nun kann das Zeichnen mit der plot-Funktion beginnen. Diesmal reicht eine direkte Ansprache des Objektes nicht aus. Wir müssen weitere Argumente angeben. In graph wird festgehalten, welches Netzwerk wir zeichnen möchten. Das Argument layout ermöglicht uns eine Konstanthaltung - hier nehmen wir natürlich das von uns bestimmte durchschnittliche Layout. Zur Differenzierung der beiden Plots geben wir ihnen noch einen Titel (title).

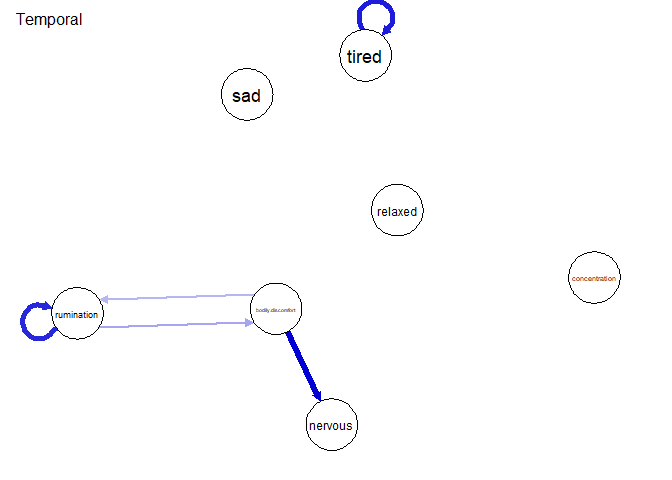
plot(res, graph = "temporal", layout = Layout, 
     title = "Temporal")

plot(res, graph = "contemporaneous", layout = Layout, 
     title = "Contemporaneous")

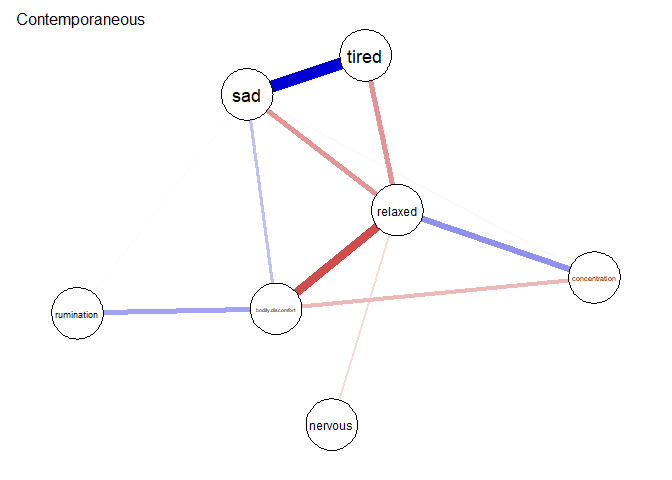
Im temporalen Teil des Netzwerkes sind zwei self-loops zu verzeichnen - also Variablen, die auf sich selbst wirken. Weiterhin sieht man auch eine Wechselwirkung zwischen rumination und bodily_discomfort. Das gleichzeitige Netzwerk ist stärker verbunden. Man sieht recht deutlich, dass relaxed viele negative Zusammenhänge zu symptomähnlichen Knoten hat. Wenn die Person sich ausgeruht fühlte, war sie gleichzeitig also weniger müde, traurig oder auch nervös.

Die gezeichnete Übersicht kann bereits einige Eindrücke über das Zusammenspiel der Symptome bieten. Doch auch darüber hinaus gibt es Ansätze für die genauere Interpretation der Ergebnisse. Wir haben bereits die Zentralitätsindizes im letzten Tutorial kennengelernt. Auch für graphicalVAR gibt es Ansätze, diese zu verwenden. Jedoch ist die Anwendung simultan auf das temporal und das contemporaneous Netzwerk noch nicht ausgereift. Die Analyse würde also getrennt für die beiden Unterformen angewendet und dann auch auf diese Weise berichtet werden. Ein weiterer bereits bekannter Vorgang ist das Bootstrapping, um die gefundenen Gewichte miteinander zu vergleichen. Auch beim Bootstrapping kommen getrennte Angaben für die beiden Unterarten der Netzwerke heraus. Es ist anzumerken, dass sich das Vorgehen bei der Erstellung eines einzelnen Boots zum querschnittlichen Netzwerk auch unterscheidet. Die zeitliche Reihenfolge der Daten muss beachtet werden. Diese können nicht einfach wild aus dem ursprünglichen Datensatz gezogen und die Daten komplett neu angeordnet werden. Aus Zeitgründen werden wir dies nicht genauer betrachten. Die Logik in der Bewertung ändert sich vom Bootstrap im querschnittlichen Format dann nicht. Wenn das Konfidenzintervall eines Gewichts größer als das eines anderen ist, kann man von einem Unterschied in den Gewichten ausgehen.

Problematiken

Wie bereits beschrieben, ist die Verwendung des graphicalVAR noch Teil des wissenschaftlichen Diskurses. Dabei gibt es einige Aspekte, die zur Diskussion gestellt sind (siehe z.B. Bringmann 2021). Wir wollen an dieser Stelle nur kurz auf drei Aspekte eingehen, die auch mit unserem jetzigen Wissen verständlich sein sollten und diese nutzen, um vor Fehlern in der Anwendung und Interpretation zu warnen. Zunächst einmal lässt sich festhalten, dass in dem Festlegen eines Erhebungszeitraums und der verwendeten Variablen bereits große Entscheidungen für die Struktur getroffen werden, die aus den Berechnungen resultieren wird. Es gibt keine allgemeingültige Regel, wie viel Zeit zwischen zwei Messzeitpunkten liegen sollte (am besten wäre natürlich eine durchgehende Messung, aber da ist die Technik dann doch noch nicht ganz so weit). Diese Unsicherheit kann man auf zwei Gründe zurückführen. Einerseits ist es interindividuell verschieden, wie schnell sich ein Symptom auf ein anderes auswirkt. Es ist etwa vorstellbar, dass bei Person A Grübeln innerhalb von wenigen Minuten zu einer traurigen Stimmung führt, wobei dies bei Person B vielleicht erst nach mehreren Stunden der Fall ist. Doch nicht nur interindividuell, sondern auch intraindividuell kann es zu Unterschieden kommen. Die Wirkung einer Variable auf eine andere kann je nach Konstrukt unterschiedlich schnell verlaufen. Während Stress bei der Arbeit womöglich innerhalb von Minuten die Anspannung einer Person erhöht, führt er vielleicht erst nach Tagen und Wochen zu Hoffnungslosigkeit. Der Abstand zwischen Erhebungen wird momentan also eher mit pragmatischen Gründen wie der Zumutbarkeit für die Teilnehmenden begründet - also, wie oft das Ausfüllen der Fragebögen an einem Tag ohne eine Beeinträchtigung des normalen Tagesablaufs möglich ist und über längere Zeit aufrechterhalten werden kann.

Eine zweite Problematik, die wir betrachten wollen, betrifft die Frage der Kausalität. Die vergleichsweise komplexer anmutende Form der Modellierung und die Einbeziehung von zeitlichen Informationen können dazu einladen, eine Kante im Netzwerk als Kausalzusammenhang zu interpretieren. Tatsächlich bedeutet das Vorhandensein einer Kante im temporalen Netzwerk ja auch, dass eine Variable eine andere über die Zeit vorhersagt, während für andere wichtige Einflüsse kontrolliert wird. Beispielsweise weist in unserem Netzwerk die Beziehung zwischen Bodily Discomfort und Nervousness eine solche Kante auf, was nach der Logik der Kausalität bedeuten würde, dass das Unwohlsein die Nervosität kausal vorhersagt. Die Argumente für Kausalität (zeitlich vorgestellt und kontrolliert für andere Einflüsse) decken sich zumindest teilweise mit einigen geläufigen Vorstellungen über Kausalität und wird daher in der Ökonomie auch als “Granger-Kausalität” bezeichnet. Allerdings gibt es hierbei mehrere Interpretationsprobleme: Es ist etwa nicht ganz klar, ob wir alle relevanten Variablen im Netzwerk eingeschlossen haben und diese für das Individuum sinnvoll erheben. Zudem kann das zuvor beschriebene Problem der Messfrequenz dazu führen, dass ein tatsächlich existierender Kausalzusammenhang von unserer Schätzmethode nicht gefunden wird, da er sich zu schnell oder zu langsam abspielt. Ebenso fehlt in der Regel eine kontrollierte Manipulation von Variablen sowie strengere theoretische Annahmen, welche für Kausalaussagen notwendig wären. Die Netzwerke werden daher in der Regel maximal als hypothesengenerierend für potenzielle Kausalzusammenhänge interpretiert.

Die dritte Problematik befasst sich mit der Annahme der Stationarität. Durch unsere Korrektur des linearen Trends konnten wir zwar für die Durchführung eine Hilfe verschaffen, aber für einige Anwendungen ist diese Korrektur inhaltlich nicht unbedingt sinnvoll. Wollten wir beispielsweise über den ganzen Verlauf einer Therapie das Zusammenspiel von Symptomen betrachten und führen daher Messungen durch, wäre eine Änderung in der Netzwerkstruktur das Ziel, was wiederum der Stationaritätsannahme widerspräche. Abhilfe kann mit den vorgestellten Mitteln zum Teil dadurch geschaffen werden, dass eine Analyse mit Patient:innen während Phasen durchgeführt wird, in denen keine allzu starken Veränderungen zu erwarten sind, wie etwa kurz vor Beginn der Therapie. Anschließend kann in der gemeinsamen Betrachtung die Struktur des Netzwerks für die Behandlung genutzt werden. Wahlweise kann natürlich auch ganz am Ende der Therapie nochmal eine Untersuchung gemacht werden. Die gefundenen Modelle zu Beginn und zum Ende der Therapie könnten dann (rein optisch) verglichen werden, wobei auch dies bisher nur in kleinen Fallstudien tatsächlich klinisch erprobt wurde.

Praktische Anwendung

Trotz der methodischen Unsicherheiten gibt es Therapeut:innen, die die Methode bereits im Rahmen ihrer Behandlung erprobt haben. Eine Studie über einen etwas größer angelegten Einsatz wurde von Frumkin et al. (2021) verfasst. Dabei wurde von Patient:innen nach einigen Gesprächen aus der eigenen Einschätzung ein Netzwerk gezeichnet, in dem visualisiert wurde, welche Variablen wie zusammenhängen. Zusätzlich haben die Patient:innen über mehrere Wochen mehrmals täglich Fragebögen ausgefüllt. Aus den resultierenden Daten wurden dann statistische Netzwerke geschätzt, welche mit den selbst eingeschätzten Netzwerken verglichen wurden. Es konnte festgestellt werden, dass die Vorhersagen der Patient:innen zum Zusammenhang ihrer Symptome von dem datengetrieben generierten Netzwerk abweichen. Trotzdem wurde die Verwendung der Netzwerke als Tool in der Therapie von Patient:innen positiv evaluiert und als hilfreich betrachtet, wodurch eine gewisse Rechtfertigung für den Einsatz abgeleitet werden kann. Es gibt jedoch zwei Aspekte zu beachten. Im Gegensatz zu den Patient:innen zeigte sich bei den Therapeut:innen ein ambivalentes Bild in der Evaluation der Technik, zudem wies die Einschätzung der Methode als hilfreich eine große Varianz auf. Weiterhin wurde die Studie auch ohne eine Kontrollgruppe durchgeführt, wodurch unklar bleibt, welchen Mehrwert Netzwerke im klinischen Alltag haben können.

Erweiterungen des idiographischen Modells

Die methodische und klinische Forschung zu Netzwerkanalysen in den letzten Jahren war äußerst produktiv und hat viele neue Analysemethoden produziert und wichtige Debatten angestoßen. Neben der hier beschriebenen Modellierung gibt es noch diverse andere Ansätze, welche die Modellierung von Netzwerken im Längsschnitt ermöglichen, wenn auch dann teilweise ohne den gleichzeitigen Anteil. Ein Vorschlag dabei ist die Integration von klinischem Vorwissen von Therapeut:innen in einem Bayesianischen Netzwerk, um die klinische Validität und Nützlichkeit zu erhöhen (bspw. Burger et al., in preparation). Ein anderer Weg besteht in der Integration von mehreren Personen zur Schätzung von Netzwerken, etwa mit einer Multilevel-Struktur, die wir bereits bei der Hierarchischen Regression gesehen haben (Epskamp et al., 2018b). Hier wird zwar die pure Idiographie hinter sich gelassen, allerdings lassen sich so immer noch temporale Zusammenhänge innerhalb von Personen über die Zeit modellieren sowie Powerprobleme tendenziell eher umgehen, da deutlich mehr Daten vorliegen. Ebenso gibt es spannende neue Ansätze, welche die Stationaritätsannahme lockern und die explizite Untersuchung von Veränderungen über die Zeit ermöglichen (Haslbeck et al., 2021).

Fazit

Insgesamt lässt sich feststellen, dass die beschriebene Methodik noch jung ist und es viele Problematiken, aber dadurch auch Entwicklungspotentiale gibt. Die ersten Anwendungen weisen auch darauf hin, dass ein direkter Einbezug in die Therapie durch den personenbezogenen Ansatz möglich ist. Jedoch steht auch hier natürlich noch eine weitere Evaluation aus.

Literatur

Bringmann, L. F. (2021). Person-specific networks in psychopathology: Past, present, and future. Current opinion in psychology, 41, 59-64. https://doi.org/10.1016/j.copsyc.2021.03.004

Burger, J., Epskamp, S,., van der Veen, D. C., Dablander, F., Schoevers, R. A., Fried, E. I., & Riese, H. (in preparation). Models that matter for patients: Integrating clinical case formulation and idiographic network estimation. https://doi.org/10.31234/osf.io/bdrs7

Epskamp, S., van Borkulo, C. D., van der Veen, D. C., Servaas, M. N., Isvoranu, A. M., Riese, H., & Cramer, A. O. J. (2018a). Personalized network modeling in psychopathology: The importance of contemporaneous and temporal connections. Clinical Psychological Science, 6(3), 416-427. https://doi.org/10.1177%2F2167702617744325

Epskamp, S., Waldorp, L. J., Mõttus, R., & Borsboom, D. (2018b). The gaussian graphical model in cross-sectional and time-series data. Multivariate Behavioral Research, 53(4), 453–480. https://doi.org/10.1080/00273171.2018.1454823

Frumkin, M.R., Piccirillo, M.L., Beck, E.D., Grossman, J.T., & Rodebaugh, T.L. (2021). Feasibility and utility of idiographic models in the clinic: A pilot study. Psychotherapy Research, 31(4), 520-534. https://doi.org/10.1080/10503307.2020.1805133

Hamaker, E. L. (2012). Why researchers should think “within-person” a paradigmatic rationale. In M. R. Mehl & T. S. Conner (Eds.), Handbook of research methods for studying daily life (p. 43-61). New York, NY: Guilford Publications.

Haslbeck, J. M., Bringmann, L. F., & Waldorp, L. J. (2021). A tutorial on estimating time-varying vector autoregressive models. Multivariate Behavioral Research, 56(1), 120-149. https://doi.org/10.1080/00273171.2020.1743630