Inhalte
- Einleitung und Datenbeispiel
- Prima-Facie-Effekt
- Effektschätzung mittels ANCOVA
- Effektschätzung mit EffectLiteR
Einleitung und Datenbeispiel
In der psychologischen Forschung ist die Bestimmung kausaler Effekte oft eine Herausforderung, dies gilt auch für die klinisch-psychologische Forschung. Wenn ein Treatment nicht randomisiert zugeordnet werden kann, besteht die Gefahr, dass andere Einflussgrößen geschätzte Wirkungen des Treatments verzerren. Bevor wir mit dem (simulierten) Beispiel beginnen, laden wir zunächst die beiden Pakete, die wir in der Sitzung brauchen werden.
Pakete laden
# Benötigte Pakete --> Installieren, falls nicht schon vorhanden
library(psych) # Für Deskriptivstatistiken
library(EffectLiteR) # Für die Schätzung adjustierter Effekte
## Warning: Paket 'EffectLiteR' wurde unter R Version 4.3.3 erstellt
library(car) # Quadratsummen in Anova-Output
Simuliertes Beispiel
In unserem fiktiven Datenbeispiel wurden Patient:innen, die an einer Depression oder einer Angststörung leiden, entweder mit einer kognitiven Verhaltenstherapie (CBT) behandelt oder in einer Wartekontrollgruppe belassen. Eine zufällige Zuordnung war nicht vollständig möglich, da die Zuordnung der Patient:innen von den überweisenden Hausärzt:innen mit beeinflusst werden konnte (z.B. durch Geltendmachung einer besonderen Dringlichkeit der Therapie). Zunächst laden wir diesen Datensatz und verschaffen uns einen Überblick:
load(url("https://pandar.netlify.app/daten/CBTdata.rda"))
head(CBTdata)
| Age | Gender | Treatment | Disorder | BDI_pre | SWL_pre | BDI_post | SWL_post |
|---|---|---|---|---|---|---|---|
| 39 | female | CBT | ANX | 27 | 10 | 24 | 15 |
| 36 | female | CBT | ANX | 22 | 13 | 13 | 17 |
| 61 | female | CBT | ANX | 24 | 11 | 17 | 14 |
| 70 | female | CBT | ANX | 30 | 15 | 22 | 19 |
| 64 | female | CBT | DEP | 32 | 12 | 26 | 20 |
| 50 | female | CBT | ANX | 24 | 15 | 23 | 22 |
Die Variablen heißen Age (Alter), Gender (Geschlecht), Treatment (Behandlungsgruppenzugehörigkeit: CBT oder Wartekontrolle), Disorder (psychische Störung: Angststörung [ANX] oder Depression [DEP]), BDI_pre (Depressionswert gemessen mit Beck Depressions-Inventar vor Therapie), SWL_pre (Lebenszufriedenheit gemessen mit Satisfaction With Life Screening vor Therapie), BDI_post (Depressionswert gemessen mit Beck Depressions-Inventar nach Therapie), SWL_post (Lebenszufriedenheit gemessen mit Satisfaction With Life Screening nach Therapie). Wir können uns die Verteilung in die Behandlungsgruppen wie folgt ansehen:
table(CBTdata$Treatment)
##
## WL CBT
## 150 176
Der Datensatz enthält Daten also 326 Patient:innen, davon 176 in der Therapiegruppe (CBT) und 150 in der Wartelisten-Bedingung (WL). Vor und nach dem Treatment wurde die Schwere der depressiven Symptomatik mit dem Beck-Depressions-Inventar erfasst (BDI_pre und BDI_post), ebenso wurde vor und nach dem Treatment die Lebenszufriedenheit mit dem Satisfaction With Life Screening gemessen (SWL_pre und SWL_post).
Kritisch für die Evaluation von Therapieeffekten sind insbesondere vorab bestehende Gruppenunterschiede in den AVs und anderen Variablen. Diese schauen wir uns mit der Funktion describeBy deskriptiv an, wobei wir zunächst den gekürzten Datensatz übergeben und dem group-Argument die Gruppenvariable zuordnen. Mit range=F machen wir die Tabelle etwas übersichtlicher.
# Deskriptivstatistiken der Gruppen für Alter und Prätest-Werte
describeBy(CBTdata[, c("Age", "BDI_pre", "SWL_pre")], group = CBTdata$Treatment, range=F)
##
## Descriptive statistics by group
## group: WL
## vars n mean sd skew kurtosis se
## Age 1 150 48.15 15.41 -0.16 -1.27 1.26
## BDI_pre 2 150 19.95 4.10 0.08 0.04 0.33
## SWL_pre 3 150 18.13 4.04 -0.08 0.31 0.33
## ----------------------------------------------------------------------------
## group: CBT
## vars n mean sd skew kurtosis se
## Age 1 176 45.47 15.94 0.02 -1.36 1.20
## BDI_pre 2 176 23.94 3.95 -0.01 -0.25 0.30
## SWL_pre 3 176 14.76 4.06 0.04 -0.28 0.31
Uns werden einige Deskriptivstatistiken ausgegeben. Einfache Mittelwertsvergleiche und Effektstärkemaße können wir so betrachten (wir sparen uns an dieser Stelle den Output und tragen die Größen nur in den Text ein, um ein besseres Gefühl dafür zu bekommen, ob Unterschiede vorliegen):
t.age <- t.test(Age ~ Treatment, data = CBTdata)
d.age <- cohen.d(Age ~ Treatment, data = CBTdata)
t.bdi <- t.test(BDI_pre ~ Treatment, data = CBTdata)
d.bdi <- cohen.d(BDI_pre ~ Treatment, data = CBTdata)
t.swl <- t.test(SWL_pre ~ Treatment, data = CBTdata)
d.swl <- cohen.d(SWL_pre ~ Treatment, data = CBTdata)
Hinsichtlich des Alters sind beide Gruppen sehr ähnlich ($t$=1.541; $p$=0.124, $d$=0.17). Die Patient:innen in der Warteliste-Gruppe haben jedoch deutlich niedrigere BDI-Werte ($t$=-8.914; $p$=0, $d$=-1) und höhere SWL-Werte ($t$=7.504; $p$=0, $d$=0.84). Das zeigt, dass die Vergleichbarkeit der Gruppen nicht gewährleistet ist - die Gruppen unterscheiden sich bereits vor dem Treatment/vor der Behandlung.
Zusammenhänge von Alter und Art der Störung mit dem Treatment können wir deskriptiv durch Kreuztabellen darstellen und mit einem $\chi^2$-Test testen. Wir sehen, dass die Verteilung des Geschlechts auf die Gruppen nicht systematisch ist ($\chi^2(1)=$ 0.02, $p=$ 0.875):
# Tabelle erzeugen
tab.gender <- table(CBTdata$Treatment, CBTdata$Gender)
# Kreuztabelle mit Anteilen Zeilenweise, durch Multiplikation mit 100 als Zeilenprozent zu lesen
round(prop.table(tab.gender, 2)*100)
##
## male female
## WL 47 45
## CBT 53 55
# Chi2-Test
chisq.test(tab.gender)
##
## Pearson's Chi-squared test with Yates' continuity correction
##
## data: tab.gender
## X-squared = 0.024746, df = 1, p-value = 0.875
Wir sehen allerdings, dass Patient:innen mit Angststörung in der Therapiegruppe überrepräsentiert sind ($\chi^2(1)=$ 40.35, $p<0.05$):
tab.disorder <- table(CBTdata$Treatment, CBTdata$Disorder)
round(prop.table(tab.disorder, 2)*100)
##
## ANX DEP
## WL 28 64
## CBT 72 36
chisq.test(tab.disorder)
##
## Pearson's Chi-squared test with Yates' continuity correction
##
## data: tab.disorder
## X-squared = 40.351, df = 1, p-value = 2.122e-10
Der table-Befehl erzeugt hierbei die jeweiligen Vierfeldertafeln. Mit prop.table werden die absoluten Häufigkeiten in relative Häufigkeiten umgerechnet. Die erstellten Tabellen können herangezogen werden, um den $\chi^2$-Unabhängigkeitstest durchzuführen. Wiederholungen zu nominalen Variablen können Sie in den Sitzungen vom Bachelor nachlesen: Deskriptivstatistik für Nominal- und Ordinalskalen und Tests für unabhängige Stichproben.
Prima-Facie-Effekt
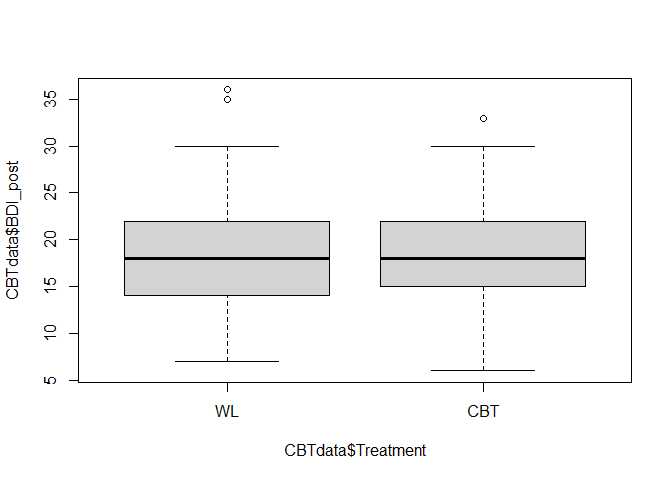
Ungeachtet der fraglichen Vergleichbarkeit schauen wir uns den augenscheinlichen Effekt der Therapie auf depressive Symptome an, grafisch als Boxplot und inferenzstatistisch mittels t-Test/Regressionsanalyse (das war ja beides das Gleiche! - siehe ANOVA vs. Regression).
boxplot(CBTdata$BDI_post ~ CBTdata$Treatment)
BDI.PFE <- lm(BDI_post ~ Treatment, data = CBTdata)
summary(BDI.PFE)
##
## Call:
## lm(formula = BDI_post ~ Treatment, data = CBTdata)
##
## Residuals:
## Min 1Q Median 3Q Max
## -12.4943 -3.4943 -0.1067 3.5057 17.8933
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 18.1067 0.4235 42.750 <2e-16 ***
## TreatmentCBT 0.3877 0.5764 0.672 0.502
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.187 on 324 degrees of freedom
## Multiple R-squared: 0.001394, Adjusted R-squared: -0.001688
## F-statistic: 0.4523 on 1 and 324 DF, p-value: 0.5017
Wir sehen bereits grafisch, dass sich beide Gruppen kaum voneinander unterscheiden. Der Unterschied von $\beta=$ 0.39 Punkten ist auch nicht signifikant ($p=$ 0.502). Diesem Ergebnis nach hat die Therapie keinen Effekt auf die Schwere der depressiven Symptomatik. Allerdings können wir diesen Effekt nicht kausal interpretieren, also das “Nichtvorliegen des Effekts” nicht auf ein nicht-funktionierendes Treatment zurückführen, da wir bereits gesehen haben, dass sich die Gruppen auch vor der Therapie schon unterschieden haben, was die Effekte somit konfundiert haben könnte.
Adjustierter Effekt mittels ANCOVA
Klassische ANCOVA
In der Annahme, dass die Selektion ins Treatment durch die vorab gemessenen Eigenschaften der Patient:innen erklärt werden kann, schätzen wir den Effekt des Treatments zunächst mit einer klassischen ANCOVA. Dabei werden die Variablen, hinsichtlich derer sich die Gruppen unterscheiden (Prätest-Werte und Art der Störung), kontrolliert:
# ANCOVA mit Treatment und Kovariaten
BDI.adj <- lm(BDI_post ~ Treatment + Disorder + BDI_pre + SWL_pre, data = CBTdata)
summary(BDI.adj)
##
## Call:
## lm(formula = BDI_post ~ Treatment + Disorder + BDI_pre + SWL_pre,
## data = CBTdata)
##
## Residuals:
## Min 1Q Median 3Q Max
## -9.6979 -1.8945 -0.0409 2.0341 8.4957
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.95691 1.45291 4.100 5.24e-05 ***
## TreatmentCBT -4.05665 0.39788 -10.196 < 2e-16 ***
## DisorderDEP 1.48794 0.38896 3.825 0.000157 ***
## BDI_pre 0.91387 0.04649 19.655 < 2e-16 ***
## SWL_pre -0.39267 0.04385 -8.955 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.059 on 321 degrees of freedom
## Multiple R-squared: 0.656, Adjusted R-squared: 0.6517
## F-statistic: 153 on 4 and 321 DF, p-value: < 2.2e-16
Unter Einbezug der Kovariaten findet sich ein signifikanter Therapieeffekt von -4.06 Punkten. Es wird auch sichtbar, dass alle Kovariaten einen Effekt auf die AV nach dem Treatment haben.
Generalisierte ANCOVA
In einer generalisierten ANCOVA nehmen wir noch die Wechselwirkungen zwischen den Kovariaten und dem Treatment hinzu und schauen uns auch den Anova-Output des car-Pakets an:
# Zentrierte Kovariaten bilden
CBTdata$BDI_pre_c <- scale(CBTdata$BDI_pre, scale = F)
CBTdata$SWL_pre_c <- scale(CBTdata$SWL_pre, scale = F)
# Generalisierte ANCOVA mit allen Wechselwirkungen zwischen Kovariaten und Treatment
BDI.adj2 <- lm(BDI_post ~ Treatment + Disorder + BDI_pre_c + SWL_pre_c +
Treatment:Disorder + Treatment:BDI_pre_c + Treatment:SWL_pre_c, data = CBTdata)
summary(BDI.adj2)
##
## Call:
## lm(formula = BDI_post ~ Treatment + Disorder + BDI_pre_c + SWL_pre_c +
## Treatment:Disorder + Treatment:BDI_pre_c + Treatment:SWL_pre_c,
## data = CBTdata)
##
## Residuals:
## Min 1Q Median 3Q Max
## -9.5620 -1.8491 -0.0809 1.9808 8.0522
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 20.08608 0.45756 43.898 < 2e-16 ***
## TreatmentCBT -4.38814 0.56952 -7.705 1.68e-13 ***
## DisorderDEP 1.16111 0.59835 1.941 0.0532 .
## BDI_pre_c 0.94310 0.06928 13.614 < 2e-16 ***
## SWL_pre_c -0.41531 0.06672 -6.224 1.52e-09 ***
## TreatmentCBT:DisorderDEP 0.60412 0.78877 0.766 0.4443
## TreatmentCBT:BDI_pre_c -0.05988 0.09366 -0.639 0.5231
## TreatmentCBT:SWL_pre_c 0.04826 0.08878 0.544 0.5871
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.062 on 318 degrees of freedom
## Multiple R-squared: 0.6585, Adjusted R-squared: 0.651
## F-statistic: 87.6 on 7 and 318 DF, p-value: < 2.2e-16
Die Effekte ändern sich kaum. Die Interaktionseffekte scheinen nicht signifikant zu sein. Trotzdem schauen wir uns nochmals die Effekte innerhalb des ANOVA-Frameworks an, um Signifikanzentscheidungen für die Gruppen kombiniert zu sehen.
Anova(BDI.adj2, type = 2)
## Anova Table (Type II tests)
##
## Response: BDI_post
## Sum Sq Df F value Pr(>F)
## Treatment 972.6 1 103.7346 < 2.2e-16 ***
## Disorder 140.4 1 14.9763 0.0001321 ***
## BDI_pre_c 3574.6 1 381.2632 < 2.2e-16 ***
## SWL_pre_c 728.8 1 77.7304 < 2.2e-16 ***
## Treatment:Disorder 5.5 1 0.5866 0.4443003
## Treatment:BDI_pre_c 3.8 1 0.4087 0.5230756
## Treatment:SWL_pre_c 2.8 1 0.2955 0.5871085
## Residuals 2981.4 318
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Diesen Analysen zufolge hat das Treatment einen Effekt. Außerdem unterscheidet sich die Depressivität je nachdem, welche Störung vorlag (wenig überraschend) und hängt von der Ausprägung der Depressivität und Lebenszufriedenheit vor Beginn der Therapie ab. Wechselwirkungen scheint es keine zu geben.
Zu guter Letzt fügen wir auch noch die Interaktion zwischen Disorder und Treatment zu den beiden kontinuierlichen Kovariaten hinzu, da dies im nächsten Abschnitt ebenfalls gemacht wird. Wir erweitern also auf eine Dreifachinteraktion. Außerdem ändern wir die Reihenfolge der Prädiktoren, da die Reihenfolge bekanntlich einen Einfluss auf die Punktschätzer haben kann. Damit wir also mit unserer ausgefalleneren ANCOVA dem nächsten Abschnitt entsprechen, müssen wir auch die entsprechende Reihenfolge der Prädiktoren einhalten:
BDI.adj3 <- lm(BDI_post ~ 1 + BDI_pre_c + SWL_pre_c + Disorder + # Interzept
Disorder:BDI_pre_c + Disorder:SWL_pre_c + # Interzept
Treatment + # Slope
Treatment:BDI_pre_c + Treatment:SWL_pre_c + Treatment:Disorder + # Slope
Treatment:Disorder:BDI_pre_c + Treatment:Disorder:SWL_pre_c, # Slope
data = CBTdata)
summary(BDI.adj3)
##
## Call:
## lm(formula = BDI_post ~ 1 + BDI_pre_c + SWL_pre_c + Disorder +
## Disorder:BDI_pre_c + Disorder:SWL_pre_c + Treatment + Treatment:BDI_pre_c +
## Treatment:SWL_pre_c + Treatment:Disorder + Treatment:Disorder:BDI_pre_c +
## Treatment:Disorder:SWL_pre_c, data = CBTdata)
##
## Residuals:
## Min 1Q Median 3Q Max
## -9.6825 -1.8013 -0.1473 1.8545 7.5690
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 20.03432 0.46219 43.347 < 2e-16 ***
## BDI_pre_c 1.05500 0.12736 8.284 3.50e-15 ***
## SWL_pre_c -0.35096 0.13813 -2.541 0.0115 *
## DisorderDEP 1.08259 0.62800 1.724 0.0857 .
## TreatmentCBT -4.50331 0.59100 -7.620 3.03e-13 ***
## BDI_pre_c:DisorderDEP -0.16040 0.15292 -1.049 0.2950
## SWL_pre_c:DisorderDEP -0.07458 0.15818 -0.471 0.6376
## BDI_pre_c:TreatmentCBT -0.13981 0.14961 -0.935 0.3508
## SWL_pre_c:TreatmentCBT -0.05871 0.15548 -0.378 0.7060
## DisorderDEP:TreatmentCBT 0.93328 0.83444 1.118 0.2642
## BDI_pre_c:DisorderDEP:TreatmentCBT 0.08140 0.20237 0.402 0.6878
## SWL_pre_c:DisorderDEP:TreatmentCBT 0.19973 0.20199 0.989 0.3235
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.068 on 314 degrees of freedom
## Multiple R-squared: 0.6615, Adjusted R-squared: 0.6497
## F-statistic: 55.8 on 11 and 314 DF, p-value: < 2.2e-16
Anova(BDI.adj3)
## Anova Table (Type II tests)
##
## Response: BDI_post
## Sum Sq Df F value Pr(>F)
## BDI_pre_c 3535.5 1 375.7025 < 2.2e-16 ***
## SWL_pre_c 715.6 1 76.0460 < 2.2e-16 ***
## Disorder 140.4 1 14.9209 0.0001362 ***
## Treatment 956.4 1 101.6326 < 2.2e-16 ***
## BDI_pre_c:Disorder 12.2 1 1.2937 0.2562377
## SWL_pre_c:Disorder 2.2 1 0.2373 0.6264934
## BDI_pre_c:Treatment 8.4 1 0.8953 0.3447726
## SWL_pre_c:Treatment 3.4 1 0.3609 0.5484181
## Disorder:Treatment 12.0 1 1.2777 0.2591840
## BDI_pre_c:Disorder:Treatment 1.5 1 0.1618 0.6877960
## SWL_pre_c:Disorder:Treatment 9.2 1 0.9778 0.3235093
## Residuals 2954.9 314
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Wir sehen, dass keine der hinzugefügten Interaktionen statistisch bedeutsam ist.
Adjustierter Effekt mittels EffectLiteR
Den adjustierten Effekt können wir auch mit EffectLiteR schätzen, hierbei wird die Gewichtung nach Kovariaten berücksichtigt. Die Funktion, die wir dazu benutzen, heißt effectLite. Das Kriterium (AV) wird dem Argument y übergeben, x wird die Gruppierungsvariable (UV) zugewiesen, z werden als Vektor die Kovariaten übergeben, k werden kategoriale Kovariaten übergeben, data schreiben wir die Daten zu und mit method = "lm" legen wir fest, dass alles auf Basis des linearen Modells geschätzt werden soll, was im Grunde einer Schätzung mittels ANCOVA entspricht.
# Schätzung des Effekts des Treatments auf BDI_post mit effectLite,
# Prätest-Werte als kontinuierliche, Störung als kategoriale Kovariate
# 'lm' als Methode für eine Schätzung per ANCOVA
effectLite(y="BDI_post", x="Treatment", z=c("BDI_pre_c", "SWL_pre_c"), k=c("Disorder"), data = CBTdata, method = "lm")
##
##
## --------------------- Variables ---------------------
##
## Outcome variable Y: BDI_post
## Treatment variable X: Treatment (Reference group: WL)
## Categorical covariates K: Disorder
## Continuous covariates in Z=(Z1,Z2): Z1=BDI_pre_c Z2=SWL_pre_c
##
## Levels of Treatment Variable X
## X Treatment (original) Indicator
## 0 WL I_X=0
## 1 CBT I_X=1
##
## Levels of Unfolded Categorical Covariate K
## K Disorder Indicator
## 0 ANX I_K=0
## 1 DEP I_K=1
##
## Cells
## Treatment (original) K Cell
## 1 WL 0 00
## 2 WL 1 01
## 3 CBT 0 10
## 4 CBT 1 11
##
##
## --------------------- Regression Model ---------------------
##
## E(Y|X,K,Z) = g0(K,Z) + g1(K,Z)*I_X=1
## g0(K,Z) = g000 + g001 * Z1 + g002 * Z2 + g010 * I_K=1 + g011 * I_K=1 * Z1 +
## + g012 * I_K=1 * Z2
## g1(K,Z) = g100 + g101 * Z1 + g102 * Z2 + g110 * I_K=1 + g111 * I_K=1 * Z1 +
## + g112 * I_K=1 * Z2
##
## Intercept Function g0(K,Z) [Reference group: WL]
##
## Coefficient Estimate SE Est./SE p-value
## g000 20.034 0.462 43.347 0.000
## g001 1.055 0.127 8.284 0.000
## g002 -0.351 0.138 -2.541 0.012
## g010 1.083 0.628 1.724 0.086
## g011 -0.160 0.153 -1.049 0.295
## g012 -0.075 0.158 -0.471 0.638
##
## Effect Function g1(K,Z) [Treatment: CBT vs. WL]
##
## Coefficient Estimate SE Est./SE p-value
## g100 -4.503 0.591 -7.620 0.000
## g101 -0.140 0.150 -0.935 0.351
## g102 -0.059 0.155 -0.378 0.706
## g110 0.933 0.834 1.118 0.264
## g111 0.081 0.202 0.402 0.688
## g112 0.200 0.202 0.989 0.324
##
##
## --------------------- Cell Counts ---------------------
##
##
## Cell Counts
##
## This table shows cell counts including missings.
## See also output under lavaan results for number of observations
## actually used in the analysis.
##
## Disorder 0 1
## Treatment
## 0 45 105
## 1 116 60
##
##
## --------------------- Main Hypotheses ---------------------
##
## H0: No average effects: E[g1(K,Z)] = 0
## H0: No covariate effects in control group: g0(K,Z) = constant
## H0: No treatment*covariate interaction: g1(K,Z) = constant
## H0: No treatment effects: g1(K,Z) = 0
##
## F value df1 df2 p-value
## No average effects 93.576 1 314 0.000
## No covariate effects in control group 65.223 5 314 0.000
## No treatment*covariate interaction 0.962 5 314 0.441
## No treatment effects 17.740 6 314 0.000
##
##
## --------------------- Adjusted Means ---------------------
##
## Estimate SE Est./SE
## Adj.Mean0 20.7 0.300 69.0
## Adj.Mean1 16.7 0.283 59.1
##
##
## --------------------- Average Effects ---------------------
##
## Estimate SE Est./SE p-value Effect Size
## E[g1(K,Z)] -3.99 0.412 -9.67 0 -0.746
##
##
## --------------------- Effects given a Treatment Condition ---------------------
##
## Estimate SE Est./SE p-value Effect Size
## E[g1(K,Z)|X=0] -3.49 0.491 -7.11 8.03e-12 -0.653
## E[g1(K,Z)|X=1] -4.41 0.458 -9.63 0.00e+00 -0.825
##
##
## --------------------- Effects given K=k ---------------------
##
## Estimate SE Est./SE p-value Effect Size
## E[g1(K,Z)|K=0] -4.72 0.586 -8.05 1.75e-14 -0.882
## E[g1(K,Z)|K=1] -3.28 0.580 -5.65 3.58e-08 -0.613
##
##
## --------------------- Effects given X=x, K=k ---------------------
##
## Estimate SE Est./SE p-value Effect Size
## E[g1(K,Z)|X=0, K=0] -4.56 0.584 -7.81 8.53e-14 -0.853
## E[g1(K,Z)|X=1, K=0] -4.78 0.621 -7.70 1.84e-13 -0.893
## E[g1(K,Z)|X=0, K=1] -3.03 0.656 -4.63 5.48e-06 -0.567
## E[g1(K,Z)|X=1, K=1] -3.71 0.606 -6.12 2.78e-09 -0.694
##
##
## --------------------- Hypotheses given K=k ---------------------
##
## H0: No average effects given K=0: E[g1(K,Z)|K=0] = 0
## H0: No average effects given K=1: E[g1(K,Z)|K=1] = 0
##
## F value df1 df2 p-value
## No average effects given K=0 64.8 1 314 1.75e-14
## No average effects given K=1 31.9 1 314 3.58e-08
Unter
## ## --------------------- Variables ---------------------
finden wir eine Zusammenfassung der Variablen, die wir als Input verwendet haben. Hier werden die kategorialen Variablen hinsichtlich ihrer Kodierung aufgedröselt. Bspw. bedeutet
## ## Levels of Treatment Variable X
## ## X Treatment (original) Indicator
## ## 0 WL I_X=0
## ## 1 CBT I_X=1
dass die Gruppierungsvariable (of interest) mit X betitelt wird und aus den Ausprägungen des Treatments besteht. Dabei ist X=0 die Wartelistenkontrolle (WL) und X=1 die Treatmentgruppe (CBT). Dahinter wird noch der Indikator I_X definiert, der entsprechend die Werte 0 und 1 annimmt. Unter ## Levels of Unfolded Categorical Covariate K steht Gleiches nochmals für die kategoriale Kovariate Disorder. Eine Übersicht über die Kombination der Gruppen steht in
## ## Cells
## ## Treatment (original) K Cell
## ## 1 WL 0 00
## ## 2 WL 1 01
## ## 3 CBT 0 10
## ## 4 CBT 1 11
Es handelt sich also um ein vollgekreuztes Design (alle Zellen sind vorhanden). Unter
## ## --------------------- Regression Model ---------------------
wird dann das Regressionsmodell definiert. Dabei wird das Modell mit Hilfe der bedingten Erwartungswert-Schreibweise dargestellt.
## ## E(Y|X,K,Z) = g0(K,Z) + g1(K,Z)*I_X=1
bedeutet dabei nichts anderes, als dass der Mittelwert von Y auf X (UV), K und Z (kategoriale und kontinuierliche Kovariaten) bedingt wird. Bedingter Mittelwert heißt wiederum nur, dass eine Art Regression durchgeführt wird. Dahinter sehen wir die Schreibweise, die wir auch aus den Folien kennen. g0 ist hierbei die Interzeptfunktion, die von K und Z abhängt. g1 ist die Slopefunktion, die von K und Z abhängt und den Effekt des Treatments darstellt.
## ## g0(K,Z) = g000 + g001 * Z1 + g002 * Z2 + g010 * I_K=1 + g011 * I_K=1 * Z1 +
## ## + g012 * I_K=1 * Z2
## ## g1(K,Z) = g100 + g101 * Z1 + g102 * Z2 + g110 * I_K=1 + g111 * I_K=1 * Z1 +
## ## + g112 * I_K=1 * Z2
beschreibt explizit die Regressionsdarstellung der Interzeptfunktion (Hautpeffekte im ANCOVA-Setting) und der Slopefunktion (Interaktionseffekte im ANCOVA-Setting) in der Reihenfolge, in der sie in die Analysen eingegangen sind. Genauso haben wir die Prädiktoren ebenfalls in die ANCOVA (BDI.adj3) aufgenommen. Die Koeffizienten werden dann in üblicher Manier dargestellt. Die Benennung ist etwas schwieriger nachzuvollziehen, aber wenn wir uns merken, in welcher Reihenfolge wir die Prädiktoren oben aufgenommen haben, erkennen wir, dass der Output im Grunde identisch ist zum Output von BDI.adj3. Bspw. ist g000 = 20.034 das Interzept und g010 = 1.083 ist der Haupteffekt von Disorder. g012 = -0.075 ist der Interaktionseffekt zwischen Disorder und SWL_pre_c (SWL_pre_c:DisorderDEP im ANCOVA-Output). Kommen wir zu den Treatment-Effekten: g100 = -4.503 ist der Haupteffekt des Treatments im ANCOVA-Sinn. Der ATE wird als der Erwartungswert der Slopefunktion g1(K,Z) geschätzt (dazu gleich mehr!). g112 = 0.2 ist die Dreifachinteraktion zwischen Treatment, Disorder und SWL_pre_c (SWL_pre_c:Disorder:Treatment).
Unter
## ## --------------------- Cell Counts ---------------------
finden wir eine Übersicht über die Häufigkeitsverteilung innerhalb der verschiedenen Gruppen. Diese entspricht tab.disorder vom Anfang der Sitzung.
Unter
## ## --------------------- Main Hypotheses ---------------------
finden wir endlich die Schätzung mit zugehöriger Signifikanzentscheidung unserer Haupthypothesen.
## ## H0: No average effects: E[g1(K,Z)] = 0
## ## H0: No covariate effects in control group: g0(K,Z) = constant
## ## H0: No treatment*covariate interaction: g1(K,Z) = constant
## ## H0: No treatment effects: g1(K,Z) = 0
beschreibt nochmals die Hypothesen, die getestet werden sollen. Die erste Hypothese bezieht sich auf den ATE (Average Treatment Effect). Wir erkennen die $H_0$ als E[g1(K,Z)] = 0. Der ATE ist also der Durchschnitt der Slopefunktion g1(K,Z). Die zweite Hypothese behandelt, ob die Kovariaten Mittelwertsunterschiede bewirken. Die dritte Hypothese untersucht, ob die Kovariaten den Effekt des Treatments beeinflussen. Die letzte Hypothese testet alle Parameter innerhalb der Slopefunktion g1(K,Z) gemeinsam. Sie wird signifikant, wenn es einen Haupteffekt oder einen Interaktionseffekt (oder beides) mit dem Treatment gibt. Der Output ist ein normaler ANOVA/ANCOVA-Output. Uns werden $F$-Werte angezeigt. Hypothese 1,2, und 4 werden durch die Daten gestützt. Die Hypothese, dass sich das Treatment je nach Ausprägung der Kovariaten unterschiedlich ausgewirkt hat, wird durch die Daten nicht gestützt. Unter
## ## --------------------- Adjusted Means ---------------------
finden wir die adjustierten Mittelwerte, mit welchen dann der ATE bestimmt wird. Dieser ist unter
## ## --------------------- Average Effects ---------------------
zu finden und beträgt -3.99. Der Wert liegt nicht sonderlich weit entfernt vom Haupteffekt im ANCOVA-Setting und ist auch hier signifikant. Es wird uns auch ein Effektstärkenmaß angeboten. Dieses liegt bei -0.75 und spricht für einen mittleren bis großen Effekt.
In den folgenden Blöcken werden jeweils bedingte Effekte dargestellt. Es beginnt mit dem ATT, dahinter folgen ATEs bedingt auf die kategorialen Prädiktoren (K) sowie eine Kombination aus beiden.
## ## --------------------- Effects given a Treatment Condition ---------------------
beschreibt die ATT (Average Treatment of the Treated) Effekte (also Effekte bedingt auf die Treatment-Bedingungen). E[g1(K,Z)|X=0] beschreibt den $ATT^0$ und E[g1(K,Z)|X=1] den $ATT^1$ Effekt (ATT0 = -3.49 und ATT1 = -4.41). Beide sind statistisch bedeutsam. Auch hier werden Effektstärken angegeben. Die Effektstärke in der Treatment-Gruppe ist etwas höher als die der Wartekontrollgruppe (-0.65 vs. -0.83).
## ## --------------------- Effects given K=k ---------------------
beschreibt die bedingten Effekte bedingt auf Disorder. Hier wird also im Grunde der Haupteffekt der Disorder untersucht. E[g1(K,Z)|K=0] beschreibt hierbei den $ATE|$ANX und E[g1(K,Z)|K=1] den $ATE|$DEP. Patient:innen mit Angstsymptomatik zeigten also eine deskriptiv größere Verbesserung durch das Treatment.
## ## --------------------- Effects given X=x, K=k ---------------------
Zeigt uns die $ATT$s in den unterschiedlichen Gruppen. E[g1(K,Z)|X=0, K=0] beschreibt also den $ATE|$WL,ANX = $ATT^0|$ANX, also gerade den $ATT$ von Personen mit Angstsymptomatik in der Wartekontrollgruppe. Genauso beschreibt E[g1(K,Z)|X=1, K=1] den $ATE|$CBT,DEP = $ATT^1|$DEP, also den $ATT$ von Personen mit Depression in der CBT-Gruppe. Alle (bedingten) $ATT$s sind statistisch bedeutsam, jedoch sind sie bei Angstsymptomatik etwas stärker ausgeprägt (ATT0|ANX = -4.56 und ATT1|ANX = -4.78) als bei Depressionen (ATT0|Dep = -3.03 und ATT1|Dep = -3.71). Auch sehen wir deskriptiv, dass in den Treatment-Bedingungen jeweils die Effekte etwas stärker ausgeprägt sind.
Zum Schluss wird noch der bedingte ATE auf Signifikanz mittels ANOVA geprüft
## ## --------------------- Hypotheses given K=k ---------------------
Die Hypothesen, die geprüft werden, sind, dass der ATE jeweils 0 ist für Angstsymptomatik (H0: No average effects given K=0: E[g1(K,Z)|K=0] = 0) und für Depressionssymptomatik (H0: No average effects given K=1: E[g1(K,Z)|K=1] = 0). Beide Tests sind statistisch bedeutsam (was wir im Grunde schon in den Outputs zuvor gesehen hatten - es hätte jedoch sein können, dass der kategoriale Prädiktor mehr als zwei Ausprägungen hat).
Zusammenfassung
Unter der Stable Unit Treatment Value Assumption (SUTVA) und der Strong Ignoribility Annahme bedeuten die Ergebnisse also, dass es einen Effekt der CBT gab (mit einer Irrtumswahrscheinlich von $5\%$) und dass dieser Effekt für unterschiedliche Symptomatiken unterschiedlich stark ausgeprägt war.
](/media/header/pendulum_chain.jpg)