Konjugierte Prior

Im ersten Beitrag hatten wir uns mal angeguckt, wie Bayes im Allgemeinen funktioniert. Auch, wenn das Ganze an einem Beispiel orientiert war, war das gesamte Vorgehen dabei eher hands-off. Das ändern wir jetzt: in diesem Beitrag gucken wir uns an, wie man Bayesianische Analysen betreiben kann, wenn man sich ein bisschen mit Verteilungen auskennt. Keine Sorge, über die grundlegenden Konzepte von Verteilungen hinaus, setzt dieser Beitrag nichts voraus - er soll eher dazu dienen, ein bisschen besser zu verstehen, wie, warum und wozu man Bayesianische Schätzung so einsetzt. Wer die Grundkonzepte von Verteilungen nochmal auffrischen möchten, kann z.B. diesen Beitrag mal querlesen (oder auch ganz).

Datenbeispiel

Wir knüpfen wieder beim gleichen Beispiel an, wie im letzten Beitrag. Es geht darum, dass Sie ein neues Ausgangskonzept für Ihre Patient:innen in einer Suchtklinik entwickelt haben. Dieses Konzept haben Sie nun ein paar Wochen getestet und dabei eine erstaunliche Erfolgsquote von 70% verbuchen können. Leider haben Sie das Ganze aber bisher nur mit $n = 10$ Personen ausprobieren können. Die Daten dazu:

# Beobachtungen
obs <- c(0, 1, 1, 0, 1, 1, 1, 0, 1, 1)

# N
length(obs)

## [1] 10

# Erfolgsquote
mean(obs)

## [1] 0.7

Wie wir schon gesehen haben, brachten uns die klassischen Analyseanstäze hier keine statistisch bedeutsamen Ergebnisse und demzufolge auch nur wenig Erkenntnisgewinn.

Die Binomialverteilung

Wenn wir in der Psychologie mit Variablen arbeiten, die nur eine von zwei Ausprägungen annehmen kann, notieren wir sie idealerweise als Dummy-Variable. Für diese Variablen nutzen wir die 0, um die Zugehörigkeit zu einer Gruppe zu notieren (z.B. Personen, bei denen keine depressive Störung vorliegt) und die 1, um die Zugehörigkeit zur anderen Gruppe festzuhalten (z.B. Personen, die an einer Depression leiden). Dabei gehen wir davon aus, dass eine Person einer und nur einer der beiden Gruppen angehört. In unserem Fall sind die beiden Gruppen Patient:innen die im Ausgang rückfällig geworden sind (obs = 0) und Patient:innen, die nicht rückfällig geworden sind (obs = 1).

Bei jeder Untersuchung versuchen wir dann möglichst voneinander unabhängige Beobachtungen als Stichprobe zu gewinnen. Bei vielen klassischen Tests ist die Unabhängigkeit der Beobachtungen eine Voraussetzung, um adäquate Inferenzstatistik betreiben zu können. Wenn wir eine Dummy-Variable mehrfach in unabhängigen Beobachtungen festhalten, folgt die Anzahl der Beobachtungen der Kategorie 1 der Binomialverteilung. In unserem Fall lässt sich die Verteilung der Anzahl der “Erfolge” (Personen, die im Ausgang nicht rückfällig werden) in einer Stichprobe so beschreiben:

$$ P(X = x | n, \pi) = {n \choose x} \cdot \pi^x \cdot (1 - \pi)^{n-x} $$ Dabei ist $x$ die Anzahl der von uns beobachteten Erfolge, $n$ die Anzahl der Beobachtungen, die wir insgesamt durchgeführt haben und $\pi$ die Grundrate in der Population. Eine super detaillierte Darstellung der Binomialverteilung haben wir z.B. in diesem Beitrag aufgeschrieben. Wie wir schon im letzten Bayes-Beitrag besprochen haben, können wir diese Formel einfach nutzen, um die Likelihood zu bestimmen:

$$ L(P = \pi | N = n, X = x) = {n \choose x} \cdot \pi^x \cdot (1 - \pi)^{n-x} $$

In unserem Fall war $n$ length(obs) also 10. Die Anzahl der Erfolge (einer der vielen Vorteile davon, mit 0 und 1 zu arbeiten und nicht z.B. mit 1 und 2, wenn man zwei Gruppen kodiert) lässt sich einfach über

sum(obs)

## [1] 7

ermitteln. Welches $\pi$ die höchste Likelihood hat, hatten wir auch bereits ausprobiert. Dazu können wir zum Beispiel einfach alle möglichen Werte für $\pi$ in die Gleichung einsetzen:

pi <- seq(0, 1, .1)
likelihood <- choose(10, 7) * pi^7 * (1 - pi)^(10 - 7)
d <- data.frame(pi, likelihood)
d

##     pi  likelihood
## 1  0.0 0.000000000
## 2  0.1 0.000008748
## 3  0.2 0.000786432
## 4  0.3 0.009001692
## 5  0.4 0.042467328
## 6  0.5 0.117187500
## 7  0.6 0.214990848
## 8  0.7 0.266827932
## 9  0.8 0.201326592
## 10 0.9 0.057395628
## 11 1.0 0.000000000

Statt immer die ganze Gleichung aufschreiben zu müssen, können wir natürlich auch die in R integrierte Verteilungsfunktionalität nutzen. Dazu gibt es ein allgemeines Muster, nach dem Verteilungsfunktionen aufgebaut sind. Für die Binomialverteilun können wir also dbinom benutzen, um uns die Dichtefunktion ausgeben zu lassen:

dbinom(7, 10, .2)

## [1] 0.000786432

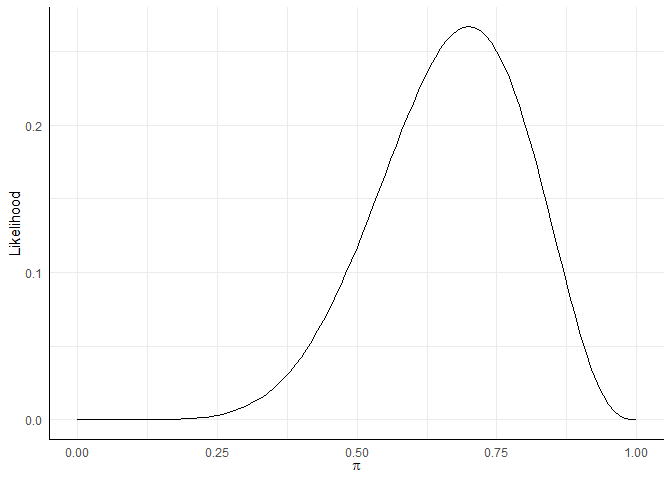
Um das Ganze in einer hübschen Abbildung darzustellen, statt eine Tabelle für alle Werte aufstellen zu müssen, hatten wir auch schon hiermit gearbeitet:

likeli_plot <- ggplot(d, aes(x = pi, y = likelihood)) + 
  xlim(0, 1) +
  geom_function(fun = dbinom, args = list(x = 7, size = 10)) +
  labs(x = expression(pi), y = 'Likelihood')
likeli_plot

Ein geeigneter Prior für Wahrscheinlichkeiten

Wie wir im Bayes-Intro besprochen haben, ist das Ziel Bayesianischer Analysen unser Vorwissen (Prior) durch Informationen aus unserer Studie (Likelihood) zu aktualisieren, um so zu einem neuen Kenntnisstand zu gelangen (Posterior). Was in unserem Prior also enthalten sein muss, sind Annahmen über die Populationsparameter - in diesem Fall die Wahrscheinlichkeit $\pi$, mit der eine Person im Ausgang nicht rückfällig wird. Im Gegensatz zu klassischen Hypothesen, stellen wir in unserem Prior für $\pi$ nicht einen Wert als unsere Annahme dar, sondern gestehen eine gewisse Unsicherheit ein. Diese Unsicherheit äußert sich darin, dass wir bestimmte Werte für wahrscheinlicher halten, der “wahre Wert” von $\pi$ zu sein - was wir benötigen ist also eine Wahrscheinlichkeitsverteilung.

Im ersten Bayes-Beitrag hatten wir bereits gesehen, wie drei unterschiedliche Prior aussehen können. Jetzt geht es darum zu bestimmen, wie wir unsere Annahmen so in eine konkrete Verteilung übersetzen können, dass sie wirklich als Prior fungieren kann. Die Verteilung einer Wahrscheinlichkeit muss bestimmte Eigenschaften haben - z.B. können Wahrscheinlichkeiten nur zwischen 0 und 1 liegen. Es hängt also von dem Parameter ab, über den wir Aussagen treffen wollen, welche Verteilung wir nutzen können.

Zum Glück haben sich Generationen von Statisker:innen bereits darüber den Kopf zerbrochen, welche Verteilungen für welche Parameter geeignet sind. Ein System hat sich dabei als besonders vielversprechend erwiesen: Prior-Verteilungen so zu gestalten, dass die Posterior-Verteilung der gleichen Verteilungsklasse angehört. Wenn das gelingt, spricht man von einem conjugate Prior. Dieser Ansatz hat den immensen Vorteil, dass wir die Posterior-Verteilung direkt berechnen können (in anderen Fällen, müssen wir auf ein simulationsbasiertes Verfahren zurückgreifen, wie im nächsten Beitrag noch genauer besprochen wird). Das Problem dabei ist nur, dass man herleiten muss, welche Verteilungen genau diese Eigenschaften aufweisen. Erneut haben wir wahnsinniges Glück, dass wir im 21. Jahrhundert leben: Fink (1997) hat bereits eine sehr ausführliche Übersicht über solche Verteilungen erstellt. Auch Wikipedia kann uns hier sehr übersichtlich weiterhelfen.

In beiden Quellen sehen wir, dass der conjugate Prior für unsere Binomialverteilung die Beta-Verteilung ist, welche genutzt werden kann, um die Verteilung von $\pi$ darzustellen. Notiert wird sie als $\text{Beta}(\alpha, \beta)$. So wie jede Normalverteilung durch Mittelwert $\mu$ und Standardabweichung $\sigma$ festgelegt ist, wird die Form der Beta-Verteilung durch die beiden Parameter $\alpha$ und $\beta$ festgelegt:

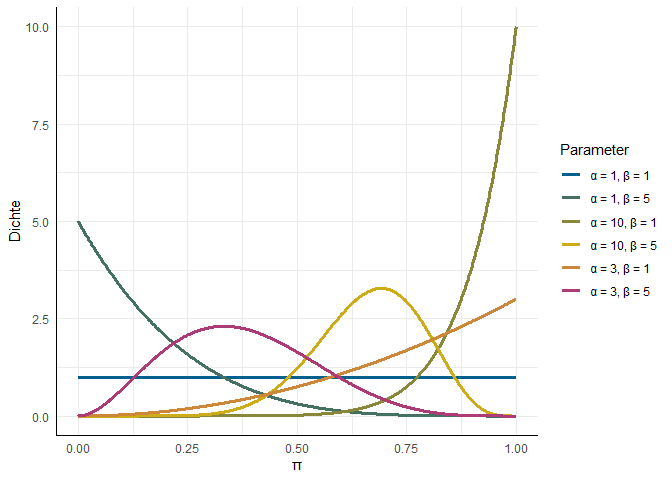
Für die beiden Parameter gibt es eine recht naheliegende (aber nicht 100% korrekte) intuitive Interpretation: $\alpha-1$ ist die Anzahl der Erfolge, $\beta-1$ die Anzahl der Misserfolge, die wir schon beobachten konnten. Wenn wir also keine Erfolge oder Misserfolge beobachtet haben ($\alpha = 1, \beta = 1$) ist jede Grundrate $\pi$ von 0 bis 1 gleich wahrscheinlich - wir haben keinerlei Vorinformation als Prior bereitgestellt. Wenn $\alpha = 10, \beta = 1$ ist es sehr wahrscheinlich, dass unsere Grundrate in der Nähe von 1 liegt und sehr unwahrscheinlich, dass sie kleiner als 0.5 ist. Weil $\alpha$ und $\beta$ Parameter sind, die die Verteilung des Parameters in unserer eigentlichen Auswertung (dem Binomialtest) bestimmen, werden sie als Hyperparameter bezeichnet.

Den Posterior händisch bestimmen

Wie schon erwähnt folgt der Posterior der gleichen Verteilung wie der Prior, wenn wir einen conjugate Prior für unsere Likelihood gefunden haben. Wir gehen mal davon aus, dass Fink seine Recherchearbeit gemacht hat, als er die Übersicht erstellt hat - also brauchen wir nur noch $\alpha$ und $\beta$ unserer resultierenden Posterior-Verteilung bestimmen.

Die angesprochene, intuitive Interpretation von $\alpha$ und $\beta$ kann uns dabei helfen: wenn $\alpha - 1$ die Anzahl der Erfolge ist und $\beta - 1$ die Anzahl der Misserfolge, dann können wir die Beobachtungen aus unseren Daten einfach dazu addieren und bekommen so unseren Posterior. Probieren wir es mal aus:

Wie in der Abbildung oben gesehen, ist bei $\text{Beta}(1, 1)$ jeder Wert von $\pi$ gleich wahrscheinlich. Kurzer Gegencheck:

pi <- seq(0, 1, .1)
dbeta(pi, 1, 1)

##  [1] 1 1 1 1 1 1 1 1 1 1 1

Das scheint soweit zu stimmen. Wir können diesen Prior also als uninformativen Prior verwenden. In unserem Versuch mit 10 Suchtpatient:innen hatten 7 Personen einen “Erfolg” (sind also ohne Rückfall wieder aus dem Ausgang zurück gekommen). In simpler Addition sollte unser Posterior also $\text{Beta}(\alpha + x, \beta + n-x) = \text{Beta}(1 + 7, 1 + 10-7) = \text{Beta}(8, 4)$

Wenn wir die ausgewählten Likelihoods von oben also nutzen, die wir in d abgelegt hatten:

d

##     pi  likelihood
## 1  0.0 0.000000000
## 2  0.1 0.000008748
## 3  0.2 0.000786432
## 4  0.3 0.009001692
## 5  0.4 0.042467328
## 6  0.5 0.117187500
## 7  0.6 0.214990848
## 8  0.7 0.266827932
## 9  0.8 0.201326592
## 10 0.9 0.057395628
## 11 1.0 0.000000000

können wir ein paar Beispieldichten der unterschiedlichen Werte erzeugen:

d$uninf_prior <- dbeta(d$pi, 1, 1)
d$uninf_post <- dbeta(d$pi, 8, 4)
d

##     pi  likelihood uninf_prior  uninf_post
## 1  0.0 0.000000000           1 0.000000000
## 2  0.1 0.000008748           1 0.000096228
## 3  0.2 0.000786432           1 0.008650752
## 4  0.3 0.009001692           1 0.099018612
## 5  0.4 0.042467328           1 0.467140608
## 6  0.5 0.117187500           1 1.289062500
## 7  0.6 0.214990848           1 2.364899328
## 8  0.7 0.266827932           1 2.935107252
## 9  0.8 0.201326592           1 2.214592512
## 10 0.9 0.057395628           1 0.631351908
## 11 1.0 0.000000000           1 0.000000000

Wichtig: der Posterior ist in diesem Fall nicht identisch zur Likelihood! Wie wir im ersten Beitrag besprochen hatten, bräuchten wir dafür eine normalisierende Konstante (nämlich die unbedingte Wahrscheinlichkeit unserer Daten). Weil wir diese nicht kennen ist unser Posterior lediglich proportional zum Produkt aus Prior und Likelihood:

$$ P(H | X) \propto P(X|H) \times P(H) $$

Also sollte das Verhältnis aus posterior und likelihood für alle Werte das Gleiche sein:

d$uninf_post / d$likelihood

##  [1] NaN  11  11  11  11  11  11  11  11  11 NaN

Die direkte Beziehung zwischen Prior und Posterior macht es in diesem Fall auch direkt erkennbar, wie wir durch unsere Annahmen Einfluss auf unsere Ergebnisse haben können. Nehmen wir das schwach informative Beispiel aus dem ersten Beitrag. Dort war der Prior auf $\text{Beta}(2, 2)$ festgelegt:

d$weak_prior <- dbeta(d$pi, 2, 2)

Nach dem gleichen Prinzip wie zuvor ist der Posterior also $\text{Beta}(9, 5)$:

d$weak_post <- dbeta(d$pi, 9, 5)
d

##     pi  likelihood uninf_prior  uninf_post weak_prior    weak_post
## 1  0.0 0.000000000           1 0.000000000       0.00 0.000000e+00
## 2  0.1 0.000008748           1 0.000096228       0.54 4.222004e-05
## 3  0.2 0.000786432           1 0.008650752       0.96 6.747587e-03
## 4  0.3 0.009001692           1 0.099018612       1.26 1.013703e-01
## 5  0.4 0.042467328           1 0.467140608       1.44 5.465545e-01
## 6  0.5 0.117187500           1 1.289062500       1.50 1.571045e+00
## 7  0.6 0.214990848           1 2.364899328       1.44 2.766932e+00
## 8  0.7 0.266827932           1 2.935107252       1.26 3.004816e+00
## 9  0.8 0.201326592           1 2.214592512       0.96 1.727382e+00
## 10 0.9 0.057395628           1 0.631351908       0.54 2.770056e-01
## 11 1.0 0.000000000           1 0.000000000       0.00 0.000000e+00

Als starker Prior hatte im Beispiel $\text{Beta}(6, 6)$ hergehalten.

d$strong_prior <- dbeta(d$pi, 6, 6)
d$strong_post <- dbeta(d$pi, 13, 9)

Wenn wir die Daten zusammenführen, wird die Tabelle langsam etwas groß, also hier die insgesamt sechs Verteilungen mal in einer Abbildung:

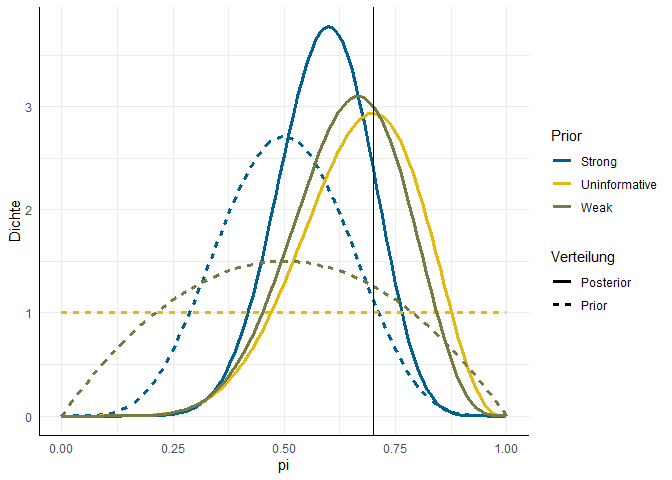
Die vertikale Linie zeigt den Wert in unserer Stichprobe ($h = .7$). Der Posterior des uninformativen Priors trifft mit seinem Modus diesen Wert natürlich genau (weil wir keine zusätzliche Information hinzugegeben hatten). Die anderen beiden Posterior-Verteilungen werden beide stärker zur Grundrate in den Prior-Annahmen ($\pi = .5$) hingezogen und dabei immer schmaler. Beide Effekte gehen damit einher, dass wir in unseren Priors mehr Information in die Analyse einspeisen. Im Fall des uninformativen Prior hatten wir mit $\text{Beta}(1, 1)$ zum ausdruck gebracht, dass wir 0 vorherige Beobachtungen haben und somit jeder Wert gleich wahrscheinlich ist. Im schwachen Prior ist die Aussage enthalten, dass wir zwei vorherige Beobachtungen gemacht haben und eine erfolgreich (kein Rückfall) und eine nicht erfolgreich war. Im starken Prior ist impliziert, dass wir zuvor schonmal zehn Beobachtungen gemacht haben, von denen fünf erfolgreich waren und fünf nicht. Unser Posterior ist also in dem Fall “die Mitte” zwischen den zehn Beobachtungen, die Sie in Ihrer Klinik gemacht haben (sieben von zehn Erfolge) und den zehn, deren Informationen schon vorab zur Verfügung standen. Dabei wird auch die Streuung unserer Posteriors kleiner, weil wir mehr Informationen als Grundlage haben und uns sicherer sein können, dass die Grundrate nicht z.B. 90% ist.

Bayes-Factor berechnen

Die Tabelle, die wir oben erstellt hatten, erlaubt uns sehr einfach auch für eine Vielzahl von Konstellationen die Savage-Dickey Density Ratio zu bestimmen. Dieser vereinfachte Annäherung des Bayes-Factors kann genutzt werden, um zu gucken wie sich unser Wissensstand durch die neue Datenlage verändert hat. Wenn wir unsere Daten auf die Fälle mit starkem Prior reduzieren:

d_strong <- subset(d, select = c('pi', 'strong_prior', 'strong_post'))

können wir für alle .1 Abstände von $\pi$ ermitteln, wie viel wahrscheinlicher jeder Wert unter dem Posterior ist:

d_strong$bayes_factor <- d_strong$strong_post / d_strong$strong_prior
d_strong

##     pi strong_prior  strong_post bayes_factor
## 1  0.0   0.00000000 0.000000e+00          NaN
## 2  0.1   0.01636838 1.138745e-06 0.0000695698
## 3  0.2   0.29066527 1.817884e-03 0.0062542196
## 4  0.3   1.13211280 8.104492e-02 0.0715873195
## 5  0.4   2.20723937 7.454462e-01 0.3377278604
## 6  0.5   2.70703125 2.522821e+00 0.9319513494
## 7  0.6   2.20723937 3.773822e+00 1.7097472931
## 8  0.7   1.13211280 2.402332e+00 2.1219895577
## 9  0.8   0.29066527 4.653784e-01 1.6010802269
## 10 0.9   0.01636838 7.471306e-03 0.4564474280
## 11 1.0   0.00000000 0.000000e+00          NaN

Natürlich können wir für jeden einzelnen Wert diesen Bayes Factor bestimmen. Für $\pi = 0.75$ z.B.

dbeta(.75, 13, 9) / dbeta(.75, 6, 6)

## [1] 1.990408

Eine Erfolgsrate von .75 ist also fast doppelt so wahrscheinlich, nachdem wir unsere Studie durchgeführt haben und sieben der zehn Teilnehmer:innen ohne Rückfall geblieben sind.

Um das Ganze nicht nur für einzelne Werte, sondern ganze Bereiche der Verteilungen zu bestimmen, brauchen wir nicht die Dichte, sondern die Fläche unter der Kurve. Diese ermitteln wir bekanntlich mit der Verteilungsfunktion - die gleiche Funktion, mit der wir auch im frequentistischen Fall $p$-Werte bestimmen. Wenn wir beispielsweise untersuchen wollen, wie die Wahrscheinlichkeit sich verändert hat, dass $\pi$ über 0.75 liegt, können wir das mit der pbeta Funktion herausfinden:

pbeta(.75, 13, 9, lower.tail = FALSE) / pbeta(.75, 6, 6, lower.tail = FALSE)

## [1] 1.635622

In diesem Bereich findet sich also eher wenig Evidenz. Wie genau diese Information genutzt werden kann, um auch Aussagen bezüglich der Gültigkeit von Nullhypothesen zu machen, sehen wir in einem späteren Beitrag.

In diesem Beitrag haben wir uns angesehen, wie man Bayesianische Analysen “per Hand” durchführen kann. Was dies erfordert ist Kenntnis von Verteilungen: zum Einen müssen wir wissen, welche Verteilung unser Parameter in der Population folgt und zum Anderen benötigen wir Informationen darüber, welche Verteilung dazu einen conjugate Prior darstellt. Wenn beides gegeben ist, können wir unsere Analysen sehr einfach durchführen. Wenn wir die Verteilungen nicht kennen oder sie zu komplex sind, um einen einfachen conjugate Prior zuzulassen, müssen wir uns einer simulationsbasierten Strategie bedienen, die wir im dritten Beitrag kennenlernen werden.