Einführung in lavaan
Das Instrument für die multivariate Datenanalyse
Einleitung
Im Verlauf dieses Seminars soll neben der Einführung in die Theorie und die Hintergründe multivariater Verfahren auch eine Einführung in deren Umsetzung gegeben werden, sodass Sie in der Lage sind, diese Verfahren in Ihrem zukünftigen akademischen und beruflichen Werdegang zu nutzen. Diese Umsetzung möchten wir Ihnen mit lavaan zeigen - dem meistverbreiteten Paket für multivariate Verfahren wie z.B. konfirmatorische Faktorenanalyse (CFA), Pfadanalyse oder Strukturgleichungsmodellierung (SEM) in R. Das Paket wird derzeit pro Woche ca. 12500 mal herunter geladen; es wird in allen Bereichen der psychologischen Forschung genutzt und wurde in über 23 000 wissenschaftlichen Veröffentlichungen zitiert.
Dieses Tutorial bietet eine Einführung in lavaan. Im Zentrum stehen dabei die Grundgedanken und die typische Vorgehensweise, in der man in lavaan arbeitet. Um diese Ideen und Vorgehensweisen zu erkunden, betrachten wir ein Beispiel aus dem letzten Semester mal aus dieser neuen Perspektive.
Wir beginnen das Tutorial aber zunächst mit einer Auffrischung Ihrer R-Fähigkeiten. Auch wenn Sie im Umgang mit R sehr geübt sind, nehmen Sie sich bitte trotzdem ein paar Minuten Zeit, um sich noch einmal intensiv mit den Befehlen auseinanderzusetzen, die für dieses Semester von zentraler Bedeutung sind. Sollten Sie wenig Übung im Umgang mit R haben, oder wenn Sie einfach noch einmal eine etwas detaillierte Einführung in R lesen möchten, finden Sie hier auch die R-Einführung aus dem Bachelorstudiengang.
Nach dem Ende der Übung finden Sie im Moodle-Kurs ein kurzes Quiz mit Bezug zu den Inhalten dieser Sitzung.
R-Grundlagen Wiederbelebung
In diesem Abschnitt gucken wir uns zur Wiederholung noch einmal ein paar Grundzüge des Datenmanagements in R an, bevor wir eine multiple Regression durchführen und deren Ergebnisse genauer inspizieren.
Beispieldatensatz
Der Datensatz, den wir in dieser Sitzung benutzen, stammt aus einer Studie von Bull, Schultze & Scheithauer (2009), in der die Effektivität eines Interventionsprogramms zur Bullyingprävention bei Jugendlichen untersucht wurde. Der Datensatz liegt bereits im R-eigenen .rda-Format vor, sodass uns ein Import der Daten erspart bleibt. Sie können den Datensatz entweder hier herunterladen und mit load arbeiten, um die Daten zu laden:
load('fairplayer.rda')
oder den Datensatz direkt von dieser Website in R laden:
load(url("https://pandar.netlify.app/daten/fairplayer.rda"))
Wir können uns mit den üblichen Befehlen einen Überblick über die Daten verschaffen:
# Namen der Variablen abfragen
names(fairplayer)
## [1] "id" "class" "grp" "sex" "ra1t1" "ra2t1" "ra3t1" "ra1t2" "ra2t2" "ra3t2" "ra1t3"
## [12] "ra2t3" "ra3t3" "em1t1" "em2t1" "em3t1" "em1t2" "em2t2" "em3t2" "em1t3" "em2t3" "em3t3"
## [23] "si1t1" "si2t1" "si3t1" "si1t2" "si2t2" "si3t2" "si1t3" "si2t3" "si3t3"
# Anzahl der Zeilen und Spalten
dim(fairplayer)
## [1] 155 31
# Struktur des Datensatz - Informationen zur Variablentypen
str(fairplayer)
## 'data.frame': 155 obs. of 31 variables:
## $ id : int 1 2 3 4 5 6 7 8 9 10 ...
## $ class: int 1 1 1 1 1 1 1 1 1 1 ...
## $ grp : Factor w/ 3 levels "CG","IGS","IGL": 3 3 3 3 3 3 3 3 3 3 ...
## $ sex : Factor w/ 2 levels "female","male": 1 2 1 1 2 2 2 2 1 1 ...
## $ ra1t1: int 2 1 1 1 2 1 1 1 1 1 ...
## $ ra2t1: int 1 3 2 1 1 3 1 1 1 1 ...
## $ ra3t1: int 1 1 1 1 1 1 1 1 1 1 ...
## $ ra1t2: int 2 1 1 1 1 1 3 1 1 1 ...
## $ ra2t2: int 1 1 1 1 5 2 2 1 3 1 ...
## $ ra3t2: int 1 1 1 1 1 1 2 1 2 1 ...
## $ ra1t3: int 1 1 1 1 1 1 2 1 1 1 ...
## $ ra2t3: int 1 1 2 1 2 3 3 1 1 1 ...
## $ ra3t3: int 1 1 1 1 1 1 2 1 1 1 ...
## $ em1t1: int 3 4 3 5 3 4 3 2 4 4 ...
## $ em2t1: int 5 4 3 5 3 3 4 2 4 4 ...
## $ em3t1: int 4 3 2 5 4 4 3 1 5 4 ...
## $ em1t2: int 4 4 2 4 3 3 3 4 4 4 ...
## $ em2t2: int 4 5 2 4 4 4 3 4 4 4 ...
## $ em3t2: int 3 5 1 4 3 4 4 4 4 5 ...
## $ em1t3: int 3 4 3 3 3 4 3 3 4 4 ...
## $ em2t3: int 4 3 2 4 4 4 3 3 5 5 ...
## $ em3t3: int 5 3 2 5 4 4 4 4 5 4 ...
## $ si1t1: int 2 2 1 4 2 2 3 2 4 3 ...
## $ si2t1: int 2 1 2 1 2 2 1 1 1 2 ...
## $ si3t1: int 3 3 2 5 2 3 4 3 3 3 ...
## $ si1t2: int 3 4 1 4 2 3 4 3 3 3 ...
## $ si2t2: int 2 2 1 4 3 3 4 2 3 2 ...
## $ si3t2: int 3 3 2 4 2 4 3 4 4 2 ...
## $ si1t3: int 2 3 1 4 3 4 4 3 3 3 ...
## $ si2t3: int 1 2 1 1 5 3 1 3 2 3 ...
## $ si3t3: int 3 3 2 4 3 4 5 3 3 3 ...
# Ersten Zeilen des Datensatzes ansehen
head(fairplayer)
## id class grp sex ra1t1 ra2t1 ra3t1 ra1t2 ra2t2 ra3t2 ra1t3 ra2t3 ra3t3 em1t1 em2t1 em3t1
## 1 1 1 IGL female 2 1 1 2 1 1 1 1 1 3 5 4
## 2 2 1 IGL male 1 3 1 1 1 1 1 1 1 4 4 3
## 3 3 1 IGL female 1 2 1 1 1 1 1 2 1 3 3 2
## 4 4 1 IGL female 1 1 1 1 1 1 1 1 1 5 5 5
## 5 5 1 IGL male 2 1 1 1 5 1 1 2 1 3 3 4
## 6 6 1 IGL male 1 3 1 1 2 1 1 3 1 4 3 4
## em1t2 em2t2 em3t2 em1t3 em2t3 em3t3 si1t1 si2t1 si3t1 si1t2 si2t2 si3t2 si1t3 si2t3 si3t3
## 1 4 4 3 3 4 5 2 2 3 3 2 3 2 1 3
## 2 4 5 5 4 3 3 2 1 3 4 2 3 3 2 3
## 3 2 2 1 3 2 2 1 2 2 1 1 2 1 1 2
## 4 4 4 4 3 4 5 4 1 5 4 4 4 4 1 4
## 5 3 4 3 3 4 4 2 2 2 2 3 2 3 5 3
## 6 3 4 4 4 4 4 2 2 3 3 3 4 4 3 4
Der Datensatz, den wir hier betrachten, enthält verhaltensbezogene Selbstberichte auf jeweils drei Items zur relationalen Aggression (ra), Empathie (em) und sozialen Intelligenz (si). Diese insgesamt 9 Indikatoren liegen zu drei Messzeitpunkten (t1, t2 und t3) vor. Die über den Befehl str angeforderte Struktur verrät uns außerdem, dass diese Variablen allesamt integer (int), also ganzzahlig, sind. Über die Items hinaus sind vier weitere Variablen im Datensatz enthalten, die den Personenidentifikator (id), die Klasse (class), die Interventionsgruppe (grp) und das Geschlecht (sex) der Jugendlichen kodieren.
Die Items sind jeweils eine Auswahl aus den gesamten Skalen, die genutzt wurden, um die drei Konstrukte zu erheben. Fur Empathie ist eines der Items z.B. “Ich kann mich über die Erfolge anderer Freuen.”, für die relationale Aggression z.B. “Ich habe versucht, andere dazu zu bringen, einen bestimmten Mitschüler auszuschließen, indem ich Gerüchte verbreitet habe”.
Datenmanagement
Eines der großen Themen in diesem Semester wird es sein, möglichst gute und zuverlässige Schätzungen für die Werte einzelner Personen auf verschiedenen psychologischen Konstrukten zu erhalten. Traditionellerweise werden dafür häufig sogenannte Skalenwerte genutzt. Diese werden meistens als Mittelwerte der Items, die ein gemeinsames Konstrukt erheben sollen, berechnet.
Für die weiteren Analysen in dieser Sitzung werden wir die Skalenwerte der relationalen Aggression, Empathie und sozialen Intelligenz zum ersten Zeitpunkt benötigen. Naheliegend wäre es, diese durch einfache Arithmetik zu bestimmen, z.B. für die relationale Aggression:
fairplayer$rat1 <- (fairplayer$ra1t1 + fairplayer$ra2t1 + fairplayer$ra3t1) / 3
Von diesem Vorgehen möchten wir an dieser Stelle explizit abraten. Grund dafür ist, dass es hier nicht möglich ist, den Umgang mit fehlenden Werte zu beeinflussen. Darüber hinaus wird diese Strategie mit zunehmender Anzahl von Items pro Skala sehr schreibaufwändig. Daher sollten wir dieses Vorgehen nicht nur aus Faulheit umgehen, sondern auch, weil mehr Syntax auch immer mehr mögliche Fehlerquellen bedeutet. Stattdessen empfehlen wir, mit dem rowMeans-Befehl zu arbeiten. Z.B. für die relationale Aggression:
fairplayer$rat1 <- rowMeans(fairplayer[, c('ra1t1', 'ra2t1', 'ra3t1')],
na.rm = TRUE)
Das Argument na.rm = TRUE bewirkt, dass wir den Skalenwert auch dann berechnen, wenn fehlende Werte auf einzelnen Items vorliegen. Das Ganze ist natürlich auch für die Empathie und die soziale Intelligenz nötig:
fairplayer$emt1 <- rowMeans(fairplayer[, c('em1t1', 'em2t1', 'em3t1')],
na.rm = TRUE)
fairplayer$sit1 <- rowMeans(fairplayer[, c('si1t1', 'si2t1', 'si3t1')],
na.rm = TRUE)
Deskriptivstatistik
Die drei Skalenwerte aus dem letzten Abschnitt sollten wir uns - zusammen mit ein paar anderen Variablen - mal genauer angucken, um ein Gefühl dafür zu entwickeln, wie die Lage in dieser Erhebung ist. Der Klassiker, um sich einen Überblick zu verschaffen, ist die R-eigene summary-Funktion. Dabei handelt es sich um eine generische Funktion, die man auf viele verschiedene Objekte in R anwenden kann. Die Aufbereitung des Ergebnisses hängt dabei immer davon ab, auf was für ein Objekt man sie angewendet hat.
Nehmen wir unsere drei Skalenwerte: bei allen handelt es sich um numerische Variablen (in R: num) - in R wird also davon ausgegangen, dass es Variablen mit mindestens Intervallskalenniveau sind (mehr Informationen zu Skalenniveaus in der psychologischen Methodenlehre finden Sie in Eid, Gollwitzer und Schmitt (2017) im Kapitel 5). Für solche Variablen wird in R mit summary eine sogenannte Fünf-Punkt-Zusammenfassung ausgegeben:
summary(fairplayer$rat1)
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 1.000 1.000 1.000 1.363 1.667 3.667 30
Den Spitzfindigen unter Ihnen fällt auf, dass hier mehr als fünf Informationen ausgegeben werden. Die klassische Fünf-Punkt-Zusammenfassung besteht aus Minimum, Maximum und den drei Quartilen. In R wird zusätzlich noch das arithmetische Mittel und die Anzahl der fehlenden Werte ausgegeben.
Für nominalskalierte Variablen, wie z.B. die Gruppenzugehörigkeit grp, sieht die Zusammenfassung ein wenig anders aus:
summary(fairplayer$grp)
## CG IGS IGL NA's
## 48 48 45 14
Weil diese Variable in R als factor angelegt ist, wird sie als nominalskaliert behandelt und es werden keine Statistiken berechnet, die für solche Variablen nicht aussagekräftig sind. Stattdessen wird lediglich eine Häufigkeitstabelle erzeugt. Neben diesen globalen Funktionen können diverse Deskriptivstatistiken natürlich auch einzeln erzeugt werden, z.B. mit mean, median oder sd.
Kovarianzen und Korrelationen
Neben univariaten Statistiken sind für eine Veranstaltung mit dem Titel “Multivariate Verfahren” natürlich Zusammenhangsmaße von zentraler Bedeutung. Die beiden gängigsten Formen, um Zusammenhänge in der Psychologie zu untersuchen, sind Kovarianzen und Korrelationen. Bivariat können wir diese in R sehr einfach über cov bzw. cor anfordern:
cov(fairplayer$rat1, fairplayer$sit1, use = 'complete')
## [1] 0.1390892
cor(fairplayer$rat1, fairplayer$sit1, use = 'complete')
## [1] 0.2727377
Mit dem Argument use wird der Umgang mit fehlenden Werten gesteuert - in diesem Fall sollen alle listenweise vollständigen Beobachtungen genutzt werden, also alle Fälle, in denen keine der beteiligten Variablen fehlt. Das ist im Moment noch kein Unterschied zum paarweisen Fallausschluss, weil wir immer nur zwei Variablen betrachten. Unten werden wir aber Korrelationen und Kovarianzen für mehrere Variablen gleichzeitig bestimmen. Eine kurze Wiederholung aus Statistik I im Bachelorstudiengang: die Produkt-Moment-Korrelation ergibt sich aus $\frac{\mathbb{C}ov[X, Y]}{Sd[X]Sd[Y]}$.
Um Zusammenhänge nicht immer nur für zwei Variablen bestimmen zu können, ist es auch möglich, die Funktionen cov und cor auf ganze Matrizen und Datensätze anzuwenden. Nehmen wir unsere drei Skalen in einen gemeinsamen Datensatz auf:
scales <- fairplayer[, c('rat1', 'emt1', 'sit1')]
Jetzt können wir die Korrelationsmatrix für die drei Variablen gleichzeitig bestimmen:
cor(scales, use = 'complete')
## rat1 emt1 sit1
## rat1 1.00000000 -0.09925784 0.2727377
## emt1 -0.09925784 1.00000000 0.2769676
## sit1 0.27273770 0.27696758 1.0000000
Das Gleiche funktioniert natürlich auch mit der Kovarianzmatrix:
cov(scales, use = 'complete')
## rat1 emt1 sit1
## rat1 0.29089810 -0.04138619 0.1390892
## emt1 -0.04138619 0.59764111 0.2024543
## sit1 0.13908923 0.20245432 0.8940376
Letztere ist für viele Analysen, die wir in diesem Semester behandeln werden, zentral, weil sie in einer Matrix (beinahe) alle relevanten Informationen über interindividuelle Unterschiede (Varianzen) und deren Zusammenhänge (Kovarianzen) enthält. Die Verwendung von use = 'complete' bewirkt hier, dass nur Personen in die Berechnung aufgenommen werden, die auf keiner der drei Variablen fehlende Werte haben. In unserem Fall bleiben also von den ursprünglich 155 Personen noch 124 übrig.
Varianzen sind in der Diagonale der Matrix enthalten:
diag(cov(scales, use = 'complete'))
## rat1 emt1 sit1
## 0.2908981 0.5976411 0.8940376
Einen Überblick über die Befehle für Matrix-Algebra in R finden Sie auf der Quick-R Website.
Wiederholung: Regression
Im letzten Semester haben Sie die lm-Funktion kennengelernt, um lineare Modelle in R zu berechnen. Um diese Funktion zu verwenden, müssen meist zwei Argumente an lm weitergegeben werden:
formula: Das Modell in klassischerR-Formelschreibweisedata: Der Datensatz, auf den dieses Modell angewendet werden soll
Die Formelschreibweise folgt in R einer einfachen Grundstruktur: Y ~ X. Gelesen werden kann $Y$ “vorhergesagt durch” $X$. Mehrere unabhängige Variablen, z.B. $X_1$ und $X_2$, können im Wesentlichen durch drei Operatoren verbunden sein:
X1 + X2: Für additive Modelle (nur Haupteffekte von $X_1$ und $X_2$)X1 : X2: Für Interaktionen (nur der Interaktionseffekt $X_1 \cdot X_2$)X1 * X2: Als Kurzschreibweise fürX1 + X2 + X1:X2
Darüber hinaus können noch einige andere Operatoren genutzt werden (mehr Informationen finden Sie mit ?formula) - z.B. kann mit - ein Effekt bewusst unterdrückt werden. Eine “Variable”, die in Regressionen häufig als Prädiktor aufgenommen wird, ist die Konstante 1. Wenn man eine abhängige Variable auf eine Konstante regressiert, ist das entsprechende Regressionsgewicht der (bedingte) Mittelwert - in Regressionsanalysen häufig als Achsenabschnitt oder Interzept bezeichnet. Für eine Wiederholung der Grundgedanken der Regressionsanalyse können Sie einen Blick in Eid et al. (2017) Kapitel 17 und 19) werfen.
Modell erstellen
Im Beispiel geht es um die drei Konstrukte relationale Aggression, soziale Intelligenz und Empathie von Jugendlichen. Da durch Interventionen soziale Intelligenz als Kompetenz gut vermittelbar ist, ist von Interesse, wie sich höhere soziale Intelligenz auf relationale Aggression auswirkt. Wichtig ist dabei, dass auch Empathie in die Gleichung einbezogen wird, weil diese konsistent ein negativer Prädiktor relationaler Aggression ist; wenn ich negative Empfindungen anderer mitfühlen kann, ist es weniger wahrscheinlich, dass ich durch mein Verhalten solche negativen Empfindungen hervorrufen möchte. Die Beziehung zu sozialer Intelligenz war in der Literatur lange aber nicht so eindeutig - erst in den späten 2000er Jahren wurde die Befundlage hierzu klarer (aus dieser Zeit stammt der Datensatz).
Um diese Fragestellung zu bearbeiten, können wir mit dem Datensatz eine multiple Regression zur Vorhersage relationaler Aggression durch Empathie und soziale Intelligenz durchführen.
mod <- lm(rat1 ~ 1 + sit1 + emt1, fairplayer)
Die 1 im Prädiktorenteil der Formel bezeichnet das Interzept und wird in R üblicherweise nicht explizit aufgeführt. Per Voreinstellung wird davon ausgegangen, dass ein Interzept geschätzt werden soll. Wenn wir dieses unterbinden wollen würden, müssten wir z.B. rat1 ~ 0 + sit1 + emt1 als Regressionsgleichung benutzen. Sie ist hier trotzdem explizit aufgeführt, weil sie gleich wieder von Relevanz sein wird.
Regressionergebnisse
Es gibt jetzt eine Vielzahl von Möglichkeiten, um die Ergebnisse des Modells zu inspizieren. Mit dem einfachen Aufruf des Modells erhalten wir zunächst nur die Regressiongewichte:
mod
##
## Call:
## lm(formula = rat1 ~ 1 + sit1 + emt1, data = fairplayer)
##
## Coefficients:
## (Intercept) sit1 emt1
## 1.3536 0.1855 -0.1321
Wir können uns die Koeffizienten mit coef auch als Vektor ausgeben lassen, was den Vorteil hat, dass wir sie in anderen Funktionen weiterverwenden können. Wenn wir uns z.B. die Ergebnisse grafisch darstellen lassen wollen, können wir die Ergebnisse einfach an ggplot weitergeben (zur Erinnerung an ggplot2 gibt es z.B. hier eine Einführung):
# Koeffizienten als Objekt ablegen
b <- coef(mod)
# Scatterplot mit Regressionslinie
library(ggplot2)
## Want to understand how all the pieces fit together? Read R for Data Science:
## https://r4ds.hadley.nz/
ggplot(fairplayer, aes(x = sit1, y = rat1)) +
geom_point() +
geom_abline(intercept = b['(Intercept)'], slope = b['sit1'],
color = '#00618f', lwd = 1.5) +
labs(x = 'Soziale Intelligenz', y = 'Relationale Aggression')
## Warning: Removed 31 rows containing missing values or values outside the scale range
## (`geom_point()`).
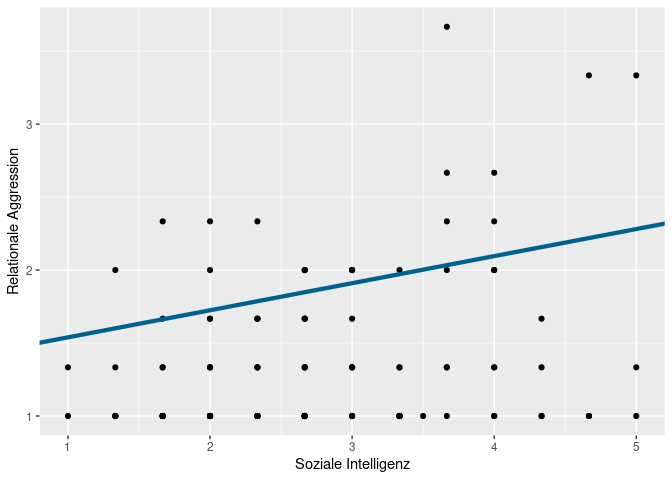
geom_line zu gehen, könnten wir auch mit geom_smooth(method = 'lm') eine Regressionsgerade von ggplot erzeugen lassen - dann hätte ich allerdings kein Beispiel mehr dafür, warum die Ausgabe der Koeffizienten als Objekt so super praktisch ist.
Üblicherweise wird aber auch bei lm-Objekten der summary-Befehl genutzt, um die Ergebnisse genauer zu inspizieren. Diese enthält z.B. auch die inferenzstatistische Prüfung der Regressionsgewichte und den Determinationskoeffizient $R^2$.
summary(mod)
##
## Call:
## lm(formula = rat1 ~ 1 + sit1 + emt1, data = fairplayer)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.6469 -0.3633 -0.1401 0.2825 2.1612
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.35364 0.24299 5.571 1.56e-07 ***
## sit1 0.18548 0.05098 3.638 0.000405 ***
## emt1 -0.13208 0.06236 -2.118 0.036211 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.5137 on 121 degrees of freedom
## (31 observations deleted due to missingness)
## Multiple R-squared: 0.1075, Adjusted R-squared: 0.09273
## F-statistic: 7.285 on 2 and 121 DF, p-value: 0.001029
Der Abschnitt Coefficients enthält die relevanten Aussagen zu den Regressionsgewichten. Um uns nur diesen anzusehen, können wir das $ benutzen, um, wie bei allen R-Objekten, nur einen spezifischen Abschnitt zu betrachten.
summary(mod)$coef
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.3536402 0.24299389 5.570676 1.560459e-07
## sit1 0.1854844 0.05098476 3.638036 4.050164e-04
## emt1 -0.1320831 0.06235884 -2.118114 3.621134e-02
Die Zeilennamen dieser Tabelle ((Intercept), sit1, emt1) geben an, zu welchem Prädiktor das Regressiongewicht gehört. In der Spalte Estimate wird das Regressionsgewicht angegeben. Hier wird also für zwei Jugendliche, die sich um eine Einheit in sozialer Intelligenz (sit1) unterscheiden, aber das gleiche Ausmaß an Empathie (emt1) haben, ein Unterschied in der relationalen Aggression von 0.19 Einheiten vorhergesagt. Bei gleicher Empathie führt höhere soziale Intelligenz also zu mehr relationaler Aggression. Die nächste Spalte Std. Error gibt den Standardfehler an, welcher das Ausmaß an Unsicherheit quantifiziert, das wir in der Schätzung des Populationswertes dieses Regressionsgewichts aufgrund unserer Stichprobe haben. Das Verhältnis aus Regressionsgewicht und Standardfehler ($\frac{0.19}{0.05} = 3.64$) folgt - wenn die Voraussetzungen der Regressionsanalyse halten - einer $t$-Verteilung mit $n - k - 1$ Freiheitsgraden und wird deswegen in der Tabelle als t Value geführt. Bei der Bestimmung der Freiheitsgrade entspricht $n$ der Anzahl der Beobachtungen und $k$ der Anzahl der Prädiktoren. Bei ausreichend großer Anzahl von Freiheitsgraden ist die $t$-Verteilung nicht mehr von der Standardnormalverteilung unterscheidbar, sodass in anderer Software hier häufig der $z$-Test genutzt wird.
Weil wir wissen, wie wahrscheinlich es ist, unter der $t$-Verteilung mit 121 Freiheitsgraden einen Wert von 3.64 zu beobachten, können wir (in der letzten Spalte) einen $p$-Wert bestimmen. In diesem Fall heißt es also, dass, wenn in der Population der wahre Wert dieses Regressionsgewichts 0 wäre, die Wahrscheinlichkeit, in unserer Stichprobe ein Regressionsgewicht von 0.19 oder extremer zu finden, 0.00041 ist. “Extremer” heißt hierbei, dass das Regressionsgewicht vom Betrag her größer sein müsste.
Nach dem gleichen Prinzip lassen sich auch andere Parameter aus der Zusammenfassung extrahieren, z.B. das $R^2$:
summary(mod)$r.squared
## [1] 0.1074785
Hier zeigt sich, dass wir mit unseren beiden Prädiktoren ca. 10.7% der Varianz in der relationalen Aggression der Jugendlichen aufklären können.
lavaan
Alle Dinge, die wir in den bisherigen Abschnitten besprochen haben, sind eine Wiederholung von Konzepten aus dem Bachelorstudium oder der vergangenen Semester gewesen. In diesem Semester werden wir hauptsächlich mit dem R-Paket lavaan arbeiten. Der Name ist dabei ein Akronym für latent variable analysis. Im Rest dieser Sitzung werden wir uns die Kerngedanken des Pakets und das grundsätzliche Vorgehen zur Modellschätzung am Beispiel der multiplen Regression ansehen. Mehr Informationen zu lavaan finden Sie unter lavaan.org.
Drei-Schritt-Verfahren
Der Grundlegende Prozess der Modellierung folgt in lavaan drei Schritten. Folgende Abbildung soll das etwas verdeutlichen:

Im 1. Schritt schreiben wir ein Modell als Text und legen es in einem Objekt (z.B. mod) ab. Dieses Modell geben wir dann im 2. Schritt an die Kernfunktionen von lavaan weiter und halten die Ergebnisse wieder in einem Objekt (z.B. fit) fest. Der Name fit verdeutlicht dabei, dass das Model auf die Daten angepasst wurde, die Ergebnisse also eine durch Empirie aktualisierte Fassung unseres ursprünglich rein theoretischen Modells sind. Die Ergebnisse, die in diesem Objekt enthalten sind, können wir im 3. Schritt mit einer Vielzahl von “Helferfunktionen”, wie dem allgemeinen summary, genauer untersuchen.
Pfaddiagramme
Die Model-Syntax von lavaan ist eine grafische Sprache. Das heißt, dass die Syntax so gedacht ist, dass man dabei das Pfaddiagramm in Worten beschreibt. Im Verlauf des Semesters werden wir noch diverse Modelle mit Pfaddiagrammen darstellen und dabei immer mal wieder neue Komponenten kennenlernen. Im Wesentlichen bilden Pfaddiagramme aber die beiden möglichen Beziehungen zwischen drei Typen von “Variablen” ab.

Mit diesen fünf sehr grundlegenden Elementen lassen sich erstaunlich viele Modelle darstellen, die in der psychologischen Forschung genutzt werden. Wir können z.B. eine einfache Regression zur Vorhersage eines Kriteriums $Y$ durch einen Prädiktor $X$ aufstellen. Wir haben also zwei manifeste Variablen (in Rechtecken) und eine gerichtete Verbindung zwischen den beiden (die Regression). Wie üblich, benennen wir die Regression mit $\beta$:

Was diese Abbildung also darstellt, ist $Y = \beta \cdot X$. Für eine vollständige Regressionsgleichung fehlen allerdings noch ein paar Dinge. Als erstes nehmen wir das Interzept hinzu - also den Wert, der für $Y$ bei $X = 0$ vorhergesagt wird. Wie in der Übersicht oben dargestellt, fügen wir Konstanten hinzu, indem wir das Dreieick nutzen:

Wir fügen also eine zweite Regression hinzu (der Pfeil), in der $Y$ auf 1 regressiert wird. In der Regressionsgleichung sieht das so aus: $Y = \alpha \cdot 1 + \beta \cdot X$. Wir nutzen hier $\alpha$ und nicht $\beta_0$ für das Interzept, weil das die von lavaan verwendete Notation ist. An der Bedeutung ändert sich dadurch aber nichts. Weil $\alpha \cdot 1 = \alpha$ ergibt, können wir die Regressionsgleichung auf $Y = \alpha + \beta \cdot X$ kürzen. Jetzt fehlt noch das Residuum, also die Komponenten in $Y$, die nicht durch $X$ vorhergesagt werden können. Bei diesem Residuum handelt es sich um eine nicht-beobachtbare, bzw. latente Variable. Diese Variable entsteht durch unsere Berechnung, sie existiert ohne das Modell nicht im Datensatz. In der Abbildung fügen wir also eine Ellipse hinzu und nutzen diese zur Vorhersage von $Y$:

In der Regressionsgleichung ergibt sich dadurch $Y = \alpha + \beta \cdot X + 1 \cdot \epsilon$. Nach dem gleichen Prinzip wie eben kürzt sich das auf die traditionelle Regressionsgleichung: $Y = \alpha + \beta \cdot X + \epsilon$.
Nehmen wir das bisherige Beispiel der Regression, in der wir relationale Aggression zum 1. Zeitpunkt ($RA_1$) durch soziale Intelligenz ($SI_1$) und Empathie ($EM_1$) vorhersagen. In diesem Fall haben wir drei beobachtbare Variablen: die drei Skalenwerte, die wir erzeugt haben. Die Beziehung zwischen $RA_1$ und $SI_1$ ($\beta_1$) bzw. $EM_1$ ($\beta_2$) ist regressiv. Zusätzlich regressieren wir die relationale Aggression auf die Konstante 1, um so eine Schätzung für das Interzept $\alpha$ zu erhalten.

In dieser Abbildung wird die Regression $RA_1 = \alpha + \beta_1 SI_1 + \beta_2EM_1 + \epsilon$ dargestellt. Häufig wird natürlich auf die detaillierte Beschriftung in solchen Abbildungen verzichtet, sodass eine typische Abbildung dieser Regression so aussehen würde:

In vielen Fällen wird von dieser (sehr rigiden) Auslegung der Darstellungsregeln abgewichen und stattdessen Folgendes Schema verwendet:

Hier wird das Residuum nicht als latente Variable eingezeichnet, sondern als Kovarianz der abhängigen Variable mit sich selbst. So soll verdeutlicht werden, dass diese Varianz geschätzt werden muss (weil es meist das Einzige ist, was uns an Residuen interessiert). Leider ist diese Darstellungsform etwas uneinheitlich mit der klassichen Notation der Regressionsgleichungen, aber sie ist so weit verbreitet, dass sie auch die Variante ist, mit der lavaan in seiner Syntax arbeitet.
Modell-Syntax
Wie oben erwähnt, wird in der Modell-Syntax von lavaan das Pfaddiagramm eines Modells beschrieben. In folgender Tabelle sind alle Befehle in lavaan Modell-Syntax zusammengetragen.
| Bezeichnung | Befehl | Bedeutung |
|---|---|---|
| Regression | ~ | wird vorhergesagt durch |
| Kovarianz | ~~ | kovariiert mit |
| Interzept | ~1 | wird auf 1 regressiert |
| Faktorladung | =~ | wird gemessen durch |
| Formative Faktoren | <~ | wird konstruiert durch |
| Schwellenparameter | |t... | Schwelle Nummer … |
In lavaan, wie in beinahe jeder Statistik-Software, wird bei ~~ nicht die Korrelation, sondern stets die Kovarianz angesprochen. Von diesen sechs Befehlen sind für uns zunächst nur drei relevant: die Regression, die Kovarianz und das Interzept. Wie auch in der R-internen Formelnotation wird die Tilde genutzt, um Regressionen darzustellen.
Anhand der Tabelle für die lavaan-Syntax lässt sich erkennen, dass hier die klassische Notation erneut benutzt werden kann, um Regressionen durchzuführen. Der grundlegende Unterschied besteht lediglich darin, dass wir im Drei-Schritt-Verfahren vorgehen müssen, also zunächst das Modell als Text in einem Objekt anlegen müssen:
mod <- 'rat1 ~ 1 + sit1 + emt1'
Für den lm-Befehl reicht es aus, die Regression zu definieren, um das Modell aufzustellen. In lavaan ist das nicht der Fall. Das liegt daran, dass lavaan im Gegensatz zu lm in der Lage ist, mehrere abhängige Variablen und komplexe Beziehungen zwischen diesen gleichzeitig darzustellen. Daher müssen alle Elemente des Pfaddiagramms angesprochen werden, wenn nicht angenommen werden soll, dass die Parameter 0 sind. Aus dem Pfaddiagramm zur multiplen Regression fehlt jetzt im Modell noch die latente Variable $\epsilon$. Da wir sie im Modell noch nicht angesprochen haben, existiert diese für lavaan auch noch nicht. Um dem Residuum eine Existenz zu verschaffen, können wir dessen Varianz anfordern. Weil das Residuum untrennbar mit der abhängigen Variable verbunden ist, erreichen wir das, indem wir die (Residual-)Varianz der relationalen Aggression anfordern:
mod <- 'rat1 ~ 1 + sit1 + emt1
rat1 ~~ rat1'
Wie oben dargestellt, können wir in lavaan die ~~ nutzen, um eine Kovarianz anzufordern. Die Kovarianz einer Variable mit sich selbst ist deren Varianz.
In der Modellsyntax von lavaan können wir Zeilenumbrüche nutzen, um einzelne Modellabschnitte voneinander abzugrenzen. Wir haben z.B. eine Zeile mit der Regression und dann eine weitere mit der Varianz der Residualvarianz. Wir können nach diesem Schema auch die Regression in ihre Einzelteile zerlegen:
mod <- '
# Regression
rat1 ~ 1
rat1 ~ sit1
rat1 ~ emt1
# Residuum
rat1 ~~ rat1'
Wie Sie sehen, können wir in lavaan-Modellen auch weiterhin mit # Kommentare beginnen. Diese aufgeschlüsselte Variante ist mit der kürzeren Schreibweise oben identisch. Welche Sie bevorzugen, ist ganz allein Ihnen überlassen.
Modellschätzung
Den ersten der drei Schritte bei der Modellierung mit lavaan haben wir abgeschlossen. Jetzt wo wir ein Modell haben, müssen wir dieses Modell mit der empirischen Realität (also unseren Daten) konfrontieren. Dafür ist der Kernbefehl des Pakets der lavaan-Befehl. Dieser nimmt eine ganze Reihe an Argumenten entgehen, von denen allerdings nur zwei zwingend erforderlich sind:
model: Das zu schätzende Modelldata: Der Datensatz auf den das Modell angepasst werden soll
Alle anderen Argumente haben - für die meisten Analysen sinnvolle - Voreinstellungen. Weil die Modellschätzung mit lavaan sehr viele Ergebnisse und Details zum Schätzverfahren erzeugt, ist es ratsam, das angepasste Modell in einem Objekt abzulegen.
fit <- lavaan(mod, fairplayer)
Sofern keine Warn- oder Fehlermeldungen erzeugt werden, war die Schätzung des Modells erfolgreich. Wie auch bei lm oder anderen Funktionen aus dem letzten Semester kann der Datensatz, der an lavaan gegeben wird, auch Variablen enthalten, die für das Modell irrelevant sind. Alle manifesten Variablen, auf die im Modell Bezug genommen wird, sucht sich lavaan aus dem Datensatz heraus.
Ergebnisinspektion
lavaan bietet eine ganze Reihe von Möglichkeiten, die Ergebnisse von Modellen genauer unter die Lupe zu nehmen. Die naheliegendste ist - wie schon bei lm - der allgemeine summary-Befehl:
summary(fit)
## lavaan 0.6-19 ended normally after 1 iteration
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 4
##
## Used Total
## Number of observations 124 155
##
## Model Test User Model:
##
## Test statistic 0.000
## Degrees of freedom 0
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## rat1 ~
## sit1 0.185 0.050 3.683 0.000
## emt1 -0.132 0.062 -2.144 0.032
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|)
## .rat1 1.354 0.240 5.639 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## .rat1 0.258 0.033 7.874 0.000
Diese Ausgabe enthält neben Modellergebnissen auch einige Informationen zur Schätzprozedur, auf die wir hier erst einmal noch nicht eingehen werden. Die erste Zahl, mit der wir uns näher auseinandersetzen können, ist die Number of free parameters in der 3. Zeile der Ausgabe. Hier wird uns gesagt, dass wir vier Paramter schätzen mussten. Wenn wir uns das Pfaddiagramm für diese Regression noch einmal vor Augen führen, wird schnell deutlich, welche vier das sind:
- Regressionsgewicht $\beta_1$ von $SI_1$
- Regressionsgewicht $\beta_2$ von $EM_1$
- Achsenabschnitt / Interzept $\alpha$
- Varianz der Residuen $\epsilon$
Die nächste für uns relevante Information ist die Number of observations, welche in Used und Total unterteilt wird. Hier wird uns verraten, dass wir zwar 155 Personen im Datensatz haben, aber für unsere Analyse aufgrund fehlender Werte nur 124 genutzt werden konnten.
Dann springen wir direkt runter zu den Modellergebnissen, die mit der Zeile Regressions: beginnen. Wie diese Überschrift verrät, erhalten wir zuerst Informationen über die Regressionsparameter. Hier der relevante Ausschnitt:
## [...]
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## rat1 ~
## sit1 0.185 0.050 3.683 0.000
## emt1 -0.132 0.062 -2.144 0.032
## [...]
Dieser Abschnitt beginnt mit der Zeile rat1 ~, was uns verdeutlichen soll, dass die folgenden Regressionsergebnisse sich auf eine Regression mit relationaler Aggression als abhängige Variable beziehen. Die anschließende Tabelle enthält die gleichen vier Spalten, die wir schon bei der Wiederholung der Regression gesehen haben: das geschätzte Regressionsgewicht (Estimate), den Standardfehler (Std.Err.), den $z$-Wert (z-value) und den daraus resultierenden $p$-Wert (P(>|z|)). Wie Ihnen mit Sicherheit sofort aufgefallen ist, arbeitet lavaan nicht mit $t$-, sondern mit $z$-Werten. Das heißt, dass hier von vornherein eine größere Stichprobe angenommen wird, um korrekte inferenzstatistische Schlüsse ziehen zu können. Wir können diese Ergebnisse direkt noch einmal mit den Ergebnissen aus lm vergleichen:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.3536402 0.24299389 5.570676 1.560459e-07
## sit1 0.1854844 0.05098476 3.638036 4.050164e-04
## emt1 -0.1320831 0.06235884 -2.118114 3.621134e-02
Wie Sie sehen, sind die Parameter zwar identisch, die Inferenzstatistik unterscheidet sich zwischen beiden Herangehensweisen aber. Woher das kommt, werden wir im Verlauf des Semesters noch genauer untersuchen.
Anders als bei lm werden in lavaan die Interzepts von den Regressionsgewichten getrennt ausgegeben:
## [...]
## Intercepts:
## Estimate Std.Err z-value P(>|z|)
## .rat1 1.354 0.240 5.639 0.000
## [...]
Hier wird das Interzept von rat1 ausgegeben. Der . vor dem Variablennamen verrät uns, dass es sich um einen bedingten Mittelwert handelt, die Variable rat1 also irgendwo im Modell eine abhängige Variable ist. Diese Notation hilft besonders bei sehr komplexen Modellen, auch wenn es in unserem Beispiel noch leicht ist, den Überblick zu behalten.
Zu guter Letzt folgt ein Abschnitt mit Varianzen - in unserem Fall nur eine:
## [...]
## Variances:
## Estimate Std.Err z-value P(>|z|)
## .rat1 0.258 0.033 7.874 0.000
Auch hier verrät uns der ., dass rat1 irgendwo im Modell eine abhängige Variable ist, sodass es sich bei dieser Varianz um eine Residualvarianz handelt.
Wir können die summary in lavaan auch noch um diverse Aspekte erweitern. Für Regressionsmodelle ist es z.B. üblich, dass wir uns standardisierte Ergebnisse ansehen:
summary(fit, standardized = TRUE)
## lavaan 0.6-19 ended normally after 1 iteration
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 4
##
## Used Total
## Number of observations 124 155
##
## Model Test User Model:
##
## Test statistic 0.000
## Degrees of freedom 0
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## rat1 ~
## sit1 0.185 0.050 3.683 0.000 0.185 0.325
## emt1 -0.132 0.062 -2.144 0.032 -0.132 -0.189
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .rat1 1.354 0.240 5.639 0.000 1.354 2.520
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .rat1 0.258 0.033 7.874 0.000 0.258 0.893
In diesem Fall tauchen im Output zwei zusätzliche Spalten auf: std.lv und std.all. Die erste liefert die Ergebnisse, wenn alle latenten Variablen standardisiert wurden. In unserem Modell gibt es nur eine manifeste AV und zwei manifeste UVs, sodass dieser Ergebnisse exakt die gleichen sind, wie die unstandardisierten Regressionsgewichte. In std.all hingegen stehen die Parameter, wenn alle Variablen im Modell standardisiert werden - in diesem Fall also die standardisierten Regressionsgewichte. Zusätzlich ist außerdem die standardisierte Residualvarianz interessant - diese gibt den Anteil an Varianz an, der nicht durch die Prädiktoren erklärt wird (also den Indeterminationskoeffizienten). Das $R^2$ lässt sich also hier als $ 1 - .893 = .107$ berechnen.
Zusätzlich zur Standardisierung, kann in der summary noch ein breites Bouquet an Zusatzinformationen angefordert werden. Ein paar Möglichkeiten (die uns auch in den späteren Sitzungen noch begegnen werden) sind:
| Argument | Output |
|---|---|
standardized | Standardisierte Parameter |
ci | Konfidenzintervalle |
fitmeasures | Informationen zur Modellgüte |
rsquare | $R^2$-Werte |
Gezielter Informationen finden
Weil der Output der summary Funktion sehr schnell sehr lang wird und es nicht erlaubt, einzelne Ergebnisse direkt als Objekte weiterzuverwenden, gibt es in lavaan ein paar Möglichkeiten, gezielter an Ergebnisse zu kommen. Die allgemeinste Fassung ist die Funktion inspect. Diese nimmt zwei Argumente entgegen:
object: Das Ergebnisobjekt (bei uns alsofit)what: Was inspiziert werden soll
Die Liste möglicher whats ist mehrere Seiten lang. Sie finden Sie bei ?inspect. Eine Sache, die uns schon bei der lm-Regression interessiert hat, war das $R^2$. Hierfür können wir inspect nutzen:
inspect(fit, 'rsquare')
## rat1
## 0.107
Dieser Befehl wird im Verlauf des Semesters noch sehr praktisch, weil wir uns so nicht immer durch den gesamten Output wühlen müssen, sondern uns stets auf das beschränken können, was gerade relevant ist.
Darüber hinaus gibt es noch die Abkürzung zur Parametertabelle in unstandardisierte und standardisierter Form:
# Unstandardisierte Parameter
parameterEstimates(fit)
## lhs op rhs est se z pvalue ci.lower ci.upper
## 1 rat1 ~1 1.354 0.240 5.639 0.000 0.883 1.824
## 2 rat1 ~ sit1 0.185 0.050 3.683 0.000 0.087 0.284
## 3 rat1 ~ emt1 -0.132 0.062 -2.144 0.032 -0.253 -0.011
## 4 rat1 ~~ rat1 0.258 0.033 7.874 0.000 0.193 0.322
## 5 sit1 ~~ sit1 0.887 0.000 NA NA 0.887 0.887
## 6 sit1 ~~ emt1 0.201 0.000 NA NA 0.201 0.201
## 7 emt1 ~~ emt1 0.593 0.000 NA NA 0.593 0.593
## 8 sit1 ~1 2.743 0.000 NA NA 2.743 2.743
## 9 emt1 ~1 3.782 0.000 NA NA 3.782 3.782
# Standardisierte Parameter
standardizedSolution(fit)
Letztere habe ich uns hier erspart - Sie können sie Sich sicherlich vorstellen. Im restlichen Semester werden für uns noch ein paar weitere relevant werden, die wir dann aber einfach genauer besprechen.
Literatur
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden (5. Auflage, 1. Auflage: 2010). Weinheim: Beltz.
Rosseel, Y. (2012). lavaan: An R Package for Structural Equation Modeling. Journal of Statistical Software, 48(2), 1 - 36. doi:http://dx.doi.org/10.18637/jss.v048.i02
Blau hinterlegte Autor:innenangaben führen Sie direkt zur universitätsinternen Ressource.
](/media/header/guitars.jpg)