Tests für abhängige Stichproben - Lösungen

Hypothesen

• Art des Effekts: Unterschiedshypothese
• Richtung des Effekts: ungerichtete Hypothese
• Größe des Effekts: Unspezifisch

Hypothesenpaar (inhaltlich):
H0: Die Teilnahme am Statistikpraktikum wirkt sich nicht auf das Wachempfinden der Studierenden aus. H1: Die Teilnahme am Statistikpraktikum wirkt sich auf das Wachempfinden der Studierenden aus.

Hypothesenpaar (statistisch):

• $H_0$: $\eta_\text{nachher} = \eta_\text{vorher}$ bzw. $\mu_{d} = 0$
• $H_1$: $\eta_\text{nachher} \neq \eta_\text{vorher}$ bzw. $\mu_{d} \neq 0$

Spezifikation des Signifikanzniveaus

$\alpha = .05$

Bevor es weiter geht:

Ein Blick in den fb25-Datensatz verrät, dass auf dem Skalenwert wm_post, der Messung des Wachempfindens zum zweiten Zeitpunkt, Werte fehlen. Diese fehlenden Werte werden als NA abgebildet.

Um verfälschte deskriptiv- und inferenzstatistische Ergebnisse zu vermeiden, werden alle Personen aus der weiteren Berechung ausgeschlossen, die einen fehlenden Wert auf wm_post (oder wm_pre) aufweisen. Damit wir den Datensatz fb25 aber nicht generell verändern, legen wir estmal einen neuen Datesatz an, der nur die beiden interessierenden Variablen enthält.

wach <- fb25[, c("wm_pre", "wm_post")] #Erstellung eines neuen Datensatzes, welcher nur die für uns wichtigen Variablen enthält

wach <- na.omit(wach) #Entfernt alle Beobachtungen, die auf einer der beiden Variable einen fehlenden Wert haben

str(wach) #Ablesen der finalen Stichprobengröße

## 'data.frame':	191 obs. of  2 variables:
##  $ wm_pre : num  3.5 2.75 2.5 3.5 3.25 2 2.75 2.5 3.25 2.75 ...
##  $ wm_post: num  3.25 2.75 3.25 2.75 3.25 2.25 1.75 2.25 2 2.75 ...
##  - attr(*, "na.action")= 'omit' Named int [1:20] 2 7 16 19 32 36 52 87 89 108 ...
##   ..- attr(*, "names")= chr [1:20] "2" "7" "16" "19" ...

Nach dem Entfernen der fehlenden Werte haben wir eine Stichprobengröße von $n = 147$.

Deskriptivstatistische Überprüfung der Hypothesen: grafisch

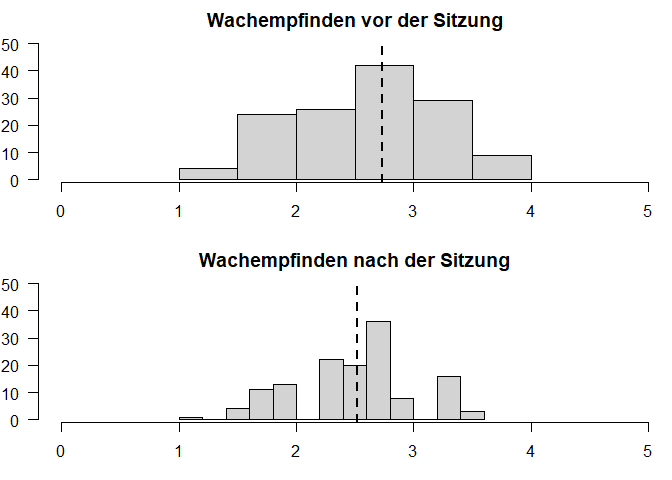
Histogramme (weil die Skalenwerte Intervallskalenqualität haben): Je ein Histogramm pro Gruppe, untereinander dargestellt, vertikale Linie für den jeweiligen Mittelwert.

par(mfrow=c(2,1), mar=c(3,2,2,0)) # Zusammenfügen der zwei Histogramme in eine Plot-Datei und ändern der Ränder (margins) des Plot-Fensters

hist(wach[, "wm_pre"], xlim=c(0,5), ylim=c(1,50), main="Wachempfinden vor der Sitzung", xlab="", ylab="", las=1)
abline(v=mean(wach[, "wm_pre"]), lty=2, lwd=2)

hist(wach[, "wm_post"], xlim=c(0,5), ylim=c(1,50), main="Wachempfinden nach der Sitzung", xlab="", ylab="", las=1)
abline(v=mean(wach[, "wm_post"]), lty=2, lwd=2)

par(mfrow=c(1,1)) #Zurücksetzen auf default

Deskriptivstatistische Beantwortung der Fragestellung: statistisch

summary(wach[, "wm_pre"])

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   1.500   2.500   3.000   2.894   3.250   4.000

summary(wach[, "wm_post"])

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   1.500   2.250   2.500   2.596   3.000   3.750

# aus dem Paket psych, das wir bereits installiert haben
library(psych)
describe(wach[, "wm_pre"])

##    vars   n mean   sd median trimmed  mad min max range  skew kurtosis   se
## X1    1 191 2.89 0.57      3    2.92 0.74 1.5   4   2.5 -0.31    -0.62 0.04

describe(wach[, "wm_post"])

##    vars   n mean   sd median trimmed  mad min  max range skew kurtosis   se
## X1    1 191  2.6 0.48    2.5     2.6 0.37 1.5 3.75  2.25 0.01    -0.79 0.03

Der Mittelwert vorher ($M$ = 2.89, $SD$ = 0.57) ist deskriptiv höher als Mittelwert nachher ($M$ = 2.6, $SD$ = 0.48).

Die deskriptivstatistischen Maße unterscheiden sich.

Voraussetzungen für t-Test für abhängige Stichproben

1. Die abhängige Variable ist intervallskaliert $\rightarrow$ ok

2. Die Messwerte innerhalb der Paare dürfen sich gegenseitig beeinflussen/voneinander abhängig sein; keine Abhängigkeiten zwischen den Messwertpaaren $\rightarrow$ ok

3. Die Stichprobenkennwerteverteilung der mittleren Mittelwertsdifferenz muss in der Population normalverteilt sein (ist gegeben, wenn die Verteilung der Mittelwertsdifferenzen in der Stichprobe normalverteilt ist) $\rightarrow$ ab $n > 30$ ist Normalverteilung der Stichprobenkennwerteverteilung durch zetralen Grenzwertsatz gegeben, ansonsten grafische Prüfung oder Hintergrundwissen $\rightarrow$ mit $n = 147$ erfüllt; Überprüfung der Normalverteilung von d wird hier aus Übungszwecken trotzdem mit aufgeführt.

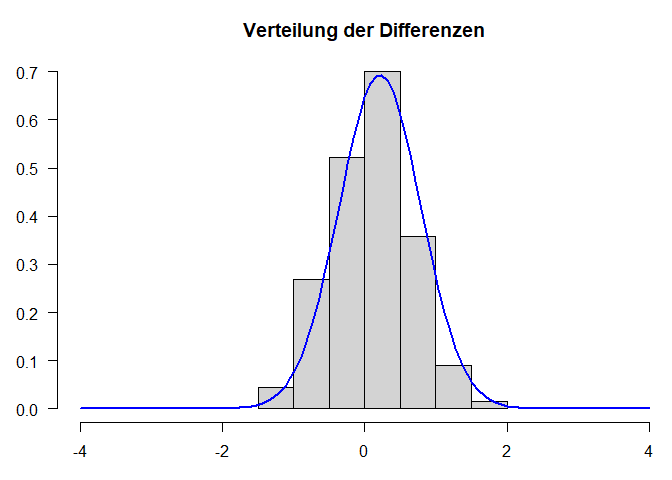
Grafische Voraussetzungsprüfung: Normalverteilung von d

par(mar=c(3,3,3,0)) #ändern der Ränder (margins) des Plot-Fensters
difference <- wach[, "wm_pre"]-wach[, "wm_post"]
hist(difference, xlim=c(-4,4), main="Verteilung der Differenzen", xlab="Differenzen", ylab="", las=1,freq=F)
curve(dnorm(x, mean=mean(difference), sd=sd(difference)), col="blue", lwd=2, add=T)

par(mfrow=c(1,1)) #Zurücksetzen auf default
qqnorm(difference,las=1)
qqline(difference, col="blue")

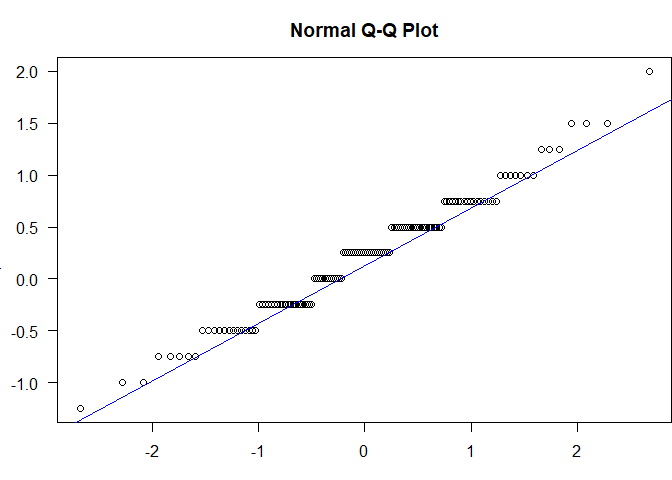
$\Rightarrow$ Differenzen weisen leichte Abweichungen zur Normalverteilung auf. Symmetrie trotzdem gegeben und auf Grund des zentralen Grenzwertsatzes und der Stichprobengröße $\Rightarrow$ Durchführung des t-Tests für abhängige Stichproben

Durchführung des t-Tests für abhängige Stichproben in R

t.test(x = wach[, "wm_pre"], y  = wach[, "wm_post"], # die Werte vorher und nachher
       paired = T,                                   # Stichproben sind abhängig
       alternative = "two.sided",                    # unggerichtete Hypothese -> zweiseitig Testung
       conf.level = .95)                             # alpha = .05

## 
## 	Paired t-test
## 
## data:  wach[, "wm_pre"] and wach[, "wm_post"]
## t = 7.6318, df = 190, p-value = 1.091e-12
## alternative hypothesis: true mean difference is not equal to 0
## 95 percent confidence interval:
##  0.2212972 0.3755614
## sample estimates:
## mean difference 
##       0.2984293

# Alternative Schreibweise
t.test(x = wach$wm_pre, y = wach$wm_post, 
       paired = T,
       alternative = "two.sided",
       conf.level = .95)

• Zur Erinnerung: $df$ bei $t$-test mit abhängigen Stichproben: $n - 1$ (wobei $n$ die Anzahl der Paare darstellt)
• t(190) = 7.632, $p $ <0.001 $\rightarrow$ ist signifikant, H0 wird verworfen.

Schätzung des standardisierten Populationseffekts

mean_d <- mean(difference) # Mittelwert der Differenzen
sd.d.est <- sd(difference) # geschätzte Populationsstandardabweichung der Differenzen
d <- mean_d/sd.d.est
d

## [1] 0.5522208

$\Rightarrow$ Der standardisierte Populationseffekt beträgt d2’’ = 0.55 und ist laut Konventionen nach Cohen (1988) ein mittlerer Effekt.

Zur Berechnung der Differenzvariable wurden von den Prä-Messungen die Post-Messungen abgezogen. Ein positives Vorzeichen des standardisierten Populationseffektes deutet also, wie auch unsere deskriptivstatistischen Ergebnisse, darauf hin, dass die Teilnahme am Statistikpraktikum einen negativen Effekt auf das Wachempfinden haben könnte. Dies könnte man in einer weiteren Studie inferenzstatistisch überprüfen.

Formales Berichten des Ergebnisses

Es wurde in einer Wiederholungsmessung untersucht, ob sich die Teilnahme am Statistikpraktikum auf das Wachempfinden auswirkt. Zunächst findet sich deskriptiv folgender Unterschied: Vor der Praktikumssitzung liegt der durchschnittliche Zufriedenheitswert bei 2.89 (SD = 0.57), während er nach der Praktikumssitzung bei 2.6 (SD = 0.48) liegt.

Zur Beantwortung der Fragestellung wurde ein ungerichteter $t$-Test für abhängige Stichproben durchgeführt. Der Gruppenunterschied ist signifikant ($t$(190) = 7.632, $p =$ 0), somit wird die Nullhypothese verworfen und wir gehen davon aus, dass sich die Teilnahme am Statistikpraktikum die Wachheit verändert.

Der standardisierte Populationseffekt von d’’ = 0.55 ist laut Konventionen nach Cohen (1988) mittelgroß.