Tests für abhängige Stichproben
Kernfragen dieser Lehreinheit über Gruppenvergleiche
- Wie fertige ich Deskriptivstatistiken (Grafiken, Kennwerte) zur Veranschaulichung des Unterschieds zwischen zwei Gruppen an?
- Was sind Voraussetzungen des abhängigen t-Tests und wie prüfe ich sie?
- Wie führe ich einen abhängigen t-Test in R durch?
- Wie berechne ich den standardisierten Populationseffekt für abhängige Stichproben?
- Wie führe ich einen abhängigen Wilcoxon-Test in R durch?
- Wie berichte ich statistische Ergebnisse formal?
Vorbereitende Schritte
Den Datensatz fb25 haben wir bereits über diesen Link heruntergeladen und können ihn über den lokalen Speicherort einladen oder Sie können Ihn direkt mittels des folgenden Befehls aus dem Internet in das Environment bekommen. In den vorherigen Tutorials und den dazugehörigen Aufgaben haben wir bereits Änderungen am Datensatz durchgeführt, die hier nochmal aufgeführt sind, um den Datensatz auf dem aktuellen Stand zu haben:
#### Was bisher geschah: ----
# Daten laden
load(url('https://pandar.netlify.app/daten/fb25.rda'))
# Nominalskalierte Variablen in Faktoren verwandeln
fb25$hand_factor <- factor(fb25$hand,
levels = 1:2,
labels = c("links", "rechts"))
fb25$fach <- factor(fb25$fach,
levels = 1:5,
labels = c('Allgemeine', 'Biologische', 'Entwicklung', 'Klinische', 'Diag./Meth.'))
fb25$ziel <- factor(fb25$ziel,
levels = 1:4,
labels = c("Wirtschaft", "Therapie", "Forschung", "Andere"))
fb25$wohnen <- factor(fb25$wohnen,
levels = 1:4,
labels = c("WG", "bei Eltern", "alleine", "sonstiges"))
# Rekodierung invertierter Items
fb25$mdbf4_r <- -1 * (fb25$mdbf4 - 5)
fb25$mdbf11_r <- -1 * (fb25$mdbf11 - 5)
fb25$mdbf3_r <- -1 * (fb25$mdbf3 - 5)
fb25$mdbf9_r <- -1 * (fb25$mdbf9 - 5)
# Berechnung von Skalenwerten
fb25$gs_pre <- fb25[, c('mdbf1', 'mdbf4_r',
'mdbf8', 'mdbf11_r')] |> rowMeans()
fb25$ru_pre <- fb25[, c("mdbf3_r", "mdbf6",
"mdbf9_r", "mdbf12")] |> rowMeans()
# z-Standardisierung
fb25$ru_pre_zstd <- scale(fb25$ru_pre, center = TRUE, scale = TRUE)
Nachdem wir uns mit unabhängige Stichproben in der letzten Sitzung beschäftigt haben, wollen wir uns diesmal mit abhängigen Stichproben beschäftigen. Abhängige Stichproben können in diversen Kontexten entstehen, beispielsweise wenn man Zwillinge und Paare untersucht oder wenn man Messwiederholungen durchführt. Im vorliegenden Beitrag werden die Fragestellungen an abhängigen Stichproben aufgrund von Messwiederholungen dargestellt. Die Methoden sind aber auf andere Arten abhängiger Stichproben übertragbar.
Mittelwertvergleich für abhängige Stichproben
Für den ersten Teil des Tutorials beschäftigen wir uns mit folgender Fragestellung: Gibt es einen Unterschied in den Werten der Subskalen ‘Ruhige vs. Unruhige Stimmung’ bei Psychologiestudierenden vor und nach der ersten Sitzung des Kurses? Wir geben in der Fragestellung keine Richtung des Effekts vor, da wir für Unterschiede in beide Richtungen uns Erklärungen vorstellen können. Ist nach dem Praktikum die Stimmung ruhiger, weil die Aufregung von der ersten Veranstaltung verflogen ist? Oder ist die Stimmung unruhiger, weil der erste Kontakt mit R stattgefunden hat?
Die Werte dieser Variablen zum zweiten Messzeitpunkt sind insofern voneinander abhängig, als dass jede Person dieselben Fragen zweimal beantwortet hat (Messwiederholung). Es gibt daher Faktoren innerhalb der Person, die einen gemeinsamen Teil der Varianz erzeugen. Im Datensatz fb25 ist der Skalenwert zur Ruhigen vs. Unruhigen Stimmung für den zweiten Messzeitpunkt bereits als ru_post hinterlegt. Den Skalenwert für die Ruhig vs. Unruhig Skala haben wir bereits bei den Aufgaben zur Deskriptivstatistik für Intervallskalen gebildet und passenderweise ru_pre genannt.
Deskriptivstatistik
Wie immer beginnen wir mit der deskriptivstatistischen Analyse unserer Daten. Die beiden Variablen können wir bspw. mit dem summary()-Befehl näher betrachten.
summary(fb25$ru_pre)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.000 2.500 3.000 2.847 3.250 4.000
summary(fb25$ru_post)
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 1.25 2.00 2.25 2.34 2.50 3.25 20
# oder mittels der Funktion describe() aus dem Package 'psych'
library(psych)
describe(fb25$ru_pre)
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 211 2.85 0.67 3 2.89 0.74 1 4 3 -0.56 -0.09 0.05
describe(fb25$ru_pos)
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 191 2.34 0.4 2.25 2.34 0.37 1.25 3.25 2 0.07 -0.19 0.03
Zunächst einmal ist offensichtlich, dass sich die Mittelwerte vor und nach der Sitzung unterscheiden. Die Frage bleibt aber bestehen, ob sich dieser Unterschied auf die Population verallgemeinern lässt. Weiterhin sticht hier direkt ins Auge, dass es in der Post-Variable fehlende Werte (20) gibt. Diese Personen können in die abhängige Testung nicht einbezogen werden, was im Folgenden berücksichtigt werden muss.
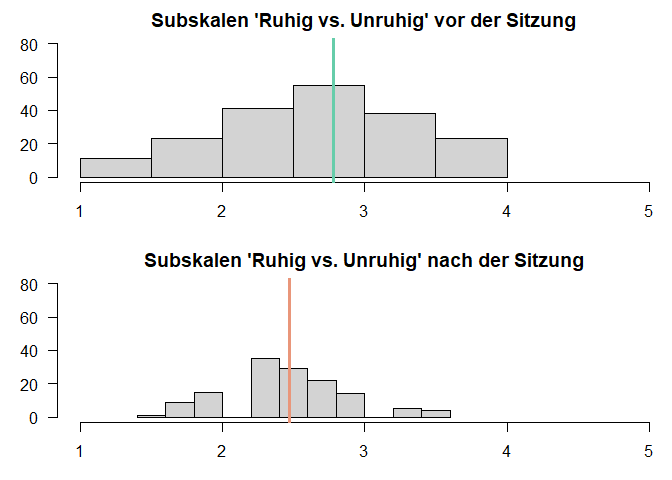
Mithilfe von Histogrammen stellen wir jeweils die Verteilungen der Werte vor und nach der Sitzung dar, wobei in den Histogrammen eine vertikale Linie eingefügt wird, die den jeweiligen Mittelwert anzeigt.
# Je ein Histogramm pro Werte, untereinander dargestellt, vertikale Linie für den jeweiligen Mittelwert
par(mfrow=c(2,1), mar=c(3,3,2,0))
hist(fb25$ru_pre,
xlim=c(1,5),
ylim = c(0,110),
main="Subskalen 'Ruhig vs. Unruhig' vor der Sitzung",
xlab="",
ylab="",
las=1)
abline(v=mean(fb25$ru_pre, na.rm = T),
lwd=3,
col="aquamarine3")
hist(fb25$ru_post,
xlim=c(1,5),
ylim = c(0,110),
main="Subskalen 'Ruhig vs. Unruhig' nach der Sitzung",
xlab="",
ylab="",
las=1)
abline(v=mean(fb25$ru_post, na.rm = T),
lwd=3,
col="darksalmon")
par(mfrow=c(1,1)) #Zurücksetzen des Plotfensters, zuvor hatten wir "dev.off()" kennengelernt
Die Funktion abline() fügt diese zusätzliche Linie in die Grafik ein. Mit dem Zusatzargument v geben wir an, dass es sich um eine vertikale Linie handeln soll. Der Ort der vertikalen Linie wird auch direkt über das Argumen v gesteuert. In dem Code soll diese jeweils den Mittelwert der beiden Gruppen kennzeichnen. Insgesamt scheinen sich die beiden Verteilungen zu unterscheiden: Der Mittelwert der Skala vor der Sitzung liegt höher als der nach der Sitzung. Beachten Sie jedoch, dass hier Personen mit fehlenden Werten auf der Post-Variable noch nicht ausgeschlossen sind, wodurch die späteren Ergebnisse anders ausfallen könnten.
Voraussetzungsprüfung
Um unsere inferenzstistische Entscheidung mittels der $t$-Verteilung abzusichern, müssen dessen Voraussetzungen erfüllt sein:
Voraussetzungen für die Durchführung des t-Tests für abhängige Stichproben:
- Die abhängige Variable ist intervallskaliert $\rightarrow$ ok
- Die Messwerte innerhalb der Paare dürfen sich gegenseitig beeinflussen/voneinander abhängig sein; keine Abhängigkeiten zwischen den Messwertpaaren $\rightarrow$ ok
- Die Differenzvariable $d$ muss in der Population normalverteilt sein $\rightarrow$ ggf. grafische Prüfung
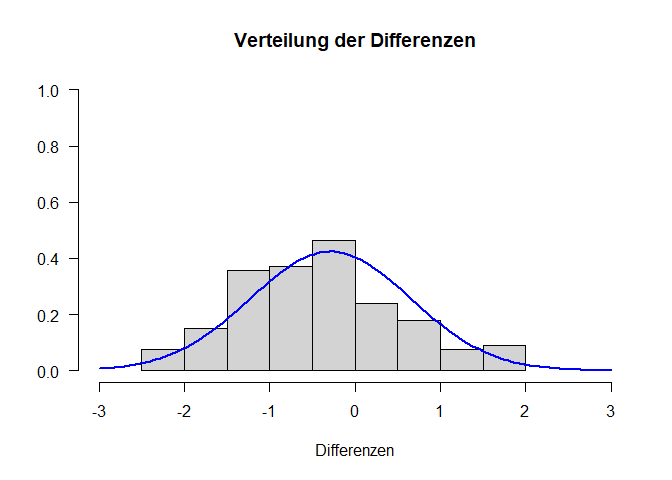
Wir müssen also nur die Voraussetzung der Normalverteilung der Differenzvariable $d$ zusätzlich prüfen. Analog zu den unabhängigen Tests ist es üblich, diese Annahme grafisch basierend auf der Stichprobe zu testen. Da wir hier die Differenzvariable betrachten wollen, müssen wir diese zunächst erstellen. Dies geht zum Glück sehr einfach, indem wir die Werte aller Personen auf ru_pre jeweils von ihren ru_post Werten abziehen. Personen mit einem fehlenden Wert auf einer der beien Variable erhalten auf difference jetzt automatisch ein NA. Somit sind alle Werte in den Grafiken diejenigen, die dann auch in unsere inferenzstatistische Prüfung eingehen. Daraufhin schauen wir uns das Histogramm der Differenzvariable und den QQ-Plot an:
difference <- fb25$ru_post - fb25$ru_pre
par(mfrow=c(1,2), mar=c(3,3,2,2))
hist(difference,
xlim=c(-3,3),
ylim = c(0,1),
main="Verteilung der Differenzen",
xlab="Differenzen",
ylab="",
las=1,
freq = F)
curve(dnorm(x, mean=mean(difference, na.rm = T), sd=sd(difference, na.rm = T)),
col="blue",
lwd=2,
add=T)
qqnorm(difference)
qqline(difference, col="blue")
par(mfrow=c(1,1))
Auf den Abbildungen sind kleine Abweichungen der Differenzen von der Normalverteilung zu sehen. Allerdings gilt (analog zu den Einstichproben- und unabhängigen Tests) der zentrale Grenzwertsatz. In Fällen, in denen die Stichprobe (also die Anzahl an Messwertpaaren) ausreichend groß ist, folgt die Stichprobenkennwerteverteilung auch unabhängig von der Verteilung der Differenzen in der Population der $t$-Verteilung. “Ausreichend groß” ist natürlich Auslegungssache, aber nochmal zur Erinnerung: Bei Stichproben ab $n \geq 30$ greift der Effekt, wenn das Merkmal zumindest symmetrisch verteilt ist. Andere Empfehlungen gehen besonders bei sehr schiefen Verteilungen in Richtung von 80 Messwertpaaren. Die kleinen Abweichungen von der Normalverteilung und die große Stichproben sprechen also dafür, dass unsere Stichprobenkennwerteverteilung der $t$-Verteilung folgt. Wir können also mit der inferenzstatistischen Überprüfung starten.
Durchführung des $t$-Test für abhängige Stichproben
Aus der Fragestellung lässt sich ableiten, dass es sich bei unserer Untersuchung um eine Unterschiedshypothese handelt, in der wir keine Richtung angenommen haben. Beginnen wir also damit, das Hypothesenpaar auszuarbeiten.
- $H_0$: Studierende sind vor und nach dem Praktikum gleich ruhig.
- $H_1$: Studierende sind vor und nach dem Praktikum unterschiedlich ruhig.
Etwas formaler ausgedrückt:
- $H_0$: $\mu_\text{vor} = \mu_\text{nach}$ bzw. $\mu_{d} = 0$
- $H_1$: $\mu_\text{vor} \ne \mu_\text{nach}$ bzw. $\mu_{d} \ne 0$
Bevor wir jetzt die Rechnungen durchführen, sollten wir noch das Signifikanzniveau der Untersuchung festlegen. Es soll hier 5% betragen. $\rightarrow$ $\alpha=.05$
Wir verwenden hier die Funktion t.test(). Diesmal müssen wir allerdings die beiden Variablen einzeln der Funktion übergeben. Dies geschieht über die Argumente x und y. Das Argument paired = T führt dazu, dass der t-Test für abhängige (gepaarte) Stichproben durchgeführt wird.
t.test(x = fb25$ru_post, y = fb25$ru_pre, # die beiden abhaengigen Variablen
paired = T, # Stichproben sind abhaengig
conf.level = .95)
##
## Paired t-test
##
## data: fb25$ru_post and fb25$ru_pre
## t = -7.6826, df = 190, p-value = 8.063e-13
## alternative hypothesis: true mean difference is not equal to 0
## 95 percent confidence interval:
## -0.6514056 -0.3852436
## sample estimates:
## mean difference
## -0.5183246
Auf den ursprünglichen Variablen sind immer noch die Personen mit fehlenden Werten enthalten. Trotzdem meldet die Funktion t.test() kein Problem. Was passiert hier also? Ein Indiz können uns die Freiheitsgrade bieten, die mit $n-1$ bestimmt werden. Hier wird deutlich, dass Personen mit fehlenden Werten auf einer der beiden Variablen einfach ignoriert werden. Aber man bekommt (außer der überraschend kleinen Freiheitsgrade im Vergleich zur Größe des Datensatzes) keine Warnung oder Fehlermeldung dazu. Hinsichtlich der Interpretation können wir aus dem Befehl folgende Ergebnisse entnehmen: $t$(190) = -7.68 mit einem zugehörigen p-Wert ($p < .01$). Da unser p-Wert unter dem festgelegten $\alpha$-Fehlerniveau liegt, verwerfen wir die $H_0$ und nehmen die $H_1$ an.
Schätzung des standardisierten Populationseffekts
Formel: $$\text{Cohen’s } d’’ = \frac{\bar{d}} {\hat{sd}_{d}}$$ wobei
- $\bar{d}$: Mittelwert der Differenz aller Wertepaare
- $\hat{sd}_{d}$: geschätzte SD der Differenzen
Wir führen die Berechnung von Cohen’s $d$ für abhängige Stichproben zunächst händisch durch. Dafür speichern wir die nötigen Größen ab und wenden dann die präsentierte Formel an:
mean_d <- mean(difference, na.rm = T)
sd.d.est <- sd(difference, na.rm = T)
d_Wert <- mean_d/sd.d.est
d_Wert
## [1] -0.5558943
Berechnung mit Funktion cohen.d()
if (!requireNamespace("effsize", quietly = TRUE)) {
install.packages("effsize")
}
library("effsize")
##
## Attaching package: 'effsize'
## The following object is masked from 'package:psych':
##
## cohen.d
d2 <- cohen.d(fb25$ru_post, fb25$ru_pre,
paired = TRUE, #paired steht fuer 'abhaengig'
within = FALSE, #wir brauchen nicht die Varianz innerhalb
na.rm = TRUE)
d2
##
## Cohen's d
##
## d estimate: -0.5558943 (medium)
## 95 percent confidence interval:
## lower upper
## -0.7087619 -0.4030266
Mit dem Argument within = T, was der Default ist, wird für die Varianzberechnung die Varianz innerhalb der Gruppen herangezogen (vergleiche Formel Cohen’s $d$ für unanghängige Stichproben). Neben der Punktschätzung der Effektstärke erhalten wir auch eine Einordnung über die Größe (large) und ein Konfidenzintervall.
Die Einordnung durch das Paket unterscheidet sich aber teils von den Konventionen nach Cohen (1988), die es auch für abhängige Stichproben gibt (Konventionen für den abhängigen und unabhängigen $t$-Test unterscheiden sich auch!). Die unterschiedlich Einordnung des Paketes zu der Tabelle macht nochmal deutlich, dass diese Konventionen nur grobe Orientierungen sind, die nur bei völliger Ahnungslosigkeit genutzt werden sollten und sonst Effekstärken im Rahmen des Anwendungsgebietes eingeordnet werden sollten.
| d’’ | Interpretation |
|---|---|
| ~ .14 | kleiner Effekt |
| ~ .35 | mittlerer Effekt |
| ~ .57 | großer Effekt |
Zusammenfassend lässt sich sagen: Der standardisierte Populationseffekt beträgt $d_2’’$ = -0.56 und ist laut Konventionen groß, laut der Aussage des Paketes auch large.
Ergebnisinterpretation
Bereits auf deskriptivstatistischer Ebene stellen wir einen Unterschied fest: Der Mittelwert der Differenzen zwischen ruhig und unruhig beträgt -0.52. Zur Beantwortung der Fragestellung wurde ein ungerichteter $t$-Test für abhängige Stichproben durchgeführt. Der Unterschied zwischen den beiden Messzeitpunkten ist signifikant ($t$(190) = -7.68, $p < .01$), somit wird die Nullhypothese verworfen. Dieser Unterschied ist nach dem standardisierten Populationseffekt von $d_2’’$ = -0.56 groß.
Medianvergleich für abhängige Stichprobe
Auch für die abhängigen Stichproben lernen wir wieder einen Test kennen, bei den es uns um den Vergleich von Medianen anstatt Mittelwerten gehen. Der präsentierte Wilcoxon-Vorzeichen-Rangtest ist eine Option, wenn wir eine stetige Variable haben, für die der Mittelwert keine sinnvolle Repräsentation der zentralen Tendenz darstellt. Ein häufiges Anwendungsbeispiel ist dabei die Antwortzeit von Proband:innen. Spezifisch haben wir sowohl bei der ersten Erhebung vor dem Praktikum als auch bei der zweiten Erhebung nach dem Praktikum die Zeit gemessen, die Sie für das Ausfüllen des MDBF benötigt haben. Wir möchten der Fragestellung, ob die Bearbeitungszeit sich zwischen den beiden Zeitpunkten unterscheidet nachgehen. Waren Sie bei der zweiten Erhebung schneller - bspw. weil Sie die Fragen schon kannten? Oder waren Sie bei der ersten Erhebung schneller, da Sie dort noch Energie hatten?
Deskriptivstatistik
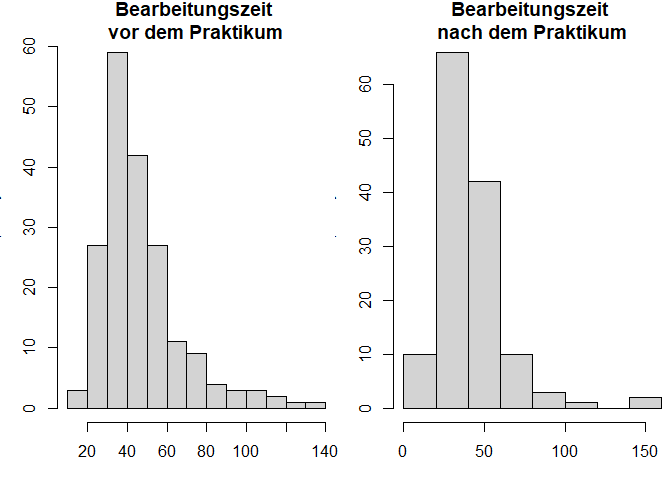
Schauen wir uns zunächst in der deskriptivstatistischen Betrachtung an, warum wir für die Bearbeitungszeit des MDBF einen Median- und keinen Mittelwertvergleich durchführen wollen. Dafür erstellen wir ein Histogramm für die Bearbeitungszeit vor und nach dem Praktikum.
par(mfrow=c(1,2), mar=c(3,3,2,0))
hist(fb25$time_pre,
main="Bearbeitungszeit \nvor dem Praktikum",
breaks = 10)
hist(fb25$time_post,
main="Bearbeitungszeit \nnach dem Praktikum",
breaks = 10)
par(mfrow=c(1,1)) #Zurücksetzen des Plotfensters
Die hier gefundenen Bearbeiungszeiten stellen ein typisches Bild für das Verhalten von Antwortzeiten dar. Es gibt eine große Anzahl an Personen, die relativ schnell antworten, aber auch einige Personen, die sehr lange brauchen. Die Verteilung ist daher linkssteil und rechtsschief. Der Median wird als besserer Repräsentant für die mittlere Ausprägung angesehen, da er weniger anfällig für die Schiefe ist.
Den Median und weitere deskriptive Statistiken können wir uns mit dem summary()-Befehl anzeigen lassen.
summary(fb25$time_pre)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 18.0 34.5 44.0 50.2 56.5 256.0
summary(fb25$time_post)
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 3.00 28.00 33.00 36.72 45.00 104.00 19
Es zeigt sich auch hier wieder, dass es nach dem Praktikum einige fehlende Werte gibt. Das heißt, dass unsere deskriptiven Betrachtungen nicht so aussagekräftig sind an dieser Stelle. Diese würde eine Veränderung in der mittleren Ausprägung der Bearbeitungszeit zeigen, da die Mediane sich unterscheiden.
Voraussetzungsprüfung
Bevor wir aber in die inferenzstatistische Betrachtung gehen, prüfen wir, ob wir zur Beantwortung der Fragestellung einen Wilcoxon-Vorzeichen-Rangtest verwenden können anhand der Voraussetzungen:
- die Messwerte innerhalb der Paare dürfen sich gegenseitig beeinflussen/voneinander abhängig sein; keine Abhängigkeiten zwischen den Messwertpaaren $\rightarrow$ ok
- die Variable ist stetig $\rightarrow$ ok
- die Differenzvariable ist hinsichtlich der Größe reliabel $\rightarrow$ bedeutet für uns, dass wir eine Intervallskalierung brauchen, damit die Differenzen zweier Messwertpaare vergleichbar sind
- die Differenzvariable ist symmetrisch verteilt (nicht notwendigerweise normalverteilt; ggf. grafische Prüfung oder Hintergrundwissen)
Die erste Voraussetzung nehmen wir, wie beschrieben, als gegeben an, da die Messwerte Prä und Post einer Messwiederholung entsprechen und zwischen den einzelnen Personen keine Abhängigkeiten bestehen sollten. Durch die Verwendung der Reaktionszeiten handelt es sich um eine stetige Variable. Hinsichtlich der Skalierung unserer Variable gehen wir davon aus, dass sie mindestens intervallskaliert ist. Diese Skalierung wird benötigt, da im ersten Schritt die Differenzen zwischen dem Prä- und dem Post-Wert berechnet wird.
Zuletzt bleibt noch die Voraussetzung, dass die Differenzvariable symmetrisch verteilt ist. Wir betrachten die Differenzwerte, indem wir zunächst einen Vektor mit dem Namen dif_time definieren, der die Differenzen aller Personen enthält. Anschließend schauen wir uns auch zu diesem Vektor das Histogramm an.
dif_time <- fb25$time_post - fb25$time_pre
hist(dif_time,
main="Differenzen Bearbeitungszeiten",
breaks = 10)
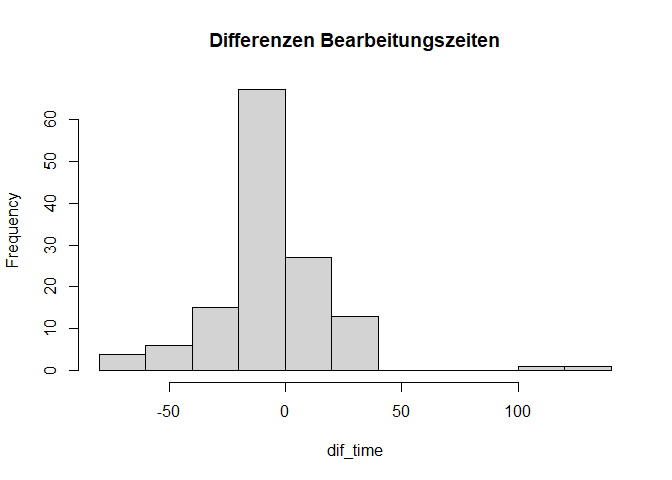
Die Differenzen weisen Abweichungen von der Symmetrie-Annahme vor, die vor allem von Ausreißern bestimmt wird. Die Verteilung der Differenzen ist aufgrund der hohen Anzahl negativer Differenzen und einiger negativer Ausreißer linksschief. Jedoch sind dies nur einzelne, wenige Fälle, weshalb wir die inferenzstatistische Testung trotzdem durchführen. Mehr Informationen zu Ausreißern und deren Behandlung erhalten Sie im nächsten Semester hier.
Durchführung des Wilcoxon-Vorzeichen-Rangtest für abhängige Stichproben
Aus unserer Fragestellung wird eine Unterschiedsyhpothese deutlich, die keine Richtung vorgibt - schließlich haben wir Überlegungen in beide Richtungen anstellen können. Das Hypothesenpaar sieht folgendermaßen aus:
- $H_0$: $\eta_\text{nach} = \eta_\text{vor}$
- $H_1$: $\eta_\text{nach} \ne \eta_\text{vor}$
Weiterhin muss das Signifikanzniveau vor der Untersuchung festgelegt werden. Es soll hier 5% betragen. $\rightarrow$ $\alpha=.05$.
Die Argumente der Funktion für den Wilcoxon-Vorzeichen-Rangsummentest für abhängige Stichproben sehen dem des $t$-Tests für abhängige Stichproben sehr ähnlich.
wilcox.test(x = fb25$time_pre,
y = fb25$time_post, # die beiden abhängigen Gruppen
paired = T, # Stichproben sind abhängig
alternative = "two.sided", # ungerichtete Hypothese
exact = F, # Approximation?
conf.level = .95) # alpha = .05
##
## Wilcoxon signed rank test with continuity correction
##
## data: fb25$time_pre and fb25$time_post
## V = 14748, p-value < 2.2e-16
## alternative hypothesis: true location shift is not equal to 0
Durch das Argument exact kann angegeben werden, ob man einen exakten p-Wert oder eine Approximation ausgeben lassen will – in spezifischen Konstellationen kann man diese Wahl treffen. Für Fälle mit Rangbindungen und Differenzen von 0 wird eine Approximation genutzt, die wir hier auch uns anzeigen lassen. Hinsichtlich der Signifikanzentscheidung ist aus dem Output ersichtlich, dass der empirische Wert bei V = 1.47485\times 10^{4} liegt und der zugehörige p-Wert bei $p < .01$. Wir würden dementsprechend die H0 verwerfen. Im Gegensatz zum $t$-Test fällt uns auch auf, dass kein Konfidenzintervall ausgegeben wird, was uns aber nicht weiter stört, da wir unsere Hypothesen prüfen konnten.
Ergebnisinterpretation
Da der Mittelwert für die Bearbeitungszeiten kein sinnvolles Maß für die zentrale Tendenz darstellt, wurde ein Wilcoxon-Vorzeichen-Rangtest für abhängige Stichproben durchgeführt, um die Mediane zu vergleichen. Zunächst findet sich deskriptiv ein Unterschied: Vor der Praktikum ist der Median der Bearbeiungszeit (44) anders als nach der Therapie (33). Der Unterschied wurde bei einem Signifikanzniveau von $\alpha = .05$ signifikant (V = 1.47485\times 10^{4}, $p$ < .01). Somit wird die Nullhypothese verworfen und es wird angenommen, dass sich die mittlere Bearbeitungszeit vor und nach dem Praktikum unterscheidet.
](/media/header/consent_checkbox.jpg)