Vorbereitung
Laden Sie zunächst den Datensatz
fb25von der pandar-Website. Alternativ können Sie die fertige R-Daten-Datei hier herunterladen. Beachten Sie in jedem Fall, dass die Ergänzungen im Datensatz vorausgesetzt werden, teils inklusive derer, die erst im Beitrag vorgenommen werden. Die Bedeutung der einzelnen Variablen und ihre Antwortkategorien können Sie dem Dokument Variablenübersicht entnehmen.
Datenaufbereitung
#### Was bisher geschah: ----
# Daten laden
load(url('https://pandar.netlify.app/daten/fb25.rda'))
# Nominalskalierte Variablen in Faktoren verwandeln
fb25$hand_factor <- factor(fb25$hand,
levels = 1:2,
labels = c("links", "rechts"))
fb25$fach <- factor(fb25$fach,
levels = 1:5,
labels = c('Allgemeine', 'Biologische', 'Entwicklung', 'Klinische', 'Diag./Meth.'))
fb25$ziel <- factor(fb25$ziel,
levels = 1:4,
labels = c("Wirtschaft", "Therapie", "Forschung", "Andere"))
fb25$wohnen <- factor(fb25$wohnen,
levels = 1:4,
labels = c("WG", "bei Eltern", "alleine", "sonstiges"))
fb25$fach_klin <- factor(as.numeric(fb25$fach == "Klinische"),
levels = 0:1,
labels = c("nicht klinisch", "klinisch"))
fb25$ort <- factor(fb25$ort, levels=c(1,2), labels=c("FFM", "anderer"))
fb25$job <- factor(fb25$job, levels=c(1,2), labels=c("nein", "ja"))
fb25$unipartys <- factor(fb25$uni3,
levels = 0:1,
labels = c("nein", "ja"))
# Rekodierung invertierter Items
fb25$mdbf4_r <- -1 * (fb25$mdbf4 - 4 - 1)
fb25$mdbf11_r <- -1 * (fb25$mdbf11 - 4 - 1)
fb25$mdbf3_r <- -1 * (fb25$mdbf3 - 4 - 1)
fb25$mdbf9_r <- -1 * (fb25$mdbf9 - 4 - 1)
fb25$mdbf5_r <- -1 * (fb25$mdbf5 - 4 - 1)
fb25$mdbf7_r <- -1 * (fb25$mdbf7 - 4 - 1)
# Berechnung von Skalenwerten
fb25$wm_pre <- fb25[, c('mdbf1', 'mdbf5_r',
'mdbf7_r', 'mdbf10')] |> rowMeans()
fb25$gs_pre <- fb25[, c('mdbf1', 'mdbf4_r',
'mdbf8', 'mdbf11_r')] |> rowMeans()
fb25$ru_pre <- fb25[, c("mdbf3_r", "mdbf6",
"mdbf9_r", "mdbf12")] |> rowMeans()
# z-Standardisierung
fb25$ru_pre_zstd <- scale(fb25$ru_pre, center = TRUE, scale = TRUE)
Aufgabe 1
Unterscheiden sich Studierende, die sich für Allgemeine Psychologie (Variable “fach”) interessieren, im Persönlichkeitsmerkmal Offenheit für neue Erfahrungen (auch Intellekt, “offen”) von Studierenden, die sich für Klinische Psychologie interessieren? Normalverteilung des Merkmals in der Population darf angenommen werden.
Lösung
Deskriptivstatistische Beantwortung der Fragestellung: grafisch
data1 <- fb25[ (which(fb25$fach=="Allgemeine"|fb25$fach=="Klinische")), ]
data1$fach <- droplevels(data1$fach)
boxplot(data1$offen ~ data1$fach,
xlab="Interessenfach", ylab="Offenheit für neue Erfahrungen",
las=1, cex.lab=1.5,
main="Interessenfach und Offenheit")
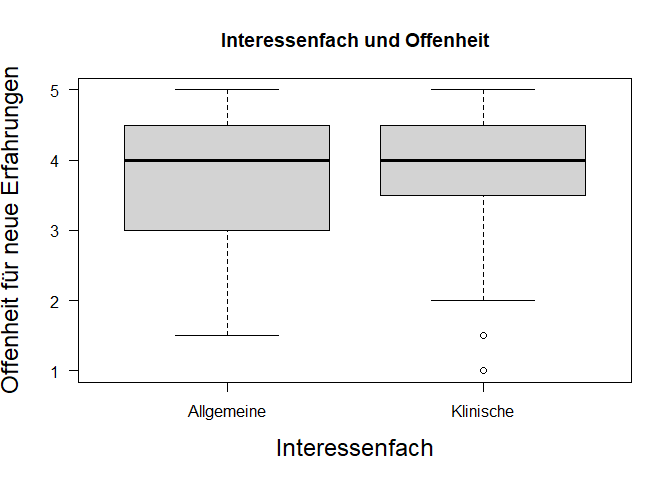
Deskriptivstatistische Beantwortung der Fragestellung: statistisch
# Überblick
library(psych)
describeBy(data1$offen, data1$fach)
##
## Descriptive statistics by group
## group: Allgemeine
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 32 3.81 0.93 4 3.85 1.48 2 5 3 -0.13 -1.28 0.16
## ------------------------------------------------------------------
## group: Klinische
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 93 3.91 0.95 4 4.01 0.74 1 5 4 -0.75 0.04 0.1
# Berechnung der empirischen Standardabweichung, da die Funktion describeBy() nur Populationsschätzer für Varianz und Standardabweichung berichtet
offen.A <- data1$offen[(data1$fach=="Allgemeine")]
sigma.A <- sd(offen.A)
n.A <- length(offen.A[!is.na(offen.A)])
sd.A <- sigma.A * sqrt((n.A-1) / n.A)
sd.A
## [1] 0.9164299
offen.B <- data1$offen[(data1$fach=="Klinische")]
sigma.B <- sd(offen.B)
n.B <- length(offen.B[!is.na(offen.B)])
sd.B <- sigma.B * sqrt((n.B-1) / n.B)
sd.B
## [1] 0.9464809
Mittelwert der Allgemeinen Psychologen (M = 3.81, SD = 0.92) unterscheidet sich deskriptivstatistisch vom Mittelwert der Klinischen (M = 3.91, SD = 0.95).
Voraussetzungsprüfung: Normalverteilung
Nicht nötig, da Normalverteilung in der Population angenommen werden darf (s. Aufgabenstellung).
Hypothesen
- Art des Effekts: Unterschiedshypothese
- Richtung des Effekts: Ungerichtet $\rightarrow$ ungerichtete Hypothesen
- Größe des Effekts: Unspezifisch
Hypthesenpaar (statistisch):
- $H_0$: $\mu_\text{Allgemeine} = \mu_\text{Klinische}$
- $H_1$: $\mu_\text{Allgemeine} \ne \mu_\text{Klinische}$
Spezifikation des Signifikanzniveaus
$\alpha = .05$
Voraussetzungsprüfung: Varianzhomogenität
library(car)
leveneTest(data1$offen ~ data1$fach)
## Levene's Test for Homogeneity of Variance (center = median)
## Df F value Pr(>F)
## group 1 0.0601 0.8068
## 123
levene <- leveneTest(data1$offen ~ data1$fach)
f <- round(levene$`F value`[1], 2)
p <- round(levene$`Pr(>F)`[1], 3)
F(1, 123) = 0.06, p = 0.807 $\rightarrow$ Das Ergebnis ist nicht signifikant, die $H_0$ wird beibehalten und Varianzhomogenität angenommen.
Durchführung des t-Tests
t.test(data1$offen ~ data1$fach, # abhängige Variable ~ unabhängige Variable
#paired = F, # Stichproben sind unabhängig
alternative = "two.sided", # zweiseitige Testung
var.equal = T, # Varianzhomogenität ist gegeben (-> Levene-Test)
conf.level = .95) # alpha = .05
##
## Two Sample t-test
##
## data: data1$offen by data1$fach
## t = -0.52315, df = 123, p-value = 0.6018
## alternative hypothesis: true difference in means between group Allgemeine and group Klinische is not equal to 0
## 95 percent confidence interval:
## -0.4854446 0.2824876
## sample estimates:
## mean in group Allgemeine mean in group Klinische
## 3.812500 3.913978
Formales Berichten des Ergebnisses
Es wurde untersucht, ob sich Studierende, die sich für Allgemeine Psychologie interessieren, im Persönlichkeitsmerkmal Offenheit für neue Erfahrungen von Studierenden, die sich für Klinische Psychologie interessieren, unterscheiden. Deskriptiv liegt ein solcher Unterschied vor: Die Mittelwerte betragen 3.81 (Allgemeine, SD = 0.92) und 3.91 (Klinische, SD = 0.95). Der entsprechende t-Test zeigt jedoch ein nicht signifikantes Ergebnis (t(df = 123, zweis.) = -0.52, p = 0.602). Die Nullhypothese konnte nicht verworfen werden und wird beibehalten. Die Studierenden sind im Persönlichkeitsmerkmal ‘Offenheit für neue Erfahrungen’ unabhängig davon, ob sie sich für Allgemeine Psychologie oder für Klinische Psychologie interessieren.
Aufgabe 2
Sind Studierende, die außerhalb von Frankfurt wohnen (“ort”), zufriedener im Leben (“lz”) als diejenigen, die innerhalb von Frankfurt wohnen?
Lösung
Deskriptivstatistische Beantwortung der Fragestellung: grafisch
boxplot(fb25$lz ~ fb25$ort,
xlab="Wohnort", ylab="Lebenszufriedenheit",
las=1, cex.lab=1.5,
main="Wohnort und Lebenszufriedenheit")

Deskriptivstatistische Beantwortung der Fragestellung: statistisch
library(psych)
describeBy(fb25$lz, fb25$ort)
##
## Descriptive statistics by group
## group: FFM
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 126 4.93 1.33 5.1 5.05 1.33 1 7 6 -0.76 -0.14 0.12
## ------------------------------------------------------------------
## group: anderer
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 81 4.88 1.27 5 4.98 1.19 1 6.8 5.8 -0.78 0.4 0.14
summary(fb25[which(fb25$ort=="FFM"), "lz"])
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.000 4.200 5.100 4.933 6.000 7.000
summary(fb25[which(fb25$ort=="anderer"), "lz"])
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.000 4.200 5.000 4.881 5.800 6.800
Der Mittelwert der Frankfurter:innen ist deskriptiv höher als der der Nicht-Frankfurter:innen. Der Median der Nicht-Frankfurter:innen und der Frankfurter:innen zeigt das gleiche Muster.
Voraussetzungsprüfung: Normalverteilung
par(mfrow=c(1,2))
lz.F <- fb25[which(fb25$ort=="FFM"), "lz"]
hist(lz.F, xlim=c(1,9), ylim=c(0,0.5), main="Lebenzufriedenheit\n(Frankfurter)", xlab="", ylab="", las=1, prob=T)
curve(dnorm(x, mean=mean(lz.F, na.rm=T), sd=sd(lz.F, na.rm=T)), col="red", lwd=2, add=T)
qqnorm(lz.F)
qqline(lz.F, col="red")
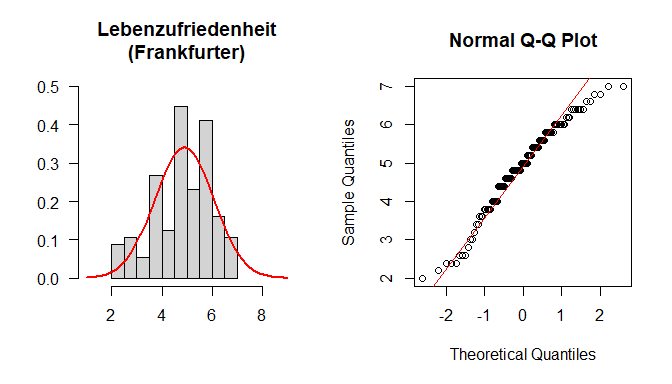
$\rightarrow$ Entscheidung: Normalverteilung wird nicht angenommmen
par(mfrow=c(1,2))
lz.a <- fb25[which(fb25$ort=="anderer"), "lz"]
hist(lz.a, xlim=c(1,9), main="Lebenszufriedenheit\n(Nicht-Frankfurter)", xlab="", ylab="", las=1, prob=T)
curve(dnorm(x, mean=mean(lz.a, na.rm=T), sd=sd(lz.a, na.rm=T)), col="red", lwd=2, add=T)
qqnorm(lz.a)
qqline(lz.a, col="red")

$\rightarrow$ Entscheidung: Normalverteilung wird nicht angenommmen
Hypothesen
- Art des Effekts: Unterschiedshypothese
- Richtung des Effekts: Gerichtet $\rightarrow$ gerichtete Hypothesen
- Größe des Effekts: Unspezifisch
Hypthesenpaar (statistisch):
- $H_0$: $\eta_\text{Frankfurter} \le \eta_\text{nicht-Frankfurter}$
- $H_1$: $\eta_\text{Frankfurter} > \eta_\text{nicht-Frankfurter}$
Spezifikation des Signifikanzniveaus
$\alpha = .05$
Durchführung des Wilcoxon-Tests
wilcox.test(fb25$lz ~ fb25$ort, # abhängige Variable ~ unabhängige Variable
#paired = F, # Stichproben sind unabhängig (Default)
alternative = "greater", # einseitige Testung: Gruppe1 (Frankfurter:innen) > Gruppe2 (Nicht-Frankfurter:innen)
conf.level = .95) # alpha = .05
##
## Wilcoxon rank sum test with continuity correction
##
## data: fb25$lz by fb25$ort
## W = 5320.5, p-value = 0.3026
## alternative hypothesis: true location shift is greater than 0
Formales Berichten des Ergebnisses
Es wurde untersucht, ob in Frankfurt wohnende Studierende zufriedener im Leben sind als die außerhalb von Frankfurt wohnenden. Deskriptiv zeigt sich, dass die Frankfurter:innen zufriedener sind (Mdn = 5.1, IQB = [4.2 ; 6]) als die Nicht-Frankfurter:innen (Mdn = 5, IQB = [4.2 ; 5.8]). Der entsprechende Wilcoxon-Test zeigt ein nicht signifikantes Ergebnis (W = 5320.5, p = 0.303). Die Nullhypothese konnte nicht verworfen werden und wird beibehalten. Die Studierenden sind gleich zufrieden, unabhängig von ihrem Wohnort.
Aufgabe 3
Ist die Wahrscheinlichkeit dafür, neben dem Studium einen Job (“job”) zu haben, die gleiche für Erstsemesterstudierende der Psychologie die in einer Wohngemeinschaft wohnen wie für Studierenden die bei ihren Eltern wohnen (“wohnen”)?
Lösung
Beide Variablen sind nominalskaliert $\rightarrow \chi^2$-TestVoraussetzungen
- Die einzelnen Beobachtungen sind voneinander unabhängig $\rightarrow$ ok
- Jede Person lässt sich eindeutig einer Kategorie bzw. Merkmalskombination zuordnen $\rightarrow$ ok
- Zellbesetzung für alle $n_{ij}$ > 5 $\rightarrow$ Prüfung anhand von Häufigkeitstabelle
wohnsituation <- fb25[(which(fb25$wohnen=="WG"|fb25$wohnen=="bei Eltern")),] # Neuer Datensatz der nur Personen beinhaltet, die entweder bei den Eltern oder in einer WG wohnen
levels(wohnsituation$wohnen)
## [1] "WG" "bei Eltern" "alleine" "sonstiges"
wohnsituation$wohnen <- droplevels(wohnsituation$wohnen)
# Levels "alleine" und "sonstiges" wurden eliminiert
levels(wohnsituation$wohnen)
## [1] "WG" "bei Eltern"
tab <- table(wohnsituation$wohnen, wohnsituation$job)
tab
##
## nein ja
## WG 36 29
## bei Eltern 42 16
$\rightarrow n_{ij}$ > 5 in allen Zellen gegeben
Hypothesen
- Art des Effekts: Zusammenhangshypothese
- Richtung des Effekts: Ungerichtet
- Größe des Effekts: Unspezifisch
Hyothesenpaar (inhaltlich):
- $H_0$: Studierende die in einer WG wohnen und Studierende die bei ihren Eltern wohnen haben mit gleicher Wahrscheinlichkeit einen Job bzw. keinen Job.
- $H_1$: Studierende die in einer WG wohnen und Studierende die bei ihren Eltern wohnen unterscheiden sich in der Wahrscheinlichkeit einen Job bzw. keinen Job neben dem Studium zu haben.
Hypothesenpaar (statistisch):
- $H_0$: $\pi_{ij} = \pi_{i\bullet} \cdot \pi_{\bullet j}$
- $H_1$: $\pi_{ij} \neq \pi_{i\bullet} \cdot \pi_{\bullet j}$
Durchführung des $\chi^2$-Test in R
chisq.test(tab, correct=FALSE)
##
## Pearson's Chi-squared test
##
## data: tab
## X-squared = 3.8311, df = 1, p-value = 0.05031
$\chi^2$ = 3.831, df = 1, p = 0.05 $\rightarrow H_0$
Effektstärke Phi ($\phi$)
library(psych)
phi(tab)
## [1] -0.18
Ergebnisinterpretation
Es wurde untersucht, ob sich Studierende die in einer WG wohnen und Studierende die bei ihren Eltern wohnen darin unterscheiden, ob sie einen Job haben oder nicht (Job vs. kein Job). Zur Beantwortung der Fragestellung wurde ein Vierfelder-Chi-Quadrat-Test für unabhängige Stichproben berechnet. Der Zusammenhang zwischen Wohnsituation und Berufstätigkeit ist nicht signifikant ($\chi^2$(1) = 3.831, p = 0.05), somit wird die Nullhypothese beibehalten. Der Effekt ist von vernachlässigbarer Stärke ($\phi$ = -0.18). Studierende die in einer WG wohnen und Studierende die bei ihren Eltern wohnen haben also mit gleicher Wahrscheinlichkeit einen Job bzw. keinen Job.
](/media/header/writing_math.jpg)