Vorbereitung
Laden Sie zunächst den Datensatz
fb25von der pandar-Website. Alternativ können Sie die fertige R-Daten-Datei hier herunterladen. Beachten Sie in jedem Fall, dass die Ergänzungen im Datensatz vorausgesetzt werden. Die Bedeutung der einzelnen Variablen und ihre Antwortkategorien können Sie dem Dokument Variablenübersicht entnehmen.
Prüfen Sie zur Sicherheit, ob alles funktioniert hat:
dim(fb25)
## [1] 211 56
names(fb25)
## [1] "mdbf1" "mdbf2" "mdbf3" "mdbf4" "mdbf5" "mdbf6"
## [7] "mdbf7" "mdbf8" "mdbf9" "mdbf10" "mdbf11" "mdbf12"
## [13] "time_pre" "lz" "extra" "vertr" "gewis" "neuro"
## [19] "offen" "prok" "trust" "uni1" "uni2" "uni3"
## [25] "uni4" "sicher" "angst" "fach" "ziel" "wissen"
## [31] "therap" "lerntyp" "hand" "job" "ort" "ort12"
## [37] "wohnen" "attent_pre" "gs_post" "wm_post" "ru_post" "time_post"
## [43] "attent_post" "hand_factor" "fach_klin" "unipartys" "mdbf4_r" "mdbf11_r"
## [49] "mdbf3_r" "mdbf9_r" "mdbf5_r" "mdbf7_r" "wm_pre" "gs_pre"
## [55] "ru_pre" "ru_pre_zstd"
Der Datensatz besteht aus 211 Zeilen (Beobachtungen) und 56 Spalten (Variablen). Falls Sie bereits eigene Variablen erstellt haben, kann die Spaltenzahl natürlich abweichen.
Aufgabe 1
Das Paket psych enthält vielerlei Funktionen, die für die Analyse von Datensätzen aus psychologischer Forschung praktisch sind. Eine von ihnen (describe()) erlaubt es, gleichzeitig verschiedene Deskriptivstatistiken für Variablen zu erstellen.
- Installieren (falls noch nicht geschehen) und laden Sie das Paket
psych. - Nutzen Sie den neugewonnen Befehl
describe(), um sich gleichzeitig die verschiedenen Deskriptivstatistiken für Lebenszufriedenheit (lz) ausgeben zu lassen.
Lösung
# Paket installieren
install.packages('psych')
# Paket laden
library(psych)
- Nutzen Sie den neugewonnen Befehl
describe(), um sich gleichzeitig die verschiedenen Deskriptivstatistiken für Lebenszufriedenheit (lz) ausgeben zu lassen.
Lösung
describe(fb25$lz)
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 210 4.89 1.32 5 5.01 1.48 1 7 6 -0.78 0.12 0.09
- Die Funktion
describeBy()ermöglicht außerdem Deskriptivstatistiken in Abhängigkeit einer gruppierenden Variable auszugeben. Machen Sie sich diesen Befehl zunutze, um sich die Lebenszufriedenheit (lz) abhängig von der derzeitigen Wohnsituation (wohnen) anzeigen zu lassen.
Lösung
describeBy(fb25$lz, group = fb25$wohnen)
##
## Descriptive statistics by group
## group: WG
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 65 5 1.42 5.4 5.09 1.48 1.4 7 5.6 -0.55 -0.74 0.18
## ------------------------------------------------------------------
## group: bei Eltern
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 59 4.98 1.12 5 5.04 1.19 1.8 7 5.2 -0.51 -0.16 0.15
## ------------------------------------------------------------------
## group: alleine
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 55 4.79 1.32 5 4.96 1.19 1 6.6 5.6 -1.14 0.69 0.18
## ------------------------------------------------------------------
## group: sonstiges
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 26 4.76 1.42 5 4.85 1.04 1.4 6.8 5.4 -0.72 -0.39 0.28
describe()kann auch genutzt werden, um gleichzeitig Deskriptivstatistiken für verschiedene Variablen zu berechnen. Nutzen Sie diese Funktionalität, um sich gleichzeitg die univariaten Deskriptivstatistiken für die fünf Persönlichkeitsdimensionen ausgeben zu lassen.
Lösung
describe(fb25[,c("extra","vertr","gewis","neuro","offen")])
## vars n mean sd median trimmed mad min max range skew kurtosis se
## extra 1 210 3.38 0.97 3.5 3.41 0.74 1.0 5 4.0 -0.29 -0.65 0.07
## vertr 2 211 3.51 0.82 3.5 3.55 0.74 1.5 5 3.5 -0.35 -0.45 0.06
## gewis 3 211 3.60 0.79 3.5 3.61 0.74 2.0 5 3.0 -0.10 -0.80 0.05
## neuro 4 211 3.19 0.99 3.0 3.21 1.48 1.0 5 4.0 -0.15 -0.67 0.07
## offen 5 211 3.92 0.89 4.0 4.01 0.74 1.0 5 4.0 -0.69 0.02 0.06
Aufgabe 2
In der Befragung am Anfang des Semesters wurde gefragt, ob Sie neben der Uni einen Nebenjob (job) ausüben und mit welcher Hand sie primär schreiben (hand). Erstellen Sie für diese beiden Variablen eine Kreuztabelle mit Randsummen.
- Stellen Sie zunächst sicher, dass die Variablen als Faktoren vorliegen und die Kategorien beider Variablen korrekt bezeichnet sind.
Lösung
Zunächst können wir überprüfen, ob die Variablen als Faktor vorliegen.
#Labels
is.factor(fb25$job)
## [1] TRUE
is.factor(fb25$hand)
## [1] FALSE
Wenn Sie die Datensatzvorbereitung aus dem Skript kopiert haben, sollte die Variable job bereits ein Faktor sein.
Die Variable hand jedoch nicht. Dies müssen wir ändern.
fb25$hand <- factor(fb25$hand,
levels = c(1, 2),
labels = c("links", "rechts"))
Für den Fall, dass die Variable job noch nicht als Faktor im Datensatz vorliegt, kann folgender Code durchgeführt werden. Achten Sie aber drauf, dass dieser Befehl auf eine Variable nicht angewendet werden sollte, wenn diese bereits ein Faktor ist. Ansonsten kommt es zu dem Fehler, dass die Variable keine Informationen mehr enthält.
fb25$job <- factor(fb25$job, levels = c(1, 2),
labels = c('nein', 'ja'))
Die Variablen sehen dann folgendermaßen aus.
str(fb25$job)
## Factor w/ 2 levels "nein","ja": 2 1 2 2 1 1 1 1 2 2 ...
str(fb25$hand)
## Factor w/ 2 levels "links","rechts": 2 2 2 2 2 2 2 2 1 2 ...
- Wie viele Personen sind Linkshänder und haben keinen Nebenjob?
Lösung
# Kreuztabelle absolut
tab <- table(fb25$hand, fb25$job)
addmargins(tab)
##
## nein ja Sum
## links 14 3 17
## rechts 117 66 183
## Sum 131 69 200
14 Personen schreiben primär mit der linken Hand und haben keinen Nebenjob.
- Was ist der relative Anteil aller Teilnehmenden, die einem Nebenjob nachgehen?
Lösung
# Relative Häufigkeiten, mit Randsummen
addmargins(prop.table(tab))
##
## nein ja Sum
## links 0.070 0.015 0.085
## rechts 0.585 0.330 0.915
## Sum 0.655 0.345 1.000
34.5% aller Teilnehmenden gehen einer Nebentätigkeit nach.
- Berechnen Sie nun mit Hilfe des
psych-Pakets die Korrelationskoeffizienten Phi ($\phi$) und Yules Q für das oben genannte Beispiel.
Lösung
phi(tab, digits = 3)
## [1] 0.108
Yule(tab) |> round(digits = 3) #da die Yule()-Funktion nicht direkt runden kann geben wir das Ergebnis an die round()-Funktion weiter
## [1] 0.449
Beide Koeffizienten sprechen für eine wenn überhaupt schwache Korrelation.
Aufgabe 3
Welche der fünf Persönlichkeitsdimensionen Extraversion (extra), Verträglichkeit (vertr), Gewissenhaftigkeit (gewis), Neurotizismus (neuro) und Offenheit für neue Erfahrungen (offen) ist am stärksten mit der Lebenszufriedenheit korreliert (lz)?
- Überprüfen Sie die Voraussetzungen für die Pearson-Korrelation.
Lösung
Voraussetzungen Pearson-Korrelation:
- Skalenniveau: intervallskalierte Daten $\rightarrow$ ok\
- Linearität: Zusammenhang muss linear sein $\rightarrow$ Grafische überprüfung (Scatterplot)
# Scatterplot
plot(fb25$extra, fb25$lz,
xlim = c(0, 6), ylim = c(0, 7), pch = 19)
plot(fb25$vertr, fb25$lz,
xlim = c(0, 6), ylim = c(0, 7), pch = 19)
plot(fb25$gewis, fb25$lz,
xlim = c(0, 6), ylim = c(0, 7), pch = 19)
plot(fb25$neuro, fb25$lz,
xlim = c(0, 6), ylim = c(0, 7), pch = 19)
plot(fb25$offen, fb25$lz,
xlim = c(0, 6), ylim = c(0, 7), pch = 19)
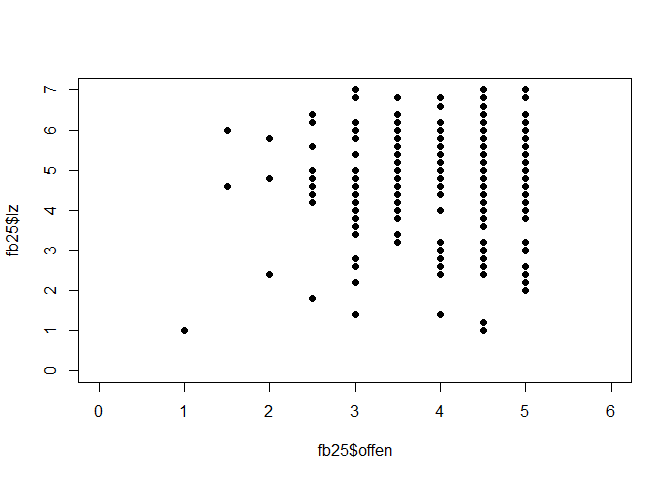
Die fünf Scatterplots lassen allesamt auf einen linearen Zusammenhang zwischen den Variablen schließen.
- Normalverteilung $\rightarrow$ QQ-Plot, Histogramm oder Shapiro-Wilk-Test
#QQ
qqnorm(fb25$extra)
qqline(fb25$extra)
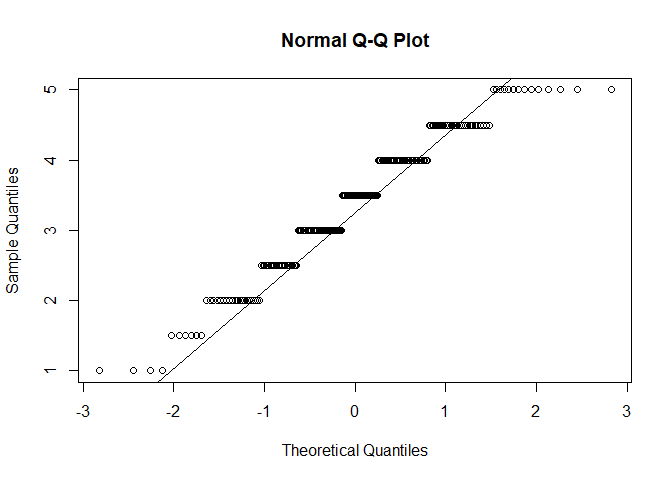
qqnorm(fb25$vertr)
qqline(fb25$vertr)
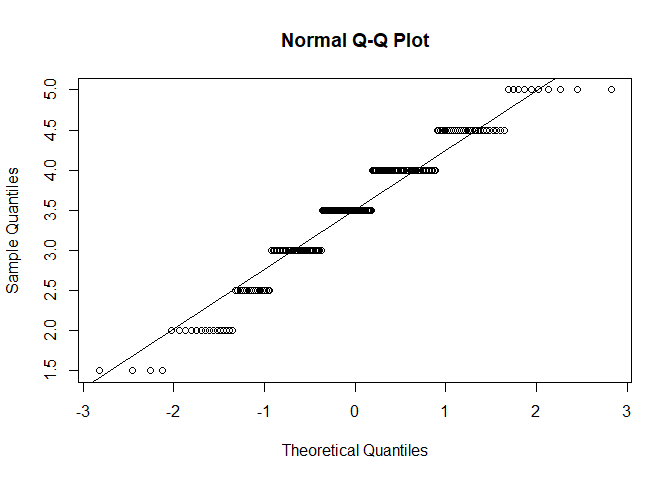
qqnorm(fb25$gewis)
qqline(fb25$gewis)
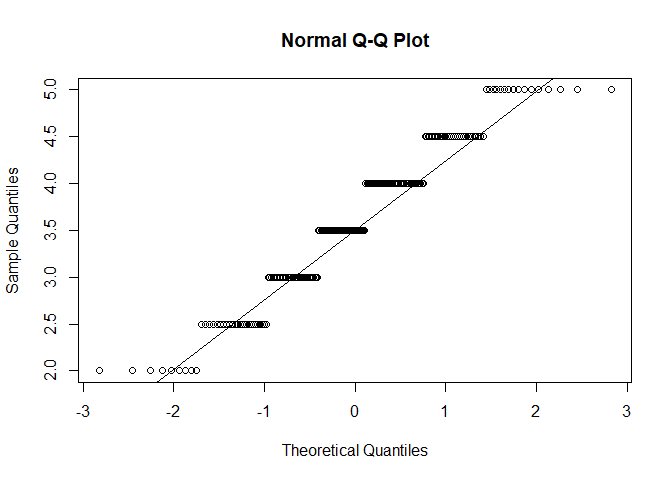
qqnorm(fb25$neuro)
qqline(fb25$neuro)
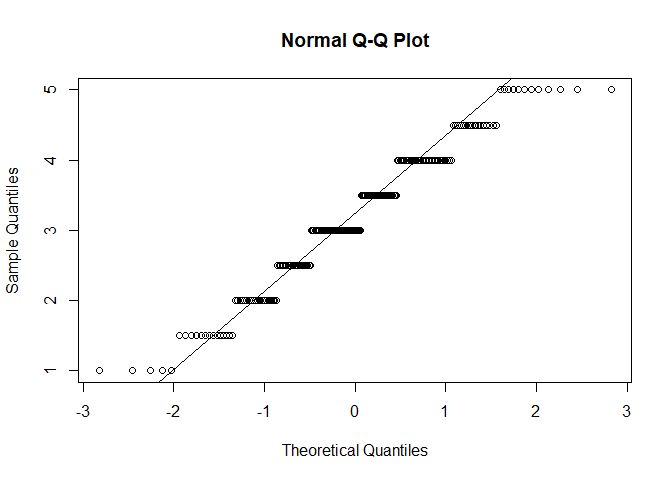
qqnorm(fb25$offen)
qqline(fb25$offen)
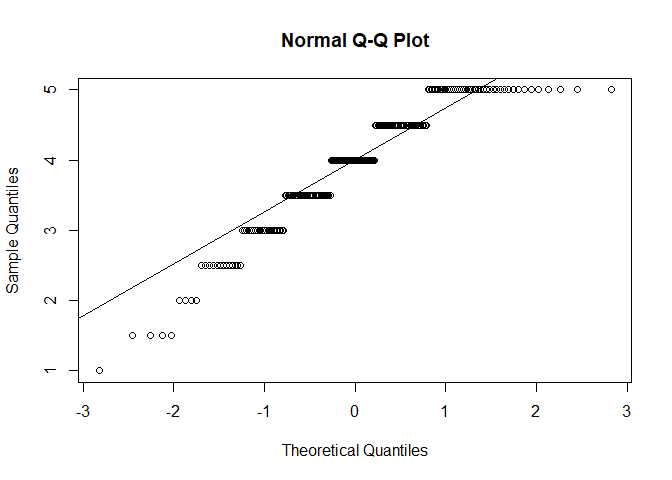
qqnorm(fb25$lz)
qqline(fb25$lz)
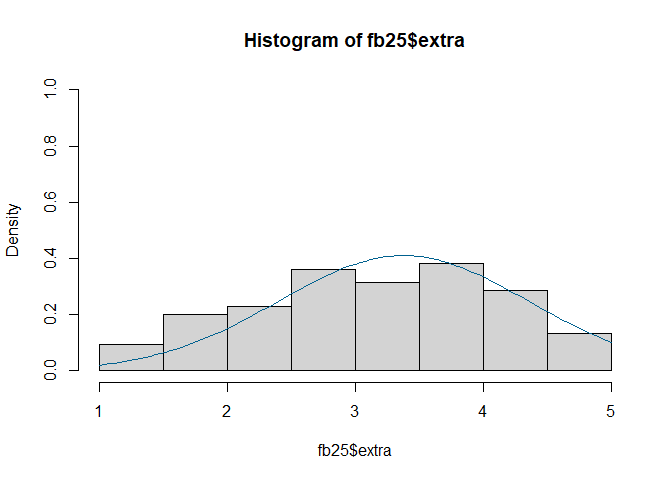
#Histogramm
hist(fb25$extra, prob = TRUE, ylim = c(0, 1))
curve(dnorm(x, mean = mean(fb25$extra, na.rm = TRUE), sd = sd(fb25$extra, na.rm = TRUE)), col = "#00618F", add = TRUE)
hist(fb25$vertr, prob = TRUE, ylim = c(0, 1))
curve(dnorm(x, mean = mean(fb25$vertr, na.rm = TRUE), sd = sd(fb25$vertr, na.rm = TRUE)), col = "#00618F", add = TRUE)
hist(fb25$gewis, prob = TRUE, ylim = c(0, 1))
curve(dnorm(x, mean = mean(fb25$gewis, na.rm = TRUE), sd = sd(fb25$gewis, na.rm = TRUE)), col = "#00618F", add = TRUE)
hist(fb25$neuro, prob = TRUE, ylim = c(0, 1))
curve(dnorm(x, mean = mean(fb25$neuro, na.rm = TRUE), sd = sd(fb25$neuro, na.rm = TRUE)), col = "#00618F", add = TRUE)
hist(fb25$offen, prob = TRUE, ylim = c(0, 1))
curve(dnorm(x, mean = mean(fb25$offen, na.rm = TRUE), sd = sd(fb25$offen, na.rm = TRUE)), col = "#00618F", add = TRUE)
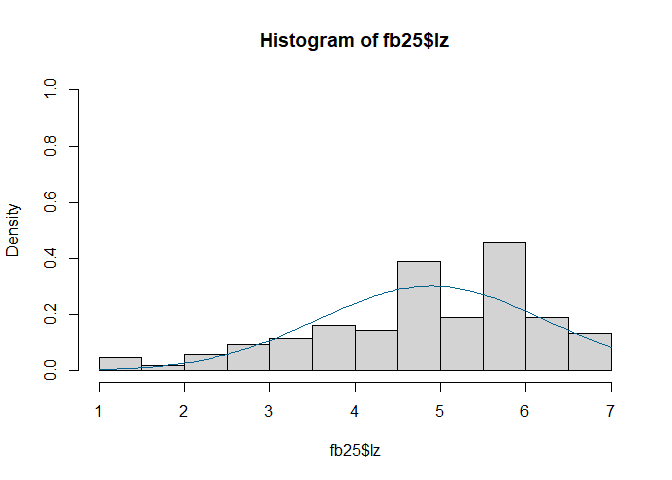
hist(fb25$lz, prob = TRUE, ylim = c(0, 1))
curve(dnorm(x, mean = mean(fb25$lz, na.rm = TRUE), sd = sd(fb25$lz, na.rm = TRUE)), col = "#00618F", add = TRUE)
#Shapiro
shapiro.test(fb25$extra)
##
## Shapiro-Wilk normality test
##
## data: fb25$extra
## W = 0.95659, p-value = 5.236e-06
shapiro.test(fb25$vertr)
##
## Shapiro-Wilk normality test
##
## data: fb25$vertr
## W = 0.95088, p-value = 1.284e-06
shapiro.test(fb25$gewis)
##
## Shapiro-Wilk normality test
##
## data: fb25$gewis
## W = 0.94854, p-value = 7.546e-07
shapiro.test(fb25$neuro)
##
## Shapiro-Wilk normality test
##
## data: fb25$neuro
## W = 0.96305, p-value = 2.605e-05
shapiro.test(fb25$offen)
##
## Shapiro-Wilk normality test
##
## data: fb25$offen
## W = 0.91578, p-value = 1.369e-09
shapiro.test(fb25$lz)
##
## Shapiro-Wilk normality test
##
## data: fb25$lz
## W = 0.94472, p-value = 3.444e-07
$p < \alpha$ $\rightarrow$ H1: Normalverteilung kann für alle Variablen nicht angenommen werden. Somit ist diese Voraussetzung für alle Variablen verletzt. Daher sollten wir fortlaufend die Rangkorrelation nach Spearman nutzen.
- Erstellen Sie für diese Frage eine Korrelationsmatrix, die alle Korrelationen enthält. Verwenden Sie die Funktion
round()(unter Betrachtung der Hilfe), um die Werte auf zwei Nachkommastellen zu runden und die Tabelle dadurch übersichtlicher darzustellen.
Lösung
# Korrelationstabelle erstellen und runden
cor_mat <- round(cor(fb25[,c('lz', 'extra', 'vertr', 'gewis', 'neuro', 'offen')],
use = 'pairwise',
method = 'spearman'),3)
cor_mat
## lz extra vertr gewis neuro offen
## lz 1.000 0.305 0.226 0.189 -0.240 0.095
## extra 0.305 1.000 0.065 0.031 -0.411 0.143
## vertr 0.226 0.065 1.000 0.133 -0.032 0.064
## gewis 0.189 0.031 0.133 1.000 0.106 0.029
## neuro -0.240 -0.411 -0.032 0.106 1.000 -0.026
## offen 0.095 0.143 0.064 0.029 -0.026 1.000
- Wie würden Sie das Ausmaß der betragsmäßig größten Korrelation mit der Lebenszufriedenheit nach den Richtlinien von Cohen (1988) einschätzen?
Lösung
Die betragsmäßig größte Korrelation mit der Lebenszufriedenheit hat der Neurotizismus. Nach den Richtlinien ist dieser mit 0.189 einem negativen mittleren Effekt, der ungefähr 0.3 beträgt, zuzuordnen.
- Ist der Korrelationskoeffizient von Lebenszufriedenheit und Neurotizismus statistisch signifikant?
Lösung
cor.test(fb25$lz, fb25$neuro,
alternative = "two.sided",
method = "spearman",
use = "pairwise")
## Warning in cor.test.default(fb25$lz, fb25$neuro, alternative = "two.sided", : Kann
## exakten p-Wert bei Bindungen nicht berechnen
##
## Spearman's rank correlation rho
##
## data: fb25$lz and fb25$neuro
## S = 1914429, p-value = 0.0004418
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
## rho
## -0.240345
$p < \alpha$ $\rightarrow$ H1. Die Korrelation ist mit einer Irrtumswahrscheinlichkeit von 5% signifikant von 0 verschieden.
Aufgabe 4
Untersuchen Sie die Korrelation zwischen Gewissenhaftigkeit (gewis) und Prokrastinationstendenz (prok). Berechnen Sie dafür ein geeignetes Korrelationsmaß und testen Sie dieses auf Signifikanz.
Lösung
Um das geeignete Korrelationsmaß zu bestimmen überprüfen wir zunächst die Vorrausetzungen der Pearson-Korrelation:
- Skalenniveau: intervallskalierte Daten $\rightarrow$ ok\
- Linearität: Zusammenhang muss linear sein $\rightarrow$ Grafische überprüfung (Scatterplot)
# Scatterplot
plot(fb25$gewis, fb25$prok,
xlim = c(0, 6), ylim = c(0, 7), pch = 19)
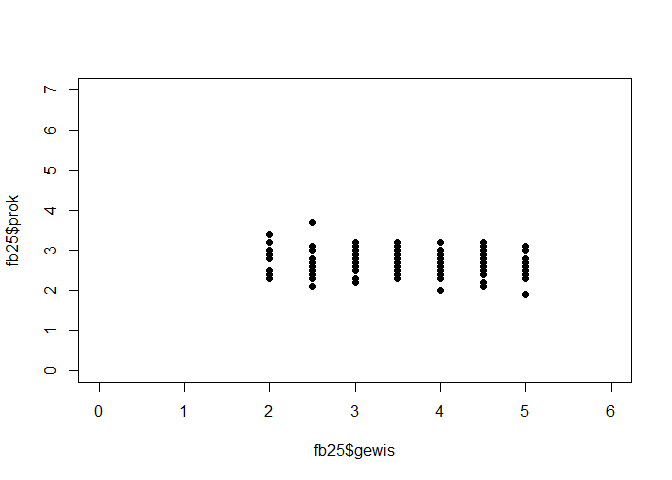
Es ist kein klarer linearer Zusammenhang zwischen gewis und prok zu erkennen.
Gleichzeitig ist keine andere Art des Zusammenhangs (polynomial, exponentiell etc.) offensichtlich. Daher gehen wir für diese Aufgabe, um im Rahmen des Erstsemester Statistik Praktikums zu bleiben, davon aus dass die Vorraussetzung der Linearität erfüllt ist.
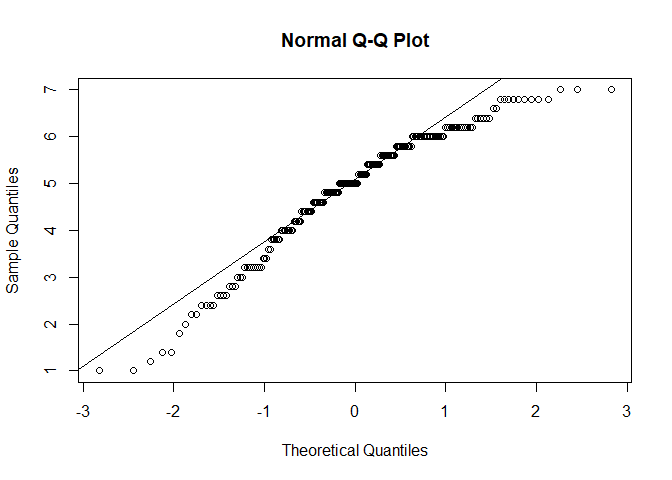
- Normalverteilung $\rightarrow$ QQ-Plot, Histogramm oder Shapiro-Wilk Test
#Car-Paket laden
library(car)
#QQ-Plot
qqPlot(fb25$gewis)
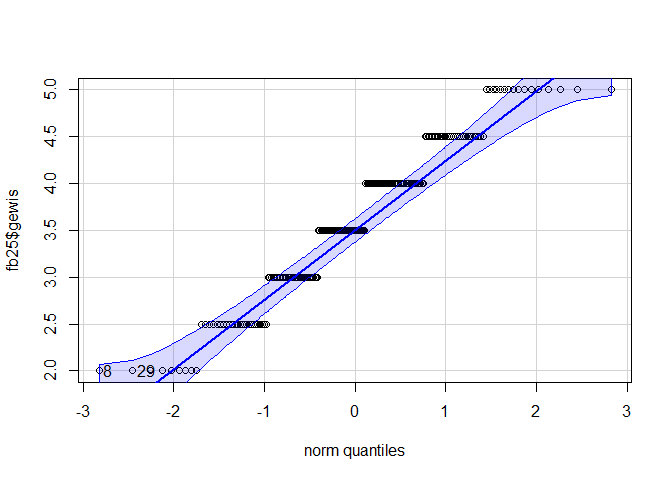
## [1] 8 29
qqPlot(fb25$prok)
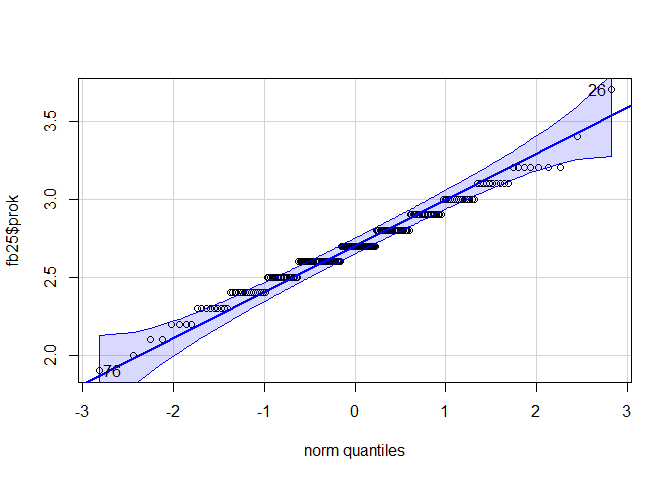
## [1] 26 76
#Histogramm
hist(fb25$gewis, prob = TRUE, ylim = c(0, 1))
curve(dnorm(x, mean = mean(fb25$gewis, na.rm = TRUE), sd = sd(fb25$gewis, na.rm = TRUE)), col = "#00618F", add = TRUE)
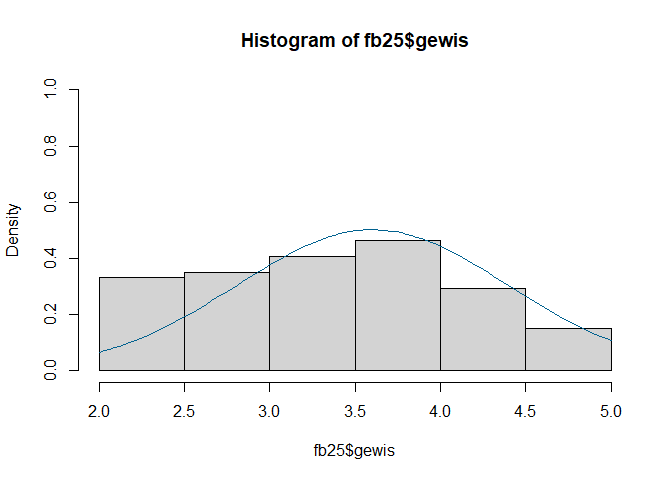
hist(fb25$prok, prob = TRUE, ylim = c(0, 1))
curve(dnorm(x, mean = mean(fb25$prok, na.rm = TRUE), sd = sd(fb25$prok, na.rm = TRUE)), col = "#00618F", add = TRUE)
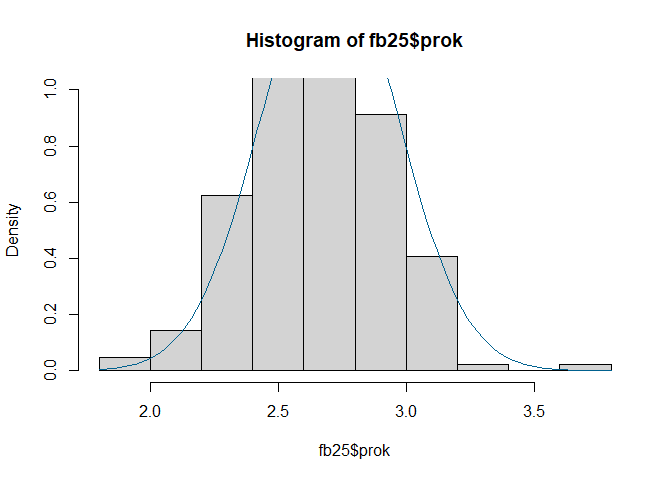
#Shapiro-Wilk Test
shapiro.test(fb25$gewis) #signifikant
##
## Shapiro-Wilk normality test
##
## data: fb25$gewis
## W = 0.94854, p-value = 7.546e-07
shapiro.test(fb25$prok) #signifikant
##
## Shapiro-Wilk normality test
##
## data: fb25$prok
## W = 0.98261, p-value = 0.01142
Auf Basis der zwei graphischen und dem inferenzstatistischen Verfahren kommen wir zum Schluss das beide Variablen nicht normalverteilt vorliegen.
Somit kommen wir zum Schluss das die Spearman-Rangkorrelation hier das richtige Korrelationsmaß ist.
cor.test(fb25$gewis, fb25$prok,
alternative = "two.sided",
method = "spearman",
use = "pairwise")
## Warning in cor.test.default(fb25$gewis, fb25$prok, alternative = "two.sided", : Kann
## exakten p-Wert bei Bindungen nicht berechnen
##
## Spearman's rank correlation rho
##
## data: fb25$gewis and fb25$prok
## S = 1563827, p-value = 0.5403
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
## rho
## -0.04270148
## Warning in cor.test.default(fb25$gewis, fb25$prok, alternative = "two.sided", : Kann
## exakten p-Wert bei Bindungen nicht berechnen
Die Spearman-Rangkorrelation (p = 0.5402615) ist nicht signifikant von 0 verschieden.
Aufgabe 5 Bonus
Im vorherigen Kapitel haben wir die Poweranalyse behandelt. Solche Analysen kann man auch für Korrelationen vornehmen. Frischen Sie gerne Ihren Wissensstand hier noch einmal auf.
Daher, führen sie mit Hilfe des Pakets WebPower eine Sensitivitätsanalyse für den Datensatz fb25 unter folgenden Parametern durch:
- Fehler 1. Art ($\alpha = 5%$)
- Fehler 2. Art ($\beta = 20%$)
- Alternativhypothese ($H_1$: $\rho_1 \neq 0$)
Lösung
Bei einer Sensitivitätsanalyse interessiert uns wie stark ein Effekt sein muss damit wir ihn gegeben der Stichprobengröße (n) und $\alpha$-Fehlerniveau mit einer Wahrscheinlichkeit (Power = 1 - $\beta$) finden. Einfach gesagt, gesucht ist die aufdeckbare Effektstärke. Außerdem sind Korrelationen ihre eigenen Effektgrößen, daher müssen wir nicht noch etwa Cohens d berechnen.
library(WebPower)
wp.correlation(n = nrow(fb25),
r = NULL, #gesucht
power = 0.8, #Power = 1 - Beta
alternative = "two.sided") #leitet sich aus der H1 ab
## Power for correlation
##
## n r alpha power
## 211 0.1913989 0.05 0.8
##
## URL: http://psychstat.org/correlation
Gegeben es gibt eine von null verschiedene (signifikante) Pearson-Korrelation muss diese mindestens 0.191 groß sein, damit wir diese mit einer Power von 80%, auf einem $\alpha$-Fehlerniveau von 5% in unserem Datensatz, mit n = 211 finden könnten.
](/media/header/storch_with_baby.jpg)