Korrelation
Kernfragen dieser Lehreinheit
- Welche zwei Varianten gibt es, Varianzen und Kovarianzen zu bestimmen?
- Wie kann die Produkt-Moment-Korrelation, die Rang-Korrelation nach Spearman und Kendalls $\tau$ bestimmt werden?
- Wie wird bei der Berechnung von Korrelationen mit fehlenden Werten umgegangen?
- Wie können Kreuztabellen in R erstellt werden? Welche Varianten gibt es, relative Häufigkeitstabellen zu erstellen?
- Wie kann ein gemeinsames Balkendiagramm für zwei Variablen erstellt werden?
- Wie lässt sich der Zusammenhang zweier dichotomer (nominaler) Variablen berechnen?
Vorbereitende Schritte
Den Datensatz fb25 haben wir bereits über diesen Link heruntergeladen und können ihn über den lokalen Speicherort einladen oder Sie können Ihn direkt mittels des folgenden Befehls aus dem Internet in das Environment bekommen. In den vorherigen Tutorials und den dazugehörigen Aufgaben haben wir bereits Änderungen am Datensatz durchgeführt, die hier nochmal aufgeführt sind, um den Datensatz auf dem aktuellen Stand zu haben:
#### Was bisher geschah: ----
# Daten laden
load(url('https://pandar.netlify.app/daten/fb25.rda'))
# Nominalskalierte Variablen in Faktoren verwandeln
fb25$hand_factor <- factor(fb25$hand,
levels = 1:2,
labels = c("links", "rechts"))
fb25$fach <- factor(fb25$fach,
levels = 1:5,
labels = c('Allgemeine', 'Biologische', 'Entwicklung', 'Klinische', 'Diag./Meth.'))
fb25$ziel <- factor(fb25$ziel,
levels = 1:4,
labels = c("Wirtschaft", "Therapie", "Forschung", "Andere"))
fb25$wohnen <- factor(fb25$wohnen,
levels = 1:4,
labels = c("WG", "bei Eltern", "alleine", "sonstiges"))
fb25$ort <- factor(fb25$ort,
levels=c(1,2),
labels=c("FFM", "anderer"))
fb25$job <- factor(fb25$job,
levels=c(1,2),
labels=c("nein", "ja"))
# Rekodierung invertierter Items
fb25$mdbf4_r <- -1 * (fb25$mdbf4 - 5)
fb25$mdbf11_r <- -1 * (fb25$mdbf11 - 5)
fb25$mdbf3_r <- -1 * (fb25$mdbf3 - 5)
fb25$mdbf9_r <- -1 * (fb25$mdbf9 - 5)
# Berechnung von Skalenwerten
fb25$gs_pre <- fb25[, c('mdbf1', 'mdbf4_r',
'mdbf8', 'mdbf11_r')] |> rowMeans()
fb25$ru_pre <- fb25[, c("mdbf3_r", "mdbf6",
"mdbf9_r", "mdbf12")] |> rowMeans()
# z-Standardisierung
fb25$ru_pre_zstd <- scale(fb25$ru_pre, center = TRUE, scale = TRUE)
Nachdem wir uns in den letzten Wochen mit der Testung von Unterschieden beschäftigt haben, untersuchen wir in den folgenden Sitzungen den Zusammenhang von Variablen. Auch wenn wir dabei sehen werden, dass sich die verwendeten Analysen ineinander überführen lassen, werden Hypothesen trotzdem häufig in diese Kategorien eingeordnet. Wir starten mit einem sehr typischen Beispiel aus der psychologischen Praxis - der Zusammenhang zwischen zwei Fragebogenscores soll untersucht werden. Spezifisch verfolgen wir die folgende Fragestellung: Hängt die Extraversion (extra) mit der Gewissenhaftigkeit (gewis) zusammen?
Besonderes Augenmaß richten wir bei dieser Fragestellung auf die Produkt-Moment-Korrelation, allerdings betrachten wir auch die Bestimmung der Kovarianz und zunächst schauen wir uns grafisch den Zusammenhang der beiden Variablen an, um einen generellen Eindruck zu gewinnen.
Der Zusammenhang zwischen zwei Variablen kann in einem Scatterplot bzw. Streupunktdiagramm dargestellt werden. Dafür kann man die plot()-Funktion nutzen. Als Argumente können dabei x für die Variable auf der x-Achse, y für die Variable auf der y-Achse, xlim, ylim für eventuelle Begrenzungen der Achsen und pch für die Punktart angegeben werden.
plot(x = fb25$extra, y = fb25$gewis, xlim = c(1,5) , ylim = c(1,5))
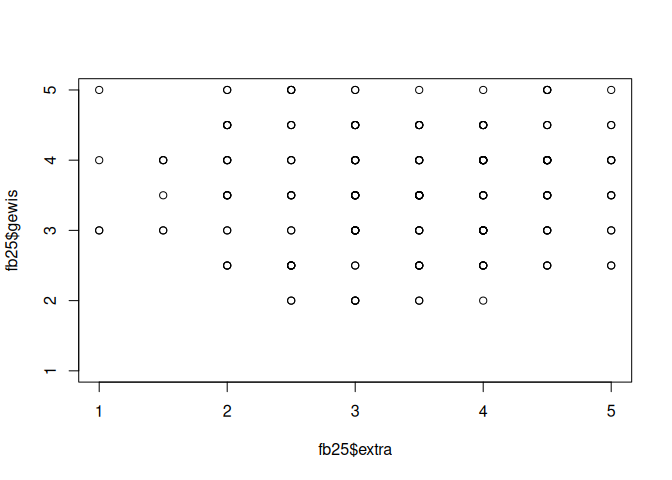
Die Produkt-Moment-Korrelation ist nur dann ein sinnvoller Kennwert für die Stärke eines Zusammenhangs, wenn der Zusammenhang zwischen den Variablen linearer Natur ist. Sollte eine andere Form des Zusammenhangs vorliegen, kann die Stärke für den linearen Zusammenhang zwar bestimmt werden, aber sie ist dann nicht das, was einen inhaltlich interessiert. Bei beispielsweise einem quadratischen Zusammenhang würde die Produkt-Moment-Korrelation einen Wert von 0 erreichen - das ist auch nicht falsch, da in den Daten eben kein linearer Zusammenhang vorliegt. Aber inhaltlich ist es nicht das, was von Interesse wäre.
In der vorliegenden Grafik können wir leider keine gute Aussage darüber finden, ob ein anderer Verlauf als der lineare vorliegt. Dadurch, dass es nur so wenig mögliche Ausprägungen auf beiden Variablen gibt, haben viele Personen dieselben Werte. Wir wissen aber anhand der Grafik nicht, welcher Punkt wie viele Personen repräsentiert. Mit der plot()-Funktion können wir auch erstmal keine Abhilfe schaffen - im nächsten Semester lernen wir noch andere Wege der Grafik-Gestaltung kennen. Jetzt gehen wir einmal davon aus, dass es hier keine andere Form des Zusammenhangs in den Daten gibt.
Varianz, Kovarianz und Korrelation
Für die Streuung einer Variable haben wir bereits die Varianz als deskriptives Maß kennengelernt. Der Zusammenhang zwischen zwei Variablen kann daher als Kovarianz, also die gemeinsame Streuung zwischen zwei Variablen bezeichnet werden. In R können wir die Kovarianz mittels der cov() Funktion bestimmen - dabei müssen die beiden interessierenden Variablen an die Funktion übergeben werden.
cov(fb25$extra, fb25$gewis) # Kovarianz Extraversion und Gewissenhaftigkeit
## [1] NA
Wenn wir das einfach so eingeben, erhalten wir als Ergebnis NA. Wie gewohnt weist das daraufhin, dass irgendwo in unseren Variablen ein Wert nicht vorliegt. Bisher haben wir in solch einem Fall das zusätzliche Argument na.rm genutzt und auf TRUE gesetzt. Bei der Bestimmung von Kovarianzen (und auch der Korrelationen) gibt es aber verschiedene Möglichkeiten zur Behandlung der fehlenden Werte und das Argument ist daher ein anderes (use). An dieser Stelle füllen wir es zunächst einfach mit einer Option aus, die uns ein Ergebnis erzeugt ("pairwise"). Die genaue Bedeutung davon folgt später.
cov(fb25$extra, fb25$gewis, use = "pairwise") # Kovarianz Extraversion und Gewissenhaftigkeit
## [1] 0.01549897
Wir sehen an dieser Stelle schon, dass es einen positiven Zusammenhang zwischen den Daten gibt. Das heißt, dass höhere Werte auf der Extraversion mit höheren Werten auf der Gewissenhaftigkeit einhergehen. Allerdings ist die Kovarianz ein unstandardisiertes Maß, das von der Skalierung der beiden Variablen X und Y abhängt. Wir können an dieser Stelle also noch gar keine Aussage darüber treffen, wie stark der gefundene Zusammenhang ist.
Anmerkung: In der Vorlesung haben Sie gelernt, dass es für Kovarianzen und Varianzen empirische und geschätzte Werte gibt. Wir haben bereits gelernt, dass R für die Varianz, die Populationsschätzung mit der var() Funktion ausgibt.
Dasselbe gilt auch für die Kovarianz - die Funktion cov() erzeugt die Populationsschätzung für Kovarianz.
Produkt-Moment-Korrelation (Pearson-Korrelation)
Wie in der Vorlesung besprochen, sind für verschiedene Skalenniveaus verschiedene Zusammenhangsmaße verfügbar, die im Gegensatz zur Kovarianz auch eine Vergleichbarkeit zwischen zwei Zusammenhangswerten sicherstellen. Für zwei metrisch skalierte Variablen gibt es dabei die Produkt-Moment-Korrelation. In der Funktion cor() werden dabei die Argumente x und y für die beiden betrachteten Variablen benötigt. use beschreibt weiterhin den Umgang mit fehlenden Werten. Die Bestimmung der Pearson-Korrelation ist dabei der Default und muss daher nicht nochmal festgehalten werden.
cor(x = fb25$extra, y = fb25$gewis, use = 'pairwise') # Bestimmung Pearson-Korrelation
## [1] 0.02004818
Die Stärke des korrelativen Zusammenhangs wird mit dem Korrelationskoeffizienten ausgedrückt, der zwischen -1 und +1 liegt. Bei einer positiven Korrelation gilt (je mehr Variable x… desto mehr Variable y) bzw. umgekehrt, bei einer negativen Korrelation (je mehr Variable x… desto weniger Variable y) bzw. umgekehrt. Korrelationen sind immer ungerichtet, das heißt, sie enthalten keine Information darüber, welche Variable eine andere vorhersagt - beide Variablen sind gleichberechtigt. Korrelationen (und Regressionen, die wir später in einem Tutorial kennen lernen werden) liefern keine Hinweise auf Kausalitäten. Sie sagen beide etwas über den (linearen) Zusammenhang zweier Variablen aus.
Es handelt sich um eine schwache positive Korrelation von r = 0.02. Der Effekt ist nach Cohens (1988) Konvention als vernachlässigbar bis schwach zu bewerten. D.h. es gibt keinen nennenswerten Zusammenhang zwischen der Ausprägung in Extraversion und der Ausprägung in der Gewissenhaftigkeit.
Cohens (1988) Konvention zur Interpretation von $|r|$
- ~ .10: schwacher Effekt
- ~ .30: mittlerer Effekt
- ~ .50: starker Effekt
Die Bestimmung der Pearson-Korrelation ist zunächst einmal ein deskriptives Vorgehen. Wir beschreiben den Zusammenhang der beiden Variablen in unserer Stichprobe. Typischerweise wollen wir aber nicht nur das machen, sondern auf eine dahinterliegende Population schließen. Wir müssen unser Ergebnis also inferenzstatistisch absichern. Die häufigste Weise ist dabei die Absicherung des Zusammenhangs gegen das Vorliegen von keinem Zusammenhang. Wie wir es bereits gewohnt sind, hat aber jede Inferenzstatistik Voraussetzungen, die wir zunächst betrachten müssen.
Inferenzstatistische Prüfung der Pearson-Korrelation
Folgende Voraussetzungen sind für die inferenzstatistische Prüfung notwendig:
- Unabhängigkeit der Beobachtungen (Zufallsstichproben)
- Bivariate Normalverteilung
Weiterhin ist anzumerken, dass die Korrelation an sich sensibel auf Ausreißer reagiert. Das ist darauf zurückzuführen, dass Mittelwerte und Standardabweichungen in ihrer Berechnung genutzt werden, die ja wie besprochen selbst sensibel für Ausreißer sind. Die Diagnostik von Ausreißern besprechen wir in zukünftigen Tutorials. Bei unseren Durchgeführten Untersuchungen hätten wir sie aber besonders im Histogramm auch schon erkennen können. Die Nutzung von Mittelwerten und Standardabweichungen in der Berechnung erklärt auch, dass die Daten mindestens auf Intervallskalenniveau vorliegen sollten (mit Ausnahme des später besprochenen, dichotomen Falles), damit die Pearson-Korrelation überhaupt die sinnvolle Wahl eines Korrelationskoeffizienten ist.
Unabhängigkeit der Beobachtungen
Die Voraussetzung kennen wir schon aus der Unterscheidung des unabhängigen vs. des abhängigen t-Tests. Wie auch dort wird die Voraussetzung vor allem durch das Versuchsdesign sichergestellt - es soll eine echte Zufallsstichprobe aus der Population gezogen werden. Für unsere Testung nehmen wir diese Voraussetzung an.
Bivariate Normalverteilung
Bivariate Normalverteilung heißt, dass die beiden beteiligten Variablen gemeinsam einer Normalverteilung im drei-dimensionalem Raum folgen. Da dies schwieriger zu visualisieren ist, wird stattdessen häufig die Normalverteilung einzeln für die beiden Variablen geprüft.
Für die Testung der Normalverteilung gibt es zwei grobe Bereiche von Methoden. Die Normalverteilung kann durch grafische Darstellung beurteilt oder mit inferenzstatistischen Methoden getestet werden.
Die einfachste Möglichkeit zur grafischen Überprüfung ist dabei die Anwendung eines Histogramms. Die Funktion curve() zeichnet zusätzlich den Verlauf der theoretischen Normalverteilung ein, damit wir die empirisch beobachteten Werte im Histogramm besser abgleichen können.
# Histogramme
hist(fb25$extra, prob = T, ylim = c(0, 1))
curve(dnorm(x, mean = mean(fb25$extra, na.rm = T), sd = sd(fb25$extra, na.rm = T)), col = "blue", add = T)
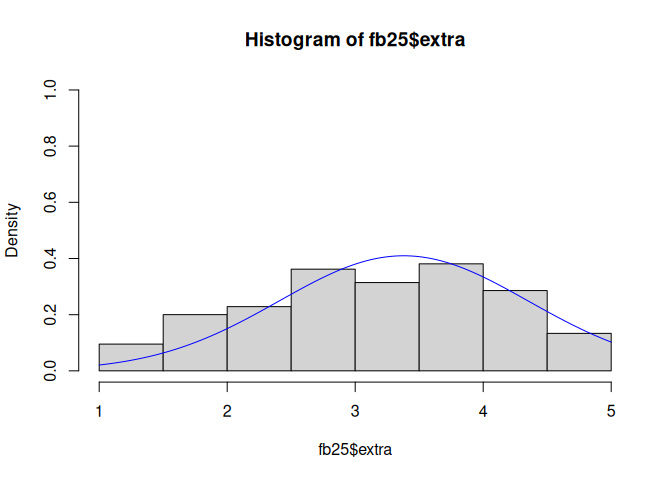
hist(fb25$gewis, prob = T, ylim = c(0,1))
curve(dnorm(x, mean = mean(fb25$gewis, na.rm = T), sd = sd(fb25$gewis, na.rm = T)), col = "blue", add = T)
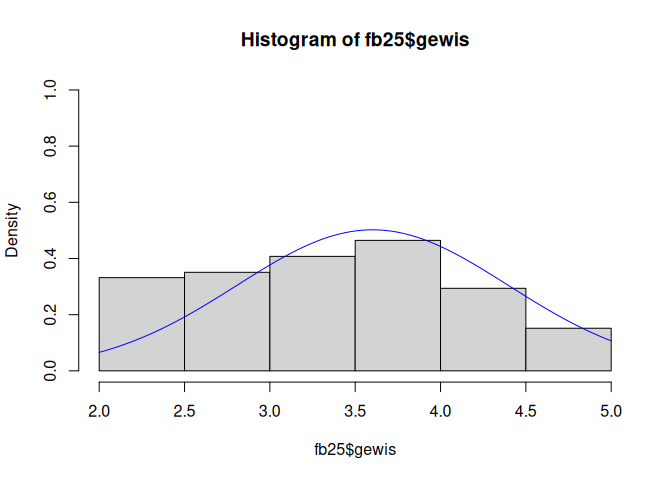
Während es für die Extraversion eher kleine Abweichungen gibt, ist die Verteilung der Gewissenhaftigkeit als rechtssteil einzuordnen.
Eine zweite Möglichkeit ist die Anwendung der qqPlot() Funktion. Diese kommt aus dem Paket car und hat ein paar mehr Features in der Anzeige als die Base-Funktion.
# car-Paket laden
library(car)
# qq-Plots
qqPlot(fb25$extra)
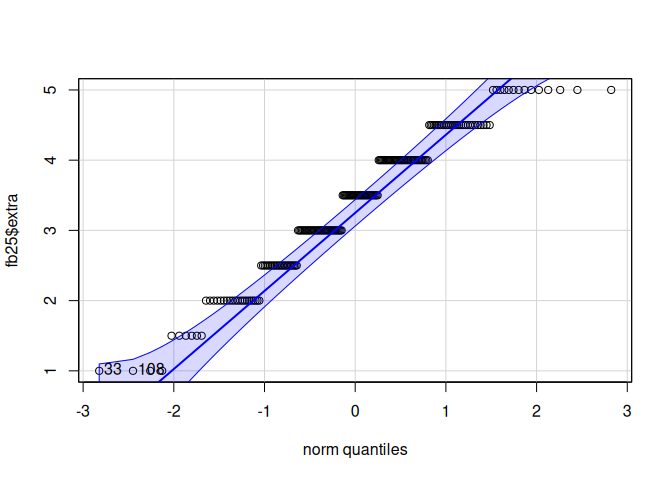
## [1] 33 108
qqPlot(fb25$gewis)
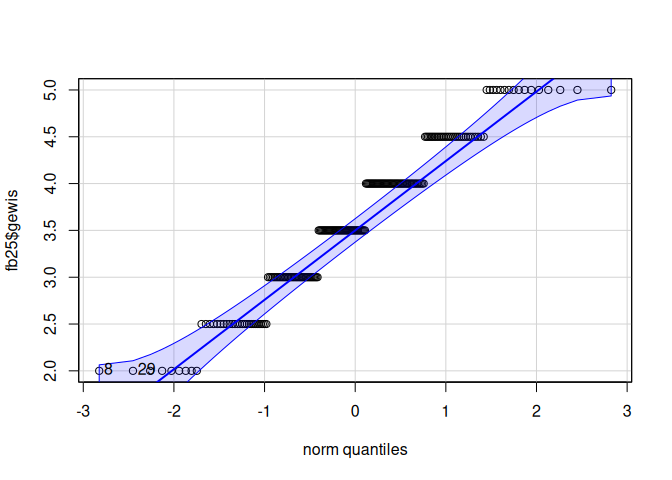
## [1] 8 29
Wir sehen für beide Variablen wieder Abweichungen von der Normalverteilung - leichte Abweichungen bei der Extraversion und deutliche bei der Gewissenhaftigkeit.
Kommen wir jetzt zur inferenzstatistischen Prüfung der Normalverteilung. Der Shapiro-Wilk-Test liefert eine Entscheidungsgrundlage dafür, ob die Annahme einer Normalverteilung für die vorliegenden Daten plausibel ist. Die Nullhypothese des Tests besagt, dass die Daten aus einer normalverteilten Grundgesamtheit stammen, während die Alternativhypothese das nicht-Vorliegen einer Normalverteilung in der Grundgesamheit aufzeigen würde. Daher spricht ein p-Wert kleiner als das gewählte Signifikanzniveau (z. B. $\alpha$ = 0.05) gegen die Annahme einer Normalverteilung, ein größerer p-Wert für die Annahme der Normalverteilung. Die Funktion zur Durchführung lautet shapiro.test().
# Shapiro
shapiro.test(fb25$extra)
##
## Shapiro-Wilk normality test
##
## data: fb25$extra
## W = 0.95659, p-value = 5.236e-06
shapiro.test(fb25$gewis)
##
## Shapiro-Wilk normality test
##
## data: fb25$gewis
## W = 0.94854, p-value = 7.546e-07
Für die Entscheidung ergibt sich $p < \alpha$ $\rightarrow$ $H_1$ bei beiden Variablen. Die Normalverteilung kann nicht angenommen werden. Somit ist diese Voraussetzung für die inferenzstatistische Testung der Korrelation verletzt.
Eine Möglichkeit damit umzugehen, ist die Rangkorrelation nach Spearman. Diese ist nicht an die Voraussetzung der Normalverteilung gebunden. Das Verfahren kann über method = "spearman" angewendet werden.
Inferenzstatistische Prüfung der Spearman-Korrelation
Wenn man sich für diese Variante entscheidet, wäre es sinnvoll, auch für den deskriptiven Bericht die Spearman Korrelation zu bestimmen. Man kann diese durch die Eingabe des method Arguments anpassen, dass per Voreinstellung eben auf die Pearson-Korrelation abzielt. Die nötige Eingabe wäre "spearman".
cor(x = fb25$extra, y = fb25$gewis, use = 'pairwise', method = "spearman") # Bestimmung Pearson-Korrelation
## [1] 0.03068195
Der sehr schwache positive Zusammenhang zwischen den Variablen wird auch hier deutlich. Doch können wir diesen auf die Population übetragen? Die inferenzstatistische Testung wird durch die Funktion cor.test() durchgeführt. Vor der Durchführung sollten wir aber wieder $\alpha$ festelgen, wir nehmen hier 5% an. Außerdem sollten die Hypothesen festgehalten werden. Aus der Fragestellung lässt sich nicht ableiten, ob wir einen positiven oder negativen Effekt erwarten, weshalb wir ungerichtete Hypothesen verwenden.
- $H_0$: $\rho = 0$ $\rightarrow$ es gibt keinen Zusammenhang zwischen Extraversion und Gewissenhaftigkeit
- $H_1$: $\rho \neq 0$ $\rightarrow$ es gibt einen Zusammenhang zwischen Extraversion und Gewissenhaftigkeit
Die Argumente von cor.test() entsprechen weitesgehend denen von cor(). Der einzig zusätzliche Input für unsere Fragestellung ist alternative, das die Art des Tests beschreibt. Wir wählen hier "two.sided" für einen zweiseitigen Test aufgrund der ungerichteten Hypothesen.
cor.test(fb25$gewis, fb25$gewis,
alternative = "two.sided",
method = "spearman",
use = "complete")
## Warning in cor.test.default(fb25$gewis, fb25$gewis, alternative = "two.sided", : Cannot compute exact
## p-value with ties
##
## Spearman's rank correlation rho
##
## data: fb25$gewis and fb25$gewis
## S = 0, p-value < 2.2e-16
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
## rho
## 1
Bei der Rangkorrelation kann der exakte p-Wert nicht berechnet werden, da gebundene Ränge vorliegen. Das bedeutet, dass Personen auf den ursprünglichen Variablen Extraversion und Gewissenhaftigkeit gleiche Werte hatten und daher auch den gleichen Rang bekommen haben. Das Ergebnis ist allerdings sehr eindeutig: $p > \alpha$ $\rightarrow$ $H_0$. Die Korrelation fällt nicht signifikant von 0 verschieden aus, d.h. die $H_0$ wird beibehalten: Extraversion und Gewissenhaftigkeit weisen keinen Zusammenhang auf.
Anmerkung: Wäre die Voraussetzung für die Testung der Pearson-Korrelation nicht verletzt gewesen, könnte man in der cor.test() Funktion das method Argument entweder weglassen oder mit "pearson" füllen.
Kovarianz- und Korrelationsmatrizen
Bisher haben wir nur den Zusammenhang von zwei Variablen betrachtet und den zugehörigen Korrelationswert ausgegeben. In der Praxis ist es aber üblich, dass man mehr als zwei Variablen erhoben hat - dann will man in der Deskriptivstatistik häufig den bivariaten Zusammenhang aller Variablenpaare darstellen. In R kann man beispielsweise die Kovarianzen zwischen den verschiedenen Variablen auch mit der cov() Funktion bestimmen. Dafür gibt man die Variablen nicht getrennt durch ein Komma an, sondern einen Datensatz der alle interessierenden Variablen enthält. Wollen wir beispielsweise alle Kovarianzen für die Variablen Verträglichkeit (vertr), Gewissenhaftigkeit (gewis) und Extraversion (extra) bestimmen, können wir das folgendermaßen erreichen.
cov(fb25[, c('vertr', 'gewis', 'extra')], use = "pairwise") # Kovarianzmatrix
## vertr gewis extra
## vertr 0.67371925 0.09664861 0.04483937
## gewis 0.09664861 0.63123448 0.01549897
## extra 0.04483937 0.01549897 0.94810321
Auf den Elementen neben der Diagonalen finden wir nun alle Kovarianzen zwischen den Varibalen. Auf der Hauptdiagonale sind die Kovarianzen mit sich selbst zu finden - dies entspricht dann den Varianzen der Variablen.
Analog kann die Korrelationsmatrix mit der cor() Funktion bestimmt werden. Auch hier wird der Datensatz mit den interessierenden Variablen als Argument übergeben (wir nutzen hier wieder die Pearson-Korrelation, da wir hier keine inferenzstatistische Testung anstreben).
cor(fb25[, c('vertr', 'gewis', 'extra')], use = "pairwise") # Korrelationsmatrix
## vertr gewis extra
## vertr 1.00000000 0.14820429 0.05616607
## gewis 0.14820429 1.00000000 0.02004818
## extra 0.05616607 0.02004818 1.00000000
Diesmal sieht man auf der Diagonalen die Korrelationen der Variablen mit sich selbst - also 1 - und in den restlichen Feldern die Korrelationen der Variablen untereinander.
Anhand der Korrelationsmatrix lassen sich jetzt auch eindrucksvoll die verschiedenen Option der Behandlung fehleder Werte besprechen.
Behandlung fehlender Werte
Wie bereits angekündigt, bietet das Argument use mehr Flexibilität bietet, als na.rm bei der univariaten Betrachtung. Diese Flexibilität setzt aber nur deutlich ein, wenn mehr als zwei Variablen gleichzeitig betrachtet werden. Die folgenden Optionen gibt es hier.
- Nutzung aller Beobachtungen: Alle Zeilen (also Personen) gehen in die Berechnung aller Werte mit ein.
- Listenweiser Fallausschluss: Personen, die auf (mindestens) einer von allen Variablen
NAhaben, werden von der Berechnung ausgeschlossen. - Paarweiser Fallausschluss: Personen, die auf (mindestens) einer von zwei Variablen
NAhaben, werden von der Berechnung ausgeschlossen.
Starten wir mit der ersten Option - der Nutzung aller Beobachtungen. Dies ist die Voreinstellung der Funktion - ausgeschrieben würde das Argument mit "everything" befüllt werden. Da dabei alle Zeilen einfach in die Berechnung eingehen, werden NA-Werte nicht ausgeschlossen und für die Zusammenhänge daher keine Kennwerte erzeugt. Wir können diese Schlussfolgerug auch nochmal überprüfen.
cor(fb25[, c('vertr', 'gewis', 'extra')]) # Nutzung aller Beobachtungen
## vertr gewis extra
## vertr 1.0000000 0.1482043 NA
## gewis 0.1482043 1.0000000 NA
## extra NA NA 1
cor(fb25[, c('vertr', 'gewis', 'extra')], use = "everything") # Nutzung aller Beobachtungen
## vertr gewis extra
## vertr 1.0000000 0.1482043 NA
## gewis 0.1482043 1.0000000 NA
## extra NA NA 1
Die Ergebnisse sind exakt gleich - "everything" ist also der Default für diese Funktion. Wir sehen, dass wir für die Variable extra fehlende Werte vorliegen haben, während die anderen Variablen vollständig beobachtet sind, denn für die Korrelation zwischen vertr und gewis erhalten wir hier Werte.
Wir haben im bisherigen Tutorial immer "pairwise" notiert, was dem paarweisem Fallausschluss entspricht.
cor(fb25[, c('vertr', 'gewis', 'extra')], use = 'pairwise') # Paarweiser Fallausschluss
## vertr gewis extra
## vertr 1.00000000 0.14820429 0.05616607
## gewis 0.14820429 1.00000000 0.02004818
## extra 0.05616607 0.02004818 1.00000000
Wie wir sehen, werden nun die Personen mit fehlenden Werten auf einer Variable ignoriert, wenn für die Variable mit fehlendem Wert ein Zusammenhangsmaß berechnet wird. Ansonsten werden Personen aber nicht aus der Berechnung ausgeschlossen, was man vor allem daran sieht, dass sich die Korrelationen von Variablen ohne fehlende Werte (vertr und gewis) nicht verändert haben im Vergleich zu der Bestimmung mit "everything"
Vergleichen wir nun dieses Ergebnis noch mit dem Ergebnis des listenweisem Fallausschluss, das über "complete" angesprochen werden kann.
cor(fb25[, c('vertr', 'gewis', 'extra')], use = 'complete') # Listenweiser Fallausschluss
## vertr gewis extra
## vertr 1.00000000 0.14261029 0.05616607
## gewis 0.14261029 1.00000000 0.02004818
## extra 0.05616607 0.02004818 1.00000000
Wie wir sehen, unterscheiden sich die Werte zwischen pairwise und complete für die Korrelation zwischen vertr und gewis. Das liegt daran, dass complete Personen mit fehlenden Werten aus der kompletten Berechnung ausgeschlossen werden. Selbst wenn sie nur auf der Extraversion (extra) einen fehlenden Wert haben, gehen sie nicht in die Berechnung des Zusammenhangs zwischen Verträglichkeit und Gewissenhaftigkeit ein.
Zusammenhang dichotomer (nominaler) Variablen
Betrachten wir nun Zusammenhangsmaße für dichotome nominalskalierte Variablen. Dazu bearbeiten wir folgende Forschungsfragestellung: Haben Studierende mit Wohnort in Uninähe (Frankfurt) eher einen Nebenjob als Studierende, deren Wohnort außerhalb von Frankfurt liegt?
Wir analysieren aus unserem Datensatz die beiden dichotomen Variablen job (ja [ja] vs. nein [nein]) und ort (Frankfurt [FFM] vs. außerhalb [andere]). Die Variablen ort und job liegen nach den vorbereitenden Schritten bereits als Faktor-Variablen mit entsprechende Labels vor. Dies wird durch die folgende Prüfung bestätigt:
is.factor(fb25$ort)
## [1] TRUE
is.factor(fb25$job)
## [1] TRUE
Bevor wir uns mit der Berechnung des Zusammenhangsmaßes beschäftigen, möchten wir zunächst die Beziehung zwischen den beiden Variablen mithilfe von Häufigkeitstabellen sowie grafisch verdeutlichen.
Häufigkeitstabellen
Die Gruppengehörigkeit verschiedener Kombinationen der dichotomen Variablen job und ort können Sie mithilfe einer sogenannten Kreuztabelle darstellen. Kreuztabellen sind Häufigkeitstabellen zur Darstellung bivariater Häufigkeiten. Sie stellen somit eine Erweiterung der Ihnen bereits bekannten Häufigkeitstabellen des univariaten Falls dar, die Sie mit dem Befehl table() erstellt haben.
Kreuztabellen liefern die Häufigkeit von Kombinationen von Ausprägungen in mehreren Variablen. In den Zeilen wird die erste Variable abgetragen und in den Spalten die zweite. Im Unterschied zum univariaten Fall muss im table()-Befehl nur die zweite interessierende Variable zusätzlich genannt werden. Tabellen können beliebig viele Dimensionen haben, werden dann aber sehr unübersichtlich.
Erstellen der Kreuztabelle als Datenbasis:
tab <- table(fb25$ort, fb25$job)
tab
##
## nein ja
## FFM 78 46
## anderer 55 24
In eine Kreuztabelle können Randsummen mit dem addmargins() Befehl hinzugefügt werden. Randsummen erzeugen in der letzten Spalte bzw. Zeile die univariaten Häufigkeitstabellen der Variablen.
addmargins(tab) #Randsummen hinzufügen
##
## nein ja Sum
## FFM 78 46 124
## anderer 55 24 79
## Sum 133 70 203
Auch für die Kreuztabelle ist die Möglichkeit der Darstellung der Häufigkeiten in Relation zur Gesamtzahl der Beobachtungen gegeben.
prop.table(tab) #Relative Häufigkeiten
##
## nein ja
## FFM 0.3842365 0.2266010
## anderer 0.2709360 0.1182266
78 von insgesamt 203 (38.42%) Studierenden wohnen in Frankfurt und haben keinen Nebenjob.
prob.table() kann allerdings nicht nur an der Gesamtzahl relativiert werden, sondern auch an der jeweiligen Zeilen- oder Spaltensumme. Dafür gibt man im Argument margin für Zeilen 1 oder für Spalten 2 an.
prop.table(tab, margin = 1) #relativiert an Zeilen
##
## nein ja
## FFM 0.6290323 0.3709677
## anderer 0.6962025 0.3037975
Von 124 Personen, die in Frankfurt Wohnen, haben 62.9% (nämlich 78 Personen) keinen Nebenjob.
prop.table(tab, margin = 2) #relativiert an Spalten
##
## nein ja
## FFM 0.5864662 0.6571429
## anderer 0.4135338 0.3428571
Von 133 Personen, die keinen Nebenjob haben, wohnen 58.65% (nämlich 78 Personen) in Frankfurt.
addmargins()und prop.table() können beliebig kombiniert werden.
prop.table(addmargins(tab)) behandelt die Randsummen als eigene Kategorie (inhaltlich meist unsinnig!).
addmargins(prop.table(tab)) liefert die Randsummen der relativen Häufigkeiten.
addmargins(prop.table(tab)) # als geschachtelte Funktion
##
## nein ja Sum
## FFM 0.3842365 0.2266010 0.6108374
## anderer 0.2709360 0.1182266 0.3891626
## Sum 0.6551724 0.3448276 1.0000000
prop.table(tab) |> addmargins() # als Pipe
##
## nein ja Sum
## FFM 0.3842365 0.2266010 0.6108374
## anderer 0.2709360 0.1182266 0.3891626
## Sum 0.6551724 0.3448276 1.0000000
Balkendiagramme
Grafisch kann eine solche Kreuztabelle durch gruppierte Balkendiagramme dargestellt werden. Das Argument beside sorgt für die Anordnung der Balken (bei TRUE nebeneinander, bei FALSE übereinander). Das Argument legend nimmt einen Vektor für die Beschriftung entgegen. Die Zeilen des Datensatzes bilden dabei stets eigene Balken, während die Spalten die Gruppierungsvariable bilden. Deshalb müssen als Legende die Namen der Reihen rownames() unserer Tabelle tab ausgewählt werden.
barplot (tab,
beside = TRUE,
col = c('mintcream','olivedrab'),
legend = rownames(tab))
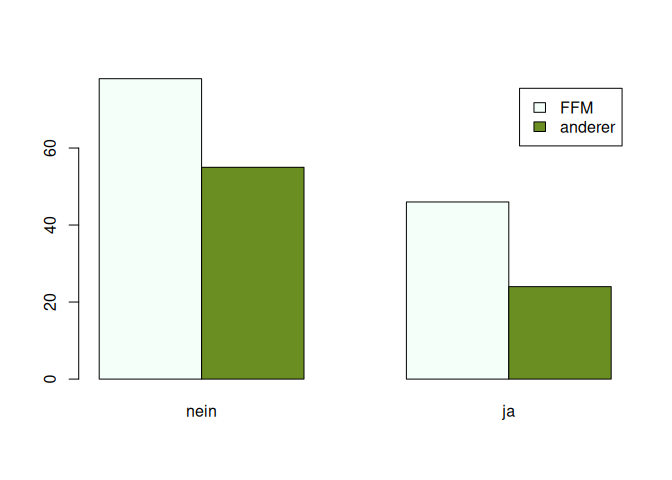
Somit haben Sie sich einen klaren Überblick über die bivariate Beziehung verschafft und können nun einen geeigneten Korrelationskoeffizienten berechnen und interpretieren.
Korrelationskoeffizient Phi ($\phi$)
Wie in der Vorlesung behandelt, berechnet sich $\phi$ folgendermaßen:
$$\phi = \frac{n_{11}n_{22}-n_{12}n_{21}}{\sqrt{(n_{11}+n_{12})(n_{11}+n_{21})(n_{12}+n_{22})(n_{21}+n_{22})}}$$ welches einen Wertebereich von [-1,1] aufweist und analog zur Korrelation interpretiert werden kann. 1 steht in diesem Fall für einen perfekten positiven Zusammenhang .
Die Berechnung muss in R natürlich nicht per Hand durchgeführt werden. Beispielsweise ist die Berechnung auch in dem uns bekannten Paket psych vorhanden, welches verschiedene psychometrische Funktionen beinhaltet. Die Funktion zur Berechnung von $\phi$ heißt phi(). Wichtig ist hier, dass nicht die beiden Variablen aus dem Datensatz als Argumente angegeben werden wie bei cor(), sondern direkt ein Tabellenobjekt mit den Häufigkeiten. Das Argument digits bietet zusätzlich die Option, die Anzahl der Nachkommastellen im Output zu definieren.
# psych Paket laden
library(psych)
phi(tab, digits = 4) #Korrelationskoeffizient Phi
## [1] -0.0689
Durch ein mathematisches Wunder (dass Sie gerne anhand der Formeln für Kovarianz und Korrelation nachvollziehen können) entspricht diese Korrelation exakt dem Wert, den wir auch anhand der Pearson-Korrelation zwischen den beiden Variablen bestimmen würden:
# Numerische Variablen erstellen
ort_num <- as.numeric(fb25$ort)
job_num <- as.numeric(fb25$job)
cor(ort_num, job_num, use = 'pairwise')
## [1] -0.06890118
Das hat gegenüber der händischen Bestimmung natürlich den Vorteil, dass wir direkt $p$-Wert und Konfidenzintervall bestimmen können:
cor.test(ort_num, job_num)
##
## Pearson's product-moment correlation
##
## data: ort_num and job_num
## t = -0.97917, df = 201, p-value = 0.3287
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## -0.20466904 0.06946779
## sample estimates:
## cor
## -0.06890118
Cohen (1988) hat folgende Konventionen zur Beurteilung der Effektstärke $\phi$ vorgeschlagen, die man heranziehen kann, um den Effekt “bei kompletter Ahnungslosigkeit” einschätzen zu können (wissen wir mehr über den Sachverhalt, so sollten Effektstärken lieber im Bezug zu anderen Studienergebnissen interpretiert werden):
| phi | Interpretation |
|---|---|
| ~ .1 | kleiner Effekt |
| ~ .3 | mittlerer Effekt |
| ~ .5 | großer Effekt |
Der Wert für den Zusammenhang der beiden Variablen ist also bei völliger Ahnungslosigkeit als klein einzuschätzen.
Yules Q
Dieses Zusammenhangsmaße berechnet sich als
$$Q=\frac{n_{11}n_{22}-n_{12}n_{21}}{n_{11}n_{22}+n_{12}n_{21}},$$
welches einen Wertebereich von [-1,1] aufweist und analog zur Korrelation interpretiert werden kann. 1 steht in diesem Fall für einen perfekten positiven Zusammenhang.
In dem vorher schon geladenen Paket psych gibt es auch die Funktion Yule():
Yule(tab) # Yules Q
## [1] -0.1494775
Händische Berechnung der beiden Zusammenhangsmaße
In R sieht eine händische Berechnung von Phi so aus:
korr_phi <- (tab[1,1]*tab[2,2]-tab[1,2]*tab[2,1])/
sqrt((tab[1,1]+tab[1,2])*(tab[1,1]+tab[2,1])*(tab[1,2]+tab[2,2])*(tab[2,1]+tab[2,2]))
korr_phi
## [1] -0.06890118
In R sieht das so aus:
YulesQ <- (tab[1,1]*tab[2,2]-tab[1,2]*tab[2,1])/
(tab[1,1]*tab[2,2]+tab[1,2]*tab[2,1])
YulesQ
## [1] -0.1494775
Odds (Wettquotient) und Odds-Ratio
Der Odds (Wettquotient, Chance) gibt das Verhältnis der Wahrscheinlichkeiten an, dass ein Ereignis eintritt bzw. dass es nicht eintritt. Das Wettquotienten-Verhältnis (Odds-Ratio) zeigt an, um wieviel sich dieses Verhältnis zwischen Ausprägungen einer zweiten dichotomen Variablen unterscheidet. Hier handelt sich also nicht um klassisches Zusammenangsmaß, das Werte zwischen -1 und 1 annehmen kann, allerdings ist es in der klinischen Forschung ein recht häufig genutztes Maß. Bleiben wir bei dem Beispiel zum Wohnort und dem Vorhandensein eines Jobs.
Zur Erinnerung lassen wir uns hier nochmal die absoluten Häufigkeiten anzeigen.
tab
##
## nein ja
## FFM 78 46
## anderer 55 24
Berechnung des Odds für FFM:
Odds_FFM = tab[1,1]/tab[1,2]
Odds_FFM
## [1] 1.695652
Für in Frankfurt Wohnende ist die Chance keinen Job zu haben demnach 1.7-mal so hoch wie einen Job zu haben.
Berechnung des Odds für anderer:
Odds_anderer = tab[2,1]/tab[2,2]
Odds_anderer
## [1] 2.291667
Für nicht in Frankfurt Wohnende ist die Chance keinen Job zu haben 2.29-mal so hoch wie einen Job zu haben.
Berechnung des Odds-Ratio:
OR = Odds_anderer/Odds_FFM
OR
## [1] 1.351496
Die Chance, keinen Job zu haben, ist für nicht in Frankfurt Wohnende 1.35-mal so hoch wie für in Frankfurt Wohnende. Man könnte auch den Kehrwert bilden, wodurch sich der Wert ändert, die Interpretation jedoch nicht.
Ergebnisinterpretation
Es wurde untersucht, ob Studierende mit Wohnort in Uninähe (also in Frankfurt) eher einen Nebenjob haben als Studierende, deren Wohnort außerhalb von Frankfurt liegt. Zur Beantwortung der Fragestellung wurden die Korrelationmaße $\phi$ und Yules Q bestimmt. Der Zusammenhang ist jeweils leicht negativ, d.h. dass Studierende, die nicht in Frankfurt wohnen, eher keinen Job haben. Der Effekt ist aber von vernachlässigbarer Größe ($\phi$ = -0.069). Diese Befundlage ergibt sich auch aus dem Odds-Ratio, das geringfügig größer als 1 aufällt (OR = 1.35).
Appendix
Zusammenhangsmaße für ordinalskalierte Daten
Vertiefung: Wie können Zusammenhangsmaße für ordinalskalierte Daten berechnet werden?
In diesem Abschnitt wird vertiefend die Bestimmung von Zusammenhangsmaßen für ordinalskalierte Variablen besprochen. Den dazugehörigen Auszug aus den Vorlesungsfolien, der in diesem Jahr herausgekürzt wurde, finden Sie im Moodle-Ordner.
Ordinalskalierte Daten können aufgrund der Verletzung der Äquidistanz zwischen bspw. Antwortstufen eines Items eines Messinstrumentes nicht schlicht mittels Pearson-Korrelation in Zusammenhang gesetzt werden. Zudem sind oft Verteilungsannahmen bei ordinalskalierten Variablen verletzt. Der Koeffizient $\hat{\gamma}$ ist zur Betrachtung solcher Zusammenhänge am besten geeignet (sogar besser als Spearman’s und Kendalls’s Rangkorrelation). Er nimmt - ähnlich wie Spearman’s und Kendall’s Koeffizenten - weder eine gewisse Verteilung der Daten an, noch deren Äquidistanz.
Zur Berechnung dieses Koeffizienten müssen wir das Paket rococo installieren, welches verschiedene Konkordanz-basierte Zusammenhangsmaße enthält. Die Installation muss dem Laden des Paketes logischerweise vorausgestellt sein. Wenn R einmal geschlossen wird, müssen alle Zusatzpakete neu geladen, jedoch nicht neu installiert werden.
if (!requireNamespace("rococo", quietly = TRUE)) {
install.packages("rococo")
}
library(rococo) #laden
Übersichten über Pakete kann man mit ?? erhalten.
??rococo
Die Funktion heißt hier zufälligerweise genau gleich wie das Paket. Wenn man nur Informationen über die Funktion statt dem Paket sucht, geht das anhand von ?.
?rococo
Dank des neuen Pakets können wir nun den Koeffizienten $\hat{\gamma}$ berechnen und damit den Zusammenhang zwischen Items betrachten. Schauen wir uns nun mal den Zusammenhang der beiden Prokrastinationsitems fb25$mdbf2 und fb25$mdbf3 an, um zu überprüfen, ob die beiden Items auch (wie beabsichtigt) etwas Ähnliches messen (nähmlich die aktuelle Stimmung). Die beiden Variablen wurden ursprünglich auf einer Skala von 1 (stimmt gar nicht) bis 4 (stimmt vollkommen) (also auf Ordinalskalenniveau) erfasst.
rococo(fb25$mdbf2, fb25$mdbf3)
## [1] -0.5505108
Um zu überprüfen, ob zwei ordinalskalierte Variablen signifikant miteinander zusammenhängen, können wir die rococo.test()-Funktion anwenden.
rococo.test(fb25$mdbf2, fb25$mdbf3)
##
## Robust Gamma Rank Correlation:
##
## data: fb25$mdbf2 and fb25$mdbf3 (length = 211)
## similarity: linear
## rx = 0.1 / ry = 0.2
## t-norm: min
## alternative hypothesis: true gamma is not equal to 0
## sample gamma = -0.5505108
## estimated p-value = < 2.2e-16 (0 of 1000 values)
Der Koeffizient von -0.55 zeigt uns, dass die Items zwar miteinander korrelieren, allerdings negativ. Ist hier etwas schief gelaufen? Nein, mdbf2_pre und mdbf3_pre repräsentieren gegenläufige Stimmungsaspekte. Mit der rekodierten Variante einer der beiden Variablen würde das - nicht da stehen, aber die Höhe der Korrelation bliebe gleich. Wir sehen daher, dass mdbf2 mit mdbf3 signifikant zusammenhängt. Die beiden Items messen demnach ein ähnliches zugrundeliegendes Konstrukt (aktuelle Stimmung).
](/media/header/storch_with_baby.jpg)