Vorbereitung
Laden Sie zunächst den Datensatz
fb25von der pandar-Website. Alternativ können Sie die fertige R-Daten-Datei hier herunterladen. Beachten Sie in jedem Fall, dass die Ergänzungen im Datensatz vorausgesetzt werden. Die Bedeutung der einzelnen Variablen und ihre Antwortkategorien können Sie dem Dokument Variablenübersicht entnehmen.
Lösung
#### Was bisher geschah: ----
# Daten laden
load(url('https://pandar.netlify.app/daten/fb25.rda'))
# Nominalskalierte Variablen in Faktoren verwandeln
fb25$hand_factor <- factor(fb25$hand,
levels = 1:2,
labels = c("links", "rechts"))
fb25$fach <- factor(fb25$fach,
levels = 1:5,
labels = c('Allgemeine', 'Biologische', 'Entwicklung', 'Klinische', 'Diag./Meth.'))
fb25$ziel <- factor(fb25$ziel,
levels = 1:4,
labels = c("Wirtschaft", "Therapie", "Forschung", "Andere"))
fb25$wohnen <- factor(fb25$wohnen,
levels = 1:4,
labels = c("WG", "bei Eltern", "alleine", "sonstiges"))
# Rekodierung invertierter Items
fb25$mdbf4_r <- -1 * (fb25$mdbf4 - 5)
fb25$mdbf11_r <- -1 * (fb25$mdbf11 - 5)
fb25$mdbf3_r <- -1 * (fb25$mdbf3 - 5)
fb25$mdbf9_r <- -1 * (fb25$mdbf9 - 5)
# Berechnung von Skalenwerten
fb25$gs_pre <- fb25[, c('mdbf1', 'mdbf4_r',
'mdbf8', 'mdbf11_r')] |> rowMeans()
fb25$ru_pre <- fb25[, c("mdbf3_r", "mdbf6",
"mdbf9_r", "mdbf12")] |> rowMeans()
# z-Standardisierung
fb25$ru_pre_zstd <- scale(fb25$ru_pre, center = TRUE, scale = TRUE)
Prüfen Sie zur Sicherheit, ob alles funktioniert hat:
dim(fb25)
## [1] 211 51
Der Datensatz besteht aus 211 Zeilen (Beobachtungen) und mindestens (unter Einbeziehung der Ergänzungen) 51 Spalten (Variablen). Falls Sie bereits weitere eigene Variablen erstellt haben, kann die Spaltenzahl natürlich abweichen.
Aufgabe 1
Im Laufe der Aufgaben sollen Sie auch Funktionen aus Paketen nutzen, die nicht standardmäßig aktiviert und auch eventuell noch nicht installiert sind. Sorgen Sie in dieser Aufgabe zunächst dafür, dass Sie Funktionen aus den Paketen psych und car nutzbar sind. Denken Sie an die beiden dargestellten Schritte aus dem Tutorial und auch daran, dass eine Installation nur einmalig notwendig ist.
Lösung
Installieren aller wichtigen Packages. Beachten Sie, dass das psych Paket eventuell schon im Tutorial installiert wurde, weshalb Sie dies nicht nochmal machen müssen.
install.packages("psych")
install.packages("car")
Damit die Funktionen ansprechbar sind, müssen die Pakete auch noch mittels library aktiviert werden.
library(psych)
library(car)
Aufgabe 2
Die mittlere Lebenszufriedenheit (lz) in Deutschland liegt bei $\mu$ = 4.4.
2.1 Was ist der Mittelwert der Stichprobe ($\bar{x}$) und die geschätzte Populations-Standardabweichung ($\hat\sigma$) der Lebenszufriedenheit in der Gruppe der Psychologie-Studierenden? Schätzen Sie außerdem ausgehend von unseren erhobenen Daten den Standardfehler des Mittelwerts ($\hat{\sigma_{\bar{x}}}$) der Lebenszufriedenheit.
Lösung
Variante 1:
mean_lz <- mean(fb25$lz, na.rm = TRUE) #Mittlere Lebenszufriedenheit
mean_lz
## [1] 4.890476
sd_lz <- sd(fb25$lz, na.rm = TRUE) #Standardabweichung (Populationsschätzer)
sd_lz
## [1] 1.320434
n_lz <- length(na.omit(fb25$lz)) #Stichprobengröße
se_lz <- sd_lz / sqrt(n_lz) #Standardfehler
se_lz
## [1] 0.09111858
- Der Mittelwert der Lebenszufriedenheit in der Stichprobe liegt bei 4.89.
- Die Standardabweichung der Lebenszufriedenheit beträgt 1.32.
- Der Standardfehler des Mittelwerts der Lebenszufriedenheit wird als 0.091 geschätzt.
Variante 2:
describe(fb25$lz) #Funktion aus Paket "psych"
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 210 4.89 1.32 5 5.01 1.48 1 7 6 -0.78 0.12 0.09
2.2 Sind die Lebenszufriedenheitswerte normalverteilt? Veranschaulichen Sie dies mit einer geeigneten optischen Prüfung. Benutzen Sie außerdem die qqPlot-Funktion aus dem car-Paket. Wann kann man in diesem Fall von einer Normalverteilung ausgehen?
Lösung
#Histogramm zur Veranschaulichung der Normalverteilung
hist(fb25$lz, xlim = c(1,7), main = "Histogramm", xlab = "Score", ylab = "Dichte", freq = FALSE)
curve(dnorm(x, mean = mean(fb25$lz, na.rm = TRUE), sd = sd(fb25$lz, na.rm = TRUE)), add = TRUE)
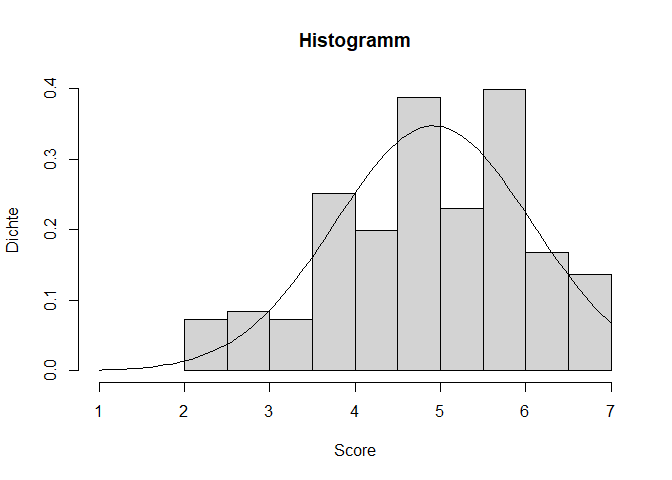
#geeigneter Plot: QQ-Plot. Alle Punkte sollten auf einer Linie liegen.
qqnorm(fb25$lz)
qqline(fb25$lz)
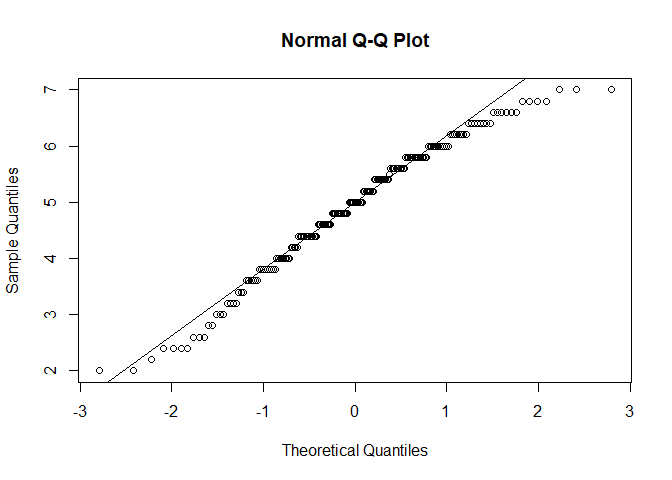
#Die qqPlot-Funktion zeichnet ein Konfidenzintervall in den QQ-Plot. Dies macht es für Betrachter:innen einfacher zu entscheiden, ob alle Punkte in etwa auf einer Linie liegen. Die Punkte sollten nicht außerhalb der blauen Linien liegen.
qqPlot(fb25$lz)
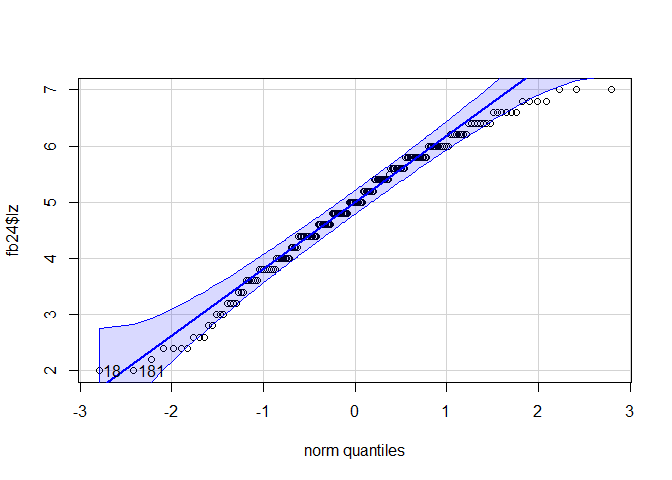
## [1] 108 146
Das Histogramm, sowie beide Darstellungsweisen des QQ-Plot weisen darauf hin, dass die Daten nicht normalverteilt sind.
2.3 Unterscheidet sich die Lebenszufriedenheit der Psychologie-Studierenden von der Lebenszufriedenheit der Gesamtbevölkerung (wie bereits geschrieben $\mu$ = 4.4)? Bestimmen Sie das 99%ige Konfidenzintervall.
Lösung
Da die Varianz der Grundgesamtheit nicht bekannt ist, wird ein t-Test herangezogen. Obwohl keine Normalverteilung vorliegt, können wir aufgrund des zentralen Grenzwertsatzes trotzdem einen t-Test rechnen.
Hypothesengenerierung:
$\alpha$ = .01
$H_0$: Die durchschnittliche Lebenzufriedenheit der Psychologie-Studierenden $\mu_1$ unterscheidet sich nicht von der Lebenszufriedenheit der Gesamtbevölkerung $\mu_0$.
$H_0$: $\mu_0$ $=$ $\mu_1$
$H_1$: Die durchschnittliche Lebenzufriedenheit der Psychologie-Studierenden $\mu_1$ unterscheidet sich von der Lebenszufriedenheit der Gesamtbevölkerung $\mu_0$.
$H_1$: $\mu_0$ $\neq$ $\mu_1$
t.test(fb25$lz, mu=4.4)
##
## One Sample t-test
##
## data: fb25$lz
## t = 5.3828, df = 209, p-value = 1.962e-07
## alternative hypothesis: true mean is not equal to 4.4
## 95 percent confidence interval:
## 4.710847 5.070105
## sample estimates:
## mean of x
## 4.890476
t.test(fb25$lz, mu=4.4, conf.level = 0.99) #Default ist 95%, deshalb erhöhen wir auf 99%
##
## One Sample t-test
##
## data: fb25$lz
## t = 5.3828, df = 209, p-value = 1.962e-07
## alternative hypothesis: true mean is not equal to 4.4
## 99 percent confidence interval:
## 4.653608 5.127344
## sample estimates:
## mean of x
## 4.890476
Zuvor ist uns aufgefallen, dass die Lebenszufriedenheit nicht normalverteilt ist. Außerdem haben wir gelernt das ab $n$ > 30 der zentrale Grenzwertsatz greift. Es gibt aber auch noch die Möglichkeit auf einen Test mit weniger strengen Voraussetzungen zurückzugreifen. Dafür büßen wir etwas Power ($1 - \beta$) ein. Das heißt, wenn ein Effekt vorliegt ist es schwerer (unwahrscheinlicher) diesen nachzuweisen. Der Ein-Stichproben Wilcoxon Tests der folgt wird nicht in der Vorlesung behandelt und ist auch nicht klausurrelevant.
wilcox.test(fb25$lz, mu = 4.4, conf.level = 0.99) #gleiche Argumente wie beim t-Test
##
## Wilcoxon signed rank test with continuity correction
##
## data: fb25$lz
## V = 14274, p-value = 5.859e-07
## alternative hypothesis: true location is not equal to 4.4
Auch dieser Test fällt signifikant aus. Daraus können wir schließen:
Mit einer Irrtumswahrscheinlichkeit von 1% kann die $H_0$ verworfen werden. Die Psychologie-Studierenden unterscheiden sich in ihrer Lebenszufriedenheit von der Gesamtbevölkerung.
Aufgabe 3
3.1 Unterscheidet sich der Mittelwert der Extraversionswerte (extra) der Studierenden der Psychologie (1. Semester) von dem der Gesamtbevölkerung ($\mu$ = 3.5, $\sigma$ = 1.2)? Bestimmen Sie den p-Wert und treffen Sie basierend auf Ihrem Ergebnis eine Signifikanzentscheidung.
Lösung
Hypothesengenerierung:
$\alpha$ = .05
$H_0$: Der Mittelwert der Extraversionswerte der Psychologie-Studierenden $\mu_1$ unterscheidet sich nicht von der Gesamtbevölkerung $\mu_0$.
$H_0$: $\mu_0$ $=$ $\mu_1$
$H_1$: Die Mittelwert der Extraversionswerte der Psychologie-Studierenden $\mu_1$ unterscheidet sich von der Gesamtbevölkerung $\mu_0$.
$H_1$: $\mu_0$ $\neq$ $\mu_1$
## Erste Schritte
anyNA(fb25$extra) #NA's vorhanden
mean_extra_pop <- 3.5 #Mittelwert der Population
sd_extra_pop <- 1.2 #empirische Standardabweichung der Population
se_extra <- sd_extra_pop / sqrt(length(na.omit(fb25$extra))) #Standardfehler
mean_extra_smpl <- mean(fb25$extra, na.rm = TRUE) #Mittelwert der Stichprobe
z-Wert bestimmen
z_extra <- (mean_extra_smpl - mean_extra_pop) / se_extra #empirischer z-Wert
p-Wert bestimmen
2 * pnorm(z_extra) #p >= .05, nicht signifikant
optionale z-Wert-Prüfung
z_krit <- qnorm(1 - 0.05/2) #kritischer z-Wert, zweiseitig
abs(z_extra) > z_krit #nicht signifikant, kann als zusätzliche Überprüfung genutzt werden
3.2 Sind die Offenheits-Werte (offen) der Psychologie-Studierenden (1. Semester) größer als die Offenheits-Werte der Gesamtbevölkerung ($\mu$ = 3.6)? Bestimmen Sie den p-Wert und treffen Sie basierend auf Ihrem Ergebnis eine Signifikanzentscheidung.
Lösung
Hypothesengenerierung:
$\alpha$ = .05
$H_0$: Die durchschnittlichen Offenheits-Werte der Psychologie-Studierenden $\mu_1$ sind geringer oder gleich groß wie die Werte der Gesamtbevölkerung $\mu_0$.
$H_0$: $\mu_0$ $\geq$ $\mu_1$
$H_1$: Die durchschnittlichen Offenheits-Werte der Psychologie-Studierenden $\mu_1$ sind größer als die Werte der Gesamtbevölkerung $\mu_0$.
$H_1$: $\mu_0$ $<$ $\mu_1$
t.test(fb25$offen, mu = 3.6, alternative = "greater")
##
## One Sample t-test
##
## data: fb25$offen
## t = 5.209, df = 210, p-value = 2.261e-07
## alternative hypothesis: true mean is greater than 3.6
## 95 percent confidence interval:
## 3.818116 Inf
## sample estimates:
## mean of x
## 3.919431
Der p-Wert beträgt 0 < .05, somit kann mit einer Irrtumswahrscheinlichkeit von 5% die $H_0$ verworfen werden. Die Psychologie-Studierenden haben höhere Offenheits-Werte im Vergleich zur Gesamtbevölkerung.
3.3 Überprüfen Sie Ihre Entscheidung aus 3.2 erneut, indem sie händisch ihren empirischen t-Wert ermitteln und mit dem entsprechenden kritischen t-Wert vergleichen.
Lösung
t_emp <- (mean(fb25$offen, na.rm = TRUE)-3.6) / (sd(fb25$offen, na.rm = TRUE)/sqrt(length(na.omit(fb25$offen)))) # (Mittelwert Stichprobe - Mittelwert Population) / Standardfehler des Mittelwerts
t_krit <- qt(0.05, df = (length(na.omit(fb25$offen))-1), lower.tail = FALSE) # Bei "Default" des vorigen Tests gehen wir von 5% beim Alphafehler aus - Alternativhypothese Größer, daher lower.tail = F
t_emp > t_krit #Vergleich
## [1] TRUE
Da der empirische Wert größer als der kritische Wert ist, können wir erneut bestätigen, dass die H0 verworfen und die H1 angenommen werden kann!
3.4 Zeigen die Psychologie-Studierenden (1. Semester) höhere Werte auf der Verträglichkeits-Skala (vertr) als die Grundgesamtheit ($\mu$ = 3.3)? Bestimmen Sie das 99%-Konfidenzintervall sowie die Effektgröße und ordnen sie diese ein.
Lösung
Hypothesengenerierung:
$\alpha$ = .01
$H_0$: Die durchschnittlichen Verträglichkeits-Werte der Psychologie-Studierenden $\mu_1$ sind geringer oder gleich groß wie die Werte der Gesamtbevölkerung $\mu_0$.
$H_0$: $\mu_0$ $\geq$ $\mu_1$
$H_1$: Die durchschnittlichen Verträglichkeits-Werte der Psychologie-Studierenden $\mu_1$ sind größer als die Werte der Gesamtbevölkerung $\mu_0$.
$H_1$: $\mu_0$ $<$ $\mu_1$
anyNA(fb25$vertr) # keine NAs
mean_vertr <- mean(fb25$vertr, na.rm = TRUE) #Mittlere Verträglichkeit der Stichprobe
sd_vertr <- sd(fb25$vertr, na.rm = TRUE) #Stichproben SD (Populationsschätzer)
mean_pop_vertr <- 3.3 #Mittlere Verträglichkeit der Grundgesamtheit
Konfidenzintervall
t_quantil_einseitig_vertr <- qt(0.01, df = length(na.omit(fb25$vertr))-1, lower.tail = FALSE)
t_lower_vertr <- mean_vertr - t_quantil_einseitig_vertr * (sd_vertr / sqrt(length(na.omit(fb25$vertr)))) # Formel für N muss angepasst werden an NAs -> Wir nehmen die Länge des Vektors der Variable ohne NA statt nrow! Siehe Deskriptivstatistik für Intervallskalen
Effektgröße
d3 <- abs((mean_vertr - mean_pop_vertr) / sd_vertr) #abs(), da Betrag
d3
## [1] 0.2552116
Da der Mittelwert der Population von 3.3 kleiner ist als das untere Konfidenzintervall mit 3.377 kann die $H_0$ verworfen werden. Die Effektgröße ist mit 0.26 nach Cohen (1988) als klein einzuordnen.
Aufgabe 4
Folgende Aufgaben haben ein erhöhtes Schwierigkeitsniveau.
Nehmen Sie für die weiteren Aufgaben den Datensatz fb25 als Grundgesamtheit (Population) an.
4.1 Sie haben eine Stichprobe mit $n$ = 42 aus dem Datensatz gezogen. Die mittlere Gewissenhaftigkeit dieser Stichprobe beträgt $\bar{x}$ = 3.6. Unterscheiden sich die Psychologie-Studierenden (1. Semester) der Stichprobe in ihrer Gewissenhaftigkeit (gewis) von der Grundgesamtheit?
Berechnen Sie den angemessenen Test und bestimmen Sie das 95%ige Konfidenzintervall.
Lösung
Hypothesengenerierung:
$\alpha$ = .05
$H_0$: Die durchschnittliche Gewissenhaftigkeit der Psychologie-Studierenden aus der Stichprobe $\mu_1$ unterscheidet sich nicht von der Gewissenhaftigkeit der Gesamtbevölkerung (Datensatz) $\mu_0$.
$H_0$: $\mu_0$ $=$ $\mu_1$
$H_1$: Die durchschnittliche Gewissenhaftigkeit der Psychologie-Studierenden aus der Stichprobe $\mu_1$ unterscheidet sich von der Gewissenhaftigkeit der Gesamtbevölkerung (Datensatz) $\mu_0$.
$H_1$: $\mu_0$ $\neq$ $\mu_1$
z-Test:
Wir arbeiten für diesen Aufgabenblock unter der Annahme, dass uns die Daten der gesamten Population, in unserem Fall aller Psychologie 1. Semester, in Form des Datensatzes fb25 vorliegen. Daher ist der angemessene Test ist in diesem Fall der z-Test.
Zuvor überprüfen wir noch ob es fehlende Werte auf der Variable gewis gibt. Sollte dies nicht der Fall sein können wir uns das Argument na.rm = TRUE sowie die Funktion na.omit() später an mehreren Stellen in der Rechnung sparen.
anyNA(fb25$gewis) #keine NAs
## [1] FALSE
Nun zur eigentlichen Rechnung:
mean_gewis_pop <- mean(fb25$gewis, na.rm = TRUE) #Mittelwert der Population
mean_gewis_smpl1 <- 3.6 #Mittelwert der Stichprobe
Weiterhin brauchen wir den Standardfehler. Dieser erechnet sich bei einem z-Test über die Standardabweichung der Population.
Da unser Datensatz nun die Population ist, können wir einfach die Standardabweichung der Werte im Datensatz bestimmen. Wir müssen hier aber nicht schätzen, da wir davon ausgehen, dass die ganze Population im Datensatz vorliegt. Deshalb muss die sd()-Funktion, die von Natur aus die geschätzte Standardabweichung berechnet, noch korrigiert werden mit dem Faktor $\sqrt\frac{n-1}{n}$. Anschließend kann der Standardfehler des Mittelwerts berechnet werden.
sd_gewis_pop <- sd(fb25$gewis, na.rm = TRUE) * sqrt((length(na.omit(fb25$gewis)) - 1) / length(na.omit(fb25$gewis))) #empirische Standardabweichung der Population
se_gewis <- sd_gewis_pop / sqrt(42) #Standardfehler des Mittelwerts
Die Teststatistik bestimmt sich mit:
z_gewis1 <- (mean_gewis_smpl1 - mean_gewis_pop) / se_gewis #empirischer z-Wert
z_krit <- qnorm(1 - 0.05/2) #kritischer z-Wert, zweiseitig
Der Abgleich des empirischen z-Werts mit dem kritischen Wert ergibt:
abs(z_gewis1) > z_krit #nicht signifikant
## [1] FALSE
Alternativ lässt sich auch noch der p-Wert über folgende Formel berechnen:
2 * pnorm(z_gewis1, lower.tail = FALSE) #p Wert
## [1] 1.012367
Da dieser größer ist als unser $\alpha = 0.05$ können wir die Nullhypothese nicht verwerfen.
Konfidenzintervall:
upper_conf_gewis <- mean_gewis_smpl1 + z_krit * se_gewis
lower_conf_gewis <- mean_gewis_smpl1 - z_krit * se_gewis
conf_int <- c(lower_conf_gewis, upper_conf_gewis)
conf_int
## [1] 3.360289 3.839711
Mit einer Irrtumswahrscheinlichkeit von 5% kann die $H_0$ nicht verworfen werden. Die Psychologie-Studierenden der Stichprobe unterscheiden sich nicht in ihrer Gewissenhaftigkeit von der Grundgesamtheit (Datensatz). Das 95%-ige Konfidenzintervall liegt zwischen 3.36 und 3.84.
4.2 Ziehen Sie nun selbst eine Stichprobe mit $n$ = 31 aus dem Datensatz (aber nur aus den Personen, die auch Beobachtungen für die Variable gewis haben. Nutzen Sie hierfür die set.seed(1234)-Funktion. Versuchen Sie zunächst selbst mit Hilfe der sample()-Funktion eine Stichprobe ($n$ = 31) zu ziehen. Falls Sie hier von alleine nicht weiterkommen, ist das kein Problem. Nutzen Sie dann für die weitere Aufgabenstellung folgenden Code:
Code
fb25_red <- fb25[!is.na(fb25$gewis),] #NA's entfernen
set.seed(1234) #erlaubt Reproduzierbarkeit
fb25_sample <- fb25_red[sample(nrow(fb25_red), size = 31), ] #zieht eine Stichprobe mit n = 31
Untersuchen Sie erneut, ob sich die Stichprobe von der Grundgesamtheit (Population) in ihrer Gewissenhaftigkeit unterscheidet. Berechnen Sie den angemessenen Test.
Lösung
Hypothesengenerierung:
$\alpha$ = .05
$H_0$: Die durchschnittliche Gewissenhaftigkeit der Psychologie-Studierenden aus der Stichprobe $\mu_1$ unterscheidet sich nicht von der Gewissenhaftigkeit der Gesamtbevölkerung (Datensatz) $\mu_0$.
$H_0$: $\mu_0$ $=$ $\mu_1$
$H_1$: Die durchschnittliche Gewissenhaftigkeit der Psychologie-Studierenden aus der Stichprobe $\mu_1$ unterscheidet sich von der Gewissenhaftigkeit der Gesamtbevölkerung (Datensatz) $\mu_0$.
$H_1$: $\mu_0$ $\neq$ $\mu_1$
Stichprobenziehung:
fb25_red <- fb25[!is.na(fb25$gewis),] #Hiemit kann man NAs entfernen, falls vorhanden, hier nicht der Fall!
set.seed(1234) #erlaubt Reproduzierbarkeit
fb25_sample <- fb25_red[sample(nrow(fb25_red), size = 31), ] #zieht eine Stichprobe mit n = 31
Mit der set.seed()-Funktion haben wir uns bereits im vorherigen Kapitel zu Verteilungen beschäftigt. Sie erlaubt uns die Ergebnisse eines Zufallsvorgangs konstant zu halten.
Die sample()-Funktion nimmt als erstes Argument keinen Datensatz entgegen sondern ausschließlich einen Vektor. Daher nutzen wir die Funktion um uns wahllos 31 Zahlen zwischen 1 und nrow(fb25_red) auszugeben. Der äußere Teil gibt uns dann die Zeilen (Personen) die mit den besagten 31 Zahlen übereinstimmen wieder.
z-Test:
Nachdem wir unsere Stichprobe gezogen haben ist die Berechnung analog zu Aufgabe 4.1. Für eine detailierte Beschreibung der Rechenschritte verweisen wir Sie auf die Lösung der vorherigen Aufgabe. Es ist allerdings wichtig zu erwähnen, das wir hier nicht mit fehlenden Werten arbeiten müssen, weshalb wir die Anzahl der genutzten Funktionen und Argumente reduzieren können, indem wir die Behandlung fehlender Werte weglassen.
anyNA(fb25$gewis) # NA's vorhanden
## [1] FALSE
anyNA(fb25_red$gewis) # keine NA's vorhanden durch Reduzierung
## [1] FALSE
anyNA(fb25_sample$gewis) # keine NA's vorhanden da Stichprobe aus fb25_red
## [1] FALSE
mean_gewis_pop <- mean(fb25_red$gewis) # Mittelwert der Population
sd_gewis_pop <- sd(fb25_red$gewis) * sqrt((length(fb25_red$gewis) - 1) / length(fb25_red$gewis)) # empirische Standardabweichung der Population - ist also die Populationsvarianz
se_gewis <- sd_gewis_pop / sqrt(length(fb25_sample$gewis)) # Standardfehler des Mittelwerts
mean_gewis_smpl2 <- mean(fb25_sample$gewis) # Mittelwert der Stichprobe
z_gewis2 <- (mean_gewis_smpl2 - mean_gewis_pop) / se_gewis #empirischer z-Wert
z_krit <- qnorm(1 - 0.05/2) # kritischer z-Wert, zweiseitig
abs(z_gewis2) > z_krit # nicht signifikant
## [1] FALSE
2 * pnorm(z_gewis2, lower.tail = FALSE) #p > .05, nicht signifikant
## [1] 0.7611888
Mit einer Irrtumswahrscheinlichkeit von 5% kann die $H_0$ nicht verworfen werden. Die Psychologie-Studierenden der Stichprobe unterscheiden sich in ihrer Gewissenhaftigkeit nicht von der Grundgesamtheit (Datensatz).
](/media/header/angel_of_the_north.jpg)