Einleitung und Datensatz
In dieser Sitzung werden wir uns mit weiteren nichtlinearen Effekte in Regressionsmodellen beschäftigen. Diese Sitzung basiert zum Teil auf der Literatur aus Eid et al. (2017) Kapitel 19 (insbesondere 19.9).
Dazu verwenden wir zunächst den Datensatz aus der Übung des letzten Themenblockes. Der Beispieldatensatz enthält Daten zur Lesekompetenz aus der deutschen Stichprobe der PISA-Erhebung in Deutschland aus dem Jahr 2009. Sie können den im Folgenden verwendeten Datensatz “PISA2009.rda” hier herunterladen.
Daten laden
Wir laden zunächst die Daten: Entweder lokal von Ihrem Rechner:
load("C:/Users/Musterfrau/Desktop/PISA2009.rda")
oder direkt über die Website:
load(url("https://pandar.netlify.app/daten/PISA2009.rda"))
Außerdem werden wir folgende R-Pakete benötigen:
library(car)
library(MASS)
library(lm.beta) # erforderlich für standardiserte Gewichte
library(ggplot2)
library(interactions) # für Interaktionsplots in moderierten Regressionen
Quadratische Verläufe in der Vorhersage von Lesekompetenz mit individuellen Merkmalen der Schüler:innen
In der Übung zur letzten Sitzung fanden wir heraus, dass der Sozialstatus (HISEI), der Bildungsabschluss der Mutter (MotherEdu) und die Zahl der Bücher zu Hause (Books) bedeutsame Prädiktoren für die Lesekompetenz der Schüler:innen sind. Jedoch zeigten Analysen, dass nicht alle Voraussetzungen erfüllt waren:
# Berechnung des Modells und Ausgabe der Ergebnisse
m1 <- lm(Reading ~ HISEI + MotherEdu + Books, data = PISA2009)
summary(lm.beta(m1))
##
## Call:
## lm(formula = Reading ~ HISEI + MotherEdu + Books, data = PISA2009)
##
## Residuals:
## Min 1Q Median 3Q Max
## -261.95 -55.34 13.83 61.24 181.60
##
## Coefficients:
## Estimate Standardized Std. Error t value Pr(>|t|)
## (Intercept) 340.7035 NA 24.0770 14.151 < 2e-16 ***
## HISEI 1.4440 0.2507 0.4769 3.028 0.00291 **
## MotherEdu 10.7052 0.1628 5.3740 1.992 0.04823 *
## Books 16.1988 0.2272 5.9608 2.718 0.00737 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 84.28 on 146 degrees of freedom
## Multiple R-squared: 0.2564, Adjusted R-squared: 0.2411
## F-statistic: 16.78 on 3 and 146 DF, p-value: 2.034e-09
Die Residuenplots sowie die Testung auf quadratische Trends, die zusammen mit dem Residuenplot ausgegeben werden, zeigen an, dass für den Bildungsabschluss der Mutter auch eine quadratische Beziehung mit der Lesekompetenz besteht, da in den Residuen quadratische Trends (ausgedrückt durch signifikante blaue Linien) zu sehen sind:
# Residuenplots
residualPlots(m1, pch = 16)
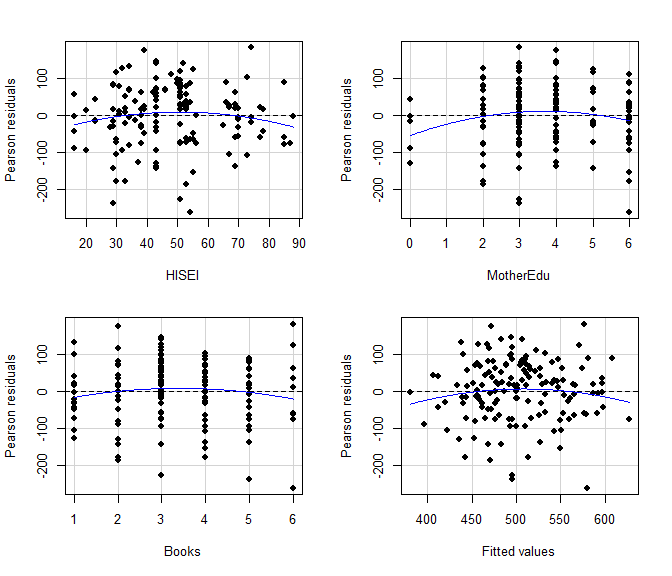
## Test stat Pr(>|Test stat|)
## HISEI -1.4084 0.16117
## MotherEdu -2.0316 0.04402 *
## Books -1.3387 0.18277
## Tukey test -1.1034 0.26986
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Die Effekte von Sozialstatus und Büchern werden durch das lineare Modell gut wiedergegeben. Für den Bildungsabschluss der Mutter ist ein leicht nicht-linearer Zusammenhang zu erkennen. Der quadratische Trend für die Residuen ist signifikant (signifikantes Ergebnis für den Bildungsabschluss der Mutter). Der Effekt ist dadurch charakterisiert, dass der Zuwachs der Lesekompetenz im unteren Bereich des mütterlichen Bildungsabschlusses stärker ist und im oberen Bereich abflacht.
Auch dem Histogramm war eine Schiefe zu entnehmen, welche durch nichtlineare Terme entstehen können (im niedrigen Bereich liegen mehr Werte; eine Linksschiefe/Rechtssteile ist zu erkennen).
res <- studres(m1) # Studentisierte Residuen als Objekt speichern
df_res <- data.frame(res) # als Data.Frame für ggplot
# Grafisch: Histogramm mit Normalverteilungskurve
library(ggplot2)
ggplot(data = df_res, aes(x = res)) +
geom_histogram(aes(y =..density..),
bins = 15, # Wie viele Balken sollen gezeichnet werden?
colour = "blue", # Welche Farbe sollen die Linien der Balken haben?
fill = "skyblue") + # Wie sollen die Balken gefüllt sein?
stat_function(fun = dnorm, args = list(mean = mean(res), sd = sd(res)), col = "darkblue") + # Füge die Normalverteilungsdiche "dnorm" hinzu und nutze den empirischen Mittelwert und die empirische Standardabweichung "args = list(mean = mean(res), sd = sd(res))", wähle dunkelblau als Linienfarbe
labs(title = "Histogramm der Residuen mit Normalverteilungsdichte", x = "Residuen") # Füge eigenen Titel und Achsenbeschriftung hinzu
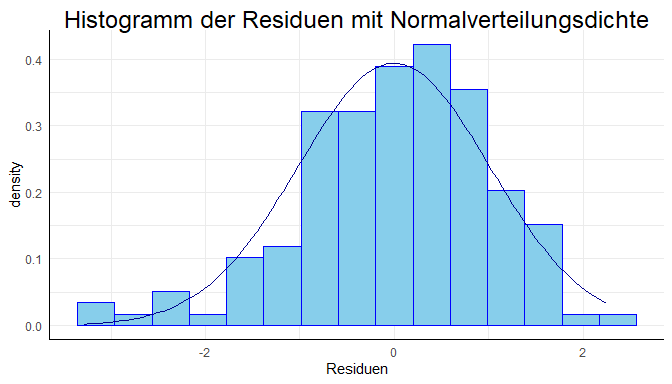
# Test auf Abweichung von der Normalverteilung mit dem Shpiro Test
shapiro.test(res)
##
## Shapiro-Wilk normality test
##
## data: res
## W = 0.97902, p-value = 0.0215
Die Frage ist nun, woher die Verstöße gegen die Normalverteilungsannahme kommen. Erste Indizien aus den Partialplots wiesen darauf hin, dass möglicherweise ein quadratischer Effekt des Bildungsabschlusses der Mutter besteht.
Aufnahme eines quadratischen Effekts
Wir wollen nun einen quadratischen Trend für den Bildungsabschluss der Mutter mit in das Regressionsmodell aufnehmen. Dies ginge beispielsweise indem wir an das Ende der Gleichung I(MotherEdu^2) aufnehmen. Die Funktion I() ermöglicht es, eine Funktion in eine Formel in R die durch ~ getrennt ist mit aufzunehmen, ohne vorher im Datensatz das Quadrat des Bildungsabschlusses der Mutter zu erstellen (was bspw. so ginge: PISA2009$MotherEdu_quadriert <- PISA2009$MotherEdu^2). Nun ist es so, dass lineare und quadratische Trends (und im Allgemeinen Trends der 2. Ordnung) korreliert sind. Daher bedienen wir uns der Funktion poly. Genauso könnten wir auch die Daten zentrieren oder standardisieren, was ebenfalls im Laufe dieser Sitzung besprochen wird.
Wird für den Bildungsabschluss der Mutter mit der Funktion poly ein linearer und ein quadratischer Trend in das Regressionsmodell aufgenommen, wird der quadratische Trend signifikant und das Modell erklärt signifikant mehr Varianz als ohne den quadratischen Trend. Um diese Ergebnisse zu sehen, müssen wir zunächst ein quadratisches Regressionsmodell schätzen. Wir interessieren uns anschließend für die standardisierten Ergebnisse (summary und lm.beta). Den quadratischen Verlauf erhalten wir, indem wir innerhalb des linearen Modells poly auf den Bildungsabschluss der Mutter anwenden. poly nimmt als zweites Argument die Potenz, für welche wir uns interessieren; hier 2:
m1.b <- lm(Reading ~ HISEI + poly(MotherEdu, 2) + Books, data = PISA2009)
summary(lm.beta(m1.b))
##
## Call:
## lm(formula = Reading ~ HISEI + poly(MotherEdu, 2) + Books, data = PISA2009)
##
## Residuals:
## Min 1Q Median 3Q Max
## -247.206 -50.365 8.392 57.886 171.694
##
## Coefficients:
## Estimate Standardized Std. Error t value Pr(>|t|)
## (Intercept) 377.9988 NA 25.4205 14.870 < 2e-16 ***
## HISEI 1.4692 0.2550 0.4720 3.113 0.00223 **
## poly(MotherEdu, 2)1 187.5689 0.1588 95.5443 1.963 0.05154 .
## poly(MotherEdu, 2)2 -169.6388 -0.1436 83.5003 -2.032 0.04402 *
## Books 16.5747 0.2324 5.9009 2.809 0.00566 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 83.4 on 145 degrees of freedom
## Multiple R-squared: 0.2769, Adjusted R-squared: 0.257
## F-statistic: 13.88 on 4 and 145 DF, p-value: 1.3e-09
poly bewirkt, dass der lineare und der quadratische Anteil von MotherEdu unkorreliert sind. Das ist sehr wichtig, da es sonst zu zu großen Standardfehlern kommen kann, wie wir in der letzten Sitzung im Themenblock der Kollinearität kennengelernt hatten.
Lineare und quadratische Funktionen von Variablen und deren Kovarianz/Korrelation
Wir bestimmen zunächst die Korrelation zwischen MotherEdu und MotherEdu^2:
cor(PISA2009$MotherEdu, PISA2009$MotherEdu^2)
## [1] 0.9665099
und erkennen, dass diese beiden “Variable” extrem hoch korreliert sind. Nun wenden wir poly an und wiederholen das Vorgehen:
cor(poly(PISA2009$MotherEdu, 2))
## 1 2
## 1 1.000000e+00 7.025821e-18
## 2 7.025821e-18 1.000000e+00
Heraus kommt eine Korrelationsmatrix und im Eintrag [1,2] erkennen wir, dass die Korrelation nun de facto 0 ist. Was genau poly macht, steht in Appendix A.
Mit dem folgenden Befehl können wir auf eine simple Weise das Inkrement des quadratischen Trends bestimmen.
# Vergleich mit Modell ohne quadratischen Trend
summary(m1.b)$r.squared - summary(m1)$r.squared # Inkrement
## [1] 0.02058156
Wir möchten dieses Inkrement auf Signifikanz prüfen. Dies geht mit dem anova-Befehl.
anova(m1, m1.b)
## Analysis of Variance Table
##
## Model 1: Reading ~ HISEI + MotherEdu + Books
## Model 2: Reading ~ HISEI + poly(MotherEdu, 2) + Books
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 146 1037169
## 2 145 1008463 1 28706 4.1274 0.04402 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Hier sollte dem anova-Befehl immer das “kleinere” (restriktivere) Modell (mit weniger Prädiktoren und Parametern, die zu schätzen sind) zuerst übergeben werden. Hier: m1, da sonst (1) die df negativ sind (und auch als solche vom Programm angezeigt werden können, obwohl dieses das oft erkennen kann und dann das Vorzeichen umdreht…) und (2) die Änderung in den Sum of Sq (Quadratsumme) negativ ist! R erkennt dies zwar und testet trotzdem die richtige Differenz auf Signifikanz, aber wir wollen uns besser vollständig korrekt verhalten! Das Inkrement des quadratischen Trends ist signifikant, der $p$-Wert liegt bei 0.044.
Erzeugt man für das erweiterte Modell Residuenplots, ist der quadratische Trend beim Bildungsabschluss komplett verschwunden - er ist ja schon im Modell enthalten und bildet sich somit nicht mehr in den Residuen ab:
residualPlots(m1.b, pch = 16)
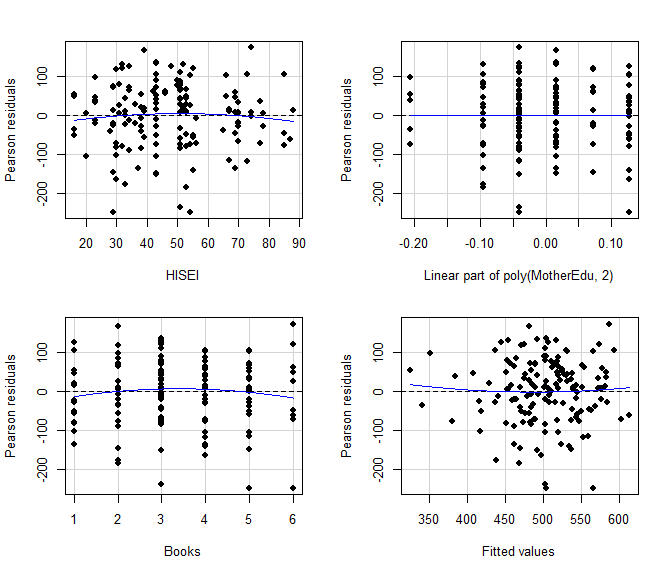
## Test stat Pr(>|Test stat|)
## HISEI -0.7518 0.4534
## poly(MotherEdu, 2)
## Books -1.1133 0.2674
## Tukey test 0.6774 0.4982
Was bedeutet nun dieser Effekt inhaltlich? Um dies genauer zu verstehen, stellen wir die um die anderen Variablen bereinigte Beziehung zwischen dem Bildungsabschluss der Mutter und der Leseleistung grafisch dar.
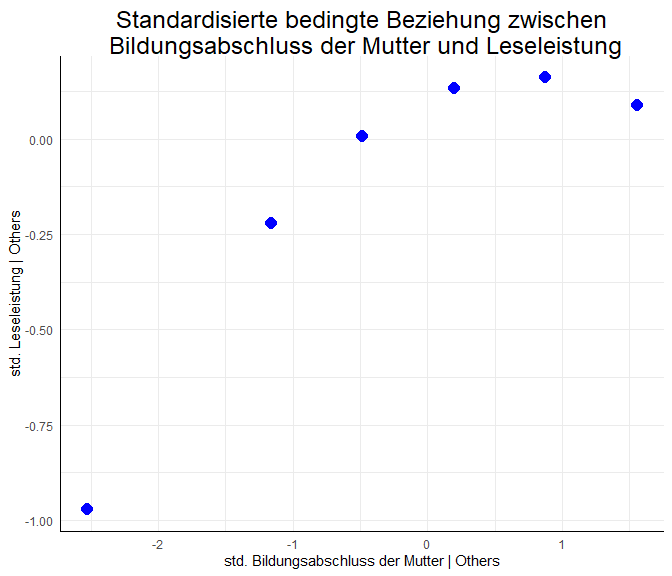
Für den Grafik-Code sowie weitere Informationen zu quadaratischen Effekten und Funktionen siehe Appendix A. Die Grafik zeigt die vorhergesagte Beziehung zwischen den standardisierten Werten des Bildungsabschlusses der Mutter und der Leseleistung. Hierbei steht erneut | für “gegeben” (wie beim Partialplot mit avPlots aus der vergangenen Sitzung). Wir sehen also den um die anderen Variablen im Modell bereinigten Effekt zwischen Bildungsabschluss und Leseleistung. Hierbei ist ein starker mittlerer Anstieg der Leseleistung (-1 bis ca. 0.1) für einen Anstieg des Bildungsabschlusses von deutlich unterdurchschnittlich bis durchschnittlich (von -2.5 bis 0) zu sehen. Danach ist die Beziehung zwischen der Leseleistung und dem Bildungsabschluss fast horizontal (Veränderung geringer als 0.1). Das spricht dafür, dass es für einen durchschnittlichen bis überdurchschnittlichen Bildungsabschluss der Mutter (von 0 bis 1.5) kaum eine Beziehung zwischen den Variablen gibt. Dies bedeutet, dass besonders im unterdurchschnittlichen Bereich der mütterlichen Bildung Unterschiede zwischen Müttern einen starken Zusammenhang mit der Leseleistung ihrer Kinder zeigen. Wenn das Bildungsniveau der Mutter jedoch durchschnittlich oder überdurchschnittlich ist, scheint der Zusammenhang beinahe zu verschwinden.
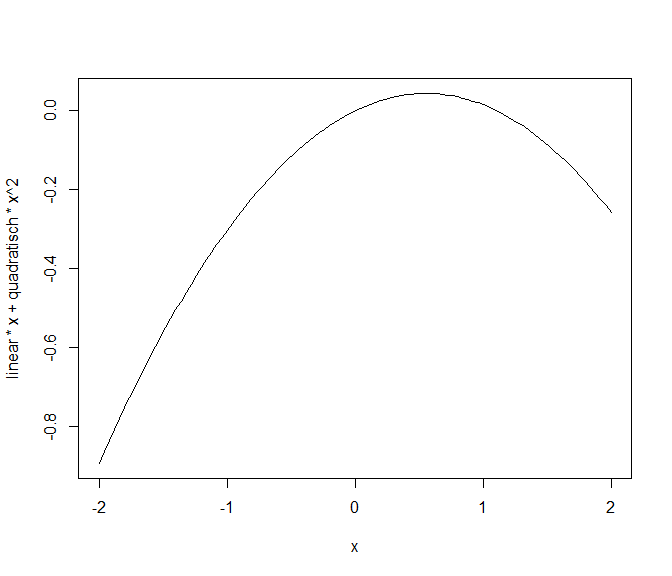
Die grobe Gestalt der Beziehung hätten wir auch aus dem Koeffizienten ablesen können. Der Koeffizient des quadratischen Teils war negativ, was für eine invers-u-förmige (konkave) Funktion steht. Das Einzeichnen hilft uns jedoch, das genaue Ausmaß zu verstehen (siehe auch Appendix A). Auch hatten wir gesehen, dass der lineare Teil des Bildungsabschlusses der Mutter keinen statistisch signifikanten Beitrag zur Vorhersage geleistet hat. Jedoch gehört zu einer quadratischen Funktion immer auch ihr linearer Anteil dazu. Aus diesem Grund können wir unsere Stichprobe nur angemessen beschreiben, wenn wir den linearen Trend des Bildungsabschlusses der Mutter im Regressionsmodell beibehalten. Um das genaue Ausmaß besser zu verstehen, manipulieren Sie doch einmal die Beziehung, die wir soeben grafisch gesehen haben, indem Sie den Code aus dem folgenden Block kopieren und die Inputvariablen verändern. Hierbei können Sie den linearen und den quadratischen Effekt verändern und sich die Auswirkungen auf die Grafik (die Beziehung zwischen dem Bildungsabschluss der Mutter und der Leseleistung) ansehen. Die Default-Einstellungen sind identisch zu der oberen Grafik. curve plottet eine Linie und nimmt x automatisch als Argument der Funktion. Somit wird $f(x)=\text{linear}*x+\text{quadratisch}*x^2$ geplottet. Probieren Sie doch einmal aus, was passiert, wenn Sie den linearen Teil auf 0 setzen oder das Vorzeichen des quadratischen Anteils ändern!
linear <- .1588
quadratisch <- -.1436
curve(linear * x + quadratisch * x^2,
xlim = c(-2, 2))
Mit Hilfe von poly(X, p) lassen sich Polynome bis zum Grad $p$ (als $X, X^2,\dots,X^{p-1},X^p$) in die Regression aufnehmen, ohne, dass sich die Parameterschätzungen der anderen Potenzen von $X$ ändern. Durch poly können also leicht Modelle mit Polynomen zur Potenz 4 und 5 verglichen werden, da die Koeffizienten des linearen ($X=X^1$), des quadratischen ($X^2$), des kubischen ($X^3$), etc. in den Modellen gleich sind. Wenn Sie noch mehr über die Funktion poly und ihre Vorteile erfahren möchten, schauen Sie sich gerne Appendix A an. Wenn wir poly nicht verwenden wollen würden, sollten wir zumindest die Prädiktoren, für welche wir quadratische Effekte annehmen, zentrieren, also den Mittelwert der Variable von dieser abziehen. Bspw. $X_i-\bar{X}$, was in R so aussieht: X-mean(X). Diese Variable würden wir dann an unseren Datensatz anhängen. Dies wird im nächsten Abschnitt zur moderierten Regression gemacht. Hierbei ist zu beachten, dass Standardisierung nichts anderes ist als Zentrierung unter zusätzlicher Setzung der Varianz/Standardbweichung auf 1 pro Variable!
Interaktionsterme: Moderierte Regression
Außerdem können auch Interaktionen zwischen Variablen in ein Regressionsmodell aufgenommen werden. Für weitere inhaltliche Details siehe Eid et al. (2017) Kapitel 19.9. Eine Regression mit einem Interaktionsterm wird häufig moderierte Regression genannt. Häufig wird dann von einem Moderator (der selbst natürlich auch ein Prädiktor im Regressionsmodell ist) gesprochen, der die Beziehung eines (anderen) Prädiktors mit dem Kriterium “moderiert”. Genaugenommen ist Moderation jedoch eine wechselseitige Beziehung, sodass es im Modell nicht nur einen Moderator gibt. Vielmehr moderieren beide beteiligten Prädiktoren jeweils den Zusammenhang des Kriteriums mit dem anderen. Dies ist leicht einzusehen, wenn wir uns die Modellgleichungen ansehen. Wir nennen den Prädiktor $X$, den Moderator $Z$ und das Kriterium $Y$. Dann ergibt sich folgende Regressionsgleichung (für eine Person $i$):
$$Y_i=\beta_0 + \beta_1X_i + \beta_2Z_i + \beta_3X_iZ_i + \varepsilon_i.$$ Der Interaktionsterm ist in diesem Beispiel $X_iZ_i$ und trägt den Koeffizienten $\beta_3$. Um sich das Ganze leichter vorstellen zu können, stellen wir diese Gleichung um und stellen die Beziehung zwischen $X$ und $Y$ mit Hilfe von $Z$ dar. Das wird auch manchmal “simple slopes” also einfache Steigungen genannt, da wir im Grunde mehrere Geraden für $X$ in Abhängigkeit von $Z$ annehmen wollen:
$$Y_i=\underbrace{(\beta_0 + \beta_2Z_i)}_{\text{Interzept}(Z_i)} + \underbrace{(\beta_1 + \beta_3Z_i)}_{\text{Slope}(Z_i)}X_i + \varepsilon_i.$$
Hier ist eigentlich gar nichts passiert - wir haben lediglich die Gleichung umgestellt. Allerdings sieht dies nun so aus, als würde vorne ein Interzept $(\beta_0 + \beta_2Z_i)$ und vor $X_i$ ein Slope (Steigungskoeffizient) $(\beta_1 + \beta_3Z_i)$ stehen - beide abhängig von $Z_i$. Deshalb haben wir sie gleich mal $\text{Interzept}(Z_i)$ und $\text{Slope}(Z_i)$ genannt. Genauso könnten wir allerdings auch alles nach $X$ umstellen: $Y_i=(\beta_0 + \beta_1X_i) + (\beta_2 + \beta_3X_i)Z_i + \varepsilon_i.$ Somit ist ersichtlich, dass es keine mathematische Begründung gibt, welche der beiden Variablen der Prädiktor und welche der Moderator ist! Manche sagen auch, dass dieses Modell “symmetrisch” in den beiden Variablen ist, man sie also leicht hinsichtlich der inhaltlichen Interpretation austauschen kann. Sich das Ganze in R anzuschauen geht sehr einfach. Wir wollen dies am Datensatz Schulleistungen.rda durchführen, den wir bereits aus vorherigen Sitzungen kennen. Wie genau wir an den Datensatz herankommen, können Sie sich in der entsprechenden Sitzung ansehen. Wir laden den Datensatz wie folgt über die Website:
load(url("https://pandar.netlify.app/daten/Schulleistungen.rda"))
head(Schulleistungen)
## female IQ reading math
## 1 1 81.77950 449.5884 451.9832
## 2 1 106.75898 544.8495 589.6540
## 3 0 99.14033 331.3466 509.3267
## 4 1 111.91499 531.5384 560.4300
## 5 1 116.12682 604.3759 659.4524
## 6 0 106.14127 308.7457 602.8577
| female | IQ | reading | math |
|---|---|---|---|
| 1 | 81.77950 | 449.5884 | 451.9832 |
| 1 | 106.75898 | 544.8495 | 589.6540 |
| 0 | 99.14033 | 331.3466 | 509.3267 |
| 1 | 111.91499 | 531.5384 | 560.4300 |
| 1 | 116.12682 | 604.3759 | 659.4524 |
| 0 | 106.14127 | 308.7457 | 602.8577 |
Auch bei Interaktionen ist es wichtig, dass die Daten zentriert sind, also einen Mittelwert von 0 aufweisen. Dies hatte im anderen Beispiel oben die Funktion poly bewirkt. Das erleichtert die Interpretation und verändert die Korrelation des Interaktionsterms (oben $X_i*Z_i$) mit den Haupteffekten von $X_i$ und $Z_i$. Daher verwenden wir die scale-Funktion, um den gesamten Datensatz zu standardisieren (also zu zentrieren und gleich noch die Varianz auf 1 zu setzen) und speichern diesen unter dem Namen Schulleistungen_std. Sind die Daten zentriert (haben einen Mittelwert von 0) oder sogar standardisiert (haben einen Mittelwert von 0 und eine Varianz/Standardabweichung von 1), dann ist in einem Modell, in dem nur lineare Effekte, quadratische- und Interaktionseffekte vorkommen (also Prädiktoren $X, Z$ und $X^2, XZ, Z^2$, wobei die Parameter vor $X, Z$ lineare Effekte und die Parameter vor $X^2, XZ, Z^2$ quadratische bzw. Interaktionseffekte genannt werden), eine Verrechnung mit poly nicht mehr nötig. poly bringt nur dann Verbesserungen, wenn bspw. noch kubische Effekte ($X^3$) mit aufgenommen werden sollen. Dies geschieht hier aber nicht, weswegen wir poly in diesem Abschnitt nicht brauchen. Lesen Sie gerne eine Gegenüberstellung von poly und Zentrierung/Standardisierung in Appendix A nach.
Schulleistungen_std <- data.frame(scale(Schulleistungen)) # standardisierten Datensatz abspeichern als data.frame
colMeans(Schulleistungen_std) # Mittelwert pro Spalte ausgeben
## female IQ reading math
## -8.215650e-17 -1.576343e-16 1.358549e-16 -6.760217e-17
apply(Schulleistungen_std, 2, sd) # Standardabweichungen pro Spalte ausgeben
## female IQ reading math
## 1 1 1 1
Nun führen wir eine moderierte Regression durch, in welcher wir in diesem Datensatz die Leseleistung reading durch den IQ sowie die Matheleistung math vorhersagen, sowie durch deren Interaktion. Die Interaktion können wir durch : ausdrücken. Falls wir einfach * verwenden, werden auch gleich noch die Haupteffekte, also die Variablen selbst, mit aufgenommen. Es gilt also: math + IQ + math:IQ = math*IQ, wobei die Interaktion math:IQ ist. Um auch wirklich die Interaktion zu testen, ist es unbedingt notwendig, die Haupteffekte der Variablen ebenfalls in das Modell mit aufzunehmen, da die Variablen trotzdem mit der Interaktion korreliert sein können, auch wenn die Variablen zentriert sind.
mod_reg <- lm(reading ~ math + IQ + math:IQ, data = Schulleistungen_std)
summary(mod_reg)
##
## Call:
## lm(formula = reading ~ math + IQ + math:IQ, data = Schulleistungen_std)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.9727 -0.5044 0.1034 0.4412 1.7998
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.10922 0.09857 -1.108 0.2706
## math -0.08142 0.11639 -0.699 0.4859
## IQ 0.63477 0.11624 5.461 3.71e-07 ***
## math:IQ 0.15815 0.07956 1.988 0.0497 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.8183 on 96 degrees of freedom
## Multiple R-squared: 0.3506, Adjusted R-squared: 0.3303
## F-statistic: 17.28 on 3 and 96 DF, p-value: 4.745e-09
Dem Output entnehmen wir, dass sowohl (1) der Haupteffekt des IQs ($p=$ 0 $<.05$) als auch (2) die Interaktion mit der Matheleistung signifikant sind ($p=$ 0.0497 $<.05$). Die Matheleistung an sich bringt aber keine signifikante Vorhersagekraft der Leseleistung ($p=$ 0.4859 $>.05$). Wie genau es hier zu diesen Ergebnissen gekommen ist, ist schwer zu sagen. Matheaufgaben von Tests bestehen häufig aus Textaufgaben, welche ein großes Maß an Textverständnis voraussetzen. Daher wäre eine Beziehung zwischen der Matheleistung und der Leseleistung zu erwarten. Wir wollen es so interpretieren, dass die Matheleistung die Beziehung zwischen dem IQ und der Leseleistung moderiert. Somit wäre $X=$ IQ (Prädiktor) und $Z=$ math (Moderator). Es gibt ein R-Paket, dass eine solche Interaktion grafisch darstellt: interactions. Nachdem Sie dieses installiert haben, können Sie es laden und die Funktion interact_plot verwenden, um diese Interaktion zu veranschaulichen. Dem Argument model übergeben wir mod_reg, also unser moderiertes Regressionsmodell. Als Prädiktor wählten wir den IQ, also müssen wir dem Argument pred den IQ übergeben. Der Moderator ist hier die Matheleistung, folglich übergeben wir math dem Argument modx.
library(interactions)
interact_plot(model = mod_reg, pred = IQ, modx = math)
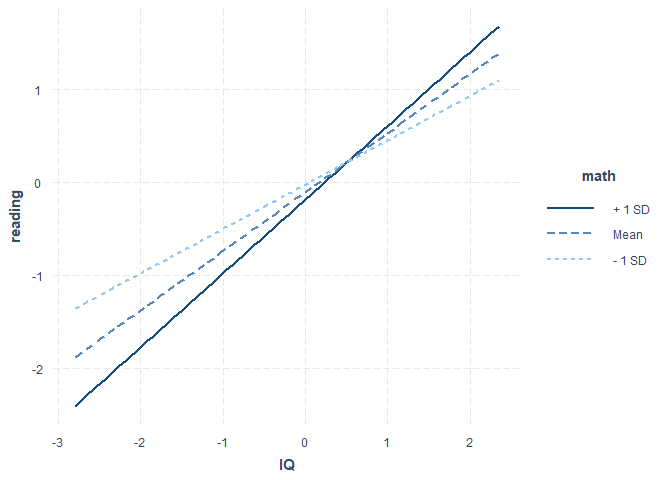
Uns wird nun ein Plot mit drei Linien ausgegeben. Dieser wird häufig “simple slopes” Plot genannt. Dargestellt sind drei Beziehungen zwischen dem IQ und reading für unterschiedliche Ausprägungen von math. Erstens für einen durchschnittlichen math-Wert und zweitens und drittens für Werte, die (1) eine Standardabweichung (SD) oberhalb oder (2) eine Standardabweichung (SD) unterhalb des Mittelwerts liegen. Damit bekommen wir ein Gefühl dafür, wie sehr sich die Beziehung (und damit Interzept und Slope) zwischen der Leseleistung und der Intelligenz verändert für unterschiedliche Ausprägungen der Matheleistung: Für eine durchschnittliche (Mean) Ausprägung, eine unter- (- 1 SD) und eine überdurchschnittliche (+ 1 SD) Ausprägung. Die Signifikanzentscheidung oben zeigte uns, dass diese Unterschiede bedeutsam sind und somit die Matheleistung entscheidend dafür ist, wie genau die Leseleistung mit der Intelligenz zusammenhängt. Die einzelnen Regressionsgeraden lassen sich ebenfalls auf signifikante Unterschiede prüfen. Es kann auch untersucht werden, welche Ausprägungen des Moderators zu unterschiedlichen “bedingten” Regressionsgewichten führen, also ab wann sich Interzept oder Slope des Prädiktors signifikant verändert, wenn sich der Moderator verändert. Inhaltlich wäre eine Post-Hoc (also nach der Analyse entstehende) Interpretation, dass intelligente Kinder, die gut in Mathematik sind, besonders gut lesen können und sich dies auch bereits in den Textaufgaben der Matheaufgaben geäußert haben könnte. Dies ist allerdings eine Interpretation, die mit Vorsicht zu genießen ist. Sie wurde quasi an die Ergebnisse angepasst. Wir wissen allerdings, dass dies ein exploratives Vorgehen ist und dass so nur bedingt wissenschaftliche Erkenntnisse gewonnen werden können Ein besseres Vorgehen wäre, dass wir im Vorhinein Hypothesen aus Theorien ableiten und diese an einem Datensatz prüfen. Außerdem müssten wir, um ganz sicher zu gehen, dass es in der Population eine Interaktion gibt (mit einem Irrtumsniveau von 5%), auch die quadratischen Effekte mit in das Modell aufnehmen! In unserem Beispiel hätten wir die quadratischen Effekte wie folgt aufnehmen können: reading ~ IQ+math+ I(math^2)+I(IQ*math) +I(IQ^2). Die Daten hatten wir zuvor schon zentriert beziehungsweise sogar standardisiert. Hier ist das I() als Funktion anzusehen, die auch “as.is” genannt wird, also “so wie es dort steht”. Dieser werden arithmetische Funktionen übergeben. Diese überschreibt die Kurzschreibweise IQ*math= IQ + math + IQ:math, da das * als Multiplikationsoperator interpretiert wird. Wir könnten also auch die beiden Schreibweisen mischend reading ~ IQ*math + I(math^2) + I(IQ^2) schreiben. Hätten wir I() nicht verwendet, hätten wir vorher alle Funktionen von Variablen an den Datensatz anhängen müssen.
Interessierte Lesende können sich bei Interesse, welches über diesen Kurs hinaus geht, dazu das R-Paket reghelper mit der Funktion simple_slopes ansehen. Nach dem Laden des Pakets kann mit ?simple_slopes die Hilfe zu dieser Funktion aufgerufen werden, die den Umgang damit und Weiteres erklärt.
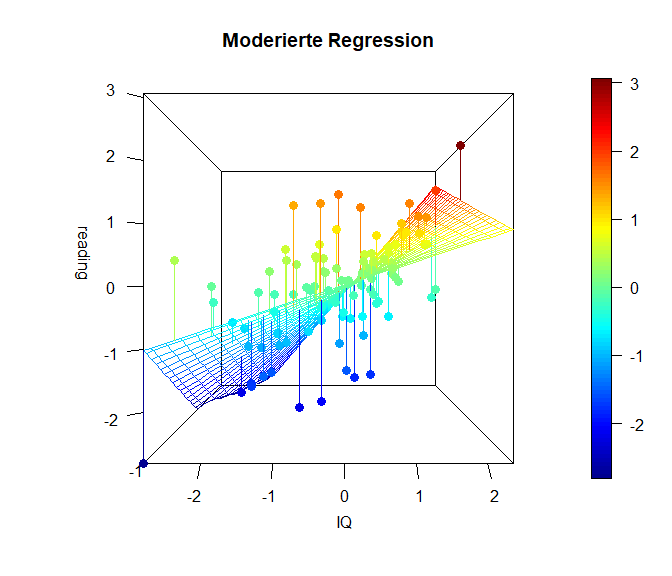
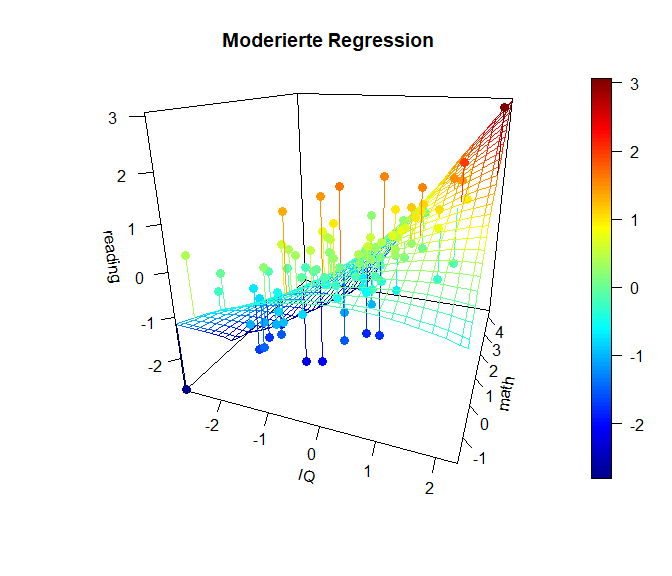
Die folgende Grafik stellt den Sachverhalt noch einmal als 3D Grafik (mit dem Paket plot3D) dar (ziemlich cool oder?). In dieser Grafik erkennen wir sehr deutlich, dass die Simple Slopes tatsächlich eine stark vereinfachte Darstellung sind und es tatsächlich unendlich viele bzw. so viele unterschiedliche Beziehungen zwischen Prädiktor (IQ) und Kriterium (reading) in Abhängigkeit des Moderators (math) gibt, wie dieser (math) Ausprägungen hat. Der Code zu den Grafiken lässt sich in Appendix B nachlesen.
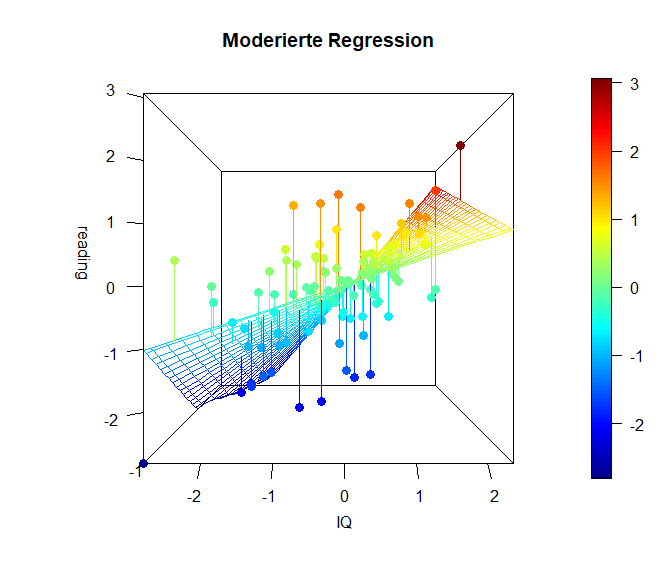
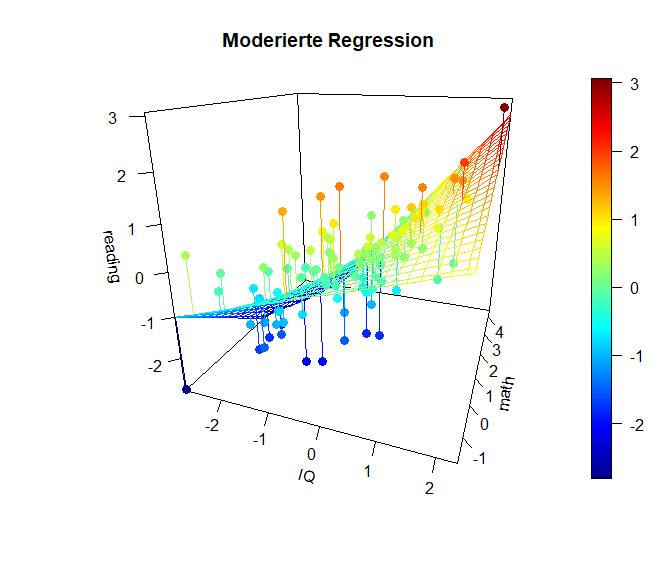
Hier ist die x-Achse ($-links\longleftrightarrow rechts+$) des IQs dargestellt und in die Tiefe ist die Matheleistung (oft z-Achse: ($-vorne\longleftrightarrow hinten+$)). Die y-Achse (im Plot heißt diese blöderweise z-Achse) stellt die Leseleistung dar. ($-unten\longleftrightarrow oben+$). Wir erkennen in dieser Ansicht ein wenig die Simple-Slopes von zuvor, denn die Achse der Matheleistung läuft ins Negative “aus dem Bildschirm hinaus”, während sie ins Positive “in den Bildschirm hinein” verläuft. Der nähere Teil der “Hyperebene” weißt eine geringere Beziehung zwischen dem IQ und der Leseleistung auf, während der Teil, der weiter entfernt liegt, eine stärkere Beziehung aufweist. Genau das haben wir auch in den Simple Slopes zuvor gesehen. Dort war für eine hohe Matheleistung die Beziehung zwischen dem IQ und der Leseleistung auch stärker. Wichtig ist, dass in diesem Plot die Beziehung zwischen dem IQ und der Leseleistung für eine fest gewählte Ausprägung der Matheleistung tatsächlich linear verläuft. Es ist also so, dass wir quasi ganz viele Linien aneinander kleben, um diese gewölbte Ebene zu erhalten. Die Ausprägung der Matheleistung ist im nächsten Plot noch besser zu erkennen, in der der Plot etwas gedreht dargestellt wird. Farblich ist außerdem die Ausprägung der Leseleistung dargestellt, damit die Werte leichter zu vergleichen sind.
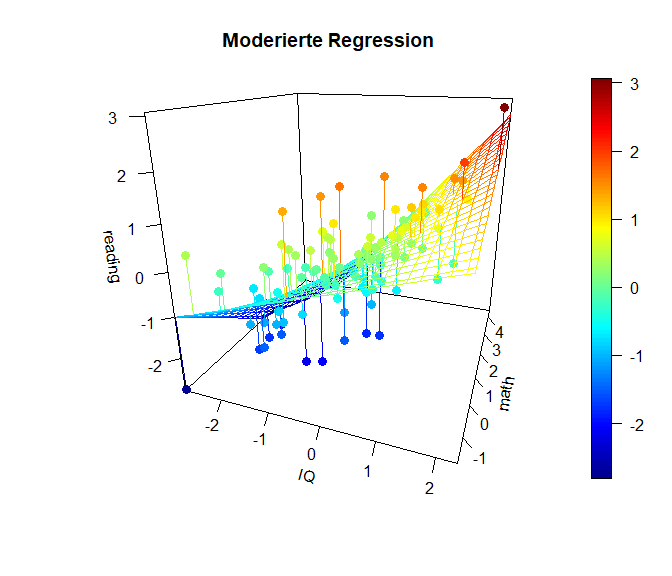
Diese Plots geben einen noch besseren Eindruck davon, was genau bei einer Interaktion passiert und wie “austauschbar” eigentlich der Moderator oder der Prädiktor sind. Außerdem kann man mit den Überlegungen aus diesem Abschnitt leicht einsehen, dass das quadratische Modell von oben tatsächlich ein Spezialfall dieses moderierten Modells ist, in welchem der Prädiktor mit sich selbst interagiert (sich selbst moderiert). Darüber, wie genau man moderierte Regressionen durchführt, gibt es viel Literatur. Einige Forschende sagen, dass man neben der Interaktion auch immer die quadratischen Effekte mit aufnehmen sollte, um auszuschließen, dass die Interaktion ein Artefakt ist, der nur auf quadratische Effekte zurückzuführen ist. Das stellt eine hervorragenden Übung dar, um sich dies einmal anzusehen! In Appendix C sehen Sie die Simple Slopes sowie die 3D-Grafiken auch noch einmal für das “volle” quadratisch-Interaktionsmodell.
Mithilfe der Funktion I() (“as is”, führt dazu, das arithmetische Operatoren als solche interpretiert werden) lassen sich innerhalb des lm Befehls zu dem noch weitere Funktionale hinzufügen, ohne diese vorher erzeugen zu müssen. Beispielsweise ließe sich durch lm(Y ~ X + I(sin(X))) + I(exp(sqrt(X)) folgendes Regressionsmodell schätzen: $Y = \beta_0+\beta_1X + \beta_2\sin(X) + \beta_3e^{\sqrt{X}} + \varepsilon$. Allerdings lassen sich so nicht die Wachstumsraten modellieren (z.B. exponentielles oder logarithmisches Wachstum). Hierzu müssten die Variablen tatsächlich transformiert werden. Dies wollen wir uns in der nächsten Sitzung zur nichtlinearen Regression genauer ansehen.
Literatur
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden (5. Auflage, 1. Auflage: 2010). Weinheim: Beltz.
Appendix A
Exkurs: Was genau macht poly?
X <- 1:10 # Variable X
X2 <- X^2 # Variable X hoch 2
X_poly <- poly(X, 2) # erzeuge Variable X und X hoch mit Hilfe der poly Funktion
colnames(X_poly) <- c("poly(X, 2)1", "poly(X, 2)2")
cbind(X, X2, X_poly)
## X X2 poly(X, 2)1 poly(X, 2)2
## [1,] 1 1 -0.49543369 0.52223297
## [2,] 2 4 -0.38533732 0.17407766
## [3,] 3 9 -0.27524094 -0.08703883
## [4,] 4 16 -0.16514456 -0.26111648
## [5,] 5 25 -0.05504819 -0.34815531
## [6,] 6 36 0.05504819 -0.34815531
## [7,] 7 49 0.16514456 -0.26111648
## [8,] 8 64 0.27524094 -0.08703883
## [9,] 9 81 0.38533732 0.17407766
## [10,] 10 100 0.49543369 0.52223297
Die Funktion poly erzeugt sogenannte orthogonale Polynome. Das bedeutet, dass zwar die $X$ und $X^2$ berechnet werden, diese Terme anschließend allerdings so transformiert werden, dass sie jeweils einen Mittelwert von 0 und die gleiche Varianz haben und zusätzlich noch unkorreliert sind. Die Unkorreliertheit ist wichtig, um z.B. einen quadratischen Effekt vom Haupteffekt des Prädiktors trennen zu können. Wenn $X$ nur positive Werte hat, sind $X$ und $X^2$ ohne zusätzliche Transformation hoch miteinander korreliert, sodass der lineare Effekt von $X$ und der quadratische Effekt von $X^2$ nur schwer voneinander getrennt werden können.
round(apply(X = cbind(X, X2, X_poly), MARGIN = 2, FUN = mean), 2) # Mittelwerte über die Spalten hinweg berechnen
## X X2 poly(X, 2)1 poly(X, 2)2
## 5.5 38.5 0.0 0.0
round(apply(X = cbind(X, X2, X_poly), MARGIN = 2, FUN = sd), 2) # Standardabweichung über die Spalten hinweg berechnen
## X X2 poly(X, 2)1 poly(X, 2)2
## 3.03 34.17 0.33 0.33
round(cor(cbind(X, X2, X_poly)),2) # Korrelationen berechnen
## X X2 poly(X, 2)1 poly(X, 2)2
## X 1.00 0.97 1.00 0.00
## X2 0.97 1.00 0.97 0.22
## poly(X, 2)1 1.00 0.97 1.00 0.00
## poly(X, 2)2 0.00 0.22 0.00 1.00
Die Funktion apply führt an der Matrix, welche dem Argument X übergeben wird, entweder über die Zeilen MARGIN = 1 oder über die Spalten MARGIN = 2 (hier jeweils gewählt) die Funktion aus, welche im Argument FUN angegeben wird. So wird zunächst mit FUN = mean der Mittelwert und anschließend mit FUN = sd die Standardabweichung von $X, X^2$ sowie poly(X, 2) berechnet. Der Korrelationsmatrix ist zu entnehmen, dass $X$ und $X^2$ in diesem Beispiel sehr hoch miteinander korrelieren und somit gleiche lineare Informationen enthalten ($\hat{r}_{X,X^2}$ = cor(X, X2) = 0.97), während die linearen und die quadratischen Anteile in poly(X, 2) keinerlei lineare Gemeinsamkeiten haben - sie sind unkorreliert (cor(poly(X,2)1 , poly(X,2)2) = 0). Ein weiterer Vorteil ist deshalb, dass sich die Parameterschätzungen des linearen Terms im Modell bei sukzessiver Aufnahme der Anteile von poly(X, 2) in ein Regressionmodell nicht (bzw. sehr wenig) ändern. Der Anteil erklärter Varianz bleibt jedoch in allen Modellen gleich - die Modelle sind äquivalent, egal auf welche Art und Weise quadratische Terme gebildet werden.
m1.b1 <- lm(Reading ~ HISEI + poly(MotherEdu, 1) + Books, data = PISA2009)
summary(lm.beta(m1.b1))
##
## Call:
## lm(formula = Reading ~ HISEI + poly(MotherEdu, 1) + Books, data = PISA2009)
##
## Residuals:
## Min 1Q Median 3Q Max
## -261.95 -55.34 13.83 61.24 181.60
##
## Coefficients:
## Estimate Standardized Std. Error t value Pr(>|t|)
## (Intercept) 380.4553 NA 25.6622 14.825 < 2e-16 ***
## HISEI 1.4440 0.2507 0.4769 3.028 0.00291 **
## poly(MotherEdu, 1) 192.2979 0.1628 96.5335 1.992 0.04823 *
## Books 16.1988 0.2272 5.9608 2.718 0.00737 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 84.28 on 146 degrees of freedom
## Multiple R-squared: 0.2564, Adjusted R-squared: 0.2411
## F-statistic: 16.78 on 3 and 146 DF, p-value: 2.034e-09
m1.b2 <- lm(Reading ~ HISEI + poly(MotherEdu, 2) + Books, data = PISA2009)
summary(lm.beta(m1.b2))
##
## Call:
## lm(formula = Reading ~ HISEI + poly(MotherEdu, 2) + Books, data = PISA2009)
##
## Residuals:
## Min 1Q Median 3Q Max
## -247.206 -50.365 8.392 57.886 171.694
##
## Coefficients:
## Estimate Standardized Std. Error t value Pr(>|t|)
## (Intercept) 377.9988 NA 25.4205 14.870 < 2e-16 ***
## HISEI 1.4692 0.2550 0.4720 3.113 0.00223 **
## poly(MotherEdu, 2)1 187.5689 0.1588 95.5443 1.963 0.05154 .
## poly(MotherEdu, 2)2 -169.6388 -0.1436 83.5003 -2.032 0.04402 *
## Books 16.5747 0.2324 5.9009 2.809 0.00566 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 83.4 on 145 degrees of freedom
## Multiple R-squared: 0.2769, Adjusted R-squared: 0.257
## F-statistic: 13.88 on 4 and 145 DF, p-value: 1.3e-09
PISA2009$MotherEdu2 <- PISA2009$MotherEdu^2 # füge dem Datensatz den quadrierten Bildungsabschluss der Mutter hinzu
m1.c1 <- lm(Reading ~ HISEI + MotherEdu + Books, data = PISA2009)
summary(lm.beta(m1.c1))
##
## Call:
## lm(formula = Reading ~ HISEI + MotherEdu + Books, data = PISA2009)
##
## Residuals:
## Min 1Q Median 3Q Max
## -261.95 -55.34 13.83 61.24 181.60
##
## Coefficients:
## Estimate Standardized Std. Error t value Pr(>|t|)
## (Intercept) 340.7035 NA 24.0770 14.151 < 2e-16 ***
## HISEI 1.4440 0.2507 0.4769 3.028 0.00291 **
## MotherEdu 10.7052 0.1628 5.3740 1.992 0.04823 *
## Books 16.1988 0.2272 5.9608 2.718 0.00737 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 84.28 on 146 degrees of freedom
## Multiple R-squared: 0.2564, Adjusted R-squared: 0.2411
## F-statistic: 16.78 on 3 and 146 DF, p-value: 2.034e-09
m1.c2 <- lm(Reading ~ HISEI + MotherEdu + MotherEdu2 + Books, data = PISA2009)
summary(lm.beta(m1.c2))
##
## Call:
## lm(formula = Reading ~ HISEI + MotherEdu + MotherEdu2 + Books,
## data = PISA2009)
##
## Residuals:
## Min 1Q Median 3Q Max
## -247.206 -50.365 8.392 57.886 171.694
##
## Coefficients:
## Estimate Standardized Std. Error t value Pr(>|t|)
## (Intercept) 283.9386 NA 36.7185 7.733 1.62e-12 ***
## HISEI 1.4692 0.2550 0.4720 3.113 0.00223 **
## MotherEdu 46.0086 0.6998 18.1726 2.532 0.01241 *
## MotherEdu2 -4.8171 -0.5597 2.3711 -2.032 0.04402 *
## Books 16.5747 0.2324 5.9009 2.809 0.00566 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 83.4 on 145 degrees of freedom
## Multiple R-squared: 0.2769, Adjusted R-squared: 0.257
## F-statistic: 13.88 on 4 and 145 DF, p-value: 1.3e-09
rbind(coef(m1.b1), coef(m1.c1)) # vgl Koeffizienten
## (Intercept) HISEI poly(MotherEdu, 1) Books
## [1,] 380.4553 1.443998 192.29788 16.19878
## [2,] 340.7035 1.443998 10.70515 16.19878
rbind(coef(m1.b2),coef(m1.c2)) # vgl Koeffizienten
## (Intercept) HISEI poly(MotherEdu, 2)1 poly(MotherEdu, 2)2 Books
## [1,] 377.9988 1.469164 187.56888 -169.638816 16.57467
## [2,] 283.9386 1.469164 46.00863 -4.817134 16.57467
rbind(summary(m1.b1)$r.squared, summary(m1.c1)$r.squared) # vgl R^2
## [,1]
## [1,] 0.2563619
## [2,] 0.2563619
rbind(summary(m1.b2)$r.squared,summary(m1.c2)$r.squared) # vgl R^2
## [,1]
## [1,] 0.2769434
## [2,] 0.2769434
Wir erkennen, dass die Funktion poly keinen Einfluss auf die Güte des Modells hat. Dies lässt sich bspw. auch an dem $R^2$ der jeweiligen Modelle ablesen. Auch die Effekte der anderen Variablen sind über die Modelle hinweg identisch.
Ähnliches hätten wir auch bewirken können, indem wir die Variablen zentriert hätten, anstatt sie mit poly zu transformieren.
Einordnung quadratischer Verläufe
Wie kommen wir nun auf die Interpretation der quadratischen Beziehung?Eine allgemeine quadratische Funktion $f$ hat folgende Gestalt: $$f(x):=ax^2 + bx + c,$$ wobei $a\neq 0$, da es sich sonst nicht um eine quadratische Funktion handelt. Wäre $a=0$, würde es sich um eine lineare Funktion mit Achsenabschnitt $c$ und Steigung (Slope) $b$ handeln. Wäre zusätzlich $b=0$, handelt es sich um eine horizontale Linie bei $y=f(x)=c$. Für betraglich große $x$ fällt $x^2$ besonders ins Gewicht. Damit entscheidet das Vorzeichen von $a$, ob es sich um eine u-förmige (falls $a>0$) oder eine umgekehrt-u-förmige (falls $a<0$) Beziehung handelt. Die betragliche Größe von $a$ entscheidet hierbei, wie gestaucht die u-förmige Beziehung (die Parabel) ist. Die reine quadratische Beziehung $f(x)=x^2$ sieht so aus:
a <- 1; b <- 0; c <- 0
x <- seq(-2,2,0.01)
f <- a*x^2 + b*x + c
data_X <- data.frame(x, f)
ggplot(data = data_X, aes(x = x, y = f)) +
geom_line(col = "black")+
labs(x = "x", y = "f(x)",
title = expression("f(x)="~x^2))
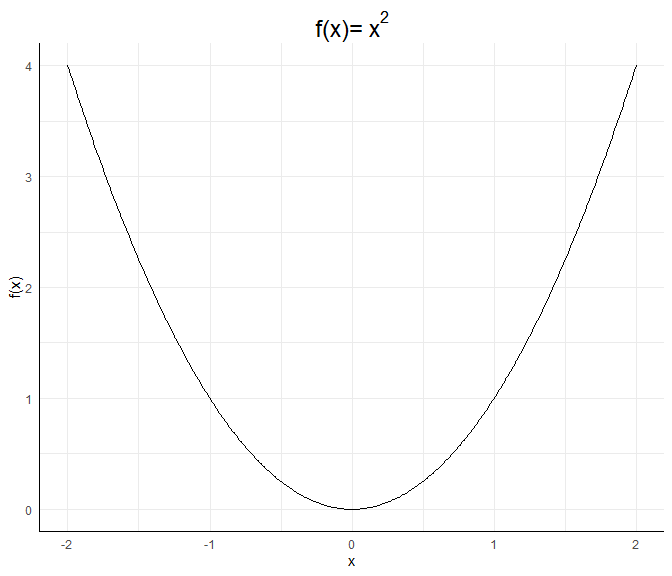 Wir werden diese Funktion immer als Referenz mit in die Grafiken einzeichnen.
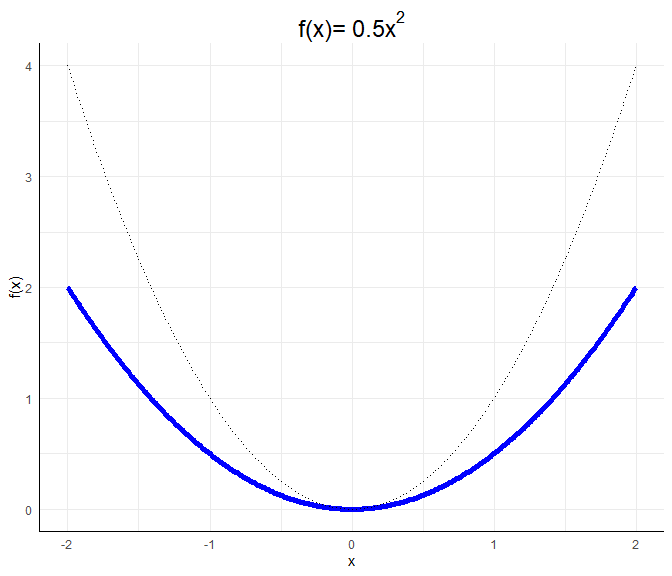
Wir werden diese Funktion immer als Referenz mit in die Grafiken einzeichnen.a <- 0.5; b <- 0; c <- 0
x <- seq(-2,2,0.01)
f <- a*x^2 + b*x + c
data_X <- data.frame(x, f)
ggplot(data = data_X, aes(x = x, y = f)) +
geom_line(col = "blue", lwd = 2)+ geom_line(mapping = aes(x, x^2), lty = 3)+
labs(x = "x", y = "f(x)",
title = expression("f(x)="~0.5*x^2))
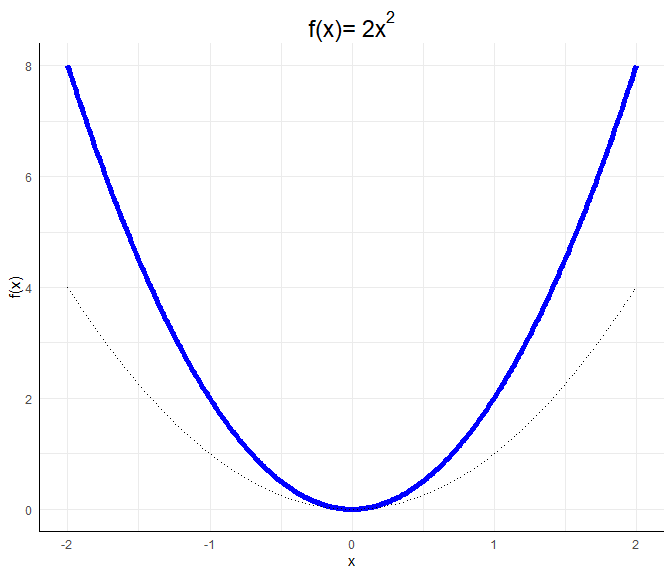
a <- 2; b <- 0; c <- 0
x <- seq(-2,2,0.01)
f <- a*x^2 + b*x + c
data_X <- data.frame(x, f)
ggplot(data = data_X, aes(x = x, y = f)) +
geom_line(col = "blue", lwd = 2)+ geom_line(mapping = aes(x, x^2), lty = 3)+
labs(x = "x", y = "f(x)",
title = expression("f(x)="~2*x^2))
a <- -1; b <- 0; c <- 0
x <- seq(-2,2,0.01)
f <- a*x^2 + b*x + c
data_X <- data.frame(x, f)
ggplot(data = data_X, aes(x = x, y = f)) +
geom_line(col = "blue", lwd = 2)+ geom_line(mapping = aes(x, x^2), lty = 3)+
labs(x = "x", y = "f(x)",
title = expression("f(x)="~-x^2))
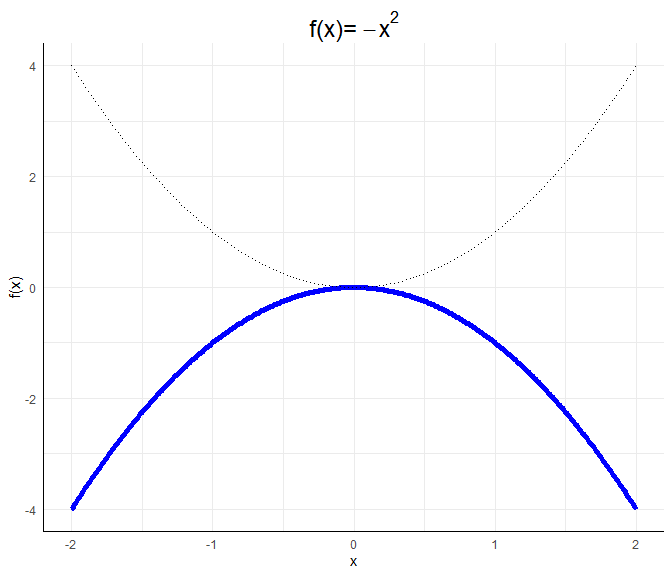
Diese invers-u-förmige Beziehung ist eine konkave Funktion. Als Eselsbrücke für das Wort konkav, welches fast das englische Wort cave enthält, können wir uns merken: Eine konkave Funktion stellt eine Art Höhleneingang dar.
$c$ bewirkt eine vertikale Verschiebung der Parabel:
a <- 1; b <- 0; c <- 1
x <- seq(-2,2,0.01)
f <- a*x^2 + b*x + c
data_X <- data.frame(x, f)
ggplot(data = data_X, aes(x = x, y = f)) +
geom_line(col = "blue", lwd = 2)+ geom_line(mapping = aes(x, x^2), lty = 3)+
labs(x = "x", y = "f(x)",
title = expression("f(x)="~x^2+1))
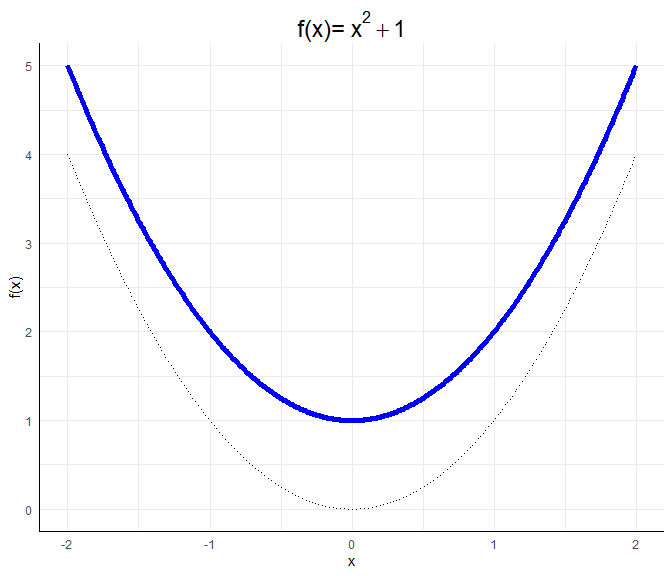
$b$ bewirkt eine horizontale und vertikale Verschiebung, die nicht mehr leicht vorhersehbar ist. Für $f(x)=x^2+x$ lässt sich beispielsweise durch Umformen $f(x)=x^2+x=x(x+1)$ leicht erkennen, dass diese Funktion zwei Nullstellen bei $0$ und $-1$ hat. Somit ist ersichtlich, dass die Funktion nach unten und nach links verschoben ist:
a <- 1; b <- 1; c <- 0
x <- seq(-2,2,0.01)
f <- a*x^2 + b*x + c
data_X <- data.frame(x, f)
ggplot(data = data_X, aes(x = x, y = f)) +
geom_line(col = "blue", lwd = 2)+ geom_line(mapping = aes(x, x^2), lty = 3)+
labs(x = "x", y = "f(x)",
title = expression("f(x)="~x^2+x))
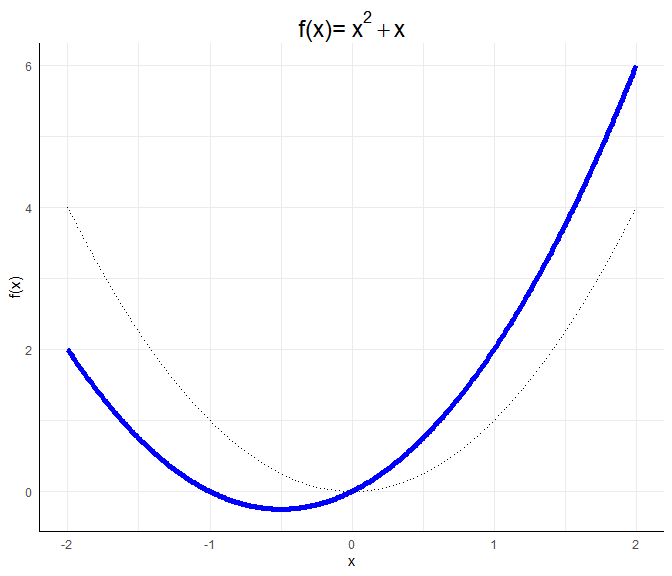
Für die genaue Gestalt einer allgemeinen quadratischen Funktion $ax^2 + bx + c$ würden wir die Nullstellen durch das Lösen der Gleichung $ax^2 + bx + c=0$ bestimmen (via p-q Formel oder a-b-c-Formel). Den Scheitelpunkt würden wir durch das Ableiten und Nullsetzen der Gleichung bestimmen. Wir müssten also $2ax+b=0$ lösen und dies in die Gleichung einsetzen. Wir könnten auch die binomischen Formeln nutzen, um die Funktion in die Gestalt $f(x):=a’(x-b’)^2+c’$ oder $f(x):=a’(x-b’_1)(x-b_2’)+c’$ zu bekommen, falls die Nullstellen reell sind (also das Gleichungssystem lösbar ist), da wir so die Nullstellen ablesen können als $b’$ oder $b_1’$ und $b_2’$, falls $c=0$. Für die Interpretation der Ergebnisse reicht es zu wissen, dass $a$ eine Stauchung bewirkt und entscheind dafür ist, ob die Funktion u-förmig oder invers-u-förmig verläuft.
a <- -0.5; b <- 1; c <- 2
x <- seq(-2,2,0.01)
f <- a*x^2 + b*x + c
data_X <- data.frame(x, f)
ggplot(data = data_X, aes(x = x, y = f)) +
geom_line(col = "blue", lwd = 2)+ geom_line(mapping = aes(x, x^2), lty = 3)+
labs(x = "x", y = "f(x)",
title = expression("f(x)="~-0.5*x^2+x+2))
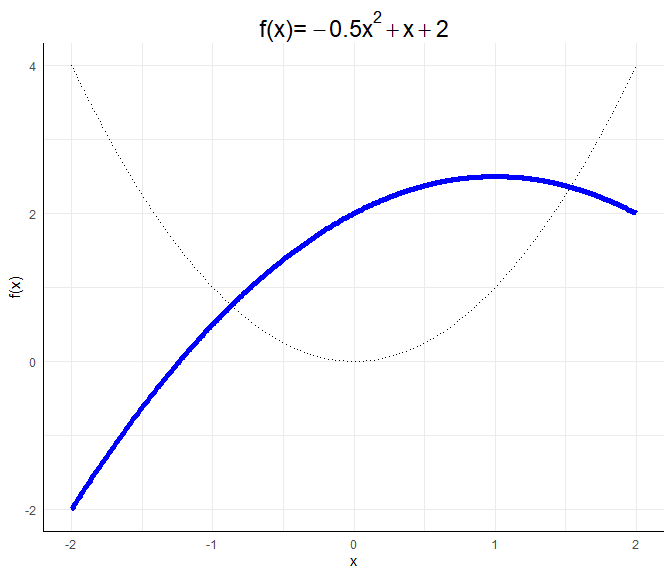 $\longrightarrow$ so ähnlich sieht die bedingte Beziehung (kontrolliert für die weiteren Prädiktoren im Modell) zwischen dem Bildungsabschluss der Mutter und der Leseleistung aus.
$\longrightarrow$ so ähnlich sieht die bedingte Beziehung (kontrolliert für die weiteren Prädiktoren im Modell) zwischen dem Bildungsabschluss der Mutter und der Leseleistung aus.Code für quadratische Verlaufsgrafik
Der Code, der die Grafik des standardisierten vorhergesagten bedingten Verlaufs des Bildungsabschlusses der Mutter erzeugt, sieht folgendermaßen aus:X <- scale(poly(PISA2009$MotherEdu, 2))
std_par_ME <- c(0.1588, -0.1436)
pred_effect_ME <- X %*% std_par_ME
std_ME <- X[,1]
data_ME <- data.frame(std_ME, pred_effect_ME)
ggplot(data = data_ME, aes(x = std_ME, y = pred_effect_ME)) + geom_point(pch = 16, col = "blue", cex = 4)+
labs(y = "std. Leseleistung | Others", x = "std. Bildungsabschluss der Mutter | Others",
title = "Standardisierte bedingte Beziehung zwischen\n Bildungsabschluss der Mutter und Leseleistung")
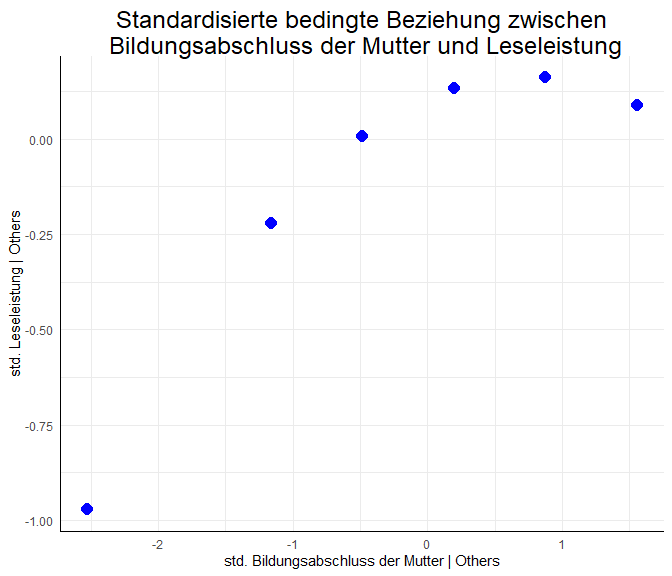
Wir verwenden scale, um die linearen und quadratischen Anteile des Bildungsabschlusses der Mutter zu standardisieren und speichern sie in X. Anschließend ist das Interzept der quadratischen Funktion 0 ($c=0$, da wir standardisiert haben). Die zugehörigen standardisierten Koeffizienten sind $b=0.1588$ und $a=-0.1436$, die wir aus der standardisierten summary abgelesen haben. Somit wissen wir, dass es sich um eine invers-u-förmige Beziehung handelt (ohne die Grafik zu betrachten). Wir speichern die standardisierten Koeffizienten unter std_par_ME ab und verwenden anschließend das Matrixprodukt X %*% std_par_ME, um die vorhergesagten Werte via $y_{std,i}=0.1588 ME - 0.1436ME^2$ zu berechnen. Diese vorhergesagten Werte pred_effect_ME plotten wir nun gegen die standardisierten Werte des Bildungsabschlusses der Mutter std_ME, welche in der ersten Spalte von X stehen: X[, 1].
Exkurs: Zentrierung vs. poly
Wir vergleichen nun an einem ganz einfachen Beispiel, was poly und was Zentrierung bewirkt. Dazu erstellen wir einen Vektor (also eine Variable) $A$ der die Zahlen von 0 bis 10 enthält in 0.1 Schritten:
A <- seq(0, 10, 0.1)
Nun bestimmen wir zunächst die Korrelation zwischen $A$ und $A^2$:
cor(A, A^2)
## [1] 0.9676503
welche sehr hoch ausfällt. Wir hatten bereits mit poly erkannt, dass diese Funktion die linearen und quadratischen Anteile trennt. Nun zentrieren wir die Daten. Das geht entweder händisch oder mit der scale Funktion:
A_c <- A - mean(A)
mean(A_c)
## [1] 2.639528e-16
A_c2 <- scale(A, center = T, scale = F) # scale = F bewirkt, dass nicht auch noch die SD auf 1 gesetzt werden soll
mean(A_c2)
## [1] 2.639528e-16
Nun vergleichen wir die Korrelationen zwischen $A_c$ mit $A_c^2$ mit den Ergebnissen von poly:
cor(A_c, A_c^2)
## [1] 1.763581e-16
cor(poly(A, 2))
## 1 2
## 1 1.000000e+00 9.847944e-17
## 2 9.847944e-17 1.000000e+00
# auf 15 Nachkommastellen gerundet:
round(cor(A_c, A_c^2), 15)
## [1] 0
round(cor(poly(A, 2)), 15)
## 1 2
## 1 1 0
## 2 0 1
beide Vorgehensweisen sind bis auf 15 Nachkommastellen identisch!
Spaßeshalber nehmen wir noch die Terme $A^3$ und $A^4$ auf und vergleichen die Ergebnisse:
# auf 15 Nachkommastellen gerundet:
round(cor(cbind(A, A^2, A^3, A^4)), 2)
## A
## A 1.00 0.97 0.92 0.86
## 0.97 1.00 0.99 0.96
## 0.92 0.99 1.00 0.99
## 0.86 0.96 0.99 1.00
round(cor(cbind(A_c, A_c^2, A_c^3, A_c^4)), 2)
## A_c
## A_c 1.00 0.00 0.92 0.00
## 0.00 1.00 0.00 0.96
## 0.92 0.00 1.00 0.00
## 0.00 0.96 0.00 1.00
round(cor(poly(A, 4)), 2)
## 1 2 3 4
## 1 1 0 0 0
## 2 0 1 0 0
## 3 0 0 1 0
## 4 0 0 0 1
Was wir nun erkennen ist, dass $A, A^2, A^3, A^4$ sehr hoch korreliert sind. Die zentrierten Variablen zeigen ein etwas anderes Bild. Hier ist $A_c$ und $A_c^3$ sehr hoch korreliert sowie $A_c^2$ und $A_c^4$ sind sehr hoch korreliert. Man sagt auch, dass nur gerade Potenzen ($A^2, A^4, A^6,\dots$) untereinander und ungerade Potenzen ($A=A^1, A^3, A^5,\dots$) untereinander korreliert sind, wenn die Daten zentriert sind. Bei poly verschwinden alle Korrelationen zwischen $A, A^2, A^3, A^4$. Hier dran erkennen wir, dass wenn wir nur Terme zur 2. Ordnung/Potenz (also $A$ und $A^2$ und natürlich Interaktionen $AB$, aber eben nicht $A^3$ bzw. $AB^2$ oder $A^2B$, etc.) im Modell haben, dann reicht die Zentrierung aus, um extreme Kollinearitäten zu zwischen linearen und nichtlinearen Termen zu vermeiden.
Da wir hier die Korrelationen betrachtet haben, kommt eine Standardisierung von $A$ zu identischen Ergebnissen, weswegen wir hierauf verzichten.
Mathematische Begründung
Dieser Abschnitt ist für die “Warum ist das so?"-Fragenden bestimmt und ist als reinen Zusatz zu erkennen.
Wir wissen, dass die Korrelation der Bruch aus der Kovarianz zweier Variablen geteilt durch deren Standardabweichung ist. Aus diesem Grund reicht es, die Kovarianz zweier Variablen zu untersuchen, um zu schauen, wann die Korrelation 0 ist. Wir hatten oben die Variablen zentriert und bemerkt, dass dann die Korrelation zwischen $A_c$ und $A_c^2$ verschwindet. Warum ist das so? Dazu stellen wir $A$ in Abhängigkeit von seinem Mittelwert $\mu_A$ und $A_c$, der zentrierten Version von $A$, dar:
$$A := \mu_A + A_c$$
So kann jede Variable zerlegt werden: in seinen Mittelwert (hier: $\mu_A$) und die Abweichung vom Mittelwert (hier: $A_c$). Nun bestimmen wir die Kovarianz zwischen den Variablen $A$ und $A^2$ und setzen in diesem Prozess $\mu_A+A_c$ für $A$ ein und wenden die binomische Formel an $(a+b)^2=a^2+2ab+b^2$.
\begin{align} \mathbb{C}ov[A, A^2] &= \mathbb{C}ov[\mu_A + A_c, (\mu_A + A_c)^2]\\ &= \mathbb{C}ov[A_c, \mu_A^2 + 2\mu_AA_c + A_c^2]\\ &= \mathbb{C}ov[A_c, \mu_A^2] + \mathbb{C}ov[A_c, 2\mu_AA_c] + \mathbb{C}ov[A_c, A_c^2] \end{align}An dieser Stelle pausieren wir kurz und bemerken, dass wir diese beiden Ausdrücke schon kennen $\mathbb{C}ov[A_c, \mu_A^2] = \mathbb{C}ov[A_c, A_c^2] = 0$. Ersteres ist die Kovarianz zwischen einer Konstanten und einer Variable, welche immer 0 ist und, dass die Kovarianz zwischen $A_c$ und $A_c^2$ 0 ist, hatten wir oben schon bemerkt! Diese Aussage, dass die Korrelation/Kovarianz zwischen $A_c$ und $A_c^2$ 0 ist, gilt insbesondere für die transformierten Daten mittels poly (hier bezeichnet $A_c^2$ quasi den quadratischen Anteil, der erstellt wird) und auch für einige Verteilungen (z.B. symmetrische Verteilungen, wie die Normalverteilung) ist so, dass die linearen Anteile und die quadratischen Anteile unkorreliert sind. Im Allgemeinen gilt dies leider nicht.
Folglich können wir sagen, dass
\begin{align} \mathbb{C}ov[A, A^2] &= \mathbb{C}ov[A_c, 2\mu_AA_c] \\ &= 2\mu_A\mathbb{C}ov[A_c,A_c]=2\mu_A\mathbb{V}ar[A], \end{align}wobei wir hier benutzen, dass die Kovarianz mit sich selbst die Varianz ist und dass die zentrierte Variable $A_c$ die gleiche Varianz wie $A$ hat (im Allgemeinen, siehe weiter unten, bleibt auch noch die Kovarianz zwischen $A_c$ und $A_c^2$ erhalten). Dies können wir leicht prüfen:
var(A)
## [1] 8.585
var(A_c)
## [1] 8.585
# Kovarianz
cov(A, A^2)
## [1] 85.85
2*mean(A)*var(A)
## [1] 85.85
# zentriert:
round(cov(A_c, A_c^2), 14)
## [1] 0
round(2*mean(A_c)*var(A_c), 14)
## [1] 0
Der zentrierte Fall ist auf 14 Nachkommastellen identisch und weicht danach nur wegen der sogenannten Maschinengenauigkeit von einander ab. Somit ist klar, dass wenn der Mittelwert = 0 ist, dann ist auch die Korrelation zwischen einer Variable und seinem Quadrat 0. Analoge Überlegungen können genutzt werden, um das gleiche für die Interaktion von Variablen zu sagen.
Im Allgemeinen:
Im Allgemeinen ist es dennoch sinnvoll die Daten zu zentrieren, wenn quadratische Effekte (oder Interaktionseffekte) eingesetzt werden, da zumindest immer gilt:
\begin{align} \mathbb{C}ov[A, A^2] &= \mathbb{C}ov[A_c, 2\mu_AA_c] + \mathbb{C}ov[A_c, A_c^2] \ &=2\mu_A\mathbb{V}ar[A]+ \mathbb{C}ov[A_c, A_c^2], \end{align}
somit wird die Kovarianz zwischen $A$ und $A^2$ künstlich vergrößert, wenn die Daten nicht zentriert sind. Denn nutzen wir zentrierte Variablen ist nur noch $\mathbb{C}ov[A_c, A_c^2]$ relevant (da $\mu_A=0$).
Appendix B
Code zu 3D Grafiken
library(plot3D)
# Übersichtlicher: Vorbereitung
x <- Schulleistungen_std$IQ
y <- Schulleistungen_std$reading
z <- Schulleistungen_std$math
fit <- lm(y ~ x*z)
grid.lines = 26
x.pred <- seq(min(x), max(x), length.out = grid.lines)
z.pred <- seq(min(z), max(z), length.out = grid.lines)
xz <- expand.grid( x = x.pred, z = z.pred)
y.pred <- matrix(predict(fit, newdata = xz),
nrow = grid.lines, ncol = grid.lines)
fitpoints <- predict(fit)
# Plot:
scatter3D(x = x, y = z, z = y, pch = 16, cex = 1.2,
theta = 0, phi = 0, ticktype = "detailed",
xlab = "IQ", ylab = "math", zlab = "reading",
surf = list(x = x.pred, y = z.pred, z = y.pred,
facets = NA, fit = fitpoints),
main = "Moderierte Regression")
scatter3D(x = x, y = z, z = y, pch = 16, cex = 1.2,
theta = 20, phi = 20, ticktype = "detailed",
xlab = "IQ", ylab = "math", zlab = "reading",
surf = list(x = x.pred, y = z.pred, z = y.pred,
facets = NA, fit = fitpoints),
main = "Moderierte Regression")
Für weitere Informationen zum Umgang mit diesem Plot siehe bspw. hier: 3D Grafiken mit plot3D .
Appendix C
Simple Slopes und 3D Grafiken für das "volle" quadratische und Interaktionsmodell
Für die Simple Slopes müssen wir nur die quadratischen Effekte aufnehmen und erkennen, dass es nun nicht mehr Geraden sondern Kurven sind:
mod_reg_full <- lm(reading ~ math + IQ + math:IQ + I(math^2) + I(IQ^2), data = Schulleistungen_std)
summary(mod_reg_full)
##
## Call:
## lm(formula = reading ~ math + IQ + math:IQ + I(math^2) + I(IQ^2),
## data = Schulleistungen_std)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.00105 -0.49725 0.09789 0.45998 1.77402
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.06917 0.11580 -0.597 0.551736
## math -0.02013 0.19700 -0.102 0.918823
## IQ 0.58110 0.16162 3.596 0.000518 ***
## I(math^2) -0.03266 0.07773 -0.420 0.675325
## I(IQ^2) -0.09759 0.12960 -0.753 0.453316
## math:IQ 0.28688 0.19461 1.474 0.143780
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.8245 on 94 degrees of freedom
## Multiple R-squared: 0.3545, Adjusted R-squared: 0.3202
## F-statistic: 10.33 on 5 and 94 DF, p-value: 6.524e-08
interact_plot(model = mod_reg_full, pred = IQ, modx = math, modx.values = c(-3, -1, 0, 1, 3))
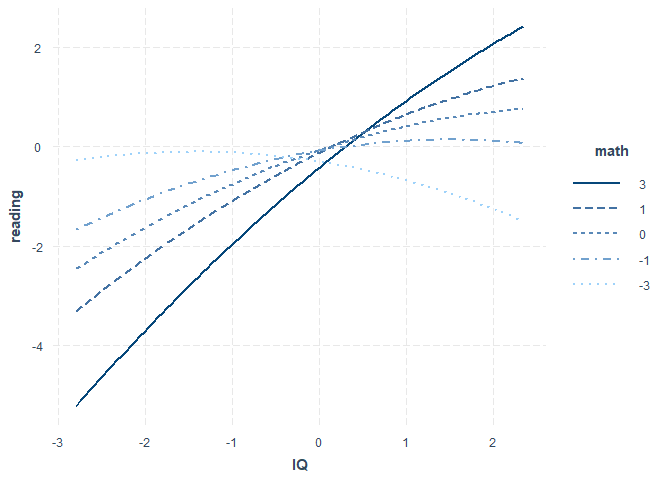
Mit modx.values = c(-3, -1, 0, 1, 3) stellen wir hier noch ein, dass wir auch Geraden für $\pm 3 SD$ und $\pm 1 SD$ des Moderators (math) sehen wollen. Wir erkennen in der Summary auch, dass im vollen Modell nur noch der IQ einen linearen Effekt auf reading hat!
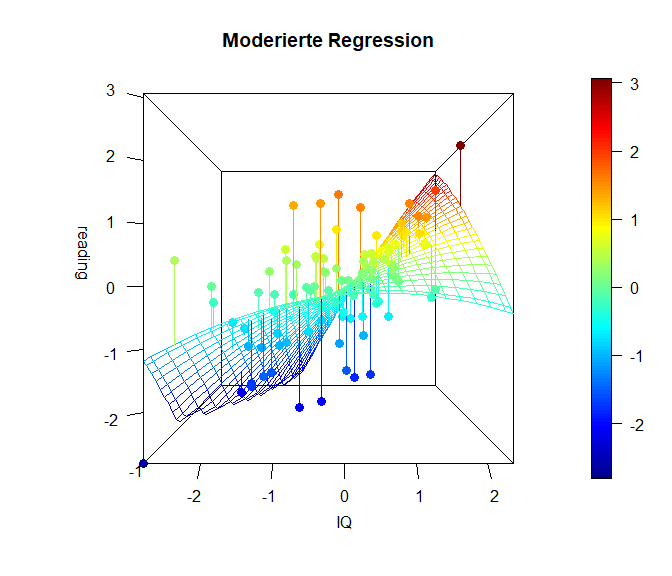
Gleiches erkennen wir auch in den 3D-Plots:
library(plot3D)
# Übersichtlicher: Vorbereitung
x <- Schulleistungen_std$IQ
y <- Schulleistungen_std$reading
z <- Schulleistungen_std$math
fit <- lm(y ~ x*z + I(x^2) + I(z^2))
grid.lines = 26
x.pred <- seq(min(x), max(x), length.out = grid.lines)
z.pred <- seq(min(z), max(z), length.out = grid.lines)
xz <- expand.grid( x = x.pred, z = z.pred)
y.pred <- matrix(predict(fit, newdata = xz),
nrow = grid.lines, ncol = grid.lines)
fitpoints <- predict(fit)
# Plot:
scatter3D(x = x, y = z, z = y, pch = 16, cex = 1.2,
theta = 0, phi = 0, ticktype = "detailed",
xlab = "IQ", ylab = "math", zlab = "reading",
surf = list(x = x.pred, y = z.pred, z = y.pred,
facets = NA, fit = fitpoints),
main = "Moderierte Regression")
scatter3D(x = x, y = z, z = y, pch = 16, cex = 1.2,
theta = 20, phi = 20, ticktype = "detailed",
xlab = "IQ", ylab = "math", zlab = "reading",
surf = list(x = x.pred, y = z.pred, z = y.pred,
facets = NA, fit = fitpoints),
main = "Moderierte Regression")
Auch die 3D-Grafiken sind nicht länger aus “Geraden zusammengesetzt”, sondern bestehen aus Parabeln/Kurven!
Literatur
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden (5. Auflage, 1. Auflage: 2010). Weinheim: Beltz.
- Blau hinterlegte Autor:innenangaben führen Sie direkt zur universitätsinternen Ressource.
](/media/header/schoolbus.jpg)