](/media/header/rice-field.jpg)
Vorbereitung
Zunächst müssen wir das readxl, forcats und das dplyr Paket wieder aktivieren und einen Teil des Code aus dem letzten Tutorial und den letzten Aufgaben wieder durchführen.
# Paket einladen
library(readxl)
library(dplyr)
library(forcats)
# Pfad setzen
rstudioapi::getActiveDocumentContext()$path |>
dirname() |>
setwd()
# Daten einladen
data <- read_excel("Pennington_2021.xlsx", sheet = "Study_Data")
# Faktoren erstellen
data$Gender <- factor(data$Gender,
levels = c(1, 2),
labels = c("weiblich", "männlich"))
data$Year <- as.factor(data$Year)
# Faktoren Rekodieren
data$Year <- fct_recode(data$Year,
"7. Schuljahr" = "Year7",
"8. Schuljahr" = "Year8")
data$Ethnicity <- as.factor(data$Ethnicity)
# NA-Werte ersetzen
data <- data %>%
mutate(across(where(is.numeric), ~ na_if(.x, -9)))
# Skalenwerte erstellen
data <- data %>%
mutate(Total_Competence = rowMeans(data[,c("Total_Competence_Maths", "Total_Competence_English", "Total_Competence_Science")]))
data$Total_SelfConcept <- rowMeans(data[, c("Total_SelfConcept_Maths", "Total_SelfConcept_Science", "Total_SelfConcept_English")])
# Gruppierungsvariablen erstellen
data <- data %>%
mutate(Achiever = case_when(
Total_Competence_Maths >= 4 &
Total_Competence_English >= 4 &
Total_Competence_Science >= 4 ~ "High Achiever",
Total_Competence_Maths == 1 &
Total_Competence_English == 1 &
Total_Competence_Science == 1 ~ "Low Achiever",
TRUE ~ "Medium Achiever" # Alle anderen Fälle
))
data <- data %>%
mutate(Career_Recommendation = case_when(
Maths_AttainmentData > 10 |
Science_AttainmentData > 10 |
Eng_AttainmentData > 10 |
Computing_AttainmentData > 10 ~ "Empfohlen",
TRUE ~ "Nicht empfohlen"
)) # Erstellen der neuen Variable
Falls Sie nicht am Workshop teilnehmen und daher keine lokale Version des Datensatzes haben, verwenden Sie diesen Code.
# Paket einladen
library(readxl)
library(dplyr)
library(forcats)
# Daten einladen
source("https://pandar.netlify.app/workshops/fdz/fdz_data_prep.R")
# Faktoren erstellen
data$Gender <- factor(data$Gender,
levels = c(1, 2),
labels = c("weiblich", "männlich"))
data$Year <- as.factor(data$Year)
# Faktoren Rekodieren
data$Year <- fct_recode(data$Year,
"7. Schuljahr" = "Year7",
"8. Schuljahr" = "Year8")
data$Ethnicity <- as.factor(data$Ethnicity)
# NA-Werte ersetzen
data <- data %>%
mutate(across(where(is.numeric), ~ na_if(.x, -9)))
# Skalenwerte erstellen
data <- data %>%
mutate(Total_Competence = rowMeans(data[,c("Total_Competence_Maths", "Total_Competence_English", "Total_Competence_Science")]))
data$Total_SelfConcept <- rowMeans(data[, c("Total_SelfConcept_Maths", "Total_SelfConcept_Science", "Total_SelfConcept_English")])
# Gruppierungsvariablen erstellen
data <- data %>%
mutate(Achiever = case_when(
Total_Competence_Maths >= 4 &
Total_Competence_English >= 4 &
Total_Competence_Science >= 4 ~ "High Achiever",
Total_Competence_Maths == 1 &
Total_Competence_English == 1 &
Total_Competence_Science == 1 ~ "Low Achiever",
TRUE ~ "Medium Achiever" # Alle anderen Fälle
))
data <- data %>%
mutate(Career_Recommendation = case_when(
Maths_AttainmentData > 10 |
Science_AttainmentData > 10 |
Eng_AttainmentData > 10 |
Computing_AttainmentData > 10 ~ "Empfohlen",
TRUE ~ "Nicht empfohlen"
)) # Erstellen der neuen Variable
Grafikerstellung
Neben der Durchführung analytischer Methoden ist auch die Grafikerstellung in Basic R grundsätzlich möglich. Die Logik dabei bleibt auch dahingehend gleich, dass eine Funktion aufgerufen wird, die bestimmte Argumente benötigt.
Wollen wir zum Beispiel uns die Häufigkeiten für Geschlecht als Balekndiagramm anzeigen lassen, können wir die barplot()-Funktion verwenden. Die Häufigkeiten selbst werden, wie bereits gelernt, mit der table() Funktion erstellt.
#### Grafikerstellung ----
gender_freq <- table(data$Gender) # absolute Häufigkeiten in Objekt ablegen
barplot(gender_freq) # Balkendiagramm erstellen
Natürlich könnten diese beiden Schritte auch in einer Zeile zusammengefasst werden, indem man die Funktion schachtelt (oder durch die Verwendung von Pipes). Durch die Nutzung der barplot() Funktion gewinnen wir schon einen guten Überblick über die Daten, doch wenn wir in die zugehörige Hilfe schauen, sehen wir, dass die optische Aufbereitung durch viele zusätzliche Argumente noch verbessert werden könnte. Einige von diesen werden wir häufiger verwenden. Bspw. verwendet man main für den Titel, xlab und ylab für die Achsenbeschriftung.
barplot(table(data$Gender),
main = "Geschlechtshäufigkeiten",
xlab = "Geschlecht",
ylab = "Absolute Häufigkeit")
Die Grafik hat dadurch an Informationsgehalt gewonnen.
Als Darstellungsform für ordinalskalierte Variablen wird häufig ein Boxplot verwendet. Auch dieser ist sehr einfach nutzbar über die Funktion boxplot(). Dabei nutzen wir direkt auch die Möglichkeit, die Grafik zu beschriften.
# Erstellung eines Boxplots mit passender Beschriftung
boxplot(data$Total_Competence_Science,
main = "Boxplot der Kompetenz in Naturwissenschaften",
ylab = "Skalenscore")
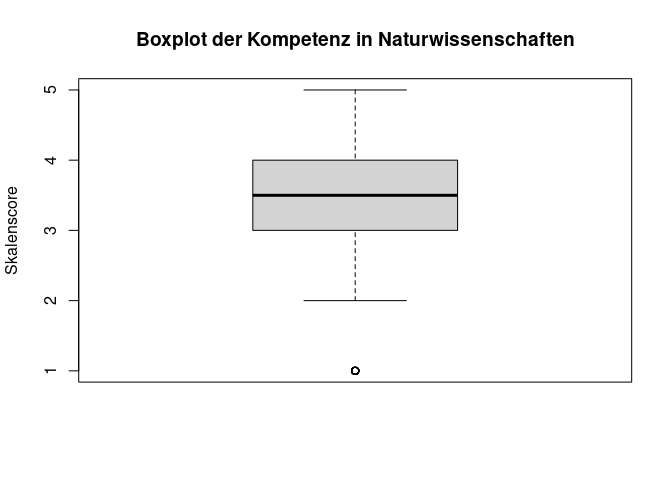
In der Hilfe der boxplot() Funktion sehen wir, dass auch hier viele weitere Argumente zur Verfügung stehen, um die Grafik zu verändern. So können wir beispielsweise die Farbe der Box (col) und die Füllung der Box (red) verändern.
# Erstellung eines Boxplots mit passender Beschriftung und Farbgebung
boxplot(data$Total_Competence_Science,
main = "Boxplot der Kompetenz in Naturwissenschaften",
ylab = "Skalenscore",
col = "blue",
border = "red")
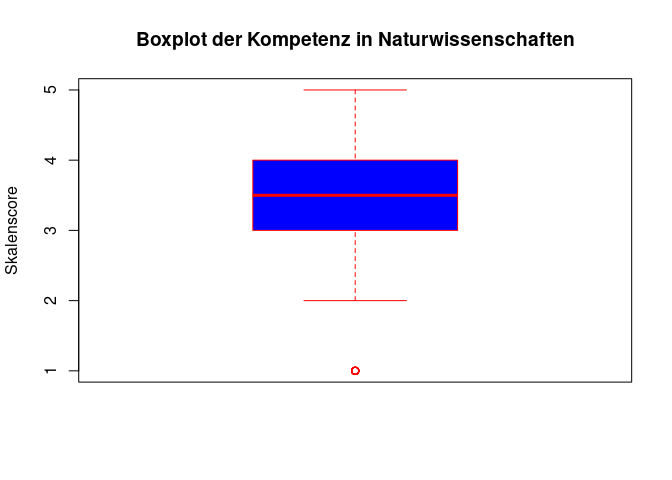
Die gerade getroffene farbliche Wahl entspricht wohl weniger einer optischen verbesserung. Deshalb gibt es auch die Möglichkeit, Farben aus einer Palette zu wählen. Hierfür gibt es in R bspw. die Funktion terrain_colors(), die eine Palette von Farben zurückgibt. Als Argument wird die Anzahl der Farben übergeben.
terrain.colors(2) # Farben aus einer Palette abrufen
## [1] "#00A600" "#F2F2F2"
Die Farben werden in Hex-Farbcode dargestellt. Die einzelnen Ergebnisse der Funktion wollen wir jetzt in unsere Zeichnung aufnehmen. Dabei können wir über die eckigen Klammern einzelne Beiträge aus dem Farbvektor ansprechen.
terrain.colors(2)[1] # Erste Farbe aus den zwei abgerufenen Farben aus der Palette
## [1] "#00A600"
Wenden wir es im Boxplot an.
# Erstellung eines Boxplots mit passender Beschriftung und Farbgebung der Palette
boxplot(data$Total_Competence_Science,
main = "Boxplot der Kompetenz in Naturwissenschaften",
ylab = "Skalenscore",
col = terrain.colors(2)[2],
border = terrain.colors(2)[1])
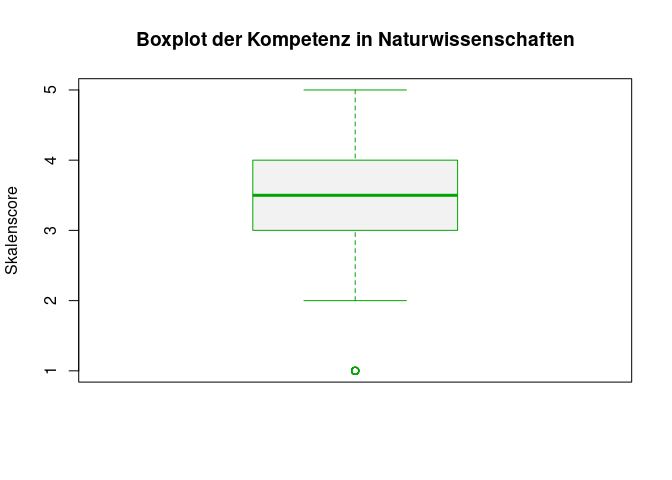
Ob das jetzt wirklich schöner ist als unsere eigene Farbgebung, ist natürlich Geschmackssache. Zumindest haben wir gelernt, dass es in R Farbpaletten gibt und wie man diese nutzt.
Für kontinuierliche Daten oder zumindest solche, die dieser Eigenschaft sehr nahe kommen, wird für die Darstellung häufig ein Histogramm verwendet. Auch hierfür gibt es eine Funktion in R, die hist() heißt. Nehmen wir als Beispiel die Variable Selbstkonzept in der Mathematik (Total_SelfConcept_Maths).
# Erstellung eines Histogramms mit passender Beschriftung
hist(data$Total_SelfConcept_Maths,
main = "Histogramm des Selbstkonzepts in Mathematik",
xlab = "Selbstkonzept Mathematik",
ylab = "Absolute Häufigkeit")
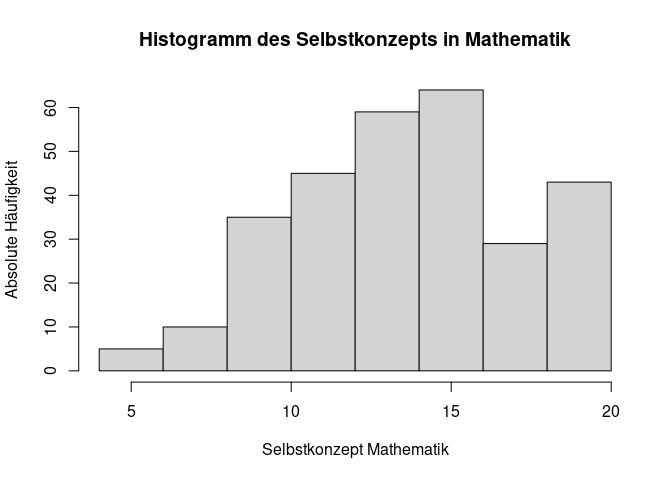
In der Hilfe sehen wir, dass für ein Histogramm das Argument breaks genutzt werden kann, um die Anzahl der Klassen zu bestimmen. Die Voreinstellung ist dabei breaks = "Sturges", was eine Methode zur Bestimmung der Anzahl der Klassen ist. Gleichzeitig kann man hier aber auch selbst alle Grenzen bestimmen oder auch einfach nur die gewünschte Anzahl an Klassen eingeben. Bspw. können wir versuchen ein Histogramm mit 10 Klassen zu erzeugen, indem wir breaks = 10 setzen.
# Erstellung eines Histogramms mit passender Beschriftung und gewünschter Anzahl an Klassen
hist(data$Total_SelfConcept_Maths,
main = "Histogramm des Selbstkonzepts in Mathematik",
xlab = "Selbstkonzept Mathematik",
ylab = "Absolute Häufigkeit",
breaks = 10)
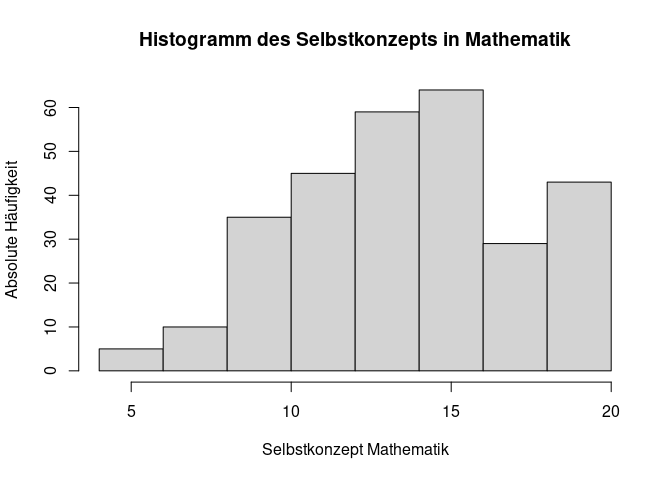
Wie wir sehen ändert sich nichts in der Anzahl der Klassen. Das liegt daran, dass die Funktion hist() die Anzahl der Klassen nur als Vorschlag sieht - das wird in der Hilfe auch beschrieben. Dieses Vorgehen ist ein seltenerer Fall in R, kommt aber durchaus vor, weshalb man sich dieser Möglichkeit generell bewusst sein sollte.
Bisher haben wir die Darstellungen auf nur eine Variable konzentriert. Doch auch die Darstellung von zwei Variablen ist möglich. Als Beispiel nutzen wir hier den Scatterplot, der die Beziehung zwischen zwei Variablen darstellt. Betrachten wir die Leistung im Fach Mathematik (Maths_AttainmentData) in Abhängigkeit vom zugehörigen Selbstkonzept Total_SelfConcept_Maths. Hier gibt es nun die Möglichkeit, die ersten beiden Argumente x und y zu nutzen, um die beiden Variablen anzugeben.
# Erstellung eines Scatterplots mit passender Beschriftung
plot(x = data$Total_SelfConcept_Maths,
y = data$Maths_AttainmentData,
main = "Scatterplot Mathematikleistung und Selbstkonzept",
xlab = "Selbstkonzept Mathematik",
ylab = "Mathematikleistung")
Es gibt auch Grafikfunktionen, die nicht direkt einen Plot erstellen, sondern in eine schon existierende Fragik zusätzlich Elemente einfügen. Ein Beispiel dafür ist die abline() Funktion, die eine Linie in den Plot einfügt. Wenn wir beispielsweise eine optische Trennung erzeugen von Schüler:innen mit niedrigeren und höheren Werten als 6 in der Mathematikleistung, können wir eine horizontale Linie in den Plot einfügen mit dem Argument h.
plot(x = data$Total_SelfConcept_Maths,
y = data$Maths_AttainmentData,
main = "Scatterplot Mathematikleistung und Selbstkonzept",
xlab = "Selbstkonzept Mathematik",
ylab = "Mathematikleistung")
abline(h = 6) # Horizontale Linie bei 6 einfügen
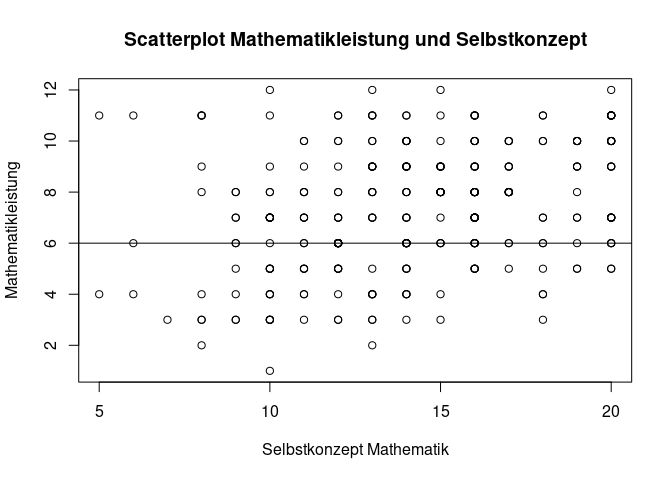
Während die Grafikerstellung mit den Basic R Funktionen, wie wir gesehen haben, sehr leicht möglich ist, stößt dieses Vorgehen bei komplexen Analysen irgendwann an ihre Grenzen. Daher gibt es ein Paket, was spezifisch Grafikerstellung als Thema hat ggplot2. Die darin verwendete Syntax unterscheidet sich ein wenig von der normalen R-Syntax, weshalb die Verwendung über diesen Workshop hinaus gehen würde. Auf pandaR gibt es dazu die Dokumentation eines ganzen Workshop oder auch ein einzelnes, einführendes Tutorial.
Lineare Modellierung
Zum Abschluss lernen wir noch die Syntax von Modellierung in Basic-R kennen. Dabei beziehen wir uns hier auf lineare Regressionsmodelle, aber auch bei hierarchischer oder generalierter Regression ist diese Syntax die Basis.
Syntax
Zunächst betrachten wir die Syntax für Abhängigkeiten in R. Dies wollen wir anhand der aggregate()-Funktion demonstrieren. Hier wird eine bestimmte Operation an einer Variable in Abhängigkeit einer anderen Variable durchgeführt.
# Berechnung des Mittelwerts der Selbstkonzeptwerte in Abhängigkeit der Gruppierung nach Achiever
aggregate(Total_SelfEsteem ~ Achiever, data = data, FUN = mean)
## Achiever Total_SelfEsteem
## 1 High Achiever 20.26437
## 2 Low Achiever 16.00000
## 3 Medium Achiever 18.44103
Das ist sozusagen die Basis R Variante für die Verwendung von group_by() und summarise() aus dem dplyr Paket. Die ~ symbolisiert die Abhängigkeit - vor der Tilde steht die abhängige Variable, nach der Tilde die unabhängige Variable.
Einfaches lineares Modell
Nun übertragen wir die eben gelernte Syntaxlogik und schauen uns die Variable zur Leistung im Fach Mathematik (Maths_AttainmentData) in Abhängigkeit vom zugehörigen Selbstkonzept Total_SelfConcept_Maths an. Die Syntax ist dabei so aufgebaut, dass im ersten Argument eine Formel verlangt wird. Unabhängige Variable und abhängige Variable müssen definiert werden, die 1 repräsentiert den Achsenabschnitt. Im zweiten Argument kann ein Datensatz aufgeführt werden, in dem die jeweiligen Variablen zu finden sind. Es ist zwar auch möglich, dass wir den Datensatznamen jeweils vor dem Variablennamen mit dem $-Zeichen angeben (data$Maths_AttainmentData ~ 1 + data$Total_SelfConcept_Maths), aber das wird vor allem bei multipler Regression unübersichtlich.
# Einfache lineare Regression
# Formel = abhängige Variable ~ unabhängige Variable
lm(formula = Maths_AttainmentData ~ 1 + Total_SelfConcept_Maths, data = data)
##
## Call:
## lm(formula = Maths_AttainmentData ~ 1 + Total_SelfConcept_Maths,
## data = data)
##
## Coefficients:
## (Intercept) Total_SelfConcept_Maths
## 4.303 0.213
Bevor wir uns um den Output kümmern, noch ein paar Hinweise zur Syntax. Da das erste Argument immer die Formel ist, wird der Argumentnamen häufig nicht mit aufgeführt. Weiterhin passiert die Schätzung des Achsenabschnitts als default, sodass wir diesen nicht explizit mit der 1 angeben müssen. In der Praxis würde man also vermutlich eher folgndenen Code sehen.
# Reduktion der Syntax
lm(Maths_AttainmentData ~ Total_SelfConcept_Maths, data = data)
##
## Call:
## lm(formula = Maths_AttainmentData ~ Total_SelfConcept_Maths,
## data = data)
##
## Coefficients:
## (Intercept) Total_SelfConcept_Maths
## 4.303 0.213
Die Funktion lm() selbst hat offenbar erstmal nur eine sehr beschränkte Ausgabe - die geschätzten Regressionsgewichte. Häufig kann man mehr aus Funktionen herausholen, wenn man ihren Output zunächst in einem Objekt ablegt:
# Speichern des Modells in einem Objekt
mod <- lm(Maths_AttainmentData ~ Total_SelfConcept_Maths, data = data)
Das Objekt mod erscheint damit im Environment. Es ist vom Typ Liste, das ist etwas anderes als ein Datensatz mit einer festen Anzahl an Spalten pro Reihe und umgekehrt. Bei Listen können in verschiedenen Bestandteilen der Liste ganz unterschiedliche Sachen liegen. Meistens ist bei der Erstellung von diesen Listen ihnen noch eine extra Klasse zugeordnet, die wir mit der Funktion class() betrachten können.
class(mod) # Klasse des Objekts
## [1] "lm"
Die Funktion lm() erstellt also eine Liste mit der Klasse lm. In dieser Liste sind verschiedene Bestandteile enthalten, die wir uns nun genauer ansehen können. Die Auswahl von Listenbestandteilen, wenn diese Namen haben, funktioniert, wie beim Datensatz, durch das $.
mod$coefficients # Koeffizienten der Regression
## (Intercept) Total_SelfConcept_Maths
## 4.3025269 0.2129649
mod$call # Aufruf der Funktion
## lm(formula = Maths_AttainmentData ~ Total_SelfConcept_Maths,
## data = data)
Neben der händischen Exploration eines Objektes können wir auch automatische Funktionen nutzen, wie beispielsweise die summary-Funktion, die wohl am häufigsten verwendet wird.
summary(mod) # Zusammenfassung des Modells
##
## Call:
## lm(formula = Maths_AttainmentData ~ Total_SelfConcept_Maths,
## data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -5.4322 -1.6289 0.1419 1.6511 5.6326
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.3025 0.5582 7.708 2.08e-13 ***
## Total_SelfConcept_Maths 0.2130 0.0381 5.589 5.30e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.28 on 288 degrees of freedom
## (10 observations deleted due to missingness)
## Multiple R-squared: 0.09785, Adjusted R-squared: 0.09472
## F-statistic: 31.24 on 1 and 288 DF, p-value: 5.295e-08
Sie zeigt uns die wichtigsten Parameter an. Die summary()-Funktion ist dahingehend besonders, dass sie auch auf Objekte anderer Klassen (eigentlich fast aller Klassen) anwendbar. Wenn wir sie beispielsweise auf den Datensatz anwenden, werden uns Zusammenfassungen der Variablen angezeigt.
summary(data) # Zusammenfassung des Datensatzes
## Year Gender Ethnicity Total_Mindset
## 7. Schuljahr:187 weiblich:151 Any other Asian background: 1 Min. :19.0
## 8. Schuljahr:113 männlich:149 Any other white background: 1 1st Qu.:29.0
## Chinese : 1 Median :32.0
## Pakistani : 1 Mean :31.6
## White and Asian : 1 3rd Qu.:35.0
## White and Black African : 2 Max. :42.0
## White British :293 NA's :7
## Total_Competence_Maths Total_Competence_English Total_Competence_Science Total_SelfEsteem
## Min. :1.000 Min. :1.000 Min. :1.000 Min. : 6.00
## 1st Qu.:3.000 1st Qu.:3.000 1st Qu.:3.000 1st Qu.:17.00
## Median :4.000 Median :4.000 Median :3.500 Median :19.00
## Mean :3.846 Mean :3.695 Mean :3.446 Mean :18.99
## 3rd Qu.:4.000 3rd Qu.:4.000 3rd Qu.:4.000 3rd Qu.:21.00
## Max. :5.000 Max. :5.000 Max. :5.000 Max. :30.00
## NA's :1 NA's :2 NA's :2 NA's :17
## Total_SocialSelfEsteem Total_AcademicSelfEfficacy Total_SelfConcept_Maths Total_SelfConcept_English
## Min. :14.00 Min. : 5.00 Min. : 5.00 Min. : 3.00
## 1st Qu.:25.00 1st Qu.:11.00 1st Qu.:12.00 1st Qu.: 9.00
## Median :29.00 Median :12.00 Median :14.00 Median :11.00
## Mean :29.25 Mean :12.64 Mean :14.22 Mean :10.61
## 3rd Qu.:33.00 3rd Qu.:15.00 3rd Qu.:16.00 3rd Qu.:12.00
## Max. :46.00 Max. :20.00 Max. :20.00 Max. :15.00
## NA's :5 NA's :8 NA's :10 NA's :3
## Total_SelfConcept_Science SubjectSTEndorsement_Maths SubjectSTEndorsement_English
## Min. : 4.00 Min. :1.000 Min. :1.000
## 1st Qu.:11.00 1st Qu.:5.000 1st Qu.:4.000
## Median :13.00 Median :5.000 Median :5.000
## Mean :13.26 Mean :5.117 Mean :4.445
## 3rd Qu.:16.00 3rd Qu.:5.000 3rd Qu.:5.000
## Max. :20.00 Max. :9.000 Max. :8.000
## NA's :5 NA's :1 NA's :1
## SubjectSTEndorsement_Science SubjectSTEndorsement_ICT CareerSTEndorsement_Maths
## Min. :1.000 Min. :2.000 Min. :1.000
## 1st Qu.:5.000 1st Qu.:5.000 1st Qu.:5.000
## Median :5.000 Median :5.000 Median :5.000
## Mean :5.341 Mean :5.692 Mean :5.634
## 3rd Qu.:6.000 3rd Qu.:6.000 3rd Qu.:6.000
## Max. :9.000 Max. :9.000 Max. :9.000
## NA's :1 NA's :1 NA's :2
## CareerSTEndorsement_English CareerSTEndorsement_Science CareerSTEndorsement_ICT Eng_AttainmentData
## Min. :1.000 Min. :1.000 Min. :1.000 Min. : 1.000
## 1st Qu.:4.000 1st Qu.:5.000 1st Qu.:5.000 1st Qu.: 6.000
## Median :5.000 Median :5.000 Median :6.000 Median : 8.000
## Mean :4.403 Mean :5.493 Mean :5.872 Mean : 8.137
## 3rd Qu.:5.000 3rd Qu.:6.000 3rd Qu.:7.000 3rd Qu.:10.000
## Max. :9.000 Max. :9.000 Max. :9.000 Max. :14.000
## NA's :2 NA's :2 NA's :2
## Maths_AttainmentData Science_AttainmentData Computing_AttainmentData Total_Competence
## Min. : 1.0 Min. : 1.000 Min. : 1.00 Min. :1.000
## 1st Qu.: 6.0 1st Qu.: 6.000 1st Qu.: 4.00 1st Qu.:3.333
## Median : 7.0 Median : 8.000 Median : 6.00 Median :3.667
## Mean : 7.3 Mean : 7.887 Mean : 6.01 Mean :3.663
## 3rd Qu.: 9.0 3rd Qu.:10.000 3rd Qu.: 8.00 3rd Qu.:4.000
## Max. :12.0 Max. :14.000 Max. :12.00 Max. :5.000
## NA's :2
## Total_SelfConcept Achiever Career_Recommendation
## Min. : 6.00 Length:300 Length:300
## 1st Qu.:11.33 Class :character Class :character
## Median :12.67 Mode :character Mode :character
## Mean :12.72
## 3rd Qu.:14.00
## Max. :18.33
## NA's :14
Eine andere Funktion, die auf mod angewendet werden kann, ist die Funktion coef(), die uns die Koeffizienten der Regression anzeigt.
coef(mod) # Koeffizienten der Regression durch Funktion
## (Intercept) Total_SelfConcept_Maths
## 4.3025269 0.2129649
Im Endeffekt ist das der Output, der uns standardmäßig von lm() angezeigt wird. Wir können unser Wissen jetzt kombinieren und in den Scatterplot zwischen den beiden Variablen der Regression auch die geschätzte Regressionsgerade einzeichnen. Dafür bauen wir wieder zunächst den Scatterplot und fügen dann über abline() die Regressionsgerade ein.
# Scatterplot mit Beschriftung
plot(x = data$Total_SelfConcept_Maths,
y = data$Maths_AttainmentData,
main = "Scatterplot Mathematikleistung und Selbstkonzept",
xlab = "Selbstkonzept Mathematik",
ylab = "Mathematikleistung")
# Regressionsgerade einzeichnen
abline(mod)
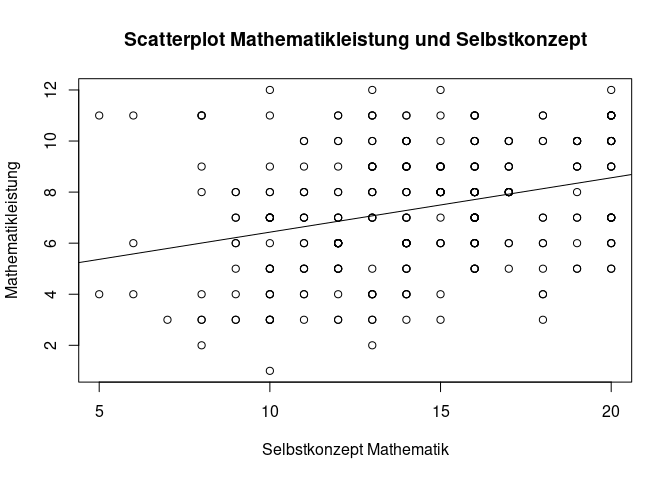
Wir können uns hier zur Nutze machen, dass abline() Achsenabschnitt und Steigung automatisch aus dem Modell ziehen kann.
Die einfache lineare Modellierung kann hier vertieft werden.
Multiple Regression
Die multiple Regression ist eine Erweiterung des Modells mit der Aufnahme von Effekten. Zur multiplen Regression gibt es viele Themen in der Übersicht von PsyBSc7.
Kontinuierliche Prädiktoren
Schauen wir uns zunächst eine einfache Erweiterung der Syntax um eine Addition an. Neben dem Selbstkonzept soll auch die eigene Einschätzung der Kompetenz in Mathematik (Total_Competence_Maths) als Prädiktor aufgenommen werden. Dies funktioniert einfach über die additive Verbindung der Prädiktoren +.
# Multiples lineares Regressionsmodell mit zwei kontinuierlichen Prädiktoren
mod_kont <- lm(Maths_AttainmentData ~ Total_SelfConcept_Maths + Total_Competence_Maths, data = data)
Die class() bleibt gleich und auch die summary() ist daher gleich aufgebaut. Die Coefficients werden logischerweise um einen Eintrag, also eine Zeile, erweitert.
class(mod_kont) # Klasse des Objekts
## [1] "lm"
summary(mod_kont) # Zusammenfassung des Modells
##
## Call:
## lm(formula = Maths_AttainmentData ~ Total_SelfConcept_Maths +
## Total_Competence_Maths, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -5.4090 -1.5913 0.0143 1.5292 6.2491
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.66959 0.61595 5.958 7.5e-09 ***
## Total_SelfConcept_Maths 0.10094 0.06026 1.675 0.0950 .
## Total_Competence_Maths 0.57668 0.24270 2.376 0.0182 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.265 on 286 degrees of freedom
## (11 observations deleted due to missingness)
## Multiple R-squared: 0.1148, Adjusted R-squared: 0.1086
## F-statistic: 18.55 on 2 and 286 DF, p-value: 2.667e-08
Aufnahme kategorialer Prädiktor
Auch die Aufnahme von kategorialen Prädiktoren in das Regressionsmodell ist möglich. Hierzu sollte die Variable in Form eines Faktors vorliegen. Beispielsweise könnte es interessat sein, ob auch das Geschlecht einen Einfluss auf die Mathematikleistung hat.
# Multiples lineares Regressionsmodell mit einem kategorialen und einem kontinuierlichen Prädiktor
mod_kat <- lm(Maths_AttainmentData ~ Total_SelfConcept_Maths + Total_Competence_Maths + Gender, data = data)
summary(mod_kat)
##
## Call:
## lm(formula = Maths_AttainmentData ~ Total_SelfConcept_Maths +
## Total_Competence_Maths + Gender, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.6873 -1.6873 0.0219 1.3965 5.9382
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.77738 0.59514 6.347 8.62e-10 ***
## Total_SelfConcept_Maths 0.15349 0.05926 2.590 0.0101 *
## Total_Competence_Maths 0.51702 0.23467 2.203 0.0284 *
## Gendermännlich -1.23728 0.26498 -4.669 4.66e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.187 on 285 degrees of freedom
## (11 observations deleted due to missingness)
## Multiple R-squared: 0.1777, Adjusted R-squared: 0.1691
## F-statistic: 20.53 on 3 and 285 DF, p-value: 4.496e-12
Wir sehen, dass Gender in der Syntax genauso notiert wird wie kontinuierlich Prädikoren. Die Zeile in der Coefficients-Tabelle zeigt uns, dass die Variable Gender in zwei Kategorien aufgeteilt wurde. Die Referenzkategorie wird nicht angezeigt, sondern nur die Differenz zur Referenzkategorie.
Moderierte Regression
Nun soll der Interaktionseffekt zwischen zwei Variablen aufgenommen werden. Bevor wir dies tun, müssen wir die Variablen zentrieren, damit Multikollinearität vorgebeugt wird. Zentrierung und Standardisierung funktionieren über die Funktion scale(). Wenn wir nur eine Zentrierung erreichen wollen, müssen wir das Argument scale auf FALSE setzen. Statt der langen Schreibweise FALSE können wir auch einfach F schreiben.
# Zentrierung der Prädiktoren
data$Total_SelfConcept_Maths_center <- scale(data$Total_SelfConcept_Maths, scale = F, center = T)
data$Total_Competence_Maths_center <- scale(data$Total_Competence_Maths, scale = F, center = T)
Wir überprüfen die Funktionalität, indem wir uns den Mittelwert der Variablen ausgeben lassen.
# Check der Mittelwerte der Variablen
mean(data$Total_SelfConcept_Maths_center, na.rm = TRUE)
## [1] -4.402414e-16
mean(data$Total_Competence_Maths_center, na.rm = TRUE)
## [1] -1.025891e-16
Wir sehen direkt, dass hier nicht einfach eine 0 steht. Das liegt aber an maschineler Ungenauigkeit - das e-symbolisert Nachkommastellen. Wir haben hier also eine sehr kleine Zahl, die maschinell gesehen nicht verschieden von 0 ist.
Setzen wir nun die lineare Modellierung mit Moderationseffekt um. Da eine Moderation eine Multiplikation der Effekte ist, würde man intuitiv den Code folgendermaßen schreiben.
# Multiple Regression mit Interaktionseffekt
mod_inter <- lm(Maths_AttainmentData ~ Total_SelfConcept_Maths_center + Total_Competence_Maths_center + Total_SelfConcept_Maths_center * Total_Competence_Maths_center, data = data)
Die intuitive Lösung mit der Multiplikation benötigt theoretisch nicht die einzelne Aufführung der Variablen, die Teil der Interaktion sind.
# Multiple Regression mit Interaktionseffekt reduzierte Schreibweise
mod_inter <- lm(Maths_AttainmentData ~ Total_SelfConcept_Maths_center * Total_Competence_Maths_center, data = data)
Allerdings hat das natürlich den Nachteil, dass man nicht spezifisch auswählt und damit nicht so stark über sein Modell nachdenken muss. Es besteht daher die Möglichkeit, Interaktionen sehr präzise mit dem : auszuwählen.
# Multiple Regression mit Interaktionseffekt präzise Schreibweise
mod_inter <- lm(Maths_AttainmentData ~ Total_SelfConcept_Maths_center + Total_Competence_Maths_center + Total_SelfConcept_Maths_center:Total_Competence_Maths_center, data = data)
Weitere Infos zur Moderation, besonders zum Zusammenspiel mit quadratischen Effekten, finden sich hier.
Zusammenfassung
In diesem Tutorial haben wir uns mit der Syntax von Grafiken und der Syntax von linearen Modellen in Basic R beschäftigt. Damit sind wir auch am Ende des Workshops angekommen. An dieser Stelle möchte ich nochmal auf die Vielzahl an Inhalten auf pandaR hinweisen, die Einführungen in die spezifischere Nutzung von R in verschiedenen Analysen bieten und auch sonst im Internet viele frei zugängliche Tutorials zu finden sind. Ansonsten sind auf den Folien noch weitere Literaturhinweise für klassische Lehrbücher.
