Simulationsstudien in R

Einleitung

Simulationsstudien können Aufschluss darüber liefern, wie gut ein statistisches Verfahren oder auch ein Schätzer funktioniert. Diese werden auch sehr häufig Monte-Carlo Simulationen oder MC-Simulationen genannt. Diese Methode wird neben der Untersuchung von statistischen Verfahren auch für die numerische Berechnung verwendet (bspw. können wir $\pi$ mit Hilfe von MC-Methoden bestimmen). Wir wollen uns eine einfache Simulationsstudie ansehen, mit welcher wir das Schätzen der Erwartung (des Mittelwerts der Population) der Normalverteilung untersuchen wollen. Dazu schauen wir uns einfache Simulationstechniken und Wiederholungssfunktionen, wie etwa die for-Schleife, in R an. Bevor wir uns mit Simulationsstudien in R beschäftigen, sollten Sie sich etwas mit R vertraut gemacht sowie die nötige Software (R als Programmiersprache und R-Studio als schöneres Interface) installiert haben. Hierzu eignet sich hervorragend der ebenfalls auf Pandar zu findende R-Crash Kurs. Auch in der ersten Sitzung aus dem Masterstudium der Psychologie wurden einige Begriffe, die für Simulationsstudien von Relevanz sind, wiederholt und es wurde auch eine kleine Simulation zum Untersuchen des $t$-Tests durchgeführt.

Daten simulieren

Wir können in R verschiedene Verteilungen simulieren. Beispielsweise erzeugt der Befehl rnorm normalverteilte Zufallsvariablen. Für weitere Informationen und Verteilungen siehe zum Beispiel R-Verteilungen auf Wiki. Wir müssen diesem Befehl lediglich übergeben, wie viele Replikationen wir wünschen und welchen Mittelwert und welche Standardabweichung die Zufallsvariablen haben sollen. Wir wollen eine Normalverteilung mit Mittelwert 4 und Standardabweichung 5 $\mathcal{N}(4,5^2)$ simulieren und legen die generierte (realisierte) Zufallsvariable in einem Objekt mit dem Namen X ab, um später gezeigte Informationen wie den Mittelwert oder die Standardabweichung abrufen zu können - dies machen wir mit dem “Zuordnungspfeil” <- (zur Erinnerung: links davon steht der Name, den wir uns ausdenken, hier: X; rechts steht das zugeordnete Objekt). Wir wollen zunächst 10 Replikationen generieren und setzen einen Seed, der für die Replizierbarkeit von Simulationen gemacht wird. Auf diese Weise erhalten wir immer die gleichen Zufallszahlen:

set.seed(1234) # Vergleichbarkeit
# (Pseudo-)Zufallsvariablen simulieren
X <- rnorm(n = 10, mean = 4, sd = 5)
X

##  [1] -2.0353287  5.3871462  9.4222059 -7.7284885  6.1456234  6.5302795  1.1263002  1.2668407  1.1777400 -0.4501891

set.seed(1234) # Vergleichbarkeit
# (Pseudo-)Zufallsvariablen simulieren
Y <- rnorm(n = 10, mean = 4, sd = 5)
Y

##  [1] -2.0353287  5.3871462  9.4222059 -7.7284885  6.1456234  6.5302795  1.1263002  1.2668407  1.1777400 -0.4501891

Z <- rnorm(n = 10, mean = 4, sd = 5)
Z

##  [1]  5.083774  1.287537  8.455723  6.979903 12.178090  7.446377 -2.406233  2.934277 13.482699 12.884316

cbind(X, Y, Z) # Vergleiche alle erzeugten Variablen

##                X          Y         Z
##  [1,] -2.0353287 -2.0353287  5.083774
##  [2,]  5.3871462  5.3871462  1.287537
##  [3,]  9.4222059  9.4222059  8.455723
##  [4,] -7.7284885 -7.7284885  6.979903
##  [5,]  6.1456234  6.1456234 12.178090
##  [6,]  6.5302795  6.5302795  7.446377
##  [7,]  1.1263002  1.1263002 -2.406233
##  [8,]  1.2668407  1.2668407  2.934277
##  [9,]  1.1777400  1.1777400 13.482699
## [10,] -0.4501891 -0.4501891 12.884316

Solche generierten Variablen werden auch häufig Pseudozufallszahlen genannt, da sie mit einem PC deterministisch simuliert wurden. Wir erkennen recht schnell, was die Funktion set.seed macht, wenn wir ihr das gleiche Argument, nämlich 1234 übergeben. Die Variablen X und Y sind identisch, Z ist allerdings deutlich unterschiedlich. Damit ist ersichtlich, dass diese Variablen nicht rein zufällig generiert wurden. Die Daten werden allerdings so erzeugt, dass sie unabhängig und damit unkorreliert sind:

cor(cbind(X, Y, Z)) # Korrelation der erstellten Zufallsvariablen

##            X          Y          Z
## X 1.00000000 1.00000000 0.06163893
## Y 1.00000000 1.00000000 0.06163893
## Z 0.06163893 0.06163893 1.00000000

Die Korrelation zwischen X und Y ist 1, da es sich hier um die “selbe” Variable handelt. Z ist gering mit X und Y korreliert. Dies liegt am Sampling Error. Würden wir diese Simulation immer wieder wiederholen, so sollte die Korrelation im Mittel Null sein.

Einfache Schätzungen und ihre Streuung

Einer der ersten Schätzer, die wir im Studium kennengelernt haben, ist der Mittelwert, welcher den Erwartungswert (Populationsmittelwert) schätzt. Der Mittelwert ist asymptotisch (sind die Daten bereits normalverteilt, sogar unmittelbar) normalverteilt mit Streuung $SE:=\frac{SD}{\sqrt{n}}$, wobei $SD$ die Standardabweichung, also die Wurzel aus der Varianz und $n$ die Stichprobengröße beschreibt. Die Verteilung des Schätzer erhalten wir nur, wenn wir immer wieder mit gleicher Stichprobengröße $n$ unter den gleichen Voraussetzungen Daten ziehen und unseren Schätzer bestimmen, wir also bspw. obigen Code immer wieder (für unterschiedliche Seeds) ausführen. Wenn wir nun für X Mittelwert und $SE$ bestimmen, so wird es nicht so sein, dass wir damit die exakten Populationsparameter erwischen. Dies liegt am Sampling Error. Unser Mittelwert ist nur eine Schätzung für die Erwartung in der Population!

mean(X) # Mittelwert

## [1] 2.084213

sd(X)   # SD

## [1] 4.978938

n <- length(X) # Stichprobenumfang (Länge des Vektors = Anzahl an Ziehungen)
sd(X)/sqrt(n)  # SE

## [1] 1.574478

length bestimmt die Länge eines Vektors und sqrt ist die Quadratwurzel. In unserer Stichprobe liegen wir mit dem Mittelwert also um circa 1.9158 neben der Erwartung. Die Standardabweichung liegt sehr nah an der vorgegebenen dran. Die Streuung des Mittelwerts ($SE$) ist recht groß. Dies liegt natürlich an der sehr geringen Stichprobengröße. Folglich ist es auch nicht verwunderlich, dass wir so weit neben der Erwartung hinsichtlich des Mittelwerts gelandet sind.

Schleifen und andere Wege in R Operationen zu wiederholen

Um Operationen immer wieder zu wiederholen, können ganz verschiedene, unterschiedlich effiziente und unterschiedlich leicht nachvollziehbare Wege gewählt werden. Ein sehr leicht verständlicher, aber ggf. nicht sehr effizienter Weg bspw. Simulationen zu wiederholen, ist die Schleife. Es gibt verschiedene Schleifen in R. Die bekannteste ist die for-Schleife. Außerdem gibt es noch die while und die repeat-Schleife (falls Sie mehr Informationen zu Schleifen wünschen, schauen Sie doch mal auf diesem Data-Camp Beitrag vorbei).

Die for-Schleife

Die for-Schleife sieht wie folgt aus:

for(Schleifen_internes_Argument in Schleifen_externes_Argument)
{
     # Schleifeninhalt, der auch auf Schleifen_internes_Argument zugreifen kann
}

Das Schleifen_interne_Argument (i.d.R. ein eindimensionales Symbol/Zahl/String) ist ein Platzhalter, der über das Schleifen_externes_Argument (i.d.R. ein Vektor) iteriert, also nach und nach die Elemente im externen Argument durchgeht. Die beiden sind durch den Ausdruck in getrennt: links davon steht das Symbol, das über die Ausprägungen im rechten Symbol iterieren soll. Zum Beispiel könnten wir über verschiedene Stichprobengrößen N iterieren. Dazu können wir zunächst N festlegen und anschließend n als das interne Argument verwenden:

N <- c(10, 50, 100)
for(n in N)
{
     
}

Bisher passiert noch nichts, da innerhalb der Schleife nichts gemacht wird. Wir wenden einfach mal print auf n an, um uns die Ausprägungen von n anzeigen zu lassen:

N <- c(10, 50, 100)
for(n in N)
{
     print(n)
}

## [1] 10
## [1] 50
## [1] 100

Wir sehen also, dass die Schleife drei Mal durchlaufen wurde und in jedem Durchlauf n eine andere Ausprägung hatte! Es ist sinnvoll, die beide Argumente einer Schleife auch namentlich sinnvoll zu wählen, damit keine Verwirrung eintreten kann. Häufig wird auch i als Laufindex in einer for-Schleife verwendet. Beliebt ist die Funktion 1:Reps, die einen Vektor erzeugt, der von 1 bis zur vorgegebenen Anzahl an Wiederholungen läuft:

Reps <- 10
for(i in 1:Reps)
{
     print(i)
}

## [1] 1
## [1] 2
## [1] 3
## [1] 4
## [1] 5
## [1] 6
## [1] 7
## [1] 8
## [1] 9
## [1] 10

Weitere Schleifen: while und repeat

Die while-Schleife führt die Schleifenoperation so lange durch, bis ein Kriterium erreicht ist. Um den letzten Output mit der while-Schleife zu replizieren, müssen wir Folgendes tun:

i <- 1 # Initialisierung
while(i <= Reps)
{
     print(i)
     i <- i + 1 # Erhöhe i um 1
}

## [1] 1
## [1] 2
## [1] 3
## [1] 4
## [1] 5
## [1] 6
## [1] 7
## [1] 8
## [1] 9
## [1] 10

Innerhalb der Schleife erhöhen wir jeweils i immer um 1 und brechen dann ab, wenn i kleiner oder gleich groß (R-Operator: <=) ist wie Reps (hier 10). Diese Schleife erscheint für diesen Zweck deutlich umständlicher, als die for-Schleife, allerdings kann sie so lange durchlaufen werden, bis ein Kriterium erreicht ist. Die repeat-Schleife funktioniert ähnlich der while-Schleife. Der Schleifeninhalt wird so lange immer wieder ausgeführt, bis wir explizit mit break die Schleife beenden. Wir kommen zum gleichen Ergebnis wie obige while-Schleife mit folgendem Code:

i <- 1 # Initialisierung
repeat
{
     if(i > Reps) # Prüfe, ob i nun größer Reps ist, falls ja, dann beende
     {
          break
     }
     
     print(i)
     i <- i + 1 # Erhöhe i um 1
}

## [1] 1
## [1] 2
## [1] 3
## [1] 4
## [1] 5
## [1] 6
## [1] 7
## [1] 8
## [1] 9
## [1] 10

In der if-Abfrage, wird geprüft, ob i bereits größer als Reps ist. Falls dem so ist, so wird die Schleife beendet. Dies ginge auch in Kurzschreibweise: if(i > Reps) break. Falls nun Ihr Interesse an Schleifen geweckt wurde, so schauen Sie doch im bereits oben Erwähnten Data-Camp Beitrag vorbei. Dort sind auch schöne Flow-Charts dargestellt, was genau die Schleifen (im Englischen Loops) genau machen.

Eine einfache Simulationsstudie mit der for-Schleife

Wenn wir nun einen weiteren Vektor erstellen, der genauso lang ist, wie wir Wiederholungen anfragen, so können wir in diesen Vektor iterationsspezifische Informationen hineinschreiben. Dazu erstellen wir mit rep einen Vektor M, der Länge Reps, der nur aus Missings (NA) besteht und schreiben in diesen Vektor jeweils an die Stelle i für wachsendes i die Ausprägung von i^2 (i zum Quadrat):

Reps <- 10
M <- rep(NA, Reps)
M # M besteht nur aus Missings

##  [1] NA NA NA NA NA NA NA NA NA NA

for(i in 1:Reps)
{
     M[i] <- i^2
}
M # M besteht aus den Zahlen von 1 bis 10 zum Quadrat

##  [1]   1   4   9  16  25  36  49  64  81 100

Wenn wir nun anstatt von i^2 den Mittelwert einer Realisierung dort hineinschreiben, so führen wir schon unsere erste kleine Simulationsstudie durch:

Reps <- 10
M <- rep(NA, Reps)
set.seed(100) # Vergleichbarkeit
for(i in 1:Reps)
{
     X <- rnorm(n = 10, mean = 4, sd = 5)
     M[i] <- mean(X)
}
M # M besteht aus den Mittelwerten der 10 Trials

##  [1] 3.910214 5.168457 3.354288 5.570583 4.034181 3.783851 4.983162 1.969181 4.389539 2.982171

Wenn wir außerdem noch eine weitere Variable SE mitführen, so können wir auch die Standardfehler des Mittelwertes direkt mit abspeichern. Dazu müssen wir nur vor der Schleife SE auf die gleiche Art und Weise wie M erzeugen und innerhalb der Schleife die nötige Berechnung und Zuordnung durchführen:

Reps <- 10
M <- rep(NA, Reps); SE <- rep(NA, Reps) # Zeilen lassen sich auch mit ";" hintereinander schreiben
set.seed(100) # Vergleichbarkeit
for(i in 1:Reps)
{
     X <- rnorm(n = 10, mean = 4, sd = 5)
     M[i] <- mean(X)
     SE[i] <- sd(X)/sqrt(length(X))
}
M # Mittelwerte der 10 Trials

##  [1] 3.910214 5.168457 3.354288 5.570583 4.034181 3.783851 4.983162 1.969181 4.389539 2.982171

SE # SEs der 10 Trials

##  [1] 0.8872064 1.3601514 1.0677863 1.1726830 1.8964952 2.4070357 1.4417604 2.0125966 1.7096845 1.9697478

Damit haben wir alle Größen, die wir für eine Simulationsstudie brauchen, um die Konsistenz sowie die Effizienz des Schätzers (hier: Mittelwert) zu untersuchen.

Advanced: replicate, apply und das Nutzen und Erstellen von Funktionen

Eine deutlich schwierigere Art, die obige Simulationsstudie durchzuführen ist mit Hilfe der apply-Funktion. Die Klasse der apply-Funktionen wendet immer wieder eine vorgegebene Funktion auf (mehrere) Datensätze oder Elemente an. Das Vorgehen ist hier ein ganz anderes. Wir erstellen zunächst die Daten und speichern diese als eine Liste. Listen sind Ansammlungen von Elementen, die nicht alle das gleiche Format haben müssen und damit deutlich flexibler als bspw. Matrizen sind. Dies geschieht mit der Funktion replicate. Anschließend wenden wir eine vorher definierte Funktion auf jeden Listeneintrag an und speichern das Ergebnis ab. Das Problem hierbei ist, dass sobald wir mehrere Informationen aus dem Datensatz haben wollen, empfiehlt es sich dafür extra Funktionen zu definieren. Wir könnten auch mehrere Schritte durchführen und immer wieder unterschiedliche Funktionen anwenden, allerdings wollen wir den Ablauf so nah an der for-Schleife halten, wie möglich! Für das iterative Anwenden unserer vorgegebener Funktion, verwenden wir eine Funktion aus der apply-Familie.

Wir beginnen mit dem Erstellen der Daten mit Hilfe von replicate, der wir drei Argumente übergeben: n ist die Anzahl an Wiederholungen, expr ist der Ausdruck/die Funktion, die repliziert werden soll und simplify = F gibt an, dass wir keine Vereinfachung der Daten vornehmen wollen, da wir eine Liste ausgegeben bekommen möchten. Dies liegt ganz einfach daran, dass wenn Sie eine Simulationsstudie durchführen, in der es mehr als eine zu simulierende Variable gibt, dann bleibt es in Listen übersichtlicher!

Reps <- 10
set.seed(100) # Vergleichbarkeit
X_data <- replicate(n = Reps, expr = rnorm(n = 10, mean = 4, sd = 5), simplify = F)
X_data

## [[1]]
##  [1]  1.4890382  4.6576558  3.6054146  8.4339240  4.5848564  5.5931504  1.0910466  7.5726636 -0.1262971  2.2006893
## 
## [[2]]
##  [1]  4.4494307  4.4813723  2.9918302  7.6992025  4.6168975  3.8534165  2.0557288  6.5542813 -0.5690709 15.5514841
## 
## [[3]]
##  [1]  1.80955009  7.82030308  5.30980646  7.86702298 -0.07189562  1.80774715  0.39889225  5.15472266 -1.78864731
## [10]  5.23537996
## 
## [[4]]
##  [1]  3.5444322 12.7868781  3.3103519  3.4440325  0.5499284  2.8910288  4.9145384  6.0866164  9.3270116  8.8510101
## 
## [[5]]
##  [1]  3.491854 11.016017 -4.883878  7.114337  1.388583 10.611155  2.182798 10.595329  4.218895 -5.393279
## 
## [[6]]
##  [1]  1.7646891 -4.6929897  4.8943242 13.4873285 -7.3596274  8.9023207 -2.9941281 13.1243621 10.9064936 -0.1942594
## 
## [[7]]
##  [1]  2.6900211  3.6557799  2.1055822 16.9097946  4.6491707  0.4348751  7.1899712  5.0084580  3.6504153  3.5375506
## 
## [[8]]
##  [1]  6.244516 -1.321778 -1.812097 12.242609 -6.310480  4.063749 -1.437642  5.352697  9.042259 -6.372024
## 
## [[9]]
##  [1]  8.484111  3.750021 -2.726747 -5.656058  7.547908  3.210475  5.081839  8.086810 12.635879  3.481149
## 
## [[10]]
##  [1]  1.214389 11.141507 -0.464787 -1.787856  1.348518 16.228414 -0.162479  6.067599 -1.893416 -1.870174

X_data ist eine Liste, die 10 Einträge enthält: jeder Eintrag besteht aus einem Vektor mit 10 Einträgen einer Normalverteilung mit Mittelwert 4 und Standardabweichung 5. Wir indizieren in Listen mit Hilfe zweier eckiger Klammern [[index]]. Bspw. können wir uns die 3. Replikation wie folgt ausgeben lassen:

X_data[[3]] # 3. Replikation

##  [1]  1.80955009  7.82030308  5.30980646  7.86702298 -0.07189562  1.80774715  0.39889225  5.15472266 -1.78864731
## [10]  5.23537996

Nun könnten wir natürlich über die Listeneinträge mit einer for-Schleife iterieren, aber das ist nicht das Ziel dieses Abschnitts. Stattdessen erstellen wir eine Funktion, die wir calculate_mean_SE nennen wollen und welche den Mittelwert und den SE eines Vektors bestimmt und diesen als Liste ausgibt. Eine Funktion wird in R erzeugt, indem wir den Namen gefolgt vom Zuordnungspfeil <- und function schreiben. Die Funktion function erstellt dann eine Funktion mit unserem vorgegebenen Namen und nimmt als Argumente entgegen, was wir in die Funktion hineingeben wollen:

calculate_mean_SE <- function(X)
{
     M <- mean(X)
     SE <- sd(X)/sqrt(length(X))
     out <- list("Mean" = M, "StdError" = SE) # Output bestimmen
     return(out) # Funktionsoutput
}

calculate_mean_SE ist der Name unserer Funktion (siehe Appendix A für eine Kurzschreibweise dieser Funktion). Das Argument, welches wir in die Funktion übergeben heißt hier X. Es ist immer so, dass wir Elemente einer Funktion übergeben und Elemente, die in einer Funktion erstellt werden, sind dann auch nur in dieser verfügbar. Innerhalb der Funktion wird dann der Mittelwert in M und der $SE$ in SE abgespeichert. Diese beiden Argumente werden anschließend in eine Liste übergeben, wobei in Anführungszeichen die Namen der Argumente angegeben werden. Da jedoch Elemente innerhalb einer Funktion nur dort verfügbar sind, müssen wir diese Liste wieder aus der Funktion herausbekommen. Dies geht ganz einfach mit return, was bestimmt, was aus der Funktion herausgegeben wird und gleichzeitig auch die Funktion beendet. Dies zeigt auch, wieso wir M und SE nicht einzeln ausgegeben haben, da sobald return das erste mal ausgeführt wird, die Funktion zu Ende ist! Durch die Liste haben wir die Möglichkeit mit beiden Argumenten weiterzumachen. Wenn wir die gesamte Funktion von calculate_mean_SE <- function(X){ bis } markieren und ausführen, dann sollte die Funktion oben rechts in Ihrem R-Studiofenster unter der Rubrik Functions zu finden sein. Wir können die Funktion nun bspw. auf X_data[[3]] anwenden:

calculate_mean_SE(X = X_data[[3]])

## $Mean
## [1] 3.354288
## 
## $StdError
## [1] 1.067786

Wir erkennen im Output die Namen der Koeffizienten, die uns ausgegeben werden. So in etwa funktionieren auch andere Outputs in R, wie bspw. der Output eines lm-Objekts. Speichern wir das Ergebnis ab, so können wir mit $ auf unsere vorgegebenen Namen zurückgreifen:

Erg3 <- calculate_mean_SE(X = X_data[[3]])
names(Erg3)

## [1] "Mean"     "StdError"

Erg3$Mean

## [1] 3.354288

Erg3$StdError

## [1] 1.067786

Diese Funktion können wir nun immer wieder auf X_data anwenden. Dies geht ganz einfach mit lapply (das l steht für listwise):

Results <- lapply(X = X_data, FUN = calculate_mean_SE)
Results[[3]] # 3. Listeneintrag

## $Mean
## [1] 3.354288
## 
## $StdError
## [1] 1.067786

Dem Argument X übergeben wir die Liste, auf welche wir unsere Funktion anwenden wollen. Dem Argument FUN übergeben wir die Funktion, die angewendet werden soll. Das Ergebnis speichern wir unter dem Namen Result ab. Es liegt als Liste vor. Wir haben uns mit Results[[3]] den 3. Listeneintrag ausgeben. Eine weitere Variante wäre sapply (s für simplified). Diese Funktion macht genau das gleiche wie lapply nur gibt sie eine Matrix aus (für weitere Information siehe bspw. auf r-Bloggers):

sResults <- sapply(X = X_data, FUN = calculate_mean_SE)
sResults

##          [,1]      [,2]     [,3]     [,4]     [,5]     [,6]     [,7]     [,8]     [,9]     [,10]   
## Mean     3.910214  5.168457 3.354288 5.570583 4.034181 3.783851 4.983162 1.969181 4.389539 2.982171
## StdError 0.8872064 1.360151 1.067786 1.172683 1.896495 2.407036 1.44176  2.012597 1.709685 1.969748

Simulationsstudien evaluieren

Wir haben zwei Wege kennengelernt eine einfache Simulationsstudie in R durchzuführen. Nun müssen wir eine Aussage über die Güte des Mittelwertschätzers treffen. Dazu müssen wir den Parameterbias sowie den relativen Parameterbias bestimmen und somit eine Aussage über die Konsistenz der Schätzung zu treffen. Ein Schätzer ist konsistent, wenn er für größer werdende Stichproben gegen den wahren Wert strebt (mathematisch bzgl. Mittelwert: $\bar{X}_n\underset{n\to\infty}{\longrightarrow}\mathbb{E}[X]$ [mindestens] in Wahrscheinlichkeit; hier ist $\bar{X}_n$ der Mittelwert einer Stichprobe der Größe $n$/ eines Datenvektors der Länge $n$; dieser Ausdruck wird auch das [schwache] Gesetz der großen Zahlen genannt).

Außerdem variiert ein Schätzer und hat somit eine Varianz $\mathbb{V}ar\left[\hat{\theta_j}\right]$. Wird ein statistisches Verfahren angewandt, so kann dieses in der Regel nur einmalig durchgeführt werden. Somit haben wir keinerlei Idee, wie stark der Schätzer durch Zufall variieren kann. Die Variation eines Schätzer kann glücklicherweise theoretisch hergeleitet werden - nämlich durch den Standardfehler eines Schätzers: diese Variation wollen wir mit dem $SE(\hat{\theta_j})$ beschreiben. Der Standardfehler gibt also eine modelltheoretische Schätzung ab, wie stark der jeweilige Schätzer gegeben diesem Modell variiert. Allerdings muss der theoretische $SE$ nicht immer die Variation der Schätzer ideal abbilden, was an Verstößen im Modell, kleinen Stichproben oder Ähnlichem liegen kann. Folglich müssen wir die Variation des Schätzers auch noch auf andere Art und Weise in der Simulation untersuchen - glücklicherweise können wir dies in einer Simulationsstudie recht einfach machen: Damit wir den SE gut vergleichen können, bestimmen wir die Standardabweichung des Schätzers $SD(\hat{\theta_j})=\sqrt{\mathbb{V}ar\left[\hat{\theta_j}\right]}$, denn diese quantifiziert die Variation des Schätzers in unserer Simulation und gibt damit eine Schätzung für die Streuung des Schätzers durch Zufall ab - genau diese Streuung wollen wir immer mit den Standardfehlern von Schätzern beschreiben! Somit vergleichen wir den mittleren $SE$ (auch MCSE für Monte-Carlo-SE) mit der Standardabweichung über alle Schätzungen (auch MCSD für Monte-Carlo-SD) und erhalten so eine Aussage darüber: 1) wie groß ist die Streuung der Schätzer und 2) wie genau wir diese durch den $SE$ beschreiben können, denn in einer Studie können wir eine Analyse in der Regel nur einmalig durchführen und müssen dann mit dem $SE$ eine Schätzung für die Streuung des Parameters erhalten – dieser muss folglich möglichst nah an der $SD$ liegen! Ein Verfahren ist effizient, wenn seine (modellimplizierten) $SE$ klein sind und genau geschätzt werden, also nah an der wahren erwarteten Variation dran liegen (also MCSE und MCSD übereinstimmen).

Sei dazu $\hat{\theta}_j$ die Schätzung (hier der Mittelwert) der $j$-ten Studie ($j=1,\dots,k$, $k$ ist die Anzahl an Replikationen, in unserem Beispiel ist $k=10$) für den wahren Wert $\theta$ und $SE(\hat{\theta}_j)$ der zugehörige Standardfehler. Dann können wir (absoluten) Bias, relativen Bias, MCSD und MCSE wie folgt definieren:

wobei der Strich über den Variablen jeweils den Mittelwert symbolisiert. Der Hut ^ symbolisiert, dass hier etwas geschätzt wird.

Außerdem wird auch häufig der $RMSE$ (Root-Mean-Square-Error; [Wurzel aus] mittlerem quadratischen Fehler) bestimmt. Zunächst betrachten wir dazu den mittlere quadratischen Fehler $MSE$:

$$MSE(\hat{\theta},\theta)=\mathbb{E}\left[(\hat{\theta}-\theta)^2\right]$$ Der $MSE$ ist also die erwartete quadratische Abweichung. In der Stichprobe bestimmen wir diesen wie folgt:

$$\hat{MSE}=\frac{1}{k}\sum_{j=1}^k(\hat{\theta}_j-\theta)^2,$$ was im Grunde eine Art Varianz ist, wobei hier nicht die quadratische Differenz vom Mittelwert, sondern vom wahren Wert betrachtet wird. Somit fließen in den $MSE$ sowohl der Bias als auch die Streuung des Schätzers ein, denn der $MSE$ kann auch wie folgt (theoretisch) beschrieben werden:

$$MSE(\hat{\theta},\theta)=\mathbb{E}\left[(\hat{\theta}-\theta)^2\right]=\mathbb{V}ar\left[\hat{\theta}\right]+Bias(\hat{\theta},\theta)^2,$$ er hängt also von der Streuung des Schätzers $\mathbb{V}ar\left[\hat{\theta}\right]$ sowie vom Bias $Bias(\hat{\theta},\theta)$ im Quadrat ab. Wir erwarten also einen großen $MSE$, wenn der Schätzer stark streut, wenn der Bias groß ist oder wenn beide stark ausgeprägt sind. Der $RMSE$ ist nun nichts Weiteres als die Wurzel aus dem $MSE$, damit man diesen wieder in der Skala des Schätzers interpretieren kann:

$$RMSE=\sqrt{MSE}.$$ Unter Konstanthaltung alles weiterem in der Simulationsstudie, sollte der Bias und die Streuung mit der Stichprobengröße kleiner werden. Dies liegt an der Konvergenz des Schätzers $\hat{\theta}$ gegen den wahren Wert $\theta$ (falls er denn konsistent ist, falls nicht, so pendelt sich dennoch der Bias um einen festen Wert ein, wenn das Verfahren denn auf einen festen Wert konvergiert - ansonsten macht das Verfahren in der Regel auch keinen Sinn!). Die kleiner werdende Streuung macht sich im kleiner werdenden $MCSD$ und $MCSE$ bemerkbar. Folglich wird auch der $RMSE$ mit steigender Stichprobengröße kleiner!

Führen wir einen Signifikanztest durch, so können wir die Power oder den Type I-Error eines Tests bestimmen (siehe auch Einführungssitzung zu PsyMSc1, wo diese Begriffe bereits behandelt werden). Der Type I-Error ist der Fehler erster Art oder $\alpha$-Fehler. Wir messen ihn in Wahrscheinlichkeiten. Wir begehen einen $\alpha$-Fehler, wenn wir die $H_0$ verwerfen, obwohl diese gilt. Diese Wahrscheinlichkeit des $\alpha$-Fehlers sollte beim vorgegebenen $\alpha$-Niveau (i.d.R. $\alpha =$ $5\%$) liegen. Gilt die $H_0$ nicht, so möchten wir, dass ein Test dies uns mit möglichst großer Wahrscheinlichkeit anzeigt. Die Wahrscheinlichkeit richtigerweise die $H_0$ zu verwerfen wird als Power bezeichnet. Hier können wir bspw. die Wahrscheinlichkeit bestimmen, dass das Konfidenzintervall nicht die 0 einschließt (somit der Effekt signifikant von 0 verschieden ist) - gleiches erreichen wir, indem wir einfach den Effekt durch seinen $SE$ teilen ($\left|\frac{Est}{SE}\right|$ und vergleiche bspw. mit 1.96). Untersuchen wir einen “richtigen” Test (z.B. ANOVA), so schauen wir uns die relative Häufigkeit eines signifikanten Ergebnisses an (also die relative Häufigkeit von $p<0.05$). Die Power sollte möglichst groß sein (z.B. hätten Methodiker gerne, dass Power $\ge 80\%$ gilt). Liegt kein Effekt vor (was wir durch Vorgaben im Modell so entscheiden), so beschreibt die Power (so wie eben beschrieben) gerade den Type I-Error, also den Fehler erster Art. Dieser sollte gerade mit Wahrscheinlichkeit des $\alpha$-Niveaus auftreten. Somit sollte der Type I-Error möglichst nah an der $5\%$-Marke liegen:

Außerdem können wir mit Hilfe der SEs von Effektparametern ein Konfidenzintervall bestimmen und dann untersuchen, wie wahrscheinlich es ist, den wahren Wert in diesem Konfidenzintervall einzuschließen. Es ergibt sich das symmetrische Konfidenzintervall (unter asymptotischer Normalverteilungsannahme des Schätzers) zu einem $\alpha$-Niveau von $5\%$ (dieses kennen Sie vielleicht noch aus dem ersten Semester): $$\Big[\hat{\theta}_j - 1.96SE(\theta_j);\ \ \hat{\theta}_j + 1.96SE(\theta_j)\Big]$$

Die Wahrscheinlichkeit, dass der wahre Werte in diesem Konfidenzintervall liegt, wird die “Coverage” genannt (im Grunde engl. für die Überdeckungswahrscheinlichkeit des wahren Wertes mit einem Konfidenzintervall) und sollte bei $95\%$ liegen (sofern $\alpha=$ $5\%$ gewählt wurde). Folglich sollte sich die Schätzung nur in $5\%$ der Fälle zufällig vom wahren Wert unterscheiden!

\begin{align} \text{Coverage}&=\mathbb{P}\left(\theta \in \left[\hat{\theta}_j - 1.96SE(\hat{\theta_j});\ \ \hat{\theta}_j + 1.96SE(\hat{\theta_j})\right]\right). \end{align}

Der Type I-Error sollte sich mit steigender Stichprobengröße bei dem vorgegebenem $\alpha$-Niveau einpendeln (i.d.R. $\alpha =$ $5\%$). Die Power sollte mit steigender Stichprobengröße steigen und irgendwann bei $100\%$ liegen; die Coverage sollte sich bei $95\%$ einpendeln.

Konsistenz und Bias

Wir bestimmen zunächst den Mittelwert über alle Mittelwertschätzungen (also $\bar{\hat{\theta}}$).

Mean_X <- mean(M) # äquivalent zu 
Mean_X2 <- mean(unlist(sResults[1, ])) #, denn die Mittelwerte stehen in der ersten Zeile 
# von sResults, die allerdings wieder als Liste ausgegeben wird und damit mit `unlist` erst
# in einen Vektor transformiert werden muss
Mean_X

## [1] 4.014563

Mean_X2

## [1] 4.014563

Die Funktion unlist wandelt eine Liste in einen Vektor um. Somit erhalten wir mit sResults[1, ] die Mittelwerte in einer Liste, die dann mit unlist in einen Vektor umgewandelt werden. Wir bestimmen den absoluten Bias, indem wir den wahren Wert von unserer Schätzung abziehen ($\bar{\hat{\theta}}-\theta$). Der wahre Mittelwert liegt bei 4:

Bias <- Mean_X - 4
Bias

## [1] 0.01456281

Der absolute Bias fällt sehr klein aus! Um den absoluten Bias besser einordnen zu können, wird er am wahren Wert relativiert: Der relative Bias ist der absolute Bias geteilt durch den wahren Wert (Achtung: dieser kann nur bestimmt werden, solange der wahre Wert $\neq0$: $\frac{\bar{\hat{\theta}}-\theta}{\theta}$).

Rel_Bias <- (Mean_X - 4)/4   # oder <- Bias/4
Rel_Bias

## [1] 0.003640703

Rel_Bias * 100 # in Prozent

## [1] 0.3640703

Der relative Bias liegt bei $0.36$ $\%$ und ist damit sehr gering. Der Mittelwert scheint bereits für kleine Stichproben konsistent für den Erwartungswert (den Populationsmittelwert) zu sein.

Effizienz und der Vergleich von MCSE und MCSD

Damit ein Verfahren gut funktioniert bzw. ein Schätzer gut funktioniert, muss der Standardfehler vertrauenerweckend sein, also die Variation des Schätzers gut abbilden. Entsprechend müssen wir den mittleren $SE$ mit der SD über die Schätzungen vergleichen (da beide Methoden der Simulation zum selben Ergebnis gekommen sind, konzentrieren wir uns auf die erste):

MCSE <- mean(SE)
MCSE2 <- mean(unlist(sResults[2,]))

MCSD <- sd(M)
MCSD2 <- sd(unlist(sResults[1,]))

MCSE

## [1] 1.592515

MCSD

## [1] 1.084299

Deskriptiv gesehen liegen die beide recht weit auseinander! Nun können wir den absoluten und den relativen Bias in der Streuung des Mittelwerts bestimmen:

Bias_SE <- MCSE - MCSD
Bias_SE

## [1] 0.5082154

Rel_Bias_SE <- (MCSE - MCSD)/MCSD
Rel_Bias_SE

## [1] 0.468704

Oft wird auch einfach MCSE durch MCSD geteilt, um den relativen Bias direkt ablesen zu können. Insgesamt liegt der relative Bias der Streuung der Mittelwertsschätzung bei circa 46.87 $\%$, was enorm groß ist. Allerdings ist die Schätzung der MCSD bei einer so geringen Replikationszahl nicht sehr genau. MCSE hingegen funktioniert bereits recht gut. Dies können wir in diesem spezifischen Beispiel auch daran erkennen, dass wir wissen, wie groß die wahre Streuung in den Daten ist, denn wir haben die Standardabweichung mit 5 vorgegeben. Anschließend müssen wir diese durch die Wurzel an Ziehungen teilen und erhalten so den wahren SE (nämlich $\frac{5}{\sqrt{10}}$):

MCSE - 5/sqrt(10)                   # Bias zum wahren SE

## [1] 0.01137591

(MCSE - 5/sqrt(10))/(5/sqrt(10))    # rel. Bias zum wahren SE

## [1] 0.007194755

Hier sehen wir nun, dass die $SE$s bereits gut funktionieren für eine Stichprobengröße von 10. Der relative Bias liegt bei unter $1\%$. Wenn wir gleiche Simulation mit wesentlich mehr Replikationen bei gleicher niedriger Stichprobengröße von 10 durchführen würden, dann sollte sich der MCSD ebenfalls bei $\frac{5}{\sqrt{10}}$ einpendeln! Insgesamt ist zu sagen, dass der Schätzer “Mittelwert” effizient ist. Das ist allerdings kein Wundernis, da dies bereits seit zahlreichen Jahrzehnten bekannt ist.

RMSE

Um nun sowohl Bias als auch Streuung des Schätzers in Einem beurteilen zu können, bestimmen wir den $RMSE$. Dazu bestimmen wir den Bias pro Replikation (also die Differenz vom wahren Wert) und berechnen davon dann die Standardabweichung:

M - 4 # die Abweichungen

##  [1] -0.08978582  1.16845730 -0.64571183  1.57058286  0.03418111 -0.21614863  0.98316187 -2.03081900  0.38953881
## [10] -1.01782852

(M-4)^2 # quadratischen Abweichungen

##  [1] 0.008061493 1.365292452 0.416943766 2.466730516 0.001168348 0.046720232 0.966607259 4.124225828 0.151740485
## [10] 1.035974905

MSE <- mean((M-4)^2) # mittleren quadratischen Abweichungen
MSE

## [1] 1.058347

RMSE <- sqrt(MSE) # Wurzel aus den mittleren quadratischen Abweichungen
RMSE

## [1] 1.02876

Wir können auch prüfen, ob der MSE sich wirklich leicht aus dem Bias zum Quadrat und der Streuung des Parameters zusammensetzt, wie wir oben gesehen hatten. Dazu müssen wir lediglich den Bias addieren, dazu die $MCSD^2$ (im Quadrat) addieren und diese noch umgewichten, da die $SD$ in R per Default mit dem Vorfaktor $\frac{1}{n-1}$ bestimmt wird, wenn wir also mit $\frac{n-1}{n}$ erweitern, erhalten wir damit das Gewicht $\frac{1}{n}$ (hier $n=k=10\hat{=}$ Anzahl Replikationen).

Bias

## [1] 0.01456281

MCSD^2

## [1] 1.175705

Beide Formeln kommen zum gleichen Ergebnis:

Bias^2 + MCSD^2 * 9/10 

## [1] 1.058347

MSE

## [1] 1.058347

Wir sehen, dass der $MSE$ hier groß ist, da die Streuung ($MCSD$) groß ist – der Bias ist (im Quadrat) klein!

RMSE

## [1] 1.02876

Der $RMSE$ sagt uns, dass die Standardabweichung um den wahren Wert bei 1.03 liegt. Da sehr viele Schätzer (asymptotisch) normalverteilt sind, können wir uns also unter dieser Standardabweichung etwas vorstellen! Jedoch hatten wir für die $MCSD$ bereits diskutiert, dass diese vermutlich so groß ist, da die Anzahl der Replikationen so klein war (hier $k=10$).

Coverage, Power und Type I-Error

Die Coverage kann für jeden Koeffizienten eines Modells bestimmt werden. Jedoch hängt es von der Ausprägung des Populationsparameters ab, ob wir die Power oder den Type I-Error bestimmen. Dies ist jedoch nur eine Namensentscheidung. Beides wird gleich bestimmt.

Power und Type I-Error bestimmen

In unserer kleinen Simulation haben wir den Mittelwert von normalverteilten Zufallsvariablen untersucht. Wir könnten uns also die Frage stellen, ob dieser Mittelwert von 0 verschieden ist. Dazu könnten wir einen Test durchführen (z.B. Einstichproben-$z$-Test) oder wir teilen den Mittelwert durch seinen modellimplizierten $SE$ (was in diesem spezifischen Beispiel gerade das selbe ist). Da wir bereits wissen, dass der wahre Mittelwert bei 4 liegt, bestimmen wir auf diese Weise die Power dieses Koeffizienten. Wir müssen zunächst prüfen, wann $\left|\frac{Est}{SE}\right|>1.96$ gilt (bzw. $\left|\frac{\bar{\hat{\theta}}}{SE(\hat{\theta}_j)}\right|>1.96$). Wir müssen hierbei den Absolutbetrag beachten, da dieser Bruch durchaus auch negativ sein kann, wir wollen aber keine gerichtete Hypothese untersuchen. Die Funktion in R heißt abs:

abs(M/SE)

##  [1] 4.4073330 3.7999131 3.1413479 4.7502887 2.1271770 1.5719964 3.4563036 0.9784281 2.5674554 1.5139865

M2 <- unlist(sResults[1,]) # andere Methode
SE2 <- unlist(sResults[2,]) # andere Methode
abs(M2/SE2) # identisch zu oben, also können wir uns auf eines der beiden konzentrieren

##  [1] 4.4073330 3.7999131 3.1413479 4.7502887 2.1271770 1.5719964 3.4563036 0.9784281 2.5674554 1.5139865

Hier alle einzeln durchzugehen und zu untersuchen, wie häufig dieser Bruch größer als 1.96 ist, ist mühselig, weswegen wir dies mit R automatisieren:

abs(M/SE) > 1.96

##  [1]  TRUE  TRUE  TRUE  TRUE  TRUE FALSE  TRUE FALSE  TRUE FALSE

An TRUE und FALSE erkennen wir, wann der Ausdruck größer als 1.96 ist. Wenn wir nun den Mittelwert auf diesen Vektor aus TRUE und FALSE anwenden, dann erhalten wir die relative Häufigkeit für Erfolg (TRUE). Die mean Funktion bestimmt die relative Häufigkeit von TRUE da TRUE R-intern als 1 und FALSE R-intern als 0 verstanden wird (siehe auch Sitzung zur logistischen Regression um relative Häufigkeiten von 01-Folgen zu wiederholen!).

mean(abs(M/SE) > 1.96)

## [1] 0.7

Die Power liegt hier bei 0.7, was $70\%$ entspricht! Die Power können wir außerdem auch in der Grafik zur Coverage im nächsten Abschnitt ablesen. Dort wird das Konfidenzintervall jeder Schätzung dargestellt. Die Power ist hier somit die Wahrscheinlichkeit, dass dieses Konfidenzintervall nicht die 0 einschließt. Da in der Grafik die 0 nur in Trial 6, 8 und 10 eingeschlossen wird, bedeutet dies, dass die $H_0$ nur in 3 von 10 Fällen nicht verworfen wird. Gleichzeitig bedeutet dies, dass sie in 7 von 10 Fällen verworfen wird, denn in Trial 1, 2, 3, 4, 5, 7 und 9 wird die 0 nicht durch das Konfidenzintervall des Schätzer mit eingeschlossen. Somit ist die $Power = \frac{7}{10}=.7$, was den eben erwähnten $70\%$ entspricht.

Coverage bestimmen

Um die Coverage zu bestimmen, müssen wir uns das Konfidenzintervall ansehen, denn wir wollen untersuchen, ob sich die Schätzung signifikant vom wahren Wert unterscheidet (das wäre nämlich nicht gewünscht!). Für unsere 10 Trials sieht das ganze so aus (Grafik-Code können Sie Appendix B entnehmen):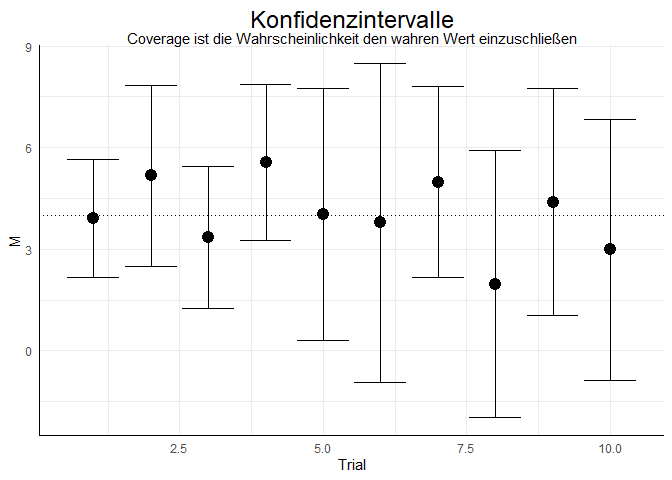

Wir sehen, dass die Konfidenzintervalle hier immer (in $100\%$ der Fälle) den wahren Wert (hier die horizontale gestrichelte Linie) enthält und somit die Schätzung sich nicht signifikant vom wahren Wert unterscheidet. Somit liegt die Coverage bei $100\%$ (für große Stichproben und viele Replikationen sollte sie bei $95\%$ liegen, bzw. allgemein bei $1-\alpha$ für beliebiges $\alpha$). In R müssen wir prüfen, ob der wahre Wert oberhalb der unteren Grenze und unterhalb der oberen Grenze des Konfidenzintervalls liegt. Wir können mehrere TRUE oder FALSE Abfragen mit & (and-Verknüpfung) verketten (es müssen beide TRUE sein, damit insgesamt TRUE entsteht). Die Coverage ergibt sich als:

mean(M - 1.96 * SE <= 4 & M + 1.96 * SE >= 4)

## [1] 1

wobei links vom & abgefragt wird, ob der wahre Wert (hier = 4) oberhalb (oder genau auf) der unteren Grenze (M - 1.96 * SE) liegt und rechts vom & wird abgefragt, ob der wahre Wert unterhalb (oder genau auf) der oberen Grenze (M + 1.96 * SE) liegt. Wenn wir uns ein paar Gedanken darüber machen, so erkennen wir, dass wir auch vom Mittelwert und von den Grenzen jeweils den wahren Wert abziehen können und anschließend prüfen können, ob die Null in diesem neuen Intervall liegt.

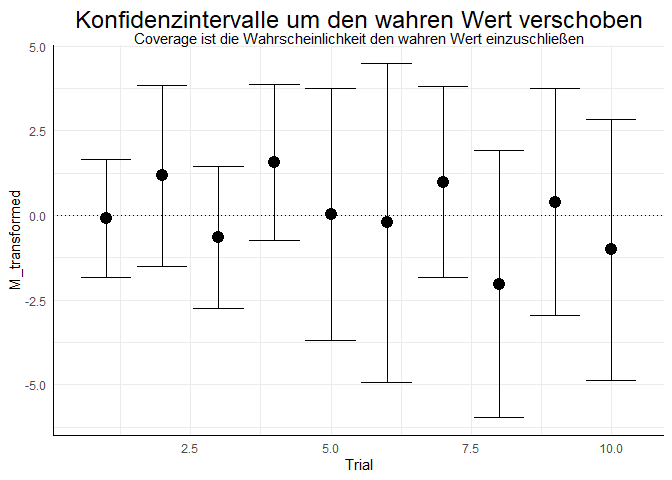
Dies ist das Gleiche, wie zu prüfen, ob der absolute Bias pro Trial geteilt durch den jeweiligen $SE$ kleiner als/gleich 1.96 (und damit nicht signifikant von Null verschieden) ist:

$$\frac{|\hat{\theta}_j-\theta|}{SE(\hat{\theta_j})}\le1.96$$

Damit ist ersichtlich, dass Bias, MCSE, MCSD und Coverage nicht unabhängig sind, denn ist der Bias groß und die Streuung klein, so sollte die Coverage ebenfalls klein sein. Bei erwartungstreuen Schätzern (jenen Schätzern, die [für große Stichproben] im Mittel beim wahren Wert rauskommen), sollte der Bias gerade nur in $5\%$ der Fälle zufällig von 0 signifikant sein, ist das Verfahren jedoch verzerrt, so ist diese Wahrscheinlichkeit deutlich größer und die Coverage entsprechend klein. Genauso können Verzerrungen der Streuung Einflüsse auf die Coverage nehmen. Ist bspw. der SE zu klein, so ist die Coverage ebenfalls kleiner als $95\%$ (in beiden Fällen ist jeweils angenommen, dass $\alpha =$ $5\%$ gewählt wurde). Es sollte folglich im Idealfall gelten:

Das sieht in R so aus:

mean(abs(M-4)/SE <= 1.96)

## [1] 1

Welche Variante für die Coverage Sie nutzen wollen, ist selbstverständlich Ihnen überlassen! Siehe Appendix A für eine zusätzliche Möglichkeit die Coverage als Funktion zu nutzen.

In Appendix C erfahren Sie, wie Sie eine Verlaufsleiste (Progress Bar) hinzufügen, um zu wissen, wie lange Ihre Simulationen noch brauchen (falls Sie dazu Lust haben!).

In Appendix D erfahren Sie, wie Sie $\pi$ mit MC-Methoden bestimmen.

Andere Modelle, wie bspw. ein Regressionsmodell, simulieren Sie, indem Sie mehrere Variablen in R simulieren und diese dann durch z.B. Addition verknüpfen, um so Ihr Populationsmodell aufstellen zu können. Danach müssen Sie entscheiden, mit welchem Analysemodell Sie die generierten Daten untersuchen wollen.

Interessante weitere Informationen bspw. zum Simulieren von SEM oder Multi-Level-Daten finden Sie bspw. in dem Online Buch Monte Carlo Simulation Examples.

Appendix

Appendix A

calculate_mean_SE_short <- function(X)
{
     return(list("Mean" = mean(X), "StdError" = sd(X)/sqrt(length(X))))
}
calculate_mean_SE_short(X = X_data[[3]])

## $Mean
## [1] 3.354288
## 
## $StdError
## [1] 1.067786

my_coverage_function <- function(Ests, SEs, truth)
{
        absBias <- abs(Ests-truth)
        coverage <- mean(absBias/SEs <= 1.96)
        return(coverage)
}

# ausprobieren:
my_coverage_function(Est = M, SE = SE, truth = 4)

## [1] 1

Appendix B

Grafik-Code

Trial <- 1:length(M) # Trial-Nr.
MSE <- data.frame(cbind(Trial, M, SE))

library(ggplot2)
ggplot(data = MSE,mapping = aes(x = Trial, y = M)) + geom_point(cex = 4)+geom_hline(yintercept = 4, lty = 3)+geom_errorbar(mapping = aes(ymin = M - 1.96*SE, ymax = M + 1.96*SE))+ggtitle("Konfidenzintervalle", subtitle = "Coverage ist die Wahrscheinlichkeit den wahren Wert einzuschließen")

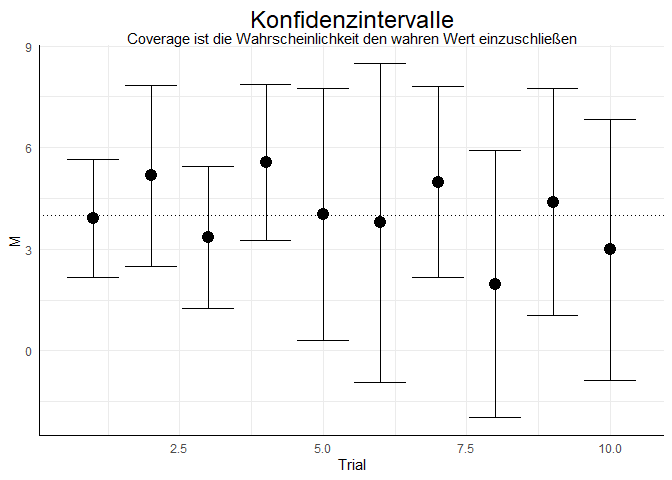
Trial <- 1:length(M) # Trial-Nr.
M_transformed <- M - 4
MSE <- data.frame(cbind(Trial, M_transformed, SE))

library(ggplot2)
ggplot(data = MSE, mapping = aes(x = Trial, y = M_transformed)) + geom_point(cex = 4)+geom_hline(yintercept = 0, lty = 3)+geom_errorbar(mapping = aes(ymin = M_transformed - 1.96*SE, ymax = M_transformed + 1.96*SE))+ggtitle("Konfidenzintervalle um den wahren Wert verschoben", subtitle = "Coverage ist die Wahrscheinlichkeit den wahren Wert einzuschließen")

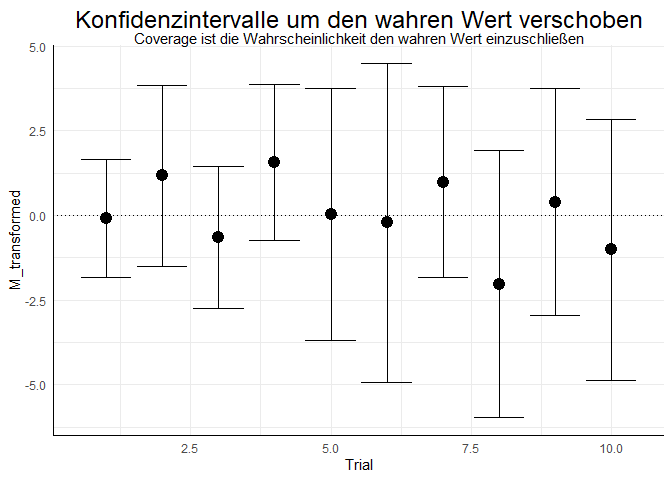
Appendix C

library(progress) # Paket laden
Reps <- 10^5 # entspricht 100000
pb <- progress_bar$new(total = Reps, 
                       format = "  |:bar| :percent elapsed = :elapsed  ~ :eta", 
                       width = 80) # Progressbar vorbereiten und als "pb" abspeichern
M <- rep(NA, Reps)
set.seed(100) # Vergleichbarkeit
for(i in 1:Reps)
{
     X <- rnorm(n = 10, mean = 4, sd = 5)
     M[i] <- mean(X)
     pb$tick() # Progress ausführen in der Schleife
}

## |=====>--------------------------------------------|  12% elapsed =  4s  ~ 26s

Reps <- 10^6 # entspricht 1000000
set.seed(100) # Vergleichbarkeit
X_data <- pbreplicate(n = Reps, expr = rnorm(n = 10, mean = 4, sd = 5), simplify = F)

## |++++++++++++++++++++                              | 39% ~03s

sResults <- pbsapply(X = X_data, FUN = calculate_mean_SE)

## |+++++++++++++++++++                               | 38% ~10s

Appendix D

Berechnung von $\pi$

Wir wissen, dass $\pi$ in etwa bei $3.14159$ liegt. Doch wie kommt man darauf? Eine Möglichkeit liefert hier die MC-Methode. Dazu brauchen wir eine Formel, in der $\pi$ vorkommt. Beispielsweise könnten wir einen Kreis mit Radius $r=1$ zeichnen:

plot(x = c(1,1,-1,-1,1), y = c(1,-1,-1,1,1), type = "l", 
     ylim = c(-1.2, 1.2), xlim = c(-1.2, 1.2), ylab = "Y", 
     xlab = "X", col = "red", lwd = 2, main = expression("Finding"~pi~"by MC-methods"))
x <- seq(-1,1,0.01)
lines(x = x, y = sqrt(1-x^2), lwd = 2, col = "blue") # Formel eines Kreises,
lines(x = x, y = -sqrt(1-x^2), lwd = 2, col = "blue") # umgestellt nach x

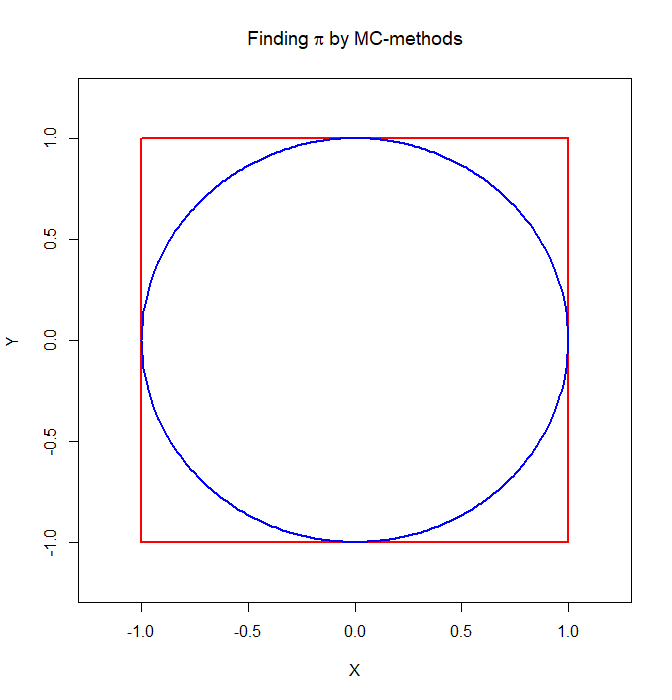
Dann wissen wir aus der Schule, dass dieser Kreis einen Flächeninhalt von $\pi r^2 = \pi$ hat. Wenn wir also den Flächeninhalt bestimmen könnten, könnten wir diese Formel und damit $\pi$ prüfen. Dazu überlegen wir uns ein Zufallsexperiment. Wir haben außen um den Kreis bereits ein rotes Viereck gezeichnet. Was wir nun machen, ist den Anteil des Kreises an dem Viereck zu bestimmen. Dazu ziehen wir unabhängige uniform-verteilte Punkte auf dem Intervall $[-1,1]$ sowohl in $x$- als auch in $y$-Richtung. Wir wissen, dass die Punkte in dem Kreis liegen, wenn sie maximal den Radius (also = 1) vom Ursprung ($(0,0)$) entfernt liegen. Also liegen Sie innerhalb des Kreises, wenn $\sqrt{x^2+y^2}=1$ gilt (die Wurzel könnten wir uns eigentlich schenken, da $\sqrt{1}=1$, was wir im Folgenden auch tun!). Wenn wir nun die Wahrscheinlichkeit bestimmen, dass die Punkte im (oder auf dem) Kreis liegen, dann erhalten wir $\pi$, denn diese Wahrscheinlichkeit ist einfach das Verhältnis der beiden Flächeninhalte. Der Flächeninhalt des Quadrats liegt bei $(1-(-1))^2=2^2=4$, der des Kreises bei $\pi$. Somit erhalten wir:

$$\mathbb{P}\left((x,y)\text{ liegt im Kreis}\right)=\mathbb{P}\left(x^2+y^2\le 1\right)=\frac{\pi}{4}.$$ Dies bedeutet, dass wir die Wahrscheinlichkeit im Kreis zu liegen, lediglich mit 4 multiplizieren müssen, um einen Schätzer für $\pi$ zu erhalten!

Diese Wahrscheinlichkeit wird durch das Verhältnis der blauen zu den gesamten Punkten dargestellt:

plot(x = c(1,1,-1,-1,1), y = c(1,-1,-1,1,1), type = "l", 
     ylim = c(-1.2, 1.2), xlim = c(-1.2, 1.2), ylab = "Y", 
     xlab = "X", col = "red", lwd = 2, main = expression("Finding"~pi~"by MC-methods"))
x <- seq(-1,1,0.01)
lines(x = x, y = sqrt(1-x^2), lwd = 2, col = "blue") # Formel eines Kreises,
lines(x = x, y = -sqrt(1-x^2), lwd = 2, col = "blue") # umgestellt nach x
data <- matrix(runif(n = 2*10^2, min = -1, max = 1), nrow = 10^2)
x <- data[,1]; y <- data[,2]
in_circle <- x^2+y^2<=1 # ! verneint eine boolsche (TRUE oder FALSE)-Variable:
points(x[in_circle], y[in_circle], col = "blue", pch = 16) # Punkte innerhalb des Kreises
points(x[!in_circle], y[!in_circle], col = "red", pch = 16) # Punkte außerhalb des Kreises

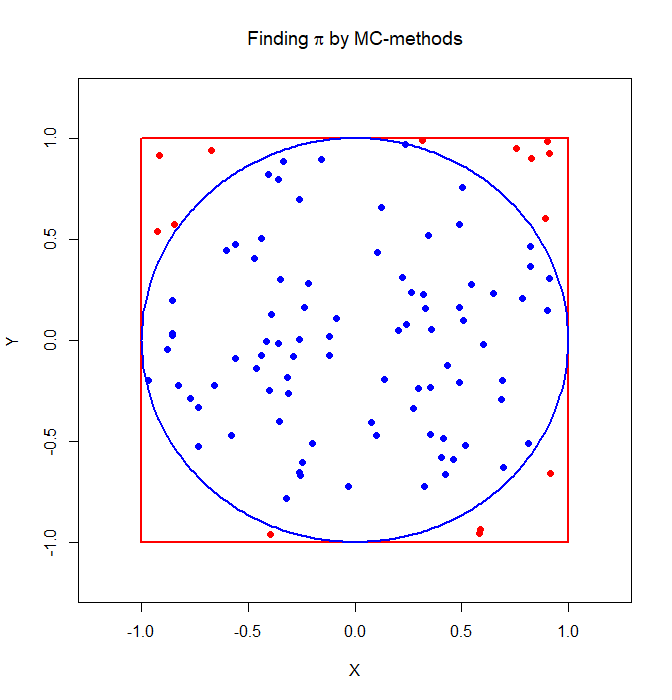
Um nun $\pi$ zu schätzen, erzeugen wir eine Matrix mit $2*10^6$ uniform auf [-1,1] verteilten Zufallsvariablen. Außerdem bestimmen wir eine Funktion inner_circle, mit welcher wir checken, ob ein Datenpunkt innerhalb des Kreises liegt, indem sie uns TRUE oder FALSE zurückgibt. Anschließend berechnen wir den relativen Anteil, dass die Punkte innerhalb des Kreises liegen mit mean (siehe auch relative Häufigkeit in 01-Folgen in der Sitzung zur logistischen Regression) und multiplizieren diese dann mit 4.

data <- matrix(runif(n = 2*10^6, min = -1, max = 1), nrow = 10^6)
inner_circle <- function(r, dat)
{
     x <- dat[1]; y <- dat[2]
     return(x^2 + y^2 <= r)
}
in_circle <- pbapply(X = data, MARGIN = 1, FUN = inner_circle, r = 1)

## |+++++                                             | 10% ~01m 50s

## [1] 3.142232

mean(in_circle)*4 # pi

## [1] 3.142232

pi # aus R

## [1] 3.141593

Uns fallen 2 Dinge auf: Die Simulation braucht extrem lang und ist nur auf 2 Nachkommastellen genau, denn in R liefert pi auch $\pi$ auf einige Nachkommastellen. Die lange Dauer liegt daran, dass dies umständlich programmiert ist. Wir können das Ganze stark verkürzen, indem wir mit Vektoren arbeiten:

# in short
x <- data[,1]; y <- data[,2]
in_circle <- x^2+y^2<=1
mean(in_circle)*4 # pi

## [1] 3.142232

pi # aus R

## [1] 3.141593

Dieser Befehl dauert nicht einmal 2 Sekunden (im Vergleich zu oben $\approx$ 2 Minuten!). Hier wird vektorbasiert quadriert, addiert und “größer/kleiner evaluiert”, was super schnell ist und sich sogar reimt! Es lohnt sich also, immer offen zu sein für verschiedene Methoden der Auswertung.

Die mangelnde Präzision allerdings liegt an der Stichprobengröße. Für eine solche Berechnung werden extrem große Stichproben benötigt. Wenn wir das Experiment bspw. mit $2*10^8$ wiederholen (also um den Faktor 100 größer als zuvor), dann erhalten wir:

# in short
data <- matrix(runif(n = 2*10^8, min = -1, max = 1), nrow = 10^8)
x <- data[,1]; y <- data[,2]
in_circle <- x^2+y^2<=1
mean(in_circle)*4 # pi

## [1] 3.141646

pi # aus R

## [1] 3.141593

Die Präzision steigt, allerdings steigt auch der Aufwand drastisch. Wenn wir die Stichprobengröße hier noch weiter erhöhen, kommen wir an den Rand der Arbeitsspeicherkapazität, weswegen wir dann uns eine andere Umsetzung überlegen müssen (z.B. viele kleine Stichproben hernehmen, $\hat{\pi}$ bestimmen und dann erneut mitteln).