Einleitung und Wiederholung

Einleitung

Im Verlauf des Seminars Forschungsmethoden und Evaluation I soll neben der Einführung in die Theorie und Hintergründe multivariater Verfahren auch eine Einführung in deren Umsetzung gegeben werden, sodass Sie in der Lage sind, diese Verfahren in Ihrem zukünftigen akademischen und beruflichen Werdegang zu benutzen. R ist eine freie Software, die vor allem für (statistische) Datenanalysen verwendet wird. Bevor wir uns die Regressionsanalyse in R ansehen wollen, sollten Sie sich etwas mit R vertraut gemacht sowie die nötige Software (R als Programmiersprache und R-Studio als schöneres Interface) installiert haben. Hierzu eignet sich hervorragend der ebenfalls auf Pandar zu findende R-Crash Kurs. Dort gibt es die Intro und Installationsanweisung sowohl in deutscher als auch in englischer Sprache. Wir gehen davon aus, dass Sie diese durchgearbeitetet haben und schauen uns als Einführung zunächst ein paar zentrale Befehle für das Dateneinlesen und -verarbeiten noch einmal an.

Nach dem Ende der Übung finden Sie in dem zu dieser Veranstaltung gehörenden OLAT Kurs Aufgaben (ein Quiz), die die Inhalte dieser Sitzung ergänzen.

Daten einlesen und verarbeiten

Falls Sie an der Goethe-Universität studiert haben, kennen Sie den Datensatz, den wir in dieser Sitzung untersuchen wollen, vielleicht aus dem Bachelorstudium: Eine Stichprobe von 100 Schülerinnen und Schülern hat einen Lese- und einen Mathematiktest, sowie zusätzlich einen allgemeinen Intelligenztest, bearbeitet. Im Datensatz enthalten ist zudem das Geschlecht (female, 0=m, 1=w). Sie können den Datensatz “Schulleistungen.rda” hier herunterladen.

Daten laden

Der Datensatz ist im R-internen “.rda” Format abgespeichert - einem datensatzspezifischen Dateiformat. Wir können diesen Datensatz einfach mit der load Funktion laden. Wir müssen R nur mitteilen, wo der Datensatz liegt und è vola, er wird uns zur Verfügung gestellt. Liegt der Datensatz bspw. auf dem Desktop, so müssen wir den Dateipfad dorthin legen und können dann den Datensatz laden (wir gehen hier davon aus, dass Ihr PC “Musterfrau” heißt):

load("C:/Users/Musterfrau/Desktop/Schulleistungen.rda")

Nun sollte in R-Studio oben rechts in dem Fenster unter der Rubrik “Data” unser Datensatz mit dem Namen “Schulleistungen” erscheinen.

Bei Dateipfaden ist darauf zu achten, dass bei Linux oder Mac OS Rechnern immer Front-Slashes ("/") zum Anzeigen von Hierarchien zwischen Ordnern verwendet werden, während auf Windows Rechnern im System aber bei Dateipfaden mit Back-Slashes gearbeitet wird ("\"). R nutzt auf Windows Rechnern ebenfalls Front-Slashes ("/"). Das bedeutet, dass, wenn wir auf Windows Rechnern den Dateipfad aus dem Explorer kopieren, wir die Slashes “umdrehen” müssen.

Genauso sind Sie in der Lage, den Datensatz direkt aus dem Internet zu laden. Hierzu brauchen Sie nur die URL und müssen R sagen, dass es sich bei dieser um eine URL handelt, indem Sie die Funktion url auf den Link anwenden. Der funktionierende Befehl sieht so aus (wobei die URL in Anführungszeichen geschrieben werden muss):

load(url("https://pandar.netlify.app/daten/Schulleistungen.rda"))

An diesem Link erkennen wir, dass Websiten im Grunde auch nur schön dargestellte Ordnerstrukturen sind. So liegt auf der Pandar-Seite, die auf netlify.app gehostet wird, ein Ordner namens daten, in welchem wiederum das Schulleistungen.rda liegt.

Ein Überblick über die Daten

Wir können uns die ersten (6) Zeilen des Datensatzes mit der Funktion head ansehen. Dazu müssen wir diese Funktion auf den Datensatz (das Objekt) Schulleistungen anwenden:

head(Schulleistungen)

##   female        IQ  reading     math
## 1      1  81.77950 449.5884 451.9832
## 2      1 106.75898 544.8495 589.6540
## 3      0  99.14033 331.3466 509.3267
## 4      1 111.91499 531.5384 560.4300
## 5      1 116.12682 604.3759 659.4524
## 6      0 106.14127 308.7457 602.8577

Wir erkennen die 4 Spalten mit dem Geschlecht, dem IQ, der Lese- und der Mathematikleistung. Außerdem sehen wir, dass die Variablen mit den Namen IQ, reading und math einige Dezimalstellen aufweisen, was daran liegt, dass diese Daten simuliert wurden (allerdings echten Daten nachempfunden sind). Da es sich bei unserem Datensatz um ein Objekt vom Typ data.frame handelt, können wir die Variablennamen des Datensatzes außerdem mit der names Funktion abfragen. Weitere interessante Funktionen sind die nrow und ncol Funktion, die, wie Sie sich sicher schon gedacht haben, die Zeilen- und die Spaltenanzahl wiedergeben (wir könnten auch dim verwenden, was diese beiden Informationen auf einmal ausgibt).

# Namen der Variablen abfragen
names(Schulleistungen)

## [1] "female"  "IQ"      "reading" "math"

# Anzahl der Zeilen
nrow(Schulleistungen)

## [1] 100

# Anzahl der Spalten
ncol(Schulleistungen)

## [1] 4

# Anzahl der Zeilen und Spalten kombiniert
dim(Schulleistungen)

## [1] 100   4

# Struktur des Datensatzes - Informationen zu Variablentypen
str(Schulleistungen)

## 'data.frame':	100 obs. of  4 variables:
##  $ female : num  1 1 0 1 1 0 1 1 1 1 ...
##  $ IQ     : num  81.8 106.8 99.1 111.9 116.1 ...
##  $ reading: num  450 545 331 532 604 ...
##  $ math   : num  452 590 509 560 659 ...

Wir entnehmen dem Output, dass die Variablen im Datensatz female, IQ, reading und math heißen, dass insgesamt $n = 100$ Schulkinder zu 4 Merkmalen befragt/untersucht wurden und dass alle diese Variablen “numerisch”, also als Zahlen, vorliegen. Eine einzelne Variable eines Datensatzes (vom Typ data.frame) können wir ansprechen, indem wir hinter den Datensatz $ schreiben und anschließend den Variablennamen. Zugriff auf den IQ der Kinder erhalten wir mit:

Schulleistungen$IQ

##   [1]  81.77950 106.75898  99.14033 111.91499 116.12682 106.14127  85.44854  93.24323
##   [9] 135.19738  89.90152  92.72073 115.90123 114.54088  83.28294 126.41670 107.20436
##  [17]  90.03418  98.34044 117.06874 115.55140  68.11351 125.64776  93.34804 106.93651
##  [25]  98.78466  78.93267 113.05378  92.86905  86.44483  70.17249 111.44613  93.78654
##  [33]  87.54754  87.01957  69.32581  92.85801  70.56712  74.17486 105.61195 110.63901
##  [41]  91.54624 105.73141 125.26215 101.14873 111.09582  79.99545  84.45429  84.50532
##  [49]  96.60821 103.90556  81.03395 126.12813  89.47650  80.78064 106.48847 103.58060
##  [57]  84.88878 115.90930  97.28407  91.60586 121.77877 110.26187 100.32137 112.65157
##  [65] 122.84032  96.45124  75.48471  91.27550 111.85776  92.72890  76.84326  92.93814
##  [73] 103.25579  81.15462  92.27190 106.40950  96.70280 104.06385 107.98499  60.76781
##  [81]  94.55947 103.55973 101.83276 113.06302  76.56824  97.56684 104.28662 106.08550
##  [89] 120.97759  82.65717 108.41181 103.38963 100.59534 122.79791  97.91853  92.96729
##  [97]  77.51862 105.01989  54.05485 106.12641

Tipp: In R-Studio können Sie sich Ihren Umgang mit der Software in vielen Dingen vereinfachen, indem Sie die automatische Vervollständigung der Software nutzen. Dies tun Sie, indem Sie bspw. Schulleistungen$ tippen und dann den Tabulator [oder “Strg” + “Leertaste” auf Windows oder Linux Rechner oder “Control” + “Leertaste” auf Mac OS Rechnern ] auf Ihrer Tastatur drücken. Ihnen werden dann Vorschläge für mögliche Argumente aufgezeigt. Das gleiche funktioniert auch in Funktionen. Hier müssen Sie zunächst den Funktionsnamen schreiben und die Klammern öffnen. Mit dem Tabulator erhalten Sie anschließend Vorschläge für mögliche Argumente, die Sie der Funktion übergeben können. Schauen Sie sich dies doch einmal an! Dies funktioniert übrigens auch für das Vervollständigen von Dateipfaden. Hierbei muss allerdings darauf geachtet werden, dass diese in Anführungsstrichen geschrieben werden und Sie müssen beachten, wo ihr aktuelles Working-Directory liegt. Sie können allerdings auch den vollständigen Pfad eingeben, indem Sie auf Windows PCs mit “C:/Users/” und auf Mac OS Rechnern mit “/Users/” beginnen und dann den Tabulator drücken und den jeweilig richtigen Ordner auswählen, bis Sie an Ihrer Zieldatei angekommen sind!

Einfache Deskriptivstatistiken

Bevor wir jetzt direkt zu komplexeren Analysen springen, wollen wir uns noch schnell mit dem Bestimmen einfacher deskriptivstatistischer Größen vertraut machen. Mit der Funktion sum können wir die Summe und mit mean können wir den Mittelwert einer Variable bestimmen. Eine Schätzung für die Populationsvarianz erhalten wir mit var. Die zugehörige Populationsschätzung für die Standardabweichung, Sie vermuten es vielleicht, erhalten wir mit sd. Es handelt sich hierbei um Populations- und nicht um Stichprobenschätzungen, da in diesen Funktionen der Vorfaktor $\frac{1}{n-1}$ genutzt wird, um einen unverzerrten Schätzer für eben die Variation in der Population zu erhalten (für mehr Informationen siehe bspw. Eid, Gollwitzer und Schmitt, 2017, S. 162-163 in Kapitel 6.4.4 und S. 246-247 in Kapitel 8.5.1 oder Agresti, & Finlay, 2013, Kapitel 3.2 und folgend).

# Summe
sum(Schulleistungen$IQ)

## [1] 9813.425

# Mittelwert
mean(Schulleistungen$IQ)

## [1] 98.13425

1/100*sum(Schulleistungen$IQ) # auch der Mittelwert

## [1] 98.13425

# Varianz
var(Schulleistungen$IQ)

## [1] 248.1075

# SD
sd(Schulleistungen$IQ)

## [1] 15.75143

sqrt(var(Schulleistungen$IQ)) # die Wurzel aus der Varianz ist die SD, hier: sqrt() ist die Wurzel Funktion

## [1] 15.75143

Mit summary können wir uns die Zusammenfassung einer Variable ansehen.

summary(Schulleistungen$IQ)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   54.05   87.42   98.56   98.13  108.09  135.20

Als Ausgabe erhalten wir den kleinsten Wert 54.05 (das Minimum, welches hier bspw. auf 2 Nachkommastellen gerundet ist; Originalwert = 54.0548457), das erste Quartil 87.42, also den 25.-Prozentrang (25% PR), den Median 98.56 (2. Quartil; 50% PR), den Mittelwert 98.13, das 3. Quartil 108.09 (75% PR) und den größten Wert 135.2 (Maximum). Wenden wir diese Funktion auf ein R-Objekt an, so gibt uns diese eine Zusammenfassung dieses Objekts aus, was häufig auch einfach die Zusammenfassung einer Analyse ist. Dies schauen wir uns später nochmals genauer an.

Als letztes gucken wir uns noch den Befehl colMeans an, welcher Mittelwerte eines Datensatzes über die Spalten (also pro Variable über alle Personen) bestimmt. Somit lassen sich ganz einfach für alle Variablen eines Datensatzes auf einmal die Mittelwerte bestimmen (rowMeans bestimmt, wie Sie sich wahrscheinlich denken, die Mittelwerte pro Zeile, also die Mittelwerte über alle Variablen pro Person):

colMeans(Schulleistungen)

##    female        IQ   reading      math 
##   0.54000  98.13425 496.06605 561.46446

Da female 0-1 kodiert ist und 1 für Mädchen steht, bedeutet die hier beobachtete Zahl von .54, dass gerade ca. 54% der Proband*innen weiblich waren.

Der $t$-Test

Ein sehr einfacher statistischer Test, ist der $t$-Test (für eine Wiederholung siehe bspw. Eid, et al., 2017, Kapitel 11.1 oder Agresti, & Finlay, 2013, Kapitel 6.2 und folgend). Mit Hilfe dieses Tests soll untersucht werden, ob die Mittelwerte in zwei Gruppen gleich sind. Dazu brauchen wir drei wichtige Annahmen:

1. die Beobachtungen stammen aus einer independent and identically distributed (i.i.d., deutsch: unabhängig und identisch verteilt) Population (dies bedeutet, dass alle Beobachtungen unabhängig sind und den gleichen Verteilungs- und Modellannahmen unterliegen),
2. die Daten in beiden Gruppen sind normalverteilt mit
3. gleicher Varianz (Varianzhomogenität).

Die 1. Annahme ist sehr kritisch und lässt sich leider nicht prüfen. Sie lässt sich aber durch das Studiendesign zumindest plausibilisieren. Für die anderen beiden Annahmen gibt es verschiedene Tests und deskriptive Verfahren, um ein Gefühl für ihr Vorliegen zu erhalten - diese schauen wir uns in der nächsten Sitzung zur Regression an. Unter diesen Annahmen stellen wir die folgenden Null-Hypothese auf - die Gleichheit der Mittelwerte in den beiden Gruppen: $$H_0: \mu_1=\mu_2$$

Diese Hypothese gilt nicht, wenn $\mu_1\neq\mu_2$. In diesem Fall gilt irgendeine Alternativhypothese ($H_1$) mit einer Mittelwertsdifferenz $d=\mu_1-\mu_2$, die nicht Null ist $(d\neq0)$. Wir sprechen hier von einer Alternativhypothese, da in der (frequentistischen) Statistik immer feste Werte für die Parameter in der Population angenommen werden müssen. Wenn die $H_0$ nicht gilt, so muss entsprechend auch ein fester Wert für die Differenz $d$ für die Mittelwerte angenommen werden.

Simulieren von Daten

Wir können in R auch Daten simulieren. Bspw. erzeugt der Befehl rnorm normalverteilte Zufallsvariablen. Für weitere Informationen siehe bspw. R-Verteilungen auf Wiki. Wir müssen diesem Befehl lediglich übergeben wie viele Replikationen wir wünschen und welchen Mittelwert und Standardabweichung die Zufallsvariablen haben sollen. Wir simulieren die Standardnormalverteilung $\mathcal{N}(0,1)$ und legen die generierte (realisierte) Zufallsvariable in einem Objekt mit dem Namen X ab, um später gezeigte Informationen wie den Mittelwert oder die Standardabweichung abrufen zu können - dies machen wir mit dem “Zuordnungspfeil” <- (zur Erinnerung: links davon steht der Name, den wir uns ausdenken; hier: X; rechts steht das zugeordnete Objekt). Um zufällige Prozesse über verschiedene Zeitpunkte hinweg konstant zu halten (damit es replizierbar ist und Sie dasselbe Ergebnis bekommen), wird zunächst ein Startpunkt für den Zufallsprozess mittels set.seed gesetzt. set.seed nimmt irgendeine ganzzahlige, positive Zahl entgegen.

set.seed(1234567) # für Replizierbarkeit (bei gleicher R Version, kommen Sie mit diesem Seed zum selben Ergebnis!)
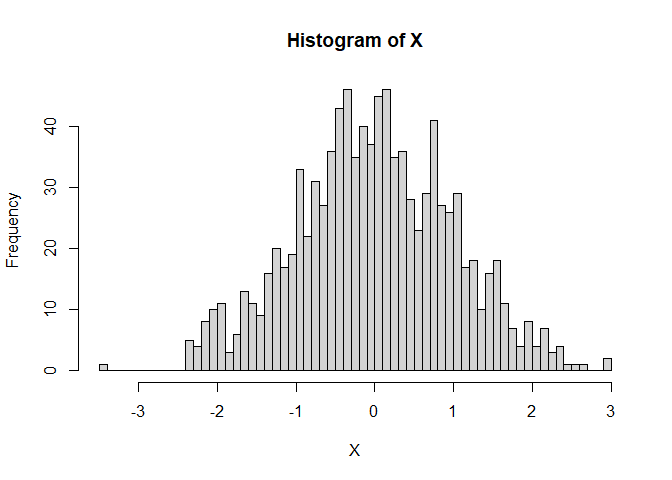
X <- rnorm(n = 1000, mean = 0, sd = 1) # Standardnormalverteilung mit n = 1000
hist(X, breaks = 50) # breaks gibt die Anzahl der Balken vor

mean(X)

## [1] -0.002997332

sd(X)

## [1] 0.9956916

Das was in rnorm drin steckt, nämlich eine Normalverteilung mit Mittelwert 0 und Standardabweichung 1, ist gerade die Population, aus der wir eine Stichprobe gezogen haben. Natürlich liegen der geschätzte Mittelwert und die geschätze Standardabweichung der Stichprobe nicht genau auf den wahren Werten der Population, was am Sampling-Error liegt. Der Sampling-Error beschreibt die zufällige Schwankung, die durch das Ziehen der Stichprobe aus einer Population (Grundgesamtheit) entsteht.

Gehen wir nun her und simulieren noch eine zweite Stichprobe standardnormalverteilter Zufallsvariablen, so können wir diese beiden Stichproben mit Hilfe des $t$-Tests vergleichen. Da in beiden Gruppen ein Mittelwert von 0 vorliegt, ziehen wir hier einen $t$-Test heran im Fall der Null-Hypothese. Die Funktion in R hierzu heißt t.test (wir müssen hier var.equal = T wählen, da sonst eine Näherung verwendet wird, die unterschiedliche Varianzen ausgleichen soll, nämlich Welch’s Two Sample $t$-Test):

set.seed(2)
Y <- rnorm(n = 1000, mean = 0, sd = 1)
t.test(X, Y, var.equal = T)

## 
## 	Two Sample t-test
## 
## data:  X and Y
## t = -1.4456, df = 1998, p-value = 0.1484
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -0.15317201  0.02317988
## sample estimates:
##    mean of x    mean of y 
## -0.002997332  0.061998736

Der Output enthält folgende Informationen:

## 
## Two Sample t-test

zeigt an, dass es sich um einen Zwei-Stichproben $t$-Test handelt.

##  data:  X and Y
##  t = -1.4456, df = 1998, p-value = 0.1484

zeigt uns die Datengrundlage (X und Y), den $t$-Wert, die $df$ und den $p$-Wert. Wir erkennen, dass die Mittelwertsdifferenz bei $d$= -0.065 liegt, mit zugehörigen $t$-Wert t(1998)=-1.4456 und $p$-Wert p=0.1484, somit ist dieser Mittelwertsvergleich auf dem 5% Niveau nicht signifikant ($p$>.05).

##  alternative hypothesis: true difference in means is not equal to 0
##  95 percent confidence interval:
##   -0.15317201  0.02317988
##  sample estimates:
##     mean of x    mean of y 
##  -0.002997332  0.061998736

zeigt uns die Alternativhypothese ($H_1:d\neq0$), das Konfidenzintervall der Mittelwertsdifferenz sowie die Mittelwerte in den beiden Gruppen ($\bar{X}=$ -0.0029973, $\bar{Y}=$ 0.0619987). Somit ist auch die Null-Hypothese klar: $H_0:d=0$.

Wir können den Test auch als R Objekt abspeichern und ähnlich wie den Datensätzen anschließend diese Informationen entlocken. Dazu müssen wir das ausgegebene Objekt t.test lediglich einem Namen zuordnen und anschließend mit $ ansprechen. Wieso nennen wir das Objekt nicht einfach ttest. Wenn wir names darauf anwenden, sehen wir alle Namen, die wir hinter $ schreiben können:

ttest <- t.test(X, Y, var.equal = T)
names(ttest)    # alle möglichen Argumente, die wir diesem Objekt entlocken können

##  [1] "statistic"   "parameter"   "p.value"     "conf.int"    "estimate"    "null.value" 
##  [7] "stderr"      "alternative" "method"      "data.name"

ttest$statistic # (empirischer) t-Wert

##       t 
## -1.4456

ttest$p.value   # zugehöriger p-Wert

## [1] 0.1484462

Da die Null-Hypothese nicht verworfen wird, bedeutet dies, dass wir weiterhin annehmen, dass die Mittelwertsdifferenz in der Population tatsächlich 0 ist. Die Mittelwertsdifferenz in der Stichprobe ist offensichtlich nicht 0. Allerdings liegt sie so nah an der 0, dass diese Abweichung wahrscheinlich durch Zufall passiert ist und sich nicht auf die Population verallgemeinern lässt (siehe als Wiederholung Eid, et al., 2017, Kapitel 11.1 für den $t$-Test und Kapitel 8 für Inferenzstatistikgrundlagen und Hypothesentests, bzw. Agresti, & Finlay, 2013, Kapitel 6).

Verteilung unter $H_0$

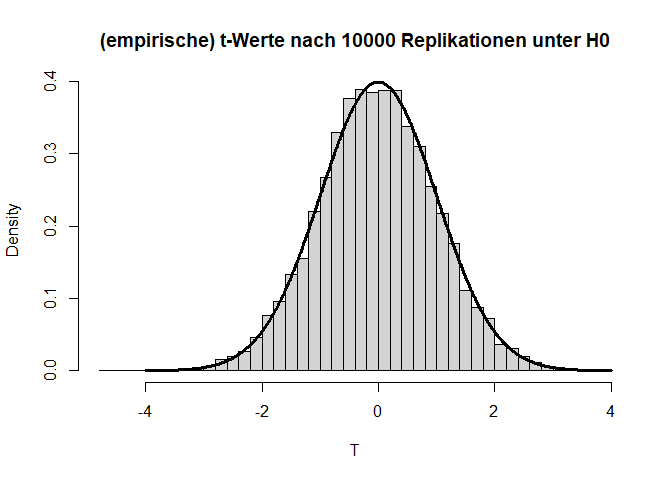
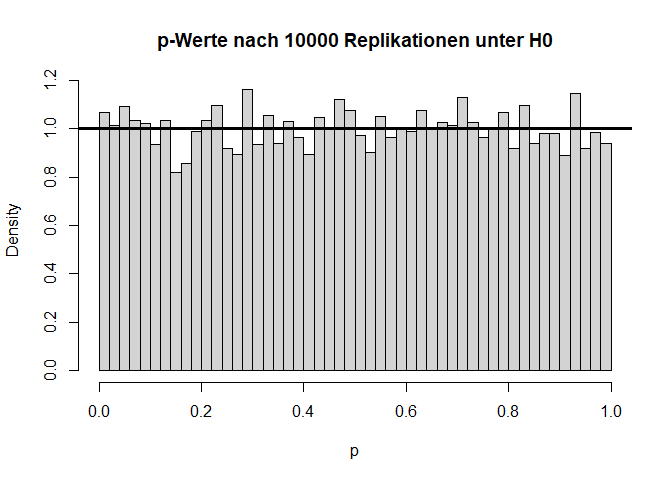
Wenn wir dieses Experiment nun ganz häufig wiederholen, dann sollte die Teststatistik $T=\frac{\bar{X}-\bar{Y}}{\sigma_p}$ (wobei $\bar{X}$ und $\bar{Y}$ die Mittelwerte von $X$ und $Y$ sind und $\sigma_p$ die gepoolte Standardabweichung beschreibt) der $t$-Verteilung folgen, welcher wir dann den $p$-Wert ablesen können. Das ist nämlich genau die Idee hinter dem inferenzstatistischen Testen. Hierbei entspricht die Teststatistik dem empirischen $t$-Wert. Die Bezeichnung kann also austauschbar verwendet werden! Wenn Sie sich für den dahinterliegenden Code interessieren, so können Sie diesen im Appendix A nachlesen.

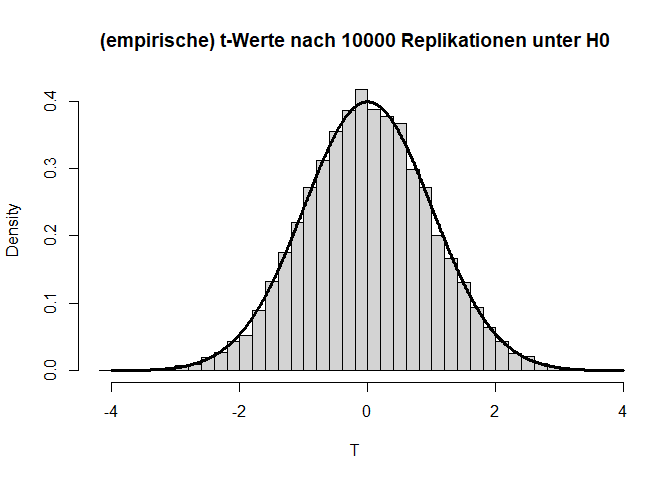
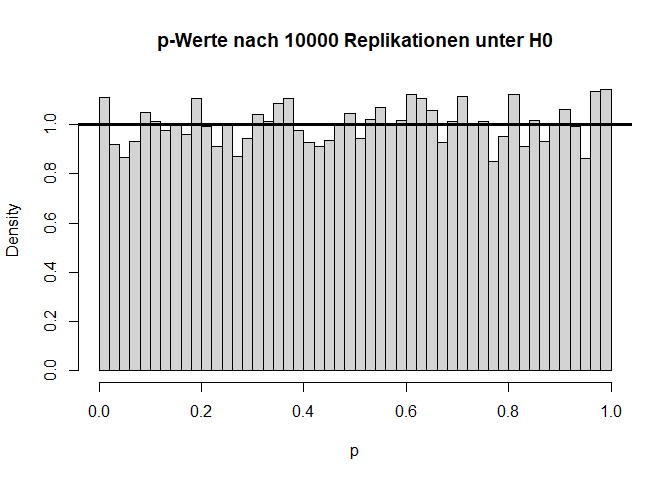
Die beiden Histogramme zeigen die empirische Verteilung der $t$- und $p$-Werte unter der $H_0$-Hypothese nach 10000 (unabhängigen) Wiederholungen und die angenommene Verteilung (fette durchgezogene schwarze Linie). Von den $p$-Werten wird erwartet, dass sie sich gleich (uniform) auf das Intervall zwischen 0 und 1 verteilen. Somit landen dann nur 5% der $p$-Werte mit zugehörig großen Teststatistiken (zufällig) im Bereich $p<0.05$.

Verteilung unter $H_1$

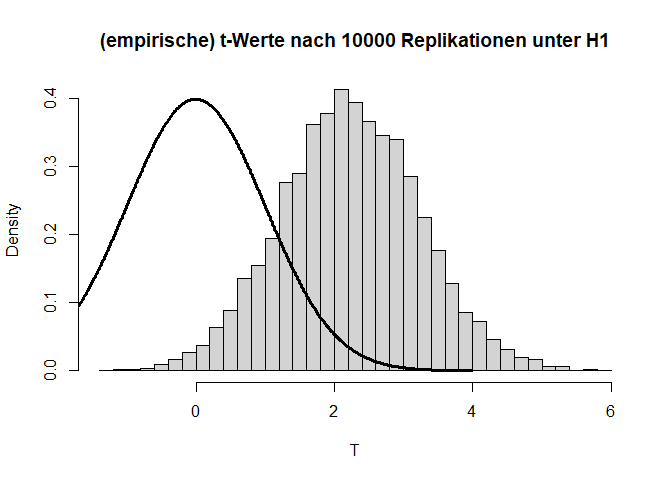
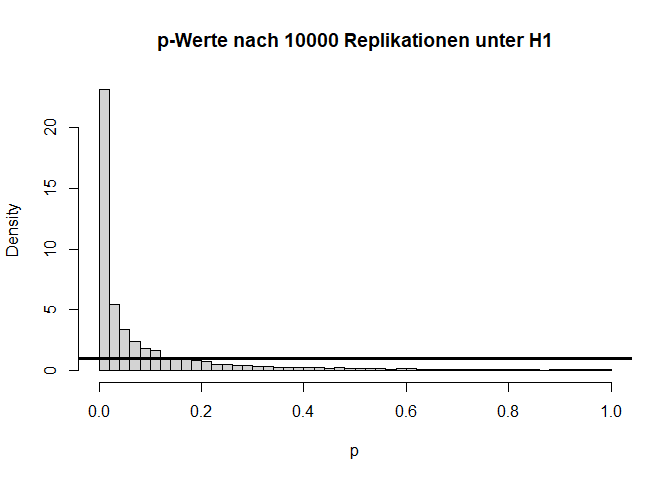
Angenommen die $H_0$-Hypothese gilt nicht und es liegt tatsächlich eine Mittelwertsdifferenz von bspw. $d=0.1$ ($H_1: \mu_1 - \mu_2 = 0.1$) vor, dann hat dies folgende Auswirkungen auf die Verteilung der Teststatistik und die zugehörigen $p$-Werte:

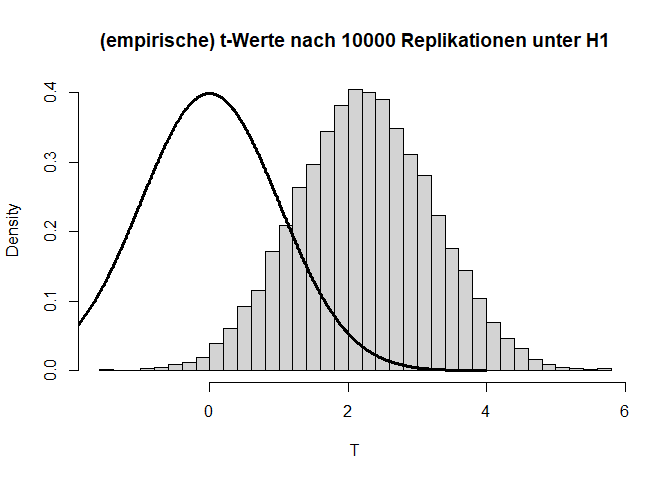
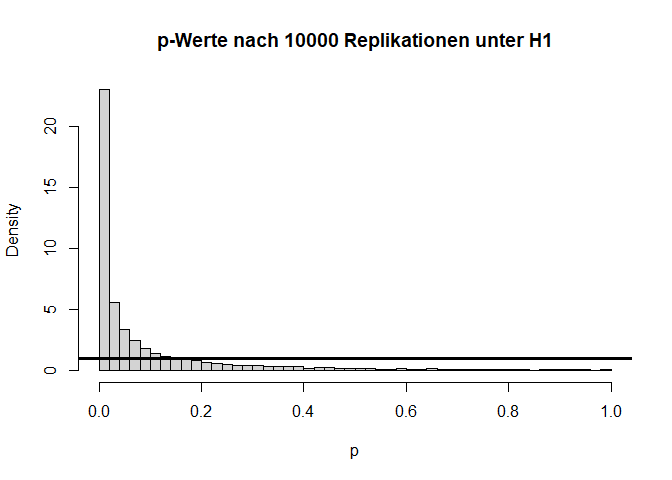
Wir sehen sehr deutlich, dass die Teststatistik $T$ deutlich nach rechts verschoben ist und nicht mehr zur theoretischen Verteilung unter der $H_0$-Hypothese passt. Auch die $p$-Werte sind alles andere als gleichverteilt. Folglich sprechen extreme $t$-Werte gegen die Null-Hypothese, weswegen wir diese verwerfen, wenn wir einen extremen Wert beobachten. Hier liegen 60.99% der $p$-Werte unterhalb von $0.05$. Dies wird auch als Power (siehe im Kapitel 8 in Eid, et al., 2017 Wiederholungen der Begriffe Power und $\alpha$-Fehler) bezeichnet. Somit hat der $t$-Test für eine Mittelwertsdifferenz von $d$=.1 und eine Stichprobengröße von insgesamt n = 2000 eine Power von rund 60.99%. Dies bedeutet, dass in diesem Fall die $H_0$ in 60.99% der Fälle richtigerweise verworfen wird. Schauen wir uns die Power der $t$-Tests einmal für verschiedene Stichprobengröße ($n$) und Mittelwertsdifferenzen ($d$) an:

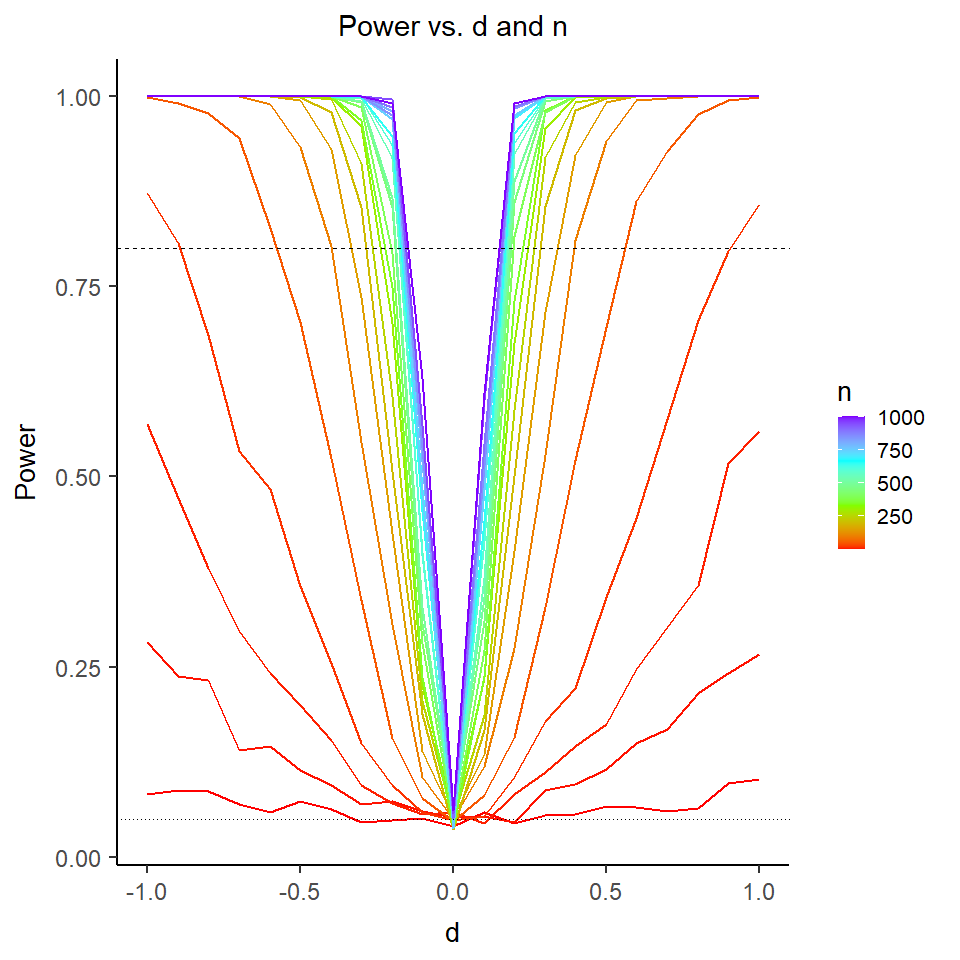
Auf der x-Achse sehen wir unterschiedliche Mittelwertsdifferenzen. Auf der y-Achse ist die Power abgetragen. Die Farbe kodiert die Stichprobengröße. Die horizontal gepunktete Linie zeigt eine Power von 5% (also das vorgegebene $\alpha$-Niveau) an und die horizontal gestrichelte Linie zeigt eine Power von 80% an.

Wir sehen sehr deutlich, dass für alle Stichprobengrößen (farblich kodiert) von $n=2$ bis $n=1000$ (pro Gruppe) die Power bei einer Mittelwertsdifferenz von 0 gerade bei ca. 5% liegt. Die Mittelwertsdifferenz von 0 beschreibt gerade die Null-Hypothese, dass es keinen Mittelwertsunterschied gibt. In diesem Fall beobachten wir den $\alpha$-Fehler dieses Tests, nämlich die Wahrscheinlichkeit, zufällig die Null-Hypothese zu verwerfen, obwohl diese gilt. Die Power von 5% war somit zu erwarten, da dies gerade das $\alpha$-Niveau dieses Tests ist (welches wir uns auch vorher so vorgegeben haben). In der Regel wird $\alpha = .05$ gewählt.

Was wir auch erkennen ist, dass für sehr große Stichproben die Power dieses Tests schon für sehr kleine Mittelwertsdifferenzen groß ist (idealerweise sprechen Methodiker von einem Test mit hinreichender Power, wenn diese größer als 80% ist). Dieses Beispiel zeigt sehr schön auf, dass damit die Power (also die Wahrscheinlichkeit einen Effekt zu finden, wenn dieser da ist) hoch ist, es einen Effekt geben muss (was sehr trivial klingt und es eigentlich auch ist) und zudem die Stichprobengröße hinreichend groß sein muss. Mit hinreichend groß hält sich der/die Statistiker/in die Hintertür offen zu sagen, dass: a) im Falle eines kleinen Effekts die Stichprobengröße eben sehr groß sein muss, um diesen zu erkennen und b) bei Vorliegen eines sehr großen Effekts schon eine kleine Stichprobengröße ausreicht, um den Effekt mit hinreichender Wahrscheinlichkeit auch als solchen zu identifizieren. Das ist auch der Grund, warum es Poweranalysen gibt, mit welchen bestimmt werden kann, wie groß die Stichprobengröße sein muss, um bei einem vorgegebenem erwarteten Effekt hinreichende Power zu haben, diese auch zu entdecken. Für sehr einfache Tests gibt es auch geschlossene Formeln, um bspw. Stichprobengröße zu finden, mit welcher vorgegebene Effekte mit hinreichend großer Wahrscheinlichkeit aufgedeckt werden können. Eines dieser Pakete ist das pwr Paket. Mit diesem können wir die oben dargestellte Grafik auch ohne Simulation (nur mit Formeln) erstellen (um das Ganze übersichtlicher zu gestalten, sind hier mehr Stichprobengrößen abgetragen, allerdings werden nur Stichproben von 2 bis 500 im Plot integriert):

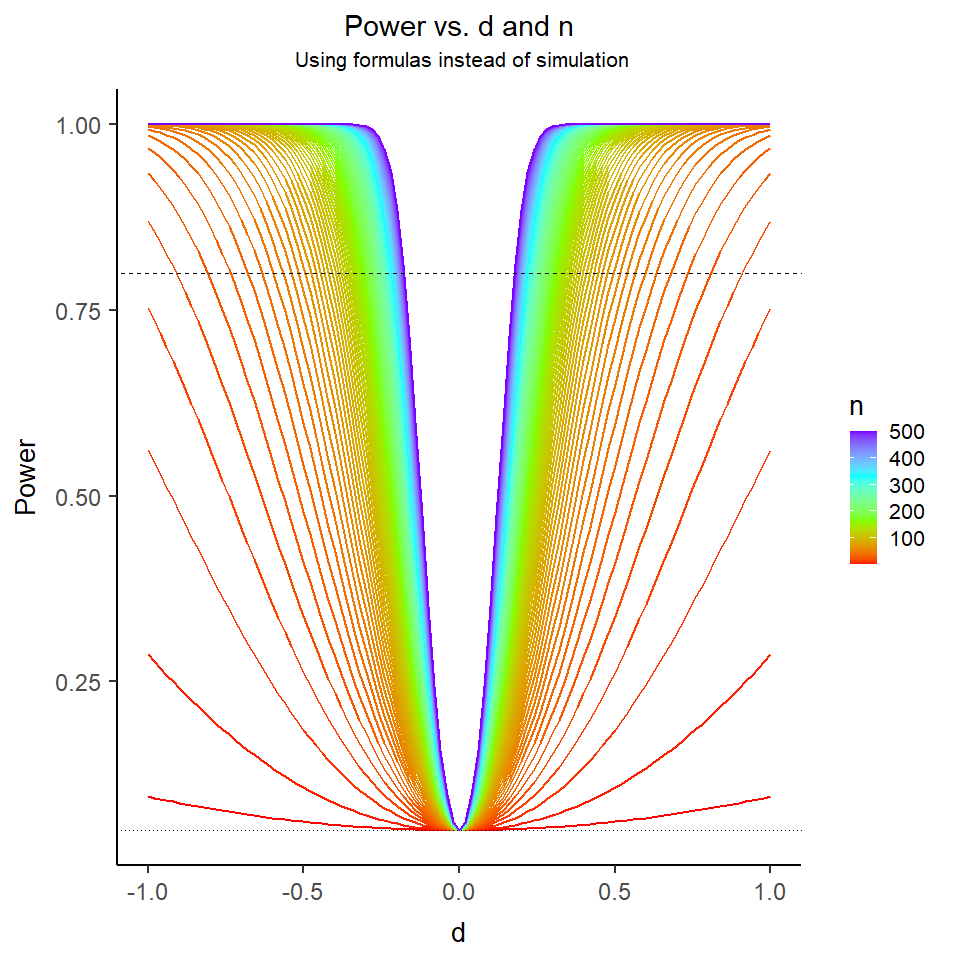
Wir erkennen deutlich, wie “smooth” der Plot eigentlich aussehen sollte. Daran ist ersichtlich, dass unsere Simulation wesentlich mehr Wiederholung benötigt, um ein solches Bild abzugeben.

Für Interessierte ist in Appendix B ein kleiner Exkurs in pwr dargestellt.

Verstöße gegen die Modellannahmen

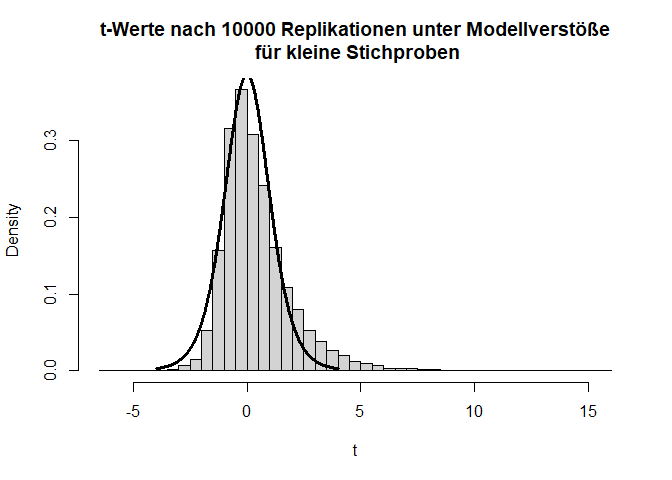
Liegen andere Verstöße gegen die Modellannahmen vor, dann kann es fälschlicherweise zu signifikanten Ergebnissen kommen, obwohl es in der Population gar keinen Effekt gibt. Dies ist oft bei kleinen Stichproben ein Problem. Nehmen wir beispielsweise an, dass die beiden Gruppen sehr gegenläufig schief verteilt sind.

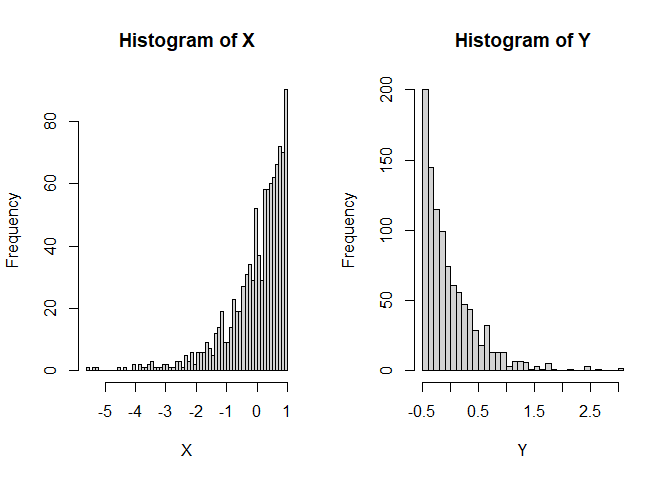
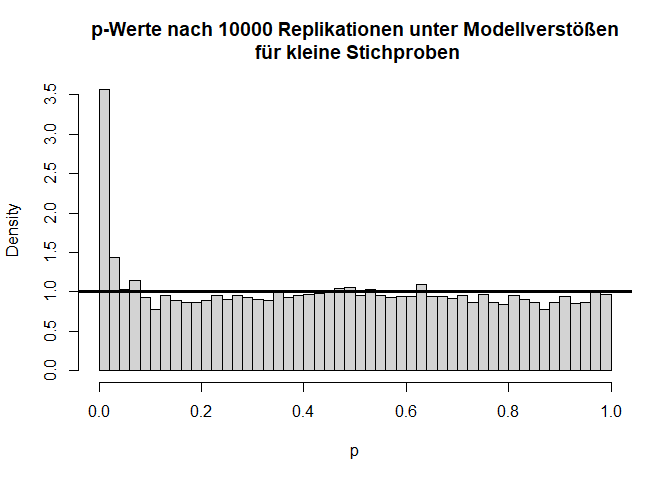
Hier gilt zwar die Null-Hypothese, da beide Verteilungen einen theoretischen Mittelwert von 0 haben, aber die Varianzen unterscheiden sich (was im Histogramm durch die extremeren Werte entlang der x-Achse zu erkennen ist) und die Variablen sind offensichtlich nicht normalverteilt. Schauen wir uns nun die Power des $t$-Tests für eine sehr kleine Stichprobe von 5 pro Gruppe an:

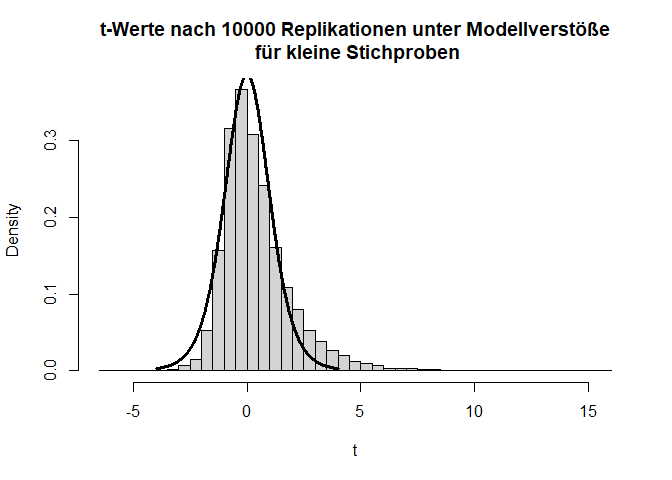
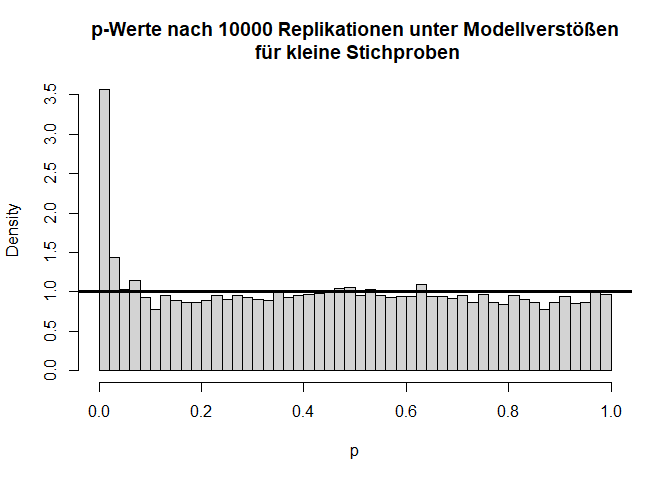
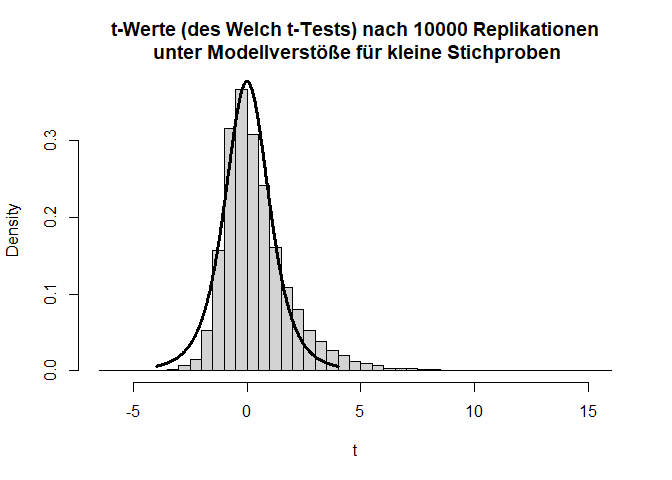
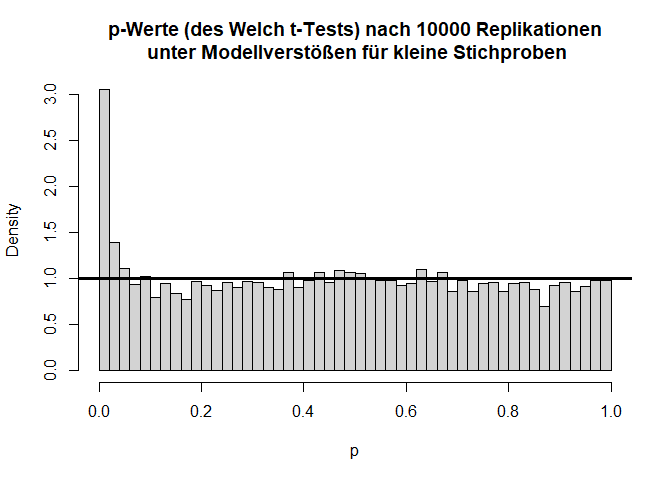
Insgesamt sieht die Verteilung der $T$-Werte einigermaßen in Ordnung, wenn auch etwas schief, aus. Doch bei den $p$-Werten fällt auf, dass die Null-Hypothese zu häufig verworfen wird, nämlich insgesamt in 11.11% der Fälle (durch Zufall, da die Null-Hypothese eigentlich gilt!); also doppelt so häufig wie von uns vorgegeben! Glücklicherweise ist der $t$-Test relativ robust, was daran zu erkennen ist, dass, wenn die Stichprobengröße für dieses Beispiel bei 50 oder gar höher liegt (pro Gruppe), das $\alpha$-Niveau schon wieder einigermaßen eingehalten wird. Außerdem gibt es geeignetere Tests zum Untersuchen von Mittelwertsunterschieden zweier Stichproben als den $t$-Test - nämlich den Welch-Test. Dies ist eine Erweiterung des $t$-Tests für ungleiche Varianzen. Dieser ist auch der Default in R. Wir rechnen ihn, indem wir nicht länger var.equal = T in t.test spezifizieren. Der Output ändert sich bis auf die Namensänderung kaum - die Freiheitsgrade des Tests werden korrigiert, um auf die ungleichen Varianzen zu reagieren (dies bedeutet, immer wenn die Freiheitsgrade nicht einfach $n-2$ sind, dann wurde der Welch-Test gerechnet; insbesondere Kommazahlen als $df$ sind möglich). Jedoch bringt diese Erweiterung ebenfalls nur für größere Stichproben etwas. Die analoge Simulationsstudie können Sie Appendix A entnehmen.

Diese Sitzung sollte als Einführung in R, Vorbereitung für die Regressionssitzung und kleine Wiederholung einiger wichtiger inferenzstatistischer Begriffe (wie etwa $\alpha$-Fehler, Power, Hypothese etc.) fungieren. Wie wir Histogramme erstellen und Verteilungen vergleichen, erfahren wir in der nächsten Sitzung im Rahmen der Voraussetzungen der Regressionsanalyse und Ausreißerdiagnostik.

Eine Übersicht über Matrixalgebra in R erhalten Sie in Appendix C.

Eine schöne Einleitung in Plots in R, wie man diese erstellt, bearbeitet und abspeichert, können Sie in den Unterlagen aus dem Bachelor (PsyBsc2) zu R Deskriptivstatistik nachlesen, wenn Sie denn wollen.

Appendix

Appendix A

Analoge Simulationsstudie

Hier ist der Code für einige Grafiken und Simulationen dargestellt. Dies geht natürlich über den Stoff des Seminars hinaus und ist nur für Interessierte bestimmt.

Verteilung unter $H_0$

ts <- c(); ps <- c() # wir brauchen zunächst Vektoren, in die wir die t-Werte und die p-Werte hineinschreiben können
for(i in 1:10000)
{
    X <- rnorm(n = 1000, mean = 0, sd = 1)
    Y <- rnorm(n = 1000, mean = 0, sd = 1)
    ttest <- t.test(X, Y, var.equal = T)
    ts <- c(ts, ttest$statistic) # nehme den Vektor ts und verlängere ihn um den neuen t-Wert
    ps <- c(ps, ttest$p.value)   # nehme den Vektor ps und verlängere ihn um den neuen p-Wert
}

hist(ts, main = "(empirische) t-Werte nach 10000 Replikationen unter H0", 
     xlab = "T", freq = F, breaks = 50)
lines(x = seq(-4,4,0.01), dt(x = seq(-4,4,0.01), df = ttest$parameter), 
      lwd = 3)

hist(ps, main = "p-Werte nach 10000 Replikationen unter H0", 
     xlab = "p", freq = F, breaks = 50)
abline(a = 1, b = 0, lwd = 3)

Verteilung unter $H_1$

ts <- c(); ps <- c() # wir brauchen zunächst Vektoren, in die wir die t-Werte und die p-Werte hineinschreiben können
for(i in 1:10000)
{
    X <- rnorm(n = 1000, mean = 0, sd = 1)
    Y <- -0.1 + rnorm(n = 1000, mean = 0, sd = 1) # Mittelwertsdifferenz ist 0.1
    ttest <- t.test(X, Y, var.equal = T)
    ts <- c(ts, ttest$statistic) # nehme den Vektor ts und verlängere ihn um den neuen t-Wert
    ps <- c(ps, ttest$p.value)   # nehme den Vektor ps und verlängere ihn um den neuen p-Wert
}

hist(ts, main = "(empirische) t-Werte nach 10000 Replikationen unter H1", 
     xlab = "T", freq = F, breaks = 50)
lines(x = seq(-4,4,0.01), dt(x = seq(-4,4,0.01), df = ttest$parameter), 
      lwd = 3)

hist(ps, main = "p-Werte nach 10000 Replikationen unter H1", 
     xlab = "p", freq = F, breaks = 50)
abline(a = 1, b = 0, lwd = 3)

Verteilung unter $H_0$ mit Modellverstößen

set.seed(1)
ts <- c(); ps <- c() # wir brauchen zunächst Vektoren, in die wir die t-Werte und die p-Werte hineinschreiben können
for(i in 1:10000)
{
       X <- -rexp(n = 5, rate = 1) # simuliere Exponentialverteilung zur Rate 1 mit n = 5
        X <- X + 1 # zentriere, sodass der Populationsmittelwert wieder 0 ist
        Y <- rexp(n = 5, rate = 2) # simuliere Exponentialverteilung zur Rate 2 mit n = 5
        Y <- Y - 1/2 # zentriere, sodass der Populationsmittelwert wieder 0 ist
        ttest <- t.test(X, Y, var.equal = T)
        ts <- c(ts, ttest$statistic) # nehme den Vektor ts und verlängere ihn um den neuen t-Wert
        ps <- c(ps, ttest$p.value)   # nehme den Vektor ps und verlängere ihn um den neuen p-Wert
}

hist(ts, main = "t-Werte nach 10000 Replikationen unter Modellverstöße\n für kleine Stichproben", 
     xlab = "t", freq = F, breaks = 50)
lines(x = seq(-4,4,0.01), dt(x = seq(-4,4,0.01), df = ttest$parameter), 
      lwd = 3)

hist(ps, main = "p-Werte nach 10000 Replikationen unter Modellverstößen\n für kleine Stichproben", 
     xlab = "p", freq = F, breaks = 50)
abline(a = 1, b = 0, lwd = 3)

Verteilung unter $H_0$ mit Modellverstößen: Welch-Test

set.seed(1)
ts <- c(); ps <- c() # wir brauchen zunächst Vektoren, in die wir die t-Werte und die p-Werte hineinschreiben können
for(i in 1:10000)
{
        X <- -rexp(n = 5, rate = 1) # simuliere Exponentialverteilung zur Rate 1 mit n = 5
        X <- X + 1 # zentriere, sodass der Populationsmittelwert wieder 0 ist
        Y <- rexp(n = 5, rate = 2) # simuliere Exponentialverteilung zur Rate 2 mit n = 5
        Y <- Y - 1/2 # zentriere, sodass der Populationsmittelwert wieder 0 ist
        ttest <- t.test(X, Y) # Welch Test
        ts <- c(ts, ttest$statistic) # nehme den Vektor ts und verlängere ihn um den neuen t-Wert
        ps <- c(ps, ttest$p.value)   # nehme den Vektor ps und verlängere ihn um den neuen p-Wert
}

hist(ts, main = "t-Werte (des Welch t-Tests) nach 10000 Replikationen\n unter Modellverstöße für kleine Stichproben", 
     xlab = "t", freq = F, breaks = 50)
lines(x = seq(-4,4,0.01), dt(x = seq(-4,4,0.01), df = ttest$parameter), 
      lwd = 3)

hist(ps, main = "p-Werte (des Welch t-Tests) nach 10000 Replikationen\n unter Modellverstößen für kleine Stichproben", 
     xlab = "p", freq = F, breaks = 50)
abline(a = 1, b = 0, lwd = 3)

Insgesamt sieht die Verteilung der Teststatistik (also quasi der empirischen $t$-Werte) einigermaßen in Ordnung aus, wenn auch etwas schief, doch bei den $p$-Werten fällt auf, dass die Null-Hypothese zu häufig verworfen wird, nämlich insgesamt in 10% der Fälle (durch Zufall, da die Null-Hypothese eigentlich gilt!); also doppelt so häufig wie von uns vorgegeben! Hier gibt es kaum Unterschiede zum ursprünglichen $t$-Test mit gleichen Varianzen. Allerdings ist die Stichprobengröße hier mit 5 pro Gruppe recht klein!

Verteilung unter $H_0$ mit Modellverstößen mit größerer Stichprobe: Welch-Test

set.seed(1234)
ts <- c(); ps <- c() # wir brauchen zunächst Vektoren, in die wir die t-Werte und die p-Werte hineinschreiben können
for(i in 1:10000)
{
        X <- -rexp(n = 100, rate = 1) # simuliere Exponentialverteilung zur Rate 1 mit n = 100
        X <- X + 1 # zentriere, sodass der Populationsmittelwert wieder 0 ist
        Y <- rexp(n = 100, rate = 2) # simuliere Exponentialverteilung zur Rate 2 mit n = 100
        Y <- Y - 1/2 # zentriere, sodass der Populationsmittelwert wieder 0 ist
        ttest <- t.test(X, Y) # Welch Test
        ts <- c(ts, ttest$statistic) # nehme den Vektor ts und verlängere ihn um den neuen t-Wert
        ps <- c(ps, ttest$p.value)   # nehme den Vektor ps und verlängere ihn um den neuen p-Wert
}

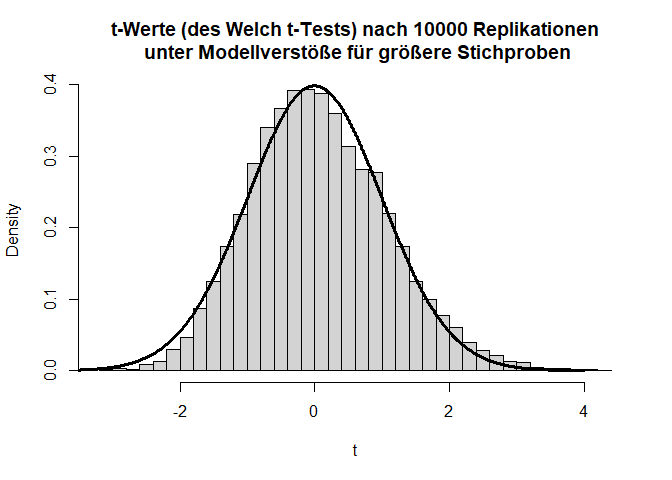
hist(ts, main = "t-Werte (des Welch t-Tests) nach 10000 Replikationen\n unter Modellverstöße für größere Stichproben", 
     xlab = "t", freq = F, breaks = 50)
lines(x = seq(-4,4,0.01), dt(x = seq(-4,4,0.01), df = ttest$parameter), 
      lwd = 3)

hist(ps, main = "p-Werte (des Welch t-Tests) nach 10000 Replikationen\n unter Modellverstößen für größere Stichproben", 
     xlab = "p", freq = F, breaks = 50)
abline(a = 1, b = 0, lwd = 3)

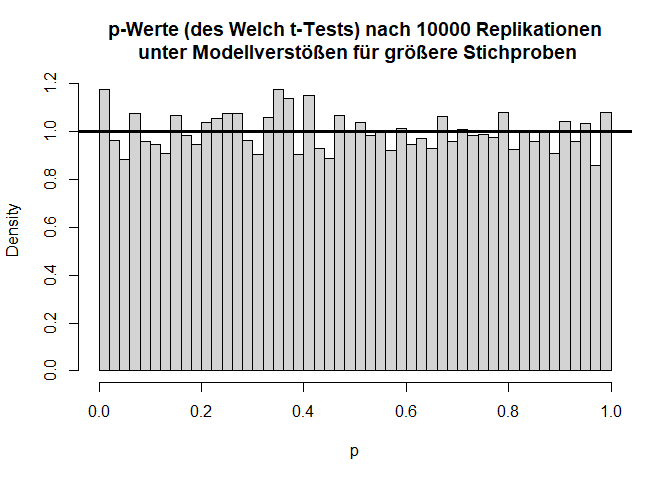
Für jeweils 100 Erhebungen pro Gruppe ist der Verstoß gegen die Normalverteilungsannahme bei ungleichen Varianzen für den Welch-Test fast zu vernachlässigen.

Appendix B

 library(pwr)
 pwr.t.test(n = 1000, d = 0.1)

## 
##      Two-sample t test power calculation 
## 
##               n = 1000
##               d = 0.1
##       sig.level = 0.05
##           power = 0.6083667
##     alternative = two.sided
## 
## NOTE: n is number in *each* group

Appendix C

X <- c(1, 2, 3)
Y <- c(10, 8, 6)

Y[2]

## [1] 8

X + Y  # Addition

## [1] 11 10  9

X - Y  # Subtraktion

## [1] -9 -6 -3

3*X    # Skalare Multiplikation

## [1] 3 6 9

1/2*X

## [1] 0.5 1.0 1.5

Z <- c(1:6) # Zahlen 1 bis 6
Z + Y

## [1] 11 10  9 14 13 12

X*Y # elementeweise Multiplikation

## [1] 10 16 18

as.matrix(X)

##      [,1]
## [1,]    1
## [2,]    2
## [3,]    3

A <- cbind(X, Y)
A

##      X  Y
## [1,] 1 10
## [2,] 2  8
## [3,] 3  6

B <- rbind(X, Y)
B

##   [,1] [,2] [,3]
## X    1    2    3
## Y   10    8    6

A[1, 2] # Eintrag 1. Zeile 2. Spalte in A

##  Y 
## 10

A[1, ] # 1. Zeile

##  X  Y 
##  1 10

A[, 2] # 2. Spalte

## [1] 10  8  6

A

##      X  Y
## [1,] 1 10
## [2,] 2  8
## [3,] 3  6

t(A)

##   [,1] [,2] [,3]
## X    1    2    3
## Y   10    8    6

B

##   [,1] [,2] [,3]
## X    1    2    3
## Y   10    8    6

A + B

## Error in A + B : non-conformable arrays

A * 2

##      X  Y
## [1,] 2 20
## [2,] 4 16
## [3,] 6 12

A %*% B # Matrixprodukt A*B

##      [,1] [,2] [,3]
## [1,]  101   82   63
## [2,]   82   68   54
## [3,]   63   54   45

B %*% A # Matrixprodukt B*A

##    X   Y
## X 14  44
## Y 44 200

diag(3) # Einheitsmatrix 3x3

##      [,1] [,2] [,3]
## [1,]    1    0    0
## [2,]    0    1    0
## [3,]    0    0    1

diag(1:3) # Diagonalmatrix mit Elementen 1,2,3 auf der Diagonalen

##      [,1] [,2] [,3]
## [1,]    1    0    0
## [2,]    0    2    0
## [3,]    0    0    3

C <- matrix(data = c(1:9), nrow = 3, ncol = 3, byrow = T)
C

##      [,1] [,2] [,3]
## [1,]    1    2    3
## [2,]    4    5    6
## [3,]    7    8    9

diag(C)

## [1] 1 5 9

solve(C)

## Error in solve.default(C) : 
##   system is computationally singular: reciprocal condition number = 2.59052e-18

det(C)

## [1] 6.661338e-16

round(det(C), 14)

## [1] 0

2*C[, 2] - C[, 1]     # 2*2.Spalte - 1. Spalte rechnen ist gleich

## [1] 3 6 9

C[, 3]               # 3. Spalte

## [1] 3 6 9

C^-1

##           [,1]  [,2]      [,3]
## [1,] 1.0000000 0.500 0.3333333
## [2,] 0.2500000 0.200 0.1666667
## [3,] 0.1428571 0.125 0.1111111

C^-1 %*% C # ist nicht die Einheitsmatrix

##          [,1]     [,2]     [,3]
## [1,] 5.333333 7.166667 9.000000
## [2,] 2.216667 2.833333 3.450000
## [3,] 1.420635 1.799603 2.178571

C^-1 * C   # elementeweise ergibt überall 1 - ist immer noch nicht die Einheitsmatrix!

##      [,1] [,2] [,3]
## [1,]    1    1    1
## [2,]    1    1    1
## [3,]    1    1    1

D <- matrix(c(1, 0, 0,
              1, 1, 1,
              2, 4, 5), 3, 3, byrow = T)
det(D)

## [1] 1

solve(D)

##      [,1] [,2] [,3]
## [1,]    1    0    0
## [2,]   -3    5   -1
## [3,]    2   -4    1

D %*% solve(D)

##      [,1] [,2] [,3]
## [1,]    1    0    0
## [2,]    0    1    0
## [3,]    0    0    1

solve(D) %*% D

##      [,1] [,2] [,3]
## [1,]    1    0    0
## [2,]    0    1    0
## [3,]    0    0    1

Literatur

Agresti, A, & Finlay, B. (2013). Statistical methods for the social sciences. (Pearson new international edition, 4th edition). Harlow, Essex : Pearson Education Limited.

Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden (5. Auflage, 1. Auflage: 2010). Weinheim: Beltz.

• Blau hinterlegte Autor:innenangaben führen Sie direkt zur universitätsinternen Ressource.