](/media/header/birds_migration.jpg)
Einleitung
In dieser Sitzung wollen wir uns die Hauptkomponentenanalyse (im Folgenden PCA, engl. Principal Component Analysis, vgl. Eid, Gollwitzer & Schmitt, 2017, Kapitel 25 und insbesondere Kapitel 25.3, Brandt, 2020, Kapitel 23 und insbesondere 23.3 und Pituch und Stevens, 2016, Kapitel 9.1 bis 9.8) genauer ansehen. Die PCA kann genutzt werden, um sich einen Überblick über die Daten zu verschaffen und kann zur Dimensionsreduktion angewandt werden, also um viele Variablen auf einige wenige Hauptkomponenten herunterzubrechen. Schwierig ist hierbei die Frage, wie viele Hauptkomponenten denn aus einem Datensatz extrahiert werden sollen. Es gibt auf diese keine pauschale Antwort, allerdings können wir uns einige Hilfsmittel heranziehen, um zumindest einen “educated guess” abzugeben. Eine weitere Frage ist, wie wir die Hauptkomponenten nach Extraktion interpretieren. Wir beginnen wie immer mit dem Einladen der Daten. Sie können den Datensatz “PCA.RData” hier herunterladen.
Daten und Pakete laden
Diesmal liegen die Daten nicht als .rda File, sondern als .RData File vor. Dieses Datenformat ist identisch zu .rda, denn .rda ist einfach eine Kurzschreibweise für .RData (es ist nur wichtig zu wissen, dass es sein kann, dass Ihnen auch dieses Datenformat unterkommt!). Wir laden es deshalb ganz einfach mit load ein (falls die Daten auf dem Desktop von Frau Musterfrau liegen).
load("C:/Users/Musterfrau/Desktop/PCA.RData")
Oder wir laden sie direkt über die Website:
load(url("https://pandar.netlify.app/daten/PCA.RData"))
Nachdem die Daten geladen sind, erkennen wir, dass wir diesmal zwei Datensätze rechts oben unter der Rubrik Data in R-Studio angezeigt bekommen: data und dataUV. Sie haben die Daten von einer Professorin bekommen, die eine geheime Pilotstudie durchgeführt hat. Sie sollen nun untersuchen, welche der Kovariaten Einfluss auf die abhängige Variable haben. Damit Sie nicht voreingenommen sind, sind die Namen recht nichtssagend. Schauen wir uns diese Datensätze einmal genauer an. Bevor wir dies tun, laden wir schnell die nötigen Paket für diese Sitzung. Das psych Paket hat einige sehr nützliche Funktionen zur Datenaufbereitung und Diagnostik. corrplot verwenden wir um Korrelationsmatrizen grafisch zu veranschaulichen.
library(psych) # Datenaufbereitung und -diagnostik
library(corrplot) # Korrelationsmatrixgrafiken
Überblick über die Daten und einfache Deskriptivstatistiken
Wir verschaffen uns einen Überblick, indem wir head auf die Datensätze data und dataUV anwenden.
head(data)
## x1 x2 x3 x4 x5 x6 y
## 1 -2.0673046 -2.1067594 2.1999414 0.6102797 1.31172684 -0.1661444 -2.9120695
## 2 0.4624190 0.4763040 -0.9814150 -1.2456641 0.39173859 -0.7428731 -0.9110541
## 3 -1.2980523 -0.1252032 -0.3915240 -1.8572746 -1.10305866 2.6331432 0.5187501
## 4 -0.9851797 0.7531473 -0.3404161 0.8214230 -0.82308313 -0.7174490 0.5631645
## 5 0.5458964 0.8963123 -0.8618176 0.3865011 0.22932366 -0.1266971 -1.2189402
## 6 -0.7262101 -1.0080812 -0.3136828 -0.6501589 -0.02115397 0.1649933 -0.2164468
head(dataUV)
## x1 x2 x3 x4 x5 x6
## 1 -2.0673046 -2.1067594 2.1999414 0.6102797 1.31172684 -0.1661444
## 2 0.4624190 0.4763040 -0.9814150 -1.2456641 0.39173859 -0.7428731
## 3 -1.2980523 -0.1252032 -0.3915240 -1.8572746 -1.10305866 2.6331432
## 4 -0.9851797 0.7531473 -0.3404161 0.8214230 -0.82308313 -0.7174490
## 5 0.5458964 0.8963123 -0.8618176 0.3865011 0.22932366 -0.1266971
## 6 -0.7262101 -1.0080812 -0.3136828 -0.6501589 -0.02115397 0.1649933
Die beiden Datensätze scheinen fast identisch zu sein. In dataUV fehlt lediglich die Variable y. Demnach enthält data die Daten für eine Regressionsanalyse mit AV und dataUV enthält nur die UVs (unabhängigen Variablen, Prädiktoren) - es fehlt das Kriterium (AV) y. Wir wollen uns noch die Mittelwerte und Standardbabweichungen der Variablen ansehen.
round(head(data),2) # noch ein Überblick: diesmal auf 2 Nachkommastellen gerundet
## x1 x2 x3 x4 x5 x6 y
## 1 -2.07 -2.11 2.20 0.61 1.31 -0.17 -2.91
## 2 0.46 0.48 -0.98 -1.25 0.39 -0.74 -0.91
## 3 -1.30 -0.13 -0.39 -1.86 -1.10 2.63 0.52
## 4 -0.99 0.75 -0.34 0.82 -0.82 -0.72 0.56
## 5 0.55 0.90 -0.86 0.39 0.23 -0.13 -1.22
## 6 -0.73 -1.01 -0.31 -0.65 -0.02 0.16 -0.22
# Mittelwerte der Daten
round(apply(X = data, MARGIN = 2, FUN = mean), 10) # identisch zu "colMeans(data)", wenn auch gerundet wird: round(colMeans(data), 10)
## x1 x2 x3 x4 x5 x6 y
## 0 0 0 0 0 0 0
# SD der Daten
round(apply(X = data, MARGIN = 2, FUN = sd), 10)
## x1 x2 x3 x4 x5 x6 y
## 1.000000 1.000000 1.000000 1.000000 1.000000 1.000000 1.350034
Damit wir nicht die SD jeder einzelnen Variablen mit Hand bestimmen müssen, benutzen wir apply. Diese Funktion wendet auf den Datensatz X, entweder über die Zeilen MARGIN = 1 oder Spalten MARGIN = 2 (hier gewählt), die Funktion, welche nur ein Argument entgegen nimmt, in FUN an. Somit führt apply(X = data, MARGIN = 2, FUN = mean) zum selben Ergebnis wie colMeans und wenn wir mean mit sd ersetzten, erhalten wir die SD für jede Spalte.
Wir erkennen, dass alle Mittelwerte der Variablen bei 0 liegen und die Standardabweichungen aller UVs 1 sind. Damit ist ersichtlich, dass die UVs standardisiert (Mittelwert = 0 & Standardabweichung = 1) wurden und die AV zumindest zentriert (Mittelwert = 0) wurde. In diesem Fall ist die Kovarianzmatrix über die UVs gerade gleich der Korrelationsmatrix über die UVs.
Berechnen der Korrelationsmatrix
Wir wollen uns die Korrelationsmatrix der UVs genauer ansehen. Dazu können wir einfach die Funktion cor auf dataUV anwenden. Da die Daten standardisiert sind, vergleichen wir das Ergebnis direkt mit dem der Kovarianzmatrix.
cor(dataUV) # Korrelationsmatrix
## x1 x2 x3 x4 x5 x6
## x1 1.00000000 0.59687989 -0.43595753 -0.16998321 -0.2712820 0.09837908
## x2 0.59687989 1.00000000 -0.63789368 -0.06529934 -0.3581969 0.07622499
## x3 -0.43595753 -0.63789368 1.00000000 0.05347046 0.4750548 -0.10391023
## x4 -0.16998321 -0.06529934 0.05347046 1.00000000 0.2141352 -0.42867869
## x5 -0.27128197 -0.35819689 0.47505483 0.21413524 1.0000000 -0.48190559
## x6 0.09837908 0.07622499 -0.10391023 -0.42867869 -0.4819056 1.00000000
cov(dataUV) # Kovarianzmatrix
## x1 x2 x3 x4 x5 x6
## x1 1.00000000 0.59687989 -0.43595753 -0.16998321 -0.2712820 0.09837908
## x2 0.59687989 1.00000000 -0.63789368 -0.06529934 -0.3581969 0.07622499
## x3 -0.43595753 -0.63789368 1.00000000 0.05347046 0.4750548 -0.10391023
## x4 -0.16998321 -0.06529934 0.05347046 1.00000000 0.2141352 -0.42867869
## x5 -0.27128197 -0.35819689 0.47505483 0.21413524 1.0000000 -0.48190559
## x6 0.09837908 0.07622499 -0.10391023 -0.42867869 -0.4819056 1.00000000
Beide Matrizen sind identisch! Anstatt des Datensatzes dataUV hätten wir auch data[,1:6] auswählen können. [,1:6] zeigt hierbei an, dass wir die 1. bis 6. Spalte von data verwenden wollen. Um dies genauer zu sehen, können Sie ja einfach mal data[,1:6] in Ihrem R-Fenster ausführen und dann die beiden Objekte vergleichen. Um damit weiterrechnen zu können, speichern wir die Korrelationsmatrix der UVs unter dem Namen R_UV ab.
R_UV <- cor(data[,1:6])
Grafische Veranschaulichung der Korrelationsmatrix
Um noch mehr auf einen Blick zu sehen, wollen wir uns die Korrelationsmatrix grafisch darstellen lassen. Dies geht mit der corrplot Funktion aus dem gleichnamigen Paket.
corrplot(R_UV)
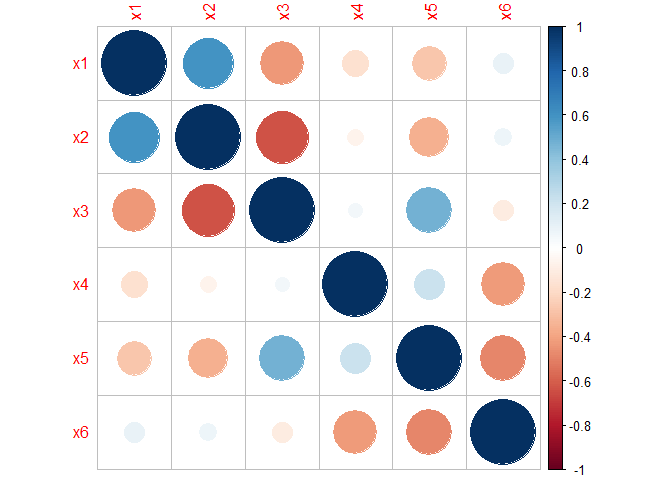
Wenn wir noch ein paar mehr Einstellungen an dieser Funktion vornehmen, erhalten wir eine Grafik, die auch die Koeffizienten enthält und noch etwas besser auf einen Blick interpretierbar ist. Wenn Sie sich für den Code interessieren, schauen Sie bitte im Appendix A nach.
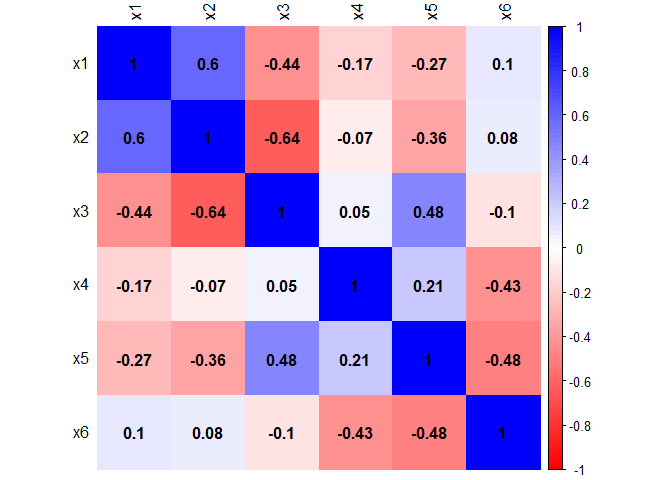
Je dunkler die Farbe (blau oder rot), desto stärker betraglich die Korrelation zwischen den Variablen. Es scheinen sich zwei Gruppen von Variablen zu bilden, die besonders stark linear zusammenzuhängen scheinen. Wir färben mal alles Rote auch Blau ein, um nur noch die Stärke der Effekte der Grafik zu entnehmen.
Grafische Veranschaulichung der absoluten Stärke der Zusammenhänge
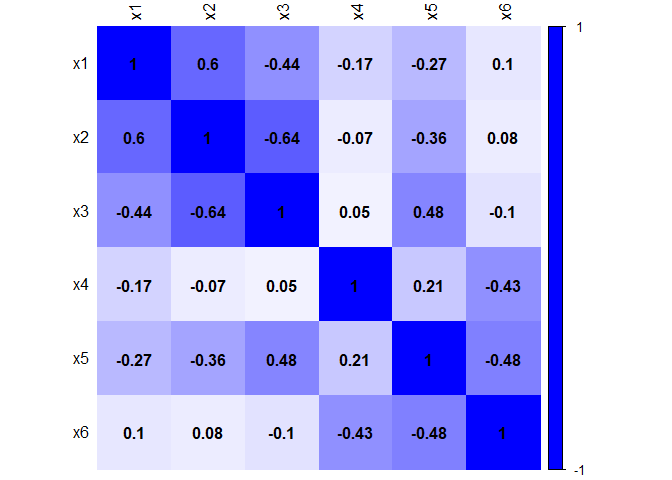
Nun ist noch stärker ersichtlich, dass jeweils die Variablen x1-x3 und die Variablen x4-x6 eine Gruppe bilden, da sie deskriptiv gesehen untereinander stärker zusammenzuhängen scheinen als zwischen den Gruppen. Diese Gruppen an Variablen haben vielleicht mehr Gemeinsamkeiten untereinander (also innerhalb einer Gruppe) als zwischen den Gruppen. Mit Hilfe einer PCA können wir nun untersuchen, auf wie viele Hauptkomponenten sich die Daten reduzieren lassen. Unserer laienhafter Einschätzung nach sollten es 2 sein!
Wiederholung der Grundbegriffe der PCA
Wenn Sie wünschen, können Sie hier die Grundbegriffe der PCA “ausklappen”.
Grundbegriffe der PCA
In der PCA bestimmen wir Hauptkomponenten $H$, die sich als Linearkombinationen der Variablen darstellen lassen mit der Eigenschaft, dass diese Hauptkomponenten unkorreliert sind und somit keine gemeinsame lineare Information enthalten. Z.B. sehen die Gleichungen zweier Hauptkomponenten, die aus zwei Variablen $Z_1$ und $Z_2$ entstehen, wie folgt aus:
\begin{align} H_1 &= \gamma_{11}Z_1 + \gamma_{12}Z_2\\ H_2 &= \gamma_{21}Z_1 + \gamma_{22}Z_2, \end{align}
wobei die $\gamma$s so gewählt sind, dass $\gamma_{11}^2 + \gamma_{12}^2 = 1$, $\gamma_{21}^2 + \gamma_{22}^2 = 1$ und $\gamma_{11}\gamma_{21} + \gamma_{12}\gamma_{22} = 0$.
In Matrixnotation sieht dies wie folgt aus: $$\mathbf{H}=\Gamma\mathbf{Z},$$ mit \begin{align} \mathbf{H} &= \begin{pmatrix}H_1\\ H_2\end{pmatrix}\\ \Gamma &= \begin{pmatrix}\gamma_{11}&\gamma_{12}\\ \gamma_{21} & \gamma_{22}\end{pmatrix}\\ \mathbf{Z} &= \begin{pmatrix}Z_1\\ Z_2\end{pmatrix}. \end{align}
Die Eigenschaft der $\gamma$s lässt sich dann wie folgt ausdrücken: $\Gamma\Gamma’=I$, wobei $I$ die Identitätsmatrix/Einheitsmatrix ist. In der Psychologie sind wir nun daran interessiert, die Daten zu reduzieren. Wir wollen also $\mathbf{Z}$ bspw. nur durch eine Hauptkomponente darstellen. Dazu müssen wir die sogenannten Ladungen der Variablen auf den Hauptkomponenten bestimmen. Diese erhalten wir, indem wir die jeweiligen Gewichte $\gamma$ mit der Wurzel aus den Eigenwerten multiplizieren (dies funktioniert nur, wenn die Variablen standardisiert sind). Dann lassen sich die Variablen durch standardisierte (Varianz = 1) Hauptkomponenten $\mathbf{H}^*$ darstellen: $$\mathbf{Z}=\Lambda\mathbf{H}^*.$$ Die Ladungsmatrix $\Lambda$ lässt sich wie folgt bestimmen: $\Lambda = \Gamma’\Theta_{std}$ mit $$\Theta_{std} = \begin{pmatrix} \sqrt{\theta_1} & 0 & 0\\ 0 & \ddots & 0\\ 0 & 0 & \sqrt{\theta_m} \end{pmatrix},$$
wobei $m$ gerade die Anzahl der Variablen ist. Hierbei ist das Transponieren wichtig, denn für das einfache Beispiel mit zwei Variablen und Hauptkomponenten ergibt sich: $\lambda_{11}=\sqrt{\theta_1}\gamma_{11}$ und $\lambda_{12}=\sqrt{\theta_2}\gamma_{21}$ (man achte auf die Indizes bei der zweiten Gleichung). Wir müssen nämlich das Gewicht der Variable $Z_1$ nehmen, welches bei der ersten Hauptkomponente gerade $\gamma_{11}$, aber bei der zweiten gerade $\gamma_{21}$ ist. Die Matrix $\Gamma$ ist gerade die Matrix der Eigenvektoren und die Eigenwerte $\theta$ repräsentieren die Varianzen der unstandardisierten Hauptkomponenten $\mathbf{H}$ (ohne $^*$). Somit sind dies gerade die Lösungen des Eigenwerteproblems zur Korrelationsmatrix unserer Daten. Die Korrelationsmatrix der Daten lässt sich auch ganz einfach mit Hilfe der Ladungsmatrix darstellen:
$$R:= \Lambda \Lambda’\quad (=\Sigma_\mathbf{Z})$$ wobei $$\Lambda’ \Lambda = \begin{pmatrix} \theta_1 & 0 & 0\\ 0 & \ddots & 0\\ 0 & 0 & \theta_m \end{pmatrix}=:\Theta$$
gerade eine Diagonalmatrix mit den Eigenwerten auf der Diagonalen ist (man achte hier auf das Transponieren!), also $\Theta_{std}\Theta_{std}=\Theta$.
Datenreduktion
Bis hierhin wurden die Daten noch nicht reduziert. Es wurde nur ein Weg präsentiert, wie die Korrelationsmatrix auch dargestellt werden kann mit Hilfe von orthogonalen (unkorrelierten) Hauptkomponenten. Wenn wir nun nur ein paar der Hauptkomponenten behalten (bspw. $k$ der $m$ Komponenten), dann geht Variation im Datensatz verloren. Hierbei ist es sinnig, dies anhand der Eigenwerte, also der Varianzen festzumachen, welche der Größe nach sortiert sind. Die Variation wird also durch die Reduktion der Hauptkomponenten verringert. Dies geschieht, indem wir aus der Matrix $\Lambda$ ein paar Spalten herausnehmen. Diese nennen wir dann $\Lambda^*$. Entsprechend verändert sich auch die resultierende Korrelationsmatrix $R^*$, welche auch häufig implizierte (durch das reduzierte “Modell”; dazu im nächsten Semester mehr) Korrelationsmatrix ($\Sigma_\mathbf{Z}$) genannt wird. Diese lässt sich immer so bestimmen:
wobei
Haben wir also nur ein paar der Hauptkomponenten gewählt, ist das resultierende $R^*$ nicht mehr gleich der Korrelationsmatrix, sondern repräsentiert die Korrelationsmatrix des reduzierten Datensatzes, wobei auf der Diagonalen keine 1en sondern die Kommunalitäten der Variablen stehen. Die ursprünglichen Variablen wurden in ihrer Variation eingeschränkt. Hier ist allerdings zu vermerken, dass wir diese reduzierte Korrelationsmatrix NICHT als Kovarianzmatrix interpretieren sollten, welche erst noch in einen Korrelationsmatrix zu überführen gilt! Sie können $R^*$ (oder $\Sigma_Z$) als Korrelationsmatrix interpretieren und sollten sich die 1en auf der Diagnale einfach denken! Jetzt aber Mal mit der dahinterliegenden Mathematik bei Seite: Wie wir dies in R umsetzen und wo wir die jeweiligen Matrizen ablesen, schauen wir uns im Folgenden an.
PCA mit der Funktion pca des psych-Pakets
Für eine PCA kann sowohl die Korrelation zwischen den Variablen (also die Korrelationsmatrix) als auch die Kovarianzen (also die Kovarianzmatrix) verwendet werden. Je nach dem welche Information genutzt wird, können unterschiedlich viele Hauptkomponenten extrahiert werden. Die beiden Datengrundlagen resultieren also nicht immer in der selben Lösung! Dazu sei gesagt, dass beim Benutzen der Kovarianz die Varianz der einzelenen Variablen eine ganz maßgebenden Rolle spielt. Dies bedeutet, dass Variablen mit großer Varianz “bevorzugt” werden und damit Hauptkomponenten sich eher aus Variablen mit große Varianz zusammensetzen. Um keine Gewichtung der Variablen vorzunehmen, wird in den meisten Fällen die Korrelationsmatrix verwendet. So werden wir auch vorgehen.
Eine PCA durchzuführen, geht sehr einfach. Wir schauen uns dies im Abschnitt PCA zu Fuß in Appendix B auch noch einmal mit den Basisfunktionen in R an. Jetzt verwenden wir aber die Funktion pca aus den psych Paket. Ihr müssen wir die Korrelationsmatrix als erstes Argument übergeben r, danach spezifizieren wir, wie viele Komponenten extrahiert werden sollen: nfactors. Da wir uns noch nicht entschieden haben, wie viele Komponenten wir extrahieren wollen, geben wir die gesamte Anzahl an Variablen an. Zuletzt spezifizieren wir, dass wir keine Rotation durchführen möchten: rotate = "none". Um das Objekt ggf. später weiter zu verwenden, ordnen wir es PCA1 zu, für die erste PCA, die wir in dieser Sitzung durchführen.
PCA1 <- pca(r = R_UV, nfactors = 6, rotate = "none")
PCA1
## Principal Components Analysis
## Call: principal(r = r, nfactors = nfactors, residuals = residuals,
## rotate = rotate, n.obs = n.obs, covar = covar, scores = scores,
## missing = missing, impute = impute, oblique.scores = oblique.scores,
## method = method, use = use, cor = cor, correct = 0.5, weight = NULL)
## Standardized loadings (pattern matrix) based upon correlation matrix
## PC1 PC2 PC3 PC4 PC5 PC6 h2 u2 com
## x1 0.71 0.29 0.44 0.40 -0.19 -0.17 1 -4.4e-16 3.1
## x2 0.78 0.41 0.10 -0.02 0.27 0.37 1 -2.2e-15 2.3
## x3 -0.78 -0.33 0.21 0.37 -0.10 0.32 1 6.7e-16 2.5
## x4 -0.36 0.66 -0.55 0.35 0.08 -0.05 1 5.6e-16 3.2
## x5 -0.72 0.28 0.48 -0.02 0.38 -0.15 1 3.3e-16 2.8
## x6 0.45 -0.75 -0.17 0.29 0.33 -0.10 1 8.9e-16 2.7
##
## PC1 PC2 PC3 PC4 PC5 PC6
## SS loadings 2.57 1.43 0.81 0.50 0.38 0.30
## Proportion Var 0.43 0.24 0.13 0.08 0.06 0.05
## Cumulative Var 0.43 0.67 0.80 0.89 0.95 1.00
## Proportion Explained 0.43 0.24 0.13 0.08 0.06 0.05
## Cumulative Proportion 0.43 0.67 0.80 0.89 0.95 1.00
##
## Mean item complexity = 2.8
## Test of the hypothesis that 6 components are sufficient.
##
## The root mean square of the residuals (RMSR) is 0
##
## Fit based upon off diagonal values = 1
Im Output ganz oben erkennen wir, dass wir eine PCA durchgeführt haben.
## Principal Components Analysis
Außerdem zeigt
## Call: principal(r = r, nfactors = nfactors, residuals = residuals,
## rotate = rotate, n.obs = n.obs, covar = covar, scores = scores,
## missing = missing, impute = impute, oblique.scores = oblique.scores,
## method = method, use = use, cor = cor, correct = 0.5, weight = NULL)
welche Funktionseinstellungen aufgerufen wurden.
Im nächsten Semester werden wir die Faktorenanalyse kennenlernen, welche einen ähnlichen Output, aber ein anderes zugrundeliegendes Modell aufweist. Aus diesem Grund heißen die Komponenten in diesem Output auch PC1 … PC6; für Principal Component 1 … 6.
## Standardized loadings (pattern matrix) based upon correlation matrix
## PC1 PC2 PC3 PC4 PC5 PC6 h2 u2 com
## x1 0.71 0.29 0.44 0.40 -0.19 -0.17 1 -4.4e-16 3.1
## x2 0.78 0.41 0.10 -0.02 0.27 0.37 1 -2.2e-15 2.3
## x3 -0.78 -0.33 0.21 0.37 -0.10 0.32 1 6.7e-16 2.5
## x4 -0.36 0.66 -0.55 0.35 0.08 -0.05 1 5.6e-16 3.2
## x5 -0.72 0.28 0.48 -0.02 0.38 -0.15 1 3.3e-16 2.8
## x6 0.45 -0.75 -0.17 0.29 0.33 -0.10 1 8.9e-16 2.7
Die Komponentenladungen zu den zugehörigen Hauptkomponenten sind unter Standardized loadings (pattern matrix) based upon correlation matrix zu sehen. Die Ladungen können hierbei als Korrelation zwischen der jeweiligen Variable und Hauptkomponente interpretiert werden. h2 steht für die Kommunalität ($h^2$), also den Anteil an systematischer Variation in der Variablen, der auf die extrahierten Komponenten zurückzuführen ist (da es sich hier um die maximale Anzahl an Komponenten handelt, ist die Kommunalität hier immer 1, da keine Datenreduktion vorliegt!). u2 ist die “uniqueness” ($u^2$), also der unerklärte Anteil der Varianz der Variable. Offensichtlich gilt $u^2 = 1-h^2$ oder $h^2 + u^2 = 1$. Unter den Ladungen erhalten wir Informationen über die Hauptkomponenten. com beschreibt die Komplexität der Items nach Hofmann (1978). In der Hilfe zur Funktion pca erhalten wir folgende Information:
$\texttt{Hoffman’s index of complexity for each item. This is just}$ $$\frac{\left(\sum_{i=1}^p\lambda_{ij}^2\right)^2}{\sum_{i=1}^p\lambda_{ij}^4}$$ $\texttt{where } \lambda_{ij} \texttt{ is the factor loading on the ith factor.}$ $\texttt{From Hofmann (1978), MBR.}$ $\texttt{See also Pettersson and Turkheimer (2010).}$
Wobei im Originaltext anstatt $\lambda$ gerade $a$ steht - es sind aber die Ladungen gemeint, weswegen ich das gleich mal angepasst habe! Insgesamt soll damit ein Kennwert angegeben werden, wie viele Komponenten im Schnitt nötig sind, um dieses Ergebnis zu erzeugen. Wir wollen diesem Koeffizienten allerdings nicht zu viel Bedeutung zuschreiben!
##
## PC1 PC2 PC3 PC4 PC5 PC6
## SS loadings 2.57 1.43 0.81 0.50 0.38 0.30
## Proportion Var 0.43 0.24 0.13 0.08 0.06 0.05
## Cumulative Var 0.43 0.67 0.80 0.89 0.95 1.00
## Proportion Explained 0.43 0.24 0.13 0.08 0.06 0.05
## Cumulative Proportion 0.43 0.67 0.80 0.89 0.95 1.00
SS loadings steht für “Sum of Squares loadings”, also die Quadratsumme der Ladungen. Diese ist gleich dem Eigenwert: $\theta_j = \Sigma_{i=1}^p\lambda_{ij}^2 = \lambda_{1j}^2+\dots+\lambda_{pj}^2$ (Spaltenquadratsumme der Komponentenladungen), mit $p=$ Anzahl an Variablen (hier $p=6$). Proportion Var betitelt den (relativen) Anteil der Variation, der durch die jeweiligen Komponenten erklärt werden kann. Cumulative Var kumuliert, also summiert, diese Anteile bis zur jeweiligen Komponente auf
(
$\text{CumVar}_i = \sum_{j=1}^i\theta_j = \theta_1+\dots+\theta_i$, also
$\text{CumVar}_1=\theta_1$
und $\text{CumVar}_2=\theta_1+\theta_2$, usw. ). Proportion Explained setzt die Variation, die durch die Komponenten erklärt wird, in Relation zur gesamten erklärten Varianz (d.h. hier summiert sich die erklärte Varianz immer zu 1, während sich die proportionale Varianz nur zu 1 aufsummiert, wenn die gesamte Variation im Datensatz auf die beiden Variablen zurückzuführen ist - da wir hier die Maximalanzahl extrahiert haben, geben beide die gleichen Zahlen wieder - dazu später mehr!). Cumulative Proportion beschreibt das gleiche wie Cumulative Var, nur bezieht sie sich hier auf die Proportion Explained.
## Mean item complexity = 2.8
## Test of the hypothesis that 6 components are sufficient.
##
## The root mean square of the residuals (RMSR) is 0
##
## Fit based upon off diagonal values = 1
Die Mean item complexity ist einfach der Mittelwert über die Komplexitäten von oben. Danach werden uns noch zwei Modellfitkriterien angegeben, die vor allem bei der Faktorenanalyse, also dem Stoff des nächsten Semesters, wichtig sind. Beim RMSR sprechen große Werte für einen schlechten Fit und bei Fit based upon off diagonal values sprechen Werte nahe 0 für einen schlechten Fit. Wir wollen diesen drei Koeffizienten nicht so viel Bedeutung zuschreiben.
Wir können dem Objekt PCA1 auch diese Informationen explizit entlocken. Dazu wenden wir einmal names auf das Objekt an, um einen Überblick zu erhalten:
names(PCA1)
## [1] "values" "rotation" "n.obs" "communality" "loadings"
## [6] "fit" "fit.off" "fn" "Call" "uniquenesses"
## [11] "complexity" "chi" "EPVAL" "R2" "objective"
## [16] "residual" "rms" "factors" "dof" "null.dof"
## [21] "null.model" "criteria" "PVAL" "weights" "r.scores"
## [26] "Vaccounted" "Structure"
Zum Beispiel stellt loadings die Ladungen dar:
PCA1$loadings
##
## Loadings:
## PC1 PC2 PC3 PC4 PC5 PC6
## x1 0.705 0.288 0.441 0.399 -0.194 -0.169
## x2 0.785 0.411 0.101 0.266 0.366
## x3 -0.775 -0.326 0.209 0.368 -0.105 0.321
## x4 -0.358 0.662 -0.548 0.354
## x5 -0.723 0.281 0.481 0.379 -0.153
## x6 0.453 -0.748 -0.169 0.291 0.333 -0.103
##
## PC1 PC2 PC3 PC4 PC5 PC6
## SS loadings 2.571 1.435 0.808 0.505 0.380 0.302
## Proportion Var 0.428 0.239 0.135 0.084 0.063 0.050
## Cumulative Var 0.428 0.668 0.802 0.886 0.950 1.000
PCA1$loadings[,] # um alle zu sehen
## PC1 PC2 PC3 PC4 PC5 PC6
## x1 0.7054183 0.2881475 0.4409241 0.39874202 -0.19365933 -0.1686499
## x2 0.7847500 0.4114272 0.1012048 -0.01687264 0.26578568 0.3656855
## x3 -0.7753742 -0.3255974 0.2089320 0.36764002 -0.10454187 0.3209991
## x4 -0.3576004 0.6615788 -0.5476874 0.35393472 0.08308031 -0.0479787
## x5 -0.7230884 0.2807451 0.4807040 -0.01616253 0.37896671 -0.1528789
## x6 0.4530308 -0.7483101 -0.1693431 0.29114954 0.33267595 -0.1033278
[,] erzwingt, dass alle Ladungen angezeigt werden, da ansonsten intern ein Cutoff-Wert herangezogen wird, um das Ganze übersichtlicher zu machen (i.d.R. betraglich > 0.2). Außerdem ändern sich die Eigenwerte, je nachdem, wie die Ladungen angezeigt werden, was sehr seltsam erscheint… Ein extremes Beispiel erkennen wir, indem wir die Komponentenladungen auf eine Nachkommastelle runden:
round(PCA1$loadings, 1)
##
## Loadings:
## PC1 PC2 PC3 PC4 PC5 PC6
## x1 0.7 0.3 0.4 0.4 -0.2 -0.2
## x2 0.8 0.4 0.1 0.3 0.4
## x3 -0.8 -0.3 0.2 0.4 -0.1 0.3
## x4 -0.4 0.7 -0.5 0.4 0.1
## x5 -0.7 0.3 0.5 0.4 -0.2
## x6 0.5 -0.7 -0.2 0.3 0.3 -0.1
##
## PC1 PC2 PC3 PC4 PC5 PC6
## SS loadings 2.670 1.410 0.750 0.570 0.400 0.340
## Proportion Var 0.445 0.235 0.125 0.095 0.067 0.057
## Cumulative Var 0.445 0.680 0.805 0.900 0.967 1.023
Für die Eigenwerte (SS loadings) werden immer noch drei Nachkommastellen angezeigt und dennoch haben sich die Werte extrem geändert. Hier müssen wir also vorsichtig sein, diese Ansicht zu interpretieren. Besser wäre es, wir lassen uns die richtigen Werte ausgeben. Diese verstecken sich hinter Vaccounted ("Variance accounted for" = erklärte Varianz):
PCA1$Vaccounted
## PC1 PC2 PC3 PC4 PC5 PC6
## SS loadings 2.5706246 1.4347873 0.8080240 0.50473814 0.38026636 0.30155966
## Proportion Var 0.4284374 0.2391312 0.1346707 0.08412302 0.06337773 0.05025994
## Cumulative Var 0.4284374 0.6675686 0.8022393 0.88636233 0.94974006 1.00000000
## Proportion Explained 0.4284374 0.2391312 0.1346707 0.08412302 0.06337773 0.05025994
## Cumulative Proportion 0.4284374 0.6675686 0.8022393 0.88636233 0.94974006 1.00000000
Die Eigenwerte/Varianzen der Hauptkomponenten sind hierbei einfach die Diagonalelemente folgenden Matrixprodukts: $\Lambda’\Lambda$ (siehe auch Grundbegriffe der PCA, diag gibt die Diagonalelemente wieder, t() transponiert die Matrix und %*% ist der Matrixproduktoperator):
diag(t(PCA1$loadings[,]) %*% PCA1$loadings[,])
## PC1 PC2 PC3 PC4 PC5 PC6
## 2.5706246 1.4347873 0.8080240 0.5047381 0.3802664 0.3015597
Jetzt haben wir uns sehr lange mit der Ladungsmatrix beschäftigt. Allerdings sind die ersten Ergebnisse, die wir bei einer PCA und dem Lösen des damit verbundenen Eigenwerteproblems erhalten, gerade die Eigenwerte sowie die Eigenvektoren. Die Eigenvektoren in einer Matrix sind gerade die Gewichte ($\Gamma$), mit welchen die Hauptkomponenten aus den Variablen erzeugt werden (siehe auch Grundbegriffe der PCA). Die Gewichte verbergen sich hinter dem gleichen Namen im R-Objekt:
PCA1$weights
## PC1 PC2 PC3 PC4 PC5 PC6
## x1 0.2744152 0.2008294 0.5456820 0.78999780 -0.5092729 -0.5592588
## x2 0.3052760 0.2867514 0.1252498 -0.03342851 0.6989461 1.2126473
## x3 -0.3016287 -0.2269308 0.2585715 0.72837774 -0.2749175 1.0644632
## x4 -0.1391103 0.4610988 -0.6778108 0.70122444 0.2184792 -0.1591019
## x5 -0.2812890 0.1956702 0.5949131 -0.03202161 0.9965823 -0.5069606
## x6 0.1762337 -0.5215478 -0.2095768 0.57683285 0.8748498 -0.3426445
Die Nebenbedingung $\Gamma’\Gamma=I$ können wir leicht untersuchen:
round(t(PCA1$weights) %*% PCA1$weights, 3)
## PC1 PC2 PC3 PC4 PC5 PC6
## PC1 0.389 0.000 0.000 0.000 0.00 0.000
## PC2 0.000 0.697 0.000 0.000 0.00 0.000
## PC3 0.000 0.000 1.238 0.000 0.00 0.000
## PC4 0.000 0.000 0.000 1.981 0.00 0.000
## PC5 0.000 0.000 0.000 0.000 2.63 0.000
## PC6 0.000 0.000 0.000 0.000 0.00 3.316
Wir erkennen, dass hier die Gewichte nicht in ihrer ursprünglichen Form angezeigt werden (keine 1en auf der Diagonale), sondern schon bereits normiert sind, sodass die Hauptkomponenten jeweils eine Varianz von 1 haben. Multiplizieren wir nun mit den Eigenwerten erhalten wir die Einheitsmatrix:
round(t(PCA1$weights) %*% PCA1$weights %*% diag(PCA1$values), 10)
## [,1] [,2] [,3] [,4] [,5] [,6]
## PC1 1 0 0 0 0 0
## PC2 0 1 0 0 0 0
## PC3 0 0 1 0 0 0
## PC4 0 0 0 1 0 0
## PC5 0 0 0 0 1 0
## PC6 0 0 0 0 0 1
Wobei mit $values gerade die Eigenwerte angesprochen werden und mit diag aus diesem Vektor aus Eigenwerten eine Diagonalmatrix erzeugt wird mit Eigenwerten auf der Diagonale und Nullen sonst (für eine Wiederholung der Matrixoperationen siehe in der Einleitungssitzung im Appendix B nach).
Bestimmung der Komponentenzahl
Die alles entscheidende Frage ist nun: Wie viele Komponenten extrahieren wir, um unsere Daten(-dimensionalität) zu reduzieren? Dazu schauen wir uns den Eigenwerteverlauf einmal an. Die Eigenwerte werden immer in absteigender Reihenfolge ausgegeben. Da wir eine Korrelationsmatrix herangezogen haben, können wir das Eigenwerte-größer-1 Kriterium (Kaiser-Gutmann Kriterium) anwenden und alle Komponenten beibehalten, deren Eigenwert größer 1 ist (hätten wir eine Kovarianzmatrix hergenommen, würde sich diese Kriterium dahingehen verändern, dass alle Hauptkomponenten beibehalten werden, deren Eigenwert größer als der durchschnittliche Eigenwert, bzw. die durchschnittliche Varianz, ist - Plottwist: Gleiches gilt auch im Korrelationsfall! Hier haben alle Variablen eine Varianz von 1, damit ist die durchschnittliche Varianz gleich dem durchschnittlichen Eigenwert und somit gleich 1). Ganz so einfach ist es allerdings nicht, denn es gibt noch das Ellbow-Kriterium (auch Scree Plot genannt), in welchem wir nach einem Knick im Eigenwerteverlauf suchen. Dies ist der Idee geschuldet, dass davon ausgegangen wird, dass Eigenwerte unbedeutsamer Hauptkomponenten substantiell kleiner ausfallen (im und nach den Knick) als Eigenwerte bedeutsamer Hauptkomponenten (vor dem Knick). Des Weiteren gibt es noch die simulationsbasierte Parallel-Analyse, welche im gleichen Stichprobenumfang sehr viele unkorrelierte Datensätze simuliert und dann einen auf unsere Bedürfnisse angepassten zufälligen durchschnittlichen Eigenwerteverlauf generiert (siehe bspw. Siehe Eid et al., 2017, Kapitel 25.3.2 oder Brandt, 2020, Kapitel 23.4). Das gleiche wird in R außerdem noch mit Neuverteilen der Datenpunkte über die Variablen hinweg gemacht (resampling). Nach diesen beiden Kriterien entscheiden wir uns für alle Hauptkomponenten deren Eigenwert größer als der durchschnittliche zufällige Eigenwert ist.
Wir können alle drei/vier Methoden in einer Funktion untersuchen, welche fa.parallel heißt. Diese führt eigentlich eine Parallelanalyse für Faktorenanalysen (FA) durch und plotten dann die Eigenwertverläufe in einer Grafik. Wenn wir allerdings das Zusatzargument fa = "pc" wählen, so wird das ganze für eine PCA gemacht. Wir müssen der Funktion lediglich die Daten übergeben (damit geresampled werden kann!). Zum Schluss malen wir noch eine horizontale Linie bei der Eigenwertsgröße von 1 hinzu, um das Eigenwerte-größer-1 Kriterium leichter prüfen zu können (abline(h = 1) ).
fa.parallel(dataUV, fa = "pc", error.bars = T)
## Parallel analysis suggests that the number of factors = NA and the number of components = 2
# Eigenwerte größer 1?
abline(h = 1)
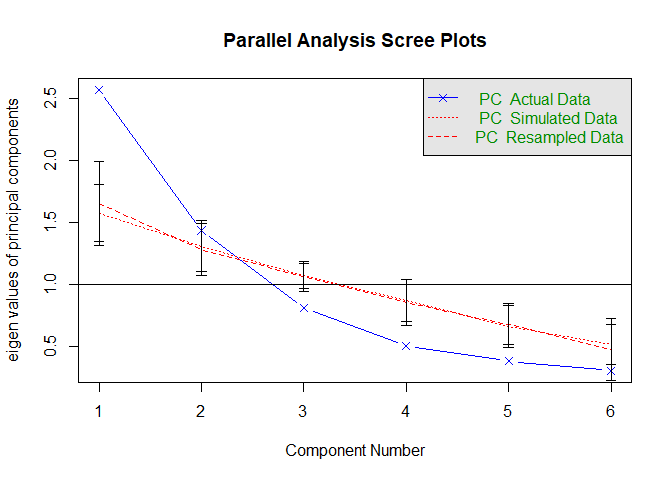
Die blaue durchgezogene Linie stellt den Eigenwerteverlauf unserer Daten dar. Die gepunktete Linie ist die Parallelanalyse auf Basis von simulierten Daten, während die gestrichelte Linie die Parallelanalyse auf Basis von Resampling darstellt.
Sowohl die Parallelanalyse als auch das Eigenwerte-Größer-1-Kriterium sprechen dafür, dass zwei Komponenten ausreichen, um die gemeinsame Varianz der Variablen zusammenzufassen. Die Funktion gibt die Entscheidung auf Basis der Parallelanalyse auch in der Konsole aus:
## Parallel analysis suggests that the number of factors = NA and the number of components = 2
Hierbei ist zu beachten, dass diese Entscheidung, die ausgegeben wird, auf Basis von Konfidenzintervallen, die um die durchschnittlichen Eigenwerte gelegt werden, bestimmt werden. Diese Konfidenzintervalle lassen sich auch anzeigen (Argument error.bars = T). Die Breite der Konfidenzintervalle und damit im Grunde die Präzision der Parallelanalyse hängen von der Anzahl an Replikationen ab. Hierbei ist es sinnvoll eine sehr große Zahl zu nehmen (n.iter = 10^3; Sie sollten beim Bearbeiten von Aufgaben immer diese zusätzliche Einstellung vornehmen - sie ist hier nicht eingestellt, da dies sonst beim Schreiben dieses Skripts zu langen Wartezeiten führen würde), damit die Schätzungen stabil sind. Allerdings kann dies zu längerer Berechnungsdauer führen!
Ein Knick im Eigenwerteverlauf ist nicht gut zu erkennen. Man könnte sich einen Knick an der 3. oder 4. Komponente einbilden (was für 2-3 Komponenten sprechen würde). Final entscheiden wir uns für 2 Komponenten und rechnen mit diesen weiter; was im Übrigen auch unsere Vermutung auf Basis der Grafik der Korrelationsmatrix war.
PCA mit zwei 2 Hauptkomponenten ohne Rotation
Um nur zwei Hauptkomponenten zu extrahieren, müssen wir lediglich in der Funktion pca das Argument nfactors ändern.
PCA2 <- pca(r = R_UV, nfactors = 2, rotate = "none")
PCA2
## Principal Components Analysis
## Call: principal(r = r, nfactors = nfactors, residuals = residuals,
## rotate = rotate, n.obs = n.obs, covar = covar, scores = scores,
## missing = missing, impute = impute, oblique.scores = oblique.scores,
## method = method, use = use, cor = cor, correct = 0.5, weight = NULL)
## Standardized loadings (pattern matrix) based upon correlation matrix
## PC1 PC2 h2 u2 com
## x1 0.71 0.29 0.58 0.42 1.3
## x2 0.78 0.41 0.79 0.21 1.5
## x3 -0.78 -0.33 0.71 0.29 1.3
## x4 -0.36 0.66 0.57 0.43 1.5
## x5 -0.72 0.28 0.60 0.40 1.3
## x6 0.45 -0.75 0.77 0.23 1.6
##
## PC1 PC2
## SS loadings 2.57 1.43
## Proportion Var 0.43 0.24
## Cumulative Var 0.43 0.67
## Proportion Explained 0.64 0.36
## Cumulative Proportion 0.64 1.00
##
## Mean item complexity = 1.4
## Test of the hypothesis that 2 components are sufficient.
##
## The root mean square of the residuals (RMSR) is 0.12
##
## Fit based upon off diagonal values = 0.89
Diesmal erkennen wir sehr deutlich, wie unterschiedlich der Output aussieht. die Kommunalitäten (h2) sind nicht mehr alle 1. Bei den Eigenwerten ändert sich nichts an der Größe (wir haben ja auch nicht rotiert), aber an den relativen Größen (Proportion Explained und Cumulative Proportion) ändert sich etwas. An den Kommunalitäten lässt sich beispielsweise ablesen, dass ca 57% der Variation von x4 durch die ersten beiden Hauptkomponenten erklärt werden kann, während es bei x2 79% sind. Außerdem können in Cumulative Var ablesen, dass nur noch ca. 67% der Variation in den Daten nach Extraktion von zwei Hauptkomponenten übrig ist. Wir wollen uns das Ladungsmuster auch nochmals grafisch veranschaulichen: besteht Einfachstruktur?
Grafische Veranschaulichungen des Ladungsmusters
In einem Balkendiagramm dargestellt sehen wir die Ladungen auf den beiden Hauptkomponenten (PC1 und PC2). Es ist keine eindeutige Zuordnung zu den beiden Komponenten zu erkennen. Was wir allerdings sehen ist, dass auf der ersten Komponenten die Ladungen im Schnitt (betraglich) größer ausfallen. Dies ist wenig überraschend, da die erste Hauptkomponente so extrahiert wird, dass sie die größte Varianz und somit den größten Eigenwert hat. Der Code zur Grafik ist in Appendix A abgedruckt.
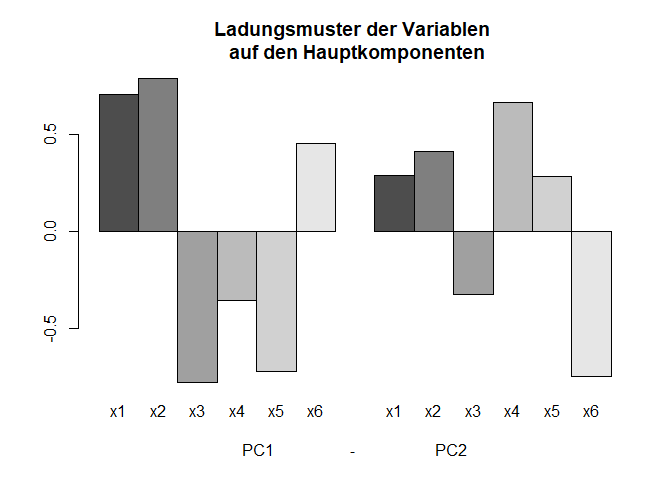
Da sich zwei Hauptkomponenten noch leicht gegeneinander abtragen lassen, können wir uns dies auch ansehen und zwar indem wir einfach plot auf das PCA-Objekt anwenden. Außerdem spezifizieren wir noch mit pch = 1, dass die Punkte anders als der Default dargestellt werden. Dies machen wir, um diese Punkte später besser von der rotierten Lösung unterscheiden zu können!
plot(PCA2, pch = 1)
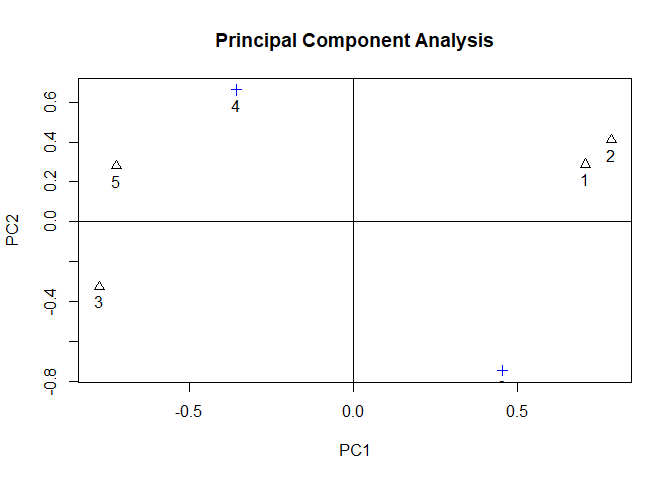
x4 und x6 liegen bspw. recht weit von beiden Achsen entfernt - sie werden keiner der beiden Hauptkomponenten eindeutig zugeordnet. Im nächsten Abschnitt erreichen wir Einfachstruktur, indem wir “varimax” rotieren.
PCA mit zwei 2 Hauptkomponenten mit Varimax-Rotation
Eine Varimax (Varianz maximierende) Rotation (für mehr Informationen zur Rotation siehe siehe bspw. Siehe Eid et al., 2017, Kapitel 25.3.3 oder Brandt, 2020, Kapitel 23.5) führen wir durch, indem wir rotate = "varimax" spezifizieren (weitere Möglichkeiten wären bspw. “quartimax” oder “bifactor” als orthogonale Roationen und “promax”, “oblimin” oder “simplimax” als Beispiele für oblique Rotationen, über welche Sie sich mit der Hilfe näher vertraut machen können).
PCA3 <- pca(r = R_UV, nfactors = 2, rotate = "varimax")
PCA3
## Principal Components Analysis
## Call: principal(r = r, nfactors = nfactors, residuals = residuals,
## rotate = rotate, n.obs = n.obs, covar = covar, scores = scores,
## missing = missing, impute = impute, oblique.scores = oblique.scores,
## method = method, use = use, cor = cor, correct = 0.5, weight = NULL)
## Standardized loadings (pattern matrix) based upon correlation matrix
## RC1 RC2 h2 u2 com
## x1 0.76 -0.09 0.58 0.42 1.0
## x2 0.89 -0.02 0.79 0.21 1.0
## x3 -0.84 0.09 0.71 0.29 1.0
## x4 0.00 0.75 0.57 0.43 1.0
## x5 -0.50 0.59 0.60 0.40 1.9
## x6 0.04 -0.87 0.77 0.23 1.0
##
## RC1 RC2
## SS loadings 2.31 1.70
## Proportion Var 0.38 0.28
## Cumulative Var 0.38 0.67
## Proportion Explained 0.58 0.42
## Cumulative Proportion 0.58 1.00
##
## Mean item complexity = 1.2
## Test of the hypothesis that 2 components are sufficient.
##
## The root mean square of the residuals (RMSR) is 0.12
##
## Fit based upon off diagonal values = 0.89
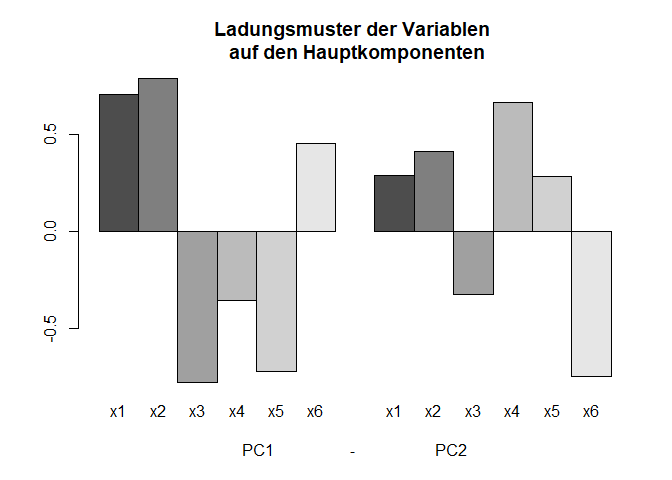
Diesmal haben sich die Komponentenladungen geändert und zwar so, dass die Komponentenladungen pro Komponente maximale Varianz haben (also möglichst unterschiedlich sind). Entsprechend fallen die Eigenwerte anders aus und auch die Komponenten heißen nicht mehr PC sondern RC für Rotated Component. Die Kommunalitäten ändern sich aber nicht - genauso wenig wie die gesamte Variation, die durch die beiden Hauptkomponenten erklärt werden kann. In den Komponentenladungen erkennen wir nun eine deutlich leichtere Zuordnung zu den Komponenten. Wir schauen uns dies nochmal grafisch an.
Grafische Veranschaulichungen des Ladungsmusters
Es wird eine stärkere Einfachstruktur sichtbar: sowohl im Barplot,
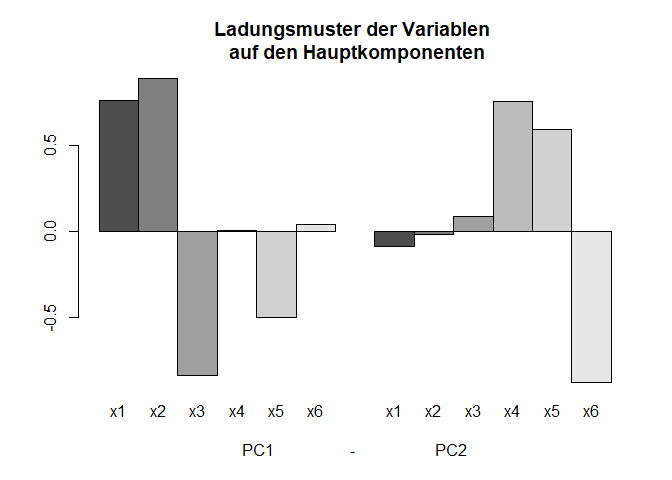
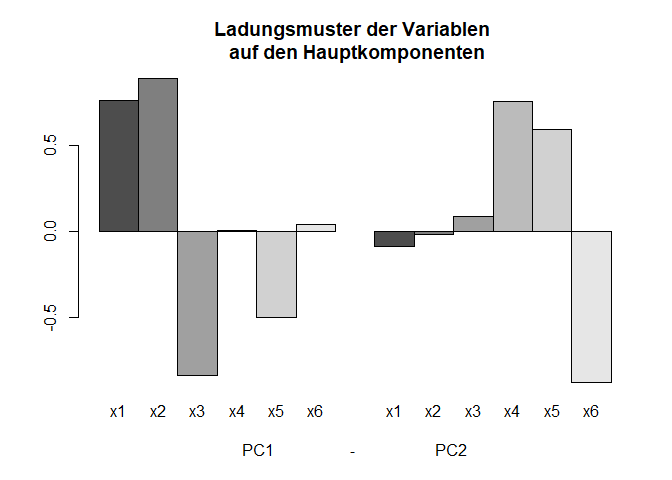
als auch in einem Plot, in welchen die Ladungen der Hauptkomponenten gegeneinander abgetragen werden (hier wählen wir mit cex = 2, dass die Punkte doppelt so groß eingezeichnet werden wie per Default, damit wir später noch stärker den Unterschied zur unrotierten Lösung sehen):
plot(PCA3, cex = 2)
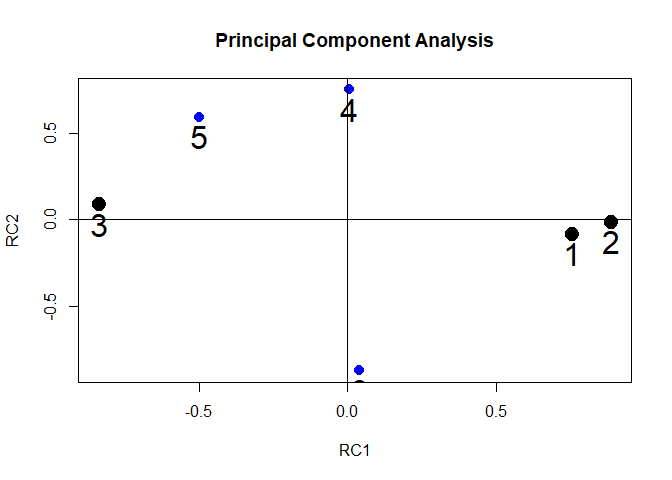
Auch hier lässt sich die Einfachstruktur dadurch erkennen, dass die Punkte mit den Zahlen (und entsprechend die Nummer der Variablen) 1-4 und 6 sehr nah an den Achsen liegen. Nur x5 wird nicht eindeutig einer Komponente zugeordnet.
Diese lässt sich auch in einem stark vereinfachten Pfaddiagramm darstellen. Dazu wenden wir fa.diagramm aus dem psych Paket auf das PCA3 Objekt an. Pfeile symbolisieren hier, dass die Variable an der Pfeilspitze eine Linearkombination aus den Variablen an den jeweiligen Pfeilenden ist (dazu mehr im nächsten Semester!). Der Default in diesem Plot ist so gewählt, dass nur sehr große Komponentenladungen auch als Pfeile eingezeichnet werden.
fa.diagram(PCA3)
Gestrichelte Pfeile zeigen entgegengesetze Vorzeichen an. Hier wird zwar x5 der 2. Hauptkomponente zugeordnet, aber es fällt schon etwas auf, dass dessen Koeffizient etwas geringer ausfällt als die der anderen. Außerdem ist hier noch zu vermerken, dass die PCA kein Erklärungsmodell liefert. Das bedeutet, dass wir den Hauptkomponenten keine inhaltliche Bedeutung unterstellen können a la: das ist die latente Variable, die die jeweilige Variation in den Daten erzeugt. Wie an den Pfeilen ersichtlich, sind die Hauptkomponenten Linearkombination der Variablen. Bei Erklärungsmodellen wäre es genau anders herum. Die Variablen würden sich aus den Hauptkomponenten zusammensetzen! Um Erklärungsmodelle anzusetzen, müssen Sie noch bis zum Kurs im Sommer warten, wenn es um latente Modellierung geht. Folglich stehen hohe Ladungen auf einer Hauptkomponenten nur für hohe Gemeinsamkeiten in der Variation der Items.
Unrotierte und rotierte Ladungen in einem Plot
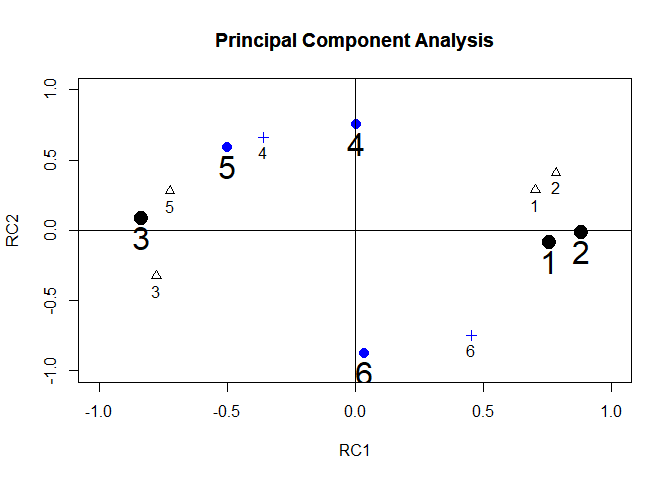
Zu guter Letzt wollen wir den Rotationseffekt noch genauer erkennen und plotten die unrotierte und die rotierte Lösung in eine Grafik:
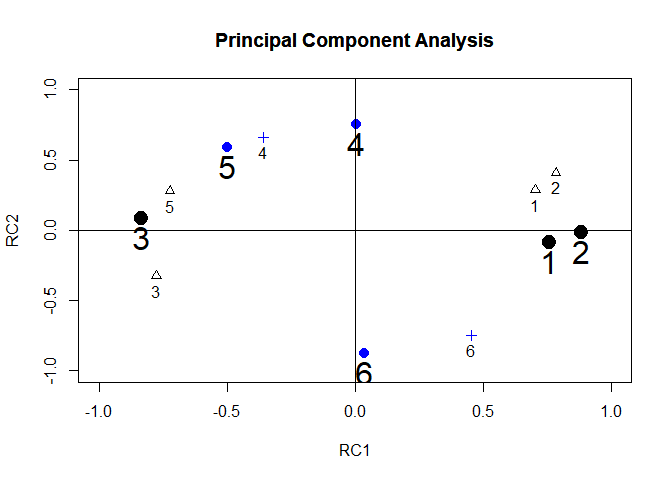
Dieser Grafik ist zu entnehmen, dass de facto alle Punkte um ca 50° (so genau man dies eben mit dem Geodreieck am Bildschirm nachmessen kann) im Uhrzeigersinn rotiert wurden und somit näher den Achsen liegen (Einfachstruktur). Die Entfernung zum Ursprung (dem Punkt $(0,0)$) wurde nicht verändert! Jetzt haben wir zwei Hauptkomponenten, von denen wir ziemlich genau wissen, was in diese drin steckt. Die Frage ist nun, wie wir mit diesen weiterrechnen können und was der Nutzen davon ist.
Bilden der Hauptkomponenten als neue Variablen
Dazu bilden wir die individuellen Werte der Hauptkomponenten (über ein Matrixprodukt) als gewichtete Linearkombinationen von x1-x6. Zuvor hatten wir geschrieben, dass $\mathbf{H}=\Gamma \mathbf{Z}$ gilt. Da die Daten jeweils in transponierter Form vorliegen, berechnen wir die Hauptkomponenten wie folgt:
PCs <- as.matrix(dataUV) %*% PCA3$weights
Wir wollen nun prüfen, ob die Komponentenladungen tatsächlich der Korrelation der Variablen und der Hauptkomponenten entsprechen. Dies gilt immer dann, wenn die Daten, die zur Berechnung verwendet werden, selbst standardisiert sind. Da sie dies waren, können wir uns einfach die Korrelation mit den Hauptkomponenten ansehen und erhalten die Ladungsmatrix:
cor(dataUV, PCs)
## RC1 RC2
## x1 0.757141041 -0.08591536
## x2 0.885919517 -0.01586164
## x3 -0.836486963 0.08665073
## x4 0.003942859 0.75202986
## x5 -0.499508846 0.59343542
## x6 0.038128536 -0.87392858
PCA3$loadings[,]
## RC1 RC2
## x1 0.757141041 -0.08591536
## x2 0.885919517 -0.01586164
## x3 -0.836486963 0.08665073
## x4 0.003942859 0.75202986
## x5 -0.499508846 0.59343542
## x6 0.038128536 -0.87392858
Tatsächlich! Falls die Daten nicht standardisiert vorliegen, so können diese leicht mit der scale Funktion standardisiert werden.
Der folgende Plot zeigt die Verteilung der individuellen Werte auf den Hauptkomponenten als Streudiagramm, welches recht unsystematisch wirkt.
plot(PCs)
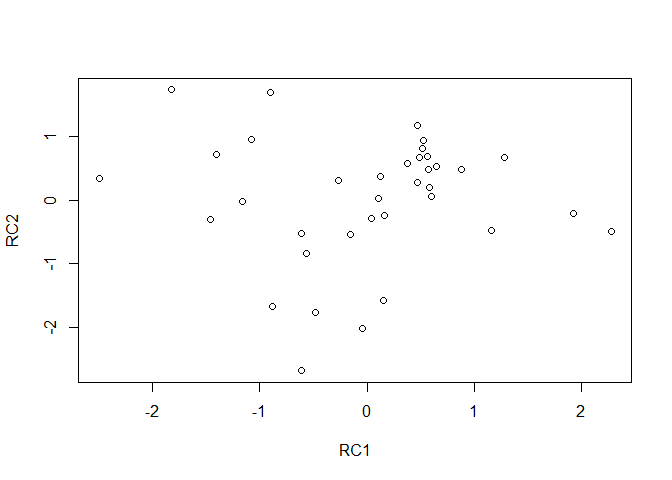
Dies liegt ganz einfach daran, dass die Werte auf den Hauptkomponenten nach orthogonaler Rotation unkorreliert sind (Korrelationsmatrix gerundet auf die 10. Nachkommastelle):
round(cor(PCs), 10)
## RC1 RC2
## RC1 1 0
## RC2 0 1
Wenn wir nun die Korrelationsmatrix der Daten mit der implizierten Korrelation vergleichen
cor(dataUV)
## x1 x2 x3 x4 x5 x6
## x1 1.00000000 0.59687989 -0.43595753 -0.16998321 -0.2712820 0.09837908
## x2 0.59687989 1.00000000 -0.63789368 -0.06529934 -0.3581969 0.07622499
## x3 -0.43595753 -0.63789368 1.00000000 0.05347046 0.4750548 -0.10391023
## x4 -0.16998321 -0.06529934 0.05347046 1.00000000 0.2141352 -0.42867869
## x5 -0.27128197 -0.35819689 0.47505483 0.21413524 1.0000000 -0.48190559
## x6 0.09837908 0.07622499 -0.10391023 -0.42867869 -0.4819056 1.00000000
PCA3$loadings %*% t(PCA3$loadings)
## x1 x2 x3 x4 x5 x6
## x1 0.58064400 0.67212878 -0.64078324 -0.06162561 -0.4291839 0.10395256
## x2 0.67212878 0.78510498 -0.74243455 -0.00843537 -0.4519375 0.04764075
## x3 -0.64078324 -0.74243455 0.70721879 0.06186579 0.4692542 -0.10762057
## x4 -0.06162561 -0.00843537 0.06186579 0.56556446 0.4443117 -0.65707005
## x5 -0.42918386 -0.45193749 0.46925425 0.44431166 0.6016747 -0.53766571
## x6 0.10395256 0.04764075 -0.10762057 -0.65707005 -0.5376657 0.76520494
erkennen wir, dass diese sich schon unterscheiden:
round(cor(dataUV) - PCA3$loadings %*% t(PCA3$loadings), 2)
## x1 x2 x3 x4 x5 x6
## x1 0.42 -0.08 0.20 -0.11 0.16 -0.01
## x2 -0.08 0.21 0.10 -0.06 0.09 0.03
## x3 0.20 0.10 0.29 -0.01 0.01 0.00
## x4 -0.11 -0.06 -0.01 0.43 -0.23 0.23
## x5 0.16 0.09 0.01 -0.23 0.40 0.06
## x6 -0.01 0.03 0.00 0.23 0.06 0.23
Auf der Diagonale steht die Uniqueness und sonst stehen dort die Residuen der implizierten Korrelationsmatrix. Einige Einträge lassen sich sehr gut replizieren (bspw. Eintrag [6,1]), während andere deutlich daneben liegen (bspw. Eintrag [3,1]). Hier erkennen wir den Datenverlust, der durch das verwerfen von 4 Hauptkomponenten entsteht. Hätten wir bspw. 5 Hauptkomponenten extrahiert, würde das Ganze deutlich genauer ausfallen:
PCA5 <- pca(r = R_UV, nfactors = 5, rotate = "varimax")
round(cor(dataUV) - PCA5$loadings %*% t(PCA5$loadings), 2)
## x1 x2 x3 x4 x5 x6
## x1 0.03 -0.06 -0.05 0.01 0.03 0.02
## x2 -0.06 0.13 0.12 -0.02 -0.06 -0.04
## x3 -0.05 0.12 0.10 -0.02 -0.05 -0.03
## x4 0.01 -0.02 -0.02 0.00 0.01 0.00
## x5 0.03 -0.06 -0.05 0.01 0.02 0.02
## x6 0.02 -0.04 -0.03 0.00 0.02 0.01
Nutzung der Hauptkomponenten als Prädiktoren in der Regression
Nun wollen wir uns endlich der Vorhersage der abhängigen Variable $y$ widmen. Dazu sagen wir diese zunächst durch alle Kovariaten im Modell mx vorher.
mx <- lm(y ~ 1 + x1 + x2 + x3 + x4 + x5 + x6, data = data)
summary(mx)
##
## Call:
## lm(formula = y ~ 1 + x1 + x2 + x3 + x4 + x5 + x6, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.7082 -0.7554 -0.0383 0.7193 2.2195
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -2.693e-16 1.757e-01 0.000 1.0000
## x1 3.317e-01 2.260e-01 1.468 0.1529
## x2 1.727e-01 2.613e-01 0.661 0.5138
## x3 2.835e-01 2.487e-01 1.140 0.2636
## x4 -2.177e-01 1.997e-01 -1.091 0.2844
## x5 -4.391e-01 2.338e-01 -1.878 0.0705 .
## x6 4.150e-01 2.227e-01 1.864 0.0725 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.054 on 29 degrees of freedom
## Multiple R-squared: 0.4951, Adjusted R-squared: 0.3906
## F-statistic: 4.739 on 6 and 29 DF, p-value: 0.001778
Der Output zeigt uns, dass kein einziger Prädiktor signifikante Vorhersagekraft leistet. Trotzdem können fast 50% der Variation von $y$ vorhergesagt werden. Tatsächlich haben die Kovariaten zu viel gemeinsam, als dass sie signifikante eigenständige Varianzanteile erklären könnten (zumindest bei dieser Stichprobengröße). Nun wollen wir die gleiche Analyse nochmals mit den beiden varimax-rotierten Hauptkomponenten durchführen, welche insgesamt 67 % der Variation in den Daten enthalten. Das Modell hierzu nennen wir mpca.
mpca <- lm(data$y ~ 1 + PCs[,1] + PCs[,2])
summary(mpca)
##
## Call:
## lm(formula = data$y ~ 1 + PCs[, 1] + PCs[, 2])
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.8714 -0.6308 -0.1829 0.8145 2.4389
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -2.224e-16 1.743e-01 0.000 1.0000
## PCs[, 1] 4.014e-01 1.768e-01 2.270 0.0298 *
## PCs[, 2] -7.937e-01 1.768e-01 -4.489 8.23e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.046 on 33 degrees of freedom
## Multiple R-squared: 0.4341, Adjusted R-squared: 0.3998
## F-statistic: 12.65 on 2 and 33 DF, p-value: 8.332e-05
Die beiden Hauptkomponenten erklären fast so viel Varianz wie die sechs einzelnen Variablen - nämlich 43.4% mit dem Unterschied, dass beide signifikante Regressionskoeffizienten aufweisen.
Interpretation
Somit lässt sich sagen, dass die Kovariaten zur Vorhersage des Kriteriums geeignet sind und dass sie jedoch sehr ähnliche Aspekte abdecken. Die Professorin sollte die Kovariaten in ihrer Studie weiter miterheben, da sie Systematiken am Kriterium erklären.
In Appendix B wird die PCA noch einmal zu Fuß durchgeführt und zudem ein Exkurs dargestellt, in dem erläutert wird, was passiert, wenn Variablen komplett linear abhängig von einander sind (und sie nicht nur stark miteinander zusammenhängen).
In Appendix C sehen Sie eine bildliche Veranschaulichung der PCA, in welcher die Pixel von Bildern mit einer PCA verrechnet werden und somit nur Teilinformationen von Bildern darstellbar sind; falls Sie dazu Lust haben!
Appendix
Appendix A
Grafische Veranschaulichung
corrplot(R_UV, method = "color",tl.col = "black", addCoef.col = "black",
col=colorRampPalette(c("red","white","blue"))(100))
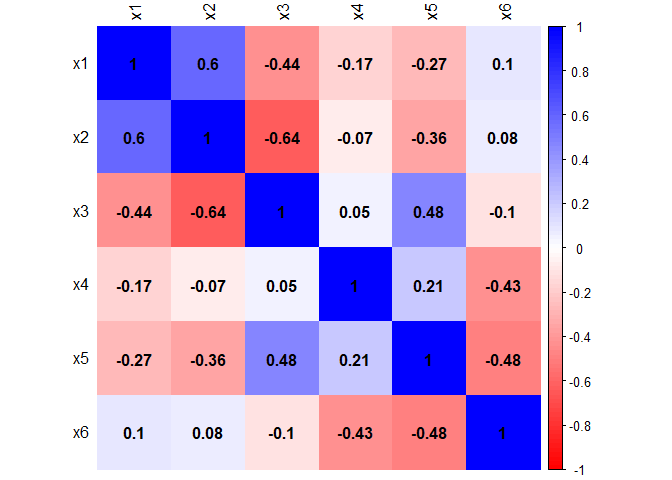
corrplot(R_UV, method = "color",tl.col = "black", addCoef.col = "black",
col=colorRampPalette(c("blue","white","blue"))(100))
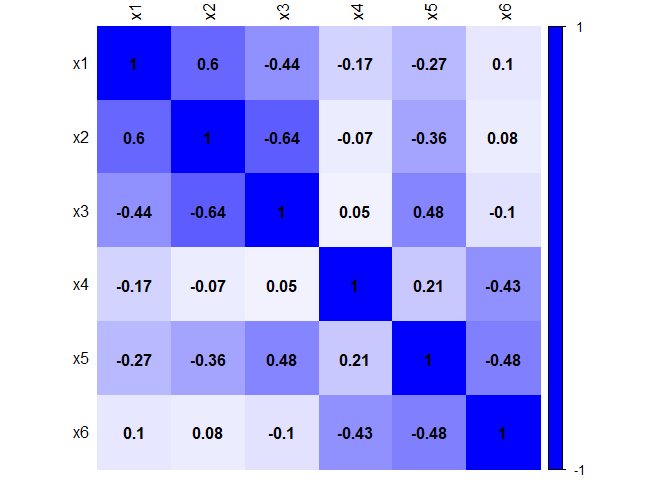
barplot(PCA2$loadings, beside = T, names.arg = rep(colnames(dataUV),2),
xlab = "PC1 - PC2",
main = "Ladungsmuster der Variablen \n auf den Hauptkomponenten")
barplot(PCA3$loadings, beside = T, names.arg = rep(colnames(dataUV),2),
xlab = "PC1 - PC2",
main = "Ladungsmuster der Variablen \n auf den Hauptkomponenten")
plot(PCA3, xlim = c(-1,1),ylim = c(-1,1), cex = 2)
par(new=TRUE) # neuen Plot erzeugen, welcher über den bereits erzeugten geplottet wird
plot(PCA2, xaxt = "n", yaxt = "n", ylab = "", xlab = "", xlim = c(-1,1),ylim = c(-1,1), pch = 1)
Appendix B
PCA zu Fuß
Wir wollen nun die PCA mit Basisfunktionen in R durchführen. Dies soll aufzeigen, wie einfach eigentlich eine solche Analyse ist! Die Funktion, die wir verwenden wollen, ist die Basis-Funktion eigen (siehe Eid et al., 2017, S. 934 und folgend im blauen Kasten):
Für jede quadratische pxp-Matrix $A$ (wobei die Nullmatrix, welche nur aus Nullen besteht, ausgeschlossen wird) können Skalare $\theta$ und Vektoren $\boldsymbol{x}$ (die nicht nur Nullen enthalten) gefunden werden, für die gilt:
$$A\boldsymbol{x}=\theta\boldsymbol{x}$$
$\theta$ ist ein Eigenwert von $A$ und $\boldsymbol{x}$ ist der zugehörige Eigenvektor von $A$ (wobei in Eid, et al. $\boldsymbol{\delta}$ anstelle von $\theta$ verwendet wird). Es existieren jeweils genau p Eigenwerte (die nicht alle verschieden sein müssen) und p Eigenvektoren. Das Verfahren, welches angewandt wird, um Eigenvektoren und -werte zu finden, heißt Lösen des Eigenwerteproblems oder Eigenwertedekomposition. Die Funktion eigen führt diese leicht für uns durch. Wir müssen sie lediglich auf eine Korrelationsmatrix (oder Kovarianzmatrix) anwenden:
eigen(cor(dataUV))
## eigen() decomposition
## $values
## [1] 2.5706246 1.4347873 0.8080240 0.5047381 0.3802664 0.3015597
##
## $vectors
## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] -0.4399744 -0.2405587 -0.4905144 0.56125334 -0.3140469 0.30711389
## [2,] -0.4894541 -0.3434783 -0.1125872 -0.02374926 0.4310103 -0.66591857
## [3,] 0.4836064 0.2718236 -0.2324303 0.51747542 -0.1695299 -0.58454407
## [4,] 0.2230379 -0.5523162 0.6092852 0.49818438 0.1347268 0.08736991
## [5,] 0.4509954 -0.2343788 -0.5347683 -0.02274973 0.6145498 0.27839460
## [6,] -0.2825585 0.6247235 0.1883889 0.40981047 0.5394826 0.18816136
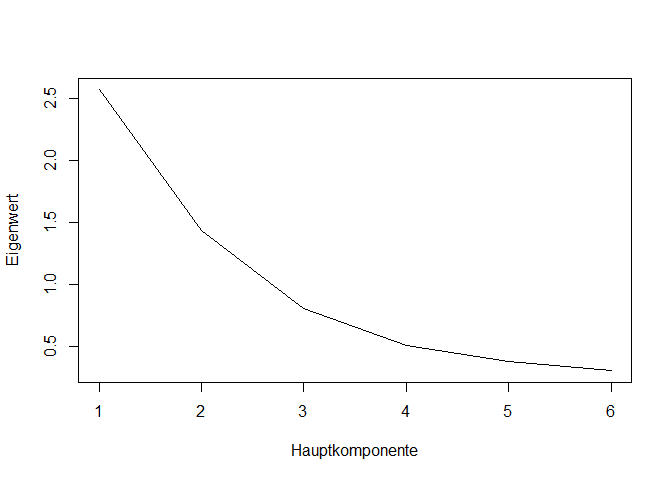
Unter values stehen (der Größe nach sortiert) die Eigenwerte, welche auch den Varianzen der Hauptkomponenten entsprechen. Unter vectors stehen die zugehörigen Eigenvektoren. Die Matrix $\Gamma$ enthält genau diese Vektoren! Wenn wir die Eigenwerte nun plotten, erhalten wir den Screeplot.
Gamma <- eigen(R_UV)$vectors
theta <- eigen(R_UV)$values
# Plot der Eigenwerte
plot(theta, type="l", ylab = "Eigenwert", xlab = "Hauptkomponente")
Durch die Funktion eigen können wir also leicht die Vektoren erzeugen und somit die Hauptkomponenten bestimmen - dazu müssen wir lediglich $\Gamma$ mit den Variablen (matrix-)multiplizieren. Die Rotation ist etwas schwieriger. Wir können für die unrotierte Lösung recht leicht die Ladungsmatrix \Lambda erstellen, indem wir $\Gamma$ mit der Wurzel aus den jeweiligen Eigenwerten multiplizieren:
Lambda <- Gamma %*% diag(sqrt(theta)) # sqrt zieht die Wurzel!
Lambda
## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] -0.7054183 -0.2881475 -0.4409241 0.39874202 -0.19365933 0.1686499
## [2,] -0.7847500 -0.4114272 -0.1012048 -0.01687264 0.26578568 -0.3656855
## [3,] 0.7753742 0.3255974 -0.2089320 0.36764002 -0.10454187 -0.3209991
## [4,] 0.3576004 -0.6615788 0.5476874 0.35393472 0.08308031 0.0479787
## [5,] 0.7230884 -0.2807451 -0.4807040 -0.01616253 0.37896671 0.1528789
## [6,] -0.4530308 0.7483101 0.1693431 0.29114954 0.33267595 0.1033278
PCA1$loadings[,] # Vergleich mit den Ladungen aus der pca-Funktion
## PC1 PC2 PC3 PC4 PC5 PC6
## x1 0.7054183 0.2881475 0.4409241 0.39874202 -0.19365933 -0.1686499
## x2 0.7847500 0.4114272 0.1012048 -0.01687264 0.26578568 0.3656855
## x3 -0.7753742 -0.3255974 0.2089320 0.36764002 -0.10454187 0.3209991
## x4 -0.3576004 0.6615788 -0.5476874 0.35393472 0.08308031 -0.0479787
## x5 -0.7230884 0.2807451 0.4807040 -0.01616253 0.37896671 -0.1528789
## x6 0.4530308 -0.7483101 -0.1693431 0.29114954 0.33267595 -0.1033278
Wir sehen, dass bis auf das Vorzeichen die Ladungsmatrizen komplett identisch sind!
Exkurs: Was passiert bei linearen Abhängigkeiten?
Wir berechnen für eine neue Variable X als Mittelwert von x1 bis x6 und bestimmen die 7x7-Korrelationsmatrix für x1-x6 und X. Es gibt in dieser Matrix keine perfekten Korrelationen, trotzdem lässt sich X vollständig aus den anderen Spalten vorhersagen.
dataUV$X <- rowMeans(dataUV)
R2 <- cor(dataUV)
round(R2,2)
## x1 x2 x3 x4 x5 x6 X
## x1 1.00 0.60 -0.44 -0.17 -0.27 0.10 0.46
## x2 0.60 1.00 -0.64 -0.07 -0.36 0.08 0.35
## x3 -0.44 -0.64 1.00 0.05 0.48 -0.10 0.20
## x4 -0.17 -0.07 0.05 1.00 0.21 -0.43 0.34
## x5 -0.27 -0.36 0.48 0.21 1.00 -0.48 0.33
## x6 0.10 0.08 -0.10 -0.43 -0.48 1.00 0.09
## X 0.46 0.35 0.20 0.34 0.33 0.09 1.00
Wenn wir nun erneut eine Eigenwertezerlegung durchführen, so erkennen wir, dass der 7. Eigenwert 0 (bzw. leicht negativ) wird. Die Matrix ist nicht mehr positiv definit, sie lässt sich auch nicht invertieren.
eigen(R2)$values
## [1] 2.575730e+00 1.782575e+00 1.172574e+00 7.596780e-01 4.057040e-01 3.037391e-01
## [7] -9.032073e-17
plot(eigen(R2)$values, type="l", ylab = "Eigenwert", xlab = "Hauptkomponente")
abline(h=0, col="red")
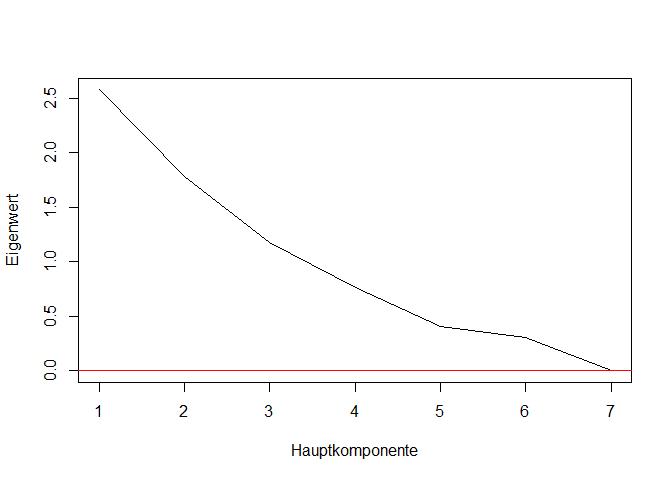
solve(R2)
## Error in solve.default(R2): system is computationally singular: reciprocal condition number = 1.817e-17
Dies bedeutet, dass sehr kleine Eigenwerte auch für komplette lineare Abhängigkeit der Daten sprechen können. In anderen Modellierungen bekommt man manchmal die Fehlermeldung, dass eine Matrix nicht positiv (semi-)definit sei. Dies bedeutet also, dass es Null-Eigenwerte oder negative Eigenwerte gibt und es sich somit nicht länger um eine Korrelations-, oder Kovarianzmatrix handeln kann (es kommt zu Schätzproblemen!).
Appendix C
PCArt
Prof. Dr. Martin Schultze hat ein kleines R Paket geschrieben, welches die PCA verbildlicht: Von bekannten Gemälden wird die Information, welche in jedem Pixel steckt, durch eine Hauptkomponentenanalyse zerlegt und das Gemälde anschließend nur durch eine Auswahl an Komponenten dargestellt. Sie können dieses Paket installieren, indem Sie zunächst devtools installieren und dann direkt vom Github Repository installieren:
install.packages("devtools")
devtools::install_github("https://github.com/martscht/PCArt")
Das erste Bild in Pixeldarstellung sieht so aus (mit PCA:: sagen wir R, dass wir in diesem Paket navigieren wollen - mit Hilfe der Autovervollständigung können wir so auch erfahren, welche weiteren Funktionen in diesem Paket enthalten sind):
PCArt::pic1$image[, , 1][1:5, 1:5]
## [,1] [,2] [,3] [,4] [,5]
## [1,] 0.3921569 0.5764706 0.6980392 0.7176471 0.6784314
## [2,] 0.8509804 0.7843137 0.6980392 0.6666667 0.6745098
## [3,] 0.7529412 0.7411765 0.7725490 0.7568627 0.6862745
## [4,] 0.7725490 0.7176471 0.7411765 0.7529412 0.7607843
## [5,] 0.7333333 0.7137255 0.7215686 0.6588235 0.6352941
PCArt::pic1$image[, , 2][1:5, 1:5]
## [,1] [,2] [,3] [,4] [,5]
## [1,] 0.2823529 0.4666667 0.5882353 0.6078431 0.5686275
## [2,] 0.7411765 0.6745098 0.5882353 0.5568627 0.5647059
## [3,] 0.6352941 0.6235294 0.6549020 0.6431373 0.5725490
## [4,] 0.6627451 0.6078431 0.6313725 0.6431373 0.6470588
## [5,] 0.6431373 0.6235294 0.6313725 0.5686275 0.5411765
PCArt::pic1$image[, , 3][1:5, 1:5]
## [,1] [,2] [,3] [,4] [,5]
## [1,] 0.1372549 0.3215686 0.4352941 0.4549020 0.4117647
## [2,] 0.5960784 0.5215686 0.4352941 0.4000000 0.4078431
## [3,] 0.4862745 0.4745098 0.5058824 0.4862745 0.4156863
## [4,] 0.5098039 0.4509804 0.4745098 0.4862745 0.4823529
## [5,] 0.4784314 0.4509804 0.4588235 0.3960784 0.3686275
Wir schauen uns hier die Intensität für die ersten 25 Pixel (1 bis 5 horizontal und 1 bis 5 vertikal) der drei Farben Gelb, Blau und Rot an. Die Intensität ist dabei von 0 bis 1 skaliert. Sie können nun die Bilder ansehen und raten, um welches es sich handelt, indem Sie Folgendes ausführen (es werden Ihnen 10 Bilder präsentiert und Sie haben die Möglichkeit, sich immer mehr Hauptkomponenten anzeigen zu lassen!). Sukzessive werden immer mehr Informationen in den Bildern dargestellt:
PCArt::PCArtQuiz()
# analog:
library(PCArt)
PCArtQuiz()
## [1] 2
Na, um welches Bild handelt es sich?
Literatur
Brandt H. (2020). Exploratorische Faktorenanalyse (EFA). In Moosbrugger H., Kelava A. (eds) Testtheorie und Fragebogenkonstruktion. Berlin, Heidelberg: Springer. https://doi.org/10.1007/978-3-662-61532-4_23
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden (5. Auflage, 1. Auflage: 2010). Weinheim: Beltz.
Pituch, K. A. & Stevens, J. P. (2016). Applied Multivariate Statistics for the Social Sciences (6th ed.). New York: Taylor & Francis.
- Blau hinterlegte Autor:innenangaben führen Sie direkt zur universitätsinternen Ressource.
