Einleitung
In der Einführungssitzung hatten wir einfache Operationen in R, das Einlesen von Datensätzen, einfache Deskriptivstatistiken, die lineare Regression, den $t$-Test und einige Grundlagen der Inferenzstatistik wiederholt. Nun wollen wir mit etwas komplexeren, aber bereits bekannten Methoden weitermachen und eine multiple Regression in R durchführen. Hierbei werden wir uns auch nochmal mit Ausreißern beschäftigen.
Bevor wir dazu die Daten einlesen, sollten wir als erstes die nötigen R-Pakete laden. R funktioniert wie eine Bibliothek, in der verschiedene Bücher (also Pakete) erst vorhanden (also installiert) sein müssen, bevor man sie dann für eine Zeit leihen (also aktivieren) kann. Die R-Pakete, die wir im weiteren Verlauf benötigen, sind das car-Paket, das MASS-Paket sowie das Paket mit dem Namen lm.beta. Diese Pakete müssen zunächst “in die Bibliothek eingelagert” werden, das heißt, sie müssen installiert werden. Dies können Sie via install.packages machen:
install.packages("car") # Die Installation ist nur einmalig von Nöten!
install.packages("lm.beta") # Sie müssen nur zu Update-Zwecken erneut installiert werden.
install.packages("MASS")
Anschließend werden Pakete mit der library-Funktion geladen (also für eine Zeit - nämlich den Verlauf einer Sitzung - ausgeliehen):
library(lm.beta) # Standardisierte beta-Koeffizienten für die Regression
library(car) # Zusätzliche Funktion für Diagnostik von Datensätzen
library(MASS) # Zusätzliche Funktion für Diagnostik von Datensätzen
Daten einladen
Der Datensatz ist derselbe wie in der Einführungssitzung: Eine Stichprobe von 90 Personen wurde hinsichtlich der Lebenszufriedenheit, der Anzahl von depressiven Emotionen, der Depressivitaet und des Neurotizismus gemessen. Weiterhin gibt es eine Variable hinsichtlich der Intervention und des Geschlechts (0=m, 1=w). Sie können den Datensatz “Depression.rda” hier herunterladen.
Nun müssen wir mit load die Daten laden. Liegt der Datensatz bspw. auf dem Desktop, so müssen wir den Dateipfad dorthin legen und können dann den Datensatz laden (wir gehen hier davon aus, dass Ihr PC “Musterfrau” heißt) Tipp: Verwenden Sie unbedingt die automatische Vervollständigung von R-Studio, wie in der letzten Sitzung beschrieben.
load("C:/Users/Musterfrau/Desktop/Depression.rda")
Genauso sind Sie in der Lage, den Datensatz direkt aus dem Internet zu laden. Hierzu brauchen Sie nur die URL und müssen R sagen, dass es sich bei dieser um eine URL handelt, indem Sie die Funktion url auf den Link anwenden. Der funktionierende Befehl sieht so aus (beachte, dass die URL in Anführungszeichen geschrieben werden muss):
load(url("https://pandar.netlify.app/daten/Depression.rda"))
Nun sollte in R-Studio oben rechts in dem Fenster Environment unter der Rubrik “Data” unser Datensatz mit dem Namen “Depression” erscheinen.
Ein Überblick über die Daten
Wir können uns die ersten (6) Zeilen des Datensatzes mit der Funktion head ansehen. Dazu müssen wir diese Funktion auf den Datensatz (das Objekt) Depression anwenden:
head(Depression)
## Lebenszufriedenheit Episodenanzahl Depressivitaet Neurotizismus Intervention Geschlecht
## 1 7 4 7 5 Kontrollgruppe 0
## 2 5 5 8 3 Kontrollgruppe 1
## 3 8 7 6 6 Kontrollgruppe 0
## 4 6 4 5 5 Kontrollgruppe 1
## 5 6 9 8 5 Kontrollgruppe 1
## 6 8 7 8 6 Kontrollgruppe 1
Wir erkennen die eben beschriebenen Spalten. Weiterhin sehen wir, dass die Änderungen aus der letzten Sitzung an der Variable Geschlecht natürlich nicht mehr enthalten sind, wenn der Datensatz neu geladen wird. Daher müssen wir die levels wieder anpassen und den falsch eingetragenen Wert für Person 5 korrigieren.
levels(Depression$Geschlecht) <- c("maennlich", "weiblich")
Depression[5, 6] <- "maennlich"
Das Folgende fundiert zum Teil auf Sitzungen zur Korrelation und Regression aus Veranstaltungen aus dem Bachelorstudium zur Statistik Vertiefung.
(Multiple-) Lineare Regression
Eine Wiederholung der Regressionsanalyse (und der Korrelation) finden Sie bspw. in Eid, Gollwitzer und Schmitt (2017), Kapitel 16 bis 19 und Pituch und Stevens (2016) in Kapitel 3.
Das Ziel einer Regression besteht darin, die Variation einer Variable durch eine oder mehrere andere Variablen vorherzusagen (Prognose und Erklärung). Die vorhergesagte Variable wird als Kriterium, Regressand oder auch abhängige Variable (AV) bezeichnet und üblicherweise mit $y$ symbolisiert. Die Variablen zur Vorhersage der abhängigen Variablen werden als Prädiktoren, Regressoren oder unabhängige Variablen (UV) bezeichnet und üblicherweise mit $x$ symbolisiert. Die häufigste Form der Regressionsanalyse ist die lineare Regression, bei der der Zusammenhang über eine Gerade bzw. eine (Hyper-)Ebene beschrieben wird. Demzufolge kann die lineare Beziehung zwischen den vorhergesagten Werten und den Werten der unabhängigen Variablen mathematisch folgendermaßen beschrieben werden:
$$y_i = b_0 +b_{1}x_{i1} + … +b_{m}x_{im} + e_i$$
- Ordinatenabschnitt/ $y$-Achsenabschnitt/ Konstante/ Interzept $b_0$:
- Schnittpunkt der Regressionsgeraden mit der $y$-Achse
- Erwartung von y, wenn alle UVs den Wert 0 annehmen
- Regressionsgewichte $b_{1},\dots, b_m$:
- beziffern die Steigung der Regressionsgeraden
- Interpretation: die Steigung der Geraden lässt erkennen, um wie viele Einheiten $y$ zunimmt, wenn (das jeweilige) x um eine Einheit zunimmt (unter Kontrolle aller weiteren Variablen im Modell)
- Regressionsresiduum (kurz: Residuum), Residualwert oder Fehlerwert $e_i$:
- die Differenz zwischen einem beobachteten und einem vorhergesagten y-Wert ($e_i=y_i-\hat{y}_i$)
- je größer die Fehlerwerte (betraglich), umso größer ist die Abweichung (betraglich) eines beobachteten vom vorhergesagten Wert
R kann natürlich die Schätzung der Regressionskoeffizienten für Sie übernehmen. Für eine händische Berechnung würde die folgende Gleichung zur Kleinste-Quadrate-Schätzung verwendet, die wir aber nicht präziser besprechen werden:
$$\hat{\mathbf{b}}=(X’X)^{-1}X’y$$
(Die Matrix X umfasst die Werte in den Prädiktoren, der Vektor y umfasst die Werte in der abhängigen Variable.)
Falls Sie sich über die mathematischen Operationen hinter der Bestimmung von verschiedenen Kennwerten in der Regression (bspw. $R^2$) informieren wollen, können Sie im Appendix A des PsyMSc Studiengangs nachlesen.
Unser Modell und das Lesen von R-Outputs
Wir wollen mit Hilfe eines Regressionsmodells die Depressivitaet durch das Geschlecht und die Lebenszufriedenheit vorhersagen. Dies funktioniert in R ganz leicht mit der lm ("linear modeling) Funktion. Dieser müssen wir zwei Argumente übergeben: 1) unsere angenommene Beziehung zwischen den Variablen; 2) den Datensatz, in welchem die Variablen zu finden sind:
lm(Depressivitaet ~ 1 + Geschlecht + Lebenszufriedenheit, data = Depression)
##
## Call:
## lm(formula = Depressivitaet ~ 1 + Geschlecht + Lebenszufriedenheit,
## data = Depression)
##
## Coefficients:
## (Intercept) Geschlechtweiblich Lebenszufriedenheit
## 7.2353 1.9117 -0.3663
Hierbei zeigt die Tilde (~) auf, welche Variable die AV ist (sie steht links der Tilde), welche Variablen die UVs sind (sie stehen rechts der Tilde und werden durch + getrennt) und ob das Interzept mitgeschätzt werden soll. (Per Default wird dieses mitgeschätzt, weshalb “1 +” redundant ist und daher hier weggelassen werden könnte - nicht mit einbezogen wird das Interzept via “0 +”.) Diese Notation wird in sehr vielen Modell verwendet, in welchen es um die Beziehung zwischen unabhängigen und abhängigen Variablen geht! Im Appendix A können Sie nachlesen, welche weiteren Befehle zum gleichen Ergebnis führen und wie bspw. explizit das Interzept in die Gleichung mit aufgenommen werden kann (oder wie darauf verzichtet wird!).
Im Output sehen wir die Parameterschätzungen unseres Regressionsmodells, das folgendermaßen aussieht:
\begin{align} \text{Depressivitaet}_i=b_0+b_1 \cdot \text{Geschlecht}_i \\ +b_2 \cdot \text{Lebenszufriedenheit}_i+\varepsilon_i, \end{align}für $i=1,\dots,100=:n$. Wir wollen uns die Ergebnisse unserer Regressionsanalyse noch detaillierter anschauen. Dazu können wir wieder die summary-Funktion anwenden. Wir weisen dafür den lm-Befehl einem Objekt zu, welches wir weiterverwenden können, um darauf beispielsweise summary auszuführen. Zur Erinnerung: Wir speichern dieses Objekt ab, indem wir eine Zuordnung durchführen via <- und einen Namen (hier: model) vergeben.
model <- lm(Depressivitaet ~ 1 + Geschlecht + Lebenszufriedenheit, data = Depression)
summary(model)
##
## Call:
## lm(formula = Depressivitaet ~ 1 + Geschlecht + Lebenszufriedenheit,
## data = Depression)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.4037 -0.6711 0.0121 0.6952 3.3289
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 7.23528 0.64773 11.17 < 2e-16 ***
## Geschlechtweiblich 1.91174 0.28879 6.62 2.83e-09 ***
## Lebenszufriedenheit -0.36632 0.09227 -3.97 0.000147 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.286 on 87 degrees of freedom
## Multiple R-squared: 0.4833, Adjusted R-squared: 0.4714
## F-statistic: 40.68 on 2 and 87 DF, p-value: 3.362e-13
Um auch die standardisierten Ergebnisse zu erhalten, verwenden wir die Funktion lm.beta. (lm steht hier für lineares Modell und beta für die standardisierten Koeffizienten. Achtung: Häufig werden allerdings auch unstandardisierten Regressionskoeffizienten als $\beta$s bezeichnet, sodass darauf stets zu achten ist.) Die Funktion muss nach dem Erstellen eines linearen Modells (in unserem Fall model) auf dieses angewendet werden. Anschließend wollen wir uns noch eine summary des Modells ausgeben lassen. So erhalten wir zusätzlich standardisierte Koeffizienten. Für die Kombination von Funktionen haben wir in der letzten Sitzung die Verwendung des Pipes |> kennen gelernt.
lm.beta(model) |> summary()
##
## Call:
## lm(formula = Depressivitaet ~ 1 + Geschlecht + Lebenszufriedenheit,
## data = Depression)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.4037 -0.6711 0.0121 0.6952 3.3289
##
## Coefficients:
## Estimate Standardized Std. Error t value Pr(>|t|)
## (Intercept) 7.23528 NA 0.64773 11.17 < 2e-16 ***
## Geschlechtweiblich 1.91174 0.53257 0.28879 6.62 2.83e-09 ***
## Lebenszufriedenheit -0.36632 -0.31940 0.09227 -3.97 0.000147 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.286 on 87 degrees of freedom
## Multiple R-squared: 0.4833, Adjusted R-squared: 0.4714
## F-statistic: 40.68 on 2 and 87 DF, p-value: 3.362e-13
model |> lm.beta() |> summary() # alternativ
##
## Call:
## lm(formula = Depressivitaet ~ 1 + Geschlecht + Lebenszufriedenheit,
## data = Depression)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.4037 -0.6711 0.0121 0.6952 3.3289
##
## Coefficients:
## Estimate Standardized Std. Error t value Pr(>|t|)
## (Intercept) 7.23528 NA 0.64773 11.17 < 2e-16 ***
## Geschlechtweiblich 1.91174 0.53257 0.28879 6.62 2.83e-09 ***
## Lebenszufriedenheit -0.36632 -0.31940 0.09227 -3.97 0.000147 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.286 on 87 degrees of freedom
## Multiple R-squared: 0.4833, Adjusted R-squared: 0.4714
## F-statistic: 40.68 on 2 and 87 DF, p-value: 3.362e-13
Nochmal zur Wiederholung: Der Pipe-Operator übergibt immer das resultiernde Objekt des vorherigen Befehls an die erste Stelle der folgenden Funktion. Somit können wir die Pipe wie folgt lesen: “Nehme model und wende darauf lm.beta() an, nehme anschließend das resultierende Objekt und wende darauf summary() an.”
summary ist eine weit verbreitete Funktion, die Objekte zusammenfasst und interessante Informationen für uns auf einmal bereitstellt. R-Outputs sehen fast immer so aus, weswegen es von unabdingbarer Wichtigkeit ist, dass wir uns mit diesem Output vertraut machen. Im Grunde werden uns alle erforderlichen Informationen über den Inhalt dieser Zusammenfassung durch die Überschriften und Spaltenüberschriften vermittelt. Was können wir dem Output nun Schritt für Schritt entnehmen?
##
## Call:
## lm(formula = Depressivitaet ~ 1 + Geschlecht + Lebenszufriedenheit,
## data = Depression)
Fasst noch einmal zusammen, welches Objekt “zusammengefasst” wird. Hier steht das zuvor untersuchte lm-Objekt (model, bzw. lm.beta(model)).
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.4037 -0.6711 0.0121 0.6952 3.3289
Diese Deskriptivstatistiken (gerundet auf 4 Nachkommastellen) geben uns ein Gefühl für die Datengrundlage: die Überschrift sagt uns, dass es hierbei um die Residuen im Regressionsmodell geht. Min steht für das Minimum (-3.4037), 1Q beschreibt das erste Quartil (-0.6711); also den Prozentrang von 25% - es liegen 25% der Werte darunter und 75% darüber, Median beschreibt den Prozentrang von 50% (0.012), 3Q beschreibt das 3. Quartil, also den Prozentrang von 75% (0.695) und Max ist der maximale Wert der Residuen (3.329). Der Mittelwert trägt hier keine Information, da die Residuen immer so bestimmt werden, dass sie im Mittel verschwinden, also ihr Mittelwert bei 0 liegt. Da der Median auch sehr nah an der 0 liegt, zeigt dies, dass die Residuen wahrscheinlich recht symmetrisch verteilt sind. Auch das 1. und 3. Quartil verteilen sich ähnlich (also entgegengesetzte Vorzeichen aber betraglich ähnliche Werte), was ebenfalls für die Symmetrie spricht. Wir können die Residuen unserem model-Objekt ganz leicht entlocken, indem wir den Befehl resid auf dieses Objekt anwenden. Bspw. ergibt sich der Mittelwert als:
mean(x = resid(model)) # Mittelwert mit Referenzierung aus dem lm Objekt "model"
## [1] -1.158362e-16
Natürlich könnte man statt der Funktion resid auch das Element Residuals im Objekt ansprechen mittels model$residuals.
Die Zahl, die beim Mittelwert ausgegeben wird, ist folgendermaßen zu lesen: e-17 steht für $*10^{-17}=0.00000000000000001$ (die Dezimalstelle wird um 17 Stellen nach links verschoben), somit ist -6.002143e-17$=-6.002143*10^{-17}=-0.00000000000000006002143\approx 0$. Hier kommt nicht exakt 0 heraus, da innerhalb der Berechnungen immer auf eine gewisse Genauigkeit gerundet wird. Diese hängt von der sogennanten Maschinengenauigkeit von R ab. Eine noch höhere Genauigkeit der Darstellung von Zahlen würde einfach zu viel Speicherplatz verbrauchen!
Nun kommen wir zum eigentlich spannenden Teil, nämlich der Übersicht über die Parameterschätzung (Coefficients). Diese sieht in sehr vielen Analysen sehr ähnlich aus (z.B. logistische Regression oder Multi-Level-Analysen/hierarchische Regression aus diesem Kurs).
##
## Coefficients:
## Estimate Standardized Std. Error t value Pr(>|t|)
## (Intercept) 7.23528 NA 0.64773 11.17 < 2e-16 ***
## Geschlechtweiblich 1.91174 0.53257 0.28879 6.62 2.83e-09 ***
## Lebenszufriedenheit -0.36632 -0.31940 0.09227 -3.97 0.000147 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Insgesamt gibt es 6 Spalten, wobei die Standardized-Spalte extra durch das Paket lm.beta angefordert wurde (sie ist also nicht immer in der Summary enthalten). In der ersten Spalte stehen die Variablennamen, die selbsterklärend sein sollten. Die Spalte Estimate zeigt den unstandardisierten Parameter (hier Regressionsgewicht). Z.B. liegt das Interzept $b_0$ bei 7.2353. Das Partialregressionsgewicht vom Geschlecht $b_\text{Geschlecht}$ liegt bei 1.9117. Da Frauen mit 1 kodiert sind, bedeutet dies: Wenn Frauen im Vergleich zu Männern betrachtet werden, so steigt die Depressivitaet durchschnittlich um 1.9117 Punkte (“durchschnittlich” in der Interpretation ist enorm wichtig, da es ja noch den Vorhersagefehler für individuelle Vergleiche gibt). Ensprechend können wir auch das Interzept interpretieren: Ein Mann mit einer Lebenszufriedenheit von 0 hat einen durchschnittlichen Depressivitaetswert von 7.2353. (Anmerkung: Ein Wert von 0 in der Lebenszufriedenheit ist leider unrealistisch, da die Skala hier nicht zentriert wurde - die Effekte von Zentrierung schauen wir uns in der Sitzung zur Hierarchischen Regression genauer an!)
In der Spalte Standardized stehen die standardisierten Regressionsgewichte. Hier werden die Daten so transformiert, dass sowohl die AV als auch die UVs jeweils Mittelwerte von 0 und Varianzen (bzw. Standardabweichungen) von 1 aufweisen. Das Interzept ist nun nicht länger interessant. Denn das Interzept ist gerade jener vorhergesagte Wert für $y$, der anfällt, wenn alle Prädiktoren den Wert 0 annehmen. Durch die Zentrierung haben $y$ und auch die unabhängigen Variablen alle einen Mittelwert von 0. Demnach entspricht in diesem Fall das Interzept genau dem y-Wert, der auftritt, wenn alle Prädiktoren ihren Mittelwert annehmen. Bei der Regression ist es nun aber so, dass an der Stelle, an der alle Prädiktoren ihren Mittelwert annehmen, auch der Mittelwert von $y$ liegt; hier also 0. Folglich ist das Interzept im zentrierten bzw. standardisierten Fall immer 0. Das standardisierte Regressionsgewicht der Lebenszufriedenheit $\beta_\text{Lebenszufriedenheit}$ liegt bei -0.3194, was bedeutet, dass bei einer Erhöhung der Lebenszufriedenheit um eine Standardabweichung die Depressivitaet im Mittel um -0.3194 Standardabweichungen fällt.
Für die Interpretation des Geschlechts als Prädiktor bringt die Standardisierung eine Erschwerung mit sich. Die beiden Ausprägungen sind nun nicht mehr eine Einheit bzw. Standardabweichung voneinander entfernt. Daher kann man den Vergleich nicht mehr mit einbeziehen. Es lässt sich nur sagen: Steigt die Variable Geschlecht um eine Standardabweichung auf der Dimension zwischen Männern und Frauen, so steigt die Depressivitaet um durchschnittlich 0.5326 Standardabweichungen.
Die Spalte Std.Error enthält die Standardfehler. Diese werden in $t$-Werte umgerechnet via $\frac{Est}{SE}$: es wird also die Parameterschätzung durch ihren Standardfehler geteilt und in der nächsten Spalte t value dargestellt. In einigen Summaries werden auch anstelle der $t$-Werte die $z$-Werte verwendet. Hierbei ändert sich nichts, nur wird zur Herleitung der $p$-Werte eben die $z$- anstelle der $t$-Verteilung verwendet. Wenn wir uns allerdings an Statistik aus dem Bachelor erinnern, so bemerken wir, dass für große Stichproben die $t$ und die $z$-Verteilung identisch (bzw. sehr nahe beieinander liegend) sind. Als groß gilt hierbei bereits eine Stichprobengröße von 50!
In der Spalte Pr(>|t|) stehen die zugehörigen $p$-Werte. “Pr” steht für die Wahrscheinlichkeit (Probability), dass die Teststatistik (hier der $t$-Wert) im Betrag ein extremeres Ergebnis aufzeigt, als das Beobachtete. Außerdem bekommen wir noch mit Sternchen angezeigt, auf welchem Signifikanzniveau die einzelnen Parameter statistisch bedeutsam sind.
Zusammenfassend entnehmen wir dem Output, dass das Interzept bedeutsam von 0 verschieden ist und auch die Effekte der Prädiktoren sind auf dem 5%-Niveau statistisch signifikant. Dies bedeutet bspw. für die Lebenszufriedenheit, dass mit einer Irrtumswahrscheinlichkeit von 5% der Regressionsparameter der Lebenszufriedenheit in der Population nicht 0 ist. Somit ist auch mit derselben Irrtumswahrscheinlichkeit in der Population von einem Effekt zu sprechen. Hierbei ist es essentiell, dass sich die statistische Interpretation immer auf die Population bezieht. Dass ein Koeffizient in der Stichprobe nicht 0 ist, erkennen wir einfach daran, dass er von 0 abweicht. Allerdings kann dieses Ergebnis eben durch Zufall aufgetreten sein. Häufig weichen Werte in unserer Stichprobe offensichtlich von 0 ab, allerdings nicht stark genug, als dass wir dies auch (mit einer Irrtumswahrscheinlichkeit von 5%) für die Population schlussfolgern (auch: schließen/inferieren, desewegen auch Inferenzstatistik/schließende Statistik) würden.
Regressionskoeffizienten können einzeln signifikant sein, ohne dass signifikante Anteile der Variation der abhängigen Variable erklärt werden.
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.286 on 87 degrees of freedom
## Multiple R-squared: 0.4833, Adjusted R-squared: 0.4714
## F-statistic: 40.68 on 2 and 87 DF, p-value: 3.362e-13
Dazu entnehmen wir dem letzten Block den Standardfehler der Residuen (Residual standard error), der im Grunde die Fehlervariation von $y$ beschreibt, sowie das multiple $R^2$ (Multiple R-squared), welches anzeigt, dass ca. 48.3% der Variation der Depressivitaet auf die Prädiktoren Geschlecht und Lebenszufriedenheit zurückgeführt werden kann. Dieses Varianzinkrement ist statistisch signifikant, was wir am $F$-Test in der letzten Zeile ablesen können. Der $F$-Wert (F-statistic) liegt bei 40.68, wobei die Hypothesenfreiheitsgrade hier gerade 2 sind ($df_h$) und die Residualfreiheitsgrade bei 87 ($df_e$) liegen. Der zugehörige $p$-Wert ist deutlich kleiner als 5% und liegt bei $3.362*10^{-13}$. Dies bedeutet, dass mit einer Irrtumswahrscheinlichkeit von 5% auch in der Population eine Vorhersage der Depressivitaet durch Geschlecht und Intelligenz gemeinsam angenommen werden kann ($R^2\neq0$). In einem Artikel (oder einer Abschlussarbeit) würden wir zur Untermauerung F(2, 87) $=$ 40.68, p<.001 in den Fließtext schreiben.
Außerdem können wir natürlich auch das mit summary erstellte Objekt unter einem Namen abspeichern und ihm dann weitere Informationen entlocken. Bspw. erhalten wir mit $coefficients die Tabelle der Koeffizienten oder mit $r.squared das multiple $R^2$.
summary_model <- summary(lm.beta(model))
summary_model$coefficients # Koeffiziententabelle
## Estimate Standardized Std. Error t value Pr(>|t|)
## (Intercept) 7.2352799 NA 0.64773072 11.170197 1.722491e-18
## Geschlechtweiblich 1.9117353 0.5325749 0.28878522 6.619921 2.834596e-09
## Lebenszufriedenheit -0.3663154 -0.3194030 0.09226649 -3.970189 1.474393e-04
summary_model$r.squared # R^2
## [1] 0.4832806
names(summary_model) # weitere mögliche Argumente, die wir erhalten können
## [1] "call" "terms" "residuals" "coefficients" "aliased" "sigma"
## [7] "df" "r.squared" "adj.r.squared" "fstatistic" "cov.unscaled"
Gleiches können wir mit allen Summary-Objekten auch in späteren Sitzungen machen!
Wenn wir diese Signifikanzentscheidungen nutzen wollen, um die Effekte in der Population derart zu interpretieren, so müssen einige Voraussetzungen erfüllt sein, die zunächst noch geprüft werden müssten. So nehmen wir bspw. für ein Regressionsmodell an, dass die Regressoren lineare Beziehungen mit dem Kriterium aufweisen. Die Personen/Erhebungen sollten außerdem unabhängig und identisch verteilt sein (sie sollten aus einer i.i.d. (independent and identically distributed) Population stammen, also keinerlei Beziehung untereinander aufweisen und dem gleichen Populationsmodell folgen). Die Residuen innerhalb der Regression werden als normalverteilt und homoskedastisch (also mit gleicher Varianz über alle Ausprägungen der Prädiktoren) angenommen. Nur unter bestimmten Voraussetzungen lassen sich Signifikanzentscheidungen im Allgemeinen überhaupt interpretieren. Außerdem beeinflussen Ausreißer die Schätzungen der Regressionskoeffizienten drastisch.
Prüfen der Voraussetzungen
Dieser Abschnitt stellt nur in einem Auszug die Prüfung der Voraussetzungen bereit. Wenn Sie alle Prüfungen wiederholen wollen, können Sie in der Bachelorsitzung zu Multipler Regression nachlesen. Die Voraussetzung der Unabhängigkeit und der Gleichverteiltheit ist und bleibt eine Annahme, die wir nicht prüfen können. Wir können jedoch durch das Studiendesign (Randomisierung, Repräsentativität) diese Annahme plausibilisieren. Die Linearitätsannahme und die Voraussetzungen der Residuen werden wir hier nicht genauer betrachten. Fokus legen wir auf die Multikollinearität und mögliche Ausreißer. Nochmal aufgezählt alle Voraussetzungen:
- korrekte Spezifikation des Modells
- Unabhängigkeit der Residuen
- Messfehlerfreiheit der unabhängigen Variablen
- Linearität bei Modellierung linearer Effekt
- Homoskedastizität (Unabhängigkeit der Residualvarianz)
- Normalverteilung der Residuen bzw. multivariate Normalverteilung
- Multikollinearität
- Identifikation von Ausreißern und einflussreichen Datenpunkten
Im Folgenden werden wir mit dem unstandardisierten Modell weiterarbeiten, welches wir im Objekt model gespeichert hatten.
Vertiefende Literatur zum folgenden Stoff finden wir bspw. in Eid, et al. (2017) in Kapitel 19.13 und Pituch und Stevens (2016) in Kapitel 3.10 - 3.14.
Multikollinearität
Multikollinearität ist ein potenzielles Problem der multiplen Regressionsanalyse und liegt vor, wenn zwei oder mehrere Prädiktoren hoch miteinander korrelieren. Hohe Multikollinearität
- schränkt die mögliche multiple Korrelation ein, da die Prädiktoren redundant sind und überlappende Varianzanteile in $y$ erklären.
- erschwert die Identifikation von bedeutsamen Prädiktoren, da deren Effekte untereinander konfundiert sind (die Effekte können schwer voneinander getrennt werden).
- bewirkt eine Erhöhung der Standardfehler der Regressionskoeffizienten (der Standardfehler ist die Standardabweichung der Verteilung der Regressionskoeffizienten bei wiederholter Stichprobenziehung und Schätzung). Dies bedeutet, dass die Schätzungen der Regressionsparameter instabil, und damit weniger verlässlich werden. Weitere Informationen zur Instabilität und zu Standardfehlern kann der/die interessierte Leser*in in Appendix D des Beitrags in PsyMSc1 nachlesen. Beachten Sie dabei, dass hier mit Matrixnotationsweise gearbeitet wird.
Multikollinearität kann durch Inspektion der bivariaten Zusammenhänge (Korrelationsmatrix) der Prädiktoren $x_j$ untersucht werden.
# Korrelation der Prädiktoren
cor(as.numeric(Depression$Geschlecht), Depression$Lebenszufriedenheit)
## [1] -0.2869571
Dieser Wert ist jedoch nur ein erstes Indiz für die Performance. Leider kann der Korrelationskoeffizient nicht alle Formen von Multikollinearität aufdecken. Darüber hinaus ist die Berechnung der sogenannten Toleranz (T) und des Varianzinflationsfaktors (VIF) für jeden Prädiktor möglich. Hierfür wird nacheinander für jeden Prädiktor $x_j$ das entsprechende $R_j^2$ berechnet, also der durch diesen Prädiktor erklärte Varianzanteil, der gleichzeitig durch alle anderen Prädiktoren in der Regression erklärt wird. Toleranz und VIF sind wie folgt definiert:
- $T_j = 1-R^2_j = \frac{1}{VIF_j}$
- $VIF = \frac{1}{1-R^2_j} = \frac{1}{T_j}$
Offensichtlich genügt eine der beiden Statistiken, da sie vollständig ineinander überführbar und damit redundant sind. Empfehlungen als Grenzwert für Kollinearitätsprobleme sind z. B. $VIF_j>10$ ($T_j<0.1$; siehe Eid, et al., 2017, S. 712 und folgend). Die Varianzinflationsfaktoren der Prädiktoren im Modell können mit der Funktion vif des car-Pakets bestimmt werden, der Toleranzwert als Kehrwert des VIFs.
car::vif(model) # VIF
## Geschlecht Lebenszufriedenheit
## 1.089733 1.089733
1/car::vif(model) # Toleranz
## Geschlecht Lebenszufriedenheit
## 0.9176556 0.9176556
In diesem Beispiel mit nur 2 Prädiktoren ist $\small R_{Geschlecht}^2=R_{Lebenszufriedenheit}^2=cor(\text{Geschlecht},\text{Lebenszufriedenheit})^2$ und die Formeln sind daher sehr einfach auch mit Hand zu bestimmen:
1/(1-cor(as.numeric(Depression$Geschlecht), Depression$Lebenszufriedenheit)^2) # 1/(1-R^2) = VIF
## [1] 1.089733
1-cor(as.numeric(Depression$Geschlecht), Depression$Lebenszufriedenheit)^2 # 1-R^2 = Toleranz
## [1] 0.9176556
Für unser Modell wird ersichtlich, dass die Prädiktoren zwar eine Korrelation haben, aber keiner der Werte außerhalb der bewährten Grenzen liegt. Dementsprechend liegt kein Multikollinearitätsproblem vor. Unabhängigkeit folgt hieraus allerdings nicht, da nicht-lineare Beziehungen zwischen den Variablen bestehen könnten, die durch diese Indizes nicht abgebildet werden.
Identifikation von Ausreißern und einflussreichen Datenpunkten
Die Plausibilität unserer Daten ist enorm wichtig. Aus diesem Grund sollten Ausreißer oder einflussreiche Datenpunkte analysiert werden. Diese können bspw. durch Eingabefehler (Alter von 211 Jahren anstatt 21), durch absichtliche Fälschung bzw. Unlust in der Beantwortung entstehen oder es sind seltene Fälle (hochintelligentes Kind in einer Normstichprobe), welche so in natürlicher Weise (aber mit sehr geringer Häufigkeit) auftreten können. Es muss dann entschieden werden, ob Ausreißer die Repräsentativität der Stichprobe gefährden und ob diese daher besser ausgeschlossen werden sollten.
Hebelwerte
Hebelwerte $h_j$ (engl.: leverage values) erlauben die Identifikation von Ausreißern aus der gemeinsamen Verteilung der unabhängigen Variablen, d.h. sie geben an, wie weit ein Wert vom Mittelwert einer Prädiktorvariable entfernt ist. Je höher der Hebelwert, desto weiter liegt der einzelne Fall vom Mittelwert der gemeinsamen Verteilung der unabhängigen Variablen entfernt und desto stärker kann somit der Einfluss auf die Regressionsgewichte sein. Hebelwerte werden mit der Funktion hatvalues ermittelt. In R werden die Hebelwerte nicht zentriert ausgegeben. Kriterien zur Beurteilung der nicht zentrierten Hebelwerte variieren, so werden von Eid et al. (2017, S. 707) in Kombination mit Pituch et al. (2016, S. 108) Grenzen von $2\cdot (k+1) / n$ für große und $3\cdot (k+1) / n$ für kleine Stichproben vorgeschlagen (mit $k$ als Anzahl der Variablen). Alternativ zu einem festen Cut-Off-Kriterium kann die Verteilung der Hebelwerte inspiziert werden, wobei diejenigen Werte als kritisch bewertet werden, die aus der Verteilung ausreißen. Eine eigene grafische Überprüfung wird empfohlen, da die Cut-Off-Werte sehr sensibel sind und viele verdächtige Werte anzeigen. Die Funktion hatvalues erzeugt die Hebelwerte aus einem Regression-Objekt. Wir wollen die Hebelwerte als Histogramm darstellen.
n <- length(residuals(model)) # Anzahl an Personen bestimmen
h <- hatvalues(model) # Hebelwerte
hist(h, breaks = 20)
abline(v = 2*(2+1)/n, col = "red") # Cut-off als große Stichprobe
abline(v = 3*(2+1)/n, col = "blue") # Cut-off als kleine Stichprobe

Hier eine kurze Beschreibung aller Argumente in der Grafik: Das Zusatzargument breaks = 20 in hist gibt an, dass 20 Balken gezeichnet werden sollen. abline ist eine Funktion, die einem Plot eine Gerade hinzufügt. Dem Argument v wird hierbei der Punkt übergeben, an welchem eine vertikale Linie eingezeichnet werden soll. col = "red" bzw. col = "blue" gibt an, dass diese Linie rot bzw. blau sein soll.
Cook’s Distanz
Cook’s Distanz $CD_i$ bezieht sich auf Ausreißer in der abhängigen Variable und gibt eine Schätzung an, wie stark sich die Regressionsgewichte verändern, wenn eine Person $i$ aus dem Datensatz entfernt wird. Fälle, deren Elimination zu einer deutlichen Veränderung der Ergebnisse führen würden, sollten kritisch geprüft werden. Als einfache Daumenregel gilt, dass $CD_i>1$ auf einen einflussreichen Datenpunkt hinweist. Cook’s Distanz kann mit der Funktion cooks.distance berechnet werden.
# Cook's Distanz
CD <- cooks.distance(model) # Cook's Distanz
hist(CD, breaks = 20)
abline(v = 1, col = "red") # Cut-off bei 1
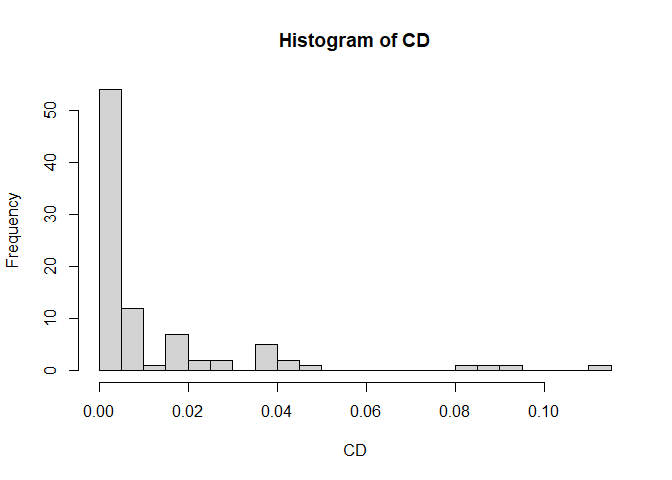
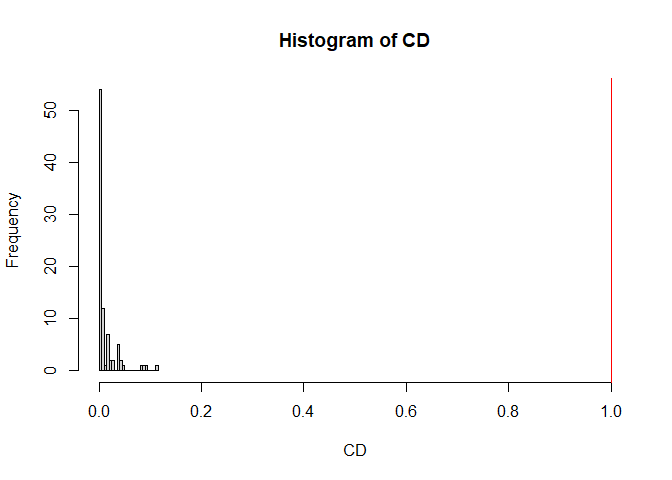
xlim = c(0,1) explizit von 0 bis 1 vorgeben:
# Cook's Distanz nochmal
hist(CD, breaks = 20, xlim = c(0, 1))
abline(v = 1, col = "red") # Cut-off bei 1
Blasendiagramm
Die Funktion influencePlot des car-Paketes erzeugt ein “Blasendiagramm” zur simultanen grafischen Darstellung von Hebelwerten (auf der x-Achse), studentisierten Residuen (auf der y-Achse) und Cook’s Distanz (als Größe der Blasen). Das Studentisieren der Residuen bezeichnet eine Art der Standardisierung, sodass anschließend der Mittelwert 0 und die Varianz 1 ist. Es ist also eine Normierung der normalen Werte des Resiuums. Somit lassen sich solche Plots immer gleich interpretieren und besser vergleichen. Horizontale Bezugslinien markieren die Werte -2, 0 und 2 auf der Skala der studentisierten Residuen, vertikale Bezugslinien das Doppelte und Dreifache des durchschnittlichen Hebelwertes. Vertikale Linien verdeutlichen die Grenzen, die für die Hebelwerte festgelegt werden (sie sind also analog zu unseren rot und blau gezeichneten Linien im Histogramm). Falls es Fälle gibt, die nach einem der drei Kriterien als Ausreißer identifiziert werden, gibt die Funktion inlfuencePlot einen Dataframe aus, der die Hebelwerte, die studentisierten Residuen und die Cook’s Distanzen dieser Ausreißer enthält. Außerdem werden solche Fälle im Streudiagramm durch ihre Zeilennummer gekennzeichent.
Wenn wir influencePlot(model) in einem Objekt (mit dem Objektnamen InfPlot ablegen), können wir durch as.numeric(row.names(InfPlot)) auf die Zeilennummern der auffälligen Werte zugreifen.
# Blasendiagramm mit Hebelwerten, studentisierten Residuen und Cook's Distanz
InfPlot <- influencePlot(model)
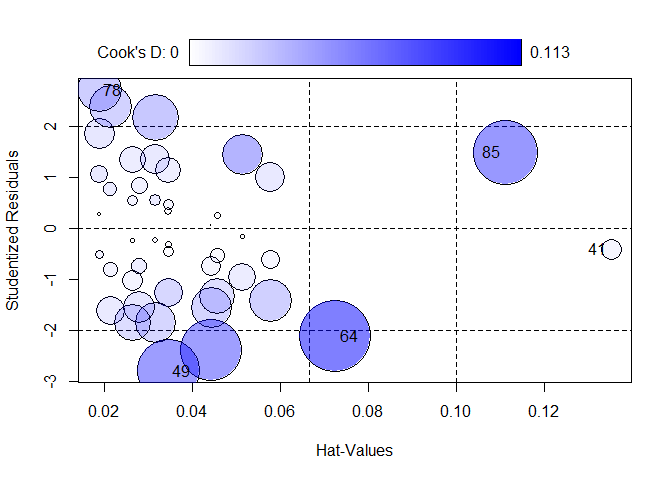
# Werte der identifizierten Fälle
InfPlot
## StudRes Hat CookD
## 41 -0.418397 0.13516814 0.009207384
## 49 -2.797895 0.03445764 0.086345854
## 64 -2.118632 0.07260556 0.112621347
## 78 2.707307 0.01881699 0.043677143
## 85 1.490516 0.11113495 0.091308435
# In "IDs" werden die Zeilennummern der auffälligen Fälle gespeichert,
# welche gleichzeitig als Zahlen im Blasendiagramm ausgegeben werden
IDs <- as.numeric(row.names(InfPlot))
Schauen wir uns die möglichen Ausreißer an und standardisieren die Ergebnisse für eine bessere Interpretierbarkeit.
# Rohdaten der auffälligen Fälle
Depression[IDs,]
## Lebenszufriedenheit Episodenanzahl Depressivitaet Neurotizismus Intervention
## 41 2 4 6 3 VT Coaching
## 49 5 4 2 8 VT Coaching
## 64 10 4 1 10 VT Coaching + Gruppenuebung
## 78 7 9 8 6 VT Coaching + Gruppenuebung
## 85 11 7 5 10 VT Coaching + Gruppenuebung
## Geschlecht
## 41 maennlich
## 49 maennlich
## 64 maennlich
## 78 maennlich
## 85 maennlich
# z-standardisierte Werte der auffälligen Fälle
scale(Depression[,1:4])[IDs,]
## Lebenszufriedenheit Episodenanzahl Depressivitaet Neurotizismus
## [1,] -2.8535787 -1.5202002 0.1947782 -2.0315461
## [2,] -0.9079568 -1.5202002 -2.0671617 0.8799053
## [3,] 2.3347462 -1.5202002 -2.6326467 2.0444859
## [4,] 0.3891244 2.1775841 1.3257481 -0.2846752
## [5,] 2.9832868 0.6984704 -0.3707068 2.0444859
Die Funktion scale z-standardisiert den Datensatz. Dies macht natürlich inhaltlich hauptsächlich für die intervallskalierten Skalen Sinn (also die ersten vier Spalten im Datensatz). Mit Hilfe von [IDs,], werden die entsprechenden Zeilen der Ausreißer aus dem Datensatz ausgegeben und anschließend auf 2 Nachkommastellen gerundet. Hierbei ist es extrem wichtig, dass wir scale(Depression[,1:4])[IDs,] und nicht scale(Depression[IDs,1:4]) schreiben, da bei der zweiten Schreibweise die Daten reskaliert (z-standardisiert) werden, allerdings auf Basis der ausgewählten Fälle (n=5) und nicht auf Basis der gesamten Stichprobe (n = 90). Mit Hilfe der z-standardisierten Ergebnisse lassen sich Ausreißer hinsichtlich ihrer Ausprägungen einordnen:
Interpretation
Was ist an den fünf identifizierten Fällen konkret auffällig? Zur Beantwortung dieser Frage sollten wir uns auf die Variablen konzentrieren, die in unserem Modell enthalten sind.
- Fall 41: durchschnittlicher Depressivitaetswert bei stark unterdurchschnittlicher Lebenszufriedenheit als Mann
- Fall 49: Sehr niedriger Depressivitaetswert bei niedriger Lebenszufriedenheit als Mann
- Fall 64: Stark überdurchschnittliche Lebenzufriedenheit und sehr stark unterdurchschnittlicher Depressivitaetswert als Mann
- Fall 78: Überdurchschnittlicher Depressivitaetswert bei durchschnittlicher Lebenszufriedenheit als Mann
- Fall 85: Leicht unterdurchschnittlicher Depressivitaetswert bei sehr hoher Lebenszufriedenheit als Mann
Die Entscheidung, ob Ausreißer oder auffällige Datenpunkte aus Analysen ausgeschlossen werden, ist schwierig und kann nicht pauschal beantwortet werden. Im vorliegenden Fall wäre z.B. zu überlegen, ob Fälle 41 und 85, den Fragebogen zur Lebenszufriedenheit ernsthaft ausgefüllt haben, da sie mit ihren Werten sehr weit außerhalb der Verteilung liegen. Allerdings liegen keine weiteren Informationen über die erhobene Gruppe vor (und es existiert eine reele Chance auf diese Daten), weshalb ein Ausschluss nicht sinnvoll zu begründen wäre.
Einfluss von Hebelwert und Cook’s Distanz
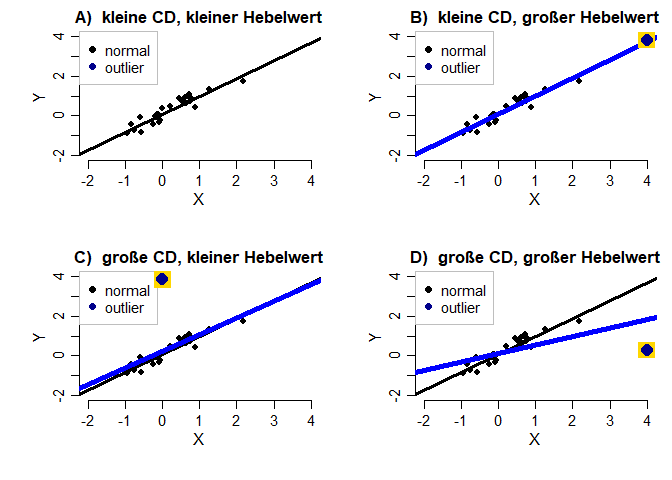
Was wäre nun gewesen, wenn die Hebelwerte oder Cook’s Distanz extreme Werte angezeigt hätten? Um dieser Frage auf den Grund zu gehen, schauen wir uns für eine Kombination der beiden Koeffizienten den Effekt auf eine Regressionsgerade an. Die vier Grafiken zeigen jeweils die Regressionsgerade in schwarz ohne den jeweiligen Ausreißer, während die Gerade in blau die Regressionsanalyse (Y ~ 1 + X) inklusive des Ausreißers symbolisiert. Falls Sie die Grafik selbst bauen wollen, finden Sie sie in Appendix B.
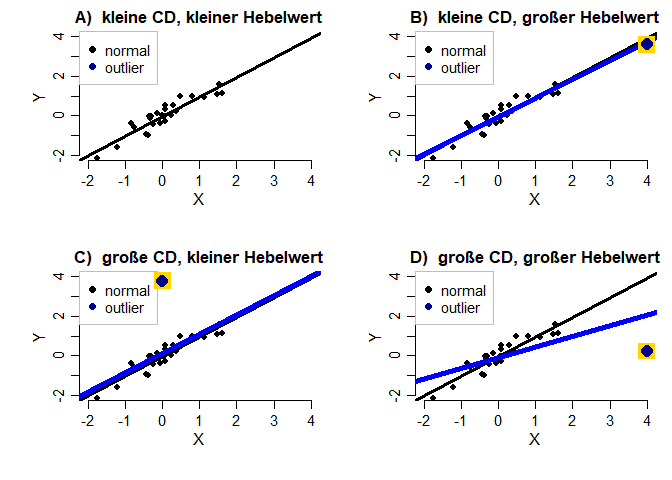
In A) ist die Regression ohne Ausreißer dargestellt. B) zeigt den Effekt, wenn nur der Hebelwert groß ist. Es ist kaum ein Einfluss auf die Regressionsgerade auszumachen. Der Mittelwert der Variable X wird stark nach rechts verschoben. Dies bedeutet, dass ein großer Hebelwert nur den Mittelwert dieser Variable in Richtung des Ausreißers “hebelt”, nicht aber zwangsweise die Regressionsgerade! C) zeigt eine große Cook’s Distanz bei gleichzeitig kleinem Hebelwert. Die Gerade ist etwas nach oben verschoben und auch die Steigung hat sich leicht verändert. Insgesamt ist mit dem bloßen Auge allerdings noch kein extremer Effekt auf die Gerade auszumachen. Dieser Effekt wird nur in D) deutlich. Hier ist sowohl Cook’s Distanz als auch der Hebelwert extrem. Dadurch verändert sich die Regressionsgerade stark. Hier könnten wir davon sprechen, dass die Gerade durch den Ausreißer nach unten “gehebelt” wird. Insgesamt zeigt diese Grafik, dass ein Koeffizient alleine nicht ausreicht, um einen Effekt auf eine Regressionsanalyse zu bewirken und dass Werte besonders dann extreme Auswirkungen haben, wenn mehrere Koeffizienten groß sind!
Interessierte Lesende können im Appendix C ein weiteres Tool zur Identifikation kennenlerenen: Die Mahalanobis-Distanz. Diese bringt den Vorteil mit sich, dass sie die Testung auf multivariate Normalverteilung auf eine Dimension runterbrechen kann.
Diese Sitzung war eine Wiederholung der multiplen Regression und einiger Konzepte in der Testung der Voraussetzungen. Es wurden nun komplexere Analysen mit R durchgeführt. In den nächsten Wochen wird die Arbeit im Linearen Modell vertieft.
Appendix
Appendix A
Regressionsmodell
Folgende Befehle führen zum gleichen Ergebnis wie:
lm(Depressivitaet ~ 1 + Geschlecht + Lebenszufriedenheit, data = Depression)
##
## Call:
## lm(formula = Depressivitaet ~ 1 + Geschlecht + Lebenszufriedenheit,
## data = Depression)
##
## Coefficients:
## (Intercept) Geschlechtweiblich Lebenszufriedenheit
## 7.2353 1.9117 -0.3663
Das Interzept kann explizit mitangegeben werden (falls Sie 0 + schreiben, setzen Sie das Interzept auf 0, was sich entsprechend auf die Parameterschätzungen auswirken wird, falls das Interzept eigentlich von 0 verschieden ist!):
lm(Depressivitaet ~ 0 + Geschlecht + Lebenszufriedenheit, data = Depression)
##
## Call:
## lm(formula = Depressivitaet ~ 0 + Geschlecht + Lebenszufriedenheit,
## data = Depression)
##
## Coefficients:
## Geschlechtmaennlich Geschlechtweiblich Lebenszufriedenheit
## 7.2353 9.1470 -0.3663
Dem Output ist zu entnehmen, dass die Parameterschätzungen sich drastisch geändert haben!
Lassen wir das Interzept in der Schreibweise weg, so wird es per Default mitgeschätzt.
lm(Depressivitaet ~ Geschlecht + Lebenszufriedenheit, data = Depression)
##
## Call:
## lm(formula = Depressivitaet ~ Geschlecht + Lebenszufriedenheit,
## data = Depression)
##
## Coefficients:
## (Intercept) Geschlechtweiblich Lebenszufriedenheit
## 7.2353 1.9117 -0.3663
Der Argumentname für das Regressionsmodell lautet formula.
lm(formula = Depressivitaet ~ 1 + Geschlecht + Lebenszufriedenheit, data = Depression)
##
## Call:
## lm(formula = Depressivitaet ~ 1 + Geschlecht + Lebenszufriedenheit,
## data = Depression)
##
## Coefficients:
## (Intercept) Geschlechtweiblich Lebenszufriedenheit
## 7.2353 1.9117 -0.3663
Wir können also auch einfach die Reihenfolge umdrehen, solange wir Argumente benutzen:
lm(data = Depression, formula = Depressivitaet ~ 1 + Geschlecht + Lebenszufriedenheit)
##
## Call:
## lm(formula = Depressivitaet ~ 1 + Geschlecht + Lebenszufriedenheit,
## data = Depression)
##
## Coefficients:
## (Intercept) Geschlechtweiblich Lebenszufriedenheit
## 7.2353 1.9117 -0.3663
Die Formel kann auch in Anführungszeichen geschrieben werden:
lm("Depressivitaet ~ 1 + Geschlecht + Lebenszufriedenheit", data = Depression)
##
## Call:
## lm(formula = "Depressivitaet ~ 1 + Geschlecht + Lebenszufriedenheit",
## data = Depression)
##
## Coefficients:
## (Intercept) Geschlechtweiblich Lebenszufriedenheit
## 7.2353 1.9117 -0.3663
Wir können auf die Datensatzspezifizierung verzichten, indem wir die Variablen direkt ansprechen (es ändern sich entsprechend die Namen der Koeffizienten im Output):
lm(Depression$Depressivitaet ~ 1 + Depression$Geschlecht + Depression$Lebenszufriedenheit)
##
## Call:
## lm(formula = Depression$Depressivitaet ~ 1 + Depression$Geschlecht +
## Depression$Lebenszufriedenheit)
##
## Coefficients:
## (Intercept) Depression$Geschlechtweiblich Depression$Lebenszufriedenheit
## 7.2353 1.9117 -0.3663
Wir können auch neue Variablen definieren, um diese dann direkt anzusprechen (es ändern sich entsprechend die Namen der Koeffizienten):
AV <- Depression$Depressivitaet
UV1 <- Depression$Geschlecht
UV2 <- Depression$Lebenszufriedenheit
lm(AV ~ 1 + UV1 + UV2)
##
## Call:
## lm(formula = AV ~ 1 + UV1 + UV2)
##
## Coefficients:
## (Intercept) UV1weiblich UV2
## 7.2353 1.9117 -0.3663
Selbstverständlich gibt es auch noch weitere Befehle, die zum selben Ergebnis kommen. Sie sehen, dass Sie in R in vielen Bereichen mit leicht unterschiedlichem Code zum selben Ergebnis gelangen!
Appendix B
Grafiken und ggplot2
Im folgenden Block sehen wir den Code für ein Histogramm in ggplot2-Notation (das Paket muss natürlich installiert sein: install.packages(ggplot2)). Hier sind einige Zusatzeinstellungen gewählt, die das Histogramm optisch aufbereiten.
Hat-Values
n <- length(residuals(model)) #Anzahl Personen
h <- hatvalues(model) # Hebelwerte
library(ggplot2)
df_h <- data.frame(h) # als Data.Frame für ggplot
ggplot(data = df_h, aes(x = h)) +
geom_histogram(aes(y =..density..),
bins = 15, # Wie viele Balken sollen gezeichnet werden?
colour = "blue", # Welche Farbe sollen die Linien der Balken haben?
fill = "skyblue") + # Wie sollen die Balken gefüllt sein?
geom_vline(xintercept = 4/n, col = "red")+ # Cut-off bei 4/n
labs(title = "Histogramm der Hebelwerte", x = "Hebelwerte") # Füge eigenen Titel und Achsenbeschriftung hinzu
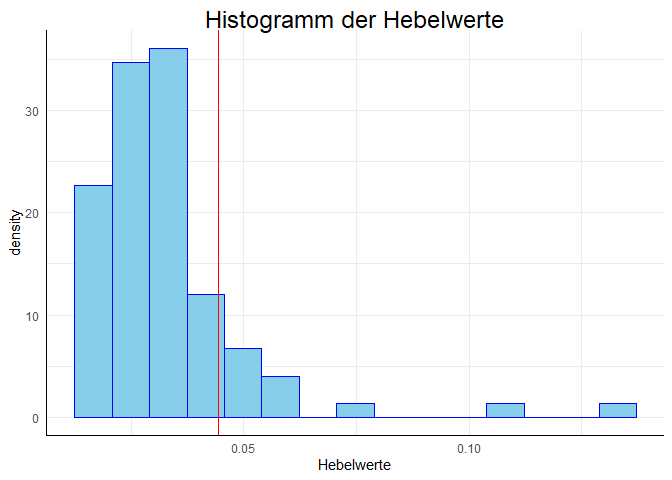
Cook’s-Distanz:
Hier nochmal der Code für das Histogramm der Cook’s-Distanz ohne die Styling-Elemente.
# Cook's Distanz
CD <- cooks.distance(model) # Cook's Distanz
df_CD <- data.frame(CD) # als Data.Frame für ggplot
ggplot(data = df_CD, aes(x = CD)) +
geom_histogram(aes(y =..density..), bins = 15)+
geom_vline(xintercept = 1, col = "red") # Cut-Off bei 1
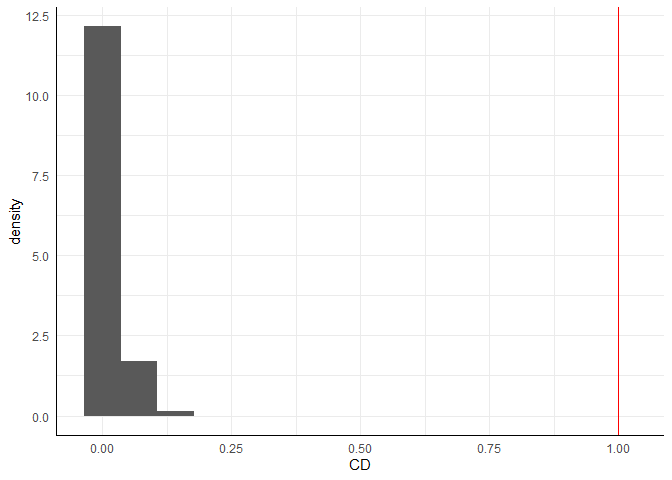
Hier finden Sie außerdem den Code zu den vier Grafiken, die den Einfluss von Hebelwerten und der Cook’s Distanz dargestellt haben.
par(mfrow=c(2,2),cex.axis = 1.1, cex.lab= 1.2, cex.main = 1.3, mar = c(5, 5, 2, 1),
bty="n",bg="white", mgp=c(2, 0.8, 0))
library(car)
X <- sort(rnorm(25))
y <- X + rnorm(25, sd = 0.3)
reg <- lm(y~X)
X_ <- c(X, 0)
y_ <- c(y, 0 + 0 + rnorm(1, sd = 0.3))
reg1 <- lm(y_ ~ X_)
plot(X_,y_, pch = 16, main = "A) kleine CD, kleiner Hebelwert", xlab = "X", ylab = "Y", xlim = c(-2,4), ylim = c(-2, 4))
abline(reg = reg, lwd = 3)
legend(x="topleft", legend = c("normal", "outlier"), col = c("black", "darkblue"), pch = 16, cex = 1.1, box.col = "grey")
X_ <- c(X, 4)
y_ <- c(y, 3.7 + rnorm(1, sd = 0.3))
reg1 <- lm(y_ ~ X_)
plot(X_,y_, pch = 16, main = "B) kleine CD, großer Hebelwert", xlab = "X", ylab = "Y", xlim = c(-2,4), ylim = c(-2, 4))
abline(reg = reg, lwd = 3)
abline(reg = reg1, lwd = 5, col = "blue")
points(X_[length(X)+1], y_[length(X)+1], pch = 15, cex = 2.8, col = "gold")
points(X_[length(X)+1], y_[length(X)+1], pch = 16, cex = 2, col = "darkblue")
legend(x="topleft", legend = c("normal", "outlier"), col = c("black", "darkblue"), pch = 16, cex = 1.1, box.col = "grey")
X_ <- c(X, 0)
y_ <- c(y, 0 + 3.7 + rnorm(1, sd = 0.3))
reg1 <- lm(y_ ~ X_)
plot(X_,y_, pch = 16, main = "C) große CD, kleiner Hebelwert", xlab = "X", ylab = "Y", xlim = c(-2,4), ylim = c(-2, 4))
abline(reg = reg, lwd = 3)
abline(reg = reg1, lwd = 5, col = "blue")
legend(x="topleft", legend = c("normal", "outlier"), col = c("black", "darkblue"), pch = 16, cex = 1.1, box.col = "grey")
points(X_[length(X)+1], y_[length(X)+1], pch = 15, cex = 2.8, col = "gold")
points(X_[length(X)+1], y_[length(X)+1], pch = 16, cex = 2, col = "darkblue")
X_ <- c(X, 4)
y_ <- c(y, 0 + rnorm(1, sd = 0.3))
reg1 <- lm(y_ ~ X_)
plot(X_,y_, pch = 16, main = "D) große CD, großer Hebelwert", xlab = "X", ylab = "Y", xlim = c(-2,4), ylim = c(-2, 4))
abline(reg = reg, lwd = 3)
abline(reg = reg1, lwd = 5, col = "blue")
legend(x="topleft", legend = c("normal", "outlier"), col = c("black", "darkblue"), pch = 16, cex = 1.1, box.col = "grey")
points(X_[length(X)+1], y_[length(X)+1], pch = 15, cex = 2.8, col = "gold")
points(X_[length(X)+1], y_[length(X)+1], pch = 16, cex = 2, col = "darkblue")
Appendix C
Mahalanobisdistanz
Die Mahalanobisdistanz (siehe z.B. Eid et al., 2017, ab Seite 707) ist ein Werkzeug, das zur Testung multivariater Normalverteilungen und zur Identifikation von multidimensionalen Ausreißern verwendet werden kann. Mit Hilfe der Mahalanobisdistanz wird die Entfernung vom zentralen Zentroiden bestimmt und mit Hilfe der Kovarianzmatrix gewichtet. Im Grunde kann man sagen, dass die Entfernung vom gemeinsamen Mittelwert über alle Variablen an der Variation in den Daten relativiert wird. Im eindimensionalen Fall ist die Mahalanobisdistanz nichts anderes als der quadrierte $z$-Wert, denn wir bestimmen dann die Mahalanobisdistanz einer Person $i$ via $$MD_i=\frac{(X_i-\bar{X})^2}{\sigma_X^2}=\left(\frac{X_i-\bar{X}}{\sigma_X}\right)^2=z^2.$$ Wir erkennen, dass wir hier den Personenwert relativ zur Streuung in den Daten betrachten. Nutzen wir nun mehrere Variablen und wollen multivariate Ausreißer interpretieren, so ist die Mahalanobisdistanz folgendermaßen definiert: $$MD_i=(\mathbf{X}_i-\bar{\mathbf{X}})’\Sigma^{-1}(\mathbf{X}_i-\bar{\mathbf{X}}).$$ Der Vektor der Mittelwertsdifferenz $\mathbf{X}_i-\bar{\mathbf{X}}$ wird durch die Kovarianzmatrix der Daten $\Sigma$ gewichtet. Sind zwei Variablen $X_1$ und $X_2$ positiv korreliert, so treten große (und auch kleine) Werte auf beiden Variablen gemeinsam häufig auf. Allerdings ist es unwahrscheinlich, dass große $X_1$ und kleine $X_2$-Werte (oder umgekehrt) gleichzeitig auftreten. Dies lässt sich anhand der Mahalanobisdistanz untersuchen. Wann ist nun ein Mahalanobisdistanzwert extrem? Dies können wir uns an einem zweidimensionalen Beispiel klarer machen. Dazu tragen wir in ein Diagramm die Ellipsen (Kurven) mit gleicher Mahalanobisdistanz ein, also jene Linien, welche in Bezug auf ihre Mahalanobisdistanz gleich weit vom Zentroiden entfernt liegen. Je dunkler die Kurven, desto weiter entfernt liegen diese Punkte vom Zentroiden (hier $(0,0)$) und desto unwahrscheinlicher sind diese Punkte in den Daten zu beobachten. In diesem Beispiel nehmen wir an, dass die Variablen positiv korreliert sind. Der Erstellungs-Code für die Grafik wird hier auch direkt eingeblendet (wenn es Ihnen mehr um den Inhalt geht, können Sie diesen auch überspringen).
library(ellipse)
mu1 <- c(0,0)
mu2 <- c(1,0)
S1 <- matrix(c(1,1,1,4),2,2)
#S2 <- matrix(c(4,0,0,1),2,2)
plot(0, col = "white", xlim = c(-3,3.5),ylim = c(-6,6), xlab = expression(X[1]), ylab = expression(X[2]),
main = "Kurven gleicher Wahrscheinlichkeit/\n Kurven gleicher Mahalanobisdistanz")
points(mu1[1],mu1[2],pch=19,col="green", cex = 3)
#points(mu2[1],mu2[2],pch=19, col = "blue", cex = 3)
# plotte einzelne Kovarianzmatrizen
color <- c("yellow","gold3", "gold3", "red")
i <- 1
for (q in c(0.5, 0.8,0.95,.99))
{
lines(ellipse(S1,level=q)[,1]+mu1[1],ellipse(S1,level=q)[,2]+mu1[2], col = color[i], lwd = 4)
#lines(ellipse(S2,level=q)[,1]+mu2[1],ellipse(S2,level=q)[,2]+mu2[2],col= color [i], lwd = 4)
i <- i +1
}
X <- ellipse(S1,level=0.8)[,1]+mu1[1]
Y <- ellipse(S1,level=0.8)[,2]+mu1[2]
i <- 25
lines(c(X[i], 0), c(Y[i], 0), lwd = 3, col = "blue")
points(X[i],Y[i], cex = 2, pch = 16)
l <- sqrt(X[i]^2 + Y[i]^2)
i <- 1
l2 <- sqrt(X[i]^2 + Y[i]^2)
lines(c(0, X[i]), c(0, Y[i]), lwd = 3)
arrows(x0=0,x1= X[i]*l/l2, y0=0,y1= Y[i]*l/l2, lwd = 3, col = "blue", code = 3, angle = 90, length = 0.1)
points(X[i],Y[i], cex = 2, pch = 16)
points(mu1[1],mu1[2],pch=19,col="green", cex = 3)
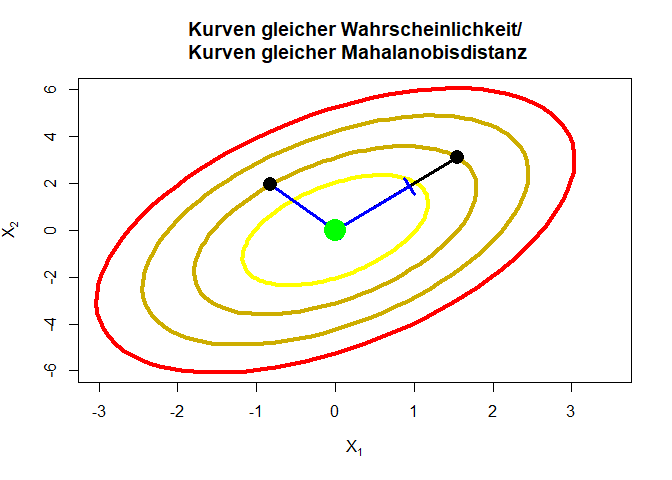
Der Ellipsenplot zeigt zwei multivariat-normalverteilte Variablen. Die Normalverteilungsdichte können wir uns dort wie einen Hügel vorstellen, der aus dem Bildschirm wächst, wobei hellere Kurven für eine größere Höhe des Hügels sprechen.
Der Zentroid ist hier in Hellgrün dargestellt. Außerdem sind zwei Punkte (in schwarz) eingezeichnet, die die gleiche Mahalanobisdistanz haben. Allerdings sehen wir, repräsentiert durch die blaue Linie, ebenfalls die euklidische Distanz. Die euklidische Distanz entspricht der Distanz, die wir nutzen, wenn wir ein Maßband anlegen würden (um bspw. ein Zimmer oder eben die Distanz der beiden Punkte vom hellgrünen Zentroiden auf dem Bildschirm zu vermessen). Das bedeutet, dass wenn wir in dieser Grafik (und damit in den Daten) die Kovariation der Variablen ignorieren würden, so würden wir den linken schwarzen Punkt und die blaue Linie als äquidistant (also gleich weit entfernt) annehmen. Berücksichtigen wir allerdings die positive Korrelation der Variablen, dann erkennen wir, dass die beiden schwarzen Punkte gleich wahrscheinlich sind und damit im Schnitt gleich häufig auftreten. Dies lässt sich folgendermaßen erklären: Wenn zwei Variablen positiv korreliert sind, sind extreme positive und extreme negative Werte auf beiden Variablen gleichzeitig recht wahrscheinlich, während es sehr unwahrscheinlich ist, dass die eine Variable eine hohe und die andere gleichzeitig eine niedrige Ausprägung aufweist (und umgekehrt). Entsprechend haben Wertekonstellationen, die sehr unwahrscheinlich sind (gegeben der Struktur in den Daten) eine große Mahalanobisdistanz - in der Grafik wächst also die Mahalanobisdistanz je dunkler die Kurve.
Außerdem gilt, dass bei multivariater Normalverteilung der Daten die Mahalanobisdistanz $\chi^2 (df=p)$-verteilt ist, wobei $p$ die Anzahl an Variablen ist. Der Vorteil hiervon ist, dass wir eine eindimensionale Verteilung untersuchen können, um ein Gefühl für multivariate Daten zu erhalten. Bspw. kann dann ein Histogramm oder ein Q-Q-Plot verwendet werden, um die Daten auf Normalverteilung zu untersuchen, bzw. es kann bspw. der Kolmogorov-Smirnov Test durchgeführt werden, um zu prüfen, ob die Mahalanobisdistanz $\chi^2(df=p)$-verteilt ist.
Der Befehl in R für die Mahalanobisdistanz ist mahalanobis. Hierfür sollten alle Prädiktoren aus einem Modell als Variablen in einen gemeinsamen Datensatz aufgenommen werden. Als Beispiel nehmen wir an dieser Stelle einfach die Depressivitaet und die Lebenszufriedenheit via Depression$... als unsere zwei Variablen auf und fassen diese zusammen zu einer Datenmatrix X mit dem Befehl cbind (column-bind), der die übergebenen Variablen als Spaltenvektoren zusammenfasst. mahalanobis braucht 3 Argumente: die Daten X, den gemeinsamen Mittelwert der Daten, den wir hier mit colMeans bestimmen (es wird jeweils der Mittelwert für die Spalten gebildet) sowie die Kovarianzmatrix der Daten cov(X), an welcher die Struktur relativiert werden soll (cor gibt die Korrelationsmatrix aus; hier wird allerdings die Kovarianzmatrix gebraucht - anhand der Korrelationsmatrix lässt sich jedoch die Beziehung der Variablen besser einordnen):
X <- cbind(Depression$Depressivitaet, Depression$Lebenszufriedenheit) # Datenmatrix mit Depressivitaet in Spalte 1 und Lebenszufriedenheit in Spalte 2
colMeans(X) # Spaltenmittelwerte (1. Zahl = Mittelwert der Depressivitaet, 2. Zahl = Mittelwert der Lebenszufriedenheit)
## [1] 5.655556 6.400000
cov(X) # Kovarianzmatrix von Depressivitaet und Lebenszufriedenheit
## [,1] [,2]
## [1,] 3.127216 -1.287640
## [2,] -1.287640 2.377528
cor(X) # zum Vergleich: die Korrelationsmatrix (die Variablen scheinen mäßig zu korrelieren, was unbedingt in die Ausreißerdiagnostik involviert werden muss)
## [,1] [,2]
## [1,] 1.0000000 -0.4722292
## [2,] -0.4722292 1.0000000
MD <- mahalanobis(x = X, center = colMeans(X), cov = cov(X))
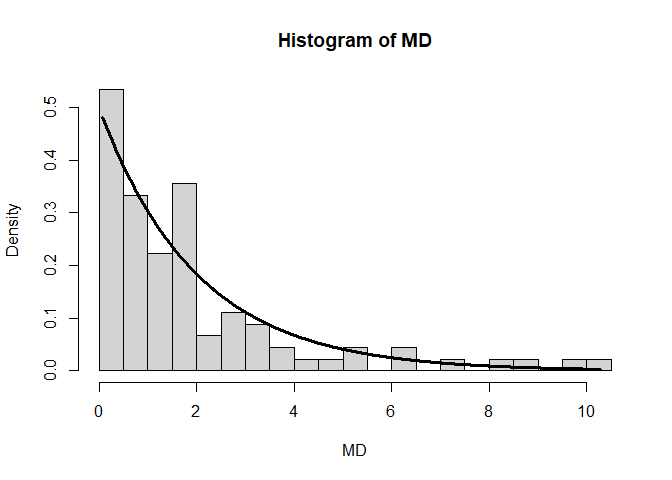
Zunächst beschäftigen wir uns mit der Überprüfung auf multivariate Normalverteilung. Die Verteilung der Mahalanobisdistanz widerspricht nicht (zu sehr) der Annahme auf multivariate Normalverteilung, da das Histogramm einigermaßen zur Dichte der $\chi^2(df=2)$-Verteilung passt:
hist(MD, freq = F, breaks = 15)
xWerte <- seq(from = min(MD), to = max(MD), by = 0.01)
lines(x = xWerte, y = dchisq(x = xWerte, df = 2), lwd = 3)
qqPlot(x = MD,distribution = "chisq", df = 2, pch = 16)
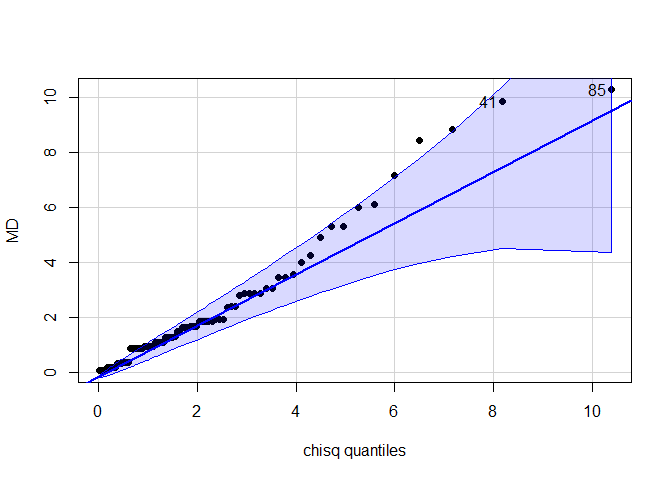
## [1] 85 41
Gleiches gilt auch für den Q-Q-Plot, der hier ebenfalls gegen die $\chi^2(df=2)$-Verteilung abgetragen wurde. Der Q-Q-Plot hat außerdem als Output die Fallnummer (Pbn-Nr) der extremeren Werte - hier Nummer 41 und 85. Insgesamt ist also zu sagen, dass die Mahalanobisdistanz nicht der multivariaten Normalverteilungsannahme widerspricht.
Da die Annahme der multivariaten Normalverteilung nicht verworfen wird, können wir jetzt einzelne extreme Werte auf Signifikanz testen. Zum Bestimmen der kritischen Distanz nehmen wir die $\chi^2$-Verteilung heran. Wir bestimmen mit qchisq den kritischen Wert, wobei als $p$-Wert hier meist ein $\alpha$-Niveau von .01 oder .001 herangezogen wird, damit wir nicht fälschlicherweise zu viele Werte aussortieren. Hierbei übergeben wir dem Argument p das $\alpha$-Niveau, lower.tail = F besagt, dass wir damit die obere Grenze meinen (also mit p gerade die Wahrscheinlichkeit meinen, einen extremeren Wert zu finden), df = 2 stellt die Freiheitsgrade ein (hier = 2, da 2 Variablen):
qchisq(p = .01, lower.tail = F, df = 2) # alpha = 1%
## [1] 9.21034
qchisq(p = .001, lower.tail = F, df = 2) # alpha = 0.1%
## [1] 13.81551
Nun können wir die Mahalanobisdistanz untersuchen:
MD
## [1] 1.29835776 1.85988286 1.68027868 0.38036881 1.93061376 5.31999173 1.29835776 0.89484803
## [9] 5.31999173 0.07401952 1.85988286 0.96581665 2.87179069 1.29835776 3.08398338 6.11730810
## [17] 0.96581665 0.33582974 1.93061376 3.99622396 0.96581665 1.85988286 1.93061376 3.57704668
## [25] 0.07401952 0.96581665 1.68027868 0.88006651 1.85988286 1.85988286 0.96581665 0.19639932
## [33] 0.07401952 2.79831527 0.19639932 1.64697702 2.42350418 0.89484803 0.96581665 0.19639932
## [41] 9.85316591 0.89484803 6.01723026 4.27802381 0.88006651 0.19639932 0.07401952 0.38036881
## [49] 8.84194961 1.64697702 0.19639932 1.29835776 2.87179069 4.92199266 7.18339325 0.19639932
## [57] 0.33582974 0.38036881 3.46236019 0.07401952 0.33582974 0.38036881 3.48368968 8.46422112
## [65] 0.19639932 0.88006651 0.07401952 0.88006651 1.09506856 1.50981570 0.38036881 0.07401952
## [73] 1.64697702 0.33582974 1.09506856 0.88006651 2.86848429 3.08398338 2.86848429 1.09506856
## [81] 2.39394112 1.50981570 1.09506856 2.42350418 10.28690861 1.33295604 0.19639932 0.88006651
## [89] 1.68027868 1.09506856
Hier alle Werte durch zugehen ist etwas lästig. Natürlich können wir den Vergleich mit den kritischen Werten auch automatisieren und z.B. uns nur diejenigen Mahalanobisdistanzwerte ansehen, die größer als der kritische Wert zum $\alpha$-Niveau von 1% sind. Wenn wir den which Befehl nutzen, so erhalten wir auch noch die Fallnummer (Pbn-Nr) der möglichen Ausreißer.
MD[MD > qchisq(p = .01, lower.tail = F, df = 2)] # Mahalanobiswerte > krit. Wert
## [1] 9.853166 10.286909
which(MD > qchisq(p = .01, lower.tail = F, df = 2)) # Pbn-Nr. 1%
## [1] 41 85
which(MD > qchisq(p = .001, lower.tail = F, df = 2)) # Pbn-Nr. 0.1%
## integer(0)
Auf dem $\alpha$-Niveau von 1% gäbe es 2 Ausreißer (Pbn-Nr = 41, 85), auf dem von 0.1% keinen.
Literatur
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden (5. Auflage, 1. Auflage: 2010). Weinheim: Beltz.
Pituch, K. A. & Stevens, J. P. (2016). Applied Multivariate Statistics for the Social Sciences (6th ed.). New York: Taylor & Francis.
- Blau hinterlegte Autor:innenangaben führen Sie direkt zur universitätsinternen Ressource.
](/media/header/frog_overencumbered.jpg)