Multiple Regression

Vorbereitende Schritte

Den Datensatz fb25 haben wir bereits über diesen Link heruntergeladen und können ihn über den lokalen Speicherort einladen oder Sie können ihn direkt mittels des folgenden Befehls aus dem Internet in das Environment bekommen. Im letzten Tutorial und den dazugehörigen Aufgaben haben wir bereits Änderungen am Datensatz durchgeführt, die hier nochmal aufgeführt sind, um den Datensatz auf dem aktuellen Stand zu haben:

#### Was bisher geschah: ----

# Daten laden
load(url('https://pandar.netlify.app/daten/fb25.rda'))

# Nominalskalierte Variablen in Faktoren verwandeln
fb25$hand_factor <- factor(fb25$hand,
                             levels = 1:2,
                             labels = c("links", "rechts"))
fb25$fach <- factor(fb25$fach,
                    levels = 1:5,
                    labels = c('Allgemeine', 'Biologische', 'Entwicklung', 'Klinische', 'Diag./Meth.'))
fb25$ziel <- factor(fb25$ziel,
                        levels = 1:4,
                        labels = c("Wirtschaft", "Therapie", "Forschung", "Andere"))
fb25$wohnen <- factor(fb25$wohnen, 
                      levels = 1:4, 
                      labels = c("WG", "bei Eltern", "alleine", "sonstiges"))
fb25$fach_klin <- factor(as.numeric(fb25$fach == "Klinische"),
                         levels = 0:1,
                         labels = c("nicht klinisch", "klinisch"))
fb25$ort <- factor(fb25$ort, levels=c(1,2), labels=c("FFM", "anderer"))
fb25$job <- factor(fb25$job, levels=c(1,2), labels=c("nein", "ja"))
fb25$unipartys <- factor(fb25$uni3,
                             levels = 0:1,
                             labels = c("nein", "ja"))

# Rekodierung invertierter Items
fb25$mdbf4_r <- -1 * (fb25$mdbf4 - 4 - 1)
fb25$mdbf11_r <- -1 * (fb25$mdbf11 - 4 - 1)
fb25$mdbf3_r <-  -1 * (fb25$mdbf3 - 4 - 1)
fb25$mdbf9_r <-  -1 * (fb25$mdbf9 - 4 - 1)
fb25$mdbf5_r <- -1 * (fb25$mdbf5 - 4 - 1)
fb25$mdbf7_r <- -1 * (fb25$mdbf7 - 4 - 1)

# Berechnung von Skalenwerten
fb25$wm_pre  <- fb25[, c('mdbf1', 'mdbf5_r', 
                        'mdbf7_r', 'mdbf10')] |> rowMeans()
fb25$gs_pre  <- fb25[, c('mdbf1', 'mdbf4_r', 
                        'mdbf8', 'mdbf11_r')] |> rowMeans()
fb25$ru_pre <-  fb25[, c("mdbf3_r", "mdbf6", 
                         "mdbf9_r", "mdbf12")] |> rowMeans()

# z-Standardisierung
fb25$ru_pre_zstd <- scale(fb25$ru_pre, center = TRUE, scale = TRUE)

Einfache lineare Regression

Im letzten Beitrag haben wir uns die einfache lineare Regression angesehen. Konkret ging es dabei darum, dass wir eine abhängige Variable (AV) durch genau eine unabhängige Variable vorhergesagt haben. Oder als Gleichung ausgedrückt:

$$ y_m = b_0 + b_1 x_m + e_m $$

In diesem Tutorial wollen nun untersuchen, ob die Lebenszufriedenheit (lz) durch den Neurotizismus (neuro) vorhergesagt wird. Die Annahme ist dabei, dass Personen, die neurotischer sind, angeben, weniger zufrieden mit ihrem Leben zu sein. Mit dem in R gelernten lm-Befehl können wir diese Hypothese einer Prüfung unterziehen.

# Einfache Regression
mod1 <- lm(lz ~ 1 + neuro, data = fb25)

# Ergebnisse
summary(mod1)

## 
## Call:
## lm(formula = lz ~ 1 + neuro, data = fb25)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -4.2471 -0.5846  0.2531  0.9529  2.3033 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  5.84733    0.29935  19.533  < 2e-16 ***
## neuro       -0.30013    0.08965  -3.348 0.000967 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.289 on 208 degrees of freedom
##   (1 observation deleted due to missingness)
## Multiple R-squared:  0.05113,	Adjusted R-squared:  0.04656 
## F-statistic: 11.21 on 1 and 208 DF,  p-value: 0.000967

Bei dieser Regression sehen wir, dass der Neurotizismus ein bedeutsamer Prädiktor der Lebenszufriedenheit ist. Dabei geht mit einem Unterschied von einer Einheit im Neurotizismus ein Unterschied von -0.3 Einheiten in der Lebenszufriedenheit einher. Der Determinationskoeffizient beträgt 0.05, was bedeutet, dass 5.11% der Varianz der Lebenszufriedenheit durch Neurotizismus erklärt werden. Wie wir auch schon gesehen hatten, entspricht dies der quadrierten Korrelation zwischen Neurotizismus und Lebenszufriedenheit und die Tests beider gegen 0 sind äquivalent:

cor.test(fb25$neuro, fb25$lz)

## 
## 	Pearson's product-moment correlation
## 
## data:  fb25$neuro and fb25$lz
## t = -3.3477, df = 208, p-value = 0.000967
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.35076363 -0.09358576
## sample estimates:
##        cor 
## -0.2261112

Multiple Regression

In diesem Beitrag geht es uns jetzt darum, diese Idee auf mehrere unabhängige Variablen zu erweitern. Das bedeutet, dass wir eine abhängige Variable durch mehrere unabhängige Variablen vorhersagen. Oder als Gleichung ausgedrückt:

$$ y_m = b_0 + b_1 x_{1m} + b_2 x_{2m} + \ldots + b_k x_{km} + e_m $$

$K$ entspricht dabei der Anzahl der Prädiktoren, die wir in das Modell aufgenommen haben. Neben dem Neurotizismus gehören noch die Verträglichkeit (vertr), die Extraversion (extra), die Gewissenhaftigkeit (gewis) und die Offenheit für neue Erfahrungen (offen) zu den Big Five Persönlichkeitsmerkmalen, die wir in der Umfrage zu Beginn des Semesters mit dem BFI-10 erhoben hatten. Wir können also ein Modell aufstellen, in dem wir das Vertrauen durch all diese Persönlichkeitsmerkmale vorhersagen.

# Multiple Regression
mod2 <- lm(lz ~ 1 + neuro + vertr + extra + gewis + offen, 
  data = fb25)

# Ergebnisse
summary(mod2)

## 
## Call:
## lm(formula = lz ~ 1 + neuro + vertr + extra + gewis + offen, 
##     data = fb25)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.2750 -0.7383  0.2575  0.9008  2.6470 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  2.02219    0.72525   2.788 0.005803 ** 
## neuro       -0.18554    0.09229  -2.010 0.045705 *  
## vertr        0.29081    0.10272   2.831 0.005105 ** 
## extra        0.35871    0.09481   3.783 0.000203 ***
## gewis        0.31307    0.10649   2.940 0.003662 ** 
## offen        0.02692    0.09428   0.286 0.775551    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.196 on 203 degrees of freedom
##   (2 observations deleted due to missingness)
## Multiple R-squared:  0.2017,	Adjusted R-squared:  0.182 
## F-statistic: 10.26 on 5 and 203 DF,  p-value: 8.844e-09

Interpretation der Gewichte

In der einfachen linearen Regression hatten wir gesagt, dass $b_1$ dem vorhergesagten Unterschied zwischen zwei Personen entspricht, die sich um eine Einheit in der unabhängigen Variable unterscheiden. Diese Interpretation lässt allerdings außer Acht, dass sich diese beiden Personen auch in anderen Eigenschaften unterscheiden können. Zum Beispiel unterscheiden sich diese beiden (fiktiven) Leute auch um ca. 0.42 Einheiten im Neurotizismus (extravertiertere Personen sind dabei weniger neurotisch). In der einfachen linearen Regression bleibt also unklar, ob der vorhergesagte Unterschied zwischen den Personen auch wirklich auf Unterschiede in unserem Prädiktor zurückzuführen ist, oder ob es auch an anderen, nicht berücksichtigten Eigenschaften liegen könnte.

In der multiplen Regression versuchen wir die Variablen aufzunehmen, die relevant sein könnten. Dadurch verändert sich auch die Interpretation des Regressionsgewichts: $b_1$ gibt jetzt den vorhergesagten Unterschied zwischen zwei Personen an, die sich um eine Einheit in der Extraversion unterscheiden, aber in allen anderen Prädiktoren gleich sind. Wir haben - so die häufig genutzte Ausdrucksweise - auf die anderen Big Five Merkmale “kontrolliert”.

Im Scatterplot wird dieser Unterschied deutlich:

# Gewichte aus der multiple Regression
b0 <- coef(mod2)[1]
b1 <- coef(mod2)[2]

# Scatterplot
plot(fb25$lz ~ fb25$neuro, 
     xlab = "Neurotizismus", 
     ylab = "Lebenszufriedenheit")

# Ergebnis aus der einfachen Regression
abline(mod1, col = "blue")

# Ergebnis der multiplen Regression
abline(a = b0, b = b1, col = "orange")

# Legende
legend("topright", legend = c("Einfache Reg.", "Multiple Reg."), col = c("blue", "orange"), lty = 1)

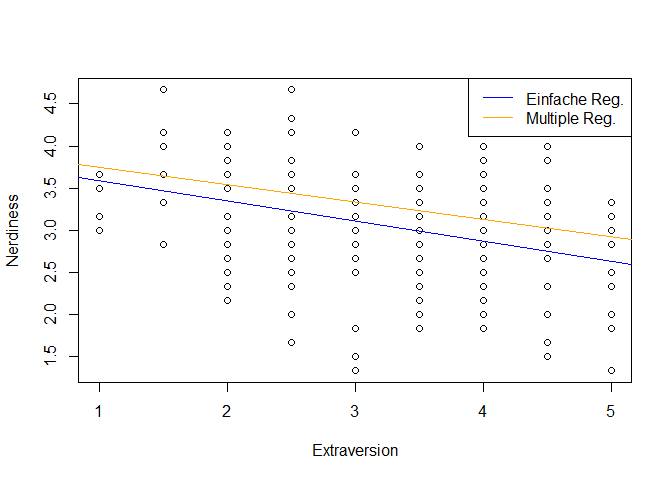
Der erste Unterschied, der zwischen den beiden Regressiongeraden auffällt ist, dass sie versetzt sind - also nicht beim gleichen Wert die y-Achse schneiden. Das liegt daran, dass nicht nur die Regressionsgewichte ihre Bedeutung verändern, sondern auch der Achsenabschnitt. Dieser ist jetzt der vorhergesagte Wert für die Lebenszufriedenheit, wenn alle Prädiktoren 0 sind:

$$ \widehat{y} = b_0 + b_1 \cdot 0 + b_2 \cdot 0 + b_3 \cdot 0 + b_4 \cdot 0 + b_5 \cdot 0 = b_0 $$

Wenn wir z.B. sehen wollen, wie sich der Neurotizismus auf das Vertrauen bei Personen auswirkt, die in ihren sonstigen Eigenschaften eher durchschnittlich sind, können wir einfach statt 0 die entsprechenden Mittelwerte in die Gleichung einsetzen. Mit unseren Kenntnissen über Matrixalgebra können wir das Ganze sogar relativ kurz halten:

# Achsenabschnitt bestimmen
X <- matrix(c(1, 0, 
  mean(fb25$vertr, na.rm = TRUE), 
  mean(fb25$extra, na.rm = TRUE), 
  mean(fb25$gewis, na.rm = TRUE), 
  mean(fb25$offen, na.rm = TRUE)))

a <- coef(mod2) %*% X

abline(a = a, b = b1, col = "darkgreen")

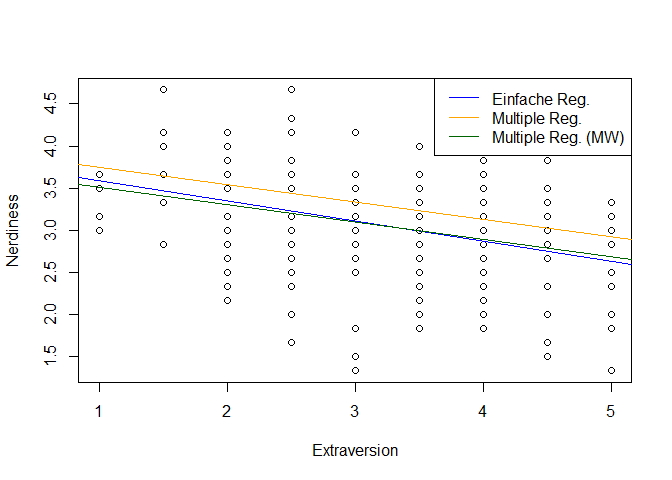
Der zweite Unterschied zwischen dieser neuen Linie (in Grün) und der Linie aus der einfachen linearen Regression (in Blau) zeigt, dass sie sich leicht im Steigungskoeffizienten unterscheiden. Das liegt eben genau daran, dass das Gewicht jetzt Unterschiede zwischen zwei Personen sind, die sich nur im Neurotizismus unterscheiden, aber sonst in allen (berücksichtigten) Belangen gleich sind.

Die anderen Gewichte können wir analog interpretieren:

summary(mod2)$coefficients |> round(3)

##             Estimate Std. Error t value Pr(>|t|)
## (Intercept)    2.022      0.725   2.788    0.006
## neuro         -0.186      0.092  -2.010    0.046
## vertr          0.291      0.103   2.831    0.005
## extra          0.359      0.095   3.783    0.000
## gewis          0.313      0.106   2.940    0.004
## offen          0.027      0.094   0.286    0.776

# Runden auf 3 Nachkommastellen für bessere Lesbarkeit

Dabei sehen wir, dass neben dem Neurotizismus auch die Verträglichkeit, Extraversion und Gewissenhaftigkeit bedeutsame Prädiktoren für die Lebenszufriedenheit sind. Das bedeutet, dass diese zwei Persönlichkeitsdimensionen einen bedeutsamen einzigartigen Beitrag zur Vorhersage der Lebenszufriedenheit leisten können. Im Umkehrschluss unterscheiden sich zwei Personen, die sich in der Offenheit um eine Einheit unterscheiden, aber hinsichtlich der anderen vier Dimensionen gleich sind, fast überhaupt nicht hinsichtlich des vorhergesagten Vertrauens.

Determinationskoeffizient

Um das Konzept des “einzigartigen Beitrags” noch einmal genauer zu beleuchten, kramen wir ein paar gute alte Venn-Diagramme aus der Schublade.

Hier sind erst einmal drei Variablen (unsere AV lz und zwei UVs neuro und vertr) dargestellt. Die Schnittmenge zwischen lz und neuro ist dabei z.B. das Ausmaß an Überlappung zwischen den beiden. Konzeptuell stellt diese Schnittmenge die Varianz dar, die zwischen den beiden geteilt wird. Diese Varianz hatten wir in der einfachen linearen Regression schon bestimmt:

summary(mod1)$r.squared

## [1] 0.05112629

Das Problem ist, dass wir dabei die gesamte Schnittmenge zwischen den beiden Variablen betrachten:

Ein Teil dieser Schnittmenge wird aber auch mit der Verträglichkeit geteilt. Für diesen Abschnitt wissen wir nicht, ob es Neurotizismus oder Verträglichkeit ist, die Unterschiede im Vertrauen bedingen. Schlimmer noch: wenn wir eine zweite einfache lineare Regression machen, wird dieser Abschnitt erneut “gezählt” - wir finden also den gleichen Effekt (zumindest in Teilen) doppelt:

Um das zu umgehen, nutzen wir die multiple Regression, um einfach die gesamte Fläche von lz zu bestimmen, die durch mindestens einen unserer Prädiktoren abgedeckt (also “aufgeklärt”) wird:

In der summary von mod2 hatten wir gesehen, wie groß dieser Anteil ist:

summary(mod2)$r.squared

## [1] 0.2016849

Im Falle dieses Modells sind es nicht nur zwei, sondern insgesamt fünf Prädiktoren, was das Venn-Diagramm allerdings ein wenig unübersichtlich machen würde. Die Gesamtheit der aufgeklärten Varianz (also der Anteil der Varianz in der AV, den unsere UVs insgesamt aufklären können) wird in der summary mittels $F$-Test geprüft:

## [...]
##  Multiple R-squared:  0.2017,	Adjusted R-squared:  0.182 
## F-statistic: 10.26 on 5 and 203 DF,  p-value: 8.844e-09

Wie wir anhand der Formel dieses Tests erkennen können, wird hier das Verhältnis von aufgeklärter zu nicht aufgeklärter Varianz geprüft:

$$ F = \frac{n - k - 1}{k} \cdot \frac{R^2}{1 - R^2} $$

Die Zählerfreiheitsgrade numdf sind dabei ungünstigerweise $k$ und die Nennerfreiheitsgrade dendf sind $n - k - 1$ - also genau das Gegenteil von dem, was aufgrund dieser Formel für $F$ zu erwarten gewesen wäre.

Modellvergleiche

Neben den Tests der einzelnen Regressionsgewichte und dem Test des gesamten $R^2$ können wir auch spezifische Modelle mit einander vergleichen. Dabei muss ein Modell immer eine eingeschränkte Fassung ($e$) eines anderen Modells ($u$) sein. Die beiden Modelle, die wir schon gesehen haben, stehen in genau so einer Relation: Die einfache lineare Regression mit Gewissenhaftigkeit als Prädiktor (mod1) ist eine eingeschränkte Version der multiplen Regression, in der wir alle Big Five Merkmale als Prädiktoren aufgenommen hatten (mod2), weil es eine Teilmenge der Prädiktoren enthält.

In solchen Fällen können wir über den Vergleich von $R^2_e$ und $R^2_u$ untersuchen, welchen Zugewinn in der Vorhersagekraft die zusätzlichen Prädiktoren so mitbringen. Rein numerisch:

# R2 durch Gewissenhaftigkeit
R2e <- summary(mod1)$r.squared

# R2 durch alle Big Five
R2u <- summary(mod2)$r.squared

R2e

## [1] 0.05112629

R2u

## [1] 0.2016849

# Inkrementelles R2 der vier anderen Prädiktoren
R2u - R2e

## [1] 0.1505586

In diesem Inkrement wird der Teil der Varianz dargestellt, den die anderen vier Big Five Merkmale zusätzlich zum Neurotizismus aufklären können. Dabei ist es wichtig zu bedenken, dass der Anteil, der durch Gemeinsamkeiten zwischen Neurotizismus und den anderen vier Merkmalen aufgeklärt wird, im ersten Schritt nur dem Neurotizismus zugute geschrieben wurde (das zweite Venn-Diagramm). Dieses Inkrement können wir natürlich auch testen:

# Test des inkrementellen R2
anova(mod1, mod2)

## Error in anova.lmlist(object, ...): models were not all fitted to the same size of dataset

Allerdings stoßen wir hier auf eine häufig vorkommende Fehlermeldung.

Intermezzo: Datenaufbereitung mit fehlenden Werten

Der von der anova-Funktion ausgegebene Fehler ## Error in anova.lmlist(object, ...): models were not all fitted to the same size of dataset zeigt, dass wir Modelle nur dann vergleichen können, wenn diese auf den gleichen Daten basieren. Das ist nicht gegeben, wenn es Personen gab, die z.B. zwar für Gewissenhaftigkeit und Vertrauen Beobachtungen hatten, für mindestens eine der anderen vier Dimensionen aber nicht. Im Beitrag zu Zusammenhangsmaßen hatten wir den Unterschied zwischen paarweisem und listenweisem Fallausschluss schon detaillierter besprochen. Im Fall mehrerer Regressionsmodelle müssen wir also vorab sicherstellen, dass wir adäquaten listenweisen Fallausschluss betreiben, wenn wir die Modelle direkt vergleichen wollen:

# Daten ohne fehlende Werte auf den relevanten Variablen
mr_dat <- na.omit(fb25[, c("lz", "neuro", "vertr", "extra", "gewis", "offen")])

Wenn wir in R Modelle aktualisieren wollen, können wir mit update arbeiten, statt die gesamte Syntax erneut eingeben zu müssen:

# Modell 1, updated
mod1_new <- update(mod1, data = mr_dat)

# Modell 2, updated
mod2_new <- update(mod2, data = mr_dat)

Modellvergleiche, Teil 2

Mit den aktualisierten Modellen können wir jetzt den Vergleich erneut probieren:

# Test des inkrementellen R2
anova(mod1_new, mod2_new)

## Analysis of Variance Table
## 
## Model 1: lz ~ 1 + neuro
## Model 2: lz ~ 1 + neuro + vertr + extra + gewis + offen
##   Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
## 1    207 344.87                                  
## 2    203 290.27  4    54.599 9.5459 4.313e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Die Ergebnistabelle gibt uns verschiedene Informationen. Zunächst wird uns noch einmal gesagt, welche Modelle wir hier eigentlich vergleichen. Die Ergebnistabelle besteht dann aus folgenden Informationen:

• Res.Df: Die Residualfreiheitsgrade ($n-k-1$)
• RSS: Die Quadratsumme der Residuen ( Residual Sum of Squares )
• Df: Der Unterschied in den Freiheitsgraden zwischen den beiden Modellen ($k_u - k_e$), hier 4, weil wir vier zusätzliche Prädiktor aufgenommen haben
• Sum of Sq: Die Quadratsumme der Residuen, die durch die zusätzlichen Prädiktoren aufgeklärt wird
• F: Der $F$-Wert
• Pr(>F): Der p-Wert des $F$-Tests

In diesem Fall ist der Modellvergleich statistisch bedeutsam, was bedeutet, dass die zusätzlichen Prädiktoren in der multiplen Regression einen statistisch relevanten Anteil der Varianz dem Vertrauen aufklären können.

Wenn wir für spezifische (Gruppen von) Prädiktoren wissen wollen, wie viel einzigartigen Beitrag sie in der Vorhersage unserer AV haben, können wir dieses Vorgehen nutzen, um die Anteile zu isolieren. Zum Beispiel, wenn wir den Anteil identifizieren wollen, den Neurotizismus aufklärt, der nicht auch durch andere Big Five Persönlichkeitsmerkmale aufgeklärt wird, können wir ein Modell aufstellen, in dem wir alle anderen Prädiktoren als eingeschränkte Version des Modells aufnehmen:

# Modell 3
mod3 <- lm(lz ~ vertr + extra + gewis + offen, data = mr_dat)

# Test des inkrementellen R2
anova(mod3, mod2_new)

## Analysis of Variance Table
## 
## Model 1: lz ~ vertr + extra + gewis + offen
## Model 2: lz ~ 1 + neuro + vertr + extra + gewis + offen
##   Res.Df    RSS Df Sum of Sq     F Pr(>F)  
## 1    204 296.05                            
## 2    203 290.27  1    5.7796 4.042 0.0457 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# Inkrementelles R2
summary(mod2_new)$r.squared - summary(mod3)$r.squared

## [1] 0.01589543

Als Venn-Diagramm ausgedrückt, prüfen wir so den hier hell markierten Abschnitt gegen 0 (nur, dass Sie sich die anderen drei Prädiktoren dazu denken müssen):

Das Ergebnis zeigt, dass Neurotizismus einen statistisch relevanten Anteil der Varianz in dem Vertrauen aufklären kann, der nicht auch durch die anderen Big Five Persönlichkeitsmerkmale aufgeklärt wird.

Voraussetzungen der multiplen Regression

Im Lehrbuch von Eid, Gollwitzer und Schmitt (2015) finden Sie auf S.720 eine Übersicht über die fünf zentralen Voraussetzungen der multiplen Regression (diese gelten in etwas simplerer Form auch für die einfache lineare Regression). Diese sind:

1. Korrekte Spezifikation des Modells
2. Messfehlerfreiheit der unabhängigen Variablen
3. Unabhängigkeit der Residuen
4. Homoskedastizität der Residuen
5. Normalverteilung der Residuen

In diesem Beitrag gucken wir uns im Folgenden noch grob an, wie man diese Voraussetzungen prüfen kann. In den meisten Fällen ist das “was mache ich, wenn die Voraussetzungen nicht erfüllt sind?” aber eine Frage mit relativ komplexen Antworten, die wir im Verlauf der (hoffentlich vielen!) weiteren Statistik Module Schritt für Schritt beantworten werden. An manchen Stellen werden wir also auf den einen oder anderen Beitrag verweisen, aber Details sprengen den Rahmen dieses sowieso schon viel zu langen Beitrags.

Korrekte Spezifikation des Modells

Die korrekte Spezifikation ist eine sehr vielseitige Voraussetzung, die eher konzeptueller und weniger statischer Natur ist. Generell wird davon ausgegangen, dass in unserem Regressionsmodell alle relevanten Prädiktoren aufgenommen wurden und dass die funktionale Form des Zusammenhangs korrekt abgebildet ist. Im Normalfall gehen wir zunächst von Linearität aus (auch wenn wir in Statistik II noch andere Formen untersuchen und testen werden). Im Beitrag zur einfachen linearen Regression hatten wir schon mit Scatterplots und LOESS-Linien geschaut, inwiefern diese Annahme realistisch ist:

plot(mr_dat$lz ~ mr_dat$neuro, 
     xlab = "Neurotizismus", 
     ylab = "Lebenszufriedenheit")
lines(loess.smooth(mr_dat$neuro, mr_dat$lz), col = "blue")
abline(mod1_new, col = "red")

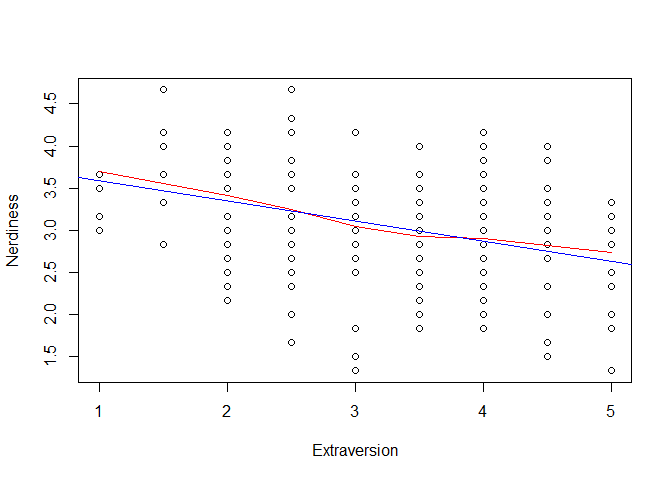
Das können wir natürlich auch für die anderen vier Prädiktoren untersuchen:

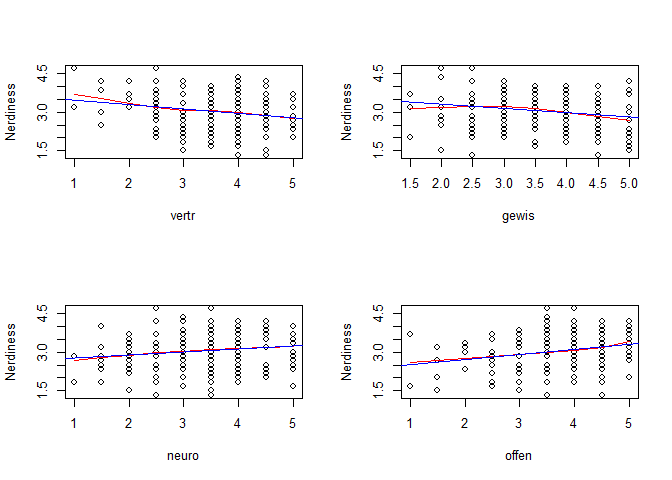
Über diese Annahme der Linearität hinaus, nehmen wir z.B. auch an, dass der Zusammenhang zwischen Neurotizismus und Lebenszufriedenheit über alle Ausprägungen des Neurotizismus hinweg gleich ist. Sollte dem nicht so sein, würden wir von moderierter Regression sprechen.

Am schwierigsten ist es, festzustellen, ob alle relevanten Prädiktoren aufgenommen wurden. In der Praxis ist das oft ein iterativer Prozess, bei dem sowohl theoriegeleitet als auch automatisiert vorgegangen werden kann. Auch das sehen wir in Statistik II noch genauer.

Messfehlerfreiheit der unabhängigen Variablen

Generell wird bei der Regression davon ausgegangen, dass die unabhängigen Variablen ohne Fehler gemessen wurden. Gerade in der Psychologie ist das aber meistens eine außerordentlich unrealistische Annahme. Durch die Verletzung dieser Annahme wird der Zusammenhang zwischen zwei Variablen systematisch unterschätzt, sodass die Regressionsgewichte und Korrelationen, die wir finden, kleiner erscheinen, als sie sind. In der abhängigen Variable ist das meist weniger dramatisch, weil Messfehler im Residuum landen, aber weil die unabhängigen Variablem im Rahmen der Regression nicht in verschiedene Varianzkomponenten unterteilt werden, wird davon ausgegangen, dass die Varianz, die wir zur Verfügung haben, potentiell auch in der Lage ist die abhängige Variable aufzuklären.

In der Praxis wird eine Einschätzung bezüglich des Ausmaß des Messfehlers durch Reliabilitätsmaße wie McDonalds Omega oder Cronbachs Alpha vorgenommen. Mehr dazu erfahren Sie z.B. in der Lehre zu Diagnostik - ein paar Schritte in R finden Sie aber auch direkt in diesem Beitrag beschrieben.

Unabhängigkeit der Residuen

Wie auch bei vielen anderen inferenzstatistischen Verfahren, die wir schon besprochen hatten, ist bei der Regression eine Voraussetzung, dass die Beobachtungen voneinander unabhängig sind. Spezifischer gesagt, sollen die Beobachtungen über die Variablen, die wir berücksichtigen hinaus unabhängig voneinander sein (also die Residuen). Wie schon bei den t-Tests gesehen, ist auch das häufig eine Annahme, die sich nicht ausschließlich statistisch prüfen lässt, sondern durch das Studiendesign und die Art der Datenerhebung beeinflusst wird. Generell wird bei der Bestimmung von Standardfehlern davon ausgegangen, dass alle Werte die Ausprägungen von Zufallsvariablen sind. Wenn dieser Zufallsprozess aber systematische Verzerrungen enthält (z.B. dadurch, dass wir die gleichen Personen mehrmals erhoben haben), wird das Ausmaß der Unterschiede zwischen Personen unterschätzt. Die Standardabweichung des Merkmals in der Population war z.B. beim $t$-Test direkt in die Berechnung des Standardfehlers eingegangen, was verdeutlichen sollte, warum eine Verschätzung dieser Unterschiede sich in Verzerrung der Standardfehler und somit auch der $p$-Werte niederschlägt.

Häufig kommt es in der Psychologie zur Verletzung dieser Annahme, wenn wir Gruppen von Personen erheben (z.B. Schüler:innen in Schulklassen, Patient:innen in Kliniken, usw.). Wenn wir die Quelle der Abhängigkeit aufgrund unseres Studiendesigns identifizieren können, können wir sog. Mehrebenenmodelle nutzen. Eine Einführung in die Grundideen und Umsetzungen, finden Sie z.B. in den Beiträgen aus dem KliPPs und dem Psychologie Master.

Homoskedastizität der Residuen

Beim $t$-Test hatten wir angenommen, dass die Varianz in allen Gruppen gleich ist, um die Standardfehler zu berechnen. In der multiple Regression ist die Definition von “Gruppe” etwas schwammig, weil theoretisch jede mögliche Kombination von Ausprägungen der unabhängigen Variablen eine “Gruppe” darstellt. Weil die Kombinationen von unabhängigen Variablen in der Regression durch die Regressionsgleichung in vorhergesagte Werte übersetzt werden, nehmen wir also an, dass die Varianz der Werte um die vorhergesagten Werte herum konstant ist. Oder anders ausgedrückt: Wir nehmen an, dass die Varianz der Residuen für alle Werte von $\widehat{y}$ die gleiche ist.

Theoretisch könnten wir das mit einem Streupunktdiagramm der Residuen gegen die vorhergesagten Werte sehen:

pred <- predict(mod2_new)
res <- resid(mod2_new)

plot(pred, res, 
     xlab = "Vorhergesagte Werte", 
     ylab = "Residuen")

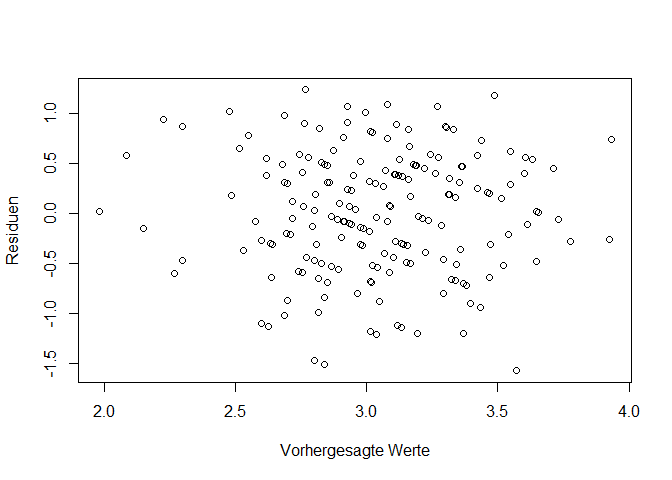
Dabei müssten die Residuen für alle Werte der x-Achse gleichmäßig entlang der y-Achse streuen. Leider ist das etwas schwer einzuschätzen, weil nicht alle Wertekombinationen gleich häufig vorkommen und somit bestimmte Regionen des Plots weniger dicht besiedelt sind, wodurch es so wirken kann, als sei dort die Varianz niedriger. Um uns das Vorgehen etwas zu vereinfachen gibt es zwei Möglichkeiten: die Darstellung der Wurzel der standardisierten Residuen in Abhängigkeit von den vorhergesagten Werten und den Breusch-Pagan Test. Ersteres wird direkt ohne Zusatzpaket in R zur Verfügung gestellt:

plot(mod2_new, which = 3)

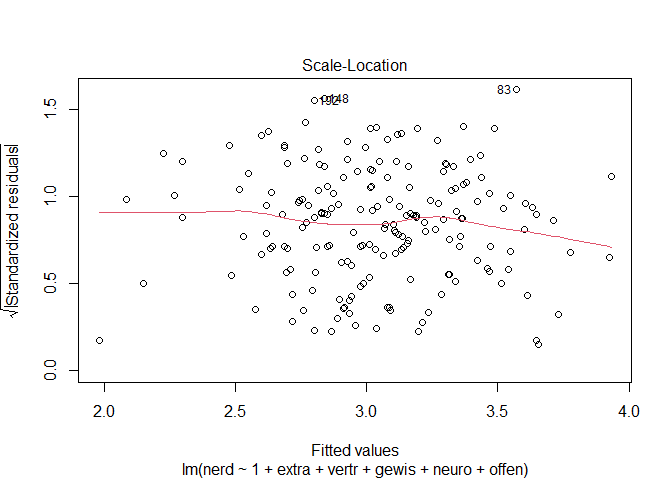
R liefert für jedes Regressionsmodell vier diagnostische Plots, um die Qualität des Modells zu beurteilen. Der dritte dieser Plots ist es, der für uns hier von Interesse ist. Wenn die Varianz der Residuen konstant ist, sollten die Wurzel der standardisierten Residuen in Abhängigkeit von den vorhergesagten Werten keine systematischen Muster aufweisen und die eingezeichnete Linie sollte relativ horizontal verlaufen.

Über die visuelle Inspektion hinaus haben wir auch noch die Möglichkeit, die Homoskedastizität der Residuen mit dem Breusch-Pagan Test zu prüfen. Dieser ist im car-Paket implementiert:

car::ncvTest(mod2_new)

## Non-constant Variance Score Test 
## Variance formula: ~ fitted.values 
## Chisquare = 5.48482, Df = 1, p = 0.019182

Wie bei allen Voraussetzungstests, wird hier die Nullhypothese geprüft, dass die Annahme hält. Bedeutsame Ergebnisse zeigen also eine deutliche Verletzung der Annahme an. An dieser Stelle sei noch einmal deutlich darauf hingewiesen, dass nicht-bedeutsame Ergebnisse nicht bedeuten, dass die Annahme erfüllt ist. Insbesondere durch das klassische Nullhypothesentesten, was in diesem Fall betrieben wird, ist die Prüfung der Annahmen als eher wenig streng anzusehen.

Normalverteilung der Residuen

Die letzte Voraussetzung haben wir bei anderen Tests schon des Öfteren geprüft. Wie auch bei $t$-Tests und der Korrelation können wir für die Prüfung der Normalverteilung der Residuen den QQ-Plot nutzen. Damit wir direkt eine Idee davon haben, wie stark die Abweichung von der Diagonale ausfällt, können wir den qqPlot aus dem car-Paket nutzen:

car::qqPlot(mod2_new)

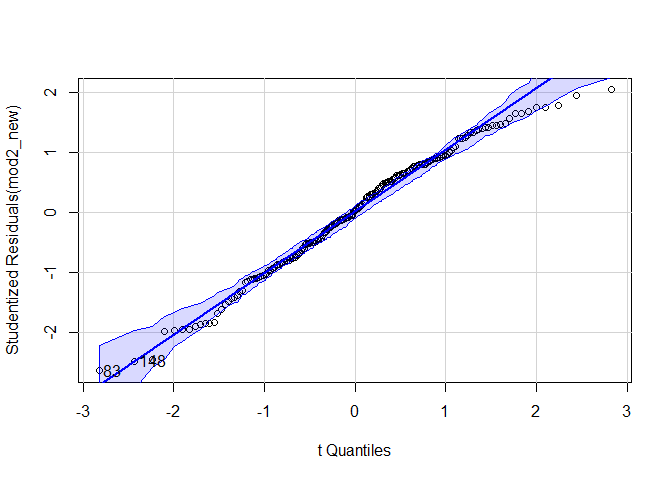
## 108 146 
## 107 144

Auch den Shapiro-Wilk-Test haben wir schon in anderen Beiträgen genutzt:

shapiro.test(resid(mod2_new))

## 
## 	Shapiro-Wilk normality test
## 
## data:  resid(mod2_new)
## W = 0.96177, p-value = 2.038e-05

Während der QQ-Plot leichte Verletzungen der Normalverteilungsannahme anzeigt, deutet das signifikante Ergebnis des Shapiro-Wilk-Tests auf eine relevante Verletzung der Annahme hin.

In Fällen, in denen wir leichte Verletzungen von der Normalverteilungsannahme feststellen, können wir verschiedene Wege nutzen, um unsere Schätzer ein wenig robuster zu machen. In Fällen, in denen wir von vornherein davon ausgehen müssen, dass die Residuen gar nicht normalverteilt sein können (z.B. weil die abhängige Variable nur zwei Ausprägungen hat), können wir andere Verteilungen annehmen. Ein klassisches Beispiel dafür ist die logistische Regression, welche in den beiden Masterstudiengängen noch einmal aufgegriffen werden wird.

Abschluss

Wie in den letzten Abschnitten zu den Voraussetzungen deutlich geworden ist, gibt es für die multiple Regression diverse Erweiterungsmöglichkeiten. Es ist von Vorteil, sich ein mal intensiv mit den Grundideen der multiple Regression auseinanderzusetzen, weil viele moderne Auswertungsverfahren letztlich genau solche Erweiterungen sind. Dabei ist egal ob logistische Regression, Mehrebenenmodelle, Strukturgleichungsmodelle oder moderne Machine-Learning-Verfahren - die Grundideen und die Interpretation der Parameter ähneln sich doch sehr.

Literatur

Eid, M., Gollwitzer, M., & Schmitt, M. (2015). Statistik und Forschungsmethoden (4., überarbeitete Auflage). Springer