Vorbereitung
Laden Sie zunächst den Datensatz fb25 von der pandar-Website und führen Sie die Ergänzungen vor, die in zurückliegenden Tutorials vorgenommen wurden.
#### Was bisher geschah: ----
# Daten laden
load(url('https://pandar.netlify.app/daten/fb25.rda'))
# Nominalskalierte Variablen in Faktoren verwandeln
fb25$hand_factor <- factor(fb25$hand,
levels = 1:2,
labels = c("links", "rechts"))
fb25$fach <- factor(fb25$fach,
levels = 1:5,
labels = c('Allgemeine', 'Biologische', 'Entwicklung', 'Klinische', 'Diag./Meth.'))
fb25$ziel <- factor(fb25$ziel,
levels = 1:4,
labels = c("Wirtschaft", "Therapie", "Forschung", "Andere"))
fb25$wohnen <- factor(fb25$wohnen,
levels = 1:4,
labels = c("WG", "bei Eltern", "alleine", "sonstiges"))
fb25$fach_klin <- factor(as.numeric(fb25$fach == "Klinische"),
levels = 0:1,
labels = c("nicht klinisch", "klinisch"))
fb25$ort <- factor(fb25$ort, levels=c(1,2), labels=c("FFM", "anderer"))
fb25$job <- factor(fb25$job, levels=c(1,2), labels=c("nein", "ja"))
fb25$unipartys <- factor(fb25$uni3,
levels = 0:1,
labels = c("nein", "ja"))
# Rekodierung invertierter Items
fb25$mdbf4_r <- -1 * (fb25$mdbf4 - 4 - 1)
fb25$mdbf11_r <- -1 * (fb25$mdbf11 - 4 - 1)
fb25$mdbf3_r <- -1 * (fb25$mdbf3 - 4 - 1)
fb25$mdbf9_r <- -1 * (fb25$mdbf9 - 4 - 1)
fb25$mdbf5_r <- -1 * (fb25$mdbf5 - 4 - 1)
fb25$mdbf7_r <- -1 * (fb25$mdbf7 - 4 - 1)
# Berechnung von Skalenwerten
fb25$wm_pre <- fb25[, c('mdbf1', 'mdbf5_r',
'mdbf7_r', 'mdbf10')] |> rowMeans()
fb25$gs_pre <- fb25[, c('mdbf1', 'mdbf4_r',
'mdbf8', 'mdbf11_r')] |> rowMeans()
fb25$ru_pre <- fb25[, c("mdbf3_r", "mdbf6",
"mdbf9_r", "mdbf12")] |> rowMeans()
# z-Standardisierung
fb25$ru_pre_zstd <- scale(fb25$ru_pre, center = TRUE, scale = TRUE)
Prüfen Sie zur Sicherheit, ob alles funktioniert hat:
dim(fb25)
## [1] 211 56
str(fb25)
## 'data.frame': 211 obs. of 56 variables:
## $ mdbf1 : num 3 3 3 4 4 3 3 3 2 3 ...
## $ mdbf2 : num 3 2 3 1 3 3 3 2 3 2 ...
## $ mdbf3 : num 1 2 2 3 1 1 1 1 3 3 ...
## $ mdbf4 : num 1 2 2 1 1 1 1 1 1 2 ...
## $ mdbf5 : num 1 2 2 2 1 1 1 3 2 3 ...
## $ mdbf6 : num 3 2 3 1 3 2 1 3 4 2 ...
## $ mdbf7 : num 1 3 2 3 2 2 2 4 2 3 ...
## $ mdbf8 : num 3 3 3 4 4 3 3 3 3 3 ...
## $ mdbf9 : num 1 3 2 2 1 4 2 1 3 4 ...
## $ mdbf10 : num 3 3 2 1 3 3 2 2 3 3 ...
## $ mdbf11 : num 1 2 2 1 1 1 2 1 3 2 ...
## $ mdbf12 : num 3 2 2 3 3 2 2 3 2 1 ...
## $ time_pre : num 43 55 79 53 28 35 44 29 30 52 ...
## $ lz : num 5 3 5 6 5.8 5.2 4.6 4.8 6.8 2.6 ...
## $ extra : num 3.5 4 2.5 4 4.5 3 2.5 2.5 3.5 2 ...
## $ vertr : num 4 3 4 3 2 4.5 2.5 4 3 2.5 ...
## $ gewis : num 2.5 4.5 3.5 4.5 3 3.5 2.5 2 4 5 ...
## $ neuro : num 2 2 3 4 4 5 4.5 1 4.5 5 ...
## $ offen : num 2.5 4.5 4.5 5 4.5 4.5 3.5 4 5 4.5 ...
## $ prok : num 2.6 2.5 2.8 3 2.5 2.9 3 3.4 3.2 2.7 ...
## $ trust : num 3.33 3.83 3.83 3.67 3.67 ...
## $ uni1 : num 0 0 1 0 0 0 0 0 0 1 ...
## $ uni2 : num 1 1 1 1 1 1 1 1 1 1 ...
## $ uni3 : num 1 0 0 1 0 1 0 0 0 0 ...
## $ uni4 : num 0 0 0 0 0 0 0 1 0 1 ...
## $ sicher : int 3 4 4 4 4 3 NA 3 4 3 ...
## $ angst : int 2 2 3 4 3 3 2 2 2 4 ...
## $ fach : Factor w/ 5 levels "Allgemeine","Biologische",..: 4 4 4 4 4 4 4 2 2 2 ...
## $ ziel : Factor w/ 4 levels "Wirtschaft","Therapie",..: 2 2 2 2 2 2 2 1 1 3 ...
## $ wissen : int NA 3 5 NA NA NA 4 NA 3 5 ...
## $ therap : int NA 5 5 NA NA NA 5 NA 5 4 ...
## $ lerntyp : int 3 3 3 3 1 3 1 3 2 1 ...
## $ hand : int 2 2 2 2 2 2 2 2 1 2 ...
## $ job : Factor w/ 2 levels "nein","ja": 2 1 2 2 1 1 1 1 2 2 ...
## $ ort : Factor w/ 2 levels "FFM","anderer": 1 2 2 1 2 1 1 2 2 1 ...
## $ ort12 : int 2 3 1 3 2 2 2 1 1 1 ...
## $ wohnen : Factor w/ 4 levels "WG","bei Eltern",..: 3 2 3 1 4 3 1 2 4 1 ...
## $ attent_pre : num 4 5 4 5 5 5 5 5 5 4 ...
## $ gs_post : num 3 NA 2.75 3.25 3 3.25 NA 3 2.75 2.25 ...
## $ wm_post : num 3.25 NA 2.75 3.25 2.75 3.25 NA 2.25 1.75 2.25 ...
## $ ru_post : num 2.25 NA 2.25 2.75 2.25 2.5 NA 2 2 2.75 ...
## $ time_post : num 18 NA 71 17 21 51 NA 31 27 34 ...
## $ attent_post: num 5 NA 5 5 5 5 NA 5 5 5 ...
## $ hand_factor: Factor w/ 2 levels "links","rechts": 2 2 2 2 2 2 2 2 1 2 ...
## $ fach_klin : Factor w/ 2 levels "nicht klinisch",..: 2 2 2 2 2 2 2 1 1 1 ...
## $ unipartys : Factor w/ 2 levels "nein","ja": 2 1 1 2 1 2 1 1 1 1 ...
## $ mdbf4_r : num 4 3 3 4 4 4 4 4 4 3 ...
## $ mdbf11_r : num 4 3 3 4 4 4 3 4 2 3 ...
## $ mdbf3_r : num 4 3 3 2 4 4 4 4 2 2 ...
## $ mdbf9_r : num 4 2 3 3 4 1 3 4 2 1 ...
## $ mdbf5_r : num 4 3 3 3 4 4 4 2 3 2 ...
## $ mdbf7_r : num 4 2 3 2 3 3 3 1 3 2 ...
## $ wm_pre : num 3.5 2.75 2.75 2.5 3.5 3.25 3 2 2.75 2.5 ...
## $ gs_pre : num 3.5 3 3 4 4 3.5 3.25 3.5 2.75 3 ...
## $ ru_pre : num 3.5 2.25 2.75 2.25 3.5 2.25 2.5 3.5 2.5 1.5 ...
## $ ru_pre_zstd: num [1:211, 1] 0.976 -0.893 -0.145 -0.893 0.976 ...
## ..- attr(*, "scaled:center")= num 2.85
## ..- attr(*, "scaled:scale")= num 0.669
Der Datensatz besteht aus 211 Zeilen (Beobachtungen) und 56 Spalten (Variablen). Falls Sie bereits eigene Variablen erstellt haben, kann die Spaltenzahl natürlich abweichen.
Aufgabe 1
Welche der fünf Persönlichkeitsdimensionen Extraversion (extra), Verträglichkeit (vertr), Gewissenhaftigkeit (gewis), Neurotizsimus (neuro) und Offenheit für neue Erfahrungen (offen) zeigt den höchsten linearen Zusammenhang mit der Lebenszufriedenheit (lz)?
- Erstellen Sie für jeden Zusammenhang je ein Streudiagramm.
Lösung
extra:
plot(fb25$extra, fb25$lz, xlim = c(0, 6), ylim = c(0, 7), pch = 19)
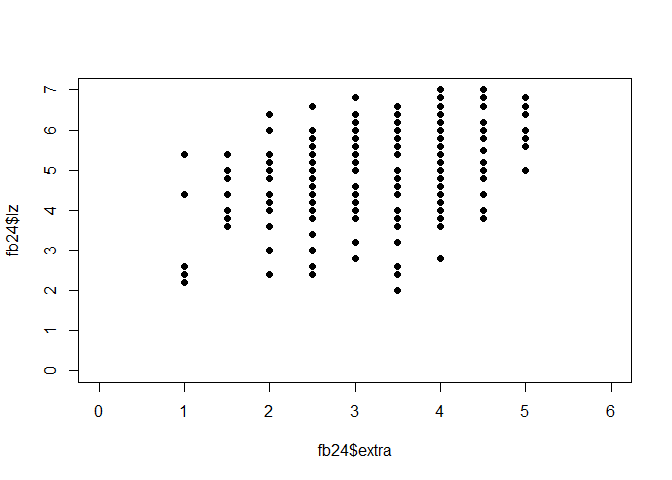
vertr:
plot(fb25$vertr, fb25$lz, xlim = c(0, 6), ylim = c(0, 7), pch = 19)
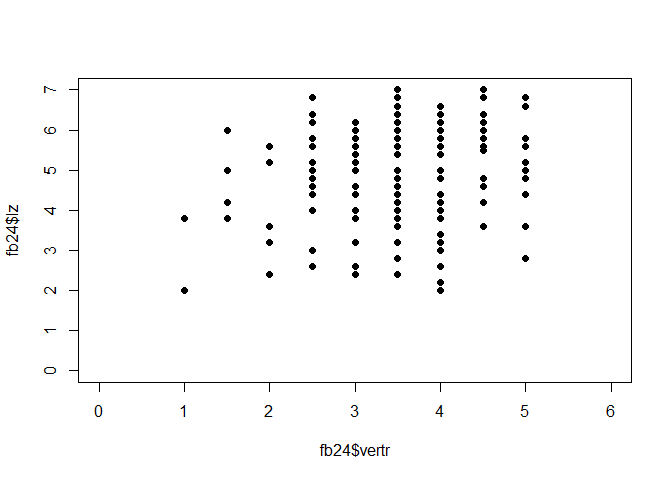
gewis:
plot(fb25$gewis, fb25$lz, xlim = c(0, 6), ylim = c(0, 7), pch = 19)
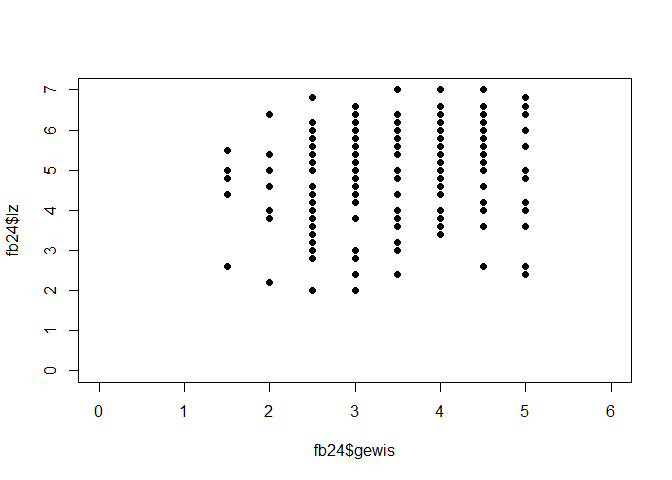
neuro:
plot(fb25$neuro, fb25$lz, xlim = c(0, 6), ylim = c(0, 7), pch = 19)
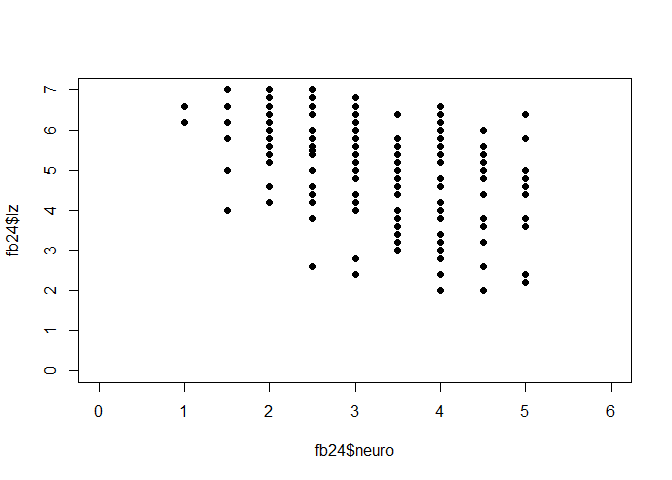
intel:
plot(fb25$offen, fb25$lz, xlim = c(0, 6), ylim = c(0, 7), pch = 19)
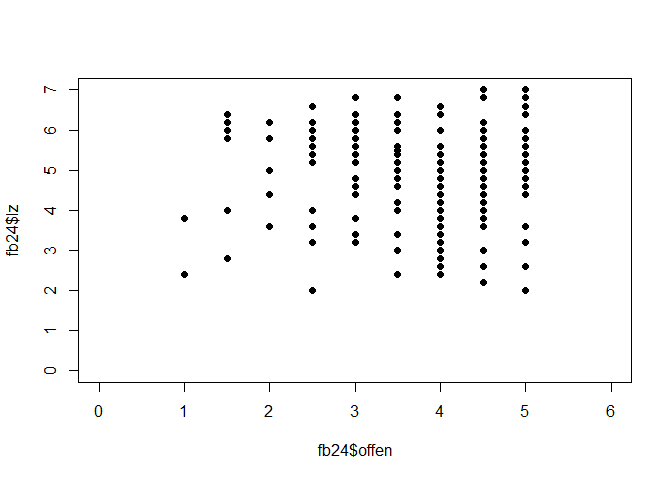
- Schätzen Sie für jeden Zusammenhang je ein Modell.
Lösung
extra:
fme <- lm(lz ~ extra, fb25)
summary(fme)
##
## Call:
## lm(formula = lz ~ extra, data = fb25)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.7172 -0.7477 0.1913 0.9744 2.3439
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.33409 0.31344 10.637 < 2e-16 ***
## extra 0.46103 0.08902 5.179 5.27e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.247 on 207 degrees of freedom
## (2 Beobachtungen als fehlend gelöscht)
## Multiple R-squared: 0.1147, Adjusted R-squared: 0.1104
## F-statistic: 26.82 on 1 and 207 DF, p-value: 5.272e-07
vertr:
fmv <- lm(lz ~ vertr, fb25)
summary(fmv)
##
## Call:
## lm(formula = lz ~ vertr, data = fb25)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.4228 -0.6662 0.2904 0.9501 2.1121
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.6399 0.3911 9.306 <2e-16 ***
## vertr 0.3566 0.1086 3.284 0.0012 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.291 on 208 degrees of freedom
## (1 Beobachtung als fehlend gelöscht)
## Multiple R-squared: 0.04928, Adjusted R-squared: 0.04471
## F-statistic: 10.78 on 1 and 208 DF, p-value: 0.001202
gewis:
fmg <- lm(lz ~ gewis, fb25)
summary(fmg)
##
## Call:
## lm(formula = lz ~ gewis, data = fb25)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.7869 -0.7282 0.2131 0.9425 2.6364
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.7050 0.4156 8.914 2.53e-16 ***
## gewis 0.3293 0.1127 2.921 0.00388 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.297 on 208 degrees of freedom
## (1 Beobachtung als fehlend gelöscht)
## Multiple R-squared: 0.0394, Adjusted R-squared: 0.03478
## F-statistic: 8.532 on 1 and 208 DF, p-value: 0.003876
neuro:
fmn <- lm(lz ~ neuro, fb25)
summary(fmn)
##
## Call:
## lm(formula = lz ~ neuro, data = fb25)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.2471 -0.5846 0.2531 0.9529 2.3033
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.84733 0.29935 19.533 < 2e-16 ***
## neuro -0.30013 0.08965 -3.348 0.000967 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.289 on 208 degrees of freedom
## (1 Beobachtung als fehlend gelöscht)
## Multiple R-squared: 0.05113, Adjusted R-squared: 0.04656
## F-statistic: 11.21 on 1 and 208 DF, p-value: 0.000967
intel:
fmo <- lm(lz ~ offen, fb25)
summary(fmo)
##
## Call:
## lm(formula = lz ~ offen, data = fb25)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.9610 -0.8110 0.1695 0.9780 2.2219
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.4124 0.4111 10.732 <2e-16 ***
## offen 0.1219 0.1022 1.192 0.234
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.319 on 208 degrees of freedom
## (1 Beobachtung als fehlend gelöscht)
## Multiple R-squared: 0.006789, Adjusted R-squared: 0.002014
## F-statistic: 1.422 on 1 and 208 DF, p-value: 0.2345
Wenn wir die Koeffizienten der Modelle vergleichen, sehen wir, dass extra den stärksten linearen Zusammenhang mit lz aufweist (Hinweis: für den Vergleich der Modelle vergleichen wir den Determinationskoeffizienten der fünf Modelle = Multiple R-squared im R-Output! Dieser ist für das Modell mit dem Prädiktor Extraversion am höchsten)
- Interpretieren Sie den standardisierten Koeffizienten des linearen Zusammenhangs zwischen Extraversion und Lebenszufriedenheit. Wie verändert sich
lz, wenn sichextraum eine Standardabweichung erhöht?
Lösung
Für diese Aufgabe gibt es zwei Lösungsansätze.
Das Einbauen der scale()-Funktion in unser Regressionsmodell.
Das Verwenden der lm.beta()-Funktion aus dem gleichnamigen Paket.
Es gilt zu Beachten: Wenn wir die Lösung zwischen den zwei Ansätzen vergleichen, ist der Wert des standardisierten Koeffizienten nicht exakt gleich. Dies ist der Fall, weil bei der standardisierten Regression mithilfe der lm()- und scale()-Befehle, das Intercept noch mitgeschätzt wird und sich dadurch auch auf die Schätzung des Koeffizienten auswirkt. Dies sollte sich aber in der Regel erst in den hinteren Nachkommastellen auswirken, sodass es für die Interpretation der Größe des Koeffizienten für gewöhnlich keine relevante Rolle spielt.
Zu 1:
sfme <- lm(scale(lz) ~ scale(extra), fb25)
sfme
##
## Call:
## lm(formula = scale(lz) ~ scale(extra), data = fb25)
##
## Coefficients:
## (Intercept) scale(extra)
## 0.0009237 0.3399672
Zu 2:
Für die Lösung der Aufgabe verwenden wir die lm.beta() Funktion. Diese stammt aus dem lm.beta-Paket, welches installiert und dann geladen werden muss.
library(lm.beta)
sfme2 <- lm.beta(fme)
summary(sfme2) # reg |> lm.beta() |> summary()
##
## Call:
## lm(formula = lz ~ extra, data = fb25)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.7172 -0.7477 0.1913 0.9744 2.3439
##
## Coefficients:
## Estimate Standardized Std. Error t value Pr(>|t|)
## (Intercept) 3.33409 NA 0.31344 10.637 < 2e-16 ***
## extra 0.46103 0.33870 0.08902 5.179 5.27e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.247 on 207 degrees of freedom
## (2 Beobachtungen als fehlend gelöscht)
## Multiple R-squared: 0.1147, Adjusted R-squared: 0.1104
## F-statistic: 26.82 on 1 and 207 DF, p-value: 5.272e-07
lm.beta() ergänzt den Output der lm()-Funktion an der Stelle der Koeffizienten um die Spalte “Standardized”. Dieser können wir den standardisierten Koeffizienten des linearen Zusammenhangs zwischen Extraversion und Lebenszufriedenheit entnehmen.
Wenn sich die Variable extra um eine Standardabweichung verändert, verändert sich das Kriterium lz um 0.34 Standardabweichungen.
Aufgabe 2
Betrachten Sie nun den Zusammenhang von Neurotizismus (neuro) und Lebenszufriedenheit (lz) etwas genauer:
- Erstellen Sie ein Streu-Punkt-Diagramm mit Regressionsgerade für den linearen Zusammenhang zwischen Neurotizismus und Lebenszufriedenheit.
Lösung
plot(fb25$neuro, fb25$lz, xlim = c(0, 6), ylim = c(0, 7), pch = 19)
abline(fmn, col = "red")
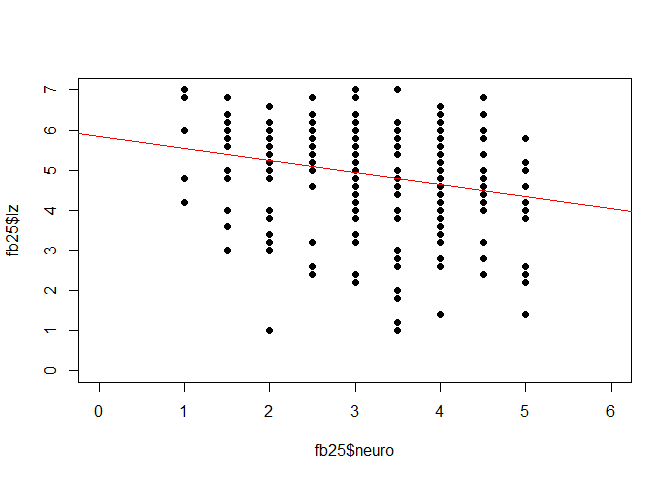
- Wie viel Prozent der Varianz werden durch das Modell erklärt?
Lösung
summary(fmn)
##
## Call:
## lm(formula = lz ~ neuro, data = fb25)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.2471 -0.5846 0.2531 0.9529 2.3033
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.84733 0.29935 19.533 < 2e-16 ***
## neuro -0.30013 0.08965 -3.348 0.000967 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.289 on 208 degrees of freedom
## (1 Beobachtung als fehlend gelöscht)
## Multiple R-squared: 0.05113, Adjusted R-squared: 0.04656
## F-statistic: 11.21 on 1 and 208 DF, p-value: 0.000967
$\rightarrow$ Das Modell erklärt 5.11% der Varianz in Lebenszufriedenheit durch Neurotizismus.
- Ein paar Studierende wurden nachträglich zum Studiengang Psychologie zugelassen und befinden sich daher nicht im Datensatz. Die neuen Studierenden wurden nachträglich befragt und weisen auf der Skala Neurotizismus folgende Werte auf: 1.25; 2.75; 3.5; 4.25; 3.75; 2.15. Machen Sie eine Vorhersage für die Lebenszufriedenheit für die neuen Studierenden.
Lösung
new <- data.frame(neuro = c(1.25, 2.75, 3.5, 4.25, 3.75, 2.15))
predict(fmn, newdata = new)
## 1 2 3 4 5 6
## 5.472165 5.021964 4.796863 4.571762 4.721829 5.202044
](/media/header/modern_buildings.jpg)