Einfache Lineare Regression
Kernfragen dieser Lehreinheit
- Wie kann ein Modell für den Zusammenhang von zwei Variablen erstellt werden?
- Wie können Streudiagramme in R erstellt werden? Wie kann die Regressionsgerade in den Plot eingefügt werden?
- Wie können standardisierte Regressionsgewichte geschätzt werden? Was ist der Unterschied zu nicht-standardisierten Regressionsgewichten?
- Wie wird der Determinationskoeffizient $R^2$ berechnet und was sagt er aus?
- Wie werden der Determinationskoeffizient $R^2$ und der Regressionsparameter b inferenzstatistisch überprüft?
Vorbereitende Schritte
Den Datensatz fb25 haben wir bereits über diesen Link heruntergeladen und können ihn über den lokalen Speicherort einladen oder Sie können Ihn direkt mittels des folgenden Befehls aus dem Internet in das Environment bekommen. Im letzten Tutorial und den dazugehörigen Aufgaben haben wir bereits Änderungen am Datensatz durchgeführt, die hier nochmal aufgeführt sind, um den Datensatz auf dem aktuellen Stand zu haben:
#### Was bisher geschah: ----
# Daten laden
load(url('https://pandar.netlify.app/daten/fb25.rda'))
# Nominalskalierte Variablen in Faktoren verwandeln
fb25$hand_factor <- factor(fb25$hand,
levels = 1:2,
labels = c("links", "rechts"))
fb25$fach <- factor(fb25$fach,
levels = 1:5,
labels = c('Allgemeine', 'Biologische', 'Entwicklung', 'Klinische', 'Diag./Meth.'))
fb25$ziel <- factor(fb25$ziel,
levels = 1:4,
labels = c("Wirtschaft", "Therapie", "Forschung", "Andere"))
fb25$wohnen <- factor(fb25$wohnen,
levels = 1:4,
labels = c("WG", "bei Eltern", "alleine", "sonstiges"))
fb25$fach_klin <- factor(as.numeric(fb25$fach == "Klinische"),
levels = 0:1,
labels = c("nicht klinisch", "klinisch"))
fb25$ort <- factor(fb25$ort, levels=c(1,2), labels=c("FFM", "anderer"))
fb25$job <- factor(fb25$job, levels=c(1,2), labels=c("nein", "ja"))
fb25$unipartys <- factor(fb25$uni3,
levels = 0:1,
labels = c("nein", "ja"))
# Rekodierung invertierter Items
fb25$mdbf4_r <- -1 * (fb25$mdbf4 - 4 - 1)
fb25$mdbf11_r <- -1 * (fb25$mdbf11 - 4 - 1)
fb25$mdbf3_r <- -1 * (fb25$mdbf3 - 4 - 1)
fb25$mdbf9_r <- -1 * (fb25$mdbf9 - 4 - 1)
fb25$mdbf5_r <- -1 * (fb25$mdbf5 - 4 - 1)
fb25$mdbf7_r <- -1 * (fb25$mdbf7 - 4 - 1)
# Berechnung von Skalenwerten
fb25$wm_pre <- fb25[, c('mdbf1', 'mdbf5_r',
'mdbf7_r', 'mdbf10')] |> rowMeans()
fb25$gs_pre <- fb25[, c('mdbf1', 'mdbf4_r',
'mdbf8', 'mdbf11_r')] |> rowMeans()
fb25$ru_pre <- fb25[, c("mdbf3_r", "mdbf6",
"mdbf9_r", "mdbf12")] |> rowMeans()
# z-Standardisierung
fb25$ru_pre_zstd <- scale(fb25$ru_pre, center = TRUE, scale = TRUE)
Einfache lineare Regression
Nachdem wir mit der Korrelation mit der gemeinsamen Betrachtung von zwei Variablen begonnen haben, werden wir jetzt lineare Modelle erstellen, uns Plots - inklusive Regressionsgerade - für Zusammenhänge anzeigen lassen und Determinationskoeffizienten berechnen. Korrelation und einfache Regression sind beides Verfahren, die sich mit dem Zusammenhang zweier Variablen befassen. Mithilfe einer Korrelation lässt sich die Stärke eines Zusammenhangs quantifizieren. Die einfache Regression hingegen verfolgt das Ziel, eine Variable mithilfe einer anderen Variable vorherzusagen. Die vorhergesagte Variable wird als Kriterium, Regressand oder auch abhängige Variable (AV) bezeichnet und üblicherweise mit $y$ symbolisiert. Die Variablen zur Vorhersage der abhängigen Variablen werden als Prädiktoren, Regressoren oder unabhängige Variablen (UV) bezeichnet und üblicherweise mit $x$ symbolisiert. Auch wenn wir in der Regression gezwungenermaßen einen gerichteten Zusammenhang angeben müssen (sprich, $x$ sagt $y$ vorher), so lässt eine Regression trotzdem keinen Schluss über kausale Zusammenhänge zu! Dies werden wir uns am Ende dieser Sitzung nochmal anschauen.
Modellschätzung
In diesem Skript beschäftigen wir uns mit der folgenden Fragestellung:
- Können wir mit der Gewissenhaftigkeit (gewis) aus dem Selbstbericht das selbst eingeschätzte “Vertrauen in die Psychologie als Wissenschaft” (trust) mit einem linearen Modell vorhersagen? Gibt es hier einen linearen Zusammenhang?
Die Modellgleichung für die lineare Regression, wie sie in der Vorlesung besprochen wurde, lautet: $y_m = b_0 + b_1 x_m + e_m$
In R gibt es eine interne Schreibweise, die sehr eng an diese Form der Notation angelehnt ist. Mit ?formula können Sie sich detailliert ansehen, welche Modelle in welcher Weise mit dieser Notation dargestellt werden können. R verwendet diese Notation für (beinahe) alle Modelle, sodass es sich lohnt, sich mit dieser Schreibweise vertraut zu machen. Die Kernelemente sind im Fall der linearen einfachen Regression:
y ~ 1 + x
Diese Notation enthält fünf Elemente:
y: die abhängige Variable~: die Notation für “regrediert auf” oder “vorhergesagt durch”1: die Konstante 1+: eine additive Verknüpfung der Elemente auf der rechten Seite der Gleichungx: eine unabhängige Variable
Die Notation beschreibt also die Aussage “$y$ wird regrediert auf die Konstante $1$ und die Variable $x$”. Die zu schätzenden Parameter $b_0$ und $b_1$ werden in dieser Notation nicht erwähnt, weil sie uns unbekannt sind. R geht generell davon aus, dass immer auch der Achsenabschnitt $b_0$ geschätzt werden soll, sodass y ~ x ausreichend ist, um eine Regression mit einem Achsenabschnitt zu beschreiben. Wenn das Intercept unterdrückt werden soll, muss das mit y ~ 0 + x explizit gemacht werden.
Starten wir nun mit unserem Anwendungsbeispiel. Für gewöhnlich würden Sie nun zuerst einmal die Voraussetzungen überprüfen. Diese werden wir in der kommenden Sitzung ausführlich besprechen. Jetzt schauen wir uns die Daten erst einmal nur an. Dies tun wir mithilfe eines Scatterplots.
plot(fb25$gewis, fb25$trust, xlab = "Gewissenhaftigkeit", ylab = "Vertrauen in die Psychologie als Wissenschaft",
main = "Zusammenhang zwischen Gewissenhaftigkeit und Vertrauen in die Psychologie als Wissenschaft", xlim = c(0, 6), ylim = c(1, 5), pch = 19)
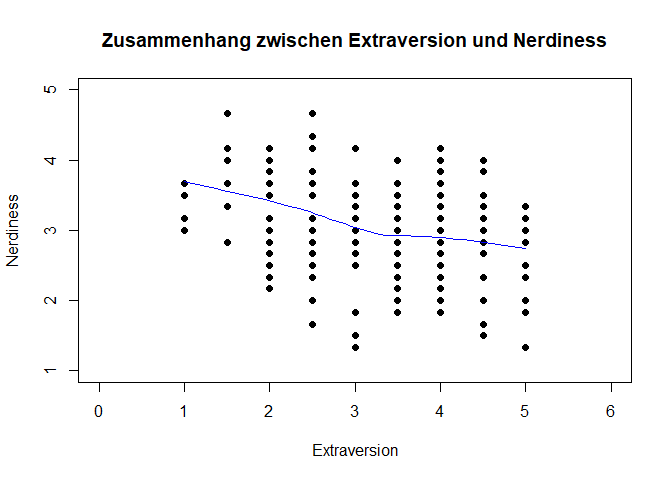
Hier erkennen wir zunächst einmal nicht so viel. Das liegt daran, dass viele Punkte übereinander liegen und es in der Grafik nicht deutlich wird, wo eigentlich die meisten Personen liegen - daher können wir auch noch nicht sagen, ob eine lineare Modellierung eine geeignete Herangehensweise für die Zusammenhang der beiden Variablen ist.
Abhilfe können wir schaffen, indem wir eine Linie zusätzlich einzeichnen, die den lokalen Zusammenhang abbildet. Die Logik bei der Erstellung kann man sich in etwa so vorstellen: Es wird für jeden kleinen Bereich der x-Variable (bspw. zwischen 2 und 2.5) geschaut wie der Zusammenhang zur y-Variable ist und eingezeichnet. Aus diesen ganzen lokalen Zusammenhängen wird dann eine durchgehende Linie gezeichnet. Wenn diese ungefähr linear ist, können wir davon ausgehen, dass die Nutzung der Linearität valide ist.
plot(fb25$gewis, fb25$trust, xlab = "Gewissenhaftigkeit", ylab = "Vertrauen in die Psychologie als Wissenschaft",
main = "Zusammenhang zwischen Gewissenhaftigkeit und Vertrauen in die Psychologie als Wissenschaft", xlim = c(0, 6), ylim = c(1, 5), pch = 19)
lines(loess.smooth(fb25$gewis, fb25$trust), col = 'blue') #beobachteter, lokaler Zusammenhang
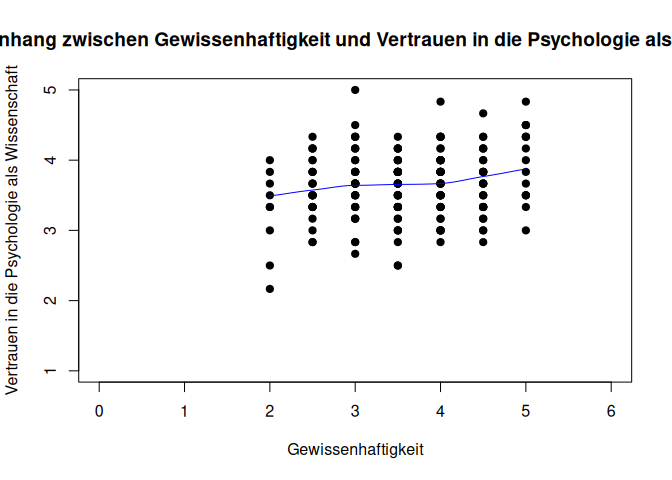
pchverändert die Darstellung der Datenpunktexlimundylimveränderen die X- bzw. Y-Achse- mit
cexkönnte man noch die Größe der Datenpunkte anpassen
Interpretation: Eine fast lineare Beziehung scheint den Zusammenhang aus gewis und trust akkurat zu beschreiben. Ein bspw. u-förmiger Zusammenhang ist nicht zu erkennen.
Wie eben gesehen ist in unserem Beispiel $x$ die Gewissenhaftigkeit (gewis) und $y$ die Vertrauen in die Psychologie als Wissenschaft (trust). Um das Modell zu schätzen, wird dann der lm() (für linear model) Befehl genutzt:
lm(formula = trust ~ 1 + gewis, data = fb25)
##
## Call:
## lm(formula = trust ~ 1 + gewis, data = fb25)
##
## Coefficients:
## (Intercept) gewis
## 3.2431 0.1157
So werden die Koeffizienten direkt ausgegeben. Wenn wir mit dem Modell jedoch weitere Analysen durchführen möchten, müssen wir es einem Objekt im Environment zuweisen. Dafür legen wir es im Objekt lin_mod (steht für lineares Modell) ab. Hier in verkürzter Schreibweise (wir lassen die 1 als Repräsentant für den Achsenabschnitt weg):
lin_mod <- lm(trust ~ gewis, fb25) #Modell erstellen und Ergebnisse im Objekt lin_mod ablegen
Falls man sich unsicher ist, wie dieses Modell zustande gekommen ist, kann man dies ausdrücklich erfragen:
formula(lin_mod)
## trust ~ gewis
Aus diesem Objekt können mit coef() oder auch lin_mod$coefficients die geschätzten Koeffizienten abgerufen werden:
coef(lin_mod)
## (Intercept) gewis
## 3.2430990 0.1157476
lin_mod$coefficients
## (Intercept) gewis
## 3.2430990 0.1157476
In lin_mod$coefficients stehen die Regressionskoeffizienten $b_0$ unter (Intercept) zur Konstanten gehörend und $b_1$ unter dem Namen der Variable, die wir als Prädiktor nutzen. In diesem Fall also gewis. Die Regressionsgleichung hat daher die folgende Gestalt: $y_i = 3.24 + 0.12 \cdot x + e_i$.
Regressionsgleichung (unstandardisiert):
$$\hat{y} = b_0 + b_1*x_m$$ $$\hat{y} = 3.24 + (0.12)*x_m$$
Interpretation der Regressionskoeffizienten:
- $b_0$ (Achsenabschnitt): beträgt die Gewissenhaftigkeit 0, wird eine Vertrauen in die Psychologie als Wissenschaft von 3.24 vorhergesagt
- $b_1$ (Regressionsgewicht): mit jeder Steigerung der Gewissenhaftigkeit um 1 Einheit wird eine um 0.12 Einheiten niedrigere (!) Vertrauen in die Psychologie als Wissenschaft vorhergesagt
Streu-Punktdiagramm mit Regressionsgerade
Das Streudiagramm haben wir zu Beginn schon abbilden lassen. Hier kann nun zusätzlich noch der geschätzte Zusammenhang zwischen den beiden Variablen als Regressiongerade eingefügt werden. Hierzu wird eine weitere Zeile mit abline() ergänzt. In abline() hätte man die Möglichkeit, Achsenabschnitt und Steigungsgewicht selbst zu definieren - aber man kann stattdessen auch einfach ein Objekt aus einer einfachen linearen Regression nutzen.
# Scatterplot zuvor im Skript beschrieben
plot(fb25$gewis, fb25$trust,
xlim = c(0, 6), ylim = c(1, 5), pch = 19)
lines(loess.smooth(fb25$gewis, fb25$trust), col = 'blue') #beobachteter, lokaler Zusammenhang
# Ergebnisse der Regression als Gerade aufnehmen
abline(lin_mod, col = 'red')
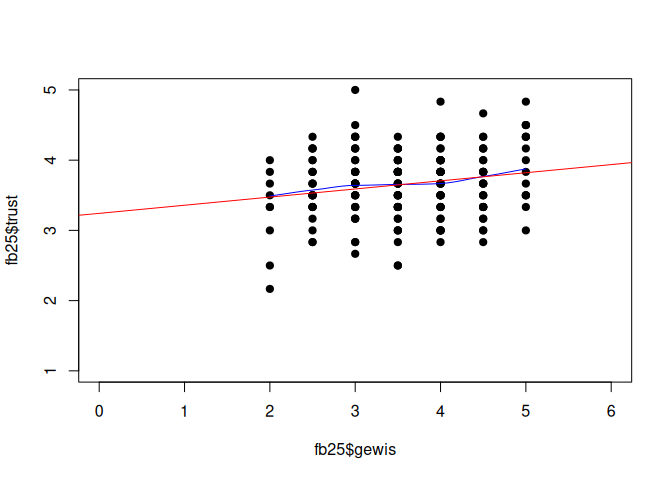
Residuen Werte
Wie wir in der eben erstellten Abbildung sehen, liegen die wahren Werte natürlich nicht genau auf der Regressionsgerade. Die Abweichungen (also die Differenz zwischen wahrem und vorhergesagten Wert) bezeichnen wir als Residuen. Mit dem Befehl lm() werden auch automatisch immer die Residuen ($e_m$) geschätzt, die mit residuals() (oder alternativ: resid()) abgefragt werden können.
residuals(lin_mod)
## 1 2 3 4 5 6 7
## -0.19913461 0.06937022 0.18511781 -0.09729644 0.07632493 0.51845114 -0.53246794
## 8 9 10 11 12 13 14
## -0.97459415 0.29391068 -0.48850357 0.01845114 -0.14821553 -0.42367507 0.06937022
## 15 16 17 18 19 20 21
## -0.70608932 0.35178447 -0.03246794 -0.70608932 -0.09034173 -0.09034173 0.80086539
## 22 23 24 25 26 27 28
## 0.18511781 0.12724401 -0.53942265 0.51845114 -0.03246794 -0.20608932 -0.37275599
## 29 30 31 34 35 36 37
## -0.14126082 0.51845114 -0.14821553 -0.31488219 -0.43062978 0.90965827 0.18511781
## 38 39 40 41 42 43 44
## -0.15517024 0.12724401 -0.19913461 0.62724401 0.01845114 -0.31488219 -0.76396311
## 45 46 47 48 50 51 52
## -0.70608932 -0.03246794 -0.42367507 0.62724401 1.12724401 0.13419872 0.07632493
## 53 54 55 56 57 58 59
## -0.14821553 -0.37275599 0.46753206 0.06937022 -0.59729644 -0.32183690 -0.43062978
## 60 61 62 63 64 65 66
## -0.14821553 -0.53942265 -1.14821553 0.40270356 -0.03942265 -0.14126082 0.18511781
## 67 68 70 71 72 73 74
## 0.23603689 -0.03246794 -0.25700840 1.40965827 -0.03246794 -0.76396311 -0.09034173
## 75 76 77 78 79 80 81
## 0.12724401 0.67816310 0.30086539 -0.09034173 0.29391068 0.29391068 0.18511781
## 82 83 84 85 86 87 88
## 0.13419872 -0.31488219 0.34482976 -0.19913461 0.68511781 0.29391068 0.18511781
## 89 90 91 92 94 95 96
## -0.25700840 -0.20608932 -0.47459415 1.01149643 0.35873918 0.62724401 0.35178447
## 97 98 99 100 101 102 103
## 0.01149643 0.67816310 -0.43062978 0.30086539 0.35178447 -0.87275599 0.07632493
## 104 105 106 107 108 110 111
## 0.24299160 -0.26396311 0.29391068 -0.42367507 -0.75700840 -0.48154886 0.56937022
## 112 113 114 115 116 117 118
## 0.29391068 0.56937022 0.12724401 0.52540585 0.63419872 0.63419872 0.07632493
## 119 120 121 122 123 124 125
## 0.19207252 0.18511781 -0.64821553 0.01845114 -0.19913461 0.18511781 -0.64821553
## 126 127 128 129 130 131 132
## 0.35178447 0.51149643 -0.14821553 0.12724401 0.57632493 -0.37275599 0.51149643
## 133 134 135 136 137 138 139
## -0.81488219 0.46057735 -0.82183690 0.57632493 -0.09729644 -0.03942265 0.12724401
## 140 141 142 143 144 145 146
## -1.14821553 0.12724401 0.40270356 0.01845114 -0.20608932 -0.26396311 0.40965827
## 147 148 149 150 151 152 153
## 0.24299160 0.24299160 -0.09729644 -0.31488219 -0.70608932 -0.64821553 -0.43062978
## 154 155 156 157 158 159 160
## -0.59729644 0.51149643 -0.75700840 0.29391068 0.01845114 0.23603689 0.12724401
## 161 162 163 164 165 166 167
## -0.09729644 0.74299160 0.06937022 0.06937022 -0.69913461 0.74299160 -0.69913461
## 168 169 170 172 173 174 175
## 0.02540585 0.07632493 -0.32183690 0.46057735 -0.03942265 -0.20608932 0.07632493
## 176 177 178 179 180 181 182
## 0.17816310 0.46753206 0.18511781 -0.92367507 0.90270356 -0.26396311 -0.03942265
## 183 184 185 186 187 188 189
## -0.31488219 -0.20608932 0.12724401 0.62724401 -0.37275599 -0.25700840 0.07632493
## 190 191 192 193 194 195 196
## 0.67816310 0.74299160 -0.70608932 0.13419872 0.63419872 -0.93062978 -1.30792748
## 197 198 199 200 201 202 203
## 0.40965827 -0.03942265 0.51845114 0.24299160 -0.20608932 0.57632493 -0.14821553
## 204 205 206 207 208 209 210
## -0.36580128 -0.48154886 0.30086539 0.24299160 0.40270356 -0.31488219 -0.32183690
## 211
## -0.43062978
Die Residuen haben die Bedeutung des “Ausmaßes an Vertrauen in die Psychologie als Wissenschaft, das nicht durch Gewissenhaftigkeit vorhergesagt werden kann” - also die Differenz aus vorhergesagtem und tatsächlich beobachtetem Wert der y-Variable (Vertrauen in die Psychologie als Wissenschaft).
Vorhergesagte Werte
Die vorhergesagten Werte $\hat{y}$ können mit predict() ermittelt werden:
predict(lin_mod)
## 1 2 3 4 5 6 7 8 9 10
## 3.532468 3.763963 3.648216 3.763963 3.590342 3.648216 3.532468 3.474594 3.706089 3.821837
## 11 12 13 14 15 16 17 18 19 20
## 3.648216 3.648216 3.590342 3.763963 3.706089 3.648216 3.532468 3.706089 3.590342 3.590342
## 21 22 23 24 25 26 27 28 29 30
## 3.532468 3.648216 3.706089 3.706089 3.648216 3.532468 3.706089 3.706089 3.474594 3.648216
## 31 34 35 36 37 38 39 40 41 42
## 3.648216 3.648216 3.763963 3.590342 3.648216 3.821837 3.706089 3.532468 3.706089 3.648216
## 43 44 45 46 47 48 50 51 52 53
## 3.648216 3.763963 3.706089 3.532468 3.590342 3.706089 3.706089 3.532468 3.590342 3.648216
## 54 55 56 57 58 59 60 61 62 63
## 3.706089 3.532468 3.763963 3.763963 3.821837 3.763963 3.648216 3.706089 3.648216 3.763963
## 64 65 66 67 68 70 71 72 73 74
## 3.706089 3.474594 3.648216 3.763963 3.532468 3.590342 3.590342 3.532468 3.763963 3.590342
## 75 76 77 78 79 80 81 82 83 84
## 3.706089 3.821837 3.532468 3.590342 3.706089 3.706089 3.648216 3.532468 3.648216 3.821837
## 85 86 87 88 89 90 91 92 94 95
## 3.532468 3.648216 3.706089 3.648216 3.590342 3.706089 3.474594 3.821837 3.474594 3.706089
## 96 97 98 99 100 101 102 103 104 105
## 3.648216 3.821837 3.821837 3.763963 3.532468 3.648216 3.706089 3.590342 3.590342 3.763963
## 106 107 108 110 111 112 113 114 115 116
## 3.706089 3.590342 3.590342 3.648216 3.763963 3.706089 3.763963 3.706089 3.474594 3.532468
## 117 118 119 120 121 122 123 124 125 126
## 3.532468 3.590342 3.474594 3.648216 3.648216 3.648216 3.532468 3.648216 3.648216 3.648216
## 127 128 129 130 131 132 133 134 135 136
## 3.821837 3.648216 3.706089 3.590342 3.706089 3.821837 3.648216 3.706089 3.821837 3.590342
## 137 138 139 140 141 142 143 144 145 146
## 3.763963 3.706089 3.706089 3.648216 3.706089 3.763963 3.648216 3.706089 3.763963 3.590342
## 147 148 149 150 151 152 153 154 155 156
## 3.590342 3.590342 3.763963 3.648216 3.706089 3.648216 3.763963 3.763963 3.821837 3.590342
## 157 158 159 160 161 162 163 164 165 166
## 3.706089 3.648216 3.763963 3.706089 3.763963 3.590342 3.763963 3.763963 3.532468 3.590342
## 167 168 169 170 172 173 174 175 176 177
## 3.532468 3.474594 3.590342 3.821837 3.706089 3.706089 3.706089 3.590342 3.821837 3.532468
## 178 179 180 181 182 183 184 185 186 187
## 3.648216 3.590342 3.763963 3.763963 3.706089 3.648216 3.706089 3.706089 3.706089 3.706089
## 188 189 190 191 192 193 194 195 196 197
## 3.590342 3.590342 3.821837 3.590342 3.706089 3.532468 3.532468 3.763963 3.474594 3.590342
## 198 199 200 201 202 203 204 205 206 207
## 3.706089 3.648216 3.590342 3.706089 3.590342 3.648216 3.532468 3.648216 3.532468 3.590342
## 208 209 210 211
## 3.763963 3.648216 3.821837 3.763963
Per Voreinstellung werden hier die vorhergesagten Werte aus unserem ursprünglichen Datensatz dargestellt. predict() erlaubt uns aber auch Werte von “neuen” Beobachtungen vorherzusagen. Nehmen wir an, wir würden die Gewissenhaftigkeit von 5 neuen Personen beobachten (sie haben - vollkommen zufällig - die Werte 1, 2, 3, 4 und 5) und diese Beobachtungen in einem neuem Datensatz gewis_neu festhalten:
gewis_neu <- data.frame(gewis = c(1, 2, 3, 4, 5))
Anhand unseres Modells können wir für diese Personen auch ihre Vertrauen in die Psychologie als Wissenschaft vorhersagen, obwohl wir diese nicht beobachtet haben:
predict(lin_mod, newdata = gewis_neu)
## 1 2 3 4 5
## 3.358847 3.474594 3.590342 3.706089 3.821837
Damit diese Vorhersage funktioniert, muss im neuen Datensatz eine Variable mit dem Namen gewis vorliegen. Vorhergesagte Werte liegen immer auf der Regressionsgeraden.
Inferenzstatistische Überprüfung der Regressionsparameter b
Signifikanztestung der Regressionskoeffizienten
Nun möchten wir aber vielleicht wissen, ob der beobachtete Zusammenhang auch statistisch bedeutsam ist oder vielleicht nur durch Zufallen zustande gekommen ist. Zuerst kann die Betrachtung der Konfidenzintervalle helfen. Der Befehl confint() berechnet die Konfidenzintervalle der Regressionsgewichte.
#Konfidenzintervalle der Regressionskoeffizienten
confint(lin_mod)
## 2.5 % 97.5 %
## (Intercept) 2.94515317 3.5410448
## gewis 0.03500078 0.1964944
Das Konfidenzintervall von 0.035 und 0.196 ist der Bereich, in dem wir den wahren Wert vermuten können. Zur Erinnerung: das 95% Konfidenzintervall besagt, dass, wenn wir diese Studie mit der selben Stichprobengröße sehr oft wiederholen, 95% aller realisierten Konfidenzintervalle den wahren Wert für $b_1$ enthalten werden. Da die 0 nicht in diesem Intervall enthalten ist, ist 0 ein eher unwahrscheinlicher wahrer Wert für $b_1$.
$b_1$
- H0: $b_1 = 0$, das Regressionsgewicht ist nicht von 0 verschieden.
- H1: $b_1 \neq 0$, das Regressionsgewicht ist von 0 verschieden.
$b_0$ (häufig nicht von Interesse)
- H0: $b_0 = 0$, der y-Achsenabschnitt ist nicht von 0 verschieden.
- H1: $b_0 \neq 0$, der y-Achsenabschnitt ist von 0 verschieden.
Für beide Parameter ($b_1$ uns $b_0$) wird die H0 auf einem alpha-Fehler-Niveau von 5% verworfen, da die 0 nicht im jeweiligen 95% Konfidenzintervall enthalten ist.
Eine andere Möglichkeit zur interferenzstatistischen Überprüfung ergibt sich über die p-Werte der Regressionskoeffizienten. Diese werden über die summary()-Funktion ausgegeben. summary() fasst verschiedene Ergebnisse eines Modells zusammen und berichtet unter anderem auch Signifikanzwerte.
#Detaillierte Modellergebnisse
summary(lin_mod)
##
## Call:
## lm(formula = trust ~ gewis, data = fb25)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.30793 -0.31488 0.01845 0.29565 1.40966
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.24310 0.15111 21.463 < 2e-16 ***
## gewis 0.11575 0.04095 2.826 0.00518 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4657 on 202 degrees of freedom
## (7 observations deleted due to missingness)
## Multiple R-squared: 0.03804, Adjusted R-squared: 0.03328
## F-statistic: 7.989 on 1 and 202 DF, p-value: 0.005179
Aus summary(): $p < \alpha$ $\rightarrow$ H1: Das Regressionsgewicht für den Prädiktor Gewissenhaftigkeit ist signifikant von 0 verschieden. Der Zusammenhang von Gewissenhaftigkeit und Vertrauen in die Psychologie als Wissenschaft ist statistisch bedeutsam.
Aus summary(): $p < \alpha$ $\rightarrow$ H1: der Achsenabschnitt ist signifikant von 0 verschieden. Beträgt die Gewissenhaftigkeit 0 wird eine von 0 verschiedene Vertrauen in die Psychologie als Wissenschaft vorhergesagt.
Konfidenzinteralle und p-Werte für Regressionskoeffizienten kommen immer zu denselben Schlussfolgerungen in Bezug darauf, ob die H0 beibehalten oder verworfen wird!
Determinationskoeffizient $R^2$
Darüber hinaus können wir uns auch anschauen, wie gut unser aufgestelltes Modell generell zu den Daten passt und Varianz erklärt. Der Determinationskoeffizient $R^2$ ist eine Kennzahl zur Beurteilung der Anpassungsgüte einer Regression. Anhand dessen kann bewertet werden, wie gut Messwerte zu einem Modell passen. Das Bestimmtheitsmaß ist definiert als der Anteil, der durch die Regression erklärten Quadratsumme an der zu erklärenden totalen Quadratsumme. Es gibt somit an, wie viel Streuung in den Daten durch das vorliegende lineare Regressionsmodell „erklärt“ werden kann. Bei einer einfachen Regression entspricht $R^2$ dem Quadrat des Korrelationskoeffizienten, wie wir später noch sehen werden.
Händische Berechnung des Determinationskoeffizienten
Für die Berechnung per Hand werden die einzelnen Varianzen benötigt:
$R^2 = \frac{s^2_{\hat{Y}}}{s^2_{Y}} = \frac{s^2_{\hat{Y}}}{s^2_{\hat{Y}} + s^2_{E}}$
# Anhand der Varianz von lz
var(predict(lin_mod)) / var(fb25$trust, use = "na.or.complete")
## [1] 0.03804456
# Anhand der Summe der Varianzen
var(predict(lin_mod)) / (var(predict(lin_mod)) + var(resid(lin_mod)))
## [1] 0.03804456
Um $R^2$ zu bestimmen, braucht es gar keinen extra Schritt. In der Funktion summary(), die wir vorhin schon kennen gelernt haben, wird der Wert mit ausgegeben. Außerdem kann anhan des p-Werts hier auch die Signifikanz des $R^2$ überprüft werden.
#Detaillierte Modellergebnisse
summary(lin_mod)
##
## Call:
## lm(formula = trust ~ gewis, data = fb25)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.30793 -0.31488 0.01845 0.29565 1.40966
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.24310 0.15111 21.463 < 2e-16 ***
## gewis 0.11575 0.04095 2.826 0.00518 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4657 on 202 degrees of freedom
## (7 observations deleted due to missingness)
## Multiple R-squared: 0.03804, Adjusted R-squared: 0.03328
## F-statistic: 7.989 on 1 and 202 DF, p-value: 0.005179
Determinationskoeffizient $R^2$ ist signifikant, da $p < \alpha$.
Der Determinationskoeffizient $R^2$ kann auch direkt über den Befehl summary(lin_mod)$r.squared ausgegeben werden:
summary(lin_mod)$r.squared
## [1] 0.03804456
3.8% der Varianz von trust können durch gewis erklärt werden. Dieser Effekt ist nach Cohens (1988) Konvention als schwach bis mittel zu bewerten, wenn keine Erkenntnisse in dem spezifischen Bereich vorliegen.
Cohens (1988) Konvention zur Interpretation von $R^2$:
Konventionen sind, wie bereits besprochen, heranzuziehen, wenn keine vorherigen Untersuchungen der Fragestellung oder zumindest in dem Forschungsbereich vorliegen. Die vorgeschlagenen Werte von $R^2$ entsprechen dabei dem Quadrat der in der letzten Sitzung genannten Konventionen für $r$.
- ~ .01: schwacher Effekt
- ~ .09: mittlerer Effekt
- ~ .25: starker Effekt
Standardisierte Regressionsgewichte
Bei einer Regression (besonders wenn mehr als ein Prädiktor in das Modell aufgenommen wird wie in der nächsten Sitzung) kann es sinnvoll sein, die standardisierten Regressionskoeffizienten zu betrachten, um die Erklärungs- oder Prognosebeiträge der einzelnen unabhängigen Variablen (unabhängig von den bei der Messung der Variablen gewählten Einheiten) miteinander vergleichen zu können, z. B. um zu sehen, welche Variable den größten Beitrag zur Prognose der abhängigen Variable leistet. Außerdem ist es hierdurch möglich, die Ergebnisse zwischen verschiedenen Studien zu vergleichen, die trust und gewis gemessen haben, jedoch in unterschiedlichen Einheiten. Durch die Standardisierung werden die Regressionskoeffizienten vergleichbar.
Die Variablen werden mit scale() standardisiert (z-Transformation; Erwartungswert gleich Null und die Varianz gleich Eins gesetzt). Mit lm() wird das Modell berechnet.
s_lin_mod <- lm(scale(trust) ~ scale(gewis), fb25) # standardisierte Regression
s_lin_mod
##
## Call:
## lm(formula = scale(trust) ~ scale(gewis), data = fb25)
##
## Coefficients:
## (Intercept) scale(gewis)
## -0.0002555 0.1941450
Gut zu wissen: scale() verwendet zur Standardisierung alle vorliegenden Werte der Variable. In unserem Datensatz gibt es allerdings einige Personen, die einen Wert auf gewis haben, jedoch einen fehlenden Wert auf trust. Die Standardisierung findet daher nicht an exakt den gleichen Personen statt.
Eine andere Variante, bei der die z-Standardisierung automatisch im Hintergrund passiert und nicht von uns manuell durch scale() erfolgen muss, liefert die Funktion lm.beta() aus dem gleichnamigen Paket lm.beta.
Nach der (ggf. nötigen) Installation müssen wir das Paket für die Bearbeitung laden.
# Paket erst installieren (wenn nötig):
if (!requireNamespace("lm.beta", quietly = TRUE)) {
install.packages("lm.beta")
}
library(lm.beta)
Die Funktion lm.beta() muss auf ein Ergebnis der normalen lm()-Funktion angewendet werden. Wir haben dieses Ergebnis im Objekt lin_mod hinterlegt. Anschließend wollen wir uns für die Interpretation wieder das summary() ausgeben lassen. Natürlich kann man diese Schritte auch mit der Pipe lösen, was als Kommentar noch aufgeführt ist.
lin_model_beta <- lm.beta(lin_mod)
summary(lin_model_beta) # lin_mod |> lm.beta() |> summary()
##
## Call:
## lm(formula = trust ~ gewis, data = fb25)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.30793 -0.31488 0.01845 0.29565 1.40966
##
## Coefficients:
## Estimate Standardized Std. Error t value Pr(>|t|)
## (Intercept) 3.24310 NA 0.15111 21.463 < 2e-16 ***
## gewis 0.11575 0.19505 0.04095 2.826 0.00518 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4657 on 202 degrees of freedom
## (7 observations deleted due to missingness)
## Multiple R-squared: 0.03804, Adjusted R-squared: 0.03328
## F-statistic: 7.989 on 1 and 202 DF, p-value: 0.005179
Wir sehen, dass die ursprüngliche Ausgabe um die Spalte standardized erweitert wurde. An der standardisierten Lösung fällt auf, dass das Intercept als NA angezeigt wird. Dies liegt wie bereits besprochen daran, dass beim Standardisieren die Mittelwerte aller Variablen (Prädiktoren und Kriterium, bzw. unabhängige und abhängige Variable) auf 0 und die Standardabweichungen auf 1 gesetzt werden. Somit muss das Intercept hier genau 0 betragen, weshalb auf eine Schätzung verzichtet werden kann.
Die Interpretation standardisierter Regressionsgewichte weicht leicht von der Interpration unstandardisierter Regressionsgewichte ab. Der Achsenabschnitt ist 0, da die Regressionsgerade durch den Mittelwert beider Variablen geht, die beide auch 0 sind. Das Regressionsgewicht hingegen beinhaltet die erwartete Veränderung von 0.12 Standardabweichungen in Vertrauen in die Psychologie als Wissenschaft bei einer Standardabweichung mehr in Gewissenhaftigkeit.
Korrelation vs. Regression
Wie bereits weiter oben angesprochen, gibt es bei der einfachen linearen Regression (1 Prädiktor) einen Zusammenhang zur Produkt-Moment-Korrelation. Dies wollen wir jetzt uns nochmal genauer anschauen.
In diesem Falle ist nämlich das standardisierte Regressionsgewicht identisch zur Produkt-Moment-Korrelation aus Prädiktor (gewis) und Kriterium (trust). Wir müssen bedenken, dass wir hier das Objekt lin_mod_beta nehmen müssen, da in s_lin_mod Personen in die Standardisierung eingeflossen sind, die bei den anderen Berechnungen komplett ausgeschlossen wurden.
cor(fb25$trust, fb25$gewis, use = "pairwise") # Korrelation
## [1] 0.1950501
coef(lin_model_beta)["gewis"] # Regressionsgewicht
## gewis
## 0.1950501
round(coef(lin_model_beta)["gewis"],2) == round(cor(fb25$trust, fb25$gewis,use = "pairwise"),2)
## gewis
## TRUE
Entsprechend ist das Quadrat der Korrelation identisch zum Determinationskoeffizienten des Modells mit standardisierten Variablen.
cor(fb25$trust, fb25$gewis, use = "pairwise")^2 # Quadrierte Korrelation
## [1] 0.03804456
summary(lin_model_beta)$r.squared # Det-Koeffizient Modell mit standardisierten Variablen
## [1] 0.03804456
round((cor(fb25$trust, fb25$gewis, use = "pairwise")^2),3) == round(summary(lin_model_beta)$r.squared, 3)
## [1] TRUE
Die Gleichheit der quadrierten Korrelation und des Determinationskoeffizienten gilt auhc für die unstandardisierten Variablen.
cor(fb25$trust, fb25$gewis, use = "pairwise")^2 # Quadrierte Korrelation
## [1] 0.03804456
summary(lin_mod)$r.squared # Det-Koeffizient Modell mit unstandardisierten Variablen
## [1] 0.03804456
round((cor(fb25$trust, fb25$gewis, use = "pairwise")^2),3) == round(summary(lin_mod)$r.squared, 3)
## [1] TRUE
Der standardisierte Korrelationskoeffizient in einer einfachen linearen Regression liefert also dieselben Informationen wie eine Produkt-Moment-Korrelation. Daraus wird auch ersichtlich, dass ein Regressionskoeffizient (genau wie eine Korrelation) nicht zulässt, auf die Richtung des Effekts (Kausalität) zu schließen.
](/media/header/modern_buildings.jpg)