Vorbereitung
Laden Sie zunächst den Datensatz
fb25von der pandar-Website. Alternativ können Sie die fertige R-Daten-Datei hier herunterladen. Beachten Sie in jedem Fall, dass die Ergänzungen im Datensatz vorausgesetzt werden. Die Bedeutung der einzelnen Variablen und ihre Antwortkategorien können Sie dem Dokument Variablenübersicht entnehmen.
Prüfen Sie zur Sicherheit, ob alles funktioniert hat:
dim(fb25)
## [1] 211 57
Der Datensatz besteht aus 211 Zeilen (Beobachtungen) und 57 Spalten (Variablen). Falls Sie bereits eigene Variablen erstellt haben, kann die Spaltenzahl natürlich abweichen.
Aufgabe 1
Ihr womöglich erstes Semester des Psychologie Studiums neigt sich dem Ende entgegen und die Klausuren rücken somit immer näher. Als vorbildliche*r Student*in sind Sie bereits fleißig am Lernen.
Jedoch beobachten Sie in manchen Kommilitoninnen und Kommilitonen, dass diese nicht so fleißig sind und eher vor sich hin prokrastinieren.
Sie vermuten, dass bestimmte Persönlichkeitsmerkmale die Prokrastinationstendenz (prok) vorhersagen könnten. Konkret vermuten Sie einen positiven Zusammenhang mit Neurotizismus (neuro) und einen negativen Zusammenhang mit Gewissenhaftigkeit (gewis). Im weiteren Verlauf sollen aber alle Eigenschaften aus dem Big Five Modell überprüft werden.
Dafür reduzieren Sie zunächst Ihren Datensatz auf die relevanten Variablen und entfernen sämtliche fehlende Werte:
fb25_short <- subset(fb25, select = c("extra", "vertr", "gewis", "neuro", "offen", "prok"))
fb25_short <- na.omit(fb25_short)
Exkurs: Warum machen wir das?
Zum einen fällt es uns so leichter den Überblick über unsere Daten zu behalten.
Zum anderen ist uns bereits im Kapitel Multiple Regression eine Fehlermeldung bei der Verwendung des Befehls anova() in Kombination mit fehlenden Werten (NA) begegnet.
Da wir im Folgenden erneut mit den Big Five Variablen arbeiten, gehen wir dieser Fehlermeldung bereits im Vorhinein aus dem Weg.
#Gibt es mindestens ein fehlenden Wert auf den 6 Variablen?
anyNA(fb25[, c("extra", "vertr", "gewis", "neuro", "offen", "prok")])
## [1] TRUE
#Auf welcher Variable und wie viele NA's gibt es?
summary(fb25[, c("extra", "vertr", "gewis", "neuro", "offen", "prok")])
## extra vertr gewis neuro offen
## Min. :1.000 Min. :1.500 Min. :2.000 Min. :1.000 Min. :1.000
## 1st Qu.:2.500 1st Qu.:3.000 1st Qu.:3.000 1st Qu.:2.500 1st Qu.:3.500
## Median :3.500 Median :3.500 Median :3.500 Median :3.000 Median :4.000
## Mean :3.379 Mean :3.509 Mean :3.602 Mean :3.187 Mean :3.919
## 3rd Qu.:4.000 3rd Qu.:4.000 3rd Qu.:4.000 3rd Qu.:4.000 3rd Qu.:4.500
## Max. :5.000 Max. :5.000 Max. :5.000 Max. :5.000 Max. :5.000
## NA's :1
## prok
## Min. :1.9
## 1st Qu.:2.5
## Median :2.7
## Mean :2.7
## 3rd Qu.:2.9
## Max. :3.7
## NA's :3
#ein NA auf vertr
- Stellen Sie das oben beschriebene lineare Regressionsmodell auf.
Lösung
mod_base <- lm(prok ~ neuro + gewis, data = fb25_short)
- Überprüfen Sie die Voraussetzungen für die multiple lineare Regression.
Lösung
Voraussetzungen:
Korrekte Spezifikation des Modells
Messfehlerfreiheit der unabhängigen Variablen
Unabhängigkeit der Residuen
Homoskedastizität der Residuen
Normalverteilung der Residuen
# Korrekte Spezifikation des Modells --> Linearität
#Einfache Regressionsmodelle aufstellen
mod_neuro <- lm(prok ~ neuro, data = fb25_short)
mod_gewis <- lm(prok ~ gewis, data = fb25_short)
#Überprüfung der Linearität
par(mfrow = c(1, 2))
plot(fb25_short$prok ~ fb25_short$neuro,
xlab = "Neurotizismus",
ylab = "Prokrastinationstendenz")
lines(lowess(fb25_short$neuro, fb25_short$prok), col = "red")
abline(mod_neuro, col = "blue")
plot(fb25_short$prok ~ fb25_short$gewis,
xlab = "Gewissenhaftigkeit",
ylab = "Prokrastinationstendenz")
lines(lowess(fb25_short$gewis, fb25_short$prok), col = "red")
abline(mod_gewis, col = "blue")
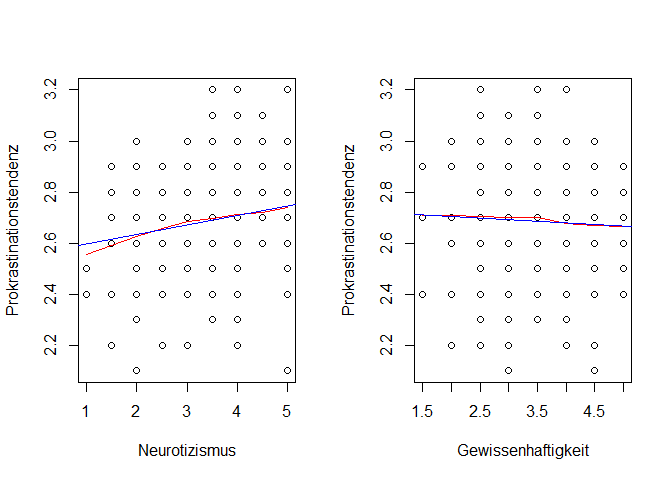
Für beide Variablen sind klare lineare Verläufe erkennbar.
#1x2 Ansicht der Plots beenden
dev.off()
## null device
## 1
Bei der Messfehlerfreiheit der unabhängigen Variablen geht man davon aus, dass der Fragebogen den man nutzt fehlerfrei misst, insbesondere unsere unabhängigen Variablen. Wie bereits im Kapitel Multiple Regression besprochen ist das selten der Fall und wir können uns Reliabilitätsmaßen wie Cronbachs Alpha und McDonalds Omega bedienen um das Ausmaß des Fehlers zu quantifizieren. Bei der Nennung dieser belassen wir es aber für diese Aufgabe mal und nehmen an dass diese Voraussetzung nicht verletzt ist.
Auch die Voraussetzung der Unabhängigkeit der Residuen ist inhaltlicher Natur. In diesem Fall gehen wir davon aus, dass Sie den Fragebogen am Anfang des Semesters weitgehend unabhängig voneinander bearbeitet haben. Somit ist auch diese Voraussetzung erfüllt.
#Homoskedastizität der Residuen
plot(mod_base, which = 3)
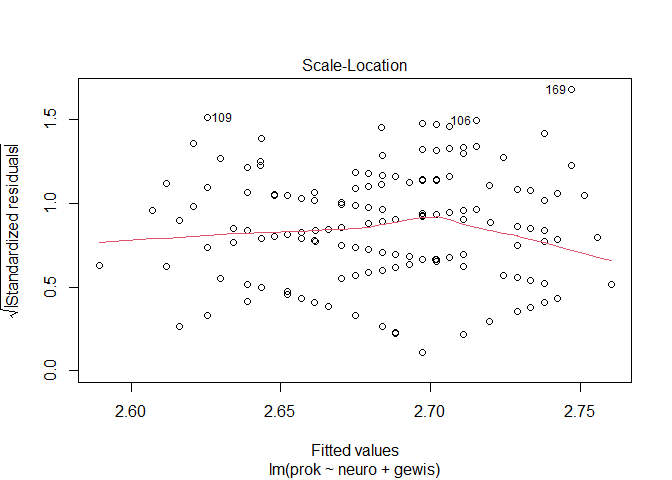
car::ncvTest(mod_base) #nicht signifikant --> Homoskedastizität wird angenommen
## Non-constant Variance Score Test
## Variance formula: ~ fitted.values
## Chisquare = 1.088653, Df = 1, p = 0.29677
#Normalverteilung der Residuen
car::qqPlot(mod_base)
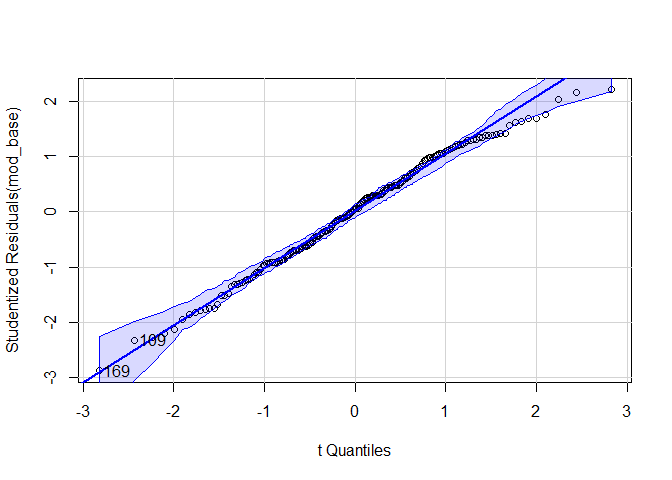
## 26 76
## 26 74
shapiro.test(mod_base$residuals) #nicht signifikant --> Normalverteilung wird angenommen
##
## Shapiro-Wilk normality test
##
## data: mod_base$residuals
## W = 0.99415, p-value = 0.5959
Anmerkung: Sowohl bei der Überprüfung der Homoskedastizität als auch der Normalverteilung bedienen wir uns Funktionen des car-Pakets. Dieses müssen wir nicht explizit mit dem library()-Befehl laden wenn wir zunächst den Namen des Pakets nennen, dann zwei Doppelpunkte und die Funktion folgen.
Dies ist selbst dann zu empfehlen wenn man die Pakete bereits geladen hat da so auch im Nachhinein ersichtlich ist aus welchem Paket welche Funktion genutzt wurde.
- Neurotizismus (
neuro) und Gewissenhaftigkeit (gewis) bilden bereits zwei der fünf Persönlichkeitsdimensionen nach dem Big Five Modell ab. Gibt es unter den verbleibenden drei Dimensionen einen weiteren signifikanten Prädiktor für die Prokrastinationstendenz (prok)? Gehen Sie schrittweise vor, indem Sie Ihr vorhandenes Modell um eine Persönlichkeitsdimension erweitern und dann testen, ob deren Inkrement signifikant ist.
Lösung
#Extraversion
mod_base_extra <- lm(prok ~ neuro + gewis + extra, data = fb25_short)
anova(mod_base, mod_base_extra) #nicht signifikant
## Analysis of Variance Table
##
## Model 1: prok ~ neuro + gewis
## Model 2: prok ~ neuro + gewis + extra
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 204 14.130
## 2 203 14.107 1 0.023431 0.3372 0.5621
#Verträglichkeit
mod_base_vertr <- lm(prok ~ neuro + gewis + vertr, data = fb25_short)
anova(mod_base, mod_base_vertr) #nicht signifikant
## Analysis of Variance Table
##
## Model 1: prok ~ neuro + gewis
## Model 2: prok ~ neuro + gewis + vertr
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 204 14.130
## 2 203 14.111 1 0.019146 0.2754 0.6003
#Offenheit für neue Erfahrungen
mod_base_offen <- lm(prok ~ neuro + gewis + offen, data = fb25_short)
anova(mod_base, mod_base_offen) #nicht signifikant
## Analysis of Variance Table
##
## Model 1: prok ~ neuro + gewis
## Model 2: prok ~ neuro + gewis + offen
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 204 14.13
## 2 203 14.13 1 0.00036366 0.0052 0.9424
#Inkrement von Extraversion
summary(mod_base_extra)$r.squared - summary(mod_base)$r.squared
## [1] 0.001621503
Keine weitere Dimension der Big Five kommt als weiterer signifikanter Prädiktor für Prokrastinationstendenz bei unserem Modell in Frage.
Somit lautet unser finales Modell weiterhin wie folgt:
mod_final <- lm(prok ~ neuro + gewis, data = fb25_short)
summary(mod_final)
##
## Call:
## lm(formula = prok ~ neuro + gewis, data = fb25_short)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.75257 -0.17894 -0.01673 0.15570 0.97362
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.69630 0.09828 27.436 <2e-16 ***
## neuro 0.03463 0.01850 1.872 0.0627 .
## gewis -0.02953 0.02325 -1.270 0.2055
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.2632 on 204 degrees of freedom
## Multiple R-squared: 0.02211, Adjusted R-squared: 0.01252
## F-statistic: 2.306 on 2 and 204 DF, p-value: 0.1022
- Interpretieren Sie das Regressionsgewicht von Gewissenhaftigkeit (
gewis).
Lösung
Zwei Personen die den gleichen Neurotizismus-Wert haben, sich aber um eine Einheit in der Gewissenhaftigkeit unterscheiden, unterscheiden sich um $\pm 0.03$ Einheiten in der Prokrastinationstendenz.
- Wie viel Varianz (in %) erklärt das finale Modell?
Lösung
summary(mod_final)$r.squared
## [1] 0.02211074
Der Determinationskoeffizient ($R^2 =$ 0.0221) besagt das 2.21% der Varianz in der Prokrastinationstendenz durch unser Modell aus zwei Prädiktoren (neuro, gewis) erklärt wird.
Aufgabe 2
Gehen Sie für die folgende Aufgabe von dem finalen Modell aus Aufgabe 1 aus.
Falls Sie dort Schwierigkeiten hatten, benutzen Sie das Kontrollergebnis.
Kontrollergebnis
mod_final <- lm(prok ~ neuro + gewis, data = fb25_short)
- Welcher Prädiktor trägt am meisten zur Prognose der Prokrastinationstendenz (
prok) bei?
Lösung
Hierfür betrachten wir unsere Regressionsgewichte:
mod_final$coefficients
## (Intercept) neuro gewis
## 2.69630191 0.03463369 -0.02952730
Diese sind jedoch noch von der benutzten Skala abhängig weswegen wir noch keine Aussage darüber treffen können welches das “beste” Regressionsgewicht ist. Daher standardisieren wir unser Modell, um uns von der Skalenabhängigkeit zu befreien. (Ausführlicher wurde dieses Vorgehen im Kapitel Einfache Lineare Regression besprochen.)
library(lm.beta)
mod_final_std <- lm.beta(mod_final)
summary(mod_final_std)
##
## Call:
## lm(formula = prok ~ neuro + gewis, data = fb25_short)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.75257 -0.17894 -0.01673 0.15570 0.97362
##
## Coefficients:
## Estimate Standardized Std. Error t value Pr(>|t|)
## (Intercept) 2.69630 NA 0.09828 27.436 <2e-16 ***
## neuro 0.03463 0.13054 0.01850 1.872 0.0627 .
## gewis -0.02953 -0.08857 0.02325 -1.270 0.2055
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.2632 on 204 degrees of freedom
## Multiple R-squared: 0.02211, Adjusted R-squared: 0.01252
## F-statistic: 2.306 on 2 and 204 DF, p-value: 0.1022
Das betragsmäßig größte standardisierte Regressionsgewicht hat der Neurotizismus mit 0.131. Somit lässt sich die Aussage treffen, das Neurotizismus im Vergleich zu Gewissenhaftigkeit am meisten zu der Vorhersage der Prokrastinationstendenz beiträgt.
- Welche Prokrastinationstendenz (
prok) sagt das finale Modell für eine Person hervor, die auf allen inkludierten Prädiktoren genau in der Mitte der Stichprobe (fb25) liegt (Mittelwerte)?
Lösung
Im Folgenden werden drei Lösungsansätze gezeigt, die sich in ihrer Komplexität unterscheiden. Sofern Sie auf einen der drei gekommen sind oder einen weiteren Ansatz gefunden haben der zum gleichen Ergebnis kommt, haben Sie die Aufgabe erfolgreich geeistert.
#1. Ansatz
means <- data.frame(neuro = mean(fb25_short$neuro),
gewis = mean(fb25_short$gewis))
predict(mod_final, newdata = means)
## 1
## 2.700483
Erklärung:
Hierbei handelt es sich um den standard Ansatz wenn es darum geht für eine neue Person mit folgenden Werten auf den Prädiktoren eine Vorhersage zu treffen.
#2. Ansatz
mod_final_sc <- lm(prok ~ scale(neuro) + scale(gewis), data = fb25_short)
mod_final_sc$coefficients[1]
## (Intercept)
## 2.700483
Erklärung:
Schematisch können wir für unser Modell folgende Formel aufstellen:
\begin{align} \hat{y} = b_1 * x_1 + b_2 * x_2 + b_0 \end{align}
Wenn wir uns an die Formel zum Standardisieren erinnern, lautet diese wie folgt:
\begin{align} x_{std} = \frac{x - \bar{x}}{\hat{\sigma}} \end{align}
Setzen wir die zweite Formel in die Erste ein erhalten wir:
\begin{align} \hat{y} = b_1 * \frac{x_1 - \bar{x_1}}{\hat{\sigma_1}} + b_2 * \frac{x_2 - \bar{x_2}}{\hat{\sigma_2}} + b_0 \end{align}
Nun interessiert uns die vorhergesagte Prokrastinationstendenz ($\hat{y}$) für eine Person die auf beiden Variablen ($x_1, x_2$) genau den Mittelwert dieser Variable ($\bar{x_1}, \bar{x_2}$) aufweist. Setzen wir für $x_1, x_2$ die Mittelwerte ein sehen wir das in den Zählern nur noch Nullen übrigbleiben.
Unsere Formel reduziert sich dann auf:
\begin{align} \hat{y} = b_0 \end{align}
$\rightarrow$ Für eine Person, die auf allen standardisierten Prädiktoren genau den Mittelwert dieser Variable als eigenen Wert hat, ist die prognostizierte Prokrastinationstendenz gleich dem Intercept.
#3. Ansatz
mean(fb25_short$prok)
## [1] 2.700483
Erklärung:
Aufgrund dessen wie unser Regressionsmodell mathematisch definiert ist, entspricht die vorhergesagte Prokrastinationstendenz für eine Person, die auf allen Prädiktorvariablen deren Mittelwert als eigenen Wert hat, der mittleren Prokrastinationstendenz in der Stichprobe aus der das Modell entstanden ist.
](/media/header/stormies.jpg)