Simulation und Poweranalyse
Kernfragen dieser Lehreinheit
- Wie können Variablen und ganze Modelle simuliert werden?
- Wie lassen sich der $\alpha$-Fehler (Type I-Error, Fehler erster Art) und die Power (Testmacht, Teststärke) empirisch bestimmen?
- Welche anderen Möglichkeiten, den $\alpha$-Fehler und die Power zu bestimmen, gibt es?
- Wie lassen sich Power-Plots erstellen und was bedeuten sie?
Einleitung
Nachdem wir uns jetzt viel mit der Durchführung der inferenzstatistischen Testung befasst haben, wollen wir den Fokus auf eine etwas übergeordnete Ebene legen. Dieses Tutorial befasst sich damit, vor einer Testung eine Stichprobe festzulegen oder diese nach der Testung zu beurteilen. Wir brauchen den Datensatz für dieses Tutorial nicht, weshalb wir ihn auch nicht einladen.
Rückblick Tests
In den vergangenen Sitzungen haben wir verschiedene Tests für unterschiedliche Fragestellungen kennengelernt: z.B. den $t$-Test und den Wilcoxon-Test für Mittelwertsvergleiche zweier Gruppen. Wie fast alle statistischen Tests folgen die erwähnten Tests einer gewissen Logik. Unter der Annahme der Nullhypothese $H_0$ und einiger weiterer Zusatzannahmen (z.B. bezüglich der Verteilung des Merkmals in der Population) folgt die jeweilige Teststatistik einer (mathematisch) herleitbaren Verteilung. Für den $t$-Test für unabhängige Stichproben ist es z.B. die $t$-Verteilung mit $n - 2$ Freiheitsgraden. Anhand der entsprechenden Verteilungsfunktion können wir die Wahrscheinlichkeit der empirischen Daten gegeben der Annahmen bestimmen und so darüber entscheiden, ob die Nullhypothese verworfen wird.
Dazu können wir ein $\alpha$-Fehlerniveau festlegen und die Nullhypothese verwerfen, wenn das Zustandekommen unserer Daten unter diesen Annahmen unwahrscheinlicher ist, als diese “akzeptierte Irrtumswahrscheinlichkeit”. Wenn dem nicht so ist, behalten wir die Nullhypothese bei. Etwas formaler:
$$ \begin{aligned} p &< \alpha\ (=5\%) \Longrightarrow \neg H_0 \implies H_1 \\\\ p &\ge \alpha\ (=5\%) \Longrightarrow H_0 \end{aligned} $$Äquivalent dazu können wir das Quantil der Verteilung bestimmen, ab dem Werte eine Wahrscheinlichkeit kleiner als $\alpha$ haben (den kritischen Wert) und unsere Teststatistik (den empirischen Wert) damit vergleichen:
$$ \begin{aligned} |t_\text{emp.}| &> t_\text{krit.} \Longrightarrow \neg H_0 \implies H_1 \\\\ |t_\text{emp.}| &\le t_\text{krit.} \Longrightarrow H_0 \end{aligned} $$Beide Ansätze kommen zum identischen Ergebnis, weil Quantil und $p$-Wert einfache Übersetzungen voneinander sind. In R können wir, wie bereits gesehen, mit p* und q* für verschiedene Verteilungen diese Übersetzung vornehmen.
Gilt die Null-Hypothese, so sollte der Test in nur höchstens $\alpha=5\%$ der Fälle ein signifikantes Ergebnis anzeigen. Die Aussage beschreibt eigentlich ein Gedankenexperiment:
Wenn wir das gleiche Experiment unendlich häufig und unabhängig voneinander wiederholen könnten und dabei unendlich häufig aus einer Population ziehen würden, in welcher es keinen Effekt gibt, dann sollte in höchstens $5\%$ der Wiederholungen (auch Replikationen genannt) rein durch Zufall ein signifikantes Ergebnis beim Durchführen des inferenzstatistischen Test herauskommen.
Andersherum sollte ein inferenzstatistischer Test die $H_0$ möglichst häufig verwerfen, wenn die $H_0$ tatsächlich nicht in der Population gilt und es somit einen bedeutsamen Effekt gibt. Die Wahrscheinlichkeit, dass wir die $H_0$ nicht verwerfen, obwohl sie falsch ist, wird $\beta$-Fehler genannt. Die Gegenwahrscheinlichkeit $1-\beta$ (also die Wahrscheinlichkeit, die $H_0$ korrekterweise zu verwerfen, weil in Wahrheit $H_1$ gilt) nennen wir die Power oder Teststärke. Sie sollte möglichst hoch sein. Es gibt verschiedene Richtlinien dazu, was “ausreichend” Power darstellt - immer in Abhängigkeit davon, welche Art von Fehlern ($\alpha$ oder $\beta$) schlimmer ist. In vielen psychologischen Studien wird eine Power von $80\%$ als Richtwert genutzt.
Zurück zu unserem Gedankenexperiment:
Eine Power von $1-\beta = 80\%$ bedeutet, wenn wir das gleiche Experiment unendlich häufig und unabhängig voneinander wiederholen könnten und dabei unendlich häufig aus einer Population ziehen würden, in welcher es einen Effekt gibt, dann sollte in mindestens $80\%$ der Fälle ein signifikantes Ergebnis beim Durchführen des inferenzstatistischen Test herauskommen, um von hinreichender Power zu sprechen.
Im Folgenden wollen wir dieses Gedankenexperiment in die Tat umsetzen und unsere Kenntnisse über das Simulieren von Zufallszahlen verwenden, um die Power und den Fehler 1. Art ($\alpha$-Fehler) empirisch zu prüfen. Hierbei beschränken wir uns auf den $t$-Test (mit der Funktion t.test()). Als Zusatz gibt es für die Korrelation als ein Zusammenhangsmaß auch ein Beispiel zum Korrelationstest in Appendix A (mit der Funktion cor.test(), welche erst in späteren Sitzungen genauer vorgestellt wird). Da wir nun also Daten simulieren brauchen wir in diesem Tutorial den Datensatz nicht.
Simulation und $\alpha$-Fehler
Sie haben nun die Möglichkeit, in einen möglichen Forschungsbereich von Methodiker:innen hineinzublicken: Simulationsstudien. Um das beschriebene Gedankenexperiment umzusetzen, müssen wir sehr häufig Stichproben aus der Population ziehen und unseren Test (z.B. einen Mittelwertsvergleich) durchführen. Die Realität hat dabei zwei grundlegende Probleme:
- Wir wissen nicht, ob in der Realität die $H_0$ oder $H_1$ gilt.
- Um zuverlässige Wahrscheinlichkeitsaussagen zu machen müssen wir die Untersuchung sehr häufig wiederholen, was in den allermeisten tatsächlich empirischen Fällen nicht praktikabel ist.
Daher behelfen wir uns in methodologischer Forschung mit Simulationsstudien.
Mittelwertsvergleiche: $t$-Test unter $H_0$
Der (klassische) $t$-Test hat folgende Voraussetzungen:
- die Erhebungen sind voneinander unabhängig
- die Varianzen in den beiden Gruppen sind gleich groß
- die Variable ist in den Populationen normalverteilt
Wir simulieren nun eine Variable $X$ für zwei Gruppen mit jeweils $N=20$. Dabei nehmen wir an, dass in beiden Gruppen die Werte standardnormalverteilt sind (also einer Normalverteilung mit einem Mittelwert von 0 und einer Standardabweichung von 1 folgen). Für die Simulation von normalverteilten Werten haben wir die Funktion rnorm() kennengelernt. Wie im Beitrag zu Verteilungen besprochen, können wir mit set.seed() die Analysen replizierbar machen. Das bedeutet, dass eure Werte mit den hier stehenden Werten übereinstimmen sollten.
N <- 20
set.seed(1234)
X_1 <- rnorm(N)
X_2 <- rnorm(N)
Die Werte der ersten Gruppe legen wir in dem Objekt X_1 ab, die Werte der zweiten Gruppe im Objekt X_2. Dadurch dass wir die Werte für beide Gruppen getrennt simuliert haben, sind die Werte voneinander unabhängig (erste Voraussetzung erfüllt). Dadurch, dass wir mit rnorm() arbeiten, machen wir außerdem explizit, dass wir Werte erzeugen, die (in der Population) der Normalverteilung folgen (dritte Voraussetzung erfüllt). Dadurch, dass wir in rnorm() außerdem für beide Variablen die Voreinstellung sd = 1 für die Standardabweichung nutzen, ist auch die zweite Voraussetzung (Homoskedastizität) erfüllt.
Zusätzlich haben wir in beiden Fällen auch die Voreinstellung mean = 0 für den Mittelwert benutzt. Dadurch gilt $\mu_{X_1}=\mu_{X_2} = 0$ für die Verteilungen aus denen beide Stichproben gezogen wurden. Da es sich hier allerdings um eine Zufallsziehung handelt, sind die Mittelwerte der beiden Gruppen natürlich nicht exakt 0:
mean(X_1)
## [1] -0.2506641
mean(X_2)
## [1] -0.5770699
Sie weichen (zufällig) von der 0 ab. Diese Abweichung wird auch Samplevariation (Stichprobenschwankung) genannt.
Die Frage, die wir uns in der Inferenzstatistik nun stellen ist, ob der Unterschied, den wir in der Stichprobe beobachten, sich auf die angenommene Grundgesamtheit verallgemeinern lässt.
Wir können nun mithilfe des $t$-Tests untersuchen, ob die beiden Variablen den gleichen Mittelwert haben (da wir den $t$-Test unter Annahme der Varianzhomogenität durchführen wollen, müssen wir var.equal = TRUE wählen, da sonst die Variante mit Welch-Korrektur gerechnet wird):
ttestH0 <- t.test(X_1, X_2, var.equal = TRUE)
ttestH0
##
## Two Sample t-test
##
## data: X_1 and X_2
## t = 1.1349, df = 38,
## p-value = 0.2635
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -0.2558241 0.9086358
## sample estimates:
## mean of x mean of y
## -0.2506641 -0.5770699
ttestH0$statistic # t-Wert
## t
## 1.134902
ttestH0$p.value # zugehöriger p-Wert
## [1] 0.2635244
Die Mittelwertsdifferenz liegt bei 0.3264, was einen $t_\text{emp}$-Wert von $t_\text{emp} =$ 1.1349 ergibt. Der zugehörige $p$-Wert liegt bei $p=$ 0.2635. Somit ist diese Mittelwertsdifferenz auf einem $\alpha$-Niveau von $5\%$ nicht statistisch bedeutsam. Die Nullyhpothese wird also nicht verworfen, was in diesem Fall die richtige Entscheidung ist, da in der Population ja die Gleichheit der Mittelwerte der beiden Gruppen gilt.
Wir sind an dieser Stelle aber nicht daran interessiert, wie der $p$-Wert in diesem spezifischen Experiment (mit Seed = 1234) ausfällt, sondern wir möchten wissen, ob die Nullhypothese in ca. $5\%$ der Fälle verworfen wird, wenn wir das Experiment häufig wiederholen. Dafür könnten wir den oben gezeigten Code immer wieder ausführen und den $p$-Wert notieren. Das erscheint sehr lästig.
Deshalb wollen wir hier bspw. die replicate()-Funktion verwenden. Mit dieser Funktion wird irgendein Stück R-Code (eine “Expression”, daher der Namen des Arguments: expr) n-mal wiederholt. Wenn wir z.B. 5 mal drei Werte aus einer Normalverteilung ziehen wollen, kann das Ganze so aussehen:
replicate(n = 5, expr = rnorm(3))
## [,1] [,2]
## [1,] 1.4494963 -0.2806230
## [2,] -1.0686427 -0.9943401
## [3,] -0.8553646 -0.9685143
## [,3] [,4]
## [1,] -1.1073182 -0.4968500
## [2,] -1.2519859 -1.8060313
## [3,] -0.5238281 -0.5820759
## [,5]
## [1,] -1.1088896
## [2,] -1.0149620
## [3,] -0.1623095
replicate() kann aber nicht nur einzelne Funktionen, sondern auch mehrere Zeilen R-Code entgegennehmen, solange diese in geschwungenen Klammern { ... } angegeben werden. Wenn wir zwei unabhängige Variablen erstellen, mit einem $t$-Test auf Mittelwertsgleichheit prüfen und uns den $p$-Wert ausgeben lassen wollen, brauchen wir die folgenden vier Zeilen:
X_1 <- rnorm(N)
X_2 <- rnorm(N)
ttestH0 <- t.test(X_1, X_2, var.equal = TRUE)
ttestH0$p.value
N hatten wir oben bereits als 20 festgelegt. Mit replicate() können wir den Code beliebig häufig durchführen. Z.B. zunächst 10 mal:
set.seed(1234)
replicate(n = 10, expr = {X_1 <- rnorm(N)
X_2 <- rnorm(N)
ttestH0 <- t.test(X_1, X_2, var.equal = TRUE)
ttestH0$p.value})
## [1] 0.26352442 0.03081077
## [3] 0.21285027 0.27429670
## [5] 0.53201656 0.79232864
## [7] 0.93976306 0.43862992
## [9] 0.96766599 0.68865560
Uns werden insgesamt 10 $p$-Werte übergeben. Wenn wir genau hinsehen, dann erkennen wir den ersten $p$-Wert wieder. Dies ist der $p$-Wert unseres Experiments weiter oben. Wiederholen wir nun das Experiment nicht nur 10 Mal, sondern 10000 Mal, dann erhalten wir eine gute Übersicht über das Verhalten der $p$-Werte unter den Bedingungen, die wir vorgegeben haben: Gültigkeit der Nullhypothese und Standardnormalverteilung der beiden voneinander unabhängigen Variablen. Damit uns die 10000 Werte nicht einfach in die Konsole gedruckt werden, legen wir sie im Objekt pt_H0 ab (für $p$-Werte für den $t$-Test unter der $H_0$-Hypothese):
set.seed(1234)
pt_H0 <- replicate(n = 10000, expr = {X_1 <- rnorm(N)
X_2 <- rnorm(N)
ttestH0 <- t.test(X_1, X_2, var.equal = TRUE)
ttestH0$p.value})
Schauen wir uns doch mal die Verteilung der $p$-Werte an:
hist(pt_H0, breaks = 20)
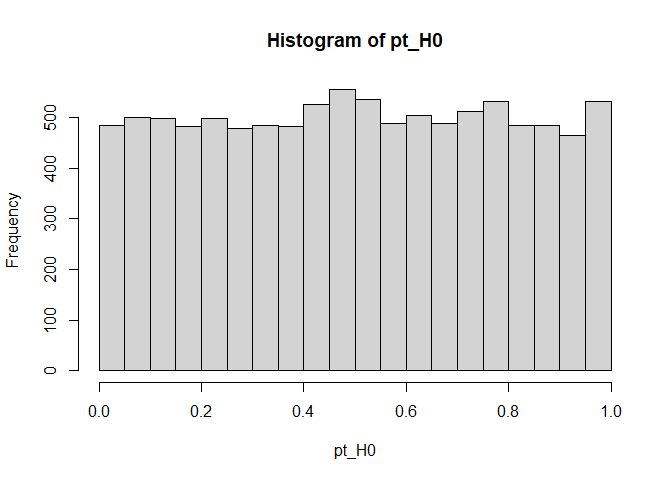
Die $p$-Werte erscheinen einigermaßen gleichverteilt auf dem Intervall [0,1], also alle Ausprägungen erscheinen gleich wahrscheinlich. Dies ist auch genau gewünscht. Unter der $H_0$-Hypothese ist der $p$-Wert uniform (gleichverteilt) auf dem Intervall [0,1]. Somit tritt jeder Wert mit der selben Wahrscheinlichkeit auf. Dies bedeutet gleichzeitig, dass in dem Intervall [0, 0.05] gerade $5\%$ der Fälle landen sollten. Dies ist gerade das Intervall, in dem die signifikanten Ergebnisse landen. Somit erkennen wir, dass unter $H_0$ die Nullhypothese nur in $5\%$ verworfen werden sollte, wenn wir uns ein $\alpha$-Niveau von $5\%$ vorgeben. Wir können prüfen, ob dem so ist, indem wir den relativen Anteil bestimmen, in welchem die $H_0$ verworfen wird. Dies ist genau dann der Fall, wenn der $p$-Wert kleiner als $0.05$ ist (siehe Einleitung). Die relative Häufigkeit bestimmen wir so:
mean(pt_H0 < 0.05)
## [1] 0.0484
Somit wird die Nullhypothese hier in 4.84% der Fälle verworfen. Dies zeigt uns, dass der $t$-Test unter $H_0$ für $N=20$ gut funktioniert, da die empirische Rate des Fehlers 1. Art bei ungefähr $5\%$ liegt. Wir könnten auch untersuchen, wie robust ein Test ist, indem wir eine Annahme verletzen (z.B. Varianzhomogenität) und untersuchen, wie sich das auf das empirische $\alpha$-Niveau und die Verteilung der Teststatistik oder der $p$-Werte ausübt.
Im Übrigen hätten wir auch die ganze Prozedur mithilfe der empirischen $t$-Werte durchführen können (diese sind als statistic im Test-Objekt angelegt):
set.seed(1234)
tt_H0 <- replicate(n = 10000, expr = {X_1 <- rnorm(N)
X_2 <- rnorm(N)
ttestH0 <- t.test(X_1, X_2, var.equal = TRUE)
ttestH0$statistic})
Wir können uns die Verteilung dieser Werte ansehen, um zu prüfen, ob die Werte annähernd $t$-verteilt sind. Die Dichte erhalten wir mit dt(x = x, df = 38), wobei x die gewünschte x-Koordinate ist:
hist(tt_H0, breaks = 50, freq = FALSE) # freq = FALSE, damit relative Häufigkeiten eingetragen werden!
x <- seq(-4, 4, 0.01) # Sequenz von -4 bis 4 in 0.01 Schritten
lines(x = x, y = dt(x = x, df = 38), lwd = 2) # lwd = Liniendicke
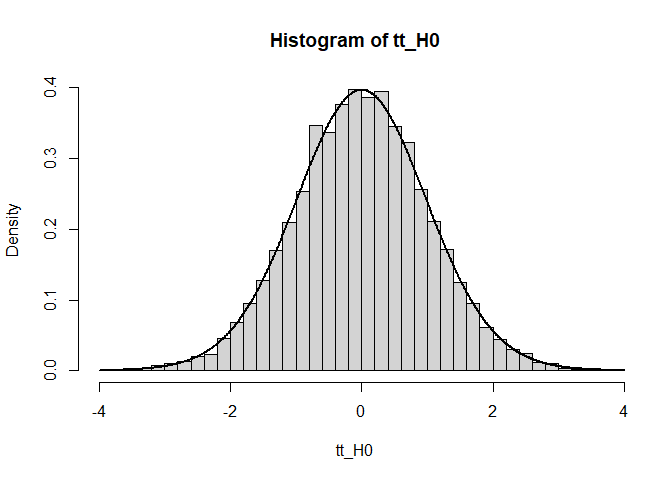
Die empirischen $t$-Werte können wir auch mit dem kritischen Wert abgleichen. Weil die $t$-Verteilung symmetrisch ist, können wir hier zweiseitig testen, indem wir einfach die Beträge (abs()) der empirischen $t$-Werte nutzen.
t_krit <- qt(p = .975, df = 38)
mean(abs(tt_H0) > t_krit) # empirischer Alpha-Fehler
## [1] 0.0484
Die Analyse kommt zum exakt gleichen Ergebnis. Das liegt daran, dass - wie oben bereits festgehalten - der $p$-Wert und der $t$-Wert ineinander überführbar sind. Das Histogramm zeigt uns außerdem die $t$-Verteilung unter der Nullhypothese mit 38 Freiheitsgraden ($N-2$). Die theoretische Kurve (mit dt()) passt sehr gut zum Histogramm!
Poweranalysen
Mit einer Power-Analyse untersuchen wir im Grunde, wie sich die Wahrscheinlichkeit die Nullhypothese zu verwerfen, verändert, je nachdem wie groß der Effekt oder die Stichprobe ist. Dem wollen wir nun nachgehen und entsprechend unsere Daten unter der Alternativhypothese simulieren.
Mittelwertsvergleiche: $t$-Test unter $H_1$
In der Inferenzstatistik gibt es im Grunde nicht “die” Alternativhypothese, sondern eine ganze Batterie an Alternativhypothesen. Beim ungerichteten Mittelwertsvergleich sieht die Alternativhypothese so aus:
$$H_1: \mu_{X_1} \neq \mu_{X_2},$$was natürlich äquivalent zur folgenden Aussage zur Differenz der beiden Mittelwerte ist: $d=\mu_{X1}-\mu_{X2}:$
$$H_1: d = \mu_{X1}-\mu_{X2} \neq 0.$$Hier wird $d$ als eine feste Zahl angenommen (z.B. 0.5, $-\sqrt{2}$, $\pi$, 123.456). Je größer der Effekt, desto größer ist die Wahrscheinlichkeit, dass dieser auch identifiziert wird. Hierbei wird die Größe des Effekts relativ zur zufälligen Streuung genommen. Da wir standardisierte (standardnormalverteilte) Variablen verwendet hatten, ist es so, dass die Mittelwertsdifferenz $d$ gerade in Vielfachen der Standardabweichung zu interpretieren ist (also Cohen’s $d’_2$ darstellt). Bspw. wäre $d=0.5$ eine halbe Standardabweichung. Wir erhalten eine Mittelwertsdifferenz von 0.5, indem wir zu dem zuvorigen Code einfach 0.5 zur 2. Variable $X_2$ dazuaddieren. “In der Population unterscheiden sich nun X_1 und X_2 um 0.5 im Mittelwert, da X_1 einen Mittelwert von 0 hat und X_2 einen Mittelwert von 0 + 0.5 = 0.5.”
set.seed(12345)
X_1 <- rnorm(N)
X_2 <- rnorm(N) + 0.5
ttestH1 <- t.test(X_1, X_2, var.equal = TRUE)
ttestH1$p.value
## [1] 0.0160865
Der empirische $p$-Wert ist diesmal kleiner als $0.05$. Die Frage ist nun, wie häufig das für eine Stichprobengröße von $N=20$ pro Gruppe vorkommt. Wir führen wieder eine Simulation dazu durch:
set.seed(12345)
pt_H1 <- replicate(n = 10000, expr = {X_1 <- rnorm(N)
X_2 <- rnorm(N) + 0.5
ttestH1 <- t.test(X_1, X_2, var.equal = TRUE)
ttestH1$p.value})
mean(pt_H1 < 0.05) # empirische Power
## [1] 0.335
hist(pt_H1, breaks = 20)
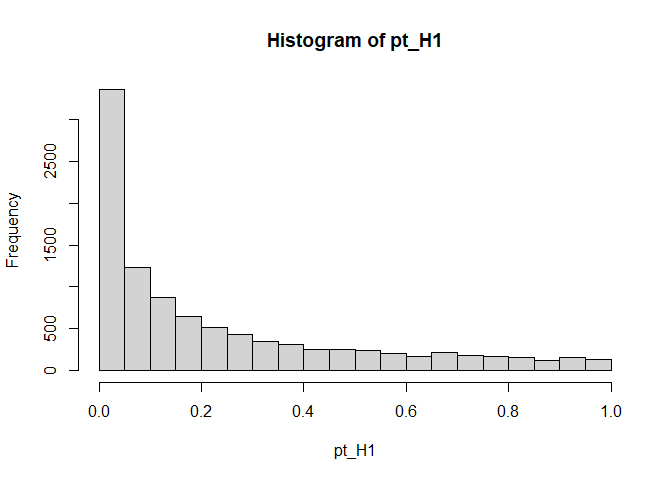
Die empirische Power (die Wahrscheinlichkeit in unserer Simulation, dass die $H_0$ verworfen wird) liegt bei 0.335. Das Histogramm ist nun alles andere als gleichverteilt. Kleine $p$-Werte nahe Null kommen wesentlich häufiger vor als große $p$-Werte nahe 1.
Woran liegt nun dieses schiefe Histogramm? Wir schauen uns dazu noch schnell die $t$-Werte an:
set.seed(12345)
tt_H1 <- replicate(n = 10000, expr = {X_1 <- rnorm(N)
X_2 <- rnorm(N) + 0.5
ttestH1 <- t.test(X_1, X_2, var.equal = TRUE)
ttestH1$statistic})
hist(tt_H1, breaks = 50, freq = FALSE) # freq = FALSE, damit relative Häufigkeiten eingetragen werden!
x <- seq(-4, 4, 0.01) # Sequenz von -4 bis 4 in 0.01 Schritten
lines(x = x, y = dt(x = x, df = 38), lwd = 2) # lwd = Liniendicke
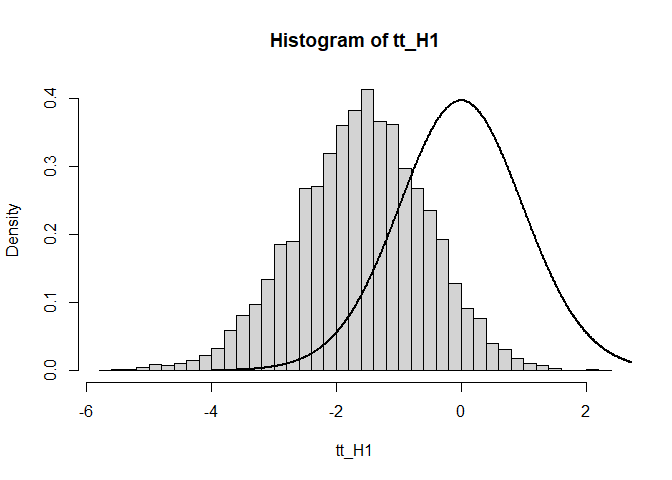
Der Grafik entnehmen wir, dass die gesamte Verteilung der empirischen t-Werte verschoben ist im Vergleich zur theoretischen Verteilung (Linie). Somit ist klar, dass die Hypothese häufiger verworfen werden muss, da die kritischen $t$-Werte unter der Alternativhypothese nicht mehr sinnvoll sind!
Nun zurück zur geschätzten Power: Eine Power von 0.335 ist allerdings nicht besonders hoch. Nur in etwas mehr als einem Drittel der Replikationen wurde die Mittelwertsdifferenz als statistisch bedeutsam betitelt. Wir wissen aber, weil wir das Modell vorgegeben haben, dass die $H_0$ tatsächlich nicht gilt. Somit wird in 2/3 der Fälle fälschlicherweise die $H_0$ nicht verworfen, obwohl sie nicht gilt. Das ist der Fehler 2. Art, auch $\beta$-Fehler genannt. Somit ist ersichtlich, dass die Power sich berechnet als $1-\beta$.
Mit größerer Stichprobe wird die Power steigen (was wir im Abschnitt Power-Plots noch deutlicher sehen werden).
Power-Plots
Mit einem einzelnen Power-Wert lässt sich in der Regel nicht so viel anfangen. Aus diesem Grund werden Power-Plots erstellt, welche darstellen, wie sich die Power bspw. über unterschiedliche Stichprobengrößen (um die Asymptotik des Tests zu prüfen) oder über unterschiedliche Effektgrößen verändert.
Power-Plots für Mittelwertsunterschiede
Wir schauen uns die Power-Plots diesmal nur für die Mittelwertsunterschiede an. Zunächst beginnen wir mit der Asymptotik. Wir wiederholen im einfachsten Fall das Experiment von oben für 5 Stichprobengrößen: $N=20, 40, 60, 80, 100$ (wobei wir das Ergebnis für $N=20$ bereits bestimmt haben). Dazu kopieren wir jeweils den Code von oben und ändern die Stichprobengröße ab:
set.seed(12345)
pt_H1_20 <- pt_H1
pt_H1_40 <- replicate(n = 10000, expr = {X_1 <- rnorm(40)
X_2 <- rnorm(40) + 0.5
ttestH1 <- t.test(X_1, X_2, var.equal = TRUE)
ttestH1$p.value})
pt_H1_60 <- replicate(n = 10000, expr = {X_1 <- rnorm(60)
X_2 <- rnorm(60) + 0.5
ttestH1 <- t.test(X_1, X_2, var.equal = TRUE)
ttestH1$p.value})
pt_H1_80 <- replicate(n = 10000, expr = {X_1 <- rnorm(80)
X_2 <- rnorm(80) + 0.5
ttestH1 <- t.test(X_1, X_2, var.equal = TRUE)
ttestH1$p.value})
pt_H1_100 <- replicate(n = 10000, expr = {X_1 <- rnorm(100)
X_2 <- rnorm(100) + 0.5
ttestH1 <- t.test(X_1, X_2, var.equal = TRUE)
ttestH1$p.value})
Nun haben wir eine ganze Menge an $p$-Werten abgespeichert. Jetzt müssen wir nur noch die Power für jede Bedingung bestimmen. Diese schreiben wir direkt in einen Vektor:
t_power <- c(mean(pt_H1_20 < 0.05),
mean(pt_H1_40 < 0.05),
mean(pt_H1_60 < 0.05),
mean(pt_H1_80 < 0.05),
mean(pt_H1_100 < 0.05))
t_power
## [1] 0.3350 0.5991 0.7700
## [4] 0.8809 0.9369
Wir sehen sehr gut, dass die Power ansteigt. Der zugehörige Power-Plot sieht nun so aus (zunächst legen wir die Stichproben in Ns ab):
Ns <- seq(20, 100, 20)
plot(x = Ns, y = t_power, type = "b",
main = "Power vs. N", xlab = "n", ylab = "Power des t-Tests mit d = .5")
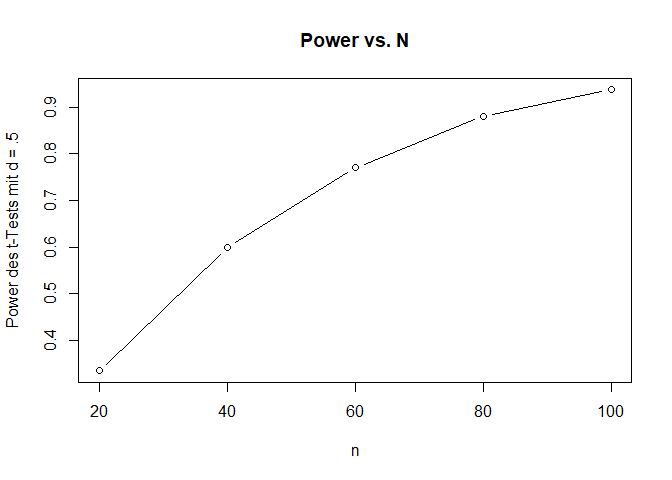
Dem Plot entnehmen wir, dass ab etwas über $N=60$ die Power oberhalb der gewünschten $80\%$-Marke liegt. Wir erkennen also, dass die Wahrscheinlichkeit einen Effekt zu finden, wenn dieser da ist, mit steigender Stichprobengröße wächst. Auf diesem Weg kann ein Experiment auch hinsichtlich der nötigen Stichprobengröße geplant werden. Wenn aus Voruntersuchungen oder der Literatur bekannt ist, wie groß ein Effekt zu erwarten ist, dann kann über Poweranalysen untersucht werden, wie groß eine Stichprobe sein muss, um einen Effekt mit hinreichend großer Wahrscheinlichkeit zu identifizieren.
Genauso könnten wir uns fragen, wie groß ein Effekt sein muss, damit mit der vorliegenden Stichprobengröße und mit hinreichend großer Wahrscheinlichkeit ein signifikantes Ergebnis gefunden wird. In diesem Fall sprechen wir von einer Sensitivitätsanalyse. Dies schauen Sie sich als Übung an!
Wenn man dies auf die Spitze treibt, dann landet man vielleicht bei diesem schönen Plot:
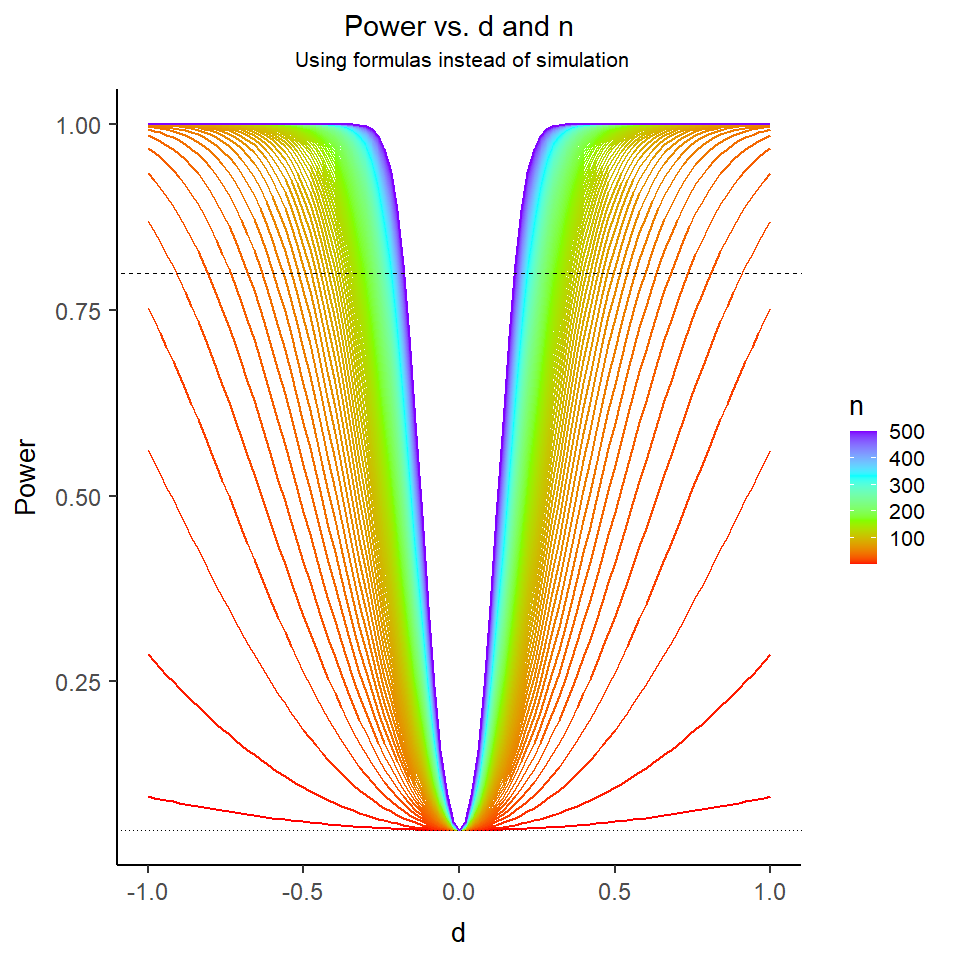
Auf der x-Achse ist die Mittelwertsdifferenz dargestellt, $N$ ist farblich kodiert. Dieser Plot enthält also sowohl Informationen über die Asymptotik (Verhalten mit steigender Stichprobengröße) und über die Auswirkung der Effektstärke. Die gestrichelte Linien symbolisiert die gewünschten $80\%$, die gepunktete Linie zeigt das $\alpha$-Fehlerniveau von $5\%$. Hier wurden allerdings keine Simulationen durchgeführt (sonst wären die Linien nicht so “smooth”), denn für den $t$-Test lässt sich die Power auch noch leicht über Formeln bestimmen. Wie das funktioniert schauen wir uns im nächsten Abschnitt an. Zuvor tauschen wir nochmal in den Power-Plot die Achsen und schreiben $n$ auf die x-Achse und kodieren die Effektgröße farbig. So sieht das Ganze unserem anderen Plot etwas ähnlicher!
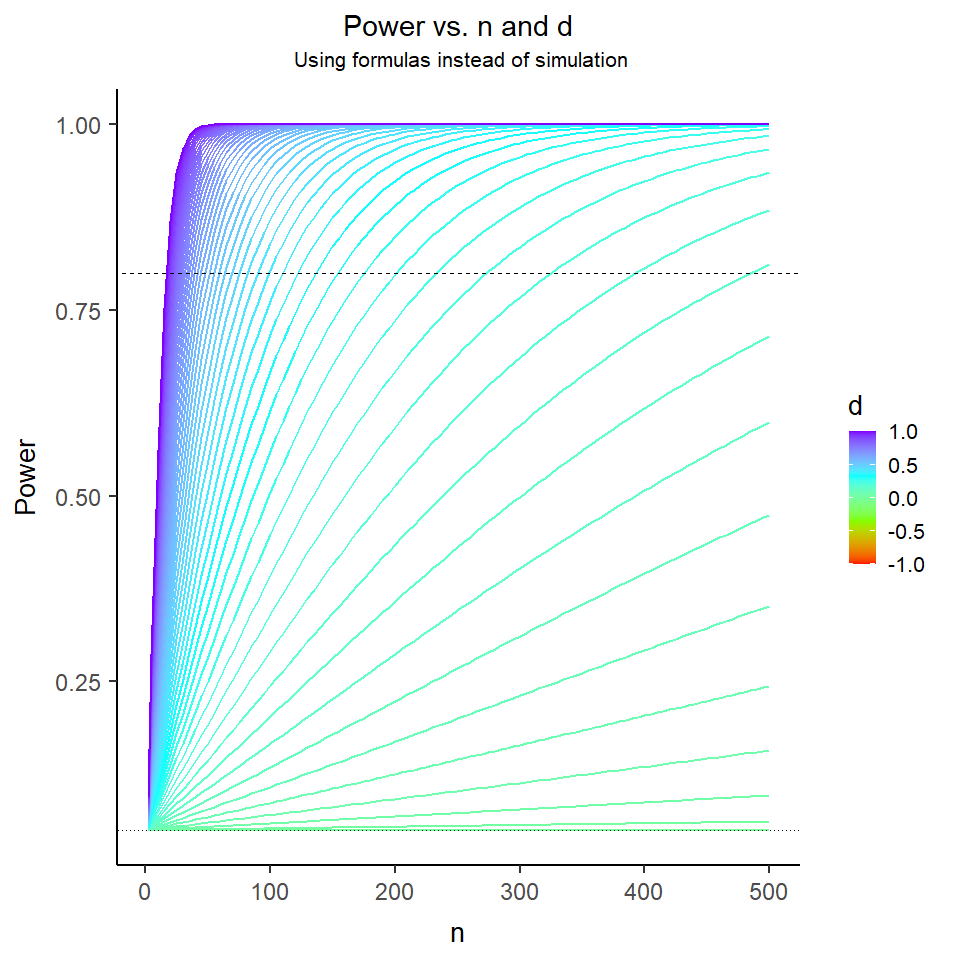
Wir sehen, dass die Power stets mit der Stichprobengröße wächst (es sei denn, der Effekt ist exakt 0, dann haben wir eine horizontale Linie auf dem $\alpha$-Fehlerniveau). Da der $t$-Test symmetrisch ist, sehen wir nur die positiven Mittelwertsdifferenzen $d$ abgebildet, während die negativen jeweils verdeckt sind ($d$ verdeckt $-d$).
Power analytisch bestimmen
Nun wollen wir die Power von Tests “analytisch” bestimmen, also durch formeln. Dazu nutzen wir das WebPower-Paket. Dieses ist eines von vielen Paketen, mit welchen die Power unterschiedlicher statistischer Tests bestimmt werden können. Wir beginnen damit das Paket zu laden (nach dem es installiert wurde mit install.packages):
library(WebPower)
## Warning: Paket 'WebPower'
## wurde unter R Version 4.3.1
## erstellt
## Warning: Paket 'Matrix' wurde
## unter R Version 4.3.2
## erstellt
## Warning: Paket 'lavaan' wurde
## unter R Version 4.3.1
## erstellt
## Warning: Paket 'PearsonDS'
## wurde unter R Version 4.3.1
## erstellt
Nun wollen wir die Power eines $t$-Tests für unabhängige Stichproben durchführen. Die nötige Funktion heißt wp.t. Das wp kürzel steht hierbei einfach nur für WebPower. Die Argumente der Funktion erhalten wir so:
args(wp.t)
## function (n1 = NULL, n2 = NULL, d = NULL, alpha = 0.05, power = NULL,
## type = c("two.sample", "one.sample", "paired", "two.sample.2n"),
## alternative = c("two.sided", "less", "greater"), tol = .Machine$double.eps^0.25)
## NULL
Mit help(wp.t) erhalten wir zu jedem dieser Argumente auch noch weitere Informationen sowie Beispiele. n1 und n2 sind die Stichprobengrößen der 1. und 2. Gruppe. Wenn wir n2 frei lassen (oder = NULL), dann wird angenommen, dass beide Stichproben gleich groß sind. d ist die standardisierte Effektgröße
sie nimmt also an, dass die Variablen standardisiert sind. alpha ist das zugehörige $\alpha$-Fehlerniveau. power können wir einen Zielwert für die Power übergeben. type gibt an, welche Art von $t$-Test durchgeführt werden soll: "two.sample", "one.sample", "paired" und "two.sample.2n". Dies steht für also 2 unabhängige Stichproben (gleiche Stichprobengröße, "two.sample"), 1-Stichprobentest ("one.sample"), gepaarter $t$-Test ("paired") und $t$-Test mit 2 unabhängigen Stichproben aber unterschiedlichen Stichprobengrößen ("two.sample.2n"). Bei $n_1=n_2=20$ hatten wir vorhin bei einer Mittelwertsdifferenz von 0.5 eine simulierte Power von 0.335 heraus. Dies untersuchen wir nun analytisch:
wp.t(n1 = 20, d = .5, type = "two.sample", alternative = "two.sided")
## Two-sample t-test
##
## n d alpha power
## 20 0.5 0.05 0.337939
##
## NOTE: n is number in *each* group
## URL: http://psychstat.org/ttest
Unsere simulierte Power von 0.335 liegt sehr nah an den theoretischen 0.337939 dran.
Sensitivitätsanalysen
Haben wir nun nur 20 Personen pro Gruppe untersucht, können wir uns fragen, wie groß denn der Effekt hätte sein müssen, damit wir eine Power von $80\%$ erhalten. Dies können wir machen, indem wir bei power = .8 eintragen und dafür d leer lassen:
wp.t(n1 = 20, power = .8, type = "two.sample", alternative = "two.sided")
## Two-sample t-test
##
## n d alpha power
## 20 0.9091587 0.05 0.8
##
## NOTE: n is number in *each* group
## URL: http://psychstat.org/ttest
Wir bräuchten also eine Mittelwertsdifferenz von 0.9091587.
Poweranalysen und Präregistrierungen
Um eine Studie sinnvoll zu planen, können wir mit Hilfe des WebPower-Pakets auch nach der nötigen Stichprobengröße fragen. Das funktioniert ähnlich wie bei der Sensitivitätsanalyse, indem wir n1 und n2 frei lassen und dafür power und d vorgeben:
wp.t(d = .5, power = .8, type = "two.sample", alternative = "two.sided")
## Two-sample t-test
##
## n d alpha power
## 63.76561 0.5 0.05 0.8
##
## NOTE: n is number in *each* group
## URL: http://psychstat.org/ttest
Für eine standardisierte Mittelwertsdifferenz von .5 brauchen wir also eine Stichprobengröße pro Gruppe von $n=$ 64, wenn wir mit einer Wahrscheinlichkeit von $80\%$ die Nullhypothese verwerfen wollen. An dieser Stelle sei angemerkt, dass diese Stichproben immer aufgerundet werden müssen und dass das eine Schätzung für $n$ pro Gruppe unter Idealbedingungen ist. Es wird angenommen, dass alle Voraussetzungen exakt erfüllt sind.
Gerichtete Hypothesen mit WebPower
Eine wichtige Ergänzung sollte an dieser Stelle für gerichtete Hypothesen erwähnt werden: wenn Sie die Hypothese richten, müssen Sie gleichzeitig auf das Vorzeichen von d achten. Wenn wir für unseren $t$-Test eine a-priori Power-Analyse durchführen wollen, um das $n$ zu bestimmen, dann könnte das z.B. so aussehen:
wp.t(d = .5, power = .8, type = "two.sample", alternative = "greater")
## Two-sample t-test
##
## n d alpha power
## 50.1508 0.5 0.05 0.8
##
## NOTE: n is number in *each* group
## URL: http://psychstat.org/ttest
Wenn wir aber annehmen, dass der Effekt umgedreht ist, bei $d$ aber den Betrag nutzen passiert Folgendes:
wp.t(d = .5, power = .8, type = "two.sample", alternative = "less")
## Error in uniroot(function(n) eval(p.body) - power, c(2 + 1e-10, 1e+07), : keine Vorzeichenwechsel nach 1000 Iterationen gefunden
Die Funktion ist nicht in der Lage, das nötige $n$ zu bestimmen, weil die Alternativ-Hypothese, dass der Mittelwert in der ersten Gruppe kleiner ist (alternative = "less") nicht zuverlässig aufgedeckt werden kann, wenn $d$ in der Population positiv ist.
Dazu hier ein Warnhinweis, bezüglich eines Bugs in WebPower: wenn Sie Sensitivitätsanalyse betreiben, funktioniert das derzeit nur für “größer als” Aussagen. Für die Gegenrichtung erhalten Sie immer eine Fehlermeldung:
wp.t(n1 = 20, n2 = 20, power = .8, type = "two.sample", alternative = "less")
## Error in uniroot(function(d) eval(p.body) - power, c(-10, 5), tol = tol, : keine Vorzeichenwechsel nach 1000 Iterationen gefunden
wp.t(n1 = 20, n2 = 20, power = .8, type = "two.sample", alternative = "greater")
## Two-sample t-test
##
## n d alpha power
## 20 0.8006879 0.05 0.8
##
## NOTE: n is number in *each* group
## URL: http://psychstat.org/ttest
Dies ist zwar in diesem Fall nicht von dramatischer Konsequenz, weil das gesamte Verfahren symmetrisch ist, aber wenn Sie z.B. ungleiche Stichproben haben (type = "two.sample.2n") sollten Sie diese explizit im Auge behalten.
Appendix A
Simulation von linearen Beziehungen
Lineare Beziehungen zwischen Variablen: Korrelationstest unter $H_0$
Der (klassische) Korrelationstest hat fast die identischen Voraussetzungen wie der $t$-Test:
- die Erhebungen sind voneinander unabhängig
- die Varianzen in den beiden Gruppen sind gleich groß
- die Variablen sind in der Population normalverteilt
- die Variablen hängen linear zusammen
Wie bei den vorherigen Berechnungen des t-Tests simulieren wirs uns wieder Daten. Die beiden Variablen, die wir gleich korrelieren wollen, nennen wir Y und Z.
set.seed(1234)
Y <- rnorm(N)
Z <- rnorm(N)
cor(Y, Z) # empirische Korrelation
## [1] -0.2765719
cortestH0 <- cor.test(Y, Z)
cortestH0$p.value # empirischer p-Wert
## [1] 0.2378304
Die empirische Korrelation liegt bei -0.28. Die wahre Korrelation liegt bei 0, da R Zufallsvektoren unabhängig voneinander simuliert. Der $p$-Wert des Korrelationstests liegt bei 0.2378. Damit ist das Ergebnis nicht statistisch bedeutsam. Die Korrelation von -0.28 ist zufällig aufgetreten. Wir wiederholen nun auch dieses Experiment:
set.seed(1234)
pcor_H0 <- replicate(n = 10000, expr = {Y <- rnorm(N)
Z <- rnorm(N)
cortestH0 <- cor.test(Y, Z)
cortestH0$p.value})
Die $p$-Werte sind wieder einigermaßen uniform auf [0,1] verteilt:
hist(pcor_H0, breaks = 20)
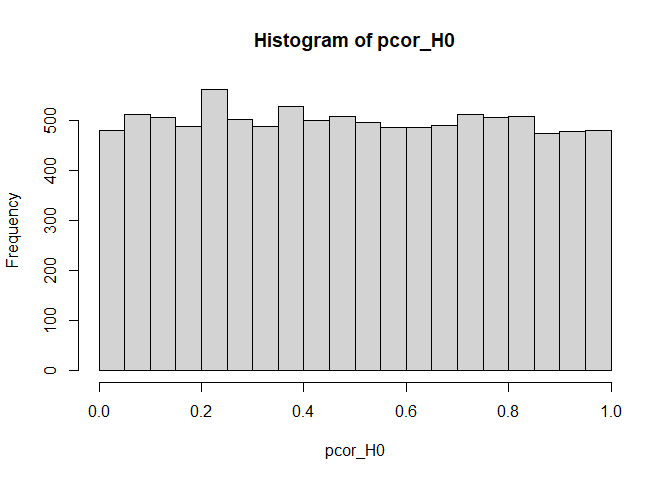
Das empirische $\alpha$-Niveau liegt bei:
mean(pcor_H0 < 0.05)
## [1] 0.0481
Somit wird die Nullhypothese hier in 4.81% der Fälle verworfen. Dies zeigt uns, dass auch der Korrelationstest unter $H_0$ für $N=20$ gut funktioniert, da die empirische Rate des Fehlers 1. Art bei ungefähr $5\%$ liegt.
Die Power für den Korrelationstest zu bestimmen, ist für diese Sitzung als Übungsaufgabe geplant!
Auch für Korrelationen können wir mit WebPower vorgehen. Die Funktion hierzu heißt wp.correlation.
](/media/header/windmills_but_fancy.jpg)