In der letzten Sitzung haben wir die einfaktorielle Varianzanalyse behandelt. Die spezifische Benennung als einfaktoriell verdeutlicht schon, dass wir hier ansetzen und Erweiterungen durch die Aufnahme von mehr Faktoren vornehmen können. In dieser Sitzung geht es vor allem um die zweifaktorielle Varianzanalyse - also das Vorliegen von zwei Faktoren. Ziel dieser Analyse ist es, gleichzeitig Gruppenunterschiede auf zwei Variablen zu untersuchen und dabei zu überprüfen, ob Kombinationen von Gruppen besondere Auswirkungen haben. Für weitere Inhalte siehe bspw. auch Eid, Gollwitzer und Schmitt (2017, Kapitel 13 und insb. 13.2 und folgend).
Wir arbeiten wieder mit dem conspiracy Datensatz. Dieser stammt aus einer Erhebung zur Validierung eines Fragebogens, aus dem Skalenwerte gebildet werden, die verschiedene Dimensionen von Verschwörungsglauben abbilden sollen.
Daten laden
Da die Rohdaten hier einige Informationen erhalten, die wir für die Durchführung des Tutorials nicht benötigen, stellen wir ein Aufbereitungsskript bereit, dass direkt eine Version des Datensatzes lädt, die für die Durchführung des Tutorials geeignet ist. Dieses kann mit dem source()-Befehl geladen und ausgeführt werden.
source("https://pandar.netlify.app/daten/Data_Processing_conspiracy.R")
Eine kurze Übersicht über den Datensatz zeigt:
dim(conspiracy)
## [1] 2451 9
Der Datensatz enthält die Werte von 2451 Personen auf 9 Variablen.
head(conspiracy)
## edu urban gender age GM
## 1 not highschool suburban female 14 4.000000
## 2 college suburban female 26 2.000000
## 3 college rural male 25 5.000000
## 4 highschool suburban male 37 5.000000
## 5 college rural male 34 1.000000
## 6 highschool suburban male 17 3.333333
## GC EC PW CI
## 1 5.000000 4.666667 3.333333 4.666667
## 2 4.000000 1.000000 2.000000 3.333333
## 3 4.333333 1.000000 3.333333 4.666667
## 4 4.333333 2.333333 3.333333 4.666667
## 5 1.000000 1.000000 1.000000 1.000000
## 6 2.666667 3.000000 2.666667 3.666667
Er stammt aus einer Untersuchung zum Thema verschwörungstheoretische Überzeugungen. Die ersten vier Variablen enthalten Informationen über den demographischen Hintergrund der Personen: höchster Bildungsabschluss (edu), Typ des Wohnortes (urban), Geschlecht (gender) und Alter (age). Die fünf restlichen Variablen sind Skalenwerte bezüglich verschiedener Subdimensionen verschwörungstheoretischer Überzeugungen: GM (goverment malfeasance), GC (malevolent global conspiracies), EC (extraterrestrial cover-up), PW (personal well-being) und CI (control of information).
Den Datensatz haben wir in der letzten Sitzung schon genutzt, haben dabei aber nicht genauer die Struktur angeschaut. Dies holen wir hier einmal nach.
str(conspiracy)
## 'data.frame': 2451 obs. of 9 variables:
## $ edu : Factor w/ 3 levels "not highschool",..: 1 3 3 2 3 2 2 1 3 2 ...
## $ urban : Factor w/ 3 levels "rural","suburban",..: 2 2 1 2 1 2 1 3 3 2 ...
## $ gender: Factor w/ 3 levels "male","female",..: 2 2 1 1 1 1 1 1 1 3 ...
## $ age : int 14 26 25 37 34 17 23 17 28 20 ...
## $ GM : num 4 2 5 5 1 ...
## $ GC : num 5 4 4.33 4.33 1 ...
## $ EC : num 4.67 1 1 2.33 1 ...
## $ PW : num 3.33 2 3.33 3.33 1 ...
## $ CI : num 4.67 3.33 4.67 4.67 1 ...
Der Output zeigt, dass wir Variablen vom Typen factor und numeric (und integer) haben. Besonderen Fokus wollen wir auf die Variablen urban, edu und ET liegen, da diese in diesem Tutorial behandelt werden. EC liegt schon als numeric vor, was an dieser Stelle für einen Fragebogenscore auch Sinn macht. Die anderen beiden Variablen sind vom Typen factor, was hier Sinn ergibt, da nur bestimmte Ausprägungen hier auftreten können (kein Freitext, sondern nominale Kategorien).
Einfaktorielle ANOVA
In der letzten Sitzung zeigte sich, dass die Überzeugung, dass die Existenz von Außerirdischen durch eine globale Verschwörung verdeckt wird (EC), von der Art des Wohngebiets (urban) abhängig ist. Zur Berechnung der einfaktoriellen ANOVA wurde das afex-Paket verwendet. Dieses Paket brauchen wir weiterhin:
library(afex)
Wir führen zur kurzen Wiederholung noch einmal die einfaktorielle ANOVA bezüglich des Bildungsniveaus (edu) durch, um uns zu vergegenwärtigen, wie der aov_4()-Befehl funktioniert! Wie schon in der letzten Sitzung ist es zunächst erforderlich, eine Personen-ID zu erzeugen. In diesem Fall kann einfach die Zeilennummer einer Person genutzt werden:
conspiracy$id <- as.factor(1:nrow(conspiracy))
Das erste Argument der aov_4()-Funktion ist im Stil der Regressionsformel - wir müssen zunächst die abhängige Variable nennen (EC), dann die unabhängige Variable (edu) nach der Tilde ~ und zum Abschluss müssen wir noch (1|id) ergänzen. Die Bedeutung dieses zusätzlichen Terms werden wir im nächsten Tutorial beleuchten. Als zweites Argument muss der Datensatz angegeben werden (data = conspiracy).
aov_4(EC ~ edu + (1|id), data = conspiracy)
## Contrasts set to contr.sum for the following variables: edu
## Anova Table (Type 3 tests)
##
## Response: EC
## Effect df MSE F ges p.value
## 1 edu 2, 2448 1.70 35.04 *** .028 <.001
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '+' 0.1 ' ' 1
Die Ergebnisse zeigen, dass es signifikante Unterschiede zwischen den verschiedenen Wohnorten gibt. Zusätzlich erhalten wir auch das generalisierte $\eta^2$, also einen Schätzer der Effektstärke, die im Grunde angibt, wie viel systematische Variation in den Daten ist, relativ zur zufälligen Schwankung. Um dies in der Skala der ursprünglichen Variablen zu interpretieren, können wir uns rein deskriptiv die gruppenspezifischen Mittelwerte angucken. Dazu kann mit einer Vielzahl von Funktionen gearbeitet werden. Eine gängige Variante ist der aggregate()-Befehl, den wir auch bereits kennengelernt haben.
aggregate(EC ~ edu, conspiracy, mean)
## edu EC
## 1 not highschool 2.422633
## 2 highschool 2.361635
## 3 college 1.929019
Deskriptive Darstellung der Kombinationen
In der mehrfaktoriellen ANOVA steht nicht nur der Vergleich von Gruppen anhand einer unabhängigen Variable im Mittelpunkt, sondern der Fokus liegt auf der Kombination von Gruppierungen anhand mehrerer unabhängiger Variablen. Deskriptiv können die Mittelwerte aus Gruppenkombinationen ebenfalls mit der aggregate()-Funktion bestimmt werden, indem in der klassischen Schreibweise eine weitere Gruppierungsvariable mit einem + aufgenommen wird:
# Kombinationsspezifische Mittelwertetabelle
aggregate(EC ~ urban + edu, conspiracy, mean)
## urban edu EC
## 1 rural not highschool 2.313433
## 2 suburban not highschool 2.364943
## 3 urban not highschool 2.577114
## 4 rural highschool 2.393519
## 5 suburban highschool 2.232493
## 6 urban highschool 2.509964
## 7 rural college 1.909722
## 8 suburban college 1.909672
## 9 urban college 1.962751
Auf den ersten Blick fällt schon einmal auf, dass Menschen, die als höchsten Bildungsabschluss das College besucht hatten, deutlich niedrigere Mittelwerte hinsichtlich der Verschwörung aufweisen als jene, die keinen High-School oder maximal einen High-School Abschluss haben. Auch wenn die tabellarische Übersicht für manche die präferierte Variante sein wird, ist es auf Postern und in Berichten häufig so, dass stattdessen Grafiken eingesetzt werden. Wir schauen uns hier erstmal an, wie man eine solche Grafik erstellen könnte mit dem ggplot2 Paket.
library(ggplot2)
Damit wir die Mittelwerte darstellen können, müssen diese natürlich auch an die Funktion gegeben werden. Dafür nutzen wir den aggregate()-Befehl und geben über die Pipe |> die resultierende Tabelle als Datensatz an die ggplot() Funktion weiter. Als nächstes ist es wichtig zu entscheiden, welcher Faktor wo abgebildet werden sollte. Wir nehmen hier urban auf der x-Achse, weshalb wir es in den Ästhetiken (aes()) auch x zuordnen. Die abhängige Variable wird y zugeordnet. Der zweite Faktor wird sowohl color als auch group zugeordnet, damit die Stufen dieses Faktors die Farbe bestimmen und auch mit Linien verbunden werden. Die passenden Geometrien sind dann geom_point() und geom_line(). Zur besseren Darstellung können bspw. die Beschriftung der Aspekte (labs()) geändert werden, aber wie wir bereits wissen, sind die Möglichkeiten in ggplot2 hier fast endlos.
aggregate(EC ~ urban + edu, conspiracy, mean) |>
ggplot(aes(x = urban, y = EC, color = edu, group = edu)) +
geom_point() +
geom_line() +
labs(x = "Urban", y = "Mean EC", color = "Education")
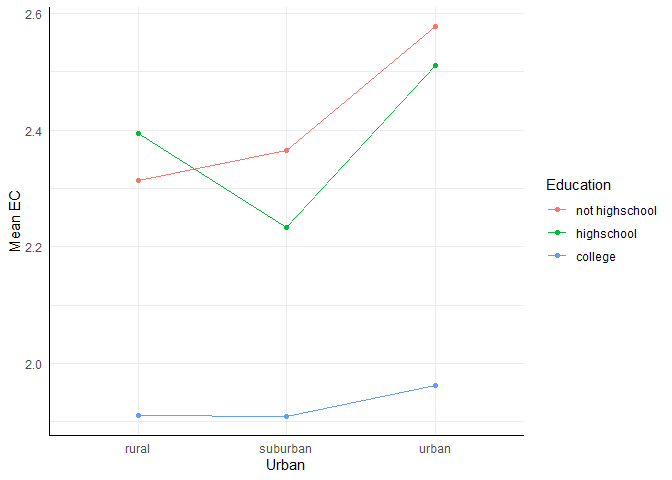
Hier werden zunächst wie von uns angefordert nur die Mittelwerte dargestellt. Wer gerne noch Balken (bspw. der geschätzte Standardfehler für den Mittelwert der Gruppen) hinzufügen möchte, kann die Vertiefung anschauen.
Mittelwertsplot mit Balken
Es gibt sehr viele Wege, um in dem Plot Unsicherheit anzuzeigen. Wie bereits geschrieben, wollen wir den geschätzten Standardfehler für den Mittelwert der einzelnen Gruppen ergänzen. Auch dafür gibt es mehrere Wege. Wir stellen an dieser Stelle einen recht einfachen vor.
Beispielsweise können wir zunächst einen Datensatz erstellen, indem sowohl die Mittelwerte als auch die geschätzten Standardfehler enthalten sind. Für die Schätzung der Standardfehler des Mittelwerts benötigen wir die Stichprobengröße und die geschätzte Populationsstandardabweichung Dafür starten wir mit der Erstellung von getrennten Datensätze.
# Mittelwert berechnen und in Datensatz ablegen
means_df <- aggregate(EC ~ urban + edu, conspiracy, mean)
# SD berechnen und in Datensatz ablegen
sds_df <- aggregate(EC ~ urban + edu, conspiracy, sd)
# Umbenennen der dritten Spalte in beiden Datensätzen für Klarheit
names(means_df)[3] <- "mean_EC"
names(sds_df)[3] <- "sd_EC"
Jetzt können wir die beiden Datensätze mit der merge() Funktion zusammenführen. Dabei füllen wir das Argument by mit den Namen der beiden Faktoren. Um die Stichprobengröße auch noch einzufügen, starten wir das Spiel nochmal.
# Zusammenführen
plot_df <- merge(means_df, sds_df, by = c("urban", "edu"))
# Datensatz erstellen und Spalte umbenennen
n_df <- aggregate(EC ~ urban + edu, conspiracy, length)
names(n_df)[3] <- "n"
# Zusammenführen
plot_df <- merge(plot_df, n_df, by = c("urban", "edu"))
Nun bestimmen wir die geschätzten Standardfehler des Mittelwerts.
plot_df$se <- plot_df$sd_EC / sqrt(plot_df$n)
Anschließend können wir den Plot erstellen. Dabei brauchen wir jetzt das zusätzlich geom_errorbar(), bei dem wir in den Ästhetiken die obere und untere Grenze der Balken festhalten können.
ggplot(plot_df, aes(x = urban, y = mean_EC, color = edu, group = edu)) +
geom_point() +
geom_line() +
geom_errorbar(aes(ymin = mean_EC - se, ymax = mean_EC + se), width = 0.1) +
labs(x = "Urban", y = "Mean ET", color = "Education")
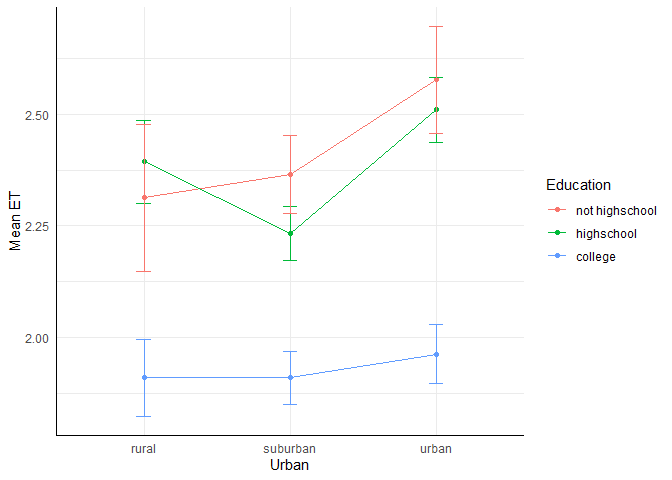
Die drei Punkte, die den jeweiligen Faktorstufen von edu angehören, scheinen sich im Mittel zu unterscheiden, was einen Unterschied auf diesem Faktor andeutet. Dasselbe gilt für das Mittel der drei Punkte, die den jeweiligen Faktorstufen von urban angehören. Außerdem sehen wir, dass die Linien sich überschneiden - für die Stufe rural liegt die mittlere Ausprägung von EC bei not highschool niedriger als highschool, während es bei allen anderen Stufen von urban andersrum ist, was ein Anzeichen für eine Interaktion der Faktoren sein kann (Hinweis: Für das Vorliegen einer Interaktion genügt es bereits, wenn die Linien unterschiedliche Steigungen aufweisen – sie müssen sich nicht zwingend schneiden. Denn bei einer Interaktion geht es darum, dass sich der Effekt einer unabhängigen Variable zwischen den Stufen der anderen unabhängigen Variable verändert). Ob diese beobachteten Unterschiede aber auch wirklich auf die Population übertragbar sind, schauen uns im Folgenden genauer an, indem wir eine zweifaktorielle ANOVA durchführen.
Zweifaktorielle Varianzanalyse
Mithilfe der zweifaktoriellen Varianzanalyse können drei zentralen Fragen beantwortet werden (Eid et al., 2017, S. 432):
- Lassen sich Unterschiede in der AV auf Unterschiede in der 1. UV zurückführen? (Haupteffekt 1, manchmal auch Haupteffekt Faktor A)
- Lassen sich Unterschiede in der AV auf Unterschiede in der 2. UV zurückführen? (Haupteffekt 2, manchmal auch Haupteffekt Faktor B)
- Hängt der Einfluss der 1. UV auf die AV von der 2. UV ab, bzw. hängt der Einfluss der 2. UV von der 1. UV ab? (Interaktionseffekt, manchmal auch Interaktionseffekt A*B)
Im Beispiel wären die Fragen also:
- Lassen sich Unterschiede in der EC-Überzeugung (
EC) auf die Art des Wohnorts (urban) zurückführen? - Lassen sich Unterschiede in der EC-Überzeugung (
EC) auf das Bildungsniveau (edu) zurückführen? - Unterschieden sich die Unterschiede aufgrund der Art des Wohnorts (
urban) zwischen den Bildungsniveaus (edu)?
Die Nullhypothesen haben wie gewohnt die Form, dass keine Effekte vorliegen. Die Alternativhypothesen besagen – ähnlich wie in der einfaktoriellen ANOVA –, dass es Effekte gibt, jedoch nicht, welche Gruppen oder Kombinationen dafür konkret verantwortlich sind. Wer sich die technischen Details nochmals ansehen möchte, kann gerne die Vertiefung öffnen.
Technische Details zu den Hypothesen
Etwas technischer ausgedrückt lassen sich die drei Fragen in Hypothesenpaaren formulieren (Eid et al., 2017, S. 442):
- $H_0: \mu_{j \bullet} - \mu = 0$, $\quad H_1: \mu_{j \bullet} - \mu \neq 0$
- $H_0: \mu_{\bullet k} - \mu = 0$, $\quad H_1: \mu_{\bullet k} - \mu \neq 0$
- $H_0: \mu_{jk} - \mu_{j \bullet} - \mu_{\bullet k} + \mu = 0$, $\quad H_1: \mu_{jk} - \mu_{j \bullet} - \mu_{\bullet k} + \mu \neq 0$
Diese können von den Gleichungen für die zweifaktorielle ANOVA abgeleitet werden. Der beobachtete Wert der i-ten Person aus Stufe j des 1. Faktors (Faktor A) und Stufe k des 2. Faktors (Faktor B) setzt sich wie folgt zusammen:
$$Y_{ijk} := \mu + \alpha_j+\beta_k + \gamma_{jk} + \varepsilon_{ijk} = \mu_{jk} + \varepsilon_{ijk},$$
wobei $\mu$ der Mittelwert über alle Messungen ist (Grand Mean). $\alpha_j$ stellt die Abweichung vom Mittelwert bedingt durch den Faktor A auf der j-ten Stufe, $\beta_k$ die Abweichung von Mittelwert bedingt durch den Faktor B auf der k-ten Stufe dar. $\gamma_{jk}$ ist die Abweichung vom Mittelwert aufgrund der spezifischen Kombination des Faktors A auf der j-ten Stufe und des Faktors B auf der k-ten, was auch die Interaktionen dieser Gruppenkombination genannt wird. Entsprechend stellt $\mu_{jk}$ auch den Mittelwert in Gruppe Faktor A Stufe j und Faktor B Stufe k dar. $\varepsilon_{ijk}$ beschreibt das Residuum, das zufällige Abweichungen in den Gruppen darstellt (dieses wird als normalverteilt und unabhängig mit gleicher Varianz über alle Gruppen hinweg angenommen!). Nun können wir die Gleichung von oben hierzu übersetzten:
$\mu_{j \bullet}$ ist der Mittelwert der j-ten Stufe auf Faktor A unabhängig von Faktor B - hier wird also über alle $\beta_k$ und $\gamma_{jk}$ gemittelt ($\beta_k$ und $\gamma_{jk}$ fallen somit weg). Somit ist $\alpha_j$ nichts anderes als die Differenz zwischen $\mu_{j \bullet}$ und $\mu$, also: $\alpha_j:=\mu_{j \bullet} - \mu$.
$\mu_{\bullet k}$ ist dementsprechend der Mittelwert der k-ten Stufe auf Faktor B unabhängig von Faktor A - $\alpha_j$ und $\gamma_{jk}$ fallen somit weg. Es ergibt sich $\beta_k:=\mu_{\bullet k}-\mu$.
$\mu_{jk}$ ist der Mittelwert der entsteht, wenn man Faktor A und Faktor B kombiniert. Da aber der alleinige Interaktionseffekt gesucht ist, muss dieser noch um die alleinigen Effekte $\mu_{j \bullet}$ und $\mu_{\bullet k}$ bereinigt werden. Daher ergibt sich $\gamma_{jk}:=\mu_{jk}-\alpha_j-\beta_k-\mu$ und daraus dann $\gamma_{jk}:=\mu_{jk}-(\mu_{j \bullet}-\mu)-(\mu_{\bullet k}-\mu)-\mu$. Wenn man dies nun vereinfacht, entsteht: $\gamma_{jk}:=\mu_{jk}-\mu_{j \bullet}-\mu_{\bullet k}+\mu$.
Da wir wissen wollen, ob sich die Effekte $\alpha_j$, $\beta_k$ und $\gamma_{jk}$ signifikant von Null unterscheiden, werden die Gleichungen in die oben genannten Hypothesen überführt. Bspw. wäre die Hypothese für Faktor A: $H_0: \alpha_1 = \dots \alpha_J = 0$ oder $H_0: \alpha_j=0$, wobei $\alpha_j:=\mu_{j \bullet} - \mu$.
Deskriptiv lassen sich Hinweise auf die drei Fragestellungen aus der erstellten Zeichnung erkennen: Für den Faktor urban, also für die erste Fragestellung, zeigen sich höhere Werte bei der gleichnamigen Ausprägung urban, während suburban und rural ähnlich erscheinen. Es könnte ein Haupteffekt vorliegen. Für den Faktor edu, die zweite Fragestellung, fällt college mit deutlich niedrigeren Werten auf, während not highschool und highschool sich weniger stark unterscheiden, was insgesamt auch auf einen Haupteffekt hindeuten könnte. Auch für die dritte Fragestellung, also den Interaktionseffekt, gibt es Hinweise, dass er vorliegen könnte. Innerhalb der Gruppe mit ländlichem Wohnort (rural) haben Personen ohne Highschool Abschluss (not highschool) eine niedrigere verschwörungstheoretische Überzeugung Personen mit Highschool Abschluss (highschool), wohingegen sie in den beiden anderen Wohnort-Gruppen einen höheren mittleren Wert (EC) aufweisen.
Die drei Nullhypothesen werden in der zweifaktoriellen ANOVA gleichzeitig geprüft. Die Schreibweise in aov_4() ist dabei ähnlich wie in der einfaktoriellen ANOVA, nur dass nun zwei unabhängige Variablen angegeben werden müssen. Die Syntax lautet: aov_4(dv ~ uv1 + uv2 + uv1 : uv 2 + (1|id), data = datensatz). Dabei ist dv die abhängige Variable, uv1 und uv2 die beiden unabhängigen Variablen und id die Personen-ID. Die gemeinsame Notation der beiden unabhängigen Variablen (uv1 : uv2) gibt an, dass die Interaktion der beiden Variablen ebenfalls berücksichtigt werden soll.
aov_4(EC ~ urban + edu + urban : edu + (1|id), data = conspiracy)
## Contrasts set to contr.sum for the following variables: urban, edu
## Anova Table (Type 3 tests)
##
## Response: EC
## Effect df MSE F ges
## 1 urban 2, 2442 1.70 4.08 * .003
## 2 edu 2, 2442 1.70 32.45 *** .026
## 3 urban:edu 4, 2442 1.70 0.96 .002
## p.value
## 1 .017
## 2 <.001
## 3 .427
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '+' 0.1 ' ' 1
Der Output zeigt uns die Ergebnisse der zweifaktoriellen ANOVA. Im Vergleich zur einfaktoriellen ANOVA erhalten wir mehr Zeilen, in denen jeweils die Variablennamen gelistet sind. Die Änderung entspricht also genau der Änderung, wenn wir in eine einfache Regression mehr Prädiktoren aufnehmen. Die erste Zeile gibt den Haupteffekt des Wohnorts (urban) an, die zweite den Haupteffekt des Bildungsniveaus (edu) und die dritte die Interaktion zwischen Wohnort und Bildungsniveau (urban:edu). In der Spalte der p-Werte sehen wir, dass sowohl der Haupteffekt des Wohnorts (urban) als auch der Haupteffekt des Bildungsniveaus (edu) statistisch bedeutsam sind. Die Interaktion zwischen Wohnort und Bildungsniveau ist jedoch nicht signifikant. Inhaltlich heißt das, dass sowohl die Art des Wohnorts als auch das Bildungsniveau einen Einfluss auf die verschwörungstheoretische Überzeugung haben. Über die jeweiligen Effekte hinaus ist die spezifische Kombination aus Wohnort und Bildungsniveau für diese Überzeugung irrelevant.
Der Output besteht allerdings nicht nur aus der Tabelle mit den Ergebnissen, sondern auch aus einer Warnung (bezüglich Kodierung) und natürlich der Überschrift (bezüglich Typen). Diese Aspekte haben wir im letzten Tutorial erstmal übersprungen, wollen uns jetzt aber mit ihnen beschäftigen.
Quadratsummen-Typen
Bei mehrfaktoriellen ANOVAs können die Quadratsummen ($QS_{A}$, $QS_{B}$ und $QS_{A\times B}$) - also die systematische Varianz, die den Faktoren zugeschrieben wird - auf unterschiedliche Arten berechnet werden. Verbreitet sind dabei drei Typen (bzw. eigentlich eher zwei zentrale Typen), zwischen denen man sich anhand der inhaltlichen Hypothesen entscheiden sollte. Wir besprechen hier im Text nur die Typen II und III - wer sich für eine genauere Betrachtung von Typ I interessiert, kann sich gerne den Appendix anschauen.
Wie die Tabellenüberschrift unseres Outputs sagt, ist der default-Typ in aov_4() Typ III. Jeder Effekt wird berechnet, nachdem alle anderen Effekte des Modells (Haupteffekte und Interaktionen) berücksichtigt wurden.
aov_4(EC ~ urban + edu + urban : edu + (1|id), data = conspiracy)
## Contrasts set to contr.sum for the following variables: urban, edu
## Anova Table (Type 3 tests)
##
## Response: EC
## Effect df MSE F ges
## 1 urban 2, 2442 1.70 4.08 * .003
## 2 edu 2, 2442 1.70 32.45 *** .026
## 3 urban:edu 4, 2442 1.70 0.96 .002
## p.value
## 1 .017
## 2 <.001
## 3 .427
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '+' 0.1 ' ' 1
Typ II berücksichtigt in der Berechnung der Quadratsummen von Effekten im Gegensatz dazu nur alle anderen Haupteffekte. In der Berechnung der Quadratsummen der Haupteffekte wird damit angenommen, dass alle Interaktionen, an denen dieser Term beteiligt ist, 0 sind. In dem Befehl kann man diese Quadratsummen mit dem Argument type = "II" anfordern:
# QS-Typ 2
aov_4(EC ~ urban + edu + urban : edu + (1|id), data = conspiracy, type = "II")
## Contrasts set to contr.sum for the following variables: urban, edu
## Anova Table (Type II tests)
##
## Response: EC
## Effect df MSE F ges
## 1 urban 2, 2442 1.70 4.44 * .004
## 2 edu 2, 2442 1.70 36.06 *** .029
## 3 urban:edu 4, 2442 1.70 0.96 .002
## p.value
## 1 .012
## 2 <.001
## 3 .427
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '+' 0.1 ' ' 1
Die Unterscheidung zwischen Typ II und Typ III ist also, dass bei Typ II die Interaktionseffekte nicht berücksichtigt werden, wenn die Quadratsumme der Haupteffekte berechnet wird. Bei Typ III hingegen werden alle anderen Haupteffekte und Interaktionen berücksichtigt. In den Zahlen merken wir das daran, dass die empirischen F-Werte, die ja die Quadratsummen der Effekte im Zähler haben, unterschiedlich sind. Spezifischer kann man sagen, dass sie bei Typ II größer sind, da die Quadratsummen der Haupteffekte nicht auf die Interaktionseffekte kontrolliert wurden. Die Quadratsummen der Interaktionseffekte sind bei Typ II und Typ III identisch, da sie in beiden Fällen die Haupteffekte in die Berechnung mit einbeziehen.
Welcher der beiden Typen ist nun der Richtige? Wie in den einleitenden Worten gesagt, sollte die Entscheidung auf den inhaltlichen Hypothesen basieren. Sind Unterschiede nur für die Haupteffekte zu erwarten und nicht für den Interaktionseffekt, sollte Typ II verwendet werden, denn hier haben wir die höhere Power. Sind hingegen Interaktionseffekte zu erwarten, sollte Typ III verwendet werden. Sollte sich bei der Testung unter Verwendung von Typ II doch ein signifikanter Interaktionseffekt ergeben, sollte die ANOVA nochmal mit Typ III durchgeführt werden - denn dann ist die Annahme für die Verwendung von Typ II ja nicht gegeben (Interaktionseffekt ist doch von 0 verschieden). Sollte sich bei der Testung mit Typ III kein signifikanter Interaktionseffekt ergeben, sollte aber nicht nochmal mit Typ II getestet werden, da dies einer Kumulation von Fehlern gleichkäme.
Kodierung der Variablen
Die Message, die wir im Output gesehen haben, bezieht sich auf die Kodierung der kategorialen Variablen mit ungeordneten Ausprägungen und deren Behandlung im Modell. Kategoriale Variablen in Analysen häufig durch sogenannte Kodiervariablen dargestellt, bei denen jeder Gruppe eine Zahl zugeordnet wird. Bei Variablen mit nur zwei Ausprägungen ist dafür lediglich eine Kodiervariable nötig, um die Informationen der ursprünglichen Variable vollständig zu repräsentieren (zum Beispiel erhält eine Gruppe den Wert 0 und die andere den Wert 1). Bei Variablen mit mehr als zwei Ausprägungen (wie in unserem Fall) sind dagegen mehrere Kodiervariablen erforderlich. Die allgemeine Regel lautet: Anzahl der Ausprägungen - 1.
Bei der Bildung der Kodiervariablen haben wir grundsätzlich zwei verschiedene Möglichkeiten. Bei der Einstellung contr.treatment (auch als Dummy-Codierung bezeichnet) wird eine der Ausprägungen als Referenzkategorie festgelegt. Die anderen Ausprägungen werden dann in Bezug auf diese Referenzkategorie kodiert. Diese Art der Kodierung ist der Standard in R und würde zum Beispiel automatisch angewendet, wenn wir unsere Variablen direkt an eine Regression mit lm() übergeben würden.
| Ausprägung | Variable 1 | Variable 2 |
|---|---|---|
| not highschool | 0 | 0 |
| highschool | 1 | 0 |
| college | 0 | 1 |
Bei der Einstellung contr.sum (bezeichnet als Effekt-Codierung) werden die Koeffizienten auf den Kodiervariablen so vergeben, dass die Abweichungen vom Mittelwert repräsentiert werden. Wir bilden hier einen ungewichteten Mittelwert der Ausprägungen, indem die Gruppengröße der einzelnen Ausprägungen nicht in die Effekt-Codierung mit einbezogen werden.
| Ausprägung | Variable 1 | Variable 2 |
|---|---|---|
| not highschool | -1 | -1 |
| highschool | 1 | 0 |
| college | 0 | 1 |
Wie die Mitteilung uns anzeigt, wird in aov_4() der Standard contr.treatment durch contr.sum ersetzt. Das liegt daran, dass contr.treatment auf dem Vergleich einer Referenzkategorie mit den anderen Gruppen basiert – was besonders dann sinnvoll ist, wenn es beispielsweise eine Kontrollgruppe und mehrere Treatment-Gruppen gibt (daher auch der Name contr.treatment). In der ANOVA liegt der Fokus jedoch nicht auf dem Vergleich zu einer einzelnen Referenzgruppe, sondern auf der Abweichung der Gruppenmittelwerte vom Gesamtmittelwert. Deshalb ist hier die Effektkodierung (contr.sum) die richtige Wahl.
Abschließende Bemerkungen zur Zweifaktoriellen ANOVA
Die Interpretation unserer Ergebnisse fällt einfach, da nur die beiden Haupteffekte signifikant sind. Es gibt also Unterschiede hinsichtlich des Wohnorts und des Bildungsniveaus hinsichtlich des Glaubens an Verschwörungstheorien über Extraterrestrische Wesen. Die Interaktion ist nicht signifikant.
Doch gerade das Vorhandensein von Interaktionseffekten kann die Interpretation der Haupteffekte sehr erschweren. Es muss geprüft werden, ob die globalen Aussagen über die Haupteffekte auch für alle Gruppen gelten. Wenn bspw. der Haupteffekt des Wohnorts nur für Personen mit College-Abschluss gilt, aber nicht für Personen ohne Highschool-Abschluss (was durch eine signifikante Interaktion deutlich wird), dann ist die Interpretation des Haupteffekts des Wohnorts schwierig. Für interessierte Lesende wird in dem folgenden Kasten eine Beschreibung der unterschiedlichen Kombinationen an Signifikanzen gegeben.
Interpretation der Haupteffekte bei signifikanter Interaktion
Die Art der Interaktion wird in der Literatur in drei Bereiche aufgeteilt. Dabei wird zwischen ordinalen, disordinalen und semidisordinalen Interaktion unterschieden. Je nach Art ist die Interpretation der Haupteffekte zulässig, schwierig oder nicht zulässig.
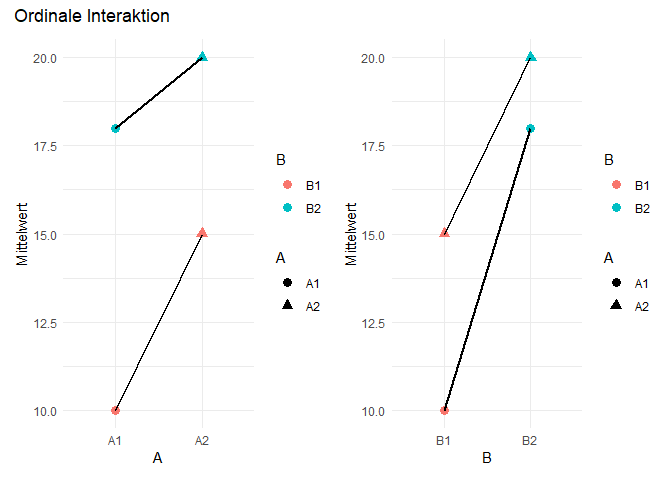
Beginnen wir in unserer Betrachtung mit einem ordinalen Interaktionseffekt. Dabei vereinfachen wir das Beispiel für die zweifaktorielle ANOVA auf Faktoren mit jeweils nur zwei Faktorstufen - es gibt also Faktor A mit den Stufen A1 und A2 und Faktor B mit den Stufen B1 und B2. Die beiden hier dargestellten Grafiken stellen die Mittelwerte der 4 Kombinationen aus zwei verschiedenen Perspektiven da - einmal mit A auf der x-Achse und einmal mit B auf der x-Achse.
## Warning: Paket 'patchwork' wurde unter R
## Version 4.3.2 erstellt
## Warning: Using `size` aesthetic for lines was
## deprecated in ggplot2 3.4.0.
## ℹ Please use `linewidth` instead.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()`
## to see where this warning was generated.
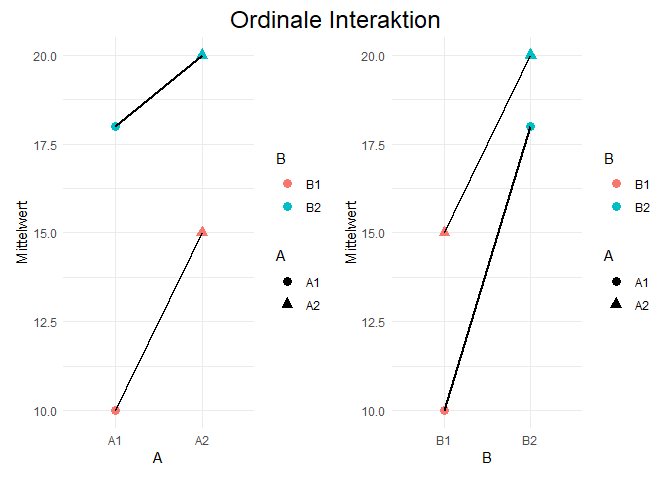
Die Farben zeigen uns stets den Faktor B an, die Formen den Faktor A. Die Linien verbinden immer die zusammengehörigen Faktorstufen auf dem Faktor, der nicht auf der x-Achse dargestellt ist. Ordinale Interaktion bedeutet nun, dass die bedingten Mittelwertsdifferenzen zwischen den Faktorstufen A (in diesem Fall A1 und A2) auf allen Stufen des Faktors B (B1 und B2) die gleichen Vorzeichen haben. Außerdem muss dasselbe für die bedingten Mittelwertsdifferenzen zwischen den Faktorstufen B (in diesem Fall B1 und B2) auf allen Stufen des Faktors A (A1 und A2) gelten.
In unserem Beispiel sind diese Ansprüche erfüllt. In der linken Grafik können wir sehen, dass die Differenz zwischen den Stufen A2 und A1 auf beiden Stufen von B positiv ist (A2 > A1). In der rechten Grafik ist die Differenz zwischen den Stufen B2 und B1 auf beiden Stufen von A ebenfalls positiv (B2 > B1).
Beim Vorliegen von ordinalen Effekten ist die Interpretation der Haupteffekte auch möglich, wenn die Interaktion signifikant ist.
Als zweites nehmen wir uns das Gegenteil - die disordinale Interaktion - vor. Auch hier zunächst eine grafische Darstellung des Falls mit der exakt selben Gestaltung wie eben.
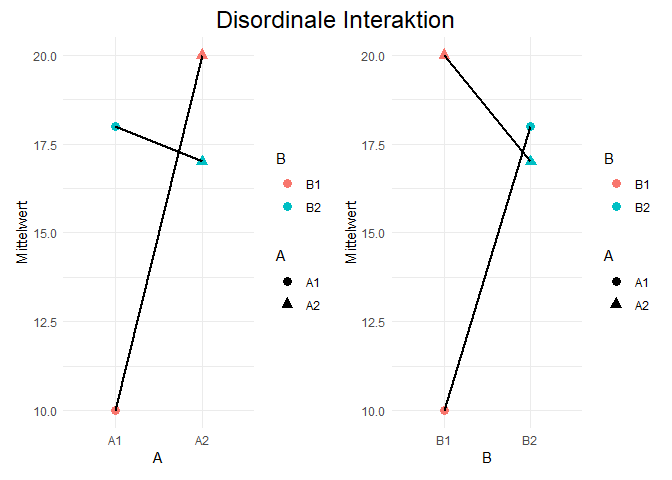
Bei einem disordinalen Interaktionseffekt ändert sich das Vorzeichen der bedingten Mittelwertsdifferenzen zwischen den Faktorstufen A (in diesem Fall A1 und A2) auf den Stufen des Faktors B (in diesem Fall B1 und B2). Weiterhin ändert sich das Vorzeichen der bedingten Mittelwertsdifferenzen zwischen den Faktorstufen B (in diesem Fall B1 und B2) auf den Stufen des Faktors A (in diesem Fall A1 und A2). In unserem Beispiel ist das der Fall, da die Differenz zwischen den Stufen A2 und A1 auf der Stufe B1 positiv ist (A2 > A1), aber auf der Stufe B2 negativ (A2 < A1). Das Gleiche gilt für die Differenz zwischen den Stufen B2 und B1 auf den Stufen von A. Auf der Stufe A1 ist die Differenz positiv (B2 > B1), auf der Stufe A2 negativ (B2 < B1).
Bei Vorliegen disordinaler Interaktionseffekte ist die Interpretation der Haupteffekte nicht zulässig - zumindest sollte nicht gesagt werden, dass eine Stufe des einen Faktors grundsätzlich höher ausgeprägt ist, da dies ja von der Ausprägung auf dem anderen Faktor abhängt.
Der letzte Fall ist die semidisordinale Interaktion. Auch hier zunächst eine grafische Darstellung des Falls mit der exakt selben Gestaltung wie eben.
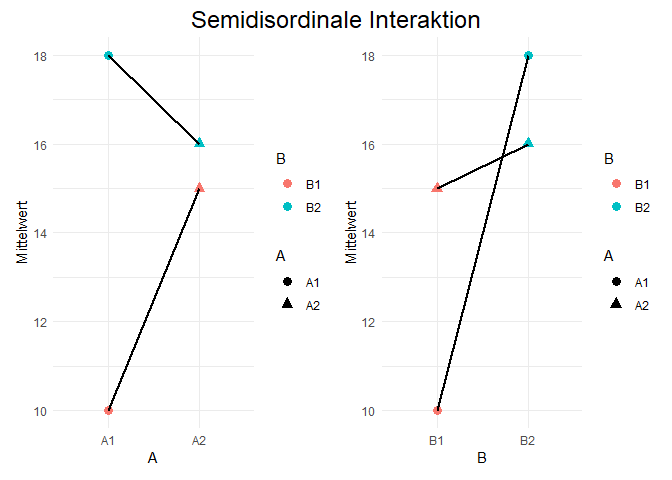
Der semidisordinale Interaktionseffekt ist eine Mischung aus den beiden vorherigen Fällen. Die bedingten Mittelwertsdifferenzen zwischen den Faktorstufen A (in diesem Fall A1 und A2) auf den Stufen des Faktors B (in diesem Fall B1 und B2) haben die gleichen Vorzeichen und die bedingten Mittelwertsdifferenzen zwischen den Faktorstufen B (in diesem Fall B1 und B2) auf den Stufen des Faktors A (in diesem Fall A1 und A2) haben unterschiedliche Vorzeichen - oder natürlich umgekehrt.
Auf den Abbildungen ist das der Fall - die Differenz zwischen den Stufen A2 und A1 auf der Stufe B1 ist positiv (A2 > A1), aber auf der Stufe B2 negativ (A2 < A1). Die Differenz zwischen den Stufen B2 und B1 auf der Stufe A1 ist positiv (B2 > B1), und auf der Stufe A2 ebenfalls positiv (B2 > B1).
Beim Vorliegen der semidisordinalen Interaktionseffekte ist die Interpretation der Haupteffekte besonders für den Faktor schwierig, bei dem die Vorzeichen wechseln, da hier wie bei der disordinalen Interaktion keine generelle Aussage getroffen werden kann. Bei der Interpretation des Faktors, bei dem die Vorzeichen gleich bleiben, kann hingegen eher eine Aussage getroffen werden, da hier die Haupteffekte auch für alle Stufen des anderen Faktors gelten.
Welche unterschiedlichen Kombinationen an Signifikanzen (der Haupt- und Interaktionseffekte) es gibt und was diese schematisch bedeuten, kann auch in Eid et al. (2017, p. 436, Abbildung 13.6) nachgelesen werden.
Post-Hoc-Analysen
Tukey-Test
Wie auch schon im letzten Tutorial können bei der zweifaktoriellen ANOVA mit der Tukeys Honest Significant Difference alle möglichen Gruppenkombinationen verglichen werden. Aufgrund der hohen Anzahl von insgesamt neun spezifischen Paarvergleichen ist es hier besonders wichtig, die Tukey-Vorgehensweise statt einer einfachen Bonferroni-Korrektur zu nutzen, um nicht zu viel Power zu verlieren. Allerdings stellt sich bei einem so großen Design die Frage, ob der stupide Vergleich aller Gruppen miteinander überhaupt sinnvoll ist. Denn dieser Ansatz setzt voraus, dass die Effekte in allen spezifischen Gruppen tatsächlich unterschiedlich sind. Wahrscheinlicher ist es jedoch, dass man gezielt bestimmte Muster oder Hypothesen verfolgt und daher nur ausgewählte Gruppenvergleiche durchführt. Trotzdem führen wir hier einmal die Tukey-Analyse durch – einerseits, um für Ausnahmefälle gewappnet zu sein, und andererseits, um die Schreibweise der zweifaktoriellen ANOVA im Paket zu üben.
Zunächst müssen wir unsere Analyse in ein Objekt ablegen.
zweifakt <- aov_4(EC ~ urban + edu + urban : edu + (1|id), data = conspiracy)
## Contrasts set to contr.sum for the following variables: urban, edu
Außerdem müssen wir wieder das Paket emmeans laden und die emmeans-Funktion verwenden, um die Post-Hoc-Analyse vorzubereiten.
library(emmeans)
emm_zweifakt <- emmeans(zweifakt, ~ urban + edu + urban : edu)
Die pairs()-Funktion erlaubt uns nun die Gegenüberstellung aller Gruppen. Als zusätzliches Argument, neben dem Objekt, brauchen wir nur die Aussage, dass die Vergleiche mit der Tukey-Methode korrigiert werden sollen.
tukey <- pairs(emm_zweifakt, adjust = "tukey")
tukey
## contrast
## rural not highschool - suburban not highschool
## rural not highschool - urban not highschool
## rural not highschool - rural highschool
## rural not highschool - suburban highschool
## rural not highschool - urban highschool
## rural not highschool - rural college
## rural not highschool - suburban college
## rural not highschool - urban college
## suburban not highschool - urban not highschool
## suburban not highschool - rural highschool
## suburban not highschool - suburban highschool
## suburban not highschool - urban highschool
## suburban not highschool - rural college
## suburban not highschool - suburban college
## suburban not highschool - urban college
## urban not highschool - rural highschool
## urban not highschool - suburban highschool
## urban not highschool - urban highschool
## urban not highschool - rural college
## urban not highschool - suburban college
## urban not highschool - urban college
## rural highschool - suburban highschool
## rural highschool - urban highschool
## rural highschool - rural college
## rural highschool - suburban college
## rural highschool - urban college
## suburban highschool - urban highschool
## suburban highschool - rural college
## suburban highschool - suburban college
## suburban highschool - urban college
## urban highschool - rural college
## urban highschool - suburban college
## urban highschool - urban college
## rural college - suburban college
## rural college - urban college
## suburban college - urban college
## estimate SE df t.ratio p.value
## -0.05151 0.1808 2442 -0.285 1.0000
## -0.26368 0.1951 2442 -1.352 0.9154
## -0.08009 0.1823 2442 -0.439 1.0000
## 0.08094 0.1701 2442 0.476 0.9999
## -0.19653 0.1732 2442 -1.135 0.9690
## 0.40371 0.1850 2442 2.182 0.4178
## 0.40376 0.1716 2442 2.353 0.3110
## 0.35068 0.1739 2442 2.016 0.5319
## -0.21217 0.1415 2442 -1.500 0.8560
## -0.02858 0.1233 2442 -0.232 1.0000
## 0.13245 0.1044 2442 1.269 0.9403
## -0.14502 0.1093 2442 -1.327 0.9235
## 0.45522 0.1272 2442 3.578 0.0106
## 0.45527 0.1068 2442 4.263 0.0007
## 0.40219 0.1105 2442 3.641 0.0085
## 0.18360 0.1434 2442 1.280 0.9371
## 0.34462 0.1275 2442 2.703 0.1473
## 0.06715 0.1316 2442 0.510 0.9999
## 0.66739 0.1468 2442 4.547 0.0002
## 0.66744 0.1295 2442 5.155 <.0001
## 0.61436 0.1325 2442 4.636 0.0001
## 0.16103 0.1070 2442 1.505 0.8534
## -0.11645 0.1118 2442 -1.042 0.9817
## 0.48380 0.1293 2442 3.741 0.0059
## 0.48385 0.1093 2442 4.426 0.0003
## 0.43077 0.1129 2442 3.816 0.0044
## -0.27747 0.0905 2442 -3.066 0.0561
## 0.32277 0.1115 2442 2.895 0.0902
## 0.32282 0.0875 2442 3.691 0.0070
## 0.26974 0.0919 2442 2.936 0.0809
## 0.60024 0.1161 2442 5.171 <.0001
## 0.60029 0.0933 2442 6.437 <.0001
## 0.54721 0.0974 2442 5.617 <.0001
## 0.00005 0.1137 2442 0.000 1.0000
## -0.05303 0.1172 2442 -0.453 1.0000
## -0.05308 0.0946 2442 -0.561 0.9998
##
## P value adjustment: tukey method for comparing a family of 9 estimates
Leider ist das Ergebnis etwas unübersichtlich, weil sich in diesem Fall 36 Vergleiche ergeben. Die erste Spalte zeigt jeweils, welche Gruppen verglichen wurden. Anschließend folgen Spalten für die Mittelwertsdifferenz, den Standardfehler, die Freiheitsgrade, die bestimmte Teststatistik und den korrigierten p-Wert. Beispielsweise könnte man erkennen, dass es signifikante Unterschiede zwischen Der Gruppe suburban / not highschool und der Gruppe suburban / college gibt, da der p-Wert kleiner als 0.05 ist.
Stattdessen können wir uns das Objekt auch sehr einfach plotten lassen:
plot(tukey)
Hier wäre es wichtig zu betrachten, welches Konfidenzintervall für die Mittelwertsdifferenz nicht die 0 enthält, um signifikante Unterschiede zu erkennen.
Spezifische Kontraste
Wie bereits erwähnt, ist es in Situationen mit vielen Gruppen eher unüblich, alle möglichen Vergleiche durchzuführen. Zum einen ist es aus theoretischer Perspektive selten plausibel, dass sich tatsächlich alle spezifischen Kombinationen voneinander unterscheiden. Zum anderen ist es aus methodischer Sicht auch wenig effizient, da die notwendige Korrektur des $\alpha-$Fehlerniveaus die Power stark reduzieren würde. An dieser Stelle bieten sich daher geplante Kontraste an: Mit ihnen können a-priori definierte, theoretisch relevante Vergleiche gezielt durchgeführt werden. So wird die Anzahl der Tests auf das Wesentliche beschränkt und die Korrektur weniger restriktiv, was insgesamt zu einer effizienteren Analyse führt.
Gehen wir einmal davon aus, dass Bildung auf College-Niveau beginnt, eigenständiges Denken und das kritische Abwägen von Informationsquellen stärker zu fördern – anders als Bildung auf niedrigeren Niveaus. Eine plausible Annahme wäre, dass insbesondere im College-Umfeld Kompetenzen wie Quellenbewertung, kritische Reflexion und analytisches Denken intensiv vermittelt werden. Daher könnte eine spezifische Hypothese in unserer Untersuchung lauten, dass sich Personen mit einem College-Abschluss hinsichtlich ihres Glaubens an Verschwörungstheorien über ein angebliches „extraterrestrisches Cover-up" von allen Personen mit einem niedrigeren Bildungsniveau unterscheiden. Diese Fragestellung müssen wir nun in einen passenden Kontrast überführen.
Um Kontraste definieren zu können, müssen wir zunächst in Erfahrung bringen, in welcher Reihenfolge die Gruppenkombinationen intern repräsentiert werden. Diese Reihenfolge können wir durch betrachten des Objektes emm_zweifakt herausfinden:
emm_zweifakt
## urban edu emmean SE df
## rural not highschool 2.31 0.1593 2442
## suburban not highschool 2.36 0.0856 2442
## urban not highschool 2.58 0.1126 2442
## rural highschool 2.39 0.0887 2442
## suburban highschool 2.23 0.0598 2442
## urban highschool 2.51 0.0680 2442
## rural college 1.91 0.0941 2442
## suburban college 1.91 0.0639 2442
## urban college 1.96 0.0698 2442
## lower.CL upper.CL
## 2.00 2.63
## 2.20 2.53
## 2.36 2.80
## 2.22 2.57
## 2.12 2.35
## 2.38 2.64
## 1.73 2.09
## 1.78 2.03
## 1.83 2.10
##
## Confidence level used: 0.95
Mithilfe eines 9 Elemente langen Vektors, in dem die Kontrastkoeffizienten stehen, können Kontraste festgelegt werden. In unserer Fragestellung sollen global die Mittelwerte der drei Gruppen, die college in ihrer Kombination haben, mit den 6 Gruppen, die not highschool oder highschool in ihrer Kombination haben, verglichen werden. Das bedeutet, dass die Koeffizienten für die Gruppen mit College-Abschluss positiv und die anderen negativ sein sollten. Eine weitere Voraussetzung für Kontrastkoeffizienten, die wir bereits kennen, lautet, dass sich die Koeffizienten zu 0 addieren müssen. Das bedeutet, dass die Summe der Koeffizienten für die Gruppen mit College-Abschluss bspw. 3 und die Summe der Koeffizienten für die anderen Gruppen -3 betragen muss. Daraus würde sich ergeben, dass alle Gruppen mit College-Abschluss den Koeffizienten 1 zugewiesen bekommen, während die anderen Gruppen den Koeffizienten -0.5 zugewiesen bekommen.
cont1 <- c(-0.5, -0.5, -0.5, -0.5, -0.5, -0.5, 1, 1, 1)
sum(cont1) == 0 # Check ob die Koeffizienten sich zu 0 addieren
## [1] TRUE
Die Nullhypothese, die durch diesen Vektor geprüft wird, lässt sich mithilfe der Reihenfolge der Gruppen leicht zusammenstellen. Wenn $j$ die drei Stufen von urban indiziert (1 = rural, 2 = suburban, 3 = urban) und $k$ die drei Stufen von edu (1 = not highschool, 2 = highschool, 3 = college), ist die durch cont1 festgelegte Nullhypothese:
$H_0: -0.5 \cdot \mu_{11} - -0.5 \cdot \mu_{21} + -0.5 \cdot \mu_{31} + -0.5 \cdot \mu_{12} + -0.5 \cdot \mu_{22} + -0.5 \cdot \mu_{32} + 1 \cdot \mu_{13} + 1 \cdot \mu_{23} + 1 \cdot \mu_{33} = 0$
Mit dem contrast-Befehl kann der festgelegte Kontrast geprüft werden, indem wir das Mittelwertsobjekt emm übergeben und anschließend die Gruppenzugehörigkeit via Kontrast als Liste list(cont1) übergeben:
contrast(emm_zweifakt, list(cont1))
## contrast
## c(-0.5, -0.5, -0.5, -0.5, -0.5, -0.5, 1, 1, 1)
## estimate SE df t.ratio p.value
## -1.41 0.182 2442 -7.762 <.0001
Der Kontrast zeigt uns hier ein signifikantes Ergebnis, was bedeutet, dass Personen, die auf dem College waren, sich signifikant von Personen unterscheiden, die nicht auf dem College waren.
Eine weitere interessante Forschungsfrage wäre hier, ob der Abstand zwischen den nicht-College Gruppen und der College Gruppe für die beiden Subgruppen rural und urban gleich groß ist. Damit kann getestet werden, ob der Effekt der höheren Bildung vielleicht vom Wohnort abhängt (diese Testung würde bei einem signifikanten Interaktionseffekt mehr Sinn machen, wird hier aber trotzdem durchgeführt). Stellen wir uns das Prinzip als Gleichung vor, um die Kontrastkoeffizienten zu vergeben:
$\frac{\mu_{11} + \mu_{12}}{2} - \mu_{13} = \frac{\mu_{31} + \mu_{32}}{2} - \mu_{33}$
Für die einfache Vergabe von Kontrastkoeffizienten sollte die Gleichung umgestellt werden:
$\frac{\mu_{11} + \mu_{12}}{2} - \mu_{13} - \frac{\mu_{31} + \mu_{32}}{2} + \mu_{33} = 0$
Daraus ergibt sich dann:
$H_0: 0.5 \cdot \mu_{11} + 0.5 \cdot \mu_{12} - 1 \cdot \mu_{13} - 0.5 \cdot \mu_{31} - 0.5 \cdot \mu_{32} + 1 \cdot \mu_{33} = 0$
Zugeordnet zur Reihenfolge der Gruppen also folgendes Muster:
cont2 <- c(0.5, 0, -0.5, 0.5, 0, -0.5, -1, 0, 1)
Weil sowohl cont1 als auch cont2 durchgeführt werden, muss für das multiple Testen der beiden korrigiert werden. Das kann dadurch erreicht werden, dass im contrast-Befehl alle Kontraste gleichzeitig eingeschlossen werden und mit adjust = 'bonferroni' z.B. die Bonferroni-Korrektur ausgewählt wird:
contrast(emm_zweifakt, list(cont1, cont2), adjust = 'bonferroni')
## contrast
## c(-0.5, -0.5, -0.5, -0.5, -0.5, -0.5, 1, 1, 1)
## c(0.5, 0, -0.5, 0.5, 0, -0.5, -1, 0, 1)
## estimate SE df t.ratio p.value
## -1.414 0.182 2442 -7.762 <.0001
## -0.137 0.162 2442 -0.844 0.7976
##
## P value adjustment: bonferroni method for 2 tests
Der erste Kontrast ist weiterhin signifikant, der zweite jedoch nicht Dieses Ergebnis ist aber auch nicht überraschend, da kein Interaktionseffekt in den Daten vorlag. Die Anzahl der geplanten Kontraste ist theoretisch endlos - der Fokus liegt hier auf den Erwartungen, die aus der Theorie abgeleitet werden.
Sollen Hypothesen möglichst effektiv getestet werden, sollten Kontraste orthogonal, das heißt voneinander unabhängig sein. Zwei orthogonale Kontraste erkennt man daran, dass die Summe aller gewichteten Kontrastprodukte gleich 0 ist. Bei geplanten Kontrasten ist dies jedoch selten der Fall, da die Fragestellungen bzw. Hypothesen, die man aus der Literatur ableitet, selten komplett voneinander unabhängig sind.
Reduzierte ANOVA
Nach einer signifikanten mehrfaktoriellen ANOVA können als Post-hoc Analyse auch weitere ANOVAs durchgeführt werden! Bspw. könnte es bei nicht signifikantem Interaktionseffekt von Interesse sein, in den Haupteffekten noch spezifischere Untersuchungen durchzuführen. Oder man reduziert bei signifikantem Interaktionseffekt die Anzahl der Ausprägungen auf beiden Faktoren, um spezifischere Aspekte des Interaktionseffektes zu untersuchen. Es zeigt sich: Die Möglichkeiten für Post-hoc-Analysen sind vielfältig und hängen stark von der Forschungsfrage ab.
Appendix A
Quadratsummen-Typ
Wie beschrieben, können bei mehrfaktoriellen ANOVAs die Quadratsummen auf unterschiedliche Arten berechnet werden.
Typ I
Typ I berücksichtigt in der Berechnung der Quadratsummen nur die vorherigen unabhängigen Variablen. Dies entspricht konzeptuell der sequenziellen Aufnahme von Prädiktoren in der Regression. In afex ist diese Berechnung gar nicht möglich, da man das Argument type nicht damit ansprechen kann.
aov_4(EC ~ urban + edu + urban : edu + (1|id), data = conspiracy, type = I)
## Contrasts set to contr.sum for the following variables: urban, edu
## Error in as.character(type): cannot coerce type 'closure' to vector of type 'character'
In der Fehlermeldung steht direkt drin, dass der Typ nicht unterstützt wird. Das deutet schonmal daraufhin, dass diese Einstellung nicht sinnvoll wäre. Um den Effekt zu betrachten, brauchen wir also ein anderes Paket - nutzen wir bspw. das Paket ez. Das müssen wir zunächst installieren und dann aktivieren.
install.packages("ez")
library(ez)
## Warning: Paket 'ez' wurde unter R Version
## 4.3.1 erstellt
In dem Paket wird die Funktion ezANOVA() verwendet, um eine ANOVA durchzuführen. Diese Funktion hat ein Argument type, welches die Quadratsummen-Typen angibt. Wir können also Typ I anfordern, indem wir type = 1 setzen. Weitere benötigte Argument sind der Datensatz, die abhängige Variable dv, die ID-Variable wid und die unabhängigen Variablen between. Diese müssen als Vektor angegeben werden, da wir hier eine mehrfaktorielle ANOVA durchführen wollen.
# QS-Typ 1, Reihenfolge 1
ezANOVA(conspiracy, dv = EC, wid = id, between = c(urban, edu), type = 1)
## Warning: Data is unbalanced (unequal N per
## group). Make sure you specified a
## well-considered value for the type argument
## to ezANOVA().
## Warning: Using "type==1" is highly
## questionable when data are unbalanced and
## there is more than one variable. Hopefully
## you are doing this for demonstration purposes
## only!
## $ANOVA
## Effect DFn DFd F p
## 1 urban 2 2442 3.5143726 2.991711e-02
## 2 edu 2 2442 36.0626891 3.672878e-16
## 3 urban:edu 4 2442 0.9624503 4.269191e-01
## p<.05 ges
## 1 * 0.002870013
## 2 * 0.028688059
## 3 0.001574014
# QS-Typ 1, Reihenfolge 2
ezANOVA(conspiracy, dv = EC, wid = id, between = c(edu, urban), type = 1)
## Warning: Data is unbalanced (unequal N per
## group). Make sure you specified a
## well-considered value for the type argument
## to ezANOVA().
## Warning: Using "type==1" is highly
## questionable when data are unbalanced and
## there is more than one variable. Hopefully
## you are doing this for demonstration purposes
## only!
## $ANOVA
## Effect DFn DFd F p
## 1 edu 2 2442 35.1355717 9.041526e-16
## 2 urban 2 2442 4.4414900 1.187368e-02
## 3 edu:urban 4 2442 0.9624503 4.269191e-01
## p<.05 ges
## 1 * 0.027971162
## 2 * 0.003624400
## 3 0.001574014
Die Reihenfolge der Prädiktoren spielt dabei eine Rolle, da die Quadratsummen in der Reihenfolge der Prädiktoren berechnet werden. Das heißt, dass die Quadratsumme für den ersten Prädiktor nur die Varianz erklärt, die nicht durch den zweiten Prädiktor erklärt wird. Daher ist es wichtig, in welcher Reihenfolge die Prädiktoren angegeben werden. Wir sehen deutlich, dass sich der $F$-Wert ändert, je nach dem in welcher Reihenfolge die Prädiktoren in die Gleichung genommen werden. Demnach kann es sein, dass die Reihenfolge die Signifikanzentscheidung beeinflusst.
Typ II und Typ 3 in ezANOVA()
Wie bereits beschrieben berücksichtigt Typ II in der Berechnung der Quadratsummen alle anderen unabhängigen Variablen. In der Berechnung der einzelnen Quadratsummen wird allerdings angenommen, dass alle Interaktionen, an denen dieser Term beteiligt ist, 0 sind. Typ II ist in ezANOVA() voreingestellt - im Gegensatz zu der Einstellung in aov_4().
# QS-Typ 2
ezANOVA(conspiracy, dv = EC, wid = id, between = c(urban, edu))
## Warning: Data is unbalanced (unequal N per
## group). Make sure you specified a
## well-considered value for the type argument
## to ezANOVA().
## Coefficient covariances computed by hccm()
## $ANOVA
## Effect DFn DFd F p
## 1 urban 2 2442 4.4414900 1.187368e-02
## 2 edu 2 2442 36.0626891 3.672878e-16
## 3 urban:edu 4 2442 0.9624503 4.269191e-01
## p<.05 ges
## 1 * 0.003624400
## 2 * 0.028688059
## 3 0.001574014
##
## $`Levene's Test for Homogeneity of Variance`
## DFn DFd SSn SSd F
## 1 8 2442 35.35671 1989.07 5.425973
## p p<.05
## 1 8.487496e-07 *
Typ III lässt sich auch durch eine einfache Einstellung in ezANOVA() anfordern. Dabei wird nicht angenommen, dass die Interaktionen 0 sind. Typ III ist z.B. auch in SPSS voreingestellt.
# QS-Typ 3
ezANOVA(conspiracy, dv = EC, wid = id, between = c(urban, edu), type = 3)
## Warning: Data is unbalanced (unequal N per
## group). Make sure you specified a
## well-considered value for the type argument
## to ezANOVA().
## Coefficient covariances computed by hccm()
## $ANOVA
## Effect DFn DFd F p
## 2 urban 2 2442 4.0803030 1.701771e-02
## 3 edu 2 2442 32.4467993 1.237413e-14
## 4 urban:edu 4 2442 0.9624503 4.269191e-01
## p<.05 ges
## 2 * 0.003330641
## 3 * 0.025886060
## 4 0.001574014
##
## $`Levene's Test for Homogeneity of Variance`
## DFn DFd SSn SSd F
## 1 8 2442 35.35671 1989.07 5.425973
## p p<.05
## 1 8.487496e-07 *
Appendix B
Voraussetzungen-Typ
Die Voraussetzungsprüfung für between-Subject Fragestellungen ist aktuell noch nicht optimiert in afex. Bspw. ist es hier auch nötig, mit dem Levene Test die Homoskedastizitätsannahme (in diesem Fall: die Varianz ist in allen 9 Gruppen identisch) zu prüfen.
Im auch in Anhang A genutzten Paket ez ist in der Funktion ezANOVA() die Prüfung der Homoskedastizität bereits integriert. Diese wird automatisch durchgeführt, wenn die ANOVA mit ezANOVA() durchgeführt wird. Auch eine Korrektur für eine signifikante Verletzung, wie sie bei dem hier verwendeten Datenbeispiel auftreten würde, ist eingebaut. Dabei handelt es sich um die HC3-Korrektur von MacKinnon & White (1985). Diese kann mit dem Argument white.adjust = TRUE aktiviert werden.
ezANOVA(conspiracy, dv = EC, wid = id, between = c(urban, edu), detailed = TRUE, white.adjust = TRUE)
## Warning: Data is unbalanced (unequal N per
## group). Make sure you specified a
## well-considered value for the type argument
## to ezANOVA().
## Coefficient covariances computed by hccm()
## $ANOVA
## Effect DFn DFd F p
## 1 urban 2 2442 3.9382419 1.960630e-02
## 2 edu 2 2442 37.0979365 1.344257e-16
## 3 urban:edu 4 2442 0.9677347 4.239611e-01
## p<.05
## 1 *
## 2 *
## 3
##
## $`Levene's Test for Homogeneity of Variance`
## DFn DFd SSn SSd F
## 1 8 2442 35.35671 1989.07 5.425973
## p p<.05
## 1 8.487496e-07 *
Literatur
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden (5. Auflage, 1. Auflage: 2010). Weinheim: Beltz.
- Blau hinterlegte Autorenangaben führen Sie direkt zur universitätsinternen Ressource.
](/media/header/heart_alien.jpg)