Einleitung
Die gewichtete Regression kann in Situationen nützlich sein, in denen die Datenpunkte unterschiedlich wichtig oder reliabel gemessen sind und wir sicherstellen wollen, dass wir nicht durch Verzerrungen in der Stichprobe oder Messfehler beeinflusst werden. Diese Methode ist besonders wertvoll, wenn es darum geht, die Repräsentativität der Stichprobe zu verbessern oder mit Heteroskedastizität umzugehen.
Es gibt verschiedene Anwendungsfälle, in denen die Gewichtung von Beobachtungen in der Regressionsanalyse sinnvoll sein kann. Zwei häufige Fälle sind:
- Sampling Representativity: Idealerweise soll die ausgewählte Stichprobe die Grundgesamtheit möglichst genau abbilden, aber in der Realität der Forschung ist das nicht immer der Fall. Oft haben wir als Forschende nur Gelegenheitsstichproben zur Verfügung. In der Umfragenforschung wird aber auch oft bewusst innerhalb verschiedener interessierender Populationsschichten (Strata - z.B. verschiedene Regionen oder Einkommensschichten), damit jede dieser Gruppen vertreten ist. Dann ist es erwünscht, die relativen Häufigkeiten der einzelnen Strata an jene in der Population anzugleichen, damit die Ergebnisse für die Population repräsentativ sind.
- Ein anderes Beispiel ist, wenn unsere Messungen Heteroskedastizität der Varianz und damit der Residuen aufweisen. Damit ist eine wichtige Voraussetzungen für die Regressionsanalyse nicht erfüllt. Eine Möglichkeit, mit diesem Problem umzugehen, besteht darin, bei der Durchführung einer Regression die Beobachtungen so zu gewichten, dass diejenigen mit einer geringen Fehlervarianz mehr Gewicht erhalten, da sie im Vergleich zu Beobachtungen mit einer größeren Fehlervarianz mehr Informationen enthalten.
Wir werden uns in diesem Tutorial auf den ersten Anwendungfall - die Bestimmung der Stichprobengewichte - konzentrieren, um das Grundprinzip der gewichteten Regression zu erklären, das auch auf andere Anwendungsszenarien übertragbar ist.
Gewichtete Regression
Wofür?
In der Forschung sind wir oft auf Gelegenheitsstichproben angewiesen, da die Ressourcen nicht ausreichen, um eine vollständig repräsentative Stichprobe zu erheben. Gelegenheitsstichproben bestehen aus den Personen, die gerade zur Verfügung stehen und teilnehmen möchten, wie z.B. Psychologiestudierende, die Versuchspersonenminuten sammeln. Allerdings gibt es auch schwerer zu erreichende und daher oft unterrepräsentierte Populationen. Inzwischen ist bekannt, dass Stichproben in der Psychologie überwiegend WEIRD sind (d.h. mehrheitlich an Probanden durchgeführt wurden, die aus “western, educated, industrial, rich and democratic societies” stammen; vgl. Henrich et al., 2010).
Daher kann es notwendig sein, eine eventuell mangelnde Repräsentativität zu korrigieren. Dies ist besonders dann wichtig, wenn die verwendeten demografischen Variablen mit wichtigen Erhebungsvariablen und/oder mit dem Antwortverhalten korreliert sind. Die gewichtete Regression bietet sich als Methode an, um eine solche Korrektur durchzuführen.
Ein populäres Beispiel aus der Umfrageforschung ist etwa die Vorhersage von politischen Einstellungen und Wahlen. Wang et al. (2015) ist es in einer Studie gelungen, Umfragedaten von Xbox-Nutzern zu verwenden, um das Ergebnis der US-Präsidentschaftswahlen 2012 vorherzusagen.
Die Stichprobe der Xbox-Spieler bestand zu 65% aus 18-29-Jährigen, und war mit 93 % überwiegend männlich - ganz anders als die Wählendenpopulation, die insgesamt nur zu 19 % 18-29-jährig und zu 47 % männlich war. Obwohl die ursprünglichen Daten also enorm verzerrt waren, konnten die Forscher durch eine geschickte Anwendung von Methoden Schätzwerte ermitteln, die mit den Werten aus tatsächlich repräsentativen, zufällig erhobenen Umfragen erstaunlich genau übereinstimmten. Das Verfahren, das sie verwendet haben, war natürlich etwas kompexer: Zuerst wurde untersucht, inwiefern demografische Charakteristika die befragten Eigenschaften innerhalb der Untergruppen vorhersagen. Diese Information wurde in einem zweiten Schritt verwendet, um je nach Region und demographischer Gruppe (auch Stratum genannt) die Regressionsgewichte festzulegen. Das nennt man auch Poststratifizierung. Falls Sie sich dafür interessieren, können Sie sich die komplette Studie unter diesem Link durchlesen.
Wir werden uns erstmal das Grundprinzip der Gewichtung, das für solche komplexeren Anwendungen vorausgesetzt wird, anschauen. In unserem Anwendungsfall wird jeder Person bzw. Beobachtung in der Umfrage ein Anpassungsgewicht zugewiesen, sodass die Verteilung der Merkmale mit der Verteilung in der Population übereinstimmt.
Ordinary Least Squares vs. Weighted Least Squares
In der Regressionsanalyse, die wir bisher kennengelernt haben, wird standardmäßig das Kleinste-Quadrate-Schätzverfahren (engl. ordinary least squares; OLS) angewandt. Bei der OLS-Regression werden die Regressionskoeffizienten $\hat{\beta}$ so geschätzt, dass die Summe der quadrierten Abweichungen der beobachteten $y_i$-Werte für jede individuelle Beobachtung $i$ von den vorhergesagten $ŷ_i$-Werten minimal wird:
OLS: $\hat{\beta} = \arg \min_{\beta} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2$
Im Anwendungsfall kann ein angepasstes, gewichtetes Kleinste-Quadrate-Schätzverfahren (engl. weighted least squares; WLS) genutzt werden. Beim gewichteten Verfahren wird jeder quadrierte Abweichungswert mit einem individuellen Gewicht $w_i$ multipliziert, sodass dann bei der Schätzung die Summe der gewichteten quadrierten Abweichungen minimiert.
WLS: $\hat{\beta} = \arg \min_{\beta} \sum_{i=1}^{n} w_i (y_i - \hat{y}_i)^2$
Wenn die Gewichte über die Beobachtungen hinweg konstant, d.h. für jede Beobachtung $w_i$ = 1 sind, entspricht diese Gleichung der gewöhnlichen OLS-Gleichung. Die Herausforderung besteht nun darin, die richtigen $w$-Gewichtskoeffizienten zu ermitteln. Für verschiedene Szenarien gibt es dafür verschiedene Methoden. Hier werden wir uns auf einen Fall konzentrieren, in dem wir Verteilung der interessierenden Merkmale in der Population bereits kennen.
Anwendungsbeispiel
Häufigkeitsverteilung von Merkmalen in der Stichprobe vs. Population
Um die Gewichtung durchzuführen, müssen wir die Häufigkeitsverteilung der interessierenden demografischer oder kategorialer Merkmale in unserer Stichprobe und in der zugrundeliegenden Population kennen und vergleichen. Typische Merkmale, die in solchen Analysen verwendet werden, sind Altersgruppe, Geschlecht, Familienstand oder Herkunft.
Für dieses Beispiel werden wir den Fragebogendatensatz aus dem ersten Semester fb22 (Link zur Beschreibung verwenden. Wir werden daraus die demografischen Variablen über das Geschlecht (geschl) und die Angaben darüber, ob die Studierenden einer Nebentätigkeit neben dem Studium nachgehen (job), verwenden. Außerdem interessieren wir uns im Besonderen für die Variablen Extraversion und Intelligenz, weshalb wir nur diese Variablen in den Datensatz aufnehmen.
# Einlesen des Datensatzes aus WiSe 22
load(url('https://pandar.netlify.app/daten/fb22.rda'))
# Nur die interessierenden Variablen reinnehmen
fb22 <- subset(fb22, select = c(geschl, job, extra, intel))
fb22 <- na.omit(fb22) # Entfernen der Beobachtungen mit NAs
Anschließend wandeln wir die kategorialen Daten noch in das korrekte Format mit entsprechenden Faktorlevels und -labels um.
# Geschlecht als Faktor
fb22$geschl <- factor(fb22$geschl, levels = c(1, 2,3 ),
labels = c("weiblich", "männlich", "anderes"))
# Job als Faktor
fb22$job <- factor(fb22$job, levels = c(1, 2),
labels = c("nein", "ja"))
Durch den Vergleich der beobachteten Häufigkeitsverteilung einer Variablen mit der Populationsverteilung können wir feststellen, ob die Umfragebeantwortung in Bezug auf diese Variable repräsentativ ist, oder ob es erhebliche Unterschiede in der Verteilung gibt. Schauen wir uns zunächst die Verteilung der relativen Häufigkeiten in der Stichprobe an, die wir uns mithilfe der table() und prop.table()-Funktionen anzeigen lassen können.
# Häufigkeitstabelle Merkmal
gender_sample <- table(fb22$geschl) |> prop.table()
gender_sample
##
## weiblich männlich anderes
## 0.837837838 0.155405405 0.006756757
job_sample <- table(fb22$job) |> prop.table()
job_sample
##
## nein ja
## 0.6486486 0.3513514
Aus Daten des HSI-Monitors finden wir heraus, dass im WiSe 2022/23 in Deutschland insgesamt 1,48 Mio. Frauen und 1,47 Mio. Männern studiert haben, was insgesamt Anteile von 50.16 % und 49.84 % ergibt. Wie wir es in einer Stichprobe aus Psychologiestudierenden erwarten würden, ist sie im Hinblick auf das Geschlecht (mit einer zu 83.78% weiblichen Stichprobe bei uns) stark verzerrt!
Das gilt auch für die Angaben zur Nebentätigkeit: In unserer Stichprobe haben 35.14% der Studierenden einen Nebenjob. Dagegen hat die DSW-Sozialerhebung 2022 herausgefunden, dass zum Erhebungszeitpunkt ganze 63% der Studierenden in Deutschland einer Nebentätigkeit nachgingen. (Diese hat zwar nicht die gesamte Population aller knapp 3 Mio. Studierenden erhoben, sondern “nur” 180,000; aber das reicht uns für die Zwecke unseres Beispiels trotzdem erstmal aus.)
Konzentrieren wir uns vorerst auf das Geschlecht, und speichern seine Populationsanteile für die weitere Bearbeitung erstmal als Objekte in R ab.
# Population der Studierenden in Deutschland 2022
studierende_total <- (1475633) + (1466282)
studierende_frauen <- 1475633
p_w <- (studierende_frauen / studierende_total) # 50.16 %
p_m <- 1 - p_w # 49.84 %
Zur Kategorie “Divers” liegen leider keine zuverlässigen Statistiken vor, denn diese Personen werden in Hochschulstatistiken immer per Zufallsprinzip den kategorien “männlich” oder “weiblich” zugeordnet. Das erfordert weitere Überlegungen dazu, inwiefern das aus methodischer Sicht ein Problem ist, bzw. die Frage, wie in Bezug auf ihr Geschlecht diverse Personen in Befragungen repräsentiert werden können, aber an dieser Stelle müssen wir diese Frage leider aussparen und aus Mangel an Information mit den beiden Geschlechtern weiterrechnen. Nach Entfernung der Kategorie anderes aus dem Datensatz können wir mit droplevels() auch das nicht mehr genutzte Faktorlevel entfernen, damit es bei den künftigen Analysen nicht mehr auftaucht:
# Geschlecht = "anderes" aus Datensatz inkl. Faktorlabels entfernen
fb22 <- fb22[fb22$geschl != "anderes", ]
fb22$geschl <- droplevels(fb22$geschl)
Führen wir zunächst eine Regression ohne Gewichtung zum Vergleich durch. Wir planen in unserer Mini-Studie die Annahme zu prüfen, dass Intelligenz im Zusammenhang mit dem Ausmaß an Extraversion stehen könnte.
# OLS-Regression
mod <- lm(extra ~ intel, fb22)
summary(mod)
##
## Call:
## lm(formula = extra ~ intel, data = fb22)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.6735 -0.4235 -0.0047 0.4141 1.5018
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.19949 0.33031 6.659 5.32e-10 ***
## intel 0.32468 0.09046 3.589 0.000453 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.69 on 145 degrees of freedom
## Multiple R-squared: 0.0816, Adjusted R-squared: 0.07527
## F-statistic: 12.88 on 1 and 145 DF, p-value: 0.0004528
Das lineare Modell zeigt in der Tat, dass Intelligenz einen signifikanten Anteil der Varianz ($R^2$ = 0.08, $p < 0.001$) in der Extraversion erklärt, und diese positiv mit Extraversion zusammenhängt.
Bestimmung der Gewichte
Das Gewicht, mit dem wir die Beobachtungen aus der $j$-ten Untergruppe versehen werden, ermitteln wir nun, indem wir die relative Häufigkeit in der Population durch die relative Häufigkeit in der Stichprobe teilen:$$ w_j = \frac{p_{j(pop)}}{p_{j(sample)}} $$
Für $j$ = Geschlecht machen wir das so:
# Berechnung der Gewichte
weight_w <- p_w / gender_sample["weiblich"]
weight_m <- p_m / gender_sample["männlich"]
weight_w
## weiblich
## 0.5986711
weight_m
## männlich
## 3.207165
Wir erkennen, dass Beobachtungen aus einer unterrepräsentierten Gruppe ein $w_j > 1$ haben und damit stärker gewichtet werden. Die überrepräsentierte Gruppe bekommt ein $w_j < 1$. In unserem Fall bekommt die Gruppe der Männer ein $w_m$ = 3.21, die Antworten der Männer werden also ganze dreimal so stark gewichtet, wie sie es in der OLS-Regression wären!
Gewichtsvariable definieren
Die individuellen Gewichte $w_{ij}$ für jede Beobachtung $i$ und Ausprägung der Gruppe $j$ werden in einer Hilfsvariable gespeichert, die die gleiche Länge hat wie die Stichprobe groß ist.
# Gewichtung nach Geschlecht
fb22$weight_gender <- ifelse(fb22$geschl == "weiblich", weight_w, weight_m)
Was hier passiert ist, dass für jede Beobachtung in der Stichprobe mit der ifelse-Funktion geprüft wird, ob sie weiblich ist. Wenn ja, wird das entsprechende Gewicht für Frauen in die neue Spaltenvariable fb22$weight_gender gepackt, andernfalls - da wir nur zwei Gewichte zur Auswahl haben - das Gewicht für Männer.
Schauen wir uns die neue Variable im Datensatz an, um uns zu vergewissern, dass wir alles richtig gemacht haben:
head(fb22)
## geschl job extra intel weight_gender
## 1897 weiblich nein 2.75 4.75 0.5986711
## 1898 männlich ja 3.75 4.00 3.2071647
## 1899 männlich nein 4.25 5.00 3.2071647
## 1900 männlich nein 4.00 4.75 3.2071647
## 1901 weiblich nein 2.50 3.50 0.5986711
## 1903 männlich ja 2.75 4.00 3.2071647
Super! Diese Variable können wir jetzt in der lm-Funktion mit der Nutzung des zusätzlichen Arguments weight einfach einbauen:
# WLS-Regression
mod_gender <- lm(extra ~ intel, fb22, weights = weight_gender)
summary(mod_gender)
##
## Call:
## lm(formula = extra ~ intel, data = fb22, weights = weight_gender)
##
## Weighted Residuals:
## Min 1Q Median 3Q Max
## -2.67789 -0.32602 0.01376 0.48721 2.71812
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.53459 0.36418 4.214 4.39e-05 ***
## intel 0.48691 0.09656 5.043 1.35e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.7247 on 145 degrees of freedom
## Multiple R-squared: 0.1492, Adjusted R-squared: 0.1433
## F-statistic: 25.43 on 1 and 145 DF, p-value: 1.351e-06
Der Zusammenhang besteht nach wie vor, aber wir sehen, dass sich u.A. das $\beta$ für Intelligenz und auch das $R^2$ etwas verändert haben. Nehmen wir das Ganze unter die Lupe:
summary(mod)$r.squared # R²
## [1] 0.08160002
summary(mod_gender)$r.squared # gewichtetes R²
## [1] 0.1491958
Wir erkennen, dass das gewichtete Modell mit 14.92% nun zumindest deskriptiv mehr Varianz erklärt als das ungewichtete Modell (8.16%).
coef(mod)[2]
## intel
## 0.324681
coef(mod_gender)[2]
## intel
## 0.4869078
Auch der Koeffizient für Intelligenz ist im gewichteten Modell deskriptiv ein wenig größer geworden.
Vorsicht: Entscheidungskriterien wie die anova()-Funktion für den Modellvergleich sind hier nicht geeignet, denn die Modelle sind nicht geschachtelt! Wir haben bereits gelernt, dass wir für den Modellvergleich auch Modellauswahlkriterien wie AIC und BIC nutzen können. Aber auch diese wären hier nur bedingt aussagekräftig, da sie den Modellfit mithilfe der Anzahl der geschätzten Modellparameter (der UVs bzw. ihrer Intercepte) ermitteln, aber nicht die Gewicht oder die Represäntativität als solche in die Bewertung einbeziehen.
Die Entscheidung, ob unser neues WLS-Modell prädiktive Validität besitzt, ließe sich am ehesten noch mithilfe von Kreuzvalidierung - der Erprobung der Vorhersagekraft an einem anderen [Teil-]Datensatz - oder durch den Abgleich mit anderen externen Kriterien bestimmen, z.B. bei der Vorhersage von Wahlergebnissen mit den tatsächlichen Wahlergebnissen am Wahltag.
Grafische Darstellung
In der folgenden Grafik ist dargestellt, wie sich die Regressionsgerade des gewichteten Modells im Gegensatz zum ungewichteten Modell verhält.
# Scatter-Plot mit ggplot2
library(ggplot2)
p <- ggplot(fb22, aes(x = intel, y = extra, color = geschl)) +
geom_point() +
# Regressionslinie und SE-Band für mod (ungewichtetes Modell)
geom_smooth(method = "lm", se = TRUE, aes(color = "ungewichtet"),
lty = "dotdash", alpha = 0.2) + # Linientyp und Transparenz für SE
# Regressionslinie und SE-Band für mod_gender (gewichtetes Modell)
geom_smooth(method = "lm", se = TRUE,
aes(weight = weight_gender, color = "gewichtet"),
alpha = 0.2) + # Transparenz für SE
labs(x = "Intelligenz", y = "Extraversion", color = "Modell") +
theme_minimal() +
scale_color_manual(values = c("gewichtet" = "#ad3b76", # Farben für Legende
"ungewichtet" = "#00618F"))
# Plot anzeigen
print(p)
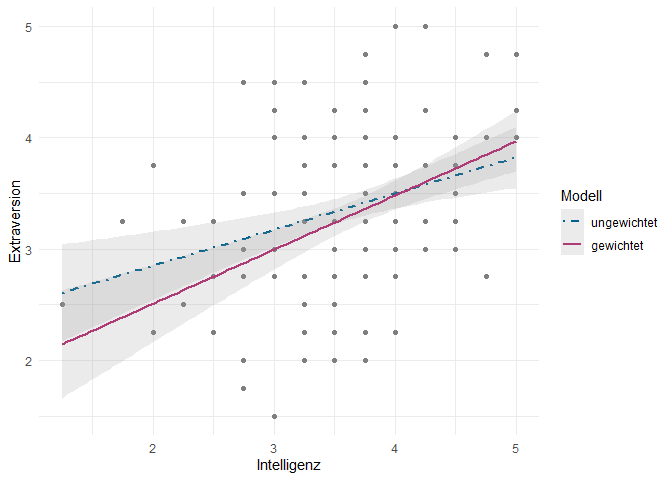
Die SE-Bänder überlappen sich und schließen die jeweils andere Regressionsgerade mit ein. Das kann man als Hinweis darauf interpretieren, dass die beiden Modelle sich in ihrer Vorhersagekraft nicht signifikant unterscheiden und beide im Hinblick auf die gegebenen Daten adäquat sind.
Um trotzdem nochmal zu verdeutlichen, weshalb die Steigung des WLS-Modells sich vom OLS-Modell unterscheidet, lohnt sich ein Blick auf die folgende Grafik. In diesem Plot sind die Beobachtungen der Männer - die stärker gewichtet sind als die der Frauen - und ihre Residuen in der Farbe des WLS-Modells hervorgehoben. Aufgrund ihres höheren Gewichts “ziehen” sie die Regressionsgerade stärker zu sich hin als die anderen Punkte. Außerdem haben wir die Datenpunkte ein bisschen verschoben (“Jitter”), um Überlappungen zu vermeiden, damit Sie die einzelnen Datenpunkte besser erkennen können. Der Code für diese Grafik mit einer zusätzlichen Erklärung ist im Appendix zu finden.
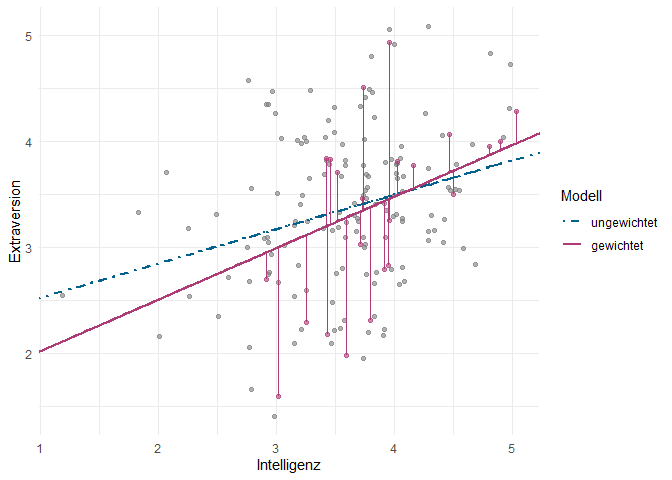
Es erinnert uns möglicherweise etwas an die Darstellung eines Interaktionseffekts aus den vergangenen Sitzungen. Jedoch ist der Effekt der Gewichtung von einem Interaktionseffekt abzugrenzen, da auch die Zielsetzung der gewichteten Regression unterschiedlich ist. Hier untersuchen wir nicht den Effekt, den eine Kovariate auf die abhängige Variable hat - dieser wird in der WLS-Regression gar nicht geschätzt.
Die Zielsetzung ist es vielmehr, die Stichprobe und die Zusammenhänge, die wir aus dieser schätzen, möglichst repräsentativ für die Grundgesamtheit zu machen und dafür zu sorgen, dass die Ergebnisse die gesamte Population besser widerspiegeln - insbesondere, wenn bestimmte Gruppen in unserer Stichprobe über- oder unterrepräsentiert sind.
Inhaltliche Interpretation
Inhaltlich könnten wir also festhalten, dass wir durch die Anwendung der gewichteten Regression in unserem Beispiel den Zusammenhang zwischen Intelligenz und Extraversion – den wir anhand einer Gelegenheitsstichprobe von 147 Psychologiestudierenden untersucht haben – so schätzen können, dass er möglichst repräsentativ für die gesamte Studierendenpopulation in Deutschland ist. Dabei haben wir die Verzerrung durch die Überrepräsentation von Frauen berücksichtigt. Hierbei zeigt sich, dass mit einer höheren Intelligenz auch ein höheres Ausmaß an Extraversion einhergeht.
Dieser Zusammenhang ist im gewichteten Modell deskriptiv etwas höher. Die Tatsache, dass sich die SE-Bänder der beiden Regressionslinien überlappen, deutet darauf hin, dass die Schätzungen der beiden Modelle nicht signifikant unterschiedlich sind. Zwar haben wir mit der gewichteten Regression eine Anpassung vorgenommen, um die Überrepräsentation von Frauen zu korrigieren, aber die grundlegenden Muster und Beziehungen in den Daten scheinen sich nicht fundamental zu unterscheiden.
Gewichtung mit > 1 Variable
Wenn wir mehr Variablen zur Gewichtung heranziehen, kann die Schätzung potenziell genauer werden. Je mehr Variablen einbezogen werden, desto mehr Kombinationen von Untergruppen entstehen, was zu einer großen Anzahl möglicher Kombinationen führen kann. Am Beispiel einer 2x2-Tabelle können wir uns das verdeutlichen. Wenn wir die hinsichtlich ihrer Häufigkeit ebenso verzerrte Variable der Nebentätigkeit einbeziehen, dann sieht die Häufigkeitstabelle in unserer Ersti-Stichprobe so aus:
table(fb22$geschl, fb22$job) |> prop.table() |> round(2)
##
## nein ja
## weiblich 0.56 0.29
## männlich 0.09 0.07
Idealerweise sollte uns bekannt sein, wie viel Prozent der Männer und Frauen in der gesamten Population der Studierenden jeweils einen Nebenjob haben. Tun wir für einen Moment so, als sei es uns tatsächlich bekannt. Die Verteilung in der Grundgesamtheit könnte dann wie folgt aussehen:
| Geschlecht | Kein Nebenjob | Nebenjob |
|---|---|---|
| Weiblich | 32.38% | 50.75% |
| Männlich | 4.63% | 12.25% |
Haben wir diese Informationen, so ist es wiederum möglich, diese für die Gewichtung heranzuziehen. In diesem Fall hätten wir also nicht nur zwei, sondern vier verschiedene Gewichte, die wir jeder Beobachtung in der Stichprobe zuweisen würden - je nachdem, welcher der vier Zellen in der oberen Tabelle sie zugehörig ist. Somit wäre das gewichtete Ergebnis in Bezug auf Geschlecht und Arbeitsstatus repräsentativ. Genauer gesagt wäre es sogar repräsentativ in Bezug auf den Arbeitsstatus innerhalb jeder Geschlechterkategorie, und repräsentativ in Bezug auf das Geschlecht innerhalb jeder Arbeitskategorie.
Je feingliedriger unsere Stratifizierung, desto genauer können wir die Schätzungen also machen. Falls wir z.B. drei Variablen mit 2 Ausprägungen hätten, hätten wir schon $2^3 = 8$ verschiedene Zellen. Und so lässt sich das Prinzip auf beliebig viele Variablen erweitern. Wang et al. (2015) kamen in ihrer Studie mit Xbox-Spielern auf ganze 76,256 (!) Zellen. So weit wollen wir aber erst einmal nicht gehen und an dieser Stelle reicht es uns, festzuhalten, dass diese potenzielle Feingliedrigkeit und Möglichkeit, auf vielfältige Art und Weise nach Relevanz der Datenpunkte zu gewichten, die Stärke der gewichteten Regression ausmacht.
Weitere Arten der Gewichtung
Inverse Probability Weighting: Wenn Häufigkeit in der Population unbekannt ist, aber die Wahrscheinlichkeit bekannt ist, dass eine Beobachtung in die Stichprobe (bzw. ein Stratum innerhalb der Stichprobe) aufgenommen wird, kann der Kehrwert dieser Wahrscheinlichkeit als Gewicht verwendet werden. Der Kehrwert der Wahrscheinlichkeit $p$, dass $i$-te Beobachtung aus der $j$-ten Kategorie in die Stichprobe aufgenommen wird, ergibt dann das Gewicht $w_i = 1/p_{ij}$. Diese Methode kann bei komplexen Stichprobenmethoden, z.B. in der Umfrageforschung, zur Anwendung kommen, bei denen ein komplexer Stichprobenerhebungsplan Quoten zur Erhebung bestimmter Untergruppen vorgibt.
Precision weights: Wenn manche Datenpunkte eine höhere Variabilität haben als andere, ist die Voraussetzung der Homoskedastizität - der konstanten Varianz der Residuen - nicht erfüllt. Präzisionsgewichte werden verwendet, um unterschiedliche Grade der Reliabilität oder Präzision in den Beobachtungen zu berücksichtigen. Diese Gewichte reflektieren die Genauigkeit oder Zuverlässigkeit der einzelnen Beobachtungen. Diese Art von Gewichten werden etwa bei Metaanalysen verwendet, um Studien mit einer höheren Reliabilität (und geringerer Variabilität) stärker zu gewichten.
Fazit
Wir haben in diesem Tutorial eine Methode kennengelernt, die es uns ermöglicht, mit einer eventuell verzerrten Stichprobe ein repräsentatives Regressionsmodell zu berechnen. Die WLS-Regression trägt dem Rechnung, dass manche Datenpunkte mehr Informationsgehalt in sich tragen als andere und sie je danach gewichtet werden können.
Jedoch kann es auch problematisch sein, wenn besonders selten auftretende Gruppen sehr stark gewichtet werden. Naturgemäß fallen insbesondere Beobachtungen in Zellen, deren Häufigkeit in der Stichprobe sehr klein ist (sogenannte “sparse cells”) stark ins Gewicht. Dadurch können aber auch kleine Schwankungen in Merkmalen, die man bei der Gewichtung ggf. nicht berücksichtigt hat, die Ergebnisse im Umkehrschluss verzerren.
Unser Beispiel war natürlich sehr vereinfacht: Mit Sicherheit haben Psychologiestudierende noch weitere Merkmale außer Geschlecht und Nebentätigkeit, die sich nicht ohne Weiteres auf die Gesamtbevölkerung aller Studierenden extrapolieren lassen. Je mehr verschiedene demografische Eigenschaften, von denen man annimmt, dass sie mit den interessierenden Variablen zusammenhängen (so wie Wang et al. dies für die Stichprobe der Xbox-Spieler eindrucksvoll demonstriert haben) in die Gewichtung einbezieht, desto mehr kann man hierfür kompensieren. Aber auch eine umfassende Gewichtung kann einen guten Stichprobenerhebungsplan und eine sinnvolle Ausreißerdiagnostik nicht vollumfänglich ersetzen.
Appendix
Code zum detaillierten Scatterplot
# Scatter-Plot mit ggplot2
# Filter für männliche Beobachtungen
fb22_male <- fb22[fb22$geschl == "männlich", ]
set.seed(36) # Für Reproduzierbarkeit
# "Jitter", um Punkte leicht zu verschieben, damit sie besser sichtbar sind
jitter_width <- 0.1
jitter_height <- 0.1
fb22_male$jittered_intel <- fb22_male$intel + runif(nrow(fb22_male), -jitter_width, jitter_width)
fb22_male$jittered_extra <- fb22_male$extra + runif(nrow(fb22_male), -jitter_height, jitter_height)
# Berechnung der vorhergesagten Werte für die jittered intel-Werte
fb22_male$predicted_weighted_jittered <- predict(mod_gender, newdata = data.frame(intel = fb22_male$jittered_intel))
# Extrahieren der Koeffizienten für die Modelle
coef_unweighted <- coef(mod)
coef_weighted <- coef(mod_gender)
# Neuer Plot mit Jitter und eingezeichneten Residuen für Männer
p2 <- ggplot(fb22, aes(x = intel, y = extra, color = geschl)) +
geom_point(position = position_jitter(width = jitter_width, height = jitter_height),
alpha = 0.6) + # Transparenz
# Regressionslinie und SE-Band für mod (ungewichtetes Modell)
# Behalten wir für eine leichtere Darstellung der Legende
geom_smooth(method = "lm", se = F, aes(color = "ungewichtet"),
lty = "dotdash", alpha = 0.2) + # Linientyp und Transparenz des SE-Bandes
# Regressionslinie und SE-Band für mod_gender (gewichtetes Modell)
geom_smooth(method = "lm", se = F,
aes(weight = weight_gender, color = "gewichtet"),
size = 1, alpha = 0.2) +
# Punkte für männliche Beobachtungen in der Farbe des gewichteten Modells
geom_point(data = fb22_male, aes(x = jittered_intel, y = jittered_extra),
color = "#ad3b76", alpha = 0.6) +
# Residuen für männliche Beobachtungen in der Farbe des gewichteten Modells
geom_segment(data = fb22_male,
aes(x = jittered_intel, xend = jittered_intel, # Beginn und Ende der Linie
y = jittered_extra, yend = predicted_weighted_jittered),
color = "#ad3b76", linetype = "solid") +
# Hinzufügen erweiterter Reg.linien, die bis zum Rand der Grafik gehen,
# für bessere Sichtbarkeit
geom_abline(intercept = coef_unweighted[1], slope = coef_unweighted[2],
linetype = "dotdash", size = 1, color = "#00618F") +
geom_abline(intercept = coef_weighted[1], slope = coef_weighted[2],
size = 1, color = "#ad3b76") + # Dicke und Farbe
labs(x = "Intelligenz", y = "Extraversion", color = "Modell") +
theme_minimal() +
scale_color_manual(values = c("gewichtet" = "#ad3b76", # Farben in der Legende
"ungewichtet" = "#00618F"))
# Plot anzeigen
print(p2)
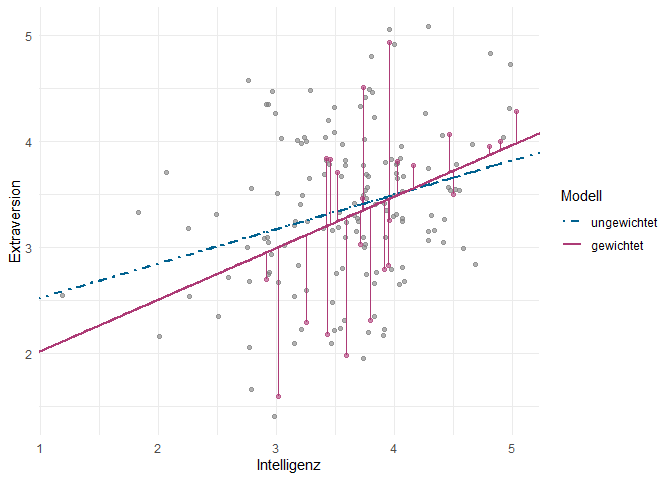
Literatur
Wang, W., Rothschild, D., Goel, S., & Gelman, A. (2015). Forecasting elections with non-representative polls. International Journal of Forecasting, 31(3), 980–991. https://doi.org/10.1016/j.ijforecast.2014.06.001
Wooldridge, J. M. (2010). Stratified Sampling. In Econometric analysis of cross section and panel data (2. ed., pp. 854-862). MIT Press. Link zur elektronischen Ressource
](/media/header/kettlebells.jpg)