[Courtesy of pexels](https://www.pexels.com/photo/aerial-view-of-road-in-the-middle-of-trees-1173777/)

Nichtlineare Regression

Martin Schultze, Julien P. Irmer, Johannes Hartig, Talha Sajjad

Zuletzt aktualisiert am 9. Juni. 2025 Statistik II

Einleitung

In der multiplen Regression haben wir uns bisher mit Modellen beschäftigt, die den linearen Zusammenhang zwischen einer abhängigen Variablen und einer Reihe von unabhängigen Variablen abbilden. In dieser Sitzung werden wir uns nun mit nichtlinearen Effekten in Regressionsmodellen befassen, insbesondere mit quadratischen Zusammenhängen und logaritmischen Effekten. Diese Sitzung basiert zum Teil auf der Literatur aus Eid et al. (2017) Kapitel 19 (insbesondere 19.9).

Quadratische Zusammenhänge

Datenbeispiel: Vegane Ernährung

Weil wir uns in diesem Beitrag mit zwei sehr unterschiedlichen Zusammenhangsformen befassen, benötigen wir auch zwei unterschiedliche Datenbeispiele. Für die quadratischen Zusammenhänge verwenden wir den Datensatz aus dem letzten Beitrag erneut. In den Daten von Stahlmann et al. (2024), geht es um die Beweggründe für und Commitment zu veganer bzw. vegetarischer Ernährung. Wir betrachten hier nur den Teildatensatz der Personen, die sich vegan ernähren (den vollen Datensatz gibt es im OSF-Repo zum Artikel). Die Datenaufbereitung und -auswahl habe ich in einem R-Skript hinterlegt, das Sie direkt ausführen können:

# Datensatz laden
source("https://pandar.netlify.app/daten/Data_Processing_vegan.R")

Für diesen Beitrag beschränken wir uns erst einmal auf die Vorhersage des Commitments zu veganer Ernährung (commitment) durch Einstellungen bezüglich des Tierwohls und der Tierrechte (animals).

Detektieren von Non-Linearität

In den meisten Fällen, in denen nicht-lineare Effekt in Regressionsmodelle aufgenommen werden, sollte das aufgrund inhaltliche Überlegungen passieren. So könnte man z.B. vermuten, dass sehr hohe und sehr niedrige Arbeitsanforderungen mit geringer Arbeitszufriedenheit, als “mittel” eingeschätzte Anforderungen aber mit hoher Zufriedenheit einhergehen. In solchen Fällen sollten wir non-lineare Effekte nicht aus Ergebnissen der Regressionsdiagnostik ableiten, sondern explizit Testen (wie wir es im nächsten Schritt tun werden).

In Fällen, in denen wir aber nicht zwingend mit Abweichungen von der Linearität rechnen, ist es trotzdem sinnvoll zu prüfen, ob das von uns posutlierte Modell (mitsamt seiner Linearitätsannahme) auch angemessen ist. Im letzten Beitrag hatten wir dafür bereits Residuenplots genutzt.

Ein kurzer Recap mit einem einfachen Modell, in dem wir commitment zur veganen Ernährung durch Einstellungen zum Tierwohl (animals) vorhersagen:

# Einfache lineare Regression
mod_lin <- lm(commitment ~ animals, data = vegan)

# Ergebnisse
summary(mod_lin)

## 
## Call:
## lm(formula = commitment ~ animals, data = vegan)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.3969 -0.3969  0.2698  0.6031  2.3150 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  2.01078    0.16328   12.31   <2e-16 ***
## animals      0.34087    0.02524   13.50   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.9051 on 985 degrees of freedom
## Multiple R-squared:  0.1562,	Adjusted R-squared:  0.1554 
## F-statistic: 182.4 on 1 and 985 DF,  p-value: < 2.2e-16

Wir sehen hier, dass der lineare Effekt ca. 16% der Unterschiede im Commitment aufklären kann. Zur Prüfung der Linearitätsannahme hatten wir dann im letzten Beitrag residualPlots() aus dem car-Paket verwendet. Für diesen Fall reicht uns der Befehl mit der Einzahl (also residualPlot()), weil wir nur eine UV haben:

# car laden
library(car)

## Loading required package: carData

# Residuenplot
residualPlot(mod_lin)

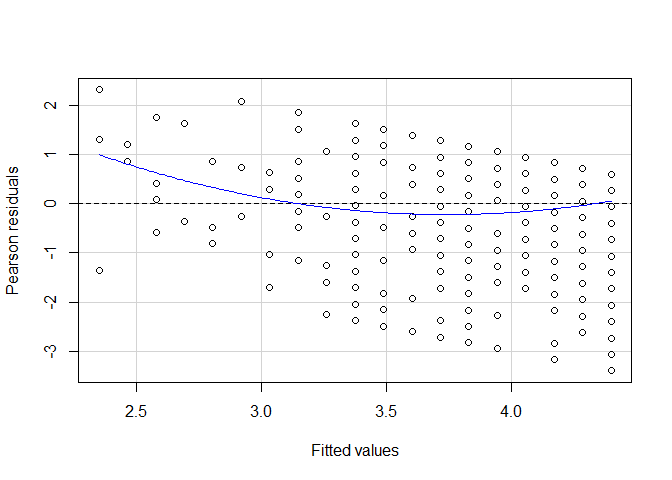
Die eingezeichnete blaue Linie stellt den quadratischen Effekt dar, wenn wir ihn explizit annehmen würden. Das ist zunächst keine Aussage darüber, ob diese Annahme korrekt ist - es könnten auch weitaus komplexere Muster vorliegen. Aber, in diesem Fall sehen wir zumindest, dass die Residuen der einfachen linearen Regression in einem quadratischen Zusammenhang mit den vorhergesagten Werten zu stehen scheinen. Wenn die linie horizontal wäre, würde kein solcher Zusammenhang bestehen.

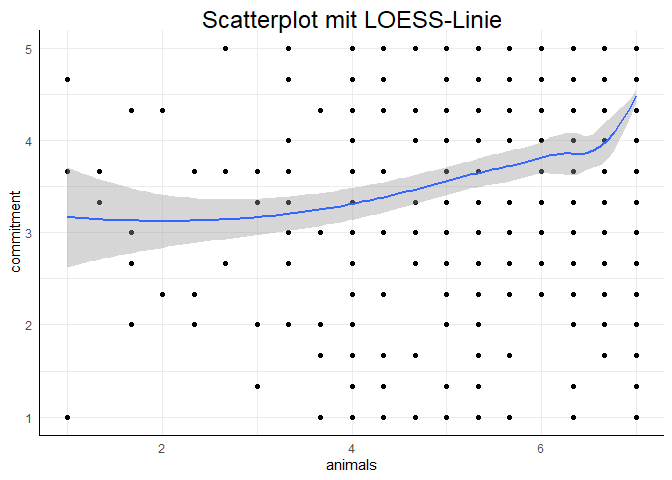
Ein anderer, häufig genutzter Ansatz sind sogenannte LOESS-Linien. Bei diesen handelt es sich um lokale Schätzer für die Zusammanhangsstruktur. Gemeint ist damit, dass an jeder Stelle der x-Achse ein nicht-lineares Regressionsmodell aufgestellt wird, welches nur die “Umgebung” (also z.B. die nähesten 50 Beobachtungen auf der x-Achse) berücksichtigt, um so detailliert die tatsächlichen Zusammenhangsstrukturen in einem Datensatz abzubilden. Dieses Vorgehen ist in der Datenexploration so gängig, dass es in ggplot z.B. die Voreinstellung ist:

# ggplot2 laden
library(ggplot2)

# Scatterplot mit LOESS-Linie
ggplot(data = vegan, aes(x = animals, y = commitment)) +
  geom_point() +
  geom_smooth() +
  labs(title = "Scatterplot mit LOESS-Linie")

## `geom_smooth()` using method = 'loess' and formula = 'y ~ x'

Wir sehen auch hier die Krümmung der Linie, die auf einen quadratischen Term hindeuten könnte. Außerdem gibt es kurz vor Ende der Skala noch einen kleinen Knick. Insbesondere bei so explorativen und lokalen Verfahren wie LOESS sollten solche Details nicht ohne Vorsicht interpretiert werden. Hier kann sich schnell sogenanntes overfitting einschleichen - also die zu starke Anpassung eines Modells an die Besonderheiten dieses spezifischen Datensatzes, sodass die Ergebnisse sich nicht generalisieren lassen.

Aufnahme eines quadratischen Effekts

Wenn im Kontext der Regression von quadratischen Effekten gesprochen wird, ist eigentlich fast immer gemeint, dass sowohl der lineare als auch der quadratische Einfluss einer Variable in die Regressionsgleichung aufgenommen wird:

$y_{m} = β_{0} + β_{1} x_{m} + β_{2} x_{m}^{2} + ε_{m}$

So wird erlaubt, dass sowohl lineare Trends als auch Krümmungen dieser Gerade abgebildet werden. Eine detaillierte Beschreibung der drei Koeffizienten verbirgt sich in dieser ausklappbaren Infobox:

Auswirkungen der drei Parameter im quadratischen Modell

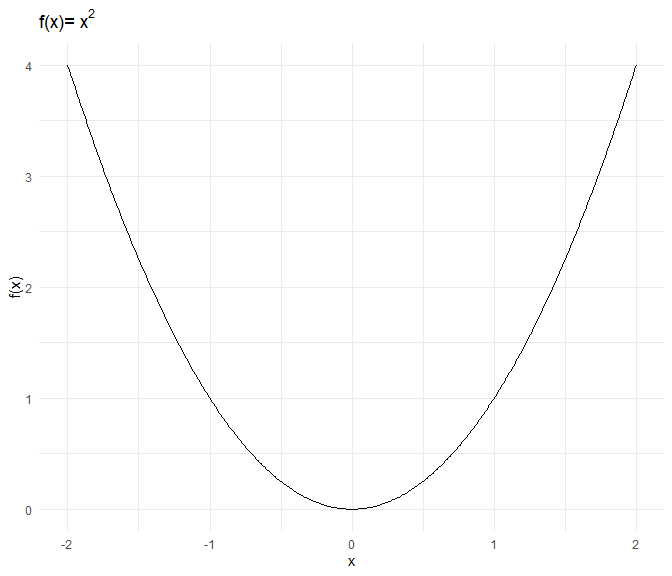
Eine allgemeine quadratische Funktion $f$ hat folgende Gestalt: $f (x) := a x^{2} + b x + c,$ wobei $a \neq 0$ , da es sich sonst nicht um eine quadratische Funktion handelt. Wäre $a = 0$ , würde es sich um eine lineare Funktion mit Achsenabschnitt $c$ und Steigung (Slope) $b$ handeln. Wäre zusätzlich $b = 0$ , handelt es sich um eine horizontale Linie bei $y = f (x) = c$ . Für betraglich große $x$ fällt $x^{2}$ besonders ins Gewicht. Damit entscheidet das Vorzeichen von $a$ , ob es sich um eine u-förmige (falls $a > 0$ ) oder eine umgekehrt-u-förmige (falls $a < 0$ ) Beziehung handelt. Die betragliche Größe von $a$ entscheidet hierbei, wie gestaucht die u-förmige Beziehung (die Parabel) ist. Die reine quadratische Beziehung $f (x) = x^{2}$ sieht so aus:

a <- 1; b <- 0; c <- 0
x <- seq(-2,2,0.01)
f <- a*x^2 + b*x + c
data_X <- data.frame(x, f)
ggplot(data = data_X, aes(x = x,  y = f)) + 
     geom_line(col = "black")+
     labs(x = "x", y =  "f(x)",
          title = expression("f(x)="~x^2))

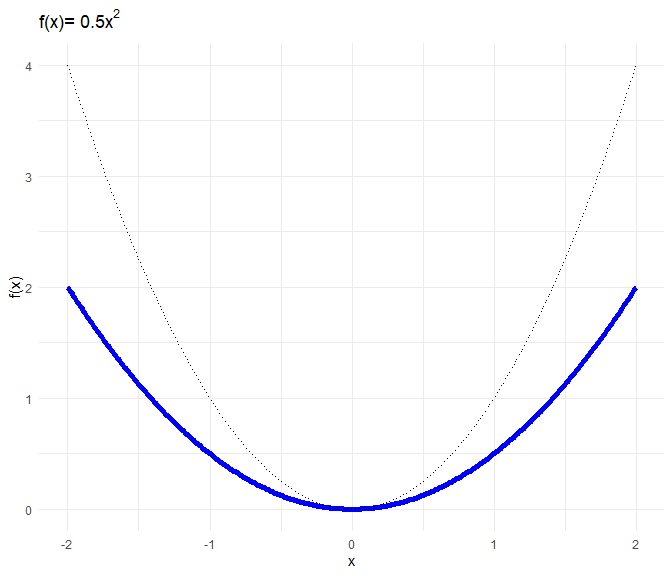
Wir werden diese Funktion immer als Referenz mit in die Grafiken einzeichnen.

a <- 0.5; b <- 0; c <- 0
x <- seq(-2,2,0.01)
f <- a*x^2 + b*x + c
data_X <- data.frame(x, f)
ggplot(data = data_X, aes(x = x,  y = f)) + 
     geom_line(col = "blue", lwd = 2)+ geom_line(mapping = aes(x, x^2), lty = 3)+
     labs(x = "x", y =  "f(x)",
          title = expression("f(x)="~0.5*x^2))

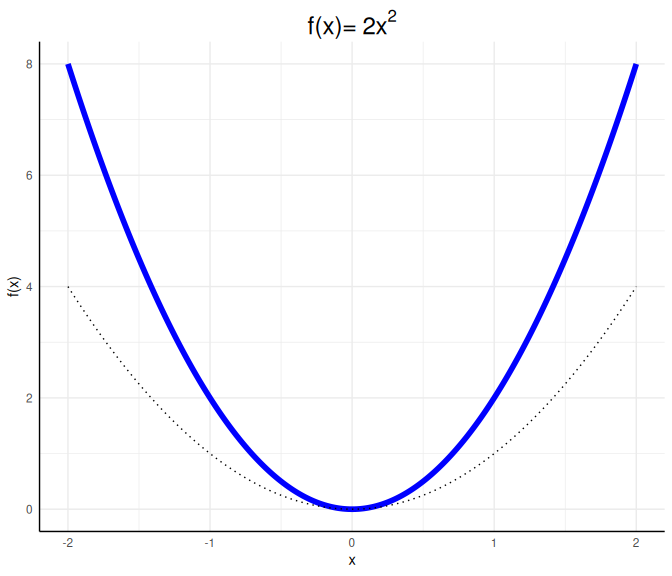
a <- 2; b <- 0; c <- 0
x <- seq(-2,2,0.01)
f <- a*x^2 + b*x + c
data_X <- data.frame(x, f)
ggplot(data = data_X, aes(x = x,  y = f)) + 
     geom_line(col = "blue", lwd = 2)+ geom_line(mapping = aes(x, x^2), lty = 3)+
     labs(x = "x", y =  "f(x)",
          title = expression("f(x)="~2*x^2))

a <- -1; b <- 0; c <- 0
x <- seq(-2,2,0.01)
f <- a*x^2 + b*x + c
data_X <- data.frame(x, f)
ggplot(data = data_X, aes(x = x,  y = f)) + 
     geom_line(col = "blue", lwd = 2)+ geom_line(mapping = aes(x, x^2), lty = 3)+
     labs(x = "x", y =  "f(x)",
          title = expression("f(x)="~-x^2))

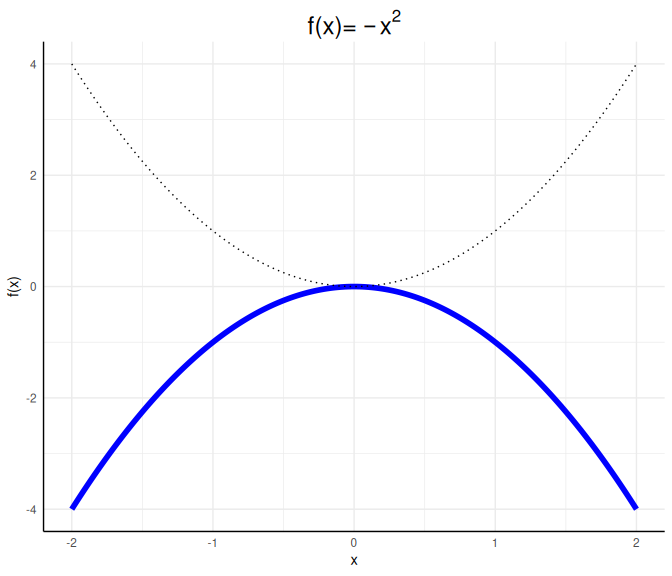
Diese invers-u-förmige Beziehung ist eine konkave Funktion. Als Eselsbrücke für das Wort konkav, welches fast das englische Wort cave enthält, können wir uns merken: Eine konkave Funktion stellt eine Art Höhleneingang dar.

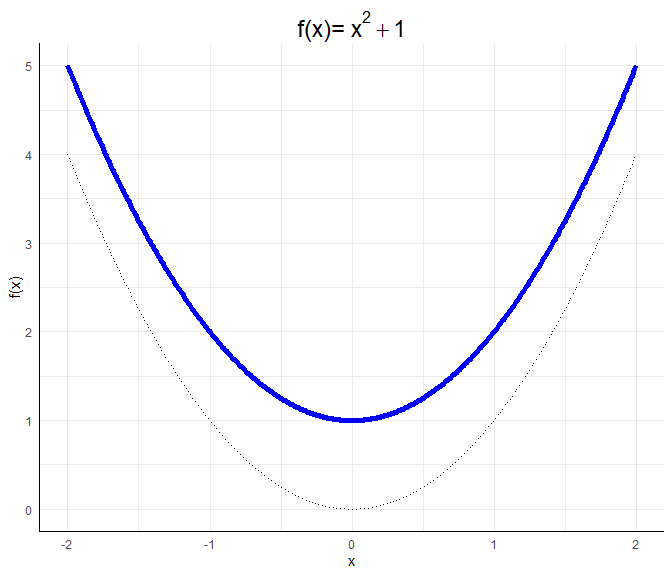
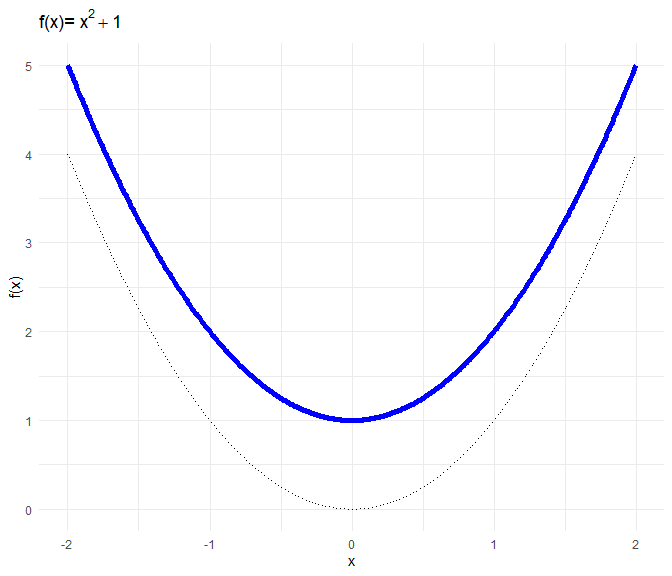
$c$ bewirkt eine vertikale Verschiebung der Parabel:

a <- 1; b <- 0; c <- 1
x <- seq(-2,2,0.01)
f <- a*x^2 + b*x + c
data_X <- data.frame(x, f)
ggplot(data = data_X, aes(x = x,  y = f)) + 
     geom_line(col = "blue", lwd = 2)+ geom_line(mapping = aes(x, x^2), lty = 3)+
     labs(x = "x", y =  "f(x)",
          title = expression("f(x)="~x^2+1))

$b$ bewirkt eine horizontale und vertikale Verschiebung, die nicht mehr leicht vorhersehbar ist. Für $f (x) = x^{2} + x$ lässt sich beispielsweise durch Umformen $f (x) = x^{2} + x = x (x + 1)$ leicht erkennen, dass diese Funktion zwei Nullstellen bei $0$ und $- 1$ hat. Somit ist ersichtlich, dass die Funktion nach unten und nach links verschoben ist:

a <- 1; b <- 1; c <- 0
x <- seq(-2,2,0.01)
f <- a*x^2 + b*x + c
data_X <- data.frame(x, f)
ggplot(data = data_X, aes(x = x,  y = f)) + 
     geom_line(col = "blue", lwd = 2)+ geom_line(mapping = aes(x, x^2), lty = 3)+
     labs(x = "x", y =  "f(x)",
          title = expression("f(x)="~x^2+x))

Für die genaue Gestalt einer allgemeinen quadratischen Funktion $a x^{2} + b x + c$ würden wir die Nullstellen durch das Lösen der Gleichung $a x^{2} + b x + c = 0$ bestimmen (via p-q Formel oder a-b-c-Formel). Den Scheitelpunkt würden wir durch das Ableiten und Nullsetzen der Gleichung bestimmen. Wir müssten also $2 a x + b = 0$ lösen und dies in die Gleichung einsetzen. Wir könnten auch die binomischen Formeln nutzen, um die Funktion in die Gestalt $f (x) := a^{'} (x - b^{'})^{2} + c^{'}$ oder $f (x) := a^{'} (x - b_{1}^{'}) (x - b_{2}^{'}) + c^{'}$ zu bekommen, falls die Nullstellen reell sind (also das Gleichungssystem lösbar ist), da wir so die Nullstellen ablesen können als $b^{'}$ oder $b_{1}^{'}$ und $b_{2}^{'}$ , falls $c = 0$ . Für die Interpretation der Ergebnisse reicht es zu wissen, dass $a$ eine Stauchung bewirkt und entscheind dafür ist, ob die Funktion u-förmig oder invers-u-förmig verläuft.

a <- -0.5; b <- 1; c <- 2
x <- seq(-2,2,0.01)
f <- a*x^2 + b*x + c
data_X <- data.frame(x, f)
ggplot(data = data_X, aes(x = x,  y = f)) + 
     geom_line(col = "blue", lwd = 2)+ geom_line(mapping = aes(x, x^2), lty = 3)+
     labs(x = "x", y =  "f(x)",
          title = expression("f(x)="~-0.5*x^2+x+2))

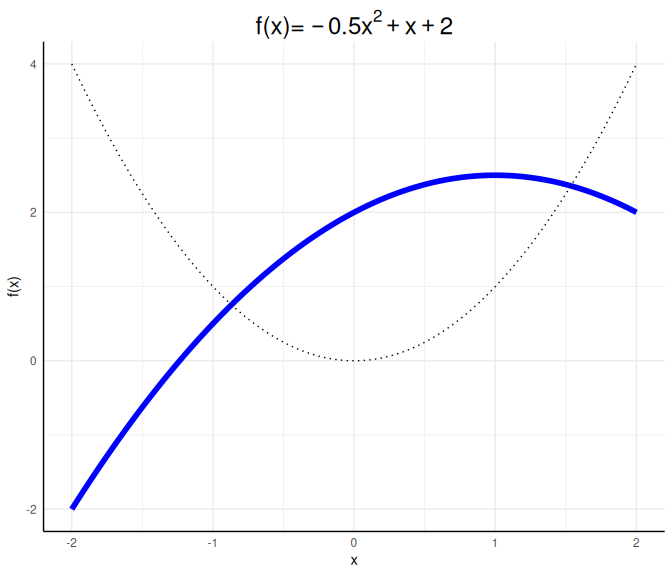
Die direkte Übersetzung der Regressionsgleichung in lm() können wir also erreichen, indem wir die Variable animals quadrieren und in die Regressionsgleichung aufnehmen:

# Quadrierter Prädiktor
vegan$animals2 <- vegan$animals^2

# Modell
mod_quad <- lm(commitment ~ animals + animals2, data = vegan)

# Ergebnisse
summary(mod_quad)

## 
## Call:
## lm(formula = commitment ~ animals + animals2, data = vegan)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.4514 -0.4514  0.2153  0.5486  1.8747 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  3.68288    0.37321   9.868  < 2e-16 ***
## animals     -0.40535    0.15224  -2.663  0.00788 ** 
## animals2     0.07359    0.01481   4.969 7.95e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.8944 on 984 degrees of freedom
## Multiple R-squared:  0.1769,	Adjusted R-squared:  0.1752 
## F-statistic: 105.7 on 2 and 984 DF,  p-value: < 2.2e-16

Wir sehen hier, dass sowohl der lineare als auch der quadratische Term statistisch bedeutsam sind. Der Zugewinn an erklärter Varianz ist mit $Δ R^{2} = 0.02$ zwar nicht überwältigend, aber unser Modell ist etwas besser geworden. Was allerdings auffällt ist, dass im zweiten Modell der Standardfehler des linearen Effekts gegenüber dem einfachen Modell fast das sechs-fache beträgt. Das liegt an einem Problem, dass wir bereits in der letzten Sitzung kurz angerissen hatten: Multikollinearität, also der gegenseitigen Abhängigkeit verschiedener Prädiktoren.

Im letzten Beitrag hatten wir Multikollinearität auf zwei wegen Entdeckt: zum Einen über die einfache Korrelation zwischen Prädiktoren und zum Anderen über die Varianzinflationsfaktor (VIF) bzw. dessen Kehrwert (der Toleranz):

# Korrelation
cor(vegan$animals, vegan$animals2)

## [1] 0.9864857

# VIF
vif(mod_quad)

##  animals animals2 
## 37.24962 37.24962

Die Korrelation zwischen den beiden Prädiktoren ist extrem hoch - wenn man genauer darüber nachdenkt aber nicht wirklich verwunderlich. Immerhin hatten wir eine Variable einfach genommen und quadriert und dann so getan, als sei es jetzt eine neue Variable.

Zentrierung

Ein einfacher Weg die nicht-essentielle Multikollinearität zu minimieren ist das einfache zentrieren des Prädiktors, bevor wir ihn quadrieren. Dadurch kann der Zusammenhang zwischen zwei Variablen entfernt werden, der lediglich aufgrund der Skalierung vorliegt.

Die Auswirkung des Zentrierens

Wie sich das Zentrieren auf die Korrelation auswirkt, lässt sich an einem einfachen Beispiel demonstrieren. Nehmen wir einfach die Zahl von 0 bis 9:

# Beispielwerte erstellen und quadrieren
A <- 0:9
A2 <- A^2

# Gegenüberstellung
cbind(A, A2)

##       A A2
##  [1,] 0  0
##  [2,] 1  1
##  [3,] 2  4
##  [4,] 3  9
##  [5,] 4 16
##  [6,] 5 25
##  [7,] 6 36
##  [8,] 7 49
##  [9,] 8 64
## [10,] 9 81

Der Zusammenhang ist direkt erkennbar: wenn A steigt, steigt auch A2. Die Korrelation ist dabei 0.96. Wenn wir A vorher zentrieren passiert folgendes:

# Zentrierung
Ac <- scale(A, scale = FALSE)
Ac2 <- Ac^2

# Gegenüberstellung
cbind(Ac, Ac2)

##       [,1]  [,2]
##  [1,] -4.5 20.25
##  [2,] -3.5 12.25
##  [3,] -2.5  6.25
##  [4,] -1.5  2.25
##  [5,] -0.5  0.25
##  [6,]  0.5  0.25
##  [7,]  1.5  2.25
##  [8,]  2.5  6.25
##  [9,]  3.5 12.25
## [10,]  4.5 20.25

Der lineare Zusammenhang zwischen den beiden Variablen verschwindet ( $r = 0$ ), weil jetzt sowohl niedrige Werte (-4.5) als auch hohe Werte (4.5) auf Ac mit hohen Werten auf Ac2 einhergehen.

Dieser Weg wird extrem häufig in psychologischen Studien eingeschlagen und in Artikeln berichtet (und auch von Eid, Gollwitzer und Schmitt, 2017, S. 675 empfohlen):

# Zentrierung des Prädiktors
vegan$animals_c <- scale(vegan$animals, scale = FALSE)

# Quadrieren
vegan$animals_c2 <- vegan$animals_c^2

# Korrelation
cor(vegan$animals_c, vegan$animals_c2)

##            [,1]
## [1,] -0.8386629

Leider verschwindet hier die Korrelation nicht, sondern wir finden stattdessen eine starke, negative Korrelation. Ein Punkt, der bedacht werden muss, wenn man die Zentrierung nutzt, um Multikollinearität für quadratische Effekte zu vermeiden ist, dass es maximal effizient ist, wenn Variablen symmetrisch verteilt sind. Je schiefer die Verteilung, desto größer ist der Zusammenhang der weiterhin besteht. Dieses Überbleibsel ist essentielle Multikollinearität, weil sehr viele gleiche (oder zumindest ähnliche) Datenkonstellationen bestehen, die diese Korrelation verursachen.

Zentrieren bei schiefen Variablen

Wenn wir das Beispiel aus der Inforbox oben so umgestalten, dass die Variable schief verteilt ist, sehen wir das Ganze erneut direkt:

# Beispielwerte erstellen und quadrieren
B <- c(0, 0, 0, 0, 0, 2, 4, 6, 8, 9)
Bc <- scale(B, scale = FALSE)
Bc2 <- Bc^2

# Gegenüberstellung
cbind(Bc, Bc2)

##       [,1]  [,2]
##  [1,] -2.9  8.41
##  [2,] -2.9  8.41
##  [3,] -2.9  8.41
##  [4,] -2.9  8.41
##  [5,] -2.9  8.41
##  [6,] -0.9  0.81
##  [7,]  1.1  1.21
##  [8,]  3.1  9.61
##  [9,]  5.1 26.01
## [10,]  6.1 37.21

# Korrelation
cor(Bc, Bc2)

##           [,1]
## [1,] 0.7334988

Hier besteht ein positiver Zusammenhang, weil niedrige Werte auf Bc (-2.9) mit “relativ” niedrigen Werte auf Bc2 einhergehen. Höhere Werte auf Bc (3.1, 5.1, 6.1) gehen allesamt mit hohen Werten auf der quadrierten Variable einher. Wenn wir B jetzt einfach so erweitern, dass auch die 9 fünf mal vorkommt, sinkt die Korrelation wieder drastisch:

# Beispielwerte erstellen und quadrieren
B <- c(0, 0, 0, 0, 0, 2, 4, 6, 8, 9, 9, 9, 9, 9)
Bc <- scale(B, scale = FALSE)
Bc2 <- Bc^2

# Korrelation
cor(Bc, Bc2)

##            [,1]
## [1,] -0.1597993

Im Fall des vegan Datensatzes ist die entstandene Korrelation negativ, was impliziert, dass sehr viele hohe Werte in der ursprünglichen Variable vorliegen.

Im Fall der animals Variable zeigt ein kurzer Blick auf das Histogramm, dass wir hier beim besten Willen nicht von einer symmetrischen Verteilung sprechen können:

# Histogramm
hist(vegan$animals)

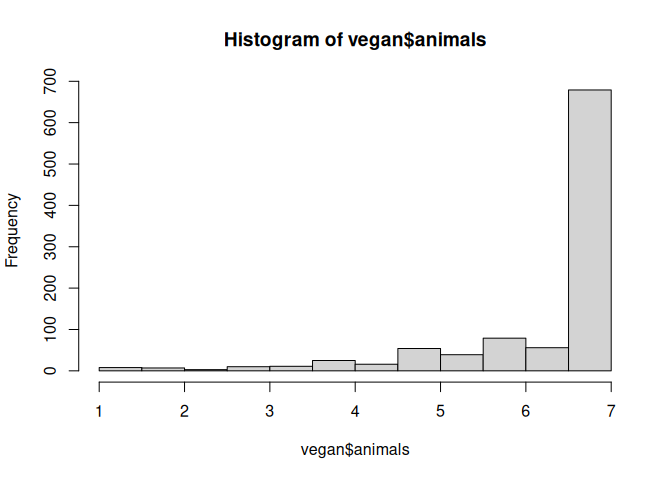
Im Fall des Modells mit zentriertem Prädiktor ist der VIF jetzt zwar unterhalb der typischen Daumenregel-Grenze von 10:

# Modell mit zentriertem Prädiktor
mod_quad_c <- lm(commitment ~ animals_c + animals_c2, data = vegan)

# VIF
vif(mod_quad_c)

##  animals_c animals_c2 
##   3.371037   3.371037

Aber die vorliegende Korrelation lässt dennoch vermuten, dass die Standardfehler unnötig groß sind.

Orthogonal Polynome

Orthogonal Polynome bieten eine Möglichkeit, eine Variable und ihre polynomialen Transformationen (nicht nur Quadrate) so zu skalieren, dass sie

alle einen Mittelwert von 0 haben,
alle die gleiche Varianz haben und
alle unkorreliert sind.

Dafür ist es allerdings notwendig für jede einzelne Anwendung eine transformation zu ermitteln, die diese Eigenschaften erfüllt. R bietet uns hierfür die poly-Funktion an, die wir direkt innerhalb des lm-Befehls nutzen können:

# Modell mit poly()-Prädiktor
mod_quad_poly <- lm(commitment ~ poly(animals, 2), data = vegan)

# Modellergebnisse
summary(mod_quad_poly)

## 
## Call:
## lm(formula = commitment ~ poly(animals, 2), data = vegan)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.4514 -0.4514  0.2153  0.5486  1.8747 
## 
## Coefficients:
##                   Estimate Std. Error t value Pr(>|t|)    
## (Intercept)        4.18102    0.02847 146.858  < 2e-16 ***
## poly(animals, 2)1 12.22236    0.89442  13.665  < 2e-16 ***
## poly(animals, 2)2  4.44405    0.89442   4.969 7.95e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.8944 on 984 degrees of freedom
## Multiple R-squared:  0.1769,	Adjusted R-squared:  0.1752 
## F-statistic: 105.7 on 2 and 984 DF,  p-value: < 2.2e-16

Während dieser Ansatz garantiert, dass wir unkorrelierte Polynome erhalten und somit die Standardfehler minimal sind, kostet uns das die direkte Interpretierbarkeit der Koeffizienten.

Vergleich der Ansätze

Wir haben drei verschiedene Ansätze zur Aufnahme quadratischer Effekte in unser Regressionsmodell betrachtet. Bevor wir debattieren, welcher Ansatz in welchen Situationen nützlich ist, macht es Sinn kurz darauf einzugehen, was zwischen den drei Ansätzen gleich ist. Zunächst ist wichtig, dass alle drei Modelle eigentlich aus den gleichen Daten die gleichen Vorhersagen versuchen und die Transformation der Daten lediglich Parameter und deren Standardfehler ändert. Die aufgeklärte Varianz hingegen, ist in allen drei Ansätzen identisch:

# R-Quadrat, Rohwerte
summary(mod_quad)$r.squared

## [1] 0.1768601

# R-Quadrat, Zentrierung
summary(mod_quad_c)$r.squared

## [1] 0.1768601

# R-Quadrat, poly()
summary(mod_quad_poly)$r.squared

## [1] 0.1768601

Da alle drei $R^{2}$ identisch sind, muss auch das $Δ R^{2}$ gegenüber dem linearen Modell (der Zugewinn durch die Aufnahme des quadratischen Terms) identisch sein. Wie schon gesehen, ist das hier $Δ R^{2} = 0.02$ . Schon in früheren Beiträgen hatten wir mittels anova geprüft, ob ein Zugewinn in der Varianzaufklärung statistisch bedeutsam ist:

# Modellvergleich, Rohwerte
anova(mod_lin, mod_quad)

## Analysis of Variance Table
## 
## Model 1: commitment ~ animals
## Model 2: commitment ~ animals + animals2
##   Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
## 1    985 806.94                                  
## 2    984 787.19  1     19.75 24.687 7.948e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# Modellvergleich, Zentrierung
anova(mod_lin, mod_quad_c)

## Analysis of Variance Table
## 
## Model 1: commitment ~ animals
## Model 2: commitment ~ animals_c + animals_c2
##   Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
## 1    985 806.94                                  
## 2    984 787.19  1     19.75 24.687 7.948e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# Modellvergleich, poly()
anova(mod_lin, mod_quad_poly)

## Analysis of Variance Table
## 
## Model 1: commitment ~ animals
## Model 2: commitment ~ poly(animals, 2)
##   Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
## 1    985 806.94                                  
## 2    984 787.19  1     19.75 24.687 7.948e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Auch diese sind allesamt identisch. Da der Modellvergleich für die Aufnahme eines Prädiktors dem Test des Regressionsgewichts entspricht, müsste auch dieser identisch sein:

# Modellergebnisse, Rohwerte
summary(mod_quad)$coef

##                Estimate Std. Error   t value     Pr(>|t|)
## (Intercept)  3.68287843 0.37321105  9.868085 5.756669e-22
## animals     -0.40534714 0.15224300 -2.662501 7.882786e-03
## animals2     0.07359022 0.01481094  4.968638 7.948045e-07

# Modellergebnisse, Zentrierung
summary(mod_quad_c)$coef

##               Estimate Std. Error    t value     Pr(>|t|)
## (Intercept) 4.08516070 0.03439098 118.785805 0.000000e+00
## animals_c   0.53171652 0.04579923  11.609726 2.702879e-29
## animals_c2  0.07359022 0.01481094   4.968638 7.948045e-07

# Modellergebnisse, poly()
summary(mod_quad_poly)$coef

##                    Estimate Std. Error    t value     Pr(>|t|)
## (Intercept)        4.181020 0.02846973 146.858440 0.000000e+00
## poly(animals, 2)1 12.222358 0.89442082  13.665109 4.716036e-39
## poly(animals, 2)2  4.444054 0.89442082   4.968638 7.948045e-07

In allen drei Fällen sehen wir als $t$ -Wert für den quadratischen Effekt 4.97 (welches, wie wir im 1. Semester gesehen hatten die Quadratwurzel des $F$ -Werts aus dem Modellvergleich ist). Die Unterschiede zwischen den Ansätzen bestehen also lediglich in den Regressionsgewichten und der Inferenz bezüglich des linearen Effekts und des Intercepts. Auch die Vorhersagen aus den drei Modellen sind identisch:

# Vorhersagen, Rohwerte
predict(mod_quad)[1:3]

##        1        2        3 
## 3.238933 4.451369 4.451369

# Vorhersagen, Zentrierung
predict(mod_quad_c)[1:3]

##        1        2        3 
## 3.238933 4.451369 4.451369

# Vorhersagen, poly()
predict(mod_quad_poly)[1:3]

##        1        2        3 
## 3.238933 4.451369 4.451369

Für die ersten drei Personen im Datensatz werden von allen drei Modellen die gleiche Werte in commitment vorhergesagt.

Wie bereits erwähnt ist in der Psychologie der Ansatz der Zentrierung am weitesten verbreitet. Er erlaubt zumindest bei (halbwegs) symmetrisch verteilten Variablen eine relativ gute Eindämmung der Multikollinearität und erzeugt gleichzeitig Regressionsgewichte, die auf den ursprünglichen Skalen interpretierbar sind.

Abbildung der Effekte

Egal ob wir uns für die Zentrierung oder die Nutzung von poly entscheiden, es macht Sinn sich das Modell ein wenig zu veranschaulichen. Zum Glück haben wir uns schon ausgiebig damit beschäftigt, wie man Grafiken mit ggplot2 erstellt. Wie weiter oben, als wir uns die LOESS-Linie angeguckt hatten, können wir auch hier mit geom_smooth arbeiten:

# Abbildung des Modells
ggplot(data = vegan, aes(x = animals, y = commitment)) +
  geom_point() +
  geom_smooth(method = "lm", formula = y ~ poly(x, 2), col = "#00618f", se = FALSE) +
  geom_smooth(method = "lm", formula = y ~ x, col = "#e3ba0f", se = FALSE)

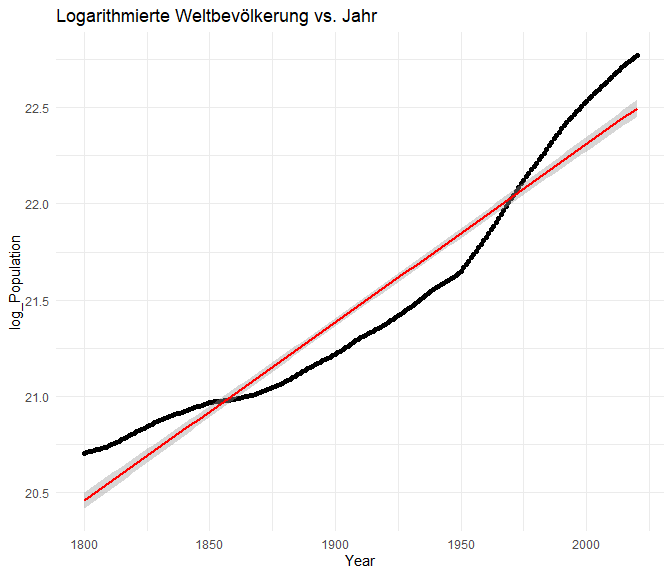
  labs(title = "Scatterplot mit quadratischer Regression")

## $title
## [1] "Scatterplot mit quadratischer Regression"
## 
## attr(,"class")
## [1] "labels"

Testen des Kubischen Effekts

Bisher hatten wir uns quadratische Effekte als die einfachste Variante von Polynomen angeguckt. Natürlich können wir die Regression aber beliebig lange komplizierter machen, in dem wir einfach immer weiter Polynome höherer Ordnung aufnehmen:

$y_{m} = β_{0} + β_{1} x_{m} + β_{2} x_{m}^{2} + β_{3} x_{m}^{3} + \dots + β_{j} x_{m}^{j} + ε_{m}$

In der Realität hört das Testen von Polynomen meistens bei der dritten Ordnung auf. Grund dafür ist, dass viele nicht-lineare Zusammenhänge nur geringfügige Unterschiede in den beobachtbaren Verteilungen erzeugen und demzufolge bei kleineren und mittelgroßen Stichproben nur sehr schwer zu entdecken sind.

Weil wir gerade gesehen haben, dass die unterschiedlichen Varianten der Prädiktorbehandlung (Rohwerte, Zentrierung, poly) für den höhesten Term (vorhin noch der quadratische) identische Inferenz liefern, wähle ich hier den poly-Ansatz, um den kubischen Effekt zu testen, weil er der einfachste in der Syntax-Umsetzung ist:

# Modell mit kubischem Effekt
mod_cubic <- lm(commitment ~ poly(animals, 3), data = vegan)

# Modellvergleich
anova(mod_quad_poly, mod_cubic)

## Analysis of Variance Table
## 
## Model 1: commitment ~ poly(animals, 2)
## Model 2: commitment ~ poly(animals, 3)
##   Res.Df    RSS Df Sum of Sq     F  Pr(>F)  
## 1    984 787.19                             
## 2    983 784.39  1    2.8024 3.512 0.06122 .
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

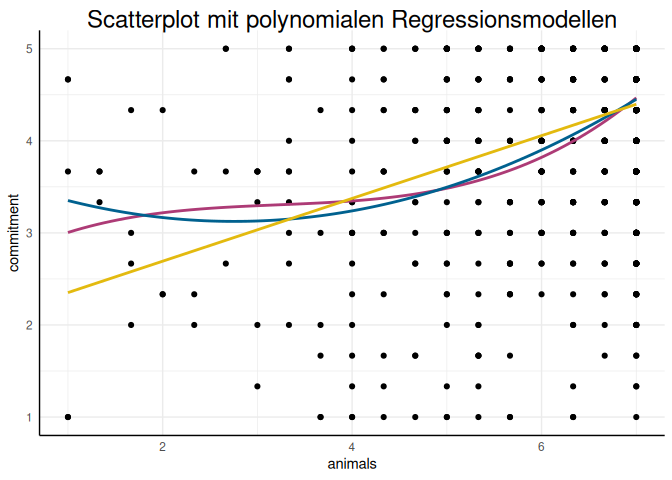
Im direkten Vergleich scheint der kubische Effekt nicht statistisch bedeutsam zu sein. Das $Δ R^{2} = 0.003$ ist auch sehr überschaubar. Auch wenn wir uns in diesem Fall für das quadratische Modell entscheiden, hier noch eine kurze Darstellung der drei Modelle (linear, quadratisch, kubisch), um die Implikationen der jeweiligen nicht-Linearität zu verdeutlichen:

# Abbildung des Modells
ggplot(data = vegan, aes(x = animals, y = commitment)) +
  geom_point() +
  geom_smooth(method = "lm", formula = y ~ poly(x, 3), col = "#ad3b76", se = FALSE) +
  geom_smooth(method = "lm", formula = y ~ poly(x, 2), col = "#00618f", se = FALSE) +
  geom_smooth(method = "lm", formula = y ~ x, col = "#e3ba0f", se = FALSE) +
  labs(title = "Scatterplot mit polynomialen Regressionsmodellen")

Logarithmische Effekte

Im vorherigen Abschnitt hatten wir quadratische und kubsiche Effekte als typische Fälle der polynomialen Regression betrachtet. Darüber hinaus sind in der Psychologie (und eigentlich sehr vielen natürlichen Phänomenen) logarithmische und exponentielle Verläufe extrem verbreitet. Letztere sehen wir z.B. in Modellen zur Ausbreitung von Krankheiten, nuklearer Kettenreaktionen oder auch Rechenkapazitäten (einen einführenden Überblick bietet Arinze, 2024). Im Genesatz zum unendlich beschleunigenden Wachstum werden logarithmische Zusammenhänge dann genutzt, wenn sich Entwicklungen verlangsamen und einer natürlichen Grenze nähern. In der Psychologie sind hierfür typische Beispiele Lernmechanismen durch Wiederholung, Gewöhnung oder auch Klassiker der frühen Psychologie wie das Weber-Fechner-Gesetz. Wenn Sie die mathematischen Grundlagen von Exponenten und Logarithmen noch einmal auffrischen wollen, bevor wir in die Umsetzung einsteigen, haben wir ein kurzes Quiz und ein paar Rechenregeln in Appendix B aufbereitet.

Datenbeispiel: Lernen falscher Information

Um uns anzugucken, wie logarithmische Effekte modelliert werden, nutzen wir Daten aus der Studie von Fazio et al. (2022). In dieser Studie wurden Personen über einen Zeitraum von zwei Wochen via Push wiederholt Aussagen präsentiert, von denen manche wahr und manche falsch waren. Effekte der Anzahl von wiederholten Präsentationen von Informationen auf das Lernen sind in experimentellen Bedingungen extrem weitreichen untersucht. Fazio et al. (2022) wollten mit ihrer Studie untersuchen, ob auch im Alltag - bei der einfachen Aufnahmen von Informationen “nebenbei”, wie sie heutzutage via Headline-Scrolling üblich ist - diese Effekte auftreten und ob sich dabei wahre von falschen Aussagen unterscheiden.

Eine volle Liste der Aussage, für die diese Effekte untersucht wurden haben wir hier bereitgestellt. Für unser Beispiel beschränken wir uns auf die Aussage “In the story of Pinnochio, the goldfish is named Cleo.” Dafür müssen wir zunächst die Daten einlesen und dann auf diese Aussage einschränken:

# Daten einlesen
source("https://pandar.netlify.app/daten/Data_Processing_trivia.R")

# Einschränken auf Pinnochio
trivia <- subset(trivia, headline == 3)

Die Variable rating gibt hier an, in welchem Ausmaß Personen diese Aussage im Abschlussquiz (nach zwei Wochen) der Studie als wahr einschätzen. Dabei heißt 1 “mit Sicherheit nicht wahr” und 6 “mit Sicherheit wahr”. In repetition ist festgehalten, wie häufig Personen diese Aussage über die zwei Wochen hinweg präsentiert bekommen haben.

Logarithmische Zusammenhänge

Um logarithmische Zusammenhänge in einer Regression darzustellen wird typischerweise die unabhängige Variable logarithmiert, sodass die Regression weiterhin linear bleibt und lediglich die UV eine Transformation darstellt:

$y_{m} = β_{0} + β_{1} \ln (x_{m}) + ε_{m}$ (Um hingegen exponentielle Zusammenhänge darzustellen würde die abhängige Variable logarithmiert werden.) Wir nutzen hier den natürlichen Logarithmus, weil er in R die Voreinstellung des log-Befehls ist. Wie immer hilft es, sich ein Bild davon zu machen, was die einzelnen Regressionsparameter in so einem Fall bewirken:

Die gepunktete und die durchgezogene Linie unterscheiden sich im Intercept

β_{0}

, wodurch der Verlauf als Ganzes nach oben bzw. unten versetzt wird. Wichtig ist dabei, dass

β_{0}

den vorhergesagten Wert für

\ln (x_{m}) = 0

angibt, also wenn

x_{m} = 1

. Die gestrichelte Linie unterscheidet sich von der durchgezogenen hingegen im Regressiongewicht

β_{1}

, sodass die Wachstumsraten sich unterscheiden. Wenn wir auf der

x

-Achse den tatsächlichen Prädiktor

\ln (x_{m})

abtragen, wird deutlich, dass wir nach wie vor einfache lineare Regression betreiben:

Logarithmische Regression in R

Wie vorhin bei den Polynomen, sollten wir auch in diesem Fall die modellierte Form des Zusammenhangs von theoretischen Überlegungen ableiten. Im Gegensatz zu den Polynomen ist es in diesem Fall aber schwieriger, den Wert der Aufnahme des logarithmischen Zusammenhangs zu quantifizieren, weil der logarithmische Term nicht einfach als weiterer Prädiktor, sondern als der einzige Prädiktor aufgenommen wird. Dadruch können wir nicht das Inkrement im $R^{2}$ und den dazugehörigen $F$ -Test bestimmen, sondern müssen uns auf andere Herangehensweisen einlassen.

Erstellen wir zunächst wieder das lineare Modell - als Baseline die einfachste Form des Zusammenhangs abzubilden:

# Lineare Regression
mod_lin <- lm(rating ~ repetition, data = trivia)

# Ergebnisse
summary(mod_lin)

## 
## Call:
## lm(formula = rating ~ repetition, data = trivia)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -4.5172 -0.5899  0.4101  1.1010  1.6419 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  4.28080    0.09410  45.494  < 2e-16 ***
## repetition   0.07727    0.01135   6.811  3.3e-11 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.27 on 428 degrees of freedom
## Multiple R-squared:  0.09779,	Adjusted R-squared:  0.09568 
## F-statistic: 46.39 on 1 and 428 DF,  p-value: 3.296e-11

Die Ergebnisse zeigen zunächst, dass es einen bedeutsamen Effekt der Anzahl der Wiederholungen auf die Wahrheitseinschätzung gibt ( $R^{2} \approx 0.1$ ). Wenn wir die unabhängige Variable (die Anzahl an Wiederholungen) logarithmieren, zeigen sich folgende Ergebnisse:

# Logarithmische Regression
mod_log <- lm(rating ~ log(repetition), data = trivia)

# Ergebnisse
summary(mod_log)

## 
## Call:
## lm(formula = rating ~ log(repetition), data = trivia)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -4.4238 -0.7510  0.2490  0.9126  1.9218 
## 
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)    
## (Intercept)      4.07819    0.10747  37.949  < 2e-16 ***
## log(repetition)  0.48534    0.06261   7.752 6.65e-14 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.252 on 428 degrees of freedom
## Multiple R-squared:  0.1231,	Adjusted R-squared:  0.1211 
## F-statistic: 60.09 on 1 and 428 DF,  p-value: 6.654e-14

Der Effekt ist ebenfalls statistisch bedeutsam, die aufgeklärte Varianz ist sogar ein bisschen größer ( $R^{2} \approx 0.12$ ). Bilden wir beide Zusammenhänge mal im Kontext der Daten ab:

# Abbildung der Modelle
ggplot(data = trivia, aes(x = repetition, y = rating)) +
  geom_point() +
  geom_smooth(method = "lm", formula = y ~ x, col = "#e3ba0f", se = FALSE) +
  geom_smooth(method = "lm", formula = y ~ log(x, base = 10), col = "#00618f", se = FALSE) +
  labs(title = "Scatterplot mit linearer und logarithmischer Regression")

Wegen des experimentellen Designs und der Einschränkung der Skalenwerte von 1 bis 6 lassen sich hier nur bedingt Effekt in den Punkten sehen. Was allerdings relativ klar wird ist, dass der Unterschied zwischen beiden Modellen relativ gering ist.

Um die beide Modelle direkt zu vergleichen hatten wir bereits im Rahmen des Beitrags zur Prädiktorauswal eine Alternative zum einfachen Modellvergleich via $F$ -Test kennengelernt: Informationskriterien wie z.B. das Akaike Informationskriterium (AIC). Während der Modellvergleich via $F$ -Test nur dann sinnvoll ist, wenn ein Modell durch Einschränkungen aus dem anderen Modell hervorgeht (und so das $Δ R^{2}$ auf diese Veränderung attribuiert werden kann), können wir Informationskriterien auch nutzen, um Modelle zu vergleichen, die nicht die gleichen Prädiktoren nutzen, solange die gleiche abhängige Variable im gleichen Datensatz vorhergesagt wird. Mit AIC können wir uns den AIC des entsprechenden Modells ausgeben lassen:

# AIC der Modelle
AIC(mod_lin, mod_log)

##         df      AIC
## mod_lin  3 1429.613
## mod_log  3 1417.367

Wie zu sehen ist, bevorzugt der AIC hier das Modell mit dem logarithmischen Prädiktor. Wenn Sie die Berechnung des AIC aus dem Beitrag zur Prädiktorenauswahl noch vor Augen haben, wird klar, dass bei gleich vielen Prädiktoren vom AIC immer das Modell mit höherem $R^{2}$ präferiert wird.

Interpretation

Neben dem (schon gezeigten) Bild, helfen auch vorhergesagte Werte immer dabei, die Regressionsparameter angemessen zu interpretieren. Durch die Logarithmierung der unabhängigen Variable, können wir die Regressionsparameter nicht wie gewohnt interpretieren, sondern müssen berücksichtigen, dass der Effekt von Unterschieden in $X$ über die Skala hinweg unterschiedlich ist. Generell finde ich es am einfachsten (und Sie können da anderer Meinung sein, was die Definition des Wortes “einfach” betrifft), Effekte von logarithmierten Variablen in Verdoppelungen zu denken. Was ich damit meine: wir können die Werte für eine Sequenz sich verdoppelnder Werte vorhersagen:

# Wertereihe
newX <- data.frame(repetition = c(1, 2, 4, 8, 16))

# Vorhersage
pred_log <- predict(mod_log, newdata = newX)
cbind(newX, pred_log)

##   repetition pred_log
## 1          1 4.078194
## 2          2 4.414604
## 3          4 4.751013
## 4          8 5.087422
## 5         16 5.423831

(Glücklicherweise sind das genau die Werte, die auch in der Studie von Fazio et al. (2022) für die Ausprägungen der Wiederholungen genutzt werden, was für ein unglaublicher Zufall.) Die Differenz zwischen diesen Werten ist immer identisch:

# Differenzen
diff(pred_log)

##        2        3        4        5 
## 0.336409 0.336409 0.336409 0.336409

Genau genommen ist diese Differenz nicht nur immer identisch, sondern sie entspricht immer $β_{1} \cdot \ln (2)$ . Wenn Sie wissen möchten warum dem so ist, gibt es hier ein bisschen Vertiefung:

Exkurs: Ein bisschen Mathe

Die Differenz zwischen zwei vorhergesagten Werten ist im Allgemeinen:

\begin{aligned} {\hat{y}}_{2} - {\hat{y}}_{1} & = (β_{0} + β_{1} \ln [x_{2}]) - (β_{0} + β_{1} \ln [x_{1}]) \\ = β_{1} (\ln [x_{2}] - \ln [x_{1}]) \\ = β_{1} \ln (\frac{x_{2}}{x_{1}}) \end{aligned}

Im ersten Schritt wird das Intercept $β_{0}$ herausgekürzt und im zweiten das Regressionsgewicht ausgeklammert. Im dritten Schritt nutzen wir die Logarithmengesetze, um den Unterschied der Logarithmen in den Logarithmus des Quotienten zu transformieren. Das heißt, für eine Verdoppelung von $X$ gilt z.B.:

$β_{1} \ln (\frac{4}{2}) = β_{1} \ln (2)$

Das Regressionsgewicht selbst ist (weil wir leichtsinnig den natürlichen Logarithmus gewählt haben) der Unterschied zwischen den vorhergesagten Werten, wenn die unabhängige Variable mit der Euler’schen Zahl $e$ multipliziert wird. Um uns selbst das Leben ein wenig einfacher zu machen, könnten wir also eine Logarithmustransformation wählen, die etwas leichter interpretierbar ist:

# Logarithmische Regression, Basis 2
mod_log2 <- lm(rating ~ log(repetition, base = 2), data = trivia)

# Ergebnisse
summary(mod_log2)

## 
## Call:
## lm(formula = rating ~ log(repetition, base = 2), data = trivia)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -4.4238 -0.7510  0.2490  0.9126  1.9218 
## 
## Coefficients:
##                           Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                 4.0782     0.1075  37.949  < 2e-16 ***
## log(repetition, base = 2)   0.3364     0.0434   7.752 6.65e-14 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.252 on 428 degrees of freedom
## Multiple R-squared:  0.1231,	Adjusted R-squared:  0.1211 
## F-statistic: 60.09 on 1 and 428 DF,  p-value: 6.654e-14

Durch die Magie der Mathematik ist das Regressionsgewicht genau der Wert, den wir gerade als Differenz der vorhergesagten Werte bestimmt haben, wenn die unabhängige Variable verdoppelt wird. Darüber hinaus sind $R^{2}$ und AIC der beiden Modelle identisch:

# R-Quadrat der Modelle
summary(mod_log)$r.squared

## [1] 0.1231201

summary(mod_log2)$r.squared

## [1] 0.1231201

# AIC der Modelle
AIC(mod_log, mod_log2)

##          df      AIC
## mod_log   3 1417.367
## mod_log2  3 1417.367

Wir können also getrost eine Basis für den Logarithmus wählen, die sich gut interpretieren lässt (ich empfehle die 2, aber auch der “klassiche” 10er Logarithmus bietet sich an).

Zusammenfassung

In diesem Tutorial haben wir nichtlineare Regressionsmodelle als Erweiterung der bisherigen Analyseverfahren kennengelernt und uns speziell mit quadratischen und logarithmischen Verläufen befasst. Abweichungen von der Normalitätsannahme der Residuen können auf unberücksichtigte nichtlineare Beziehungen zwischen der unabhängigen und der abhängigen Variable hinweisen. Die verschiedenen nichtlinearen Modelle lassen sich relativ unkompliziert mit den bereits bekannten Befehlen erstellen, zum Beispiel durch Einbeziehung höherer Ordnungspolynome mit poly oder Modellierung von logarithmischen Zusammenhängen durch das Logarithmieren der unabhängigen Variablen.

Appendix A

Exkurs: Zentrierung vs. poly

Wir vergleichen nun an einem ganz einfachen Beispiel, was poly und was Zentrierung bewirkt. Dazu erstellen wir einen Vektor (also eine Variable) $A$ der die Zahlen von 0 bis 10 enthält in 0.1 Schritten:

A <- seq(0, 10, 0.1)

Nun bestimmen wir zunächst die Korrelation zwischen $A$ und $A^{2}$ :

cor(A, A^2)

## [1] 0.9676503

welche sehr hoch ausfällt. Wir hatten bereits mit poly erkannt, dass diese Funktion die linearen und quadratischen Anteile trennt. Nun zentrieren wir die Daten. Das geht entweder händisch oder mit der scale Funktion:

A_c <- A - mean(A)
mean(A_c)

## [1] 2.639528e-16

A_c2 <- scale(A, center = T, scale = F)  # scale = F bewirkt, dass nicht auch noch die SD auf 1 gesetzt werden soll
mean(A_c2)

## [1] 2.639528e-16

Nun vergleichen wir die Korrelationen zwischen $A_{c}$ mit $A_{c}^{2}$ mit den Ergebnissen von poly:

cor(A_c, A_c^2)

## [1] 1.763581e-16

cor(poly(A, 2))

##              1            2
## 1 1.000000e+00 9.847944e-17
## 2 9.847944e-17 1.000000e+00

# auf 15 Nachkommastellen gerundet:
round(cor(A_c, A_c^2), 15)

## [1] 0

round(cor(poly(A, 2)), 15)

##   1 2
## 1 1 0
## 2 0 1

beide Vorgehensweisen sind bis auf 15 Nachkommastellen identisch!

Spaßeshalber nehmen wir noch die Terme $A^{3}$ und $A^{4}$ auf und vergleichen die Ergebnisse:

# auf 15 Nachkommastellen gerundet:
round(cor(cbind(A, A^2, A^3, A^4)), 2)

##      A               
## A 1.00 0.97 0.92 0.86
##   0.97 1.00 0.99 0.96
##   0.92 0.99 1.00 0.99
##   0.86 0.96 0.99 1.00

round(cor(cbind(A_c, A_c^2, A_c^3, A_c^4)), 2)

##      A_c               
## A_c 1.00 0.00 0.92 0.00
##     0.00 1.00 0.00 0.96
##     0.92 0.00 1.00 0.00
##     0.00 0.96 0.00 1.00

round(cor(poly(A, 4)), 2)

##   1 2 3 4
## 1 1 0 0 0
## 2 0 1 0 0
## 3 0 0 1 0
## 4 0 0 0 1

Was wir nun erkennen ist, dass $A, A^{2}, A^{3}, A^{4}$ sehr hoch korreliert sind. Die zentrierten Variablen zeigen ein etwas anderes Bild. Hier ist $A_{c}$ und $A_{c}^{3}$ sehr hoch korreliert sowie $A_{c}^{2}$ und $A_{c}^{4}$ sind sehr hoch korreliert. Man sagt auch, dass nur gerade Potenzen ( $A^{2}, A^{4}, A^{6}, \dots$ ) untereinander und ungerade Potenzen ( $A = A^{1}, A^{3}, A^{5}, \dots$ ) untereinander korreliert sind, wenn die Daten zentriert sind. Bei poly verschwinden alle Korrelationen zwischen $A, A^{2}, A^{3}, A^{4}$ . Hier dran erkennen wir, dass wenn wir nur Terme zur 2. Ordnung/Potenz (also $A$ und $A^{2}$ und natürlich Interaktionen $A B$ , aber eben nicht $A^{3}$ bzw. $A B^{2}$ oder $A^{2} B$ , etc.) im Modell haben, dann reicht die Zentrierung aus, um extreme Kollinearitäten zu zwischen linearen und nichtlinearen Termen zu vermeiden.

Da wir hier die Korrelationen betrachtet haben, kommt eine Standardisierung von $A$ zu identischen Ergebnissen, weswegen wir hierauf verzichten.

Mathematische Begründung

Dieser Abschnitt ist für die “Warum ist das so?"-Fragenden bestimmt und ist als reinen Zusatz zu erkennen.

Wir wissen, dass die Korrelation der Bruch aus der Kovarianz zweier Variablen geteilt durch deren Standardabweichung ist. Aus diesem Grund reicht es, die Kovarianz zweier Variablen zu untersuchen, um zu schauen, wann die Korrelation 0 ist. Wir hatten oben die Variablen zentriert und bemerkt, dass dann die Korrelation zwischen $A_{c}$ und $A_{c}^{2}$ verschwindet. Warum ist das so? Dazu stellen wir $A$ in Abhängigkeit von seinem Mittelwert $μ_{A}$ und $A_{c}$ , der zentrierten Version von $A$ , dar:

$A := μ_{A} + A_{c}$

So kann jede Variable zerlegt werden: in seinen Mittelwert (hier: $μ_{A}$ ) und die Abweichung vom Mittelwert (hier: $A_{c}$ ). Nun bestimmen wir die Kovarianz zwischen den Variablen $A$ und $A^{2}$ und setzen in diesem Prozess $μ_{A} + A_{c}$ für $A$ ein und wenden die binomische Formel an $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ .

$\begin{aligned} C o v [A, A^{2}] & = C o v [μ_{A} + A_{c}, (μ_{A} + A_{c})^{2}] & = C o v [A_{c}, μ_{A}^{2} + 2 μ_{A} A_{c} + A_{c}^{2}] & = C o v [A_{c}, μ_{A}^{2}] + C o v [A_{c}, 2 μ_{A} A_{c}] + C o v [A_{c}, A_{c}^{2}] \end{aligned}$

An dieser Stelle pausieren wir kurz und bemerken, dass wir diese beiden Ausdrücke schon kennen $C o v [A_{c}, μ_{A}^{2}] = C o v [A_{c}, A_{c}^{2}] = 0$ . Ersteres ist die Kovarianz zwischen einer Konstanten und einer Variable, welche immer 0 ist und, dass die Kovarianz zwischen $A_{c}$ und $A_{c}^{2}$ 0 ist, hatten wir oben schon bemerkt! Diese Aussage, dass die Korrelation/Kovarianz zwischen $A_{c}$ und $A_{c}^{2}$ 0 ist, gilt insbesondere für die transformierten Daten mittels poly (hier bezeichnet $A_{c}^{2}$ quasi den quadratischen Anteil, der erstellt wird) und auch für einige Verteilungen (z.B. symmetrische Verteilungen, wie die Normalverteilung) ist so, dass die linearen Anteile und die quadratischen Anteile unkorreliert sind. Im Allgemeinen gilt dies leider nicht.

Folglich können wir sagen, dass

$\begin{aligned} C o v [A, A^{2}] & = C o v [A_{c}, 2 μ_{A} A_{c}] & = 2 μ_{A} C o v [A_{c}, A_{c}] = 2 μ_{A} V a r [A], \end{aligned}$

wobei wir hier benutzen, dass die Kovarianz mit sich selbst die Varianz ist und dass die zentrierte Variable $A_{c}$ die gleiche Varianz wie $A$ hat (im Allgemeinen, siehe weiter unten, bleibt auch noch die Kovarianz zwischen $A_{c}$ und $A_{c}^{2}$ erhalten). Dies können wir leicht prüfen:

var(A)

## [1] 8.585

var(A_c)

## [1] 8.585

# Kovarianz 
cov(A, A^2)

## [1] 85.85

2*mean(A)*var(A)

## [1] 85.85

# zentriert:
round(cov(A_c, A_c^2), 14)

## [1] 0

round(2*mean(A_c)*var(A_c), 14)

## [1] 0

Der zentrierte Fall ist auf 14 Nachkommastellen identisch und weicht danach nur wegen der sogenannten Maschinengenauigkeit von einander ab. Somit ist klar, dass wenn der Mittelwert = 0 ist, dann ist auch die Korrelation zwischen einer Variable und seinem Quadrat 0. Analoge Überlegungen können genutzt werden, um das gleiche für die Interaktion von Variablen zu sagen.

Im Allgemeinen:

Im Allgemeinen ist es dennoch sinnvoll die Daten zu zentrieren, wenn quadratische Effekte (oder Interaktionseffekte) eingesetzt werden, da zumindest immer gilt:

$\begin{aligned} C o v [A, A^{2}] & = C o v [A_{c}, 2 μ_{A} A_{c}] + C o v [A_{c}, A_{c}^{2}] & = 2 μ_{A} V a r [A] + C o v [A_{c}, A_{c}^{2}], \end{aligned}$

somit wird die Kovarianz zwischen $A$ und $A^{2}$ künstlich vergrößert, wenn die Daten nicht zentriert sind. Denn nutzen wir zentrierte Variablen ist nur noch $C o v [A_{c}, A_{c}^{2}]$ relevant (da $μ_{A} = 0$ ).

Appendix B

Exkurs: Exponenten und Logarithmen

Um Regressionsmodelle, die exponentielles Wachstum abbilden, besser zu verstehen, sind einige grundlegende Kenntnisse im Umgang mit Exponenten erforderlich. Zum Beispiel müssen wir uns überlegen, welche Rate und welche Basis ein exponentieller Verlauf hat. Beispielsweise wächst $10^{x}$ deutlich schneller als $2^{x}$ (für gleiches wachsendes $x$ ).

Wie gut kennen Sie sich noch mit Exponenten und Logarithmen aus?

Welche der folgenden Aussagen ist richtig?

Die Gleichung $10^{x} = 100$ können wir bspw. mit dem 10er-Logarithmus $l o g_{10} (100)$ berechnen. Die Antwort ist 2.
Die Gleichung $10^{x} = 100$ können wir bspw. mit dem 10er-Logarithmus $l o g_{10} (100)$ berechnen. Die Antwort ist 3.
Logarithmen können NICHT in einander umgerechnet werden.
Es gilt: $l o g (a + b) = l o g (a) l o g (b)$ .
Es gilt: $l o g (a b) = l o g (a) + l o g (b)$ .
$l o g_{a} (x)$ ist die Umkehrfunktion zu $a^{x}$ . Dies bedeutet, dass $l o g_{a} (a^{x}) = x .$
Es gilt: $a^{c + d} = a^{c} + a^{d}$ .
Es gilt: $a^{c + d} = a^{c} a^{d}$ .
Es gilt immer $a^{x} < b^{x}$ für a < b und alle x.
Es gilt immer $a^{x} < b^{x}$ für 1 < a < b und alle x.
Es gilt immer $a^{x} < b^{x}$ für 0 < a < b und alle x > 0.
Es gilt immer $a^{x} > b^{x}$ für 0 < a < b < 1 und alle x.
Es gilt immer $a^{x} < b^{x}$ für 0 < a < b < 1 und alle x.
Es gilt immer $a^{x} > b^{x}$ für 0 < a < b und alle x < 0.

Wie gut kennen Sie sich noch mit Exponenten und Logarithmen aus? --- Antworten

In fett, kursiv und mit einem werden Ihnen die richtigen Antworten angezeigt:

Die Gleichung $10^{x} = 100$ können wir bspw. mit dem 10er-Logarithmus $l o g_{10} (100)$ berechnen. Die Antwort ist 2.
Die Gleichung $10^{x} = 100$ können wir bspw. mit dem 10er-Logarithmus $l o g_{10} (100)$ berechnen. Die Antwort ist 3.
Logarithmen können NICHT in einander umgerechnet werden.
Es gilt: $l o g (a + b) = l o g (a) l o g (b)$ .
Es gilt: $l o g (a b) = l o g (a) + l o g (b)$ .
$l o g_{a} (x)$ ist die Umkehrfunktion zu $a^{x}$ . Dies bedeutet, dass $l o g_{a} (a^{x}) = x .$
Es gilt: $a^{c + d} = a^{c} + a^{d}$ .
Es gilt: $a^{c + d} = a^{c} a^{d}$ .
Es gilt immer $a^{x} < b^{x}$ für a < b und alle x.
Es gilt immer $a^{x} < b^{x}$ für 1 < a < b und alle x.
Es gilt immer $a^{x} < b^{x}$ für 0 < a < b und alle x > 0.
Es gilt immer $a^{x} > b^{x}$ für 0 < a < b < 1 und alle x.
Es gilt immer $a^{x} < b^{x}$ für 0 < a < b < 1 und alle x.
Es gilt immer $a^{x} > b^{x}$ für 0 < a < b und alle x < 0.

Im folgenden Exkurs haben Sie die Möglichkeit Ihr Wissen nochmal aufzufrischen und zu erweitern. Ihnen werden Quellen genannt, in welchen Sie weitere Inhalte nachlesen können. Dieser Exkurs stellt eine Wiederholung dar. Sie können ihn auch überspringen.

Exkurs: Ein paar Rechenregeln zu Exponenten und Logarithmen

Um eine exponentielle Gleichung nach $x$ aufzulösen wird der Logarithmus verwendet, denn er ist die Umkehrfunktion zum Exponentiellen (siehe beispielsweise hier für eine Wiederholung zum Logarithmus und Logarithmusrechenregeln; Pierce (2018), Exponenten; Pierce (2019) oder Exponentenrechenregeln; Pierce (2018)). In der Schule wird zunächst der Logarithmus zur Basis 10 gelehrt. So kann man die Gleichung $10^{x} = 100$ leicht auflösen: Dazu müssen beide Seiten (zur Basis 10) logarithmiert werden: $\log_{10} (10^{x}) = \log_{10} (100)$ , denn es gilt im Allgemeinen:

Für Exponenten:

$a^{b + c} = a^{b} a^{c}$ $a^{b} < a^{c} ⟹ b < c, falls b, c > 0$

$a^{- b} = \frac{1}{a^{b}}$ $(a^{b})^{c} = a^{b c} = (a^{c})^{b}$ $a^{0} = 1$

Und folglich auch für Logarithmen: $\log_{a} (a) = 1$

$\log_{a} (b c) = \log_{a} (b) + \log_{a} (c)$ $\log_{a} (\frac{b}{c}) = \log_{a} (b) - \log_{a} (c)$

$\log_{a} (b^{c}) = c \log_{a} (b)$

$x = \log_{a} (a^{x}) = a^{\log_{a} (x)}$ (hier ist $\log_{a}$ der Logarithmus zur Basis $a$ und $a, b$ und $c$ sind Zahlen, wobei der Einfachheit halber $a, b, c > 0$ gelten soll)

Also rechnen wir: $\log_{10} (10^{x}) = x \log_{10} (10) = x * 1 = x$ auf der linken Seite und $\log_{10} (100) = 2$ auf der rechten Seite. So erhalten wir $x = 2$ als Lösung. Natürlich wussten wir schon vorher, dass $10^{2} = 100$ ergibt; es ist aber eine schöne Veranschaulichung, wofür Logarithmen unter anderem gebraucht werden.

Es muss allerdings nicht immer der richtige Logarithmus zur jeweiligen Basis sein. Eine wichtige Logarithmusrechenregel besagt, dass der Logarithmus zur Basis $a$ leicht mit Hilfe des Logarithmus zur Basis $b$ berechnet werden kann:

$\log_{a} (x) = \frac{\log_{b} (x)}{\log_{b} (a)},$ siehe bspw. Logarithmus und Logarithmusrechenregeln; Pierce (2018). Da diese Gesetzmäßigkeit gilt, wird in der Mathematik und auch in der Statistik meist nur der natürliche Logarithmus (ln; logarithmus naturalis) verwendet. Die Basis ist hierbei die “Eulersche Zahl” $e$ ( $e \approx 2.718 \dots$ ). Mit den obigen Rechenregeln sowie der Rechenregeln für Exponenten können wir jedes exponentielles Wachstum als Wachstum zur Basis e darstellen, denn

$a^{x} = e^{ln (a^{x})} = e^{x ln (a)}$ z.B ist $10^{3} = e^{ln (10^{3})} = e^{3 ln (10)} = 1000$

Da sich durch e und ln alle exponentiellen Verläufe darstellen lassen, wird in der Mathematik häufig log als das Symbol für den natürlich Logarithmus verwendet; so ist es auch in R: ohne weitere Einstellungen ist log der natürliche Logarithmus und exp ist die Exponentialfunktion. Mit Hilfe von log(..., base = 10) erhalten sie beispielsweise den 10er-Logarithmus. Probieren Sie die obige Gleichung selbst aus:

# gleiches Ergebnis:
10^3

## [1] 1000

exp(3*log(10))

## [1] 1000

# gleiches Ergebnis:
log(10^3, base = 10) # Logarithmus von 1000 zur Basis 10

## [1] 3

log(10^3)/log(10) # mit ln

## [1] 3

# gleiches Ergebnis:
log(9, base = 3) # Logarithmus von 9 zur Basis 3

## [1] 2

log(9)/log(3) # mit ln

## [1] 2

Literatur

Arinze, E.D. (2024). Unravelling Exponential Growth Dynamics: A Comprehensive Review. IAA Journal of Scientific Research 11(3):19-26. https://doi.org/10.59298/IAAJSR/2024/113.1926

Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden (5. Auflage, 1. Auflage: 2010). Weinheim: Beltz.

Blau hinterlegte Autor:innenangaben führen Sie direkt zur universitätsinternen Ressource.

Regression Nichtlinear Polynome Quadratisch Logarithmus