Übersicht und Vorbereitung
In den letzten Sitzungen haben wir gesehen, wie wir ein Modell für eine Multiple Regression in R aufstellen und verschiedene Modelle gegeneinander testen können. Besonders bei der Nutzung von Inferenzstatistik wissen wir aber auch, dass genutzte statistische Verfahren häufig Voraussetzungen an die Daten mitbringen. Das Thema der heutigen Sitzung ist daher die Überprüfung von Voraussetzungen im Rahmen der Regressionsdiagnostik. In Statistik I hatten wir bereits im Beitrag zur Multiplen Regression die fünf grundlegenden Voraussetzungen besprochen:
- Messfehlerfreiheit der unabhängigen Variablen
- Unabhängigkeit der Residuen
- Homoskedastizität der Residuen
- Normalverteilung der Residuen
- Korrekte Spezifikation des Modells - bspw. Linearität
In diesem Beitrag gucken wir uns diese nochmal genauer an, betrachten ein paar Details etwas präziser und gucken uns an, was man eigentlich tun kann, wenn die Voraussetzungen nicht halten sollten. Darüber hinaus werden wir zwei weitere problematische Datensituationen behandeln, welche die Analyse beeinflussen können:
Beispieldaten
In diesem Beitrag nutzen wir die Daten aus dem Artikel von Stahlmann et al. (2024), in welchem Beweggründe für und Commitment zu veganer bzw. vegetarischer Ernährung untersucht werden. Wir betrachten hier nur den Teildatensatz der Personen, die sich vegan ernähren, aber den vollen Datensatz können Sie sich im OSF-Repo zum Artikel genauer ansehen. Die Datenaufbereitung und -auswahl habe ich in einem R-Skript hinterlegt, das Sie direkt ausführen können:
# Datensatz laden
source("https://pandar.netlify.app/daten/Data_Processing_vegan.R")
Dieser reduzierte Datensatz besteht aus 987 Beobachtungen auf 10 Variablen. Für uns sind im Rahmen dieses Beitrags vor allem die commitment und die sechs Subskalen des VEMI+ relevant, die unterschiedliche Gründe für die vegane Ernährung abbilden. Mit einem Klick finden Sie hier ein paar Beispielitems:
Details zu den Variablen
| Variable | Beispielitem |
|---|---|
commitment | I am always vegan, without exception |
health | I want to be healthy |
environment | Plant-based diets are better for the environment |
animals | I don’t want animals to suffer |
social | I want to be more like people I admire |
workers | People who work in animal agriculture are exploited |
disgust | The idea of eating meat disgusts me |
Modell aufstellen
Zunächst gucken wir uns das Regressionsmodell an, mit dem wir vorhersagen, inwiefern die Gründe für den Veganismus das Commitment zum Veganismus vorhersagen können. Wie Sie in den vorangegangenen Beiträgen zur Regression wahrscheinlich mitbekommen haben, funktioniert das Ganze über den lm-Befehl:
#### Modell aufstellen ----
# Volles Regressionsmodell
mod <- lm(commitment ~ health + environment + animals + social + workers + disgust, data = vegan)
# Ergebnisse betrachten
summary(mod)
##
## Call:
## lm(formula = commitment ~ health + environment + animals + social +
## workers + disgust, data = vegan)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.4378 -0.4009 0.2042 0.5481 2.0268
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.48377 0.20111 12.350 < 2e-16 ***
## health -0.06681 0.01974 -3.385 0.000741 ***
## environment 0.04370 0.02599 1.681 0.093046 .
## animals 0.19855 0.02774 7.157 1.62e-12 ***
## social -0.10357 0.02371 -4.367 1.39e-05 ***
## workers -0.04125 0.01675 -2.463 0.013960 *
## disgust 0.18467 0.01610 11.471 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.8437 on 980 degrees of freedom
## Multiple R-squared: 0.2706, Adjusted R-squared: 0.2662
## F-statistic: 60.6 on 6 and 980 DF, p-value: < 2.2e-16
Im Output der summary sehen wir die Parameterschätzungen unseres Regressionsmodells:
Den Koeffizienten entnehmen wir, dass alle Subskalen der Beweggründe außer environment statistisch bedeutsam sind. Dabei ist besonders beachtenswert, dass drei der signifikanten Prädiktoren sich sogar negativ auf das commitment auswirken - Personen, denen ihre Gesundheit besonders wichtig ist, fühlen sich dem Veganismus also weniger stark verpflichtet (unter Konstanthaltung der Ausprägung auf den anderen fünf Subskalen). Insgesamt werden 27.06% der Variation durch die Prädiktoren erklärt.
Die Regressionskoeffizienten lm.beta() aus dem Paket lm.beta ermitteln, welches wir bereits installiert haben und nur noch aktivieren müssen.
library(lm.beta)
summary(lm.beta(mod))
##
## Call:
## lm(formula = commitment ~ health + environment + animals + social +
## workers + disgust, data = vegan)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.4378 -0.4009 0.2042 0.5481 2.0268
##
## Coefficients:
## Estimate Standardized Std. Error t value Pr(>|t|)
## (Intercept) 2.48377 NA 0.20111 12.350 < 2e-16 ***
## health -0.06681 -0.10623 0.01974 -3.385 0.000741 ***
## environment 0.04370 0.05356 0.02599 1.681 0.093046 .
## animals 0.19855 0.23022 0.02774 7.157 1.62e-12 ***
## social -0.10357 -0.12708 0.02371 -4.367 1.39e-05 ***
## workers -0.04125 -0.07499 0.01675 -2.463 0.013960 *
## disgust 0.18467 0.36468 0.01610 11.471 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.8437 on 980 degrees of freedom
## Multiple R-squared: 0.2706, Adjusted R-squared: 0.2662
## F-statistic: 60.6 on 6 and 980 DF, p-value: < 2.2e-16
Die standardisierten Regressionsgewichte für die Prädiktoren, welche in der zweiten Spalte bei den Koeffizienten abgetragen sind, geben an, um wie viele Standardabweichungen sich die Vorhersage von
Messfehlerfreiheit der unabhängigen Variablen und Unabhängigkeit der Residuen
Die beiden Voraussetzungen werden wir im Tutorial nicht genauer betrachten. Im Beitrag zur multiplen Regression hatten wir beide schon angeschnitten, weshalb wir hier nur zum Start die Bedeutung und Auswirkung kurz zusammenfassen. Messfehlerfreiheit der unabhängigen Variable umfasst, dass die Ausprägung der Variablen ohne Fehler gemessen werden können. Eine vielleicht aus der Diagnostik bekannte Größe, die den Grad an Messfehlerabhängigkeit bestimmen kann, ist die Reliabilität. Messinstrumente mit hoher Reliabilität sind demnach zu bevorzugen und resultieren in weniger Fehlern. Wenn unsere unabhängigen Variablen mit Messfehler versehen sind, kann das zu einer Unterschätzung der Regressionsgewichte führen - woher das kommt, erklären wir im Exkurs in Appendix A.
Bei der Unabhängigkeit der Residuen geht es darum, dass die Residuen voneinander unabhängig sind. Diese Annahme ist z.B. dann verletzt, wenn wir in Messwiederholungen mehrfach die gleichen Personen messen (bei
Homoskedastizität
Prüfung der Voraussetzung
Wie schon beim
Im ersten Semester hatten wir für die optische Prüfung den Scale-Location-Plot genutzt, die Homoskedastizität einzuschätzen. Weil es damals so gut funktioniert hat, gibt es zunächst keinen Grund, etwas daran zu ändern. Wir hatten damals alle diagnostischen Plots zu einem Modell über den einfachen plot-Befehl angefordert. Weil wir jetzt nur den dritten der dort erzeugten vier Plots benötigen, können wir als zweites Argument (which) einfach 3 auswählen:
# Scale-Location-Plot
plot(mod, 3)
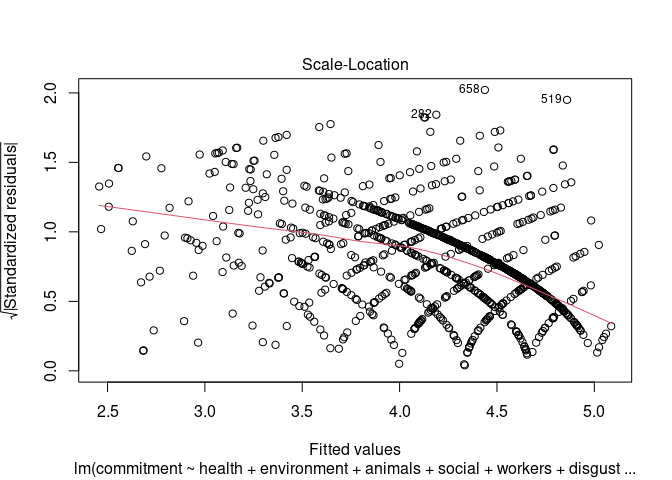
Zur Erinnerung: wenn die Varianz über alle vorhergesagten Werte gleich wäre, sollte die eingezeichnete rote LOWESS-Linie bei einem Wert von 1 parallel zur x-Achse (also horizontal) verlaufen. Die Tendenz weißt aber deutlich darauf hin, dass in diesem Fall die Varianz der Residuen bei hohen vorhergesagten Werten niedriger zu sein scheint, als bei niedrigen Werten. Zum Abgleich: die Varianz der Residuen ist für die 25% der Fälle mit den geringsten vorhergesagten Werten 1.17, bei den Fällen mit den höchsten 25% der vorhergesagten Werte hingegen 0.35.
Im Residuenplot zeichnet sich der Grund für die Heteroskedastizität ab:
# Residuenplot
plot(mod, which = 1)
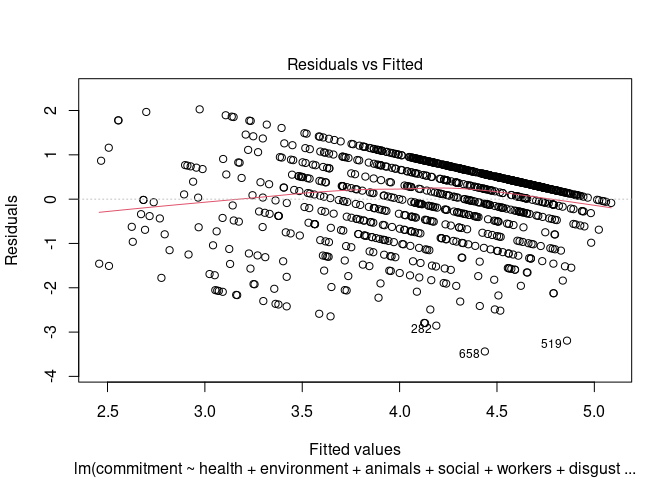
Für einen Test der Homoskedastizität, können wir die Funktion ncvTest (Test For Non-Constant Error Variance) aus dem car-Paket nutzen. Diese prüft, ob die Varianz der Residuen signifikant linear (!) mit den vorhergesagten Werten zusammenhängt. Für Gruppenvergleiche hatten wir noch den Levene-Test (leveneTest) genutzt - dieser funktioniert allerdings nur dann, wenn wir Varianzen über viele Beobachtungen in wenigen Gruppen bestimmen können. Da wir in den meisten Fällen in der Regression mehr potenzielle Ausprägungen der vorhergesagten Werte als Beobachtungen haben, benötigen wir hier eine vereinfachende Modellannahme, um eine Approximation dafür zu erhalten, ob sich Unterschiede in der Varianz finden lassen.
library(car)
# Test For Non-Constant Error Variance
ncvTest(mod)
## Non-constant Variance Score Test
## Variance formula: ~ fitted.values
## Chisquare = 104.7127, Df = 1, p = < 2.22e-16
Wie bei allen Voraussetzungstests ist auch hier die Nullhypothese, dass die Voraussetzung hält. Wird dieser Test also signifikant (wie hier), ist die Annahme der Homoskedaszidität zu verwerfen. Es ist wichtig zu bedenken, dass ein nicht signifikantes Ergebnis kein Beleg für Homoskedastizität ist - es könnte uns an Power mangeln oder die Varianzen könnten z.B. nicht-linear von den vorhergesagten Werten abhängen.
Umgang mit Heteroskedastizität
Wenn unsere Datenlage eine Voraussetzung für einen statistischen Test nicht erfüllt, ist die wichtigste anschließende Frage “warum?”. Eine pauschale Lösung, wie mit der Verletzung einer Annahme umgegangen werden soll, wird es nicht geben, weil - etwas dramatisch ausgedrückt - ein Symptom ein Indikator für verschiedene Krankheiten sein kann. Prinzipiell könnte Heteroskedasitizität z.B. entstehen, weil nicht-lineare Effekte vorliegen, die wir nicht in unserem Modell aufgenommen haben. Eine andere Möglichkeit wäre, dass die Skala, mit der wir die abhängige Variable gemessen haben, begrenzt ist, sodass die Unterschiede zwischen Personen künstlich beschnitten sind. Weil beides sehr unterschiedliche Gründe sind, unterscheiden sich auch die entsprechenden Gegenmaßnahmen dramatisch. Im ersten Fall würden wir zunächst versuchen die Annahme der korrekten Spezifikation des Modells zu erfüllen, z.B. indem wir nicht-lineare Effekte aufnehmen. Im zweiten Fall könnten wir für die nächste Studie notieren, dass wir ein anderes Messinstrument nutzen sollten (was uns bei der aktuellen Regression aber nur wenig hilft).
Wenn wir entweder nicht herausfinden können, was die Ursache für das Problem ist, dieses nicht beheben können oder - auch das soll es geben - die Varianzen einfach tatsächlich unterschiedlich sind, können wir zumindest das Symptom lindern. Wie im 1. Semester besprochen, führt die Verletzung der Annahme der Homoskedastizität zu einer Verzerrung der Standardfehler und somit der Inferenzstatistik unserer Regressionsgewichte und des
- Nutzen von weighted-least-squares (WLS) Regression
- Transformation der abhängigen Variable
- Bestimmen von robusten, korrigierten Standardfehlern
- Bootstrapping
Der Ansatz via WLS-Regression wird z.B. von Cohen et al. (2003) bei starker Verletzung der Annahme und großen Stichproben empfohlen. Dieses Vorgehen umfasst mehrere Schritte, die wir hier nicht näher erläutern werden, weil Alternativen 2 bis 4 meist ausreichend gut und sehr viel einfacher das gewünschte Ziel erreichen. Den 4. Punkt (Bootstrapping) werden wir gleich beim Umgang mit Verletzungen der Normalverteilungsannahme besprechen, weswegen wir ihn hier überspringen.
Transformation der abhängigen Variable: Box-Cox Transformation
Unterschiedliche Varianzen der Residuen bedeuten, dass die Unterschiede zwischen Personen in einigen Bereichen der Variable kleiner sind, als in anderen. Wenn wir also die Skalierung der Variable so ändern, dass Unterschiede in bestimmten Bereichen “groß gerechnet” werden, während wir sie an anderen Stellen verringern, könnte das unser Problem lösen. Die Frage, die sich aufdrängt, ist aber: welche Transformation ist in diesem spezifischen Anwendungsfall die Richtige? Je nachdem, wo Varianzen kleiner oder größer sind, werde ich andere Gleichungen brauchen, um durch die Transformation Varianzen anzugleichen, statt sie potentiell sogar unterschiedlicher zu machen.
Generell wird die Box-Cox Transformation durch folgende Gleichung ausgedrückt:
Diese Transformation ist relativ flexibel - wenn boxcox aus dem Paket MASS nutzen:
# Box-Cox Transformation
bc <- MASS::boxcox(mod, lambda = seq(-5, 5, .1))
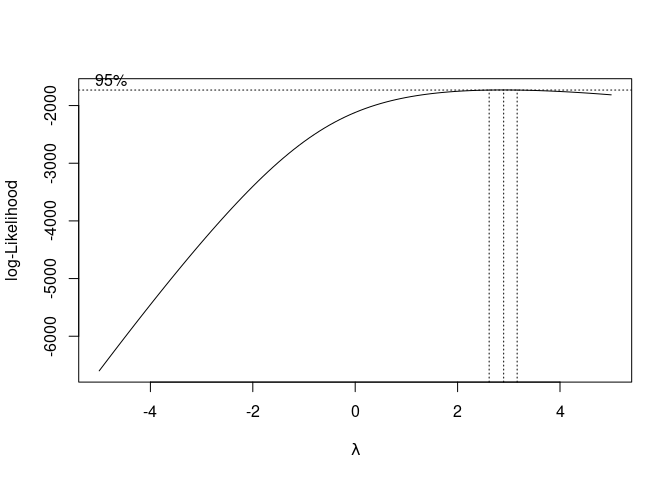
mod und die Werte, die wir für # Optimales Lambda extrahieren
lam <- bc$x[which.max(bc$y)]
lam
## [1] 2.9
Wenn wir unsere AV jetzt so transformieren, sollte sich das Problem der Heteroskedastizität erübrigen:
# Transformation der AV
vegan$commitment_bc <- (vegan$commitment^lam - 1) / lam
# Neues Modell aufstellen
mod_bc <- lm(commitment_bc ~ health + environment + animals + social + workers + disgust, data = vegan)
Und, um zu checken, ob wir tatsächlich jetzt homoskedastische Fehler haben:
# Non-Constant-Variance Test
ncvTest(mod_bc)
## Non-constant Variance Score Test
## Variance formula: ~ fitted.values
## Chisquare = 9.421633, Df = 1, p = 0.0021444
Leider konnten wir unser Problem nicht in Gänze lösen. Wie wir oben gesehen hatten, ist durch die Skala der abhängigen Variable eingeschränkt, welche Residuen möglich sind. Bei einer Transformation können wir zwar die Unterschiede zwischen Personen reskalieren, um die Varianz über alle
Robuste Standardfehler
Wie bereits erwähnt, führt Heteroskedastizität vor allem zu einer Verzerrung der Standardfehler und damit zu Fehler in der Inferenzstatistik. Wenn Heteroskedastizität also keinen tieferen Grund hat, sondern einfach tatsächliche Unterschiede in der Streuung sind, können wir “einfach” die Standardfehler korrigieren, um diesem Problem entgegenzuwirken. Solche korrigierten Standardfehler werden heteroskedasticitiy consistent (HC) genannt. Verbreitet haben sich im Wesentlichen fünf unterschiedliche Varianten (Hayes et al., 2007, bieten einen Überblick) dieser Korrektur, wobei generell empfohlen wird den HC3 Ansatz für beinahe alle Fälle zu verwenden. Die einzige Ausnahme stellen Situationen dar, in denen wir einzelne, sehr einflussreiche Datenpunkte haben (dazu gleich mehr). Daher fokussieren wir uns hier zunächst auf die HC3-Korrektur.
Für alternative Ansätze, Inferenzstatistik in Regressionen zu betreiben wurde das lmtest-Paket entwickelt. Dieses erlaubt es uns z.B. eigene Berechnungsformen der Standardfehler anzugeben. Weil wir uns ersparen wollen, die HC3-Korrektur selbst zu berechnen, benutzen wir dafür das sandwich-Paket:
# Pakete laden
library(sandwich) # für die Berechnung der HC3 Standardfehler
library(lmtest) # für die Testung der Regressionsgewichte
Das sandwich-Paket bietet uns im vcovHC-Befehl direkt die korrigierten Standardfehler. Zum Vergleich, unsere “normalen” Standardfehler entsprechen der Quadratwurzel der Diagonale des vcov-Outputs:
# Standardfehler
vcov(mod) |> diag() |> sqrt()
## (Intercept) health environment animals social workers disgust
## 0.20110858 0.01974033 0.02599389 0.02774348 0.02371486 0.01674969 0.01609833
Die korrigierte Fassung sieht so aus (der vcovHC-Befehl nutzt per Voreinstellung HC3, andere Varianten können über type angefordert werden):
# HC3 Standardfehler
vcovHC(mod) |> diag() |> sqrt()
## (Intercept) health environment animals social workers disgust
## 0.25281493 0.02042803 0.02880656 0.03358680 0.02385231 0.01707229 0.01754127
Um diese Standardfehler in der Inferenzstatistik zu nutzen, können wir die coeftest-Funktion aus dem lmtest-Paket verwenden:
# Inferenzstatistik der Regressionsgewichte
coeftest(mod, vcov = vcovHC(mod))
##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.483774 0.252815 9.8245 < 2.2e-16 ***
## health -0.066815 0.020428 -3.2707 0.00111 **
## environment 0.043700 0.028807 1.5170 0.12958
## animals 0.198554 0.033587 5.9117 4.672e-09 ***
## social -0.103572 0.023852 -4.3422 1.557e-05 ***
## workers -0.041250 0.017072 -2.4162 0.01587 *
## disgust 0.184670 0.017541 10.5277 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Inhaltlich ändert das wenig an den Aussagen - die konkreten Werte ändern sich zwar, aber bei
Normalverteilung
Die Normalverteilung der Residuen haben wir bereits in Statistik I geprüft. Dafür haben wir - analog zum Vorgehen bei der Homoskedastizität - sowohl eine optische als auch eine inferenzstatistische Prüfung kennengelernt. Im Fall der Normalverteilungsannahme basiert die visuelle Prüfung auf QQ-Plots (Quantile-Quantile-Plots) oder auf einem Histogramm der Residuen. Für den QQ-Plot hatten wir den Befehl qqPlot aus dem car-Paket genutzt:
# QQ-Plot der Residuen
qqPlot(mod)
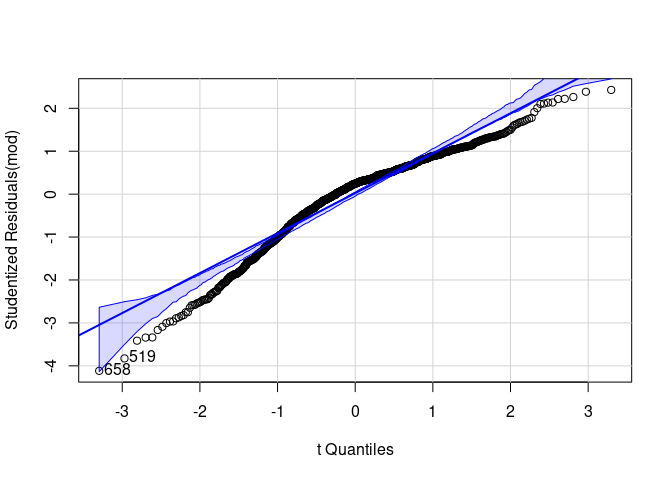
## [1] 519 658
Das Histogramm können wir mittels hist-Befehl erzeugen:
# Histogramm der Residuen
resid(mod) |> hist()
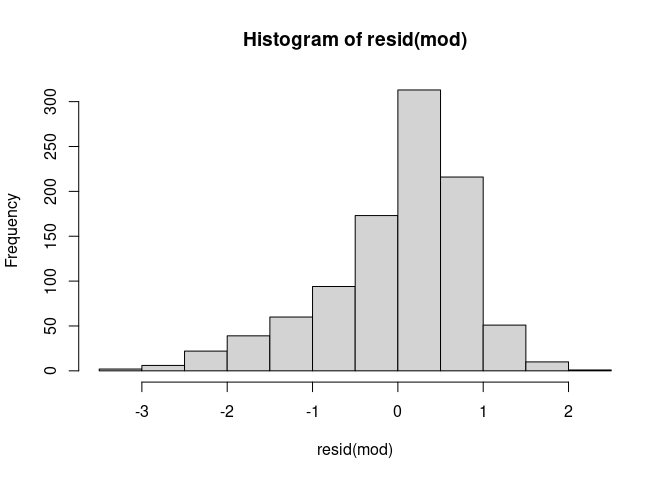
Wenn wir zusätzlich einen inferenzstatistischen Beleg der Unangemessenheit der Annahmen haben möchten, können wir den Shapiro-Wilk-Test auf Normalität (shapiro.test) nutzen.
# Shapiro-Wilk-Test auf Normalverteilung
resid(mod) |> shapiro.test()
##
## Shapiro-Wilk normality test
##
## data: resid(mod)
## W = 0.94394, p-value < 2.2e-16
Wenig überraschend verwirft dieser Test hier die Nullhypothese, dass die Residuen normalverteilt sind und wir müssen uns wieder fragen, was geeignete Vorgehensweisen für den
Umgang mit Abweichung von der Normalverteilung
sind. Im Wesentlichen lassen sich die Möglichkeiten in drei große Kategorien gliedern:
- Nutzen von generalisierten Regressionsmodellen
- Transformation der abhängigen Variable
- Bootstrapping
Die erste Möglichkeit ist etwas, dass wir z.B. im Rahmen der logistischen Regression im KliPPs- oder dem Psychologie-Master wieder aufgreifen werden. Die Grundidee ist hier, dass wir statt der Normalverteilung eine andere Verteilung der Residuen annehmen. Dieses Vorgehen ist besonders dann beliebt, wenn die Residuen die Normalverteilungsannahme gar nicht erfüllen können, z.B. weil die abhängige Variable nominalskaliert ist.
Die anderen beiden Möglichkeiten hatten wir gerade schon bei der Homoskedastizität gesehen.
Transformation der abhängigen Variable
Bei der Transformation der Variable ändert sich naheliegenderweise nicht nur deren Varianz, sondern auch deren Verteilung. Nehmen wir die gleiche Transformation, die wir vorhin aus der Box-Cox-Analyse erhalten haben:
# Vier plots gleichzeitig darstellen
par(mfrow = c(2, 2))
# QQ-Plot ohne Transformation
qqPlot(mod)
## [1] 519 658
# QQ-Plot mit Transformation
qqPlot(mod_bc)
## [1] 519 658
# Histogramm ohne Transformation
resid(mod) |> hist()
# Histogramm mit Transformation
resid(mod_bc) |> hist()
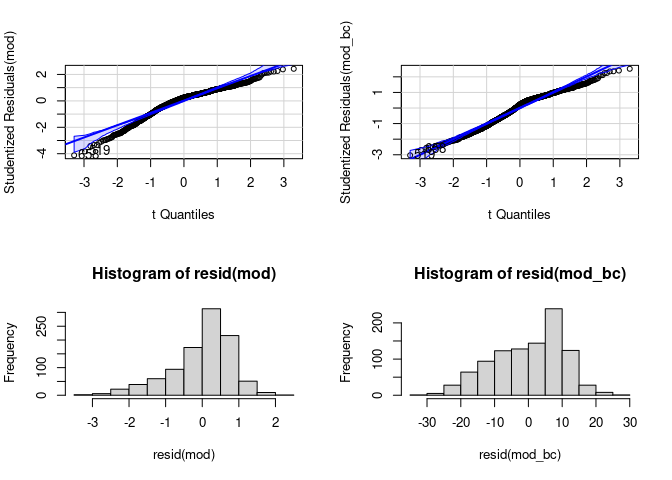
# Normale Einstellung für Plots wiederherstellen
par(mfrow = c(1, 1))
Wir sehen auch hier, dass die Transformation zumindest im unteren Bereich der Variable ein wenig Besserung vollbracht hat, allerdings insgesamt nicht in der Lage war, die Residuen in eine Normalverteilung zu überführen. So viel sagt uns auch der Shapiro-Test:
# Shapiro-Wilk-Test nach Transformation
resid(mod_bc) |> shapiro.test()
##
## Shapiro-Wilk normality test
##
## data: resid(mod_bc)
## W = 0.9734, p-value = 1.827e-12
Die Transformation der Variablen sollte stets extrem überlegt vorgenommen werden. Wie wir hier gesehen haben, hat sie gleichzeitig Auswirkungen auf Varianz und Verteilung der Variablen, aber auch die Interpretation der Modellparameter ändert sich. So bewirkt z.B. die beliebte logarithmus-Transformation von Reaktionszeiten, dass die Regression keine linearen Effekte mehr abbildet, sondern Reaktionszeiten exponentiell die Unterschiede in den unabhängigen Variablen abbilden. Bei komplexeren Transformationen (wie hier z.B. bei der Box-Cox-Transformation) wird die direkte Interpretation der Regressionsgewichte extrem schwer, sodass ich generell von einer Transformation der Variablen abraten würde, wenn sie nicht vorher theoretisch ableitbar war und die Veränderung der Interpretation der Regressionsgewichte explizit gewollt ist.
Bootstrapping
Die Voraussetzungen der Normalverteilung und Homoskedastizität sollen gewährleisten, dass das Verhältnis aus Parameterschätzer und Standardfehler der animals) sehen möchten.
Details zum Bootstrapping
Wie kurz geschildert, ziehen wir beim Bootstrapping aus unserem Datensatz wiederholt, mit Zurücklegen, einen Datensatz der gleichen Größe aus unseren Daten. Am Beispiel der ersten sieben Personen würde das z.B. so aussehen:
# Originaldatensatz
og <- vegan[1:7, c('age', 'gender', 'commitment', 'animals')]
og
## age gender commitment animals
## 1 32 male 1.666667 4
## 2 59 male 4.333333 7
## 3 25 nonconformingOther 5.000000 7
## 4 34 male 4.333333 7
## 5 26 male 4.666667 7
## 6 43 male 4.666667 5
## 7 68 male 4.000000 6
# Bootstrap-Datensatz
b1 <- og[sample(1:7, 7, replace = TRUE), ] #Wichtig: replace=TRUE --> mit Zurücklegen
b1
## age gender commitment animals
## 2 59 male 4.333333 7
## 6 43 male 4.666667 5
## 3 25 nonconformingOther 5.000000 7
## 4 34 male 4.333333 7
## 4.1 34 male 4.333333 7
## 6.1 43 male 4.666667 5
## 2.1 59 male 4.333333 7
Hier wurden die Personen 4, 6 und 2 jeweils doppelt gezogen, Personen 1, 5 und 7 kommen hingegen in dieser Zufallsziehung gar nicht vor. Wenn wir in diesem Datensatz die Regression berechnen würden, wäre sie also etwas anders als im Originaldatensatz.
Damit wir das Ganze wiederholt durchführen können, könnten wir den replicate-Befehl benutzen, den wir im letzten Semester für die Poweranalyse verwendet hatten. Beschränken wir uns zunächst auf das Regressionsgewicht von animals und erstellen eine Funktion, die einen Datensatz entgegennimmt, daraus zufällig zieht und das Regressionsgewicht ausgibt:
# Manuelle Regressionsfunktion
booting <- function(data) {
# Datensatz zufällig ziehen
b_data <- data[sample(1:nrow(data), nrow(data), replace = TRUE), ]
# Regression durchführen
mod <- lm(commitment ~ health + environment + animals + social + workers + disgust, data = b_data)
# Regressionsgewicht extrahieren
out <- coef(mod)[4]
return(out)
}
# Wiederholte anwendung
booted <- replicate(5000, booting(vegan))
Damit wir nicht jedes mal eine neue Funktion schreiben müssen, können wir Regressionsmodelle auch einfach an die Boot-Funktion aus dem car-Paket übergeben:
# Bootstrapping mit car-Paket
booted <- Boot(mod, R = 5000)
So erhalten wir die Ergebnisse für unsere Regression 5000 mal. Um zu sehen, wie sich das auf das Regressionsgewicht von animals auswirkt, können wir die angenommene Verteilung des Regressionsgewichts (eine Normalverteilung mit dem Mittelwert
# ggplot2 Paket laden
library(ggplot2)
# Original Regressionsgewicht
b_og <- coef(mod)[4]
# Standardfehler
se_og <- sqrt(diag(vcov(mod))[4])
# 5000 Regressionen
b_boot <- booted$t
# ggplot2 Plot erstellen
ggplot(b_boot, aes(x = animals)) +
geom_histogram(aes(y = after_stat(density)), bins = 50, fill = "grey90", color = "black") +
geom_function(fun = dnorm, args = list(mean = b_og, sd = se_og)) +
geom_vline(xintercept = b_og, linetype = "dashed")
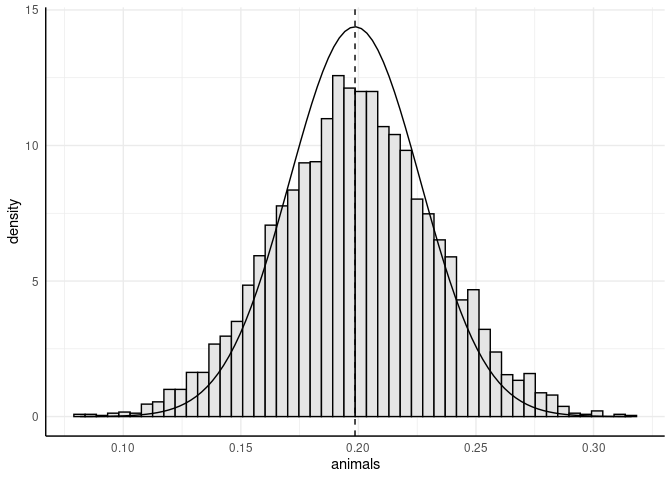
Diese Intuition können wir überprüfen, indem wir die Standardfehler aus dem Modell mit der Standardabweichung der gebootstrappten Werte vergleichen:
# Standardabweichung der gebootstrappten Werte
sd(b_boot[, 4])
## [1] 0.03388931
# Standardfehler der Regressionsgewichte
vcov(mod)[4, 4] |> sqrt()
## [1] 0.02774348
Wir sehen also, dass der Standardfehler die tatsächliche Schwankung der Regressionsgewichte um knapp 18% unterschätzt und wir (aufgrund der Verletzung der Annahmen) einen zu liberalen Test des Gewichts durchgeführt haben.
Das car-Paket liefert uns mit der Boot-Funktion die sehr einfache Möglichkeit nicht nur den Bootstrap durchzuführen, sondern auch im Anschluss direkt über Konfidenzintervalle eine aktualisierte inferenzstatistische Entscheidung treffen zu können:
# Bootstrapping mit car-Paket
booted <- Boot(mod, R = 5000)
# Zusammenfassung der Ergebnisse
confint(booted, type = 'perc')
## Bootstrap percent confidence intervals
##
## 2.5 % 97.5 %
## (Intercept) 1.97843799 2.98336045
## health -0.10734771 -0.02740971
## environment -0.01202953 0.10059435
## animals 0.13157351 0.26712685
## social -0.15082137 -0.05748843
## workers -0.07436732 -0.00848034
## disgust 0.15026793 0.21951566
Im einfachsten Fall wird das Konfidenzintervall im Bootstrap so erstellt, dass von unseren 5000 Wiederholungen die 2.5% und 97.5% Perzentile bestimmt werden. Dieses “percentile” Konfidenzintervall ist nicht immer frei von Verzerrungen, sodass die Korrektur (BCa - Bias-Corrected and Accelerated) inzwischen der Standard ist (und auch ohne Angabe von type als Voreinstellung ausgegeben werden würde). Generell werden hier keine
Korrekte Spezifikation des Modells - bspw. Linearität
In die korrekte Spezifikation des Modells fällt, dass keine als Prädiktor relevanten Variablen aus der Population ausgelassen werden und auch keine Variablen eingeschlossen werden, die nicht zur Erklärung beitragen. Ein Aspekt davon ist, dass der Zusammenhang zwischen den Prädiktoren und dem Kriterium auch so sein soll, wie von uns in der Regressionsgleichung postuliert. Bisher nutzen wir nur lineare Zusammenhänge, weshalb eine Annahme ist, dass in der Population auch wirklich ein linearer Zusammenhang zwischen den Prädiktoren und dem Kriterium besteht. Im Beitrag zur einfachen linearen Regression haben wir die Linearitätsannahme mit Hilfe von Scatterplots und LOESS-Linien betrachtet. Obwohl diese Methode auch für die multiple Regression anwendbar ist, berücksichtigt sie nicht vollständig einen zentralen Aspekt: Wir nehmen an, dass die Beziehung zwischen einer unabhängigen Variable und der abhängigen Variable bedingt auf die Ausprägungen der anderen Variablen im Modell linear ist.
Eine grafische Prüfung der partiellen Linearität zwischen den einzelnen Prädiktorvariablen und dem Kriterium kann durch Residuenplots erreicht werden. Die Residuen der Regression stellen den Rest der abhängigen Variable dar, nachdem wir alle Prädiktoren auspartialisiert haben. Da in unserem Fall ausschließlich lineare Terme enthalten sind, sind alle linearen Effekte also auspartialisiert. Wir können gucken, ob diese Residuen z.B. quadratisch mit den Prädiktoren zusammenhängen, um so zu prüfen, ob die angenommene Linearität realistisch war. car liefert hierfür den residualPlots-Befehl:
# Residuenplots
residualPlots(mod)
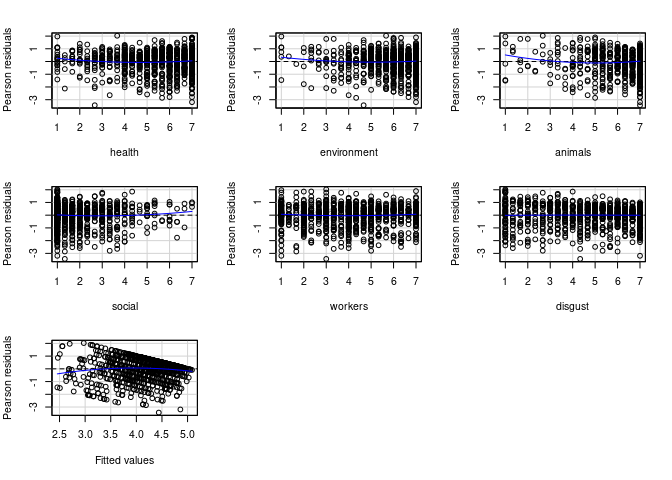
workers und disgust sehen wir zum Beispiel, dass die Kurve quasi nur eine horizontale Linie ist - hier scheint es also keine quadratischen Effekte zu geben. Für environment und animals sieht dies etwas anders aus - für beide Variablen indiziert der Plot zunächst, dass sehr niedrige Ausprägungen auf dem Prädiktor mit höheren Residuen einhergehen, als unser lineares Modell implizieren würde.Die Plots dienen hauptsächlich dem Check auf die Intensität und Richtung dieser Effekte. Per Voreinstellung liefert der residualPlots-Befehl auch eine Ergebnistabelle für die inferenzstatistische Prüfung dieser quadratischen Effekte:
## Test stat Pr(>|Test stat|)
## health 2.3849 0.017274 *
## environment 1.7593 0.078839 .
## animals 2.8367 0.004652 **
## social 1.5525 0.120877
## workers 1.5416 0.123505
## disgust -0.2139 0.830654
## Tukey test -3.0512 0.002279 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Letztlich sagt uns diese Tabelle, dass wir zumindest auf die Möglichkeit eingehen sollten, dass die Begründungsmuster health und animals quadratische Effekte vorweisen. Im nächsten Beitrag befassen wir uns genauer damit, wie solche Modelle aufgestellt werden können und welche inhaltlichen Möglichkeiten wir dadurch erschließen können.
Der letzte Test in dieser Tabelle ist der Tukey-Test für non-Additivität. Letztlich wird hier sehr grob gecheckt, ob es zwischen unseren Prädiktoren Interaktionen gibt - ob sich die Einflüsse der unabhängigen Variablen also gegenseitig beeinflussen. Mit solchen Modellen werden wir uns unter dem Begriff moderierte Regression in einem späteren Beitrag noch detaillierter beschäftigen.
Multikollinearität
Multikollinearität ist ein potenzielles Problem der multiplen Regressionsanalyse und liegt vor, wenn zwei oder mehrere Prädiktoren hoch miteinander korrelieren. Hohe Multikollinearität
- schränkt die mögliche multiple Korrelation ein, da die Prädiktoren redundant sind und überlappende Varianzanteile in
y - erschwert die Identifikation von bedeutsamen Prädiktoren, da deren Effekte untereinander konfundiert sind (die Effekte können schwer voneinander getrennt werden).
- bewirkt eine Erhöhung der Standardfehler der Regressionkoeffizienten (der Standardfehler ist die Standardabweichung zu der Varianz der Regressionskoeffizienten bei wiederholter Stichprobenziehung und Schätzung). Dies bedeutet, dass die Schätzungen der Regressionsparameter instabil, und damit weniger verlässlich, werden. Für weiterführende Informationen zur Instabilität und Standardfehlern siehe Appendix B.
Multikollinearität kann durch Inspektion der bivariaten Zusammenhänge (Korrelationsmatrix) der Prädiktoren
Offensichtlich genügt eine der beiden Statistiken, da sie vollständig ineinander überführbar und damit redundant sind. Empfehlungen als Grenzwert für Kollinearitätsprobleme sind z. B. vif des car-Paktes bestimmt werden, der Toleranzwert als Kehrwert des VIFs.
# Datensatz der Prädiktoren
UV <- vegan[, c('health', 'environment', 'animals', 'social', 'workers', 'disgust')]
# Korrelation der Prädiktoren
cor(UV)
## health environment animals social workers disgust
## health 1.0000000 0.3890467 -0.10229228 0.20984452 0.2005306 0.1885483
## environment 0.3890467 1.0000000 0.23526017 0.11503185 0.3228451 0.2647138
## animals -0.1022923 0.2352602 1.00000000 -0.00881963 0.2197142 0.4302433
## social 0.2098445 0.1150319 -0.00881963 1.00000000 0.2816703 0.1707085
## workers 0.2005306 0.3228451 0.21971420 0.28167029 1.0000000 0.2346389
## disgust 0.1885483 0.2647138 0.43024335 0.17070846 0.2346389 1.0000000
Wir sehen, dass einige der Begründungsmuster untereinander durchaus korreliert sind. So zeichnet sich z.B. eine moderate Korrelation zwischen disgust und animals ab - Personen, denen Tierwohl wichtig ist, empfinden im Mittel auch mehr Ekel bei der Vorstellung, Fleisch zu essen. Ob dieser Zusammenhang im Rahmen der multiplen Regression zu Problemen führt, können wir anhand des VIF bzw. der Toleranz untersuchen:
# Varianzinflationsfaktor:
vif(mod)
## health environment animals social workers disgust
## 1.323588 1.363915 1.390330 1.137595 1.245808 1.357881
# Toleranzwerte als Kehrwerte
1 / vif(mod)
## health environment animals social workers disgust
## 0.7555219 0.7331837 0.7192538 0.8790471 0.8026918 0.7364414
Für unser Modell wird ersichtlich, dass die Prädiktoren allesamt noch vollkommen im Rahmen sind und die als Daumenregeln propagierten Grenzwerte weit entfernt liegen.
Identifikation von Ausreißern und einflussreichen Datenpunkten
Die Plausibilität unserer Daten ist enorm wichtig. Aus diesem Grund sollten Ausreißer oder einflussreiche Datenpunkte analysiert werden. Diese können bspw. durch Eingabefehler entstehen (Alter von 211 Jahren anstatt 21) oder es sind seltene Fälle (hochintelligentes Kind in einer Normstichprobe), welche so in natürlicher Weise (aber mit sehr geringer Häufigkeit) auftreten können. Es muss dann entschieden werden, ob Ausreißer die Repräsentativität der Stichprobe gefährden und ob diese besser ausgeschlossen werden sollten.
Hebelwerte hatvalues ermittelt (die Hebelwerte spielen auch bei der Bestimmung standardisierter und studentisierter Residuen eine wichtige Rolle, sodass interessierte Lesende gerne im Appendix C mehr Informationen dazu finden). Kriterien zur Beurteilung der Hebelwerte variieren, so werden von Eid et al. (2017, S. 707 und folgend) Grenzen von
Cook’s Distanz cooks.distance ermittelt werden.
Detaillierte Betrachtung von Hebelwerten und Cook's Distanz
Wir können zunächst beide Werte für alle Personen bestimmen:
#### Ausreißerdiagnostik ----
# Hebelwerte
hebel <- hatvalues(mod) # Hebelwerte
# Cooks Distanz
cook <- cooks.distance(mod) # Cooks Distanz
Um festzustellen, welche Personen auffällig sind, können wir die verschiedenen Kriterien anlegen:
# Abgleich mit verschiedenen Grenzwerten:
n <- length(hebel) # Anzahl der Beobachtungen
which(hebel > (4/n)) |> length() # Anzahl Hebelwerte > 4/n
## [1] 733
which(hebel > (2*6/n)) |> length() # Anzahl Hebelwerte > 2*k/n
## [1] 116
which(hebel > (3*6/n)) |> length() # Anzahl Hebelwerte > 3*k/n
## [1] 36
# Abgleich für Cook
which(cook > 1) |> length() # Anzahl Cook's Distanz > 1
## [1] 0
Um zunächst einen Eindruck davon zu bekommen, wie viele Personen über den jeweiligen Grenzwerten liegen, werden hier die Vektoren der auffälligen Personen an length weitergegeben. So zeigt, dass liberalsten Ansatz immer noch 36 Personen als potentielle Ausreißer identifiziert werden. Hinsichtlich der Cooks Distanz waren keine Beobachtungen auffällig, sodass wir anscheinend viele Fälle seltener Wertkonstellationen haben, aber dabei keine extreme Verzerrung unserer Regressionsgewichte passiert.
Alternativ zu einem festen Cut-Off-Kriterium kann die Verteilung der Hebelwerte inspiziert und wir können uns damit auseinandersetzen, ob diese Personen noch aus der gleichen Verteilung kommen könnten, wie die restlichen Beobachtungen oder ob wir hier vermuten sollten, dass andere Mechanismen (z.B. Musterantworten) die Werte einzelner Personen verursacht haben könnten:
# Histogramm der Hebelwerte mit Grenzwerten
grenzen <- data.frame(h = c(4/n, 2*6/n, 3*6/n),
Grenzwerte = c("4/n", "2*k/n", "3*k/n"))
ggplot(data = as.data.frame(hebel), aes(x = hebel)) +
geom_histogram(aes(y =after_stat(density)), bins = 15, fill="grey90", colour = "black") +
geom_vline(data = grenzen, aes(xintercept = h, lty = Grenzwerte)) # Cut-off bei 4/n
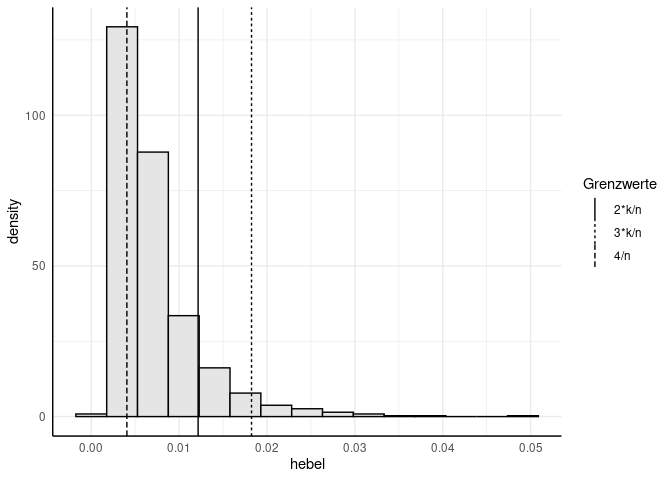
Cook’s Distanz cooks.distance ermittelt werden.
CD <- cooks.distance(mod) # Cooks Distanz
# Erzeugung der Grafik
ggplot(as.data.frame(CD), aes(x = CD)) +
geom_histogram(aes(y =after_stat(density)), bins = 15, fill="grey90", colour = "black")
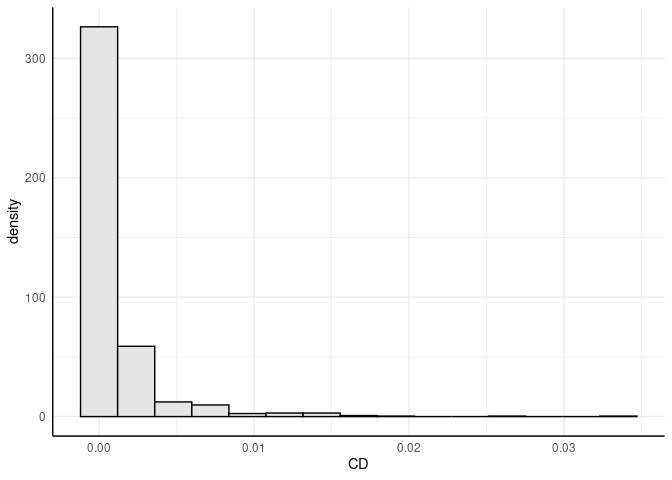
Die Funktion influencePlot des car-Paktes erzeugt ein “Blasendiagramm” zur simultanen grafischen Darstellung von Hebelwerten (auf der x-Achse), studentisierten Residuen (auf der y-Achse) und Cooks Distanz (als Größe der Blasen). Vertikale Bezugslinien markieren das Doppelte und Dreifache des durchschnittlichen Hebelwertes, horizontale Bezugslinien die Werte -2, 0 und 2 auf der Skala der studentisierten Residuen. Fälle, die nach einem der drei Kriterien als Ausreißer identifiziert werden, werden im Streudiagramm durch ihre Zeilennummer gekennzeichnet. Diese Zeilennummern können verwendet werden, um sich die Daten der auffälligen Fälle anzeigen zu lassen. Sie werden durch InfPlot ausgegeben werden. Auf diese kann durch as.numeric(row.names(InfPlot)) zugegriffen werden.
InfPlot <- influencePlot(mod)
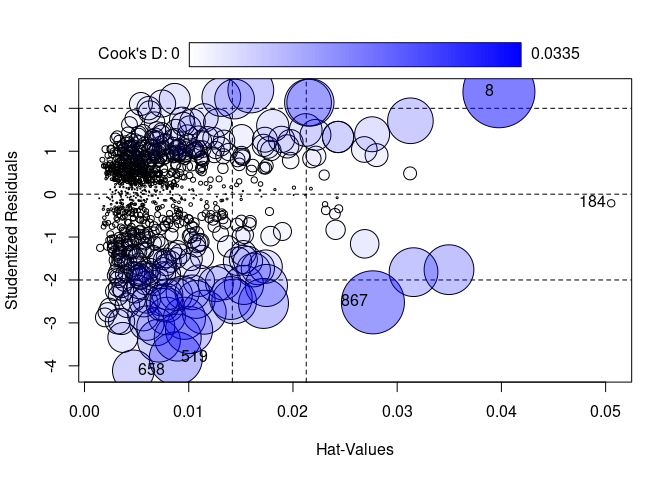
IDs <- as.numeric(row.names(InfPlot))
Schauen wir uns die möglichen Ausreißer an und standardisieren die Ergebnisse für eine bessere Interpretierbarkeit.
# Rohdaten der auffälligen Fälle
vegan[IDs, c('commitment', 'health', 'environment', 'animals', 'social', 'workers', 'disgust')]
## commitment health environment animals social workers disgust
## 8 4.666667 1.000000 1.000000 1.000000 1.000000 1.000000 1.000000
## 184 3.666667 2.000000 3.333333 1.000000 1.000000 1.000000 7.000000
## 519 1.666667 7.000000 7.000000 7.000000 1.000000 1.000000 7.000000
## 658 1.000000 2.666667 4.666667 7.000000 1.333333 3.000000 4.333333
## 867 1.000000 7.000000 2.333333 6.333333 2.000000 6.333333 1.000000
# Standardisierte Skalenwerte
std <- vegan[, c('commitment', 'health', 'environment', 'animals', 'social', 'workers', 'disgust')] |>
scale()
round(std[IDs, ], 3)
## commitment health environment animals social workers disgust
## 8 0.493 -2.826 -4.137 -4.700 -0.730 -1.651 -1.969
## 184 -0.522 -2.187 -2.204 -4.700 -0.730 -1.651 1.117
## 519 -2.553 1.006 0.833 0.555 -0.730 -1.651 1.117
## 658 -3.230 -1.761 -1.100 0.555 -0.454 -0.534 -0.255
## 867 -3.230 1.006 -3.033 -0.029 0.098 1.328 -1.969
Interpretation
Was ist an den fünf identifizierten Fällen konkret auffällig?
- Fall 8: Antwortete auf allen Prädiktoren mit dem Minimalwert - eventuell also eine Person, die den Fragebogen ab einem gewissen Punkt nicht mehr gewissenhaft ausgefüllt hat. Fällt deswegen durch ein sehr hohes Residuum auf (minimale Werte der Prädiktoren aber überdurchschnittliches Commitment)
- Fall 184: Hat einen sehr hohen Wert auf
disgustaber niedrige Werte aufhealth,animals,socialundworkers, wodurch die Person eine seltene Wertkombination hat - sie übt allerdings vernachlässigbaren Einfluss auf die Regressionsergebnisse aus (kleine Cooks Distanz, minimales Residuum) - Fall 519: Antwortet quasi ausschließlich in Extremkategorien und erzeugt dadurch eine seltene Wertekonstellation. Das sehr niedrige Commitment ist dabei unerwartet.
- Fall 658: Hat wenig spektakuläre Werte auf den UVs aber ein unerwartet niedriges Commitment, wodurch die Regressionsgerade stark nach unten gezogen wird.
- Fall 867: Relativ hohe Werte auf
health,animals,socialundworkersaber auch hier unerwartet niedriges Commitment machen die Person auffällig.
Die Entscheidung, ob Ausreißer oder auffällige Datenpunkte aus Analysen ausgeschlossen werden, ist schwierig und kann nicht pauschal beantwortet werden. Im vorliegenden Fall wäre z.B. zu überlegen, ob Person 8 und eventuell 519 aufgrund ihrer sehr auffälligen Antwortmuster von der Auswertung ausgeschlossen werden sollten. Sollte Unschlüssigkeit über den Ausschluss von Datenpunkten bestehen, bietet es sich an, die Ergebnisse einmal mit und einmal ohne die Ausreißer zu berechnen und zu vergleichen. Sollte sich ein robustes Effektmuster zeigen, ist die Entscheidung eines Ausschlusses nicht essenziell.
Appendix A
Auswirkungen des Messfehlers in den unabhängigen Variablen
Disclaimer: Dieser Block ist als Zusatz anzusehen und für Interessierte bestimmt.
Wir können die Auswirkungen von Messfehlern in den unabhängigen Variablen anhand eines Beispiels mit simulierten Daten verdeutlichen. Nehmen wir an, wir möchten die Lebenszufriedenheit (Lebenszufriedenheit) anhand der Depressivität (Depressivitaet) vorhersagen. Dazu können wir Daten simulieren, die die folgende Beziehung zwischen diesen beiden Variablen modellieren:
# Vergeichbarkeit
set.seed(1)
# Datensimulation UV (Normalverteilt)
Depressivitaet <- rnorm(n = 250) # Ohne Messfehler
Depressivitaet_mf <- sqrt(0.7)*Depressivitaet + rnorm(n = 250, sd = sqrt(0.3)) # Mit Messfehler
# Datensimulation der AV
Lebenszufriedenheit <- -0.5 * Depressivitaet
# Zusammenfassung zu einem Datensatz (relevant für ggplot)
df <- data.frame(Lebenszufriedenheit = c(Lebenszufriedenheit, Lebenszufriedenheit),
Depressivitaet = c(Depressivitaet, Depressivitaet_mf),
Messfehler = c(rep("Ohne Messfehler", 250), rep("Mit Messfehler", 250)))
# Faktorisieren der Messfehlervariable
df$Messfehler <- factor(df$Messfehler, levels = c("Ohne Messfehler", "Mit Messfehler"))
Dabei unterscheiden wir in der Datensimulation zwischen zwei Fällen: In einem Fall wird die Depressivität ohne Messfehler erfasst (Depressivitaet), und im anderen Fall enthält die unabhängige Variable einen Messfehler (Depressivitaet_mf). Außerdem nehmen wir an, dass die abhängige Variable (Lebenszufriedenheit) keinen Messfehler enthält und perfekt durch die Depressivität vorhergesagt werden kann. Diese Annahme hilft uns, den Effekt des Messfehlers auf die Schätzung der Regressionsgewichte isoliert von anderen potenziellen Einflüssen zu betrachten. Eine grafische Darstellung der beiden Variablen in Abhängigkeit vom Messfehler zeigt uns den folgenden Scatterplot:
library(ggplot2)
ggplot(data = df, aes(x = Depressivitaet, y = Lebenszufriedenheit, group = Messfehler))+
geom_point()+
geom_smooth(method = "lm", se =F)+
facet_wrap(~Messfehler)
## `geom_smooth()` using formula = 'y ~ x'
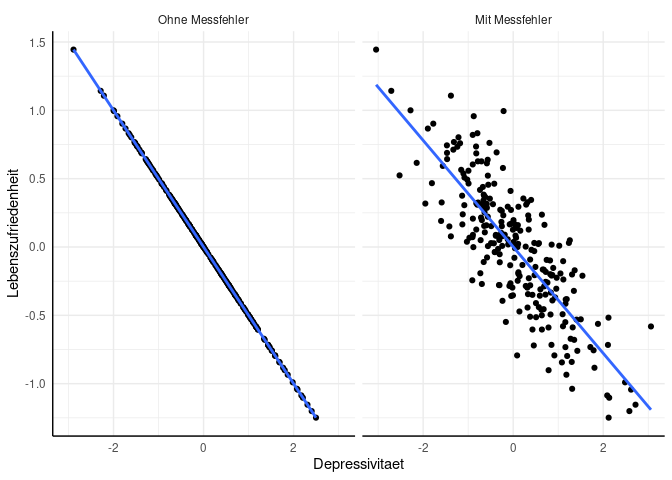
Aus dem Plot können wir erkennen, dass die Anwesenheit eines Messfehlers in der unabhängigen Variablen, also der Depressivität, dazu führt, dass die Datenpunkte aufgrund der Ungenauigkeit in der Erfassung um die Regressionslinie streuen. Dieser Effekt tritt nicht auf, wenn die Depressivität fehlerfrei gemessen wird. Der Messfehler hat auch Auswirkungen auf die Schätzung der Regressionsgewichte:
summary(lm(Lebenszufriedenheit~Depressivitaet)) # Ohne Messfehler
##
## Call:
## lm(formula = Lebenszufriedenheit ~ Depressivitaet)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.795e-16 -2.730e-17 -1.670e-17 -6.800e-18 4.276e-15
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -7.022e-18 1.741e-17 -4.03e-01 0.687
## Depressivitaet -5.000e-01 1.812e-17 -2.76e+16 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.752e-16 on 248 degrees of freedom
## Multiple R-squared: 1, Adjusted R-squared: 1
## F-statistic: 7.618e+32 on 1 and 248 DF, p-value: < 2.2e-16
summary(lm(Lebenszufriedenheit~Depressivitaet_mf)) # Mit Messfehler
##
## Call:
## lm(formula = Lebenszufriedenheit ~ Depressivitaet_mf)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.76056 -0.19503 0.01161 0.16986 0.91049
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.001072 0.017507 0.061 0.951
## Depressivitaet_mf -0.389494 0.017325 -22.482 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.2767 on 248 degrees of freedom
## Multiple R-squared: 0.6708, Adjusted R-squared: 0.6695
## F-statistic: 505.4 on 1 and 248 DF, p-value: < 2.2e-16
# Konfidenzintervall des Regressionsgewichts
confint(lm(Lebenszufriedenheit~Depressivitaet)) # Ohne Messfehler
## 2.5 % 97.5 %
## (Intercept) -4.130616e-17 2.726283e-17
## Depressivitaet -5.000000e-01 -5.000000e-01
confint(lm(Lebenszufriedenheit~Depressivitaet_mf)) # Mit Messfehler
## 2.5 % 97.5 %
## (Intercept) -0.03340876 0.03555231
## Depressivitaet_mf -0.42361637 -0.35537165
| 2.5% | 97.5% | ||
|---|---|---|---|
| Kein MF | -0.50 | -0.50 | -0.50 |
| X mit MF | -0.39 | -0.42 | -0.36 |
Während das Regressionsmodell ohne Messfehler in der unabhängigen Variablen dem Populationsmodell entspricht (
Appendix B
Multikollinearität und Standardfehler
Disclaimer: Dieser Block ist als Zusatz anzusehen und für Interessierte bestimmt.
Im Folgenden stehen
Für eine einfache Regressionsgleichung mit
Insgesamt bedeutet dies, dass die Standardfehler von der Inversen der Kovarianzmatrix unserer Daten sowie von der Residualvarianz abhängen. Sie sind also groß, wenn die Residualvarianz groß ist (damit ist die Vorhersage von
Fall 1 :
Fall 2 :
Fall 3 :
Hierbei ist zu beachten, dass
Fall 1 :
Fall 2 :
Fall 3 :
Im Fall 1 sind die zwei Variablen unkorreliert. Die Inverse ist leicht zu bilden.
XX_1 <- matrix(c(100,0,0,
0,100,0,
0,0,100),3,3)
XX_1 # Die Matrix X'X im Fall 1
## [,1] [,2] [,3]
## [1,] 100 0 0
## [2,] 0 100 0
## [3,] 0 0 100
I_1 <- solve(XX_1)*1 # I (*1 wegen Residualvarianz = 1)
I_1
## [,1] [,2] [,3]
## [1,] 0.01 0.00 0.00
## [2,] 0.00 0.01 0.00
## [3,] 0.00 0.00 0.01
sqrt(diag(I_1)) # Wurzel aus den Diagonalelementen der Inverse = SE, wenn sigma_e^2=1
## [1] 0.1 0.1 0.1
Die Standardfehler sind nicht sehr groß: alle liegen bei
Im Fall 2 sind die zwei Variablen fast perfekt (zu
XX_2 <- matrix(c(100,0,0,
0,100,99,
0,99,100),3,3)
XX_2 # Die Matrix X'X im Fall 2
## [,1] [,2] [,3]
## [1,] 100 0 0
## [2,] 0 100 99
## [3,] 0 99 100
I_2 <- solve(XX_2)*1 # I (*1 wegen Residualvarianz = 1)
I_2
## [,1] [,2] [,3]
## [1,] 0.01 0.0000000 0.0000000
## [2,] 0.00 0.5025126 -0.4974874
## [3,] 0.00 -0.4974874 0.5025126
sqrt(diag(I_2)) # SEs im Fall 2
## [1] 0.1000000 0.7088812 0.7088812
sqrt(diag(I_1)) # SEs im Fall 1
## [1] 0.1 0.1 0.1
Die Standardfehler des Fall 2 sind sehr groß im Vergleich zu Fall 1 (mehr als sieben Mal so groß); nur der Standardfehler des Interzept bleibt gleich. Die Determinante von
det(XX_2) # Determinante Fall 2
## [1] 19900
det(XX_1) # Determinante Fall 1
## [1] 1e+06
Im Fall 3 sind die zwei Variablen perfekt korreliert - es liegt perfekte Multikollinearität vor. Die Inverse kann nicht gebildet werden (da
XX_3 <- matrix(c(100,0,0,
0,100,100,
0,100,100),3,3)
XX_3 # Die Matrix X'X im Fall 3
## [,1] [,2] [,3]
## [1,] 100 0 0
## [2,] 0 100 100
## [3,] 0 100 100
det(XX_3) # Determinante on X'X im Fall 3
## [1] 0
I_3 <- solve(XX_3)*1 # I (*1 wegen Residualvarianz = 1)
I_3
sqrt(diag(I_3)) # Wurzel aus den Diagonalelementen der Inverse = SE, wenn sigma_e^2=1
# hier wird eine Fehlermeldung ausgegeben, wodurch der Code nicht ausführbar ist und I_3 nicht gebildet werden kann:
# Error in solve.default(XX_3) :
# Lapack routine dgesv: system is exactly singular: U[2,2] = 0
Der VIF bzw. die Toleranz quantifizieren die Korrelation zwischen den beiden Variablen. Der VIF wäre in diesen Analysen im 1. Fall für beide Variablen 1, im 2. Fall für beide Variabeln 50.25 und im 3. Fall nicht berechenbar (bzw.
Dieser Exkurs zeigt, wie sich die Multikolinearität auf die Standardfehler und damit auf die Präzision der Parameterschätzung auswirkt. Inhaltlich bedeutet dies, dass die Prädiktoren redundant sind und nicht klar ist, welchem Prädiktor die Effekte zugeschrieben werden können.
Die Matrix
Appendix C
Standardisierte und Studentisierte Residuen
Disclaimer: Dieser Block ist als Zusatz anzusehen und für Interessierte bestimmt.
Wir wollen uns in diesem Abschnitt verschiedene “normierte” Residuen ansehen, welche dafür genutzt werden, einflussreiche Datenpunkte und Ausreißer zu bestimmen. Diese können dann aus der Analyse ausgeschlossen werden oder zumindest genauer betrachtet werden. Normiert bedeutet hier, dass diese Residuen über Studien hinweg vergleichbar gemacht werden sollen. Der Vorteil ist somit, dass bspw. Grafiken, die auf diesen normierten Residuen beruhen, immer gleich interpretiert werden können.
Der Einfluss der Position entlang der Regressiongerade (oder Hyperebene, wenn es mehrere Prädiktoren sind) in “x”-Richtung kann mitunter enorm sein. Weit vom (gemeinsamen) Mittelwert entfernt liegende Punkte in den Prädiktoren sind hinsichtlich der Vorhersage von
# Vergleichbarkeit
set.seed(1)
# simuliere X~gamma
n <- 20
X <- rgamma(n = n, shape = .7, rate = 1)
hist(X) # recht schief
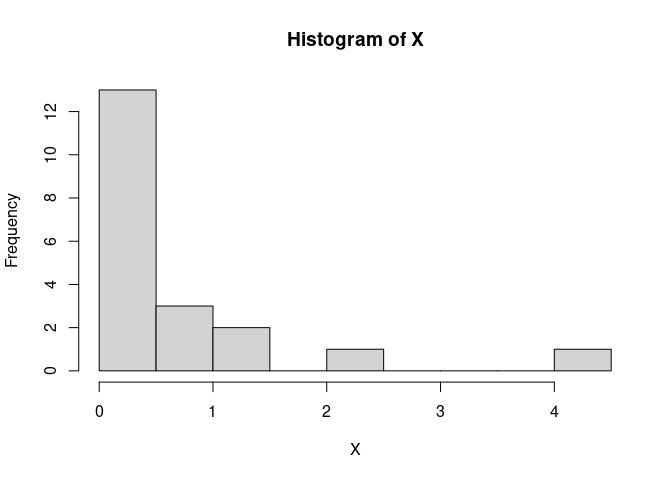
# simuliere eps~norm
eps <- rnorm(n = n, mean = 0, sd = 2)
# setzte Y zusammen
beta0 <- .5; beta1 <- .6
Y <- beta0 + beta1*X + eps
# füge X und Y in einen data.frame
df <- data.frame(X, Y)
# fitte ein Regressionsmodell
reg <- lm(Y~X, data = df)
summary(reg)
##
## Call:
## lm(formula = Y ~ X, data = df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.2530 -1.5084 -0.2787 1.2584 5.0920
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.2648 0.6378 0.415 0.683
## X 0.7395 0.5209 1.420 0.173
##
## Residual standard error: 2.283 on 18 degrees of freedom
## Multiple R-squared: 0.1007, Adjusted R-squared: 0.05076
## F-statistic: 2.016 on 1 and 18 DF, p-value: 0.1727
Wir sehen, dass die Populationsparameter, die wir vorgegeben haben, nicht exakt getroffen werden. Das Interzept ist mit ggplot veranschaulichen und einen Regressionstrend hinzuzufügen. Per Default wird dann auch direkt ein Konfidenzintervall für die Regressionsgerade eingezeichnet:
library(ggplot2)
ggplot(data = df, mapping = aes(x = X, y = Y)) + geom_point() +
geom_smooth(method = "lm", formula = "y~x")
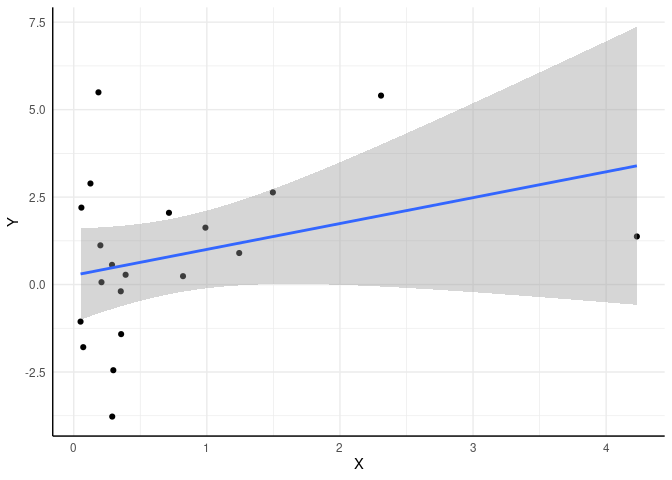
Diesem Plot entnehmen wir sehr deutlich, dass die Unsicherheit bezüglich der Vorhersage von MASS-Paket ab. In Eid et al. (2017) wird das standardisierte Residuum so definiert, dass das Residuum einfach durch seine Standardabweichung geteilt wird:
$$ \begin{equation} \hat{\varepsilon}{i,\text{std}} := \frac{\hat{\varepsilon}{i}}{\hat{\sigma}}, \end{equation} $$
wobei
So haben wir die Standardisierung auch schon vorher kennengelernt. Da bei einem Residuum der Mittelwert eh bei 0 liegt, müssen wir den Mittelwert des Residuums auch vorher nicht mehr abziehen, sondern es reicht das Residuum durch die Standardabweichung zu teilen. Gleichzeitig wird in Eid et al. (2017) das studentisierte Residuum so definiert, dass wir uns das Wissen über den Regressionzusammenhang zwischen den unabhängigen Variablen und der abhängigen Variable zu Nutze machen und einpreisen, dass wir für Punkte, die weit vom Mittelwert der Prädiktoren entfernt liegen, größere Residuen erwarten können. Das hatten wir auch in dem Plot gesehen, dass an den Rändern das Konfidenzintervall viel breiter ausfällt.
Wir bestimmen nun das standardisierte Residuum und das studentisierte Residuum für den größten Xmax:
# größtes X finden
ind_Xmax <- which.max(X)
Xmax <- X[ind_Xmax]
Xmax
## [1] 4.230831
# zugehörigen Y-Wert finden
Y_Xmax <- Y[ind_Xmax]
Y_Xmax
## [1] 1.374412
# sd_eps bestimmen
sd_eps <- summary(reg)$sigma
sd_eps
## [1] 2.282814
# vorhergesaten y-Wert bestimmen
Y_pred_Xmax <- predict(reg, newdata = data.frame("X" = Xmax))
Y_pred_Xmax
## 1
## 3.39369
In ind_Xmax steht einfach nur die Position innerhalb des Vektors, an der das Maximum angenommen wird - also quasi die Personennummer - hier ist das die 5. Wenn wir diese auf
Um zu prüfen, ob wir uns verrechnet haben, zeichnen wir den vorhergesagten
ggplot(data = df, mapping = aes(x = X, y = Y)) + geom_point() +
geom_smooth(method = "lm", formula = "y~x") +
geom_point(mapping = aes(x = Xmax, y = Y_pred_Xmax), cex = 4, col = "gold3")
## Warning in geom_point(mapping = aes(x = Xmax, y = Y_pred_Xmax), cex = 4, : All aesthetics have length 1, but the data has 20 rows.
## ℹ Please consider using `annotate()` or provide this layer with data containing a single row.
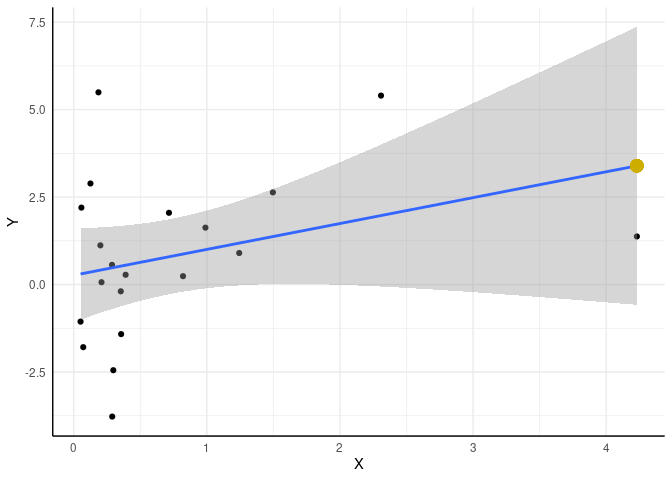
Der gelbe Punkt liegt genau auf der Gerade - super!
Das standardisierte Residuum nach Eid et al. (2017) bekommen wir nun, indem wir das Residuum durch den Standardfehler der Regression teilen. Dazu brauchen wir zunächst das Residuum:
# Residuum bestimmen
resid_Xmax <- resid(reg)[ind_Xmax]
resid_Xmax
## 5
## -2.019278
# std Residuum (nach Eid et al., 2017)
resid_Xmax_std <- resid_Xmax / sd_eps
resid_Xmax_std
## 5
## -0.8845566
Jetzt müssen wir noch die Unsicherheit einpreisen, die dadurch resultiert, dass die
Sie sind die Diagonalelemente der sogenannten Hut-Matrix.
X_mat <- cbind(1, X)
h <- diag(X_mat %*% solve(t(X_mat) %*% X_mat) %*% t(X_mat))
#Abgleich mit vorher berechneten hatvalues
round(h-hatvalues(reg), digits = 10)
## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
## 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Super, die hatvalues haben wir schon mal ausgerechnet. Nun kommen wir zu den studentisierten Residuen, welche diese Werte mit einbeziehen. Wir bestimmen hier zwei Varianten des studentisierten Residuums (Eid et al., 2017); das internal studentisierte Residuum und das external studentisierte Residuum. Internal und external bezieht sich hierbei auf dem Umstand, ob die Standardabweichung der Residuen unter Einbezug (internal) oder unter Ausschluss (external) der betrachteten Person bestimmt wird:
$$ \begin{equation} \hat{\varepsilon}{i,\text{stud, internal}} := \frac{\hat{\varepsilon}{i}}{\hat{\sigma}\sqrt{1-h_i}} \end{equation} $$
$$ \begin{equation} \hat{\varepsilon}{i,\text{stud, external}} := \frac{\hat{\varepsilon}{i}}{\hat{\sigma}_{(-i)}\sqrt{1-h_i}} \end{equation} $$
Die beiden Residuen werden also bestimmt, indem das eigentliche Residuum der Person MASS-Pakets internal-studentisierte Residuen mit dem stdres und external-studentisierte Residuen mit dem studres-Befehl bestimmt werden und es so zu einer Vermischung der Terminologien kommt:
# hatvalue für Xmax bestimmen
h_Xmax <- h[ind_Xmax]
h_Xmax
## [1] 0.686591
# Residuum internal studentisiert (Mittelwert abziehen und durch SD teilen)
resid_Xmax_stud_int <- resid_Xmax / (sd_eps*sqrt(1-h_Xmax))
resid_Xmax_stud_int
## 5
## -1.580047
# vergleich -> identisch!
MASS::stdres(reg)[ind_Xmax] # internal studentisiert nach MASS
## 5
## -1.580047
# studentisiertes Residuum bestimmen
reg2 <- lm(Y~X, data = df[-ind_Xmax,]) # Regression ohne Person i
sd_eps_Xmax <- summary(reg2)$sigma
resid_Xmax_stud_ext <- resid_Xmax / (sd_eps_Xmax*sqrt(1-h_Xmax))
resid_Xmax_stud_ext
## 5
## -1.654551
# vergleich -> identisch!
MASS::studres(reg)[ind_Xmax] # external studentisiert nach MASS
## 5
## -1.654551
Das Schöne ist nun, dass sich diese Residuen auch über Analysen hinweg vergleichen lassen, da sie eben normiert sind und den Abstand vom Mittelwert und damit auch den Einfluss auf die Analyse und die damit verbundenen Unsicherheit integrieren. Beide Arten der Normierung haben den Abstand zum Mittelwert von
resid_Xmax_std <- resid_Xmax / sd_eps
resid_Xmax_std
## 5
## -0.8845566
Also sehr viel kleiner! Somit würde sein Einfluss auf die Analyse unterschätzt, da signalisiert werden würde, dass der Vorhersagefehler nicht sonderlich groß ausfällt.
Literatur
Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. (2003). Applied multiple regression/correlation analysis for the behavioral sciences (3rd ed.). Lawrence Erlbaum Associates Publishers. Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden (5. Auflage, 1. Auflage: 2010). Weinheim: Beltz. Hayes, A.F., Cai, L. (2007). Using heteroskedasticity-consistent standard error estimators in OLS regression: An introduction and software implementation. Behavior Research Methods, 39, 709–722 (2007). https://doi.org/10.3758/BF03192961 Stahlmann, A.G., Hopwood, C.J., & Wiebke, B. (2024). The Veg*n Eating Motives Inventory Plus (VEMI+): A measure of health, environment, animal rights, disgust, social, pandemic and zoonotic diseases, and farm workers’ rights motives. Appetite, 203:107701. DOI: https://doi.org/10.1016/j.appet.2024.107701
- Blau hinterlegte Autor:innenangaben führen Sie direkt zur universitätsinternen Ressource.
](/media/header/vegan_produce.jpg)