Logistische Regression
Vorhersage von Gruppenzugehörigkeiten
Inhaltsverzeichnis
Einleitung
In diesem Beitrag geht es darum, wie wir die Prinzipien der Regression nutzen können, um Vorhersagen auch dann zu ermöglichen, wenn die abhängige Variable nominalskaliert ist. Solche Konstellationen sind insbesondere in der klinischen Forschung sehr verbreitet - die Vorhersage eines Rezidivs, einer potentiellen Diagnose oder eines Therapieerfolgs stellen allesamt häufig zentrale Fragen von Psychotherapieforschung dar.
Suizidgedanken und -versuche
Wie in den vergangenen Beiträgen auch, werden wir versuchen, die Auswertung und Ergebnisse einer Studie aus der klinischen Forschung nachzuvollziehen. In diesem Beitrag geht es um eine Studie von Lin, O’Connell und Law (2023), in welcher die Autorinnen untersuchen, inwiefern Kontrollüberzeugungen und Durchhaltevermögen (Grit) die negativen Konsequenzen von Rumination auf Suizidgedanken und -versuche abschwächen oder verstärken. Da es sich bei der Studie um eine Querschnittuntersuchung handelt, werden die Wirkmechanismen hier allerdings ungerichtet untersuchte, sodass untersucht wird, inwiefern sich drei Gruppen unterscheiden: Personen, die in der Vergangenheit Suizidgedanken hatten, Personen, die in der Vergangenheit Suizidversuche unternommen haben und Personen, auf die keines von beiden zutrifft.
Genauer konzentrieren wir uns auf folgende Hypothesen bzw. Forschungsfragen der Studie:
Given findings from past research, we hypothesize grit to be protective against the development of suicidal ideation, but associated with facilitating suicidal behaviors in the presence of ideation.
Further, we hypothesize ILOC [internal locus of control] to amplify the self-directed negative emotions of rumination, allowing one to believe their life outcomes are the result of self-determination, and increase risks of suicide.
In contrast, ELOC [external locus of control] would be protective against rumination by displacing the contents of rumination externally, thereby decreasing vulnerability to suicide.
Schauen wir uns an, wie diese Hypothesen geprüft werden können.
Daten
Die Daten wurden von den Autorinnen der Studie über das OSF zur Verfügung gestellt. Sie stellen außerdem auch eine .Rmd-Datei zur Verfügung, in der die Datenaufbereitung für den Artikel dargestellt wird. Ich habe dieses Skript ein wenig gekürzt und damit wir schnell zu den interessanten Punkten kommen können, können wir dieses Skript einfach direkt ausführen, um die Daten in R zu laden:
source('https://pandar.netlify.app/daten/Data_Processing_grit.R')
Anmerkung: Leider wurde der Datensatz aus dem OSF entfernt, nachdem ich mit den Autorinnen des Artikels Kontakt aufgenommen habe (mehr dazu später). Die Daten erhalten Sie daher derzeit nur, wenn Sie am Kurs teilnehmen.
Der Datensatz besteht aus ein paar Skalenwerten, demografischen Variablen und der für uns entscheidenen Angabe, ob Personen schon einmal Suizidgedanken oder -versuche durchlebt haben (Suicide). Eine detaillierte Darstellung der Variablen findet sich im Artikel von Lin et al. (2023), hier nur noch ein kurzer Überblick:
Variablenübersicht
| Variable | Beschreibung | Ausprägungen |
|---|---|---|
Suicide | Suizidgedanken und -versuche | None, Ideator, Attempter |
ARS | Anger Rumination Scale | Skalenwert, 0-76 |
RSS | Rumination on Sadness Scale | Skalenwert, 0-65 |
ILOC | Internal Locus of Control | Skalenwert, 0-48 |
ELOC | External Locus of Control | Skalenwert, 0-96 |
Grit | Grit Scale | Skalenmittelwert, 0-4 |
Age | Alter | in Jahren |
Sex | Geschlecht | Female, Male, Other |
Employment | Beschäftigungsverhältnis | Unemployed, Part-Time, Full-Time |
Marital | Familienstand | Never Married, Actively Married, Not Actively Married, Divorced, Widowed |
SES | Sozioökonomischer Status | Einkommensbänder |
Orientation | Sexuelle Orientierung | Heterosexual, Homosexual, Bisexual, Other/Missing |
Stichprobenbeschreibung
Die Deskriptivstatistiken der Variablen, die für uns relevant sind, werden in Tabelle 1 des Aritkels von Lin et al. (2023) dargestellt. Wir können relativ einfach prüfen, ob wir diese reproduzieren können. Weil die Tabelle die Ergebnisse nach den drei Gruppen None, Ideator und Attempter aufteilt, können wir den describeBy-Befehl aus dem psych-Paket nutzen, um diese Unterteilung direkt mitzumachen. Weil die ausgegebenen Statistiken für nominalskalierte Variablen nicht sinnvoll sind, schließen wir diese aus dem Datensatz aus, bevor wir ihn mit der Pipe |> an die Funktion weitergeben.
library(psych)
subset(grit, select = c(ARS, RSS, ELOC, ILOC, Grit, Age)) |>
describeBy(grit$Suicide)
##
## Descriptive statistics by group
## group: None
## vars n mean sd median trimmed mad min max range skew kurtosis se
## ARS 1 145 33.10 12.41 29.00 31.86 11.86 19.00 75 56.00 0.81 -0.05 1.03
## RSS 2 145 27.01 12.45 25.00 25.54 13.34 13.00 65 52.00 0.88 0.09 1.03
## ELOC 3 145 35.26 17.60 35.00 34.73 19.27 1.00 89 88.00 0.32 -0.17 1.46
## ILOC 4 145 35.90 7.48 38.00 36.62 5.93 9.00 48 39.00 -0.99 0.65 0.62
## Grit 5 145 2.76 0.67 2.83 2.79 0.74 0.92 4 3.08 -0.34 -0.55 0.06
## Age 6 145 37.34 11.15 35.00 36.57 11.86 20.00 66 46.00 0.57 -0.53 0.93
## ------------------------------------------------------------------
## group: Ideator
## vars n mean sd median trimmed mad min max range skew kurtosis se
## ARS 1 83 42.57 15.32 44.0 41.99 19.27 19.00 76.00 57.00 0.16 -1.12 1.68
## RSS 2 83 35.24 13.81 37.0 35.22 16.31 2.00 61.00 59.00 -0.09 -0.91 1.52
## ELOC 3 83 46.01 18.51 47.0 46.03 22.24 2.00 84.00 82.00 -0.04 -0.89 2.03
## ILOC 4 83 31.34 9.68 32.0 32.24 8.90 7.00 48.00 41.00 -0.78 -0.11 1.06
## Grit 5 83 2.42 0.66 2.5 2.45 0.74 0.92 3.83 2.92 -0.32 -0.74 0.07
## Age 6 83 35.78 10.86 33.0 34.49 10.38 21.00 68.00 47.00 1.03 0.69 1.19
## ------------------------------------------------------------------
## group: Attempter
## vars n mean sd median trimmed mad min max range skew kurtosis se
## ARS 1 94 42.80 13.85 44.50 42.80 17.05 19.00 70.00 51.00 -0.08 -1.18 1.43
## RSS 2 94 39.06 13.24 40.00 39.51 13.34 12.00 65.00 53.00 -0.33 -0.65 1.37
## ELOC 3 94 44.19 18.39 45.50 44.72 18.53 2.00 80.00 78.00 -0.22 -0.65 1.90
## ILOC 4 94 33.46 7.53 35.00 34.13 7.41 14.00 47.00 33.00 -0.76 -0.05 0.78
## Grit 5 94 2.42 0.60 2.42 2.40 0.74 1.33 3.92 2.58 0.31 -0.61 0.06
## Age 6 94 35.24 9.52 33.00 34.25 8.90 21.00 66.00 45.00 1.00 0.76 0.98
Insgesamt scheinen die Ergebnisse mit den Angaben im Artikel weitestgehend übereinzustimmen, lediglich bei der Gruppe None scheinen sich bei den Angaben zu den Variablen ARS und RSS Unstimmigkeiten eingeschlichen zu haben (die ich auch durche eine Nachfrage bei den Autorinnen nicht klären konnte). Die Verteilungen der nominalskalierten Variablen hingegen scheinen zu passen.
table(grit$Suicide, grit$Sex) |> addmargins()
table(grit$Suicide, grit$Employment) |> addmargins()
table(grit$Suicide, grit$Marital) |> addmargins()
table(grit$Suicide, grit$SES) |> addmargins()
table(grit$Suicide, grit$Orientation) |> addmargins()
(Die Ausgabe habe ich an dieser Stelle mal ausgespart, Sie können Sie aber einfach direkt bei sich mit dem dargestellten Code ausgeben lassen.)
Logistische Regression
In der (normalen) logistischen Regression geht es uns darum, eine dichotome abhängige Variable in einer Regression vorherzusagen. Wenn wir uns auf die erste Hypothese der Autorinnen zuückbesinnen:
[…] we hypothesize grit to be protective against the development of suicidal ideation […]
können wir uns also erst einmal damit befassen, Unterschiede zwischen Personen, die Suizidgedanken hatten und Personen, die weder Suizidgedanken hatten noch Suizidversuche unternommen haben zu untersuchen. Dazu erstellen wir erst einmal einen Datensatz, der nur diese Personen enhält:
idea <- subset(grit, grit$Suicide %in% c('None', 'Ideator'))
idea$Suicide <- droplevels(idea$Suicide)
In diesem Datensatz sind nun nur noch 228 der ursprünglichen 322 Personen enthalten, weil wir nur die beiden Gruppen betrachten. Wir führen aber später, wenn wir uns die multinomiale logistische Regression angucken angucken, wieder alle Personen zusammen und betrachten die gesamte Stichprobe.
Warum keine lineare Regression?
Bevor wir uns angucken, wie man es richtig macht, gucken wir uns zunächst an, warum die normale Regression in diesem Fall ungeeignet ist. Wie Sie vielleicht in Erinnerung haben, treffen wir in der multiplen Regression im wesentlichen fünf Annahmen (die Sie in ausuferndem Detail im Beitrag zur Multiplen Regression nochmal nachlesen können). Eine davon ist die Normalverteilung der Residuen - eine vielleicht etwas optimistische Annahme, angesichts der Tatsache, dass unsere AV nur zwei Ausprägungen hat, aber probieren wir es aus:
# Lineare Regression
mod0 <- lm(Suicide ~ 1 + Grit, idea)
## Warning in model.response(mf, "numeric"): using type = "numeric" with a factor response
## will be ignored
## Warning in Ops.factor(y, z$residuals): '-' not meaningful for factors
Wir sehen direkt, dass R sich weigert unser unlauteres Vorhaben zu unterstützen; wir müssen die Variable also zunächst in eine numerische Variable überführen:
# Lineare Regression
mod0 <- lm(as.numeric(Suicide) ~ 1 + Grit, idea)
# Ergebnisübersicht
summary(mod0)
##
## Call:
## lm(formula = as.numeric(Suicide) ~ 1 + Grit, data = idea)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.6523 -0.3732 -0.2476 0.5431 0.8361
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.80581 0.12437 14.520 < 2e-16 ***
## Grit -0.16746 0.04565 -3.669 0.000304 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4695 on 226 degrees of freedom
## Multiple R-squared: 0.05621, Adjusted R-squared: 0.05203
## F-statistic: 13.46 on 1 and 226 DF, p-value: 0.0003041
Das Ergebnis zeigt uns zunächst an, dass Personen mit mehr Grit weniger Suizidgedanken haben. Betrachten wir das Ganze mal als Abbildung:
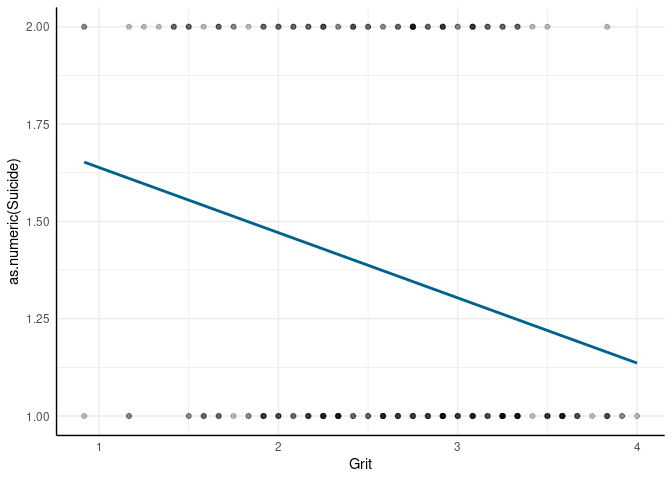
1 noch 2 sind). Noch deutlicher wird die Unzulänglichkeit der linearen Regression, wenn wir uns die Verteilung der Residuen angucken:
residuals(mod0) |> hist()
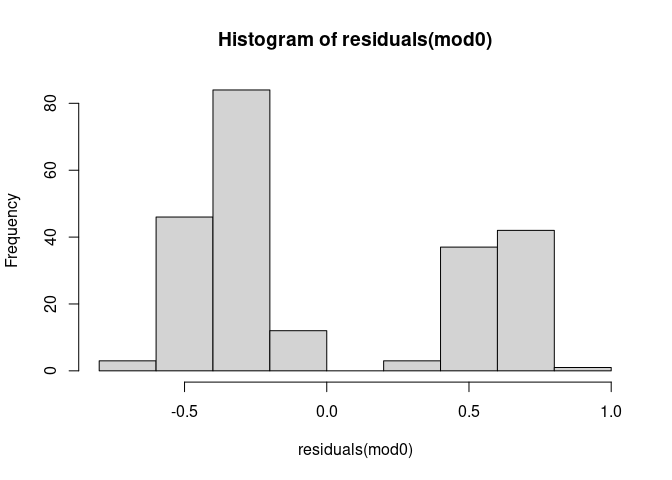
Wie bereits erwähnt, sollten diese Residuen normalverteilt sein, damit die Inferenzstatistik des Regressionsgewichts vertrauenswürdig ist. Den shapiro.test erspare ich uns angesichts dieser sehr deutlichen Lage.
Grundidee der logistischen Regression
Im Grunde ist das Problem im Fall von dichotomen abhängigen Variablen lediglich, dass Ausprägungen nicht einfach mit $Y = \widehat{Y} + e$ in zwei Teile zerlegt werden können, weil eine Annäherung des echten Wertes einer Person mit mehr oder weniger Genauigkeit etwas ungelenk scheint, wenn wir von vornherein wissen, dass die Variable nur zwei Ausprägungen haben kann. Daher wird bei der logistischen Regression die Wahrscheinlichkeit einer Kategorie (im Kontrast zu einer exklusiven anderen Kategorie) modelliert. So wird die Eigenschaft beibehalten, dass wir in der Regression Unsicherheit quantifizieren, statt im Residuum nun darüber, dass wir Wahrscheinlichkeiten statt Werte modellieren. Diese Wahrscheinlichkeit ist dabei eine Funktion der unabhängigen Variablen. Der so entstandene Ansatz ist eine Generalisierung des linearen Modells (lm) der Regression und wird daher generalisiertes lineares Modell (glm) genannt.
Wenn wir wieder auf die Annahme zurückkommen, dass Grit ein protektiver Faktor gegenüber Suizidgedanken ist, heißt das, dass die Wahrscheinlichkeit, dass eine Person Suizidgedanken hatte, ein Funktion Ihrer Werte auf der Grit Variable sein sollte. Etwas formaler ausgedrückt, wollen wir die bedingte Wahrscheinlichkeit von $Y = 1$ (also, dass es in der Vergangenheit zu Suizidgedanken kam) gegeben $X = x$ (also, dass eine Person einen bestimmten Wert $x$ auf der Grit Variable $X$ hat) modellieren. Worum es uns geht, ist in welcher Form sich Unterschiede in $X$ in Unterschiede in der Wahrscheinlichkeit übersetzen.
Weil die Wahrscheinlichkeit einen beschränkten Wertebereich hat (0 bis 1), können wir auch diese nicht einfach mit der linearen Regression vorhersagen, weil die Vorhersage sonst relativ schnell den Bereich zulässiger Werte verlassen würden. Daher ist eine Funktion von nöten, die im Wertebereich ebenfalls auf $[0; 1]$ eingeschränkt ist. Eine einfache Lösung ist dafür die Exponentialfunktion nach dem Schema
$$ \mathbb{P}(Y = 1 | X = x) = \frac{e^{\beta_0 + \beta_1x}}{1 + e^{\beta_0 + \beta_1x}} $$ zu nutzen. Hier ist der Exponent die alte bekannte Regressionsgleichung aus $\beta_0$ und $\beta_1$. Im Seminar und bei Eid, Gollwitzer und Schmitt (2017, Kap. 22.1) wird genauer besprochen, was die einzelnen Werte in diesem Fall bedeuten und warum es eigentlich drei verschiedene Formen gibt, die logistische Regression darzustellen. In den Sozialwissenschaften wird meistens der sogenannte Logit als Link-Funktion verwendet, um die Gleichung eine Form umzuwandeln, die unserer klassischen Regression entspricht:
$$ \text{logit}(p) = \ln\left(\frac{\mathbb{P}(Y = 1 | X = x)}{1 - \mathbb{P}(Y = 1 | X = x)}\right) = \beta_0 + \beta_1x $$ In der Regression, wie wir sie anwenden werden wird also das logarithmierte Verhältnis der Wahrscheinlichkeit einer Kategorie und der Gegenwahrscheinlichkeit (Odds) modelliert. Gucken wir uns am Besten am Beispiel an, was das genau bedeutet.
Einfache Logistische Regression
Wie schon angedeutet, ist der Befehl den wir nutzen werden der glm Befehl (für generalized linear model). Der Funktioniert eigentlich genau so, wie der lm-Befehl funktioniert. Als erstes Brauchen wir die Formel, in der wir festhalten, von welchen Variablen die Wahrscheinlichkeit abhängt, dass Personen in der Vergangenheit Suizidgedanken hatten. Nach Lin et al. (2023, S. 251) sollte dabei Grit eine wesentliche Rolle spielen, da
Some have also suggested grit to be protective of [suicidal thoughts and behaviors] (Marie et al., 2019), buffering against suicidal ideation by maintaining life goals and promoting a sense of purpose (Kleiman et al., 2013), as well as decreasing the impact of hopelessness (Pennings et al., 2015), negative life events (Blalock et al., 2015), and depression (Kim, 2015).
Als einfache logistische Regression ausgedrückt also:
# Logistische Regression
mod1 <- glm(Suicide ~ 1 + Grit, data = idea, family = 'binomial')
Da der Oberbegriff generalisiertes lineares Modell eine Vielzahl von verschiedenen Möglichkeiten umfasst, müssen wir im glm-Befehl mit dem Argument family = 'binomial' festlegen, dass unser Modell eine Binomialverteilung annimmt - unser abhängige Variable also binär bzw. dichotom ist.
Der Output dieser Prozedur sieht der einfachen Regression erstaunlich ähnlich:
# Ergebnisausgabe
summary(mod1)
##
## Call:
## glm(formula = Suicide ~ 1 + Grit, family = "binomial", data = idea)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.3752 0.5639 2.439 0.014745 *
## Grit -0.7446 0.2132 -3.492 0.000479 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 299.00 on 227 degrees of freedom
## Residual deviance: 286.05 on 226 degrees of freedom
## AIC: 290.05
##
## Number of Fisher Scoring iterations: 4
Konzentrieren wir uns erstmal auf die Koeffizienten. Intercept und Regressionsgewicht sind analog zur einfachen linearen Regression interpretierbar:
- $\beta_0$: Vorhergesagter Logit für Personen mit einem
Grit-Wert von 0 - $\beta_1$: Vorhergesagter Unterschied im Logit zwischen zwei Personen, die sich um eine Einheit im
Gritunterscheiden
Das Problem bei dieser Interpretation ist nur, dass der Logit nicht wirklich intuitiv interpretierbar ist. Daher werden die Ergebnisse der Regression häufig in Odds umgerechnet (zur Erinnerung an Odds und Odds-Ratios können Sie in diesem Beitrag nachgucken). Weil der Logit einfach der logarithmierte Odds ist, können wir durch exponieren auch den Odds erhalten:
# Odds
exp(coef(mod1))
## (Intercept) Grit
## 3.9557456 0.4749213
Bei einem Grit-Wert von 0 ist es also knapp 3.96-mal so wahrscheinlich in der Vergangenheit Suizidgedanken gehabt zu haben, wie es ist, sie nicht gehabt zu haben. Wenn sich zwei Personen auf der Grit-Skala um eine Einheit unterscheiden, sind die Odds der Suizidgedanken der Person mit dem höheren Wert nur ungefähr das 0.47-fache der Person mit dem niedrigeren Wert.
Für jeden einzelnen Wert können wir außerdem die Wahrscheinlichkeit berechnen, dass Person Suizidgedanken hatten. Dafür können wir zunächst, wie bei der normalen Regression, die vorhergesagten Logits bestimmen und diese dann in Wahrscheinlichkeiten umrechnen:
# Ganze Werte auf der Grit Skala
new_data <- data.frame(Grit = 0:4)
# Vorhersage
new_data$Logits <- predict(mod1, newdata = new_data)
# Umrechnung in Wahrscheinlichkeit
new_data$Probability <- exp(new_data$Logits) / (1 + exp(new_data$Logits))
# Ausgabe
new_data
## Grit Logits Probability
## 1 0 1.3751691 0.7982140
## 2 1 0.6305630 0.6526171
## 3 2 -0.1140431 0.4715201
## 4 3 -0.8586492 0.2976217
## 5 4 -1.6032553 0.1675271
Zum Glück, können wir das Ganze in predict auch abkürzen, wenn wir direkt die Wahrscheinlichkeiten anfordern:
new_data$Probability <- predict(mod1, newdata = new_data, type = 'response')
Die Ergebnisse können wir natürlich auch bildlich veranschaulichen (den entsprechenden R-Code dazu finden Sie im oben verlinkten R-Skript für diesen Beitrag):
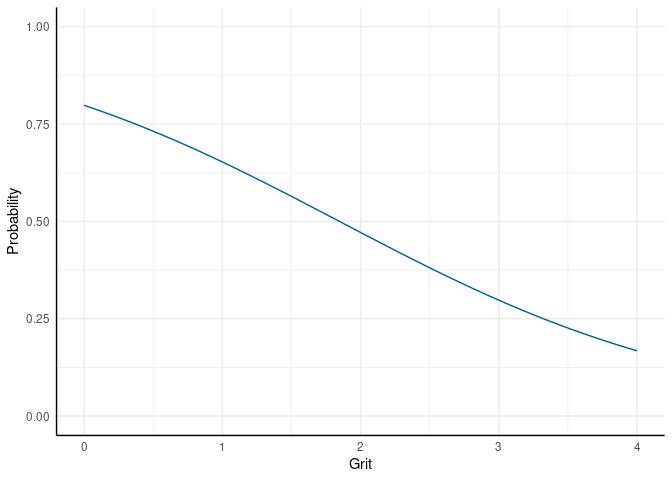
Von der APA wird empfohlen, für Ergebnisse der logistischen Regression Odds und deren Konfidenzintervalle zu präsentieren. Da wir schon wissen, wie wir die Regressiongewichte in Odds umrechnen, brauchen wir nur noch die Konfidenzintervalle. Die confint-Funktion gibt diese natürlich auch in Logits aus, aber sie sind nach dem gleichen Prinzip in Odds umrechenbar, wie die Koeffizienten selbst:
# Konfidenzintervalle
ci <- confint(mod1)
## Waiting for profiling to be done...
# Ergebnisse
results <- data.frame(
Odds = exp(coef(mod1)),
Lower = exp(ci[, 1]),
Upper = exp(ci[, 2])
)
# Ausgabe
results
## Odds Lower Upper
## (Intercept) 3.9557456 1.3279710 12.2213299
## Grit 0.4749213 0.3092452 0.7155088
Im Einklang mit den Ergebnissen der $p$-Werte aus der summary sagen uns die Konfidenzintervalle hier, dass sowohl das Intercept als auch der Regressionskoeffizient für Grit signifikant von 1 (gleicher Wahrscheinlichkeit) verschieden sind.
Mehrere Prädiktoren und Modellvergleiche
Die Erweiterung der logistischen Regression auf mehrere Prädiktoren funktionier eigentlich genauso, wie bei der linearen Regression. Wenn wir Tabelle 3 in Lin et al. (2023) betrachten, sehen wir die Ergebnisse verschiedener Modelle, mit jeweils sequentiell aufgenommenen Blöcken von Prädiktoren. In unserem eingeschränkten idea Datensatz befinden sich derzeit alle Personen, die als Ideator oder None klassifiziert wurden. Wir können also versuchen, die Ergebnisse aus der zweiten Spalte des Model 1 zu reproduzieren. Dafür brauchen wir vier Modelle:
- Block 1: Nur eine dichotomisierte
Orientation-Variable - Block 2: Zusätzlich
ARS,ILOCundGrit - Block 3: Zusätzlich die paarweisen Interaktionen zwischen
ARS,ILOCundGrit - Block 4: Zusätzlich die dreifach-Interaktion zwischen
ARS,ILOCundGrit
Die Grundideen aus der moderierten Regression und der generalisierten ANCOVA halten auch hier (wir haben ja nur ausgetauscht, wie wir unsere abhängige Variable behandeln). Deswegen müssen wir auch hier die Variablen zentrieren, um nicht-essentielle Multikollinearität zu vermeiden:
# Zentrierung
idea$ARS_c <- scale(idea$ARS, scale = FALSE)
idea$ILOC_c <- scale(idea$ILOC, scale = FALSE)
idea$Grit_c <- scale(idea$Grit, scale = FALSE)
Außerdem müssen wir - im Einklang mit dem Vorgehen von Lin et al. (2023) - die Orientation Variable so umkodieren, dass sie den dichotomen Kontrast zwischen heterosexuellen und nicht-heterosexuellen Personen abbildet:
# dichotome Orientierung
idea$Orientation_bin <- factor(idea$Orientation,
labels = c('Hetero', 'LGBTQ', 'LGBTQ', 'LGBTQ'))
Stellen wir direkt alle vier Modell auf:
# Modelle aus Tabelle 3, Model 1, Spalte 2
block1 <- glm(Suicide ~ 1 + Orientation_bin,
idea, family = 'binomial')
block2 <- glm(Suicide ~ 1 + Orientation_bin + ARS_c + ILOC_c + Grit_c,
idea, family = 'binomial')
block3 <- glm(Suicide ~ 1 + Orientation_bin + ARS_c + ILOC_c + Grit_c +
ARS_c:ILOC_c + ARS_c:Grit_c + ILOC_c:Grit_c,
idea, family = 'binomial')
block4 <- glm(Suicide ~ 1 + Orientation_bin + ARS_c + ILOC_c + Grit_c +
ARS_c:ILOC_c + ARS_c:Grit_c + ILOC_c:Grit_c +
ARS_c:ILOC_c:Grit_c,
idea, family = 'binomial')
Wie in der linearen multiple Regression, macht es auch hier Sinn erst zu beurteilen, welches Modell das Beste ist, bevor wir in die Interpretation der einzelnen Ergebnisse übergehen. In der linearen Regression hatten wir Modelle anhand der Differenz der Varianzaufklärung $R^2$ bzw. Quadratsummen verglichen. Leider funktioniert beides hier nicht mehr, da es weder Varianzaufklärung noch Residualquadratsummen gibt, wenn es keine Residuen gibt. Da die logistische Regression aber mittels Maximum-Likelihood Schätzverfahren geschätzt wird, können wir die Likelihood der beiden Modelle direkt miteinander vergleichen.
Sehr vereinfacht gesagt, stellt die Likelihood jedes Modells dar, wie wahrscheinlich die beobachteten Daten sind, wenn dieses Modell das wahre Modell wäre. Für den direkten Vergleich zwischen zwei Modellen können wir uns dies zunutze machen, weil wir das Modell bevorzugen wollen, bei dem die Daten wahrscheinlicher sind, die wir beobachtet haben. Weil mehr Parameter dabei die Daten immer wahrscheinlicher machen, müssen wir darauf achten, dass das Modell in größerem Ausmaß besser wird, als wir durch mehr Parameter unser Modell komplexer machen. Wenn die Annahmen der logistischen Regression erfüllt sind, folgt die Differenz der Log-Likelihoods von zwei Modellen einer $\chi^2$-Verteilung mit der Differenz der Parameteranzahl als Freiheitsgrade.
# Modellvergleich
anova(block1, block2, block3, block4)
## Analysis of Deviance Table
##
## Model 1: Suicide ~ 1 + Orientation_bin
## Model 2: Suicide ~ 1 + Orientation_bin + ARS_c + ILOC_c + Grit_c
## Model 3: Suicide ~ 1 + Orientation_bin + ARS_c + ILOC_c + Grit_c + ARS_c:ILOC_c +
## ARS_c:Grit_c + ILOC_c:Grit_c
## Model 4: Suicide ~ 1 + Orientation_bin + ARS_c + ILOC_c + Grit_c + ARS_c:ILOC_c +
## ARS_c:Grit_c + ILOC_c:Grit_c + ARS_c:ILOC_c:Grit_c
## Resid. Df Resid. Dev Df Deviance Pr(>Chi)
## 1 226 293.96
## 2 223 259.75 3 34.211 1.788e-07 ***
## 3 220 256.43 3 3.324 0.3443
## 4 219 256.26 1 0.160 0.6887
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Wir stellen an dieser Stelle also fest, dass die Aufnahme der Interaktionsterme in Block 3 und 4 nicht notwendig sind. Das Modell aus Block 2 ist nicht bedeutsam schlechter, als diese komplexeren Modelle. Die aufgestellten Hypothesen bezüglich der verstärkenden Effekte von ILOC bzw. schützenden Effekte von ELOC auf die Beziehung zwischen Rumination und Suizidalität scheinen also hier hinsichtlich der Ärger-Rumination keine Unterstützung zu finden. Betrachten wir aber das ausgewählte Modell (Block 2) genauer:
# Ergebnisse
summary(block2)
##
## Call:
## glm(formula = Suicide ~ 1 + Orientation_bin + ARS_c + ILOC_c +
## Grit_c, family = "binomial", data = idea)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.75683 0.16147 -4.687 2.77e-06 ***
## Orientation_binLGBTQ 1.34943 0.53062 2.543 0.01099 *
## ARS_c 0.03590 0.01146 3.133 0.00173 **
## ILOC_c -0.04310 0.01881 -2.291 0.02194 *
## Grit_c -0.44773 0.23785 -1.882 0.05978 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 299.00 on 227 degrees of freedom
## Residual deviance: 259.75 on 223 degrees of freedom
## AIC: 269.75
##
## Number of Fisher Scoring iterations: 3
Zur besseren Interpretierbarkeit ergänzen wir noch die Odds und deren Konfidenzintervalle:
# Odds
results <- data.frame(Odds = exp(coef(block2)),
Lower = exp(confint(block2)[, 1]),
Upper = exp(confint(block2)[, 2])
)
## Waiting for profiling to be done...
## Waiting for profiling to be done...
# Ausgabe
results
## Odds Lower Upper
## (Intercept) 0.4691500 0.3390869 0.639702
## Orientation_binLGBTQ 3.8552457 1.3813956 11.326587
## ARS_c 1.0365503 1.0138161 1.060593
## ILOC_c 0.9578181 0.9225228 0.993481
## Grit_c 0.6390767 0.3982674 1.015907
Wir sehen anhand dieser Ergebnisse also, dass (jeweils bei Konstanthaltung der anderen Prädiktoren):
- Personen, die sich als nicht-heterosexuell identifizieren, eine um den Faktor 3.86 höhere Wahrscheinlichkeit haben, in der Vergangenheit Suizidgedanken gehabt zu haben, als heterosexuelle Personen.
- Sich für jede Einheit Unterschied in der Ärger-Rumination die Wahrscheinlichkeit, Suizidgedanken gehabt zu haben, um den Faktor 1.04 erhöht.
- Sich für jede Einheit Unterschied in der internalen Kontrollüberzeugung die Wahrscheinlichkeit, Suizidgedanken gehabt zu haben, um den Faktor 0.96 verringert.
- Der Grit einer Personen keinen bedeutsamen Einfluss auf die Wahrscheinlichkeit hat, Suizidgedanken gehabt zu haben.
Anhand der Modellvergleiche hatten wir schon gesehen, dass der Grit (anders als ursprünglich in den Hypothsen angenommen) keine moderierende Wirkung auf diese Einflüsse hat. Wenngleich die numerischen Ergebnisse von denen in Lin et al. (2023) abweichen, scheinen die Ergebnisse inhaltlich im Einklang zu sein.
Klassifikationsgüte
Trotz diverser Vorschläge hat sich bislang kein generelles Effektstärkemaß im Sinne eines pseudo-$R^2$ zufriedenstellend durchsetzen können. Was sich hingegen, insbesondere aufgrund des rasanten Anstiegs von Machine-Learning-Verfahren, immer größerer Beliebtheit erfreut, sind Maße für die Klassifikations bzw. Vorhersagegüte. Eines der übersichtlichsten Konzepte ist dabei wahrscheinlich die treffend benannte Confusion Matrix.
Für die Beurteilung der Klassifikationsgüte müssen wir zunächst die konkreten Vorhersagen aus dem Modell ableiten. Das hatten wir schon für die Darstellung der Wahrscheinlichkeiten gemacht, nur dass wir jetzt definitive Aussagen haben wollen. Dafür müssen wir festhalten, welche Wahrscheinlichkeit als welche Vorhersage klassifiziert wird. Im Normalfall können wir dabei so vorgehen, dass alle Vorhersagen $> .5$ als $\widehat{Y} = 1$ klassifiziert werden (und natürlich andersrum). Diese Vorhersagen stellen wir dann einfach den tatsächlich beobachteten Kategorien gegenüber:
# Vorhersagen
idea$Prediction <- predict(block2, type = 'response') > .5
idea$Prediction <- factor(idea$Prediction, labels = c('None', 'Ideator'))
# Confusion
table(idea$Prediction, idea$Suicide)
##
## None Ideator
## None 124 44
## Ideator 21 39
Auf den ersten Blick scheint das nicht sonderlich zufriedenstellend. Das caret Paket bietet uns mit dem confusionMatrix-Befehl eine Möglichkeit dieses diffuse Gefühl der Unzufriedenheit numerisch auszudrücken:
library(caret)
confusionMatrix(idea$Prediction, idea$Suicide)
## Confusion Matrix and Statistics
##
## Reference
## Prediction None Ideator
## None 124 44
## Ideator 21 39
##
## Accuracy : 0.7149
## 95% CI : (0.6516, 0.7726)
## No Information Rate : 0.636
## P-Value [Acc > NIR] : 0.007248
##
## Kappa : 0.3455
##
## Mcnemar's Test P-Value : 0.006357
##
## Sensitivity : 0.8552
## Specificity : 0.4699
## Pos Pred Value : 0.7381
## Neg Pred Value : 0.6500
## Prevalence : 0.6360
## Detection Rate : 0.5439
## Detection Prevalence : 0.7368
## Balanced Accuracy : 0.6625
##
## 'Positive' Class : None
##
confuse <- table(idea$Prediction, idea$Suicide)
Im Fall der Vierfelder-Tafel sind die hier dargestellten Indikatoren relativ leicht rekonstruierbar. Die Accuracy ist der relative Anteil der korrekt klassifizierten Personen (also $(124 + 39) / 228 = 0.715$ ). Die Accuracy wird allerdings ein schlechtes Maß, wenn die Kategorien sehr ungleich groß sind - etwas das bei der Vorhersage von Störungen sehr häufig vorkommt. Wenn z.B. nur 10% der Personen Suizidgedanken gehabt hätten, könnten wir bei jeder Person einfach raten, dass sie keine Suizidgedanken hatte und würden eine Accuracy von $.9$ erreichen. Um die Accuracy also ein bisschen zu relativieren erhalten wir z.B. die Aussage No Information Rate - also was unsere Accuracy gewesen wäre, hätten wir immer die häufigste Kategorie geraten (also die relative Häufigkeit der häufigsten Kategorie in den Daten).
Für uns sind daher zunächst noch Sensitivity und Specificity von Interesse. Die Sensitivität ist in unserem Fall die relative Häufigkeit, mit der wir Personen, die keine Suizidgedanken hatten, auch korrekt als solche klassifizieren. Die 'Positive' Class: None zeigt uns im Output, welche Kategorie hier als Referenz genutzt wird. Die Spezifität ist dann, im Gegenzug, die relative Häufigkeit mit der wir Personen, die Suizidgedanken hatten, als solche identifizieren können. Hier ist die Güte mit 0.47 sogar unter 50%. Wir können anhand unseres Modells also in weniger als der Hälfte der Fälle Personen mit Suizidgedanken korrekt identifizieren. Für die Prävention also eventuell noch kein optimales Modell.
Multinomiale Logistische Regression
In der Studie von Lin et al. (2023) wird nicht nur zwischen Personen mit Suizidgedanken und Personen ohne Suizidgedanken unterschieden, sondern auch zusätzlich explizit Überlegungen zu den Unterschieden zwischen Personen mit Suizidgedanken (Ideator) und Personen mit Suizidversuchen (Attempter) angestellt. Insbesondere hinsichtlich des Grit, wird folgendes gesagt (S. 251):
Grit is commonly viewed as a character strength in overcoming challenging circumstances.
Das wird zum Einen damit in Verbindung gebracht, dass Personen mit stärkerem Grit seltener Suizidgedanken hegen sollten (weil sie besser in Lage sind auf zukünftige Ziele zu fokussieren und diese auch gegen stärkeren Widerstand aufrecht zu erhalten). Zum Anderen findet sich aber eine gegensätzliche Überlegung hinsichtlich eines tatsächlichen Suizidversuchs:
On the flip side, the ability to pursue death in the face of pain requires considerable persistence.
Daraus wird also zusammengenommen die erste Hypothese abgeleitet, die wir zu Beginn dieses Beitrags gesehen hatten:
Given findings from past research, we hypothesize grit to be protective against the development of suicidal ideation, but associated with facilitating suicidal behaviors in the presence of ideation.
Um diese Hypothese untersuchen zu können, benötigen wir also eine Methode, mit der wir gleichzeitig alle drei Gruppen untersuchen können. Das erreichen wir durch die Erweiterung der logitischen Regression in die multinomiale logistische Regression. Diese Erweiterung geht zwar technisch gesehen mit einer sehr viel komplizierteren Rechnung einher als die bisher betrachtete Regression (weswegen wir sie auch nicht mehr über den glm-Befehl anstellen können), aber inhaltlich und konzeptuell ist sie eigentlich nur ein Zusatzschritt.
Vorbereitung
Um die drei Gruppen unterscheiden zu können, müssen wir unsere Prädiktoren aus im gesamten Datensatz zentrieren und für die sexuelle Orientierung eine dichotomisierte Variable erstellen:
# Zentrierung
grit$ARS_c <- scale(grit$ARS, scale = FALSE)
grit$ILOC_c <- scale(grit$ILOC, scale = FALSE)
grit$Grit_c <- scale(grit$Grit, scale = FALSE)
# dichotome Orientierung
grit$Orientation_bin <- factor(grit$Orientation,
labels = c('Hetero', 'LGBTQ', 'LGBTQ', 'LGBTQ'))
Um später einen Fehler in der predict-Funktion zu vermeiden, müssen wir unseren zentrierten Variablen hier noch ihre besonderen Fähigkeiten entziehen (der Fehler taucht immer mal wieder bei verschiedenen Paketen auf, wenn man zentrierte Variablen in predict-Funktionen verwendet, weswegen wir ihn hier direkt vermeiden):
# Umwandlung in "numeric"
grit$ARS_c <- as.numeric(grit$ARS_c)
grit$ILOC_c <- as.numeric(grit$ILOC_c)
grit$Grit_c <- as.numeric(grit$Grit_c)
Außerdem müssen wir uns noch ein Paket besorgen, welches die multinomiale logistische Regression auch rechnen kann. Dafür gibt es zum Beispiel die funktion multinom im Paket nnet. Das Paket, wurde eigentlich dafür entwickelt, neuronale Netze zu rechnen. Aber in unserem Fall machen wir einfach nach dem ersten Schritt schluss (und verknüpfen unsere Regression nicht auch noch in einem Netz weiter).
# Paket installieren
install.packages('nnet')
# Paket laden
library(nnet)
Modell
Wie schon im Abschnitt zur einfachen logistischen Regression getan, konzentrieren wir uns zunächst auf die explizite Hypothese, dass Grit die Wahrscheinlich von Suizidgedanken verringern, die von Suizidversuchen aber erhöhen sollte. Die multinom-Funktion kann man im Wesentlichen genauso benutzen wie die lm- oder glm-Funktionen:
# Multinomiale logistische Regression
mod2 <- multinom(Suicide ~ 1 + Grit_c, grit)
## # weights: 9 (4 variable)
## initial value 353.753157
## final value 333.365834
## converged
Die Ausgabe unterscheidet sich allerdings ein wenig:
# Ergebnisse aus multinom
summary(mod2)
## Call:
## multinom(formula = Suicide ~ 1 + Grit_c, data = grit)
##
## Coefficients:
## (Intercept) Grit_c
## Ideator -0.5417195 -0.7994254
## Attempter -0.4191781 -0.8119500
##
## Std. Errors:
## (Intercept) Grit_c
## Ideator 0.1420315 0.2193857
## Attempter 0.1368580 0.2119803
##
## Residual Deviance: 666.7317
## AIC: 674.7317
Aus Gewohnheit des Lesens psychologischer, wissenschaftlicher Artikel fällt Ihnen eventuell als Erstes auf, dass hier kein $p$-Wert generiert wird. Aber auch die Gesamtstruktur unterscheidet sich ein wenig. Wir erhalten zwei Matrizen, eine enthält die Parameterschätzer (wieder im Logit-Format) und eine enthält die Standardfehler. In diesen beiden Matrizen zeigen die Zeilen die jeweilige Kategorie an, die vorhergesagt wird (in unserem Fall Ideator und Attempter). Die Spalten zeigen die Gewichte (bzw. Standardfehler) der jeweiligen Prädiktoren (hier nur das Intercept und Grit_c).
Wenn wir die Ergebnisse wieder in Odds überführen, können wir mit der Interpretation genauso verfahren, wie schon bei der “normalen” logistischen Regression:
# Odds
odds <- exp(coef(mod2))
odds
## (Intercept) Grit_c
## Ideator 0.5817471 0.4495872
## Attempter 0.6575870 0.4439914
Im ersten Intercept wird hier also festgehalten, wie viel wahrscheinlicher es ist, dass eine Person ein Ideator ist, als dass sie bislang weder Suizidgedanken noch -versuche hatte (none ist unsere Referenzkategorie), wenn sie durchschnittlichen Grit vorweisen kann (wir haben Grit zentriert). Im zweiten Intercept steht das Gleiche, aber für die Wahrscheinlichkeit, dass eine Person ein Attempter ist. Bezüglich des Grit können wir sagen, dass für jede zusätzliche Einheit in Grit, ein um das 0.45-fache geringerer Odds erwartet wird, dass eine Person schon einmal Suizidgedanken hatte.
Vorhesagen und Abbildungen
Wie schon bei der logistischen Regression, kann es immens hilfreiche sein, sich konkrete Vorhersagen anzusehen und eventuell eine Abbildung zu erstellen. Erneut können wir mit predict direkt Wahrscheinlichkeiten erzeugen lassen:
# Mittlerer Grit +/- 1 und 2 SD
new_data <- data.frame(Grit_c = c(-2*sd(grit$Grit), -sd(grit$Grit), 0, sd(grit$Grit), 2*sd(grit$Grit)))
# Vorhegesagte Wahrscheinlichkeiten
new_data$Probability <- predict(mod2, newdata = new_data, type = 'probs')
# Ausgabe
new_data
## Grit_c Probability.None Probability.Ideator Probability.Attempter
## 1 -1.3346695 0.2157771 0.3648532 0.4193697
## 2 -0.6673347 0.3202764 0.3176497 0.3620740
## 3 0.0000000 0.4465613 0.2597857 0.2936529
## 4 0.6673347 0.5801371 0.1979591 0.2219038
## 5 1.3346695 0.7029174 0.1406889 0.1563937
Wir sehen hier also, dass jetzt die Wahrscheinlichkeit für alle drei Kategorien bestimmt wird. Etwas bildlicher (der Code für die Abbildung ist wieder in der begleitenden R-Datei enthalten):
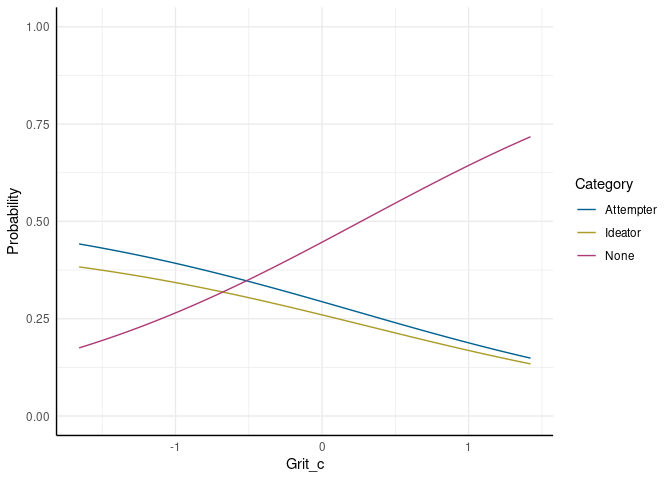
None klassifiziert zu werden, während die Wahrscheinlichkeiten für die beiden anderen Kategorien sinkt. Bisher sprechen die Ergebnisse also nur für die erste Hälfte der Hypothese.
Inferenzstatistik
Die Ergebnisse des multinom-Befehls liefern Parameterschätzer und Standardfehler. Die Konfidenzintervall der Parameter können wir allerdings - wie bei allen anderen Regressionen - mit dem confint-Befehl bestimmen:
confint(mod2)
## , , Ideator
##
## 2.5 % 97.5 %
## (Intercept) -0.8200962 -0.2633429
## Grit_c -1.2294134 -0.3694374
##
## , , Attempter
##
## 2.5 % 97.5 %
## (Intercept) -0.6874149 -0.1509413
## Grit_c -1.2274238 -0.3964762
Weil die Ergebnisse im Logit-Format sind, müssen wir hier gegen 0 prüfen. In beiden Fällen ist die 0 nicht im Konfidenzintervall enthalten - mehr Grit geht also mit einer statistisch bedeutsam geringeren Wahrscheinlichkeit einher, Suizidgedanken und -versuche durchlebt zu haben.
Um einen $p$-Wert zu erzeugen, müssen wir den $z$-Test händisch durchführen. Wie im allersten Test, den Sie im Bachelorstudium kennengelernt haben, ergibt sich die Teststatistik aus dem Verhältnis aus Parameter zum Standardfehler
$$
z = \frac{\beta}{\mathbb{SE}(\beta)}
$$
Wenn die Annahmen der multinomialen logistischen Regression halten, folgt dieser Wert asymptotisch einer Standardnormalverteilung, also können wir den $p$-Wert direkt bestimmen. Sowohl Parameter als auch Standardfehler können wir aus der summary des Modells ziehen:
# Parameter
beta <- summary(mod2)$coefficients
# Standardfehler
se <- summary(mod2)$standard.errors
# z-Werte
z <- beta/se
# p-Werte (zweiseitig)
p <- 2 * pnorm(abs(z), lower.tail = FALSE)
Volle Modelle
Um die, im Artikel von Lin et al. (2023) gezeigten Ergebnisse zu reproduzieren, müssen wir wieder die vier separaten Blöcke aufstellen und vergleichen. Im Artikel werden dann die Odds und deren Konfidenzintervalle aus dem vollen Modell berichtet.
# Blöcke aufstellen
block1 <- multinom(Suicide ~ 1 + Orientation_bin,
grit)
## # weights: 9 (4 variable)
## initial value 353.753157
## final value 339.293561
## converged
block2 <- multinom(Suicide ~ 1 + Orientation_bin + ARS_c + ILOC_c + Grit_c,
grit)
## # weights: 18 (10 variable)
## initial value 353.753157
## iter 10 value 320.636615
## final value 314.487424
## converged
block3 <- multinom(Suicide ~ 1 + Orientation_bin + ARS_c + ILOC_c + Grit_c +
ARS_c:ILOC_c + ARS_c:Grit_c + ILOC_c:Grit_c,
grit)
## # weights: 27 (16 variable)
## initial value 353.753157
## iter 10 value 324.553596
## iter 20 value 311.606052
## final value 311.601616
## converged
block4 <- multinom(Suicide ~ 1 + Orientation_bin + ARS_c + ILOC_c + Grit_c +
ARS_c:ILOC_c + ARS_c:Grit_c + ILOC_c:Grit_c +
ARS_c:ILOC_c:Grit_c,
grit)
## # weights: 30 (18 variable)
## initial value 353.753157
## iter 10 value 328.731857
## iter 20 value 311.995891
## final value 311.082859
## converged
# Modellvergleiche
anova(block1, block2, block3, block4)
## Likelihood ratio tests of Multinomial Models
##
## Response: Suicide
## Model
## 1 1 + Orientation_bin
## 2 1 + Orientation_bin + ARS_c + ILOC_c + Grit_c
## 3 1 + Orientation_bin + ARS_c + ILOC_c + Grit_c + ARS_c:ILOC_c + ARS_c:Grit_c + ILOC_c:Grit_c
## 4 1 + Orientation_bin + ARS_c + ILOC_c + Grit_c + ARS_c:ILOC_c + ARS_c:Grit_c + ILOC_c:Grit_c + ARS_c:ILOC_c:Grit_c
## Resid. df Resid. Dev Test Df LR stat. Pr(Chi)
## 1 640 678.5871
## 2 634 628.9748 1 vs 2 6 49.612275 5.622105e-09
## 3 628 623.2032 2 vs 3 6 5.771616 4.492540e-01
## 4 626 622.1657 3 vs 4 2 1.037514 5.952600e-01
Die Vergleiche zeigen, dass zumindest die Hypothesen hinsichtlich der moderierenden Effekte keine Unterstüzung finden. Im Artikel werden dennoch die Ergebnisse des vollen Modells berichtet, welche wir hier kurz rekonstruieren können.
Wie in den letzten beiden Sitzungen gesehen, bietet das Paket sjPlot eine breite Palette an Möglichkeiten, Ergebnisse schnell in die üblichen Tabellenformate für Artikel zu übertragen. Das gilt auch für die Ergebnisse aus multinom.
library(sjPlot)
tab_model(block4, show.r2 = FALSE, show.aic = TRUE)
| Suicide | ||||
|---|---|---|---|---|
| Predictors | Odds Ratios | CI | p | Response |
| (Intercept) | 0.49 | 0.36 – 0.69 | <0.001 | Ideator |
| Orientation bin [LGBTQ] | 2.71 | 0.99 – 7.44 | 0.053 | Ideator |
| ARS c | 1.04 | 1.01 – 1.06 | 0.002 | Ideator |
| ILOC c | 0.96 | 0.92 – 1.00 | 0.050 | Ideator |
| Grit c | 0.70 | 0.42 – 1.14 | 0.149 | Ideator |
| ARS c × ILOC c | 1.00 | 1.00 – 1.00 | 0.484 | Ideator |
| ARS c × Grit c | 0.98 | 0.95 – 1.02 | 0.351 | Ideator |
| ILOC c × Grit c | 1.03 | 0.97 – 1.10 | 0.332 | Ideator |
| (ARS c × ILOC c) × Grit c | 1.00 | 1.00 – 1.01 | 0.562 | Ideator |
| (Intercept) | 0.61 | 0.45 – 0.83 | 0.002 | Attempter |
| Orientation bin [LGBTQ] | 3.51 | 1.34 – 9.17 | 0.011 | Attempter |
| ARS c | 1.04 | 1.02 – 1.07 | <0.001 | Attempter |
| ILOC c | 0.98 | 0.94 – 1.02 | 0.274 | Attempter |
| Grit c | 0.59 | 0.37 – 0.94 | 0.028 | Attempter |
| ARS c × ILOC c | 1.00 | 1.00 – 1.00 | 0.688 | Attempter |
| ARS c × Grit c | 1.00 | 0.96 – 1.03 | 0.870 | Attempter |
| ILOC c × Grit c | 1.00 | 0.95 – 1.07 | 0.894 | Attempter |
| (ARS c × ILOC c) × Grit c | 1.00 | 1.00 – 1.01 | 0.314 | Attempter |
| Observations | 322 | |||
| AIC | 658.166 | |||
# Referenzlevel ändern
grit$Suicide_r <- relevel(grit$Suicide, ref = 'Attempter')
# Modell
block4b <- multinom(Suicide_r ~ 1 + Orientation_bin + ARS_c + ILOC_c + Grit_c +
ARS_c:ILOC_c + ARS_c:Grit_c + ILOC_c:Grit_c +
ARS_c:ILOC_c:Grit_c,
grit)
## # weights: 30 (18 variable)
## initial value 353.753157
## iter 10 value 324.713090
## iter 20 value 311.525627
## final value 311.082859
## converged
# Tabelle
tab_model(block4b, show.r2 = FALSE, show.aic = TRUE)
| Suicide_r | ||||
|---|---|---|---|---|
| Predictors | Odds Ratios | CI | p | Response |
| (Intercept) | 1.65 | 1.21 – 2.24 | 0.002 | None |
| Orientation bin [LGBTQ] | 0.29 | 0.11 – 0.75 | 0.011 | None |
| ARS c | 0.96 | 0.94 – 0.98 | <0.001 | None |
| ILOC c | 1.02 | 0.98 – 1.06 | 0.274 | None |
| Grit c | 1.69 | 1.06 – 2.69 | 0.028 | None |
| ARS c × ILOC c | 1.00 | 1.00 – 1.00 | 0.688 | None |
| ARS c × Grit c | 1.00 | 0.97 – 1.04 | 0.870 | None |
| ILOC c × Grit c | 1.00 | 0.94 – 1.06 | 0.894 | None |
| (ARS c × ILOC c) × Grit c | 1.00 | 0.99 – 1.00 | 0.314 | None |
| (Intercept) | 0.81 | 0.57 – 1.16 | 0.255 | Ideator |
| Orientation bin [LGBTQ] | 0.77 | 0.33 – 1.81 | 0.551 | Ideator |
| ARS c | 0.99 | 0.97 – 1.02 | 0.613 | Ideator |
| ILOC c | 0.98 | 0.94 – 1.02 | 0.381 | Ideator |
| Grit c | 1.17 | 0.70 – 1.98 | 0.548 | Ideator |
| ARS c × ILOC c | 1.00 | 1.00 – 1.00 | 0.254 | Ideator |
| ARS c × Grit c | 0.99 | 0.95 – 1.02 | 0.447 | Ideator |
| ILOC c × Grit c | 1.03 | 0.96 – 1.09 | 0.412 | Ideator |
| (ARS c × ILOC c) × Grit c | 1.00 | 1.00 – 1.00 | 0.649 | Ideator |
| Observations | 322 | |||
| AIC | 658.166 | |||
Am AIC können wir sehen, dass beide Modelle identische Passung zu den Daten aufweisen - also einfach Umformulierungen voneinander sind.
Im Artikel zwar nicht dargestellt, aber auch für multinomiale logistische Regression interessant ist die Klassifikationsgüte, welche wir für die reguläre logistische Regression anhand der Confusion Matrix untersucht hatten. Das gleiche Vorgehen können wir auch hier nutzen. Wenn wir predict auf ein multinom-Ergebnis anwenden, erhalten wir direkt die vorhergesagte Kategorie:
# Vorgesagte Kateogrien
grit$Prediction <- predict(block4)
# Confusion Matrix
confusionMatrix(grit$Prediction, grit$Suicide)
## Confusion Matrix and Statistics
##
## Reference
## Prediction None Ideator Attempter
## None 120 39 52
## Ideator 8 18 14
## Attempter 17 26 28
##
## Overall Statistics
##
## Accuracy : 0.5155
## 95% CI : (0.4595, 0.5713)
## No Information Rate : 0.4503
## P-Value [Acc > NIR] : 0.01099
##
## Kappa : 0.2039
##
## Mcnemar's Test P-Value : 4.423e-09
##
## Statistics by Class:
##
## Class: None Class: Ideator Class: Attempter
## Sensitivity 0.8276 0.2169 0.29787
## Specificity 0.4859 0.9079 0.81140
## Pos Pred Value 0.5687 0.4500 0.39437
## Neg Pred Value 0.7748 0.7695 0.73705
## Prevalence 0.4503 0.2578 0.29193
## Detection Rate 0.3727 0.0559 0.08696
## Detection Prevalence 0.6553 0.1242 0.22050
## Balanced Accuracy 0.6567 0.5624 0.55464
Erneut gibt die Accuracy den relativen Anteil der korrekt klassifzierten Personen an. In unserem Fall also $(120 + 18 + 28) / 322 = 0.52$. Senisitivtät und Spezifität werden jetzt ein wenig anders interpretiert als im Fall der binären logistischen Regression. Für die Klasse der Ideator, zum Beispiel, wurden 18 der insgesamt 83 Personen korrekt als Personen mit Suizidgedanken identifiziert (21.7%). So sensitiv ist unser Modell also in der Detektion dieser Gruppe. Auf der anderen Seite sind 18 der insgesamt 40 (45%) der Personen, für die Ideator vorhergesagt wurde auch tatsächlich Personen, die Suizidgedanken berichtet haben. So spezifisch ist unsere Vorhersage also für diese Gruppe.
Abschluss
Mit den gezeigten Schritten (und einer zusätzlichen Korrelationstablle via corr.test) können wir also versuchen alle Ergebnisse aus dem Artikel von Lin et al. (2023) zu reproduzieren. Wie Sie (als aufmerksame Leser*innen) bestimmt mitbekommen haben, sind dieser Ergebnisse allerdings nicht identisch. Zwar zweigen die Ergebnisse für das “Model 1” aus dem Artikel die gleichen Muster an bedeutsamen und nicht-bedeutsamen Prädiktoren, die tatsächlichen Zahlen weichen allerdings ab. Ich habe die Autorinnen des Papers kontaktiert, um über die Diskrepranzen zu sprechen. Meine Vermutung ist dabei, dass die Unterschiede auf den Ausschluss von Ausreißern und Extremwerten zurückgehen, welche im Paper (und dem ursprünglichen Skript auf dem OSF) nicht dokumentiert sind. Leider hat diese Kontaktaufnahme dazu geführt, dass der Beitrag im OSF verschwunden ist, bis diese Diskrepanzen geklärt werden können, sodass es mir zum Zeitpunkt, zu dem ich diesen Beitrag schreibe nicht möglich ist, eine definitive Aussage dazu zu treffen, woher diese Unterschiede kommen. Dennoch sind Sie jetzt in der Lage, für die anderen drei berichteten Modelle zu prüfen, ob es auch dort zu solchen Diskrepanzen kommt und ob sich die Interpretation im Artikel dadurch verändern würden.
Literatur
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden (5. Auflage, 1. Auflage: 2010). Weinheim: Beltz.
Lin, Y.-C., O’Connell, K.L., & Law, K.C. (2023). Moderating roles of grit and locus of control on rumination and suicidality. Journal of Affective Disorders, 330, 250-258. doi: 10.1016/j.jad.2023.02.148.
Pituch, K. A. & Stevens, J. P. (2016). Applied Multivariate Statistics for the Social Sciences (6th ed.). New York: Taylor & Francis.
- Blau hinterlegte Autor:innenangaben führen Sie direkt zur universitätsinternen Ressource.
](/media/header/talking_beach.jpg)