Regression mit nominalskalierten Prädiktoren
In den bisherigen Sitzungen zur multiplen Regression haben wir als Prädiktoren hauptsächlich intervallskalierte Variablen betrachtet. In einigen Beispielen ist aber z.B. das Geschlecht aufgetaucht. In diesem Beitrag gucken wir uns etwas genauer an, was passiert, wenn Prädiktoren nominalskaliert sind.
Hier wird es, wie immer auf pandaR, vor allem um die Umsetzung in R und die Interpretation von Ergebnissen gehen. Für eine etwas genauere Einleitung in Regression mit nominalskalierten (oder auch “kategorialen”) Prädiktoren, empfiehlt sich ein Blick in Kapitel 19.11 und 19.12 von Eid et al. (2017).
Datenbeispiel
Das Beispiel, was wir in diesem Beitrag betrachten, dreht sich um Daten aus der ersten Studie im Artikel von Hong-Zhi et al. (2021). Weil die Daten für unsere Berechnungen ein wenig gekürzt und umbenannt werden müssen, können wir das dafür vorbereitete Skript ausführen:
source("https://pandar.netlify.app/lehre/statistik-ii/Data_Processing_punish.R")
Die vollständigen Daten können aber auch direkt vom OSF heruntergeladen werden.
Der Datensatz, der durch das Vorbereitungsskript entsteht heißt punish und sieht auf den ersten Blick so aus:
head(punish)
## country bribe age gender gains
## 1 China individual 21-30 female 8.6
## 2 China individual 31-40 female 10.0
## 3 China individual 31-40 male 9.2
## 4 China individual 31-40 female 10.0
## 5 China individual 31-40 female 9.0
## 6 China individual 31-40 male 9.0
## difficult notice probable severe
## 1 3.0 3.8 3.0 2.8
## 2 3.8 1.6 1.0 1.2
## 3 1.6 2.0 2.2 2.4
## 4 1.2 0.8 2.4 4.6
## 5 1.4 1.2 4.2 4.6
## 6 8.0 6.0 7.8 8.6
In der Studie, aus der diese Daten kommen, wurden kulturelle Unterschiede in der Einschätzung von und Reaktion auf Bestechung untersucht. Spezifisch ging es darum, wie sich Personen in China und den USA darin unterscheiden, wie sie individuelle und gruppenbezogene Bestechung wahrnehmen und für wie wahrscheinlich und schwer sie Bestrafungen für diese halten. Dabei wurden fünf verschiedene Situationen als Text dargestellt. In Tabelle 1 des Artikels von Hong-Zhi et al. (2021) sind die fünf Situationen dargestellt. Der erste Text dreht sich um Bestechung im Gesundheitswesen, welche im individuellen Fall so aussieht:
Um die Verkaufszahlen eines Medikaments zu steigern, gibt ein Pharmaunternehmen einem Arzt Geld und Geschenke. Der Arzt akzeptiert diese Vorzüge und beginnt das Medikament absichtlich mehr Patientinnen und Patienten zu verschreiben.
In der zweiten experimentellen Bedingung ist der Text hingegen:
Um die Verkaufszahlen eines Medikaments zu steigern, gibt ein Pharmaunternehmen einer Krankhausabteilung Geld und Geschenke. Alle Ärztinnen und Ärzte der Abteilung profitieren gleichmäßig von diesen Vorzügen und beginnen das Medikament absichtlich mehr Patientinnen und Patienten zu verschreiben.
Jede Situation wurde auf fünf Eigenschaften hin eingeschätzt:
- das Ausmaß an Vorteilen, dass sich die Person erschleicht, die die Bestechung akzeptiert (
gains), - wie schwer es wäre das erkaufte Verhalten umzusetzen (
difficult), - wie wahrscheinlich es ist, dass das Verhalten bemerkt wird (
notice), - wie wahrscheinlich es ist, dass das Verhalten bestraft wird (
probable) - wie schwer die Bestrafung ausfallen wird (
severe)
Im Folgenden werden wir versuchen, die eingeschätzte schwere der Bestrafung (severe) unter anderem durch verschiedene nominalskalierte Variablen vorherzusagen:
- das Land, aus dem die befragte Person kommt (
country) - welche Art von Bestechung dargestellt wird (
bribe) - wie alt die befragte Person ist (
age) - welches Geschlecht die befragte Person hat (
gender)
Einfache Regression mit Dummy-Kodierung
Wie wir schon in der Vorlesung aus dem 1. Semester gesehen hatten, können wir Regressionen auch mit dichotomen Prädiktoren durchführen und dabei das gleiche Ergebnis erhalten, wie von einem $t$-Test für unabhängige Stichproben.
Als ersten Prädiktor nutzen wir das Land (country) um festzustellen, ob es globale Unterschiede zwischen China und den USA im Ausmaß von vorhergesagter Bestrafungsschwere gibt:
mod1 <- lm(severe ~ country, punish)
summary(mod1)
##
## Call:
## lm(formula = severe ~ country, data = punish)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.7902 -1.9902 -0.0669 1.6448 5.4565
##
## Coefficients:
## Estimate Std. Error t value
## (Intercept) 4.5435 0.2378 19.11
## countryChina 0.4468 0.3463 1.29
## Pr(>|t|)
## (Intercept) <2e-16 ***
## countryChina 0.199
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.28 on 172 degrees of freedom
## Multiple R-squared: 0.009582, Adjusted R-squared: 0.003824
## F-statistic: 1.664 on 1 and 172 DF, p-value: 0.1988
Wie wir sehen, zeigt die Ausgabe der Regression als Prädiktor countryChina. Das liegt daran, dass die Variable country im Datensatz als factor vorliegt:
class(punish$country)
## [1] "factor"
Per Voreinstellung wandelt R factor-Variablen, die als Prädiktoren in Regressionen aufgenommen werden in sogenannte dummy-Variablen um. Diese sind numerisch als 0 und 1 kodiert. Welches Land mit 0 und welches mit 1 kodiert wird können wir mit contrasts einsehen:
contrasts(punish$country)
## China
## U.S 0
## China 1
Diese Kodierung wird gewählt, weil 0 und 1 ein paar sehr schöne mathematische Eigenschaften haben, die die Interpretation der Regressionsergebnisse sehr einfach machen. Sehen wir uns die Regressionsgleichung für die vorhergesagten Werte von severe mal an:
$$
\hat{y}_{m} = b_0 + b_1 \cdot x_{m}
$$
Dadurch, dass der Prädiktor den Wert 0 annimmt, wenn eine Person aus den USA kommt, vereinfacht sich die Gleichung:
\begin{equation}
\begin{split}
&\hat{y}_{m} = b_0 + b_1 \cdot 0 \\
&\hat{y}_{m} = b_0
\end{split}
\end{equation}
Heißt, das Intercept entspricht dem vorhergesagten Wert für Personen aus den USA. Weil keine weiteren Informationen in der Regression genutzt werden, sagen wir für Personen aus den USA den Mittelwert dieser Gruppe vorher. Für Personen aus China ist $x_m = 1$ also:
\begin{equation}
\begin{split}
&\hat{y}_{m} = b_0 + b_1 \cdot 1 \\
&\hat{y}_{m} = b_0 + b_1
\end{split}
\end{equation}
Der vorhergesagte Wert ist auch in dieser Gruppe der Mittelwert. Er ergibt sich aus $b_0 + b_1$; $b_1$ ist also der Mittelwertsunterschied zwischen den beiden Gruppen. Prüfen wir, ob ich nicht einfach unhaltbare Behauptungen in den Raum stelle:
# Gruppenmittelwerte
tapply(punish$severe, punish$country, mean)
## U.S China
## 4.543478 4.990244
# Koeffizienten
coef(mod1)[1] # USA
## (Intercept)
## 4.543478
coef(mod1)[1] + coef(mod1)[2] # China
## (Intercept)
## 4.990244
Weil in $b_1$ der Mittelwertsunterschied dargestellt wird, entspricht auch das Ergebnis dem des t-Tests für unabhängige Stichproben:
t.test(punish$severe ~ punish$country, var.equal = TRUE)
##
## Two Sample t-test
##
## data: punish$severe by punish$country
## t = -1.29, df = 172, p-value = 0.1988
## alternative hypothesis: true difference in means between group U.S and group China is not equal to 0
## 95 percent confidence interval:
## -1.1303844 0.2368531
## sample estimates:
## mean in group U.S mean in group China
## 4.543478 4.990244
Die Äquivalenz der Ergebnisse erkennen wir bspw. an der Gleichheit der $p$-Werte in der Signifikanzentscheidung und der betraglichen Gleichheit der zugehörigen $t$-Werte.
Effektkodierung
In der Dummy-Kodierung, die in R voreinstellung ist, wird die zweite Gruppe mit der ersten Gruppe verglichen. Das Intercept stellt dabei den Mittelwert der ersten Gruppe dar und das Regressionsgewicht ist die Abweichung der zweiten Gruppe von der ersten Gruppe. In Fällen mit nur zwei Gruppen, ist die logische Frage “na und?”, aber für Fälle, in denen wir mehr als nur zwei Gruppen untersuchen, könnte das ein Problem darstellen (auf das wir später noch eingehen werden).
Obwohl die Dummy-Kodierung auch in der Psychologie die verbreitetste Kodierung darstellt, wird auch die sogenannte Effekt-Kodierung von Zeit zu Zeit verwendet. Dabei ist das Ziel, dass das Intercept nicht mehr an eine Gruppe gebunden ist, sondern die gesamte Stichprobe beschreibt und das Regressionsgewicht die Abweichung einzelnen Gruppen von diesem globalen Wert darstellt. In R können wir die Kodierung eines factor mit contrasts nicht nur abfragen, sondern auch einstellen:
contrasts(punish$country) <- contr.sum(2)
In R können verschiedene Kontrastypen genutzt werden - alle Funktionen dafür beginnen mit contr.. Für die Effektkodierung nutzen wir contr.sum und die 2 stellt dar, wie viele Ausprägungen unsere Variable hat.
contrasts(punish$country)
## [,1]
## U.S 1
## China -1
Das sum in der Benennung kommt daher, dass die Summe dieser Kontraste Null ist. Die Regression verändert sich ein wenig:
mod1b <- lm(severe ~ country, punish)
summary(mod1b)
##
## Call:
## lm(formula = severe ~ country, data = punish)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.7902 -1.9902 -0.0669 1.6448 5.4565
##
## Coefficients:
## Estimate Std. Error t value
## (Intercept) 4.7669 0.1732 27.53
## country1 -0.2234 0.1732 -1.29
## Pr(>|t|)
## (Intercept) <2e-16 ***
## country1 0.199
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.28 on 172 degrees of freedom
## Multiple R-squared: 0.009582, Adjusted R-squared: 0.003824
## F-statistic: 1.664 on 1 and 172 DF, p-value: 0.1988
Das Intercept ist jetzt der Mittelwert der Gruppenmittelwerte (wir geben die oben erstellten Gruppenmittelwerte mit |> an den mean-Befehl weiter:
# Mittel der Gruppenmittelwerte
tapply(punish$severe, punish$country, mean) |> mean()
## [1] 4.766861
Das Regressionsgewicht ist jetzt der Effekt (daher die Bezeichnung Effektkodierung) den das Land auf die Schwere der Bestrafung hat. Dies entspricht dem Vergleich eines Landes mit einem durchschnittlichen Land. Der Effekt ist vom Betrag die Hälfte dessen, was wir in der Dummy-Kodierung gesehen haben, weil das durchschnittliche Land bei zwei untersuchten Ländern einfach genau dem Mittelwert der beiden Länder entspricht und jedes Land von diesem Mittelwert um genau die Hälfte ihres Gesamtunterschieds abweicht.
Kombination mehrerer dichotomer Prädiktoren
Im Folgenden arbeiten wir mit dummy-kodierten Prädiktoren weiter, weil diese in der Psychologie der häufigste Fall sind. Weil wir im vorherigen Abschnitt die Kodierung aber händisch umgestellt hatten, müssen wir erst einmal wieder den Ausgangszustand herstellen (die zweiten Zeile garantiert, dass in unseren Ausgaben in Zukunft auch weiterhin China erscheint und nicht 2):
contrasts(punish$country) <- contr.treatment(2)
dimnames(contrasts(punish$country))[[2]] <- 'China'
Als nächstes nehmen wir in unsere Analysen die Art der Bestechung auf (bribe). Die Hypothese ist, dass in Ländern mit kollektivistischeren Grundhaltungen (wie z.B. China) Korruption durch ein Kollektiv einer strengeren Strafe unterliegt, weil dem Kollektiv die Aufgabe der Einhaltung moralischer Regeln zugeschrieben wird. In Ländern mit stärker ausgeprägten individualisitischen Grundhaltungen (wie z.B. die USA) hingegen, wird diese Aufgabe dem Individuum zugeschrieben, sodass dessen Verstoß durch die Annahme von Bestechung stärker bestraft werden muss.
Um verschiedene Analyseansätze zu verstehen, bietet es sich an, die vorhergesagten Werte genauer zu betrachten. Wir erzeugen uns eine Tabelle mit vier Einträgen: Gruppenbestechung in den USA, individuelle Bestechung in den USA, Gruppenbestechung in China und individuelle Bestechung in China:
tab <- data.frame(country = c('U.S', 'U.S', 'China', 'China'),
bribe = c('group', 'individual', 'group', 'individual'))
Wie wir schon in der Sitzung zur Regression im 1. Semester gesehen haben, können wir einen data.frame benutzen, um für alle Einträge darin aus unserem Modell eine Vorhersage generieren zu lassen. Gucken wir uns zunächst das Modell an, in dem wir das Ausmaß der Bestrafung nur durch das Land vorhergesagt haben:
tab$mod1 <- predict(mod1, tab)
tab
## country bribe mod1
## 1 U.S group 4.543478
## 2 U.S individual 4.543478
## 3 China group 4.990244
## 4 China individual 4.990244
Für beide Einträge aus den USA wird 4.54 - also $b_0$ - vorhergesagt. Im Modell haben wir nicht zwischen Bestechungsarten unterschieden, also ist das zunächst relativ naheliegend. Für Fans der bunten Bilder, können wir das auch in einen ggplot überführen:
pred_plot <- ggplot(tab, aes(x = bribe,
group = country, color = country)) +
geom_point(aes(y = mod1)) + geom_line(aes(y = mod1)) +
theme_minimal() +
ylim(c(4, 5.5))
pred_plot
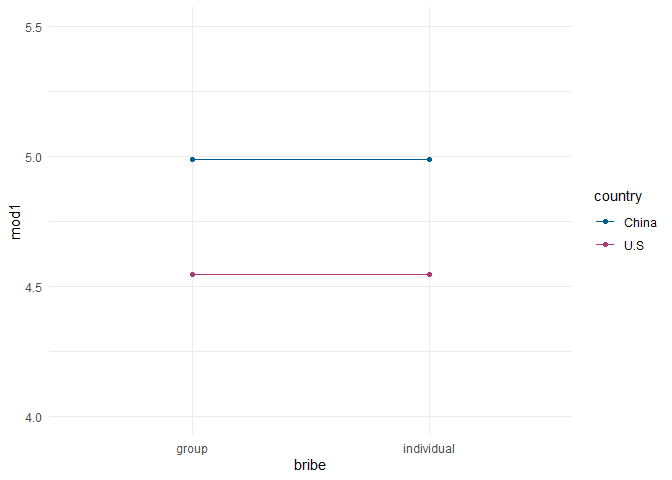
Wenn wir zusätzlich in einer multiple Regression die Art der Bestechung aufnehmen, erweitert sich unser Modell in bekannter Manier:
mod2 <- lm(severe ~ country + bribe, punish)
summary(mod2)
##
## Call:
## lm(formula = severe ~ country + bribe, data = punish)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.8853 -1.9040 -0.0947 1.5573 5.3620
##
## Coefficients:
## Estimate Std. Error t value
## (Intercept) 4.4568 0.2903 15.351
## countryChina 0.4472 0.3471 1.289
## bribeindividual 0.1812 0.3469 0.523
## Pr(>|t|)
## (Intercept) <2e-16 ***
## countryChina 0.199
## bribeindividual 0.602
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.285 on 171 degrees of freedom
## Multiple R-squared: 0.01116, Adjusted R-squared: -0.0004046
## F-statistic: 0.965 on 2 and 171 DF, p-value: 0.383
Die Regressionsgewichte haben sich analog zu denen einer multiplen Regression mit intervallskalierten Prädiktoren verändert: $b_1 = 0.45$ bezieht sich auf den Unterschied zwischen zwei Personen, deren country Variable sich um eine Einheit unterscheidet (USA = 0 zu China = 1), die auf der bribe Variable aber die gleiche Ausprägung haben. In der Tabelle der Vorhersagen und der Abbildung wird dies noch einmal deutlich:
tab$mod2 <- predict(mod2, tab)
pred_plot <- pred_plot +
geom_point(aes(y = tab$mod2)) + geom_line(aes(y = tab$mod2), lty = 2)
pred_plot
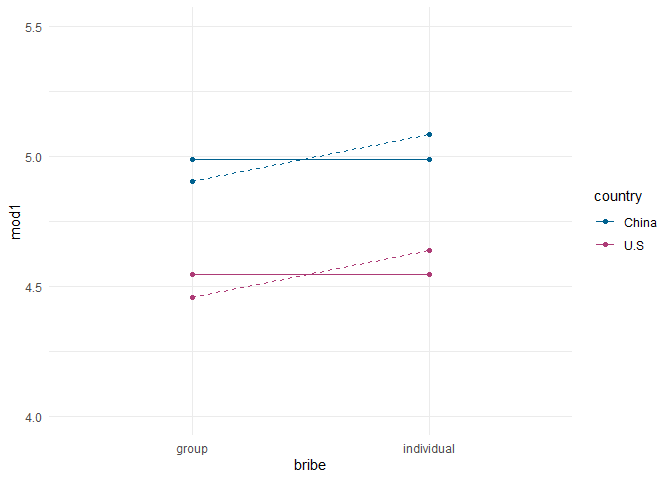
tab$mod2 arbeiten und nicht einfach nur mit mod2 in geom_point und geom_line, da sich die Daten geändert hatten und wir den Plot ansonsten nochmals hätten aufrufen müssen, was wir uns hier ersparen wollten): Die beiden Linien haben jetzt einen Anstieg - dieser Anstieg entspricht dem Regressionsgewicht von bribe: $b_2 =$ 0.18 und somit dem Unterschied zwischen den Vorhersagen für Gruppenbestechung und individuelle Bestechung:
# Übersicht über die Vorhersagten Werte
tab
## country bribe mod1 mod2
## 1 U.S group 4.543478 4.456796
## 2 U.S individual 4.543478 4.638041
## 3 China group 4.990244 4.904042
## 4 China individual 4.990244 5.085287
# Unterschied der Bestechungstypen in den beiden Ländern
tab$mod2[2] - tab$mod2[1]
## [1] 0.1812452
tab$mod2[4] - tab$mod2[3] # identisch
## [1] 0.1812452
Weil die Linien parallel sind, ist egal in welchem Land wir den Unterschied berechnen. Das Modell nimmt an, dass der Unterschied zwischen individueller und kollektiver Bestechung über die Länder hinweg gleich ist.
Die oben dargestellte Hypothese geht aber davon aus, dass die Länder sich im Ausmaß der Bestrafung unterscheiden, je nachdem um welche Art von Bestechung es sich handelt. Wir müssen also die Restriktion additiver Effekte aufheben, indem wir, wie auch bei der moderierten Regression, einen Interaktionsterm in das Modell aufnehmen. Weil die beiden Prädiktoren nominalskaliert sind, können wir sie nicht zentrieren (nominalskalierte Variablen haben kein arithmetisches Mittel) - das ist nicht weiter tragisch, weil wir bei diesen Variablen in geringerem Ausmaß skalierungsbedingte Probleme mit der Multikollinearität haben.
mod3 <- lm(severe ~ country + bribe + country:bribe, punish)
summary(mod3)
##
## Call:
## lm(formula = severe ~ country + bribe + country:bribe, data = punish)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.1182 -1.7436 0.0564 1.5993 5.0564
##
## Coefficients:
## Estimate
## (Intercept) 4.0167
## countryChina 1.3787
## bribeindividual 1.1015
## countryChina:bribeindividual -1.9533
## Std. Error
## (Intercept) 0.3231
## countryChina 0.4700
## bribeindividual 0.4672
## countryChina:bribeindividual 0.6806
## t value Pr(>|t|)
## (Intercept) 12.432 < 2e-16
## countryChina 2.933 0.00382
## bribeindividual 2.358 0.01952
## countryChina:bribeindividual -2.870 0.00463
##
## (Intercept) ***
## countryChina **
## bribeindividual *
## countryChina:bribeindividual **
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.238 on 170 degrees of freedom
## Multiple R-squared: 0.05685, Adjusted R-squared: 0.04021
## F-statistic: 3.416 on 3 and 170 DF, p-value: 0.01874
Im Gegensatz zu den bisherigen Modellen, sind nun alle Effekte bedeutsam. Das liegt daran, dass die Bedeutung der Regressionsgewichte sich verändert hat. Gucken wir uns erst die Abbildung an, um zu sehen was das Modell insgesamt darstellt:
tab$mod3 <- predict(mod3, tab)
pred_plot <- pred_plot +
geom_point(aes(y = tab$mod3)) + geom_line(aes(y = tab$mod3), lty = 3)
pred_plot
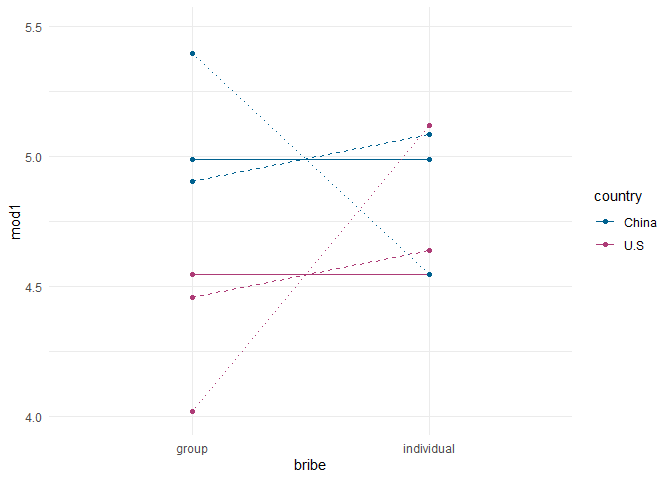
lty = 3) erlaubt jetzt, dass der Einfluss der Bestechungsart sich über die Länder hinweg unterscheiden kann (bzw. dass der Einfluss des Landes sich über die Bestechungsarten hinweg unterscheidet - weil es sich um Multiplikation handelt, ist dieser Effekt symmetrisch bzw. ungerichtet). Hier lohnt es sich noch einmal einen genaueren Blick in die Regressionsgleichung zu werfen:
$$
\hat{y}_{m} = b_0 + b_1 \cdot x_{1m} + b_2 \cdot x_{2m} + b_3 \cdot (x_{1m} \cdot x_{2m}) \\
$$
Und auf die vier Vorhersagen, die durch dieses Modell getätigt werden:
tab
## country bribe mod1 mod2
## 1 U.S group 4.543478 4.456796
## 2 U.S individual 4.543478 4.638041
## 3 China group 4.990244 4.904042
## 4 China individual 4.990244 5.085287
## mod3
## 1 4.016667
## 2 5.118182
## 3 5.395349
## 4 4.543590
Wir sollten uns wieder vor Augen führen, dass die unabhängigen Variablen mit 0 und 1 kodiert sind, da es sich um dummy-Variablen handelt. Für Personen aus den USA (country = 0), die kollektive Bestechung (bribe = 0) gesehen haben vereinfacht sich die Regressionsgleichung also zu:
\begin{equation}
\begin{split}
&\hat{y}_{m} = b_0 + b_1 \cdot 0 + b_2 \cdot 0 + b_3 \cdot (0 \cdot 0) \\
&\hat{y}_{m} = b_0 \\
\end{split}
\end{equation}
Das Intercept entspricht also dem Wert, der für diese Referenzgruppe vorhergesagt wird. Wenn wir Personen betrachten, die aus China kommen (country = 1), und ebenfalls kollektive Bestechung (bribe = 0) gesehen haben, ergibt sich Folgendes:
\begin{equation}
\begin{split}
&\hat{y}_{m} = b_0 + b_1 \cdot 1 + b_2 \cdot 0 + b_3 \cdot (1 \cdot 0) \\
&\hat{y}_{m} = b_0 + b_1\\
\end{split}
\end{equation}
Die Vorhersage für die Gruppe (in tab: 5.4) setzt sich also aus dem Wert für Amerikaner:innen, die kollektive Bestechung gesehen haben ($b_0$) und dem Unterschied zwischen diesen und Personen aus China, die kollektive Bestechung gesehen haben ($b_1$) zusammen. Das heißt, dass das Regressionsgewicht diesen spezifischen Gruppenvergleich prüft.
In gleicher Weise fungiert $b_2$ als der Vergleich zwischen der Referenzgruppe und Personen aus den USA, die individuelle Bestechung gesehen haben:
\begin{equation}
\begin{split}
&\hat{y}_{m} = b_0 + b_1 \cdot 0 + b_2 \cdot 1 + b_3 \cdot (0 \cdot 1) \\
&\hat{y}_{m} = b_0 + b_2
\end{split}
\end{equation}
Etwas komplexer wird das Problem, wenn wir die letzte Gruppe betrachten: Personen aus China, die individuelle Bestechung gesehen haben:
\begin{equation}
\begin{split}
&\hat{y}_{m} = b_0 + b_1 \cdot 1 + b_2 \cdot 1 + b_3 \cdot (1 \cdot 1) \\
&\hat{y}_{m} = b_0 + b_1 + b_2 + b_3
\end{split}
\end{equation}
Weil für diese Gruppe der Mittelwert nicht mehr aus dem Intercept und einem einfachen Vergleich bestimmt wird, ist auch die Interpretation des entsprechenden Regressionsgewichts ein bisschen schwieriger. Dieses Gewicht stellt den Unterschied dar zwischen dem Mittelwert der Gruppe und dem, was wir erwartet hätten, hätte es in der Chinesischen Gruppe den gleichen Effekte der Bestechungsart gegeben wie in den USA. Erneut: weil der Interaktionsterm einfache Multiplikation ist, ist es genauso zulässig diese Aussage umzudrehen: dieses Gewicht stellt den Unterschied dar zwischen dem Mittelwert der Gruppe und dem, was wir erwartet hätten, hätte es beim sehen individueller Bestechung den gleichen Länderunterschied gegeben, wie bei kollektiver Bestechung. Die Inferenzstatistik dieses Interaktionseffekts prüft also, ob die Effekte gleich sind. Wie wir in der summary gesehen haben, ist dem nicht so:
## Estimate
## (Intercept) 4.016667
## countryChina 1.378682
## bribeindividual 1.101515
## countryChina:bribeindividual -1.953274
## Std. Error
## (Intercept) 0.3230915
## countryChina 0.4700153
## bribeindividual 0.4671896
## countryChina:bribeindividual 0.6806394
## t value
## (Intercept) 12.431978
## countryChina 2.933271
## bribeindividual 2.357748
## countryChina:bribeindividual -2.869764
## Pr(>|t|)
## (Intercept) 1.183591e-25
## countryChina 3.817026e-03
## bribeindividual 1.952359e-02
## countryChina:bribeindividual 4.629547e-03
Dies bedeutet auch, dass es auf die spezifische Kombination aus Land und Art der Bestechung ankommt, für die Vorhersage der eingeschätzten Schwere der Bestrafung. Für die Grafik bedeutet die Signifikanz des Interaktionseffektes, dass die Geraden sich signifikant von der Parallelität unterscheiden.
Modellvergleiche
Wie wir in der Sitzung zur Modelloptimierung gesehen haben, können wir die drei Modelle über anova() vergleichen, um zu prüfen, ob sie sich hinsichtlich der Vorhersagekraft der eingeschätzten Schwere der Bestrafung unterscheiden. Die Modelle sind ineinander geschachtelt, weil wir in jedem Schritt lediglich einen weiteren Prädiktor aufgenommen haben.
anova(mod1, mod2, mod3)
## Analysis of Variance Table
##
## Model 1: severe ~ country
## Model 2: severe ~ country + bribe
## Model 3: severe ~ country + bribe + country:bribe
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 172 894.50
## 2 171 893.07 1 1.426 0.2846 0.59441
## 3 170 851.81 1 41.265 8.2355 0.00463
##
## 1
## 2
## 3 **
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Deskriptiv
summary(mod2)$r.squared - summary(mod1)$r.squared
## [1] 0.001578844
summary(mod3)$r.squared - summary(mod2)$r.squared
## [1] 0.04569026
Was wir hier sehen ist also wieder: für die Untersuchung von Interaktionseffekten ist es nicht zwingend notwendig, dass die additiven Modellkomponenten statistisch bedeutsam sind. Gegenläufige Effekte können sich über die verschiedenen Ausprägungen der unabhängigen Variablen hinweg ausmitteln, sodass sie verdeckt werden.
Nominalsklierte Prädiktoren mit mehr als zwei Kategorien
In dem Datenbeispiel, das wir hier nutzen gibt es leider keine nominalskalierte Variable, die mehr als zwei Ausprägungen hat. Allerdings werden (wie wir es jetzt auch tun werden) ordinalskalierte UVs in den meisten Fällen nach dem gleichen Prinzipien behandelt, wie nominalskalierte. In den hier vorliegenden Daten ist das Alter (wie aus Datenschutzgründen üblich) in Segmenten und nicht in Jahren erhoben:
table(punish$age)
##
## 21-30 31-40 41-50 over 50
## 42 80 33 19
Die Stichprobe ist also in vier Alterskategorien eingeteilt. Diese Variable als numerischen Prädiktor aufzunehmen, hätte den Nachteil, dass ein konstanter, linearer Effekt über alle Alterstufen hinweg angenommen wird. In diesem Fall ist aber besonders die vierte Kategorie (over 50) sehr viel heterogener als die vorangegangenen drei.
Gucken wir uns den Einfluss an, den das Alter auf die eingeschätzte Schwere der Bestrafung hat:
mod4 <- lm(severe ~ age, punish)
summary(mod4)
##
## Call:
## lm(formula = severe ~ age, data = punish)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.2650 -1.8150 -0.0951 1.5152 5.1152
##
## Coefficients:
## Estimate Std. Error t value
## (Intercept) 4.12857 0.34659 11.912
## age31-40 1.13643 0.42800 2.655
## age41-50 0.55628 0.52250 1.065
## ageover 50 -0.02331 0.62101 -0.038
## Pr(>|t|)
## (Intercept) < 2e-16 ***
## age31-40 0.00868 **
## age41-50 0.28855
## ageover 50 0.97010
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.246 on 170 degrees of freedom
## Multiple R-squared: 0.05035, Adjusted R-squared: 0.03359
## F-statistic: 3.004 on 3 and 170 DF, p-value: 0.03196
Wie wir schon bei den beiden dichotomen Prädiktoren gesehen hatten, übernimmt R die Kodierung der unabhängigen Variable für uns, wenn wir die Variable als factor deklarieren. Per Voreinstellung wird auch in diesem Fall die Dummykodierung genutzt. Wie genau die hier aussieht, können wir uns wieder mit contrasts ansehen:
contrasts(punish$age)
## 31-40 41-50 over 50
## 21-30 0 0 0
## 31-40 1 0 0
## 41-50 0 1 0
## over 50 0 0 1
Unsere vier Kategorien (Zeilen) werden also in drei Prädiktoren (Spalten) umgewandelt. Diese Tabelle sagt uns also, dass Personen die z.B. zwischen 41 und 50 Jahre alt sind (dritte Zeile) auf der ersten Dummyvariable (erste Spalte) eine 0 erhalten, auf der zweiten Dummyvariable eine 1 und auf der dritten Dummyvariablen eine 0. Generell ist das System der Dummykodierung immer so angelegt, dass wir $k-1$ Prädiktoren erhalten, die den Unterschied eine spezifischen Gruppen gegenüber der Referenzkategorie darstellen. Als Referenzkategorie gilt immer die Kategorie, deren Mitglieder auf allen Prädiktoren den Werte 0 haben, weil das genau die Personen sind, für die das Intercept vorhergesagt wird und gegen deren Ausprägung die anderen Gruppen kontrastiert werden. Wieder etwas formeliger ausgedrückt: $$ \hat{y}_m = b_0 + b_1 \cdot x_{1m} + b_2 \cdot x_{2m} + b_3 \cdot x_{3m} $$ Dabei wird - wie oben dargelegt - $x_{2m} = 1$ immer dann, wenn die Person $m$ zwischen 41 und 50 Jahre alt ist: \begin{equation} \begin{split} &\hat{y}_m = b_0 + b_1 \cdot 0 + b_2 \cdot 1 + b_3 \cdot 0 \\ &\hat{y}_m = b_0 + b_2 \end{split} \end{equation}
Wie wir in der 1. Sitzung des 1. Semesters gesehen hatten, ist eine zentrale Eigenschaft des Nominalskalenniveaus, dass Personen einer und nur einer Kategorie zugeordnet werden können. Das heißt für jede Person kann immer höchstens eine dieser drei Variablen den Wert 1 annehmen.
Die Ergebnisse unserer Regression sagen uns jetzt also, dass Personen zwischen 31 und 40 (sogenannte “Millenials”) bedeutend mehr Bestrafung erwarten als die Referenzkategorie (21 bis 30 - “Zoomer”). Wir können uns die Mittelwerte wieder nach dem gleichen Verfahren angucken, wie vorhin:
tab <- data.frame(age = levels(punish$age))
tab$mod4 <- predict(mod4, tab)
tab
## age mod4
## 1 21-30 4.128571
## 2 31-40 5.265000
## 3 41-50 4.684848
## 4 over 50 4.105263
Kombination nominal- und intervallskalierter Prädiktoren
Der Kombination von unabhängigen Variablen mit Nominal- und Intervallskalenniveau kommt in der Psychologie eine so große Bedeutung zu, dass wir diese z.B. im Rahmen der Methodenlehre im Master für klinische Psychologie und Psychotherapie noch einmal sehr detailliert behandeln werden. Diese Kombination ist deswegen so wichtig, weil wir in der Psychologie besonders Gruppenunterschiede untersuchen und dabei z.B. Interventions- vs. Kontrollgruppe als nominalskalierten Prädiktor nutzen. Gleichzeitig ist es aber auch wichtig, Interventionseffekte entweder um den Einfluss bestimmter psychologischer Eigenschaften zu bereinigen oder explizit den Effekt zu untersuchen, den Interventionen auf den Zusammenhang zwischen Variablen haben.
Für unseren Fall hatten wir schon gesehen, dass es Unterschiede zwischen den USA und China in der Einschätzung darüber gibt, welche Art von Bestechung mehr oder weniger stark bestraft werden wird. Damit das Modell übersichtlich bleibt, nutzen wir hier erst einmal nur die Daten aus den USA weiter, aber das volle Modell findet sich in Appendix A.
usa <- subset(punish, country == 'U.S')
Für die Bestrafung sollte idealerweise die Schwere des Vergehens eine Bedeutung haben. Im Datensatz gibt es z.B. die Variable gains, die beschreibt, in welchem Ausmaß die Person oder Gruppe Vorzüge durch die Bestechung erhält. Eine einfache Regression zeigt dabei Folgendes:
mod5 <- lm(severe ~ gains, usa)
summary(mod5)
##
## Call:
## lm(formula = severe ~ gains, data = usa)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.6008 -1.9318 0.2474 1.5992 5.3905
##
## Coefficients:
## Estimate Std. Error t value
## (Intercept) 4.4212 0.6766 6.534
## gains 0.0219 0.1138 0.192
## Pr(>|t|)
## (Intercept) 3.74e-09 ***
## gains 0.848
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.224 on 90 degrees of freedom
## Multiple R-squared: 0.0004112, Adjusted R-squared: -0.0107
## F-statistic: 0.03702 on 1 and 90 DF, p-value: 0.8479
Interessanterweise scheint es also keinen Einfluss auf das erwartete Ausmaß an Bestrafung zu haben, wie groß der Gewinn durch die Bestechung eingeschätzt wird. In diese Regression können wir zusätzlich die Art der Bestechung aufnehmen, von der wir ja bereits gesehen hatten, dass sie einen großen Einfluss auf das eingeschätzte Ausmaß der Bestrafung hat.
mod6 <- lm(severe ~ gains + bribe, usa)
summary(mod6)
##
## Call:
## lm(formula = severe ~ gains + bribe, data = usa)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.2272 -1.5163 0.0983 1.5606 4.9696
##
## Coefficients:
## Estimate Std. Error t value
## (Intercept) 4.19277 0.66516 6.303
## gains -0.03392 0.11311 -0.300
## bribeindividual 1.12940 0.46126 2.449
## Pr(>|t|)
## (Intercept) 1.09e-08 ***
## gains 0.7650
## bribeindividual 0.0163 *
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.165 on 89 degrees of freedom
## Multiple R-squared: 0.0635, Adjusted R-squared: 0.04245
## F-statistic: 3.017 on 2 and 89 DF, p-value: 0.05397
Das aufgestellte Modell ist eine sogenannte Kovarianzanalyse (oder ANCOVA, für Analysis of Covariance). Hier wird - analog zum mod2 - angenommen, dass der Zusammenhang zwischen gains und severe über die beiden Bestechungstypen gleich ist:
# Scatterplot erstellen
scatter <- ggplot(usa, aes(x = gains, y = severe, color = bribe)) +
geom_point()
# Regressionsgerade aus mod6 hinzufügen
scatter +
# Kollektive Bestechung
geom_abline(intercept = coef(mod6)[1], slope = coef(mod6)[2],
color = '#00618F') +
# Individuelle Bestechung
geom_abline(intercept = coef(mod6)[1] + coef(mod6)[3], slope = coef(mod6)[2],
color = '#ad3b76')
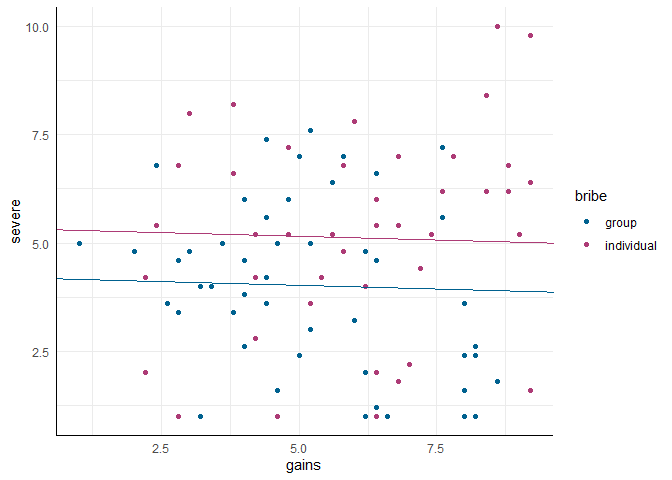
Um zu prüfen, ob der Zusammenhang zwischen dem Ausmaß erwarteter Bestrafung und dem Bestechungsgewinn wirklich über beide Arten der Bestechung hinweg gleich ist, können wir - für alle, die meine bisherigen Ausführungen gelesen haben wenig überraschend - einen Interaktionsterm in das Modell aufnehmen. Damit wird aus der ANCOVA eine generalisierte ANCOVA. In diesem Fall können wir gains zentrieren, aber im Gegensatz zum Fall mit der Interaktion zwischen zwei intervallskalierten Prädiktoren ist dies hier nicht zwingend erforderlich.
mod7 <- lm(severe ~ gains + bribe + gains:bribe, usa)
summary(mod7)
##
## Call:
## lm(formula = severe ~ gains + bribe + gains:bribe, data = usa)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.2442 -1.2632 -0.0587 1.3676 4.2925
##
## Coefficients:
## Estimate Std. Error
## (Intercept) 5.6659 0.8784
## gains -0.3177 0.1588
## bribeindividual -1.9180 1.3089
## gains:bribeindividual 0.5455 0.2201
## t value Pr(>|t|)
## (Intercept) 6.450 5.86e-09 ***
## gains -2.001 0.0485 *
## bribeindividual -1.465 0.1464
## gains:bribeindividual 2.478 0.0151 *
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.105 on 88 degrees of freedom
## Multiple R-squared: 0.1246, Adjusted R-squared: 0.09475
## F-statistic: 4.175 on 3 and 88 DF, p-value: 0.008194
Wieder macht es Sinn, sich die Regressionsgleichung anzusehen, um besser zu verstehen, was hier passiert:
$$
\hat{y}_m = b_0 + b_1 \cdot x_{1m} + b_2 \cdot x_{2m} + b_3 \cdot (x_{1m} \cdot x_{2m})
$$
$x_{1m}$ ist jetzt unsere intervallskalierter Prädiktor (gains) und $x_{2m}$ unser dummykodierter Indikator für bribe. Diese Variable nimmt wieder dann den Wert 0 an, wenn die Person eine Gruppenbestechung gesehen hat. Also ergibt sich dann für die Regressionsgleichung:
\begin{equation} \begin{split} &\hat{y}_m = b_0 + b_1 \cdot x_{1m} + b_2 \cdot 0 + b_3 \cdot (x_{1m} \cdot 0) \\ &\hat{y}_m = b_0 + b_1 \cdot x_{1m} \end{split} \end{equation} $b_0$ ist also das Intercept für Personen, die eine Gruppenbestechung gesehen haben - der Wert den wir für Personen vorhersagen, die in dieser Gruppe sind und den Gewinn durch die Bestechung mit 0 einschätzen. Das Regressionsgewicht ist dementsprechend der Unterschied zwischen zwei Personen, die beide die kollektive Bestechung gesehen haben und sich um eine Einheit in der Gewinneinschätzung unterscheiden. Ich weise an dieser Stelle noch einmal darauf hin, dass sich die Interpretation durch Interaktionsterme gegenüber “normalen” Regressionen ändert: es ist nun nicht erforderlich, dass zwei Personen die selbe Ausprägung haben, sondern der Steigungskoeffizient gilt nur für Leute, die eine bestimmte Ausprägung haben (in diesem Fall, dass sie aus der Gruppe “kollektive Bestechung” kommen).
Für Personen aus der Gruppe, die individuelle Bestechung gesehen haben ergibt sich hingegen folgende Regressionsgleichung:
\begin{equation} \begin{split} &\hat{y}_m = b_0 + b_1 \cdot x_{1m} + b_2 \cdot 1 + b_3 \cdot (x_{1m} \cdot 1) \\ &\hat{y}_m = (b_0 + b_2) + (b_1 + b_3) \cdot x_{1m} \end{split} \end{equation}$b_2$ ist also der Unterschied zwischen den Intercepts, also der Unterschied zwischen zwei Personen, die beide den Wert 0 bei der Gewinneinschätzung angeben, aber unterschiedliche Formen der Bestechung (Gruppe vs. individuell) gesehen haben. $b_3$ ist der Unterschied in den Regressionsgewichten der intervallskalierten Variable zwischen den beiden Gruppen, also das Ausmaß an Unterschied im Zusammenhang zwischen $x_1$ und unserer AV, der durch die gesehene Art von Bestechung erklärt wird. Wir erhalten nun also zwei voneinander unterschiedliche Regressionsgerade - für jede der beiden Gruppen eine. Wir sehen, dass die Regressionsgleichung quasi identisch ist zu der einer moderierten Regression, mit dem einzigen Unterschied, dass $x_{2}$ ein nominaler Prädiktor ist:
$$ \hat{y}_m = (b_0 + b_2x_{2m}) + (b_1 + b_3x_{2m}) \cdot x_{1m} $$Für die grafische Darstellung können wir die Regressionsgewichte genauso in geom_abline einsetzen, wie wir es gerade in der Gleichung gemacht haben:
scatter +
# Kollektive Bestechung
geom_abline(intercept = coef(mod7)[1], slope = coef(mod7)[2],
color = '#00618f') +
# Individuelle Bestechung
geom_abline(intercept = coef(mod7)[1] + coef(mod7)[3], slope = coef(mod7)[2] + coef(mod7)[4],
color = '#ad3b76')
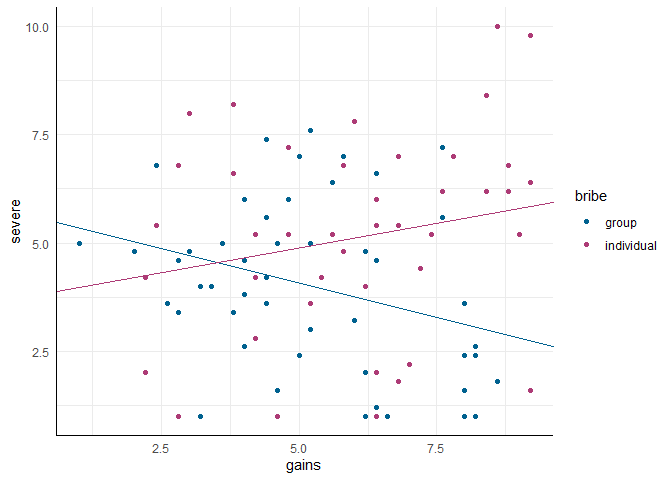
Im Beitrag zu Interaktionen zwischen intervallskalierten Variablen hatten wir Simple Slopes - also bestimmte einzelne Regressionsgeraden - kennengelernt, die wir mit dem Paket interactions grafisch veranschaulichen konnten und mit Hilfe welcher wir die Effekte in der moderierter Regression genauer inspizieren können. Wie so oft gibt es in R Pakete, die sehr ähnliches tun. So enthält das Paket reghelper auch Funktionen, mit welcher wir Simple Slopes betrachten können. Die summary unseres Modell hat uns zwar gezeigt, dass der negative Zusammenhang bei Gruppenbestechung bedeutsam ist (die Testung von $b_1$) und dass der Unterschied im Regressionsgewicht zwischen den beiden Gruppen bedeutsam ist (die Testung von $b_3$), aber nicht ob der positive Zusammenhang für individuelle Bestechung positiv ist. Dafür können wir uns die Simple Slopes näher angucken:
library(reghelper)
## Warning: Paket 'reghelper' wurde unter R
## Version 4.3.2 erstellt
simple_slopes(mod7)
## gains bribe Test Estimate
## 1 3.536522 sstest 0.0113
## 2 5.584783 sstest 1.1287
## 3 7.633043 sstest 2.2461
## 4 sstest group -0.3177
## 5 sstest individual 0.2279
## Std. Error t value df Pr(>|t|) Sig.
## 1 0.6362 0.0178 88 0.985874
## 2 0.4485 2.5167 88 0.013660 *
## 3 0.6357 3.5330 88 0.000657 ***
## 4 0.1588 -2.0010 88 0.048475 *
## 5 0.1525 1.4943 88 0.138685
Die ersten drei Zeilen zeigen uns Gruppenunterschiede zwischen individueller und kollektiver Bestechung bei verschiedenen Ausprägungen von gains - per Voreinstellung eine Standardabweichung unter dem Mittelwert, dem Mittelwert und eine Standardabweichung darüber. Die letzten beiden Zeilen zeigen uns die gruppenspezifischen Regressionsgewichte. Für bribe = 'group' entspricht dies genau der Testung, die wir schon in der normalen summary gesehen haben. Nun erhalten wir auch das Gegenstück und sehen, dass der positive Effekt in der Gruppe, die individuelle Bestechung gesehen hat, nicht statistisch bedeutsam von 0 abweicht.
Erkenntnisse wie diese sind für die Überprüfung von Interventionsmaßnahmen von zentraler Bedeutung, daher werden wir sie in den Sitzungen für den Master klinische Psychologie und Psychotherapie wiedersehen.
Appendix A
Vollständiges Modell zur Kombination von `country`, `bribe` und `gains`
Um vollständig untersuchen zu können, wie die Effekte des Landes, der Bestechungsart und des Ausmaß an erwartetem Profit mit einander interagieren, können wir ein Modell aufstellen, welches alle drei Variablen gleichzeitig als Prädiktoren enthält. Das additive Modell ist zunächst relativ simpel:
mod8 <- lm(severe ~ country + bribe + gains, punish)
summary(mod8)
##
## Call:
## lm(formula = severe ~ country + bribe + gains, data = punish)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.883 -1.878 -0.125 1.577 5.406
##
## Coefficients:
## Estimate Std. Error t value
## (Intercept) 4.54433 0.59165 7.681
## countryChina 0.47596 0.38691 1.230
## bribeindividual 0.19243 0.35402 0.544
## gains -0.01663 0.09786 -0.170
## Pr(>|t|)
## (Intercept) 1.19e-12 ***
## countryChina 0.220
## bribeindividual 0.587
## gains 0.865
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.292 on 170 degrees of freedom
## Multiple R-squared: 0.01133, Adjusted R-squared: -0.006118
## F-statistic: 0.6493 on 3 and 170 DF, p-value: 0.5844
Dieses Modell impliziert wieder, dass die Effekte der einzelnen Variablen über die Ausprägungen der anderen Variablen hinweg gleich sind (also z.B. dass der Zusammenhang zwischen Profit und Ausmaß der Bestrafung in China und den USA der Gleiche ist). Wie wir bereits in den anderen Abschnitten gesehen hatten, ist diese Annahme nicht haltbar, aber als Ausgangspunkt für die Interpretation ist es dennoch nützlich, sich das einfache Modell vor Augen zu führen:
$$
\hat{y}_{m} = b_0 + b_1 \cdot x_{1m} + b_2 \cdot x_{2m} + b_3 \cdot x_{3m}
$$
Hier sind $x_{1m}$ und $x_{2m}$ unsere dummykodierten Indikatoren für country und bribe und $x_{3m}$ ist die intervallskalierte Variable gains. Wieder macht es Sinn, die behaupteten Effekte in einer Abbildung zu inspizieren.
scatter <- ggplot(punish, aes(x = gains, y = severe, color = country:bribe)) +
geom_point()
Mit country:bribe wird - wie wir es schon in den Regressionen gesehen haben - die Kreuzung von zwei Variablen erstellt. In unserem Fall erhalten wir im Scatterplot also vier Gruppen, die zur Färbung der Punkte genutzt werden. Weil wir wieder vier Linien anlegen müssen und diese nicht komplett händisch eintragen und idealerweise in der entsprechenden Farbe halten wollen, legen wir einen data.frame an, in dem wir die Intercepts und Slopes für abline hinterlegen:
tmp <- coef(mod8)
tab <- data.frame(country = as.factor(c('U.S', 'U.S', 'China', 'China')),
bribe = as.factor(c('group', 'individual', 'group', 'individual')),
intercept = NA,
slope = NA)
tab$intercept <- c(tmp[1], sum(tmp[c(1, 3)]), sum(tmp[1:2]), sum(tmp[1:3]))
tab$slope <- tmp[4]
Intercepts und Slopes ergeben sich nach dem gleichen Prinzip, das wir in den vorherigen Abschnitten für die kleineren Modelle gesehen hatten.
scatter +
geom_abline(data = tab, aes(intercept = intercept, slope = slope,
color = country:bribe))
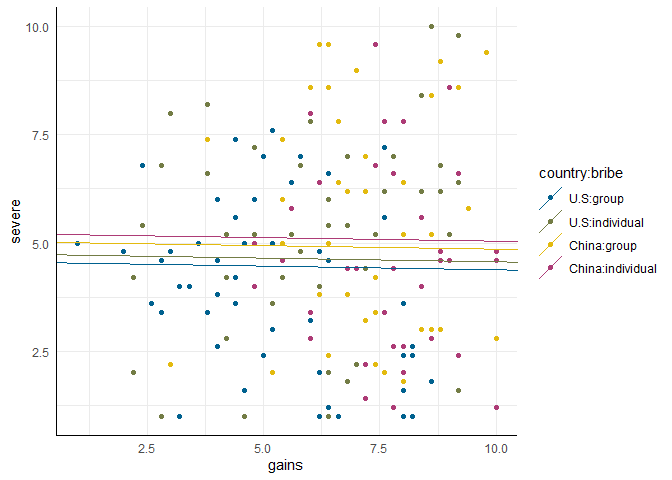
# Modell
mod9 <- lm(severe ~ country + bribe + gains + country:bribe, punish)
# Plot vorbereitung
tmp <- coef(mod9)
tab$intercept <- c(tmp[1], sum(tmp[c(1, 3)]), sum(tmp[1:2]), sum(tmp[c(1:3, 5)]))
tab$slope <- tmp[4]
# Plot
scatter +
geom_abline(data = tab, aes(intercept = intercept, slope = slope,
color = country:bribe))
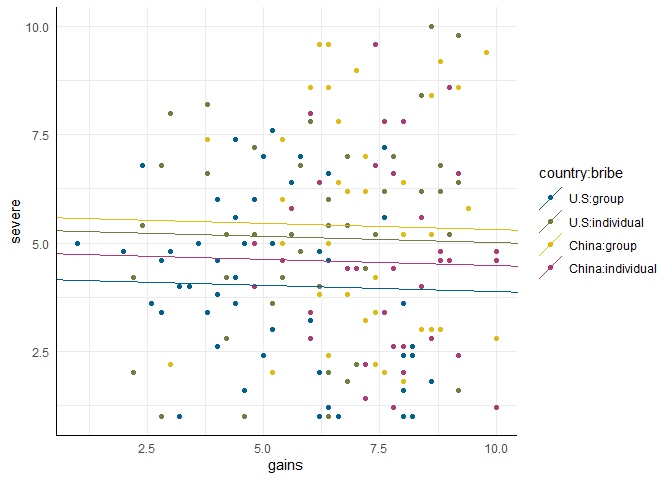
gains und severe in allen Bedingungen der Gleiche ist. Es handelt sich also auch hier um eine klassische ANCOVA.
Es ist möglich, für jeden der dummykodierten Prädiktoren einzeln den Interaktionseffekt mit der intervallskalierten Variable in das Modell aufzunehmen. Hier die Schritte im Schnelldurchlauf mit anschließender Modellauswahl über das Informationskriterium $AIC$:
# Schrittweise Modelle mit Interaktionen
mod10 <- lm(severe ~ country + bribe + gains + country:bribe + country:gains, punish)
mod11 <- lm(severe ~ country + bribe + gains + country:bribe + bribe:gains, punish)
mod12 <- lm(severe ~ country + bribe + gains + country:bribe + country:gains + bribe:gains, punish)
mod13 <- lm(severe ~ country + bribe + gains + country:bribe + country:gains + bribe:gains + country:bribe:gains, punish)
# AIC Tabelle
aics <- rbind(extractAIC(mod8),
extractAIC(mod9),
extractAIC(mod10),
extractAIC(mod11),
extractAIC(mod12),
extractAIC(mod13)) |> data.frame()
names(aics) <- c('df', 'AIC')
aics$model <- 8:13
aics
## df AIC model
## 1 4 292.5670 8
## 2 5 286.2715 9
## 3 6 288.2659 10
## 4 6 286.3236 11
## 5 7 288.2826 12
## 6 8 285.7176 13
Wie wir sehen, bevorzugt der AIC das Modell 13 - ein Modell mit beiden paarweisen Interaktionen und der dreifach Interaktion. Diese Interaktion gibt in dieser Konstellation an, dass das Regressionsgewicht wieder für jede der vier Gruppen individuell sein darf. Es folgt dem gleichen Prinzip, wie wir es schon für die Interaktionen der nominalskalierten Variablen in der Vorhersage des Schweregrads gesehen hatten. Nur dass sich der Effekt diesmal nicht auf Mittelwerte, sondern auf Regressionsgewichte bezieht. In der Abbildung:
# Plot vorbereitung
tmp <- coef(mod13)
tab$intercept <- c(tmp[1], sum(tmp[c(1, 3)]), sum(tmp[1:2]), sum(tmp[c(1:3, 5)]))
tab$slope <- c(tmp[4], sum(tmp[c(4, 7)]), sum(tmp[c(4, 6)]), sum(tmp[c(4, 6:8)]))
# Plot
scatter +
geom_abline(data = tab, aes(intercept = intercept, slope = slope,
color = country:bribe))
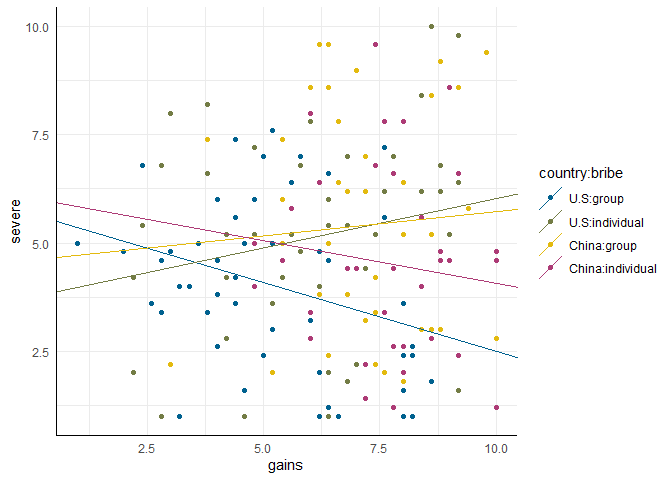
gains und severe bestehen: in den USA geht mit größerem Gewinn bei Gruppenbestechung (rote Linie) eine geringere Erwartung der Schwere der Bestrafung einher; in China hingegen eine höhere (türkise Linie). Wir können wieder über simple_slopes die gruppenspezifischen Regressionsgewichte prüfen:
simple_slopes(mod13, levels = list(gains = 'sstest'))
## country bribe gains Test Estimate
## 1 U.S group sstest -0.3177
## 2 China group sstest 0.1126
## 3 U.S individual sstest 0.2279
## 4 China individual sstest -0.1968
## Std. Error t value df Pr(>|t|) Sig.
## 1 0.1676 -1.8950 166 0.05983 .
## 2 0.2177 0.5172 166 0.60573
## 3 0.1610 1.4151 166 0.15890
## 4 0.2534 -0.7767 166 0.43844
Wir sehen also, dass trotz der großen optischen Unterschiede in den Regressionsgewichten, keins der gruppenspezifischen Regressionsgewichte statistisch bedeutsam von 0 abweicht.
Literatur
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden (5. Auflage, 1. Auflage: 2010). Weinheim: Beltz.
Liu, H.-Z., Wang, X.-Z., Sun, X. and Wei, Z.-H. (2022). Group punishment does not always discount: Cultural difference in punishment of individuals and groups. Asian Journal of Social Psychology.
](/media/header/transaction_50_euros.jpg)