Gemischte Modelle
Gemischte Lineare Modelle für den Längsschnitt
Inhaltsverzeichnis
Einleitung
Daten in der klinisch-psychologischen Forschung haben häufig eine sogenannte hierarchische Struktur oder Mehrebenen-Struktur, in der Beobachtungen auf einer ersten Ebene in Beobachtungseinheiten auf einer übergeordneten Ebene gruppiert sind. Typische Strukturen sind Individuen in Gruppen (z. B. Patient*innen in Therapiepraxen oder in Kliniken) oder Messzeitpunkte in Personen (z. B. Befragungszeitpunkte im Verlauf einer Therapiestudie).
Ziel der Analyse ist es in solchen Fällen zum Einen die Verzerrung der Inferenzstatistik, die aus diesen Abhängigkeiten in den Daten resultieren kann, zu korrigieren, zum Anderen aber auch die unterschiedlichen Ebene explizit zu berücksichtigen, um so Effekte besser lokalisieren zu können. Wie immer, versuchen wir uns das Ganze an einem relativ aktuellen Artikel aus der klinischen Forschung zu veranschaulichen.
Studie zur Interpersonellen Emotionsregulation
In den letzten Jahren haben Experience Sampling Methoden (ESM) in der klinischen Forschung immer mehr an Relevanz gewonnen. Dabei ist das Ziel durch sehr häufige, kleine Befragungen oder Erhebungen, Personen in alltäglichen Situationen zu erfassen, um so die ökologische Validität der Schlüsse zu maximieren. Darüber hinaus können so relevante, detaillierte Informationen über Veränderungen (auch innerhalb eines Tages) gewonnen werden.
Auch bei der Studie, die wir hier betrachten, handelt es sich um eine solche ESM Studie. Liu et al. (2024) haben in ihrer Studie die Prozesse der interpersonellen Emotionsregulation (IER) untersucht und dabei besonderen Fokus darauf gelegt, inwiefern diese durch eine Major Depression (MD) gestört sind. Interpersonelle Emotionsregulation beschreiben sie dabei relativ direkt als “goal-directed process of regulating emotion through social interactions” (Liu et al. (2024, S. 62)). Für den Erfolg dieses Vorhabens sind dabei zwei wesentliche Komponenten relevant: intrinsische Zielsetzungen - was möchte die Person erreichen, die hier versucht ihre Emotionen zu regulieren? - und extrinsische Strategien - welche Verhaltensweisen legt die andere Person an den Tag?
Um eine möglichst unverzerrte, direkte und spontane Einschätzung solcher sozialer Verhaltensweisen zu erhalten, haben sich Liu et al. (2024) eines ESM Ansatzes bedient und insgesamt 215 Personen über 14 Tage hinweg fünf mal am Tag befragt, ob eine solche Situation aufgetreten ist, welche Ziele sie dabei verfolgt haben und welche Strategien der bzw. die Gegenüber an den Tag gelegt haben.
Den Kern der Studie machen drei wesentliche Forschungsfragen aus:
- Geht MD mit seltenerer IER einher?
- Geht MD mit spezifischen Strategien des Gegenüber einher?
- Wird die Beziehung von Strategien und Outcomes durch MD moderiert?
Wie zu sehen ist, befassen sich alle drei Forschungsfragen mit Konzepten auf unterschiedlichen Ebenen. MD ist eine (für die Zwecke dieser ESM-Untersuchung) “stabile” Personeneigenschaft. Die genutzten Strategien des Gegenübers und der erlebte Erfolg von IER sind hingegen sehr variabel - beziehen sich also in der Regel nur auf eine spezifische Situation.
Überblick über die Daten
Wie auch schon in den letzten Beiträgen, wurden die Rohdaten zur Studie über das OSF bereitgestellt. Sie können direkt eine aufbereitete Fassung der Daten laden, indem Sie das Skript ausführen, dass ich dafür vorbereitet habe:
source('https://pandar.netlify.app/daten/Data_Processing_esm.R')
Die Daten liegen im long-format vor - jede Zeile stellt also eine Beobachtung dar, nicht eine Person. Über die Grundkonzepte von long und wide Formaten haben wir im Beitrag zur ANOVA mit Messwiederholung schon einmal geschrieben - dort können Sie auch herausfinden, wie man in R zwischen den beiden Formaten hin und her transponieren kann. Eine Übersicht über die Variablen finden Sie wieder hier:
Übersicht über die Variablen
| Variable | Beschreibung | Ausprägungen |
|---|---|---|
id | Eindeutige ID der Person | Code |
daynumber | Tag der Erhebung | 1 - 14 |
index1 | Fortlaufender Index des Messzeitpunkts | 1 - 70 |
group | Erhebungsgruppe | current in MDE, healthy control, remitted MDD |
occurance | IER seit der letzten Erhebung? | no, yes |
close | Bezug zum Gegenüber | close (Familie, Partner*in, Freunde), non-close (Kolleg*innen, Fremde, Bekannte) |
goal | Ziel der IER | advice only, both, empathy only |
reappraisal | Reappraisal-Strategie des/der Gegenübers | 0 = nein, 1 = ja |
solving | Lösungsvorschläge des/der Gegenübers | 0 = nein, 1 = ja |
invalidation | Invalidierung des Problems durch den/die Gegenüber | 0 = nein, 1 = ja |
blaming | Schuldzuweisung durch den/die Gegenüber | 0 = nein, 1 = ja |
sharing | Bekräftigung der Hilfesuche durch den/die Gegenüber | 0 = nein, 1 = ja |
affection | Demonstration der Zuneigung durch den/die Gegenüber | 0 = nein, 1 = ja |
other | Andere Strategien des/der Gegenübers | 0 = nein, 1 = ja |
warmth | Wie Einfühlsam wird Gegenüber erlebt | -5 bis 5 |
problem | Hat IER zu Lösung des Problems beigetragen | -5 bis 5 |
interpersonal | Hat IER zu Verbesserung der emotionalen Zustands beigetragen | -5 bis 5 |
gender | Geschlecht | female, male |
age | Alter in Jahren | Zahl |
race | Ethnie | character Vektor |
education | Bildungsabschluss | character Vektor |
relationshipstatus | Derzeitiger Familienstand | character Vektor |
Für diesen Beitrag wird der Fokus auf dem Outcome problem liegen, bei dem die befragten Personen angeben sollten, inwiefern sich ihre Einschätzung des ursprünglichen Problems durch die Interaktion verändert hat (von -5 “much worse” bis 5 “much better”). Im Artikel von Liu et al. (2024) werden die Analysen, die wir hier durchführen, auch für interpersonal, also die Veränderung der Beziehung zum Gegenüber durch die Interaktion, berichtet.
Nullmodell
Im ersten Schritt können wir zunächst versuchen das Outcome in stabile und situative Komponenten zu unterteilen. Die Idee, die diesem Schritt zugrunde liegt ist, dass es Eigenschaften der spezifichen Interaktion geben wird, die beeinflussen, ob eine Person sich bezüglich des ursprünglich berichteten Problems besser fühlt oder nicht. Gleichzeitig sind Personen aber auch in Ihrer “Grundtendenz” unterschiedlich, aus der IER für sich positive Outcomes herausziehen zu können. Genau genommen zielen die Kernfragen dieser Studie auf genau diese Unterschiede ab, weil die Behauptung untersucht wird, dass sich Personen in diesen Tendenzen aufgrund ihrer MD von gesunden Personen unterscheiden.
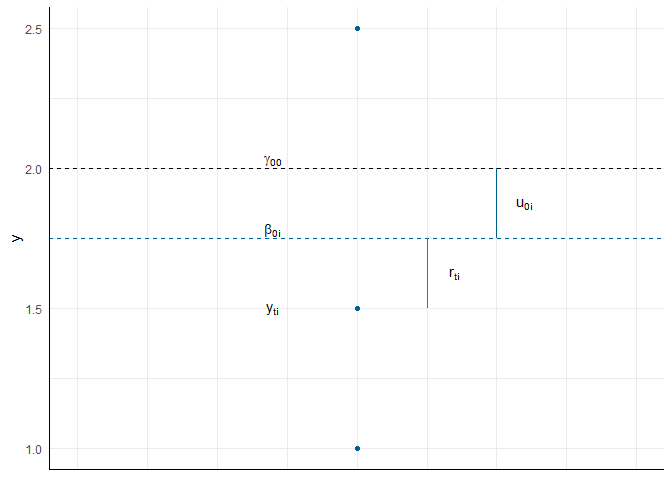
Um das Outcome $y_{ti}$ (hier problem) so zu unterteilen nutzen wir das Nullmodell. Beachtenswert ist, dass diese Variable zwei Indizes hat: $t$ (für time) kennzeichnet den Zeitpunkt der Erhebung und $i$ (für individual) die Person, die erhoben wurde. Die Kombination aus beiden Indizes teilt uns mit, in welcher Zeile im Datensatz wir diesen Wert nachschlagen können, wobei die Variable index1 unser $t$ und die Variable id unser $i$ ist. Dabei ergibt sich also schon anhand der Daten die Zweiteilung der Effekte: stabile Eigenschaften der einzelnen Personen ($\beta_{0i}$) und situative Eigenschaften der einzelnen Messung dieser Person ($r_{ti}$). Dieser Unterteilung passiert innerhalb der Messungen einer Person, also auf dem 1. Level:
$$ \text{Level 1:} \qquad y_{ti} = \beta_{0i} + r_{ti} $$ Die Eigenschaften der Person können dann noch weiter zerlegt werden, in den mittleren Effekt von IER über alle Personen und Situationen hinweg ($\gamma_{00}$) und die Abweichung einer Person von diesem globalen Effekt ($u_{0i}$). Diese Zerlegung passiert zwischen den Personen, also auf dem 2. Level:
$$ \text{Level 2:} \qquad \beta_{0i} = \gamma_{00} + u_{0i} $$ Wenn wir die zweite Gleichung in die erste einsetzen, erhalten wir die gesamte Zerlegung des Effektes:
$$ \text{Gesamt:} \qquad y_{ti} = \gamma_{00} + u_{0i} + r_{ti} $$ Da $\gamma_{00}$ den Erwartungswert aller Beobachtungen darstellt, sind $u_{0i}$ und $r_{ti}$ als Residuen zu verstehen. Sie sollten also die üblichen Eigenschaften haben, die wir in unserer bisherigen Modellierung auch immer von Residuen erwartet haben: sie sollten unabhängig, heteroskedastisch und normalverteilt sein und dabei einen Mittelwert von 0 haben.
Die Erklärung nochmal als Bild
Im folgenden Bild habe ich den Versuch unternommen, diese einzelnen Komponenten noch einmal alle zu verdeutlichen:
Umsetzung in R
In R gibt es eine ganze Reihe an Paketen, mit denen gemischte Modelle und (beinahe) jede Abwandlungsform davon umgesetzt werden können. Am weitesten hat sich das Paket lme4 verbreitet, das sowohl Modelle für kontinuierliche Variablen, als auch diverse Formen der generalisierten gemischten Modelle erlaubt. Für Fälle, in denen wir mit kontinuierlichen Variablen und der Annahme normalverteilter Residuen arbeiten bietet lme4 per Voreinstellung allerdings keine $p$-Werte an - zum Glück können wir diese Lücke aber mit lmerTest schließen. Daher benötigen wir zunächst die beiden Pakete:
# Pakete installieren
install.packages("lme4")
install.packages("lmerTest")
# Pakete laden
library(lme4)
library(lmerTest)
Die Grundfunktion von lme4 ist lmer() und folgt den gleichen Grundprinzipien wie die lm-Funktion zur Schätzung von Regressionen. Wir müssen lediglich zusätzlich deutlich machen, anhand welcher Variable die Beobachtungen in unserem Datensatz gruppiert sind. In unserem Fall ist das die id-Variable, die kenntlich macht, dass mehrere Messungen zur gleichen Person gehören.
# Nullmodell in lme4
mod0 <- lmer(problem ~ 1 + (1 | id), data = esm)
Die Modellgleichung enthält auf der linken Seite, wie immer, unsere AV (hier das Ausmaß, in dem die Einstellung zum Problem als verändert wahrgenommen wird). Hinter der ~ kommen die unabhängigen Variablen, im Nullmodell also keine, hier deklariert die 1 lediglich das Intercept. Der Ausdruck (1 | id) gibt an, dass dieses Intercept sich dann wiederum über Personen hinweg unterscheiden darf. Gucken wir uns die Ergebnisse mal an:
# Modellzusammenfassung
summary(mod0)
## Linear mixed model fit by REML. t-tests use Satterthwaite's method ['lmerModLmerTest']
## Formula: problem ~ 1 + (1 | id)
## Data: esm
##
## REML criterion at convergence: 6973.3
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.9378 -0.5351 0.0128 0.6392 3.0516
##
## Random effects:
## Groups Name Variance Std.Dev.
## id (Intercept) 0.938 0.9685
## Residual 3.709 1.9259
## Number of obs: 1632, groups: id, 198
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) 1.42603 0.08913 178.14457 16 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Gegenüber der Zusammenfassung eines Regressionsergebnisses ist vor allem der Abschnitt Random effects neu. Hier wird die Unterschiedlichkeit der Personen im Intercept (Zeile id - (Intercept)) und die Unterschiedlichkeit der Beobachtungen innerhalb der Personen (Zeile Residual) dargestellt angegeben. Dass wir für Letztere nur eine Zahl erhalten macht eine weitere Annahme deutlich: das Ausmaß an Unterschiedlichkeit der situativen Komponenten wird alle Personen hinweg als gleich angenommen. Weil diese beiden Komponenten - wie oben erwähnt - Residuen in Bezug auf die fixed effects (hier $\gamma_{00}$) sind, sind deren Mittelwerte 0 und werden hier nirgendwo angegeben. Darüber hinaus wird angenommen, dass die Effekte normalverteilt sind, sodass die Varianz bzw. Standardabweichung ausreicht, um die Verteilung der Effekte zu beschreiben.
Zusätzlich finden wir im Abschnitt Fixed effects die Schätzung des globalen Effektes $\gamma_{00}$, der hier als (Intercept) bezeichnet wird. Die Ergebnisse dieses Modells werden auch von Liu et al. (2024, S. 67) berichtet:
According to estimates of unconditional (i.e., intercept-only) models, on average, participants […] reported somewhat improved problem outcome, $b = 1.43$, $SE = 0.09$, $p < .001$
Die Ergebnisse können wir soweit schon einmal reproduzieren.
Intraklassenkorrelationskoeffizient (ICC)
Im letzten Abschnitt haben wir die beiden random effects, das random intercept $u_{0i}$ und das Residuum $r_{ti}$ Anhand ihrer Varianz bzw. Standardabweichung beschrieben, dabei stellt $\mathbb{V}ar(u_{0i})$ die Unterschiede zwischen Personen $\mathbb{V}ar(r_{ti})$ und Unterschiede zwischen Situationen dar. Weil Varianzen meist schwierig zu interpretieren sind, können wir die beiden Komponenten in Anteile übersetzen und der Anteil der Varianz, der auf Unterschiede zwischen Personen (oder im Allgemeinen auf die Cluster) zurückzuführen ist, wird als Intraklassenkorrelationskoeffizient bezeichnet:
$$ ICC = \frac{\mathbb{V}ar(u_{0i})}{\mathbb{V}ar(u_{0i}) + \mathbb{V}ar(r_{ti})} $$
Wir könnten diesen zwar aus den Ergebnissen des Modells händisch berechnen, aber zum Glück liefert uns hier die icc-Funktion des performance-Pakets eine kürzere Fassung, das ganze zu bestimmen:
# Paket laden
library(performance)
## Warning: Paket 'performance' wurde unter R Version 4.3.2 erstellt
# ICC berechnen
icc(mod0)
## # Intraclass Correlation Coefficient
##
## Adjusted ICC: 0.202
## Unadjusted ICC: 0.202
Ungefähr 20% der Unterschiede zwischen allen Beobachtungen, die wir hinsichtlich der Einschätzung der Veränderung der Probleminterpretation gemacht haben gehen also auf stabile Eigenschaften der Personen zurück. Die restlichen 80% sind situative Komponenten, die z.B. durch Eigenschaften oder Verhalten des Interaktionspartners, das eigentliche Problem oder auch die aktuelle Stimmung beeinflusst werden könnten.
Random Intercept Modell
Das Nullmodell hat uns zwar eine Einschätzung dazu gegeben, in welchem Ausmaß wir unterschiede in der Problemeinschätung auf die situativen bzw. individuellen Komponenten attribuieren können, aber es hat noch keinen Versuch der Erklärung oder Vorhersage enthalten. Im “Aim 3” des Artikels von Liu et al. (2024) stehen zunächst die an den Tag gelegten Verhaltensweisen des Gegenübers im Zentrum der Aufmerksamkeit. Auf S. 66 berichten die Autor*innen ihr Vorgehen dabei wie folgt:
For each outcome, we first entered the six (uncentered) IER strategy variables at Level 1 to examine associations between each strategy and the outcome (Step 1)
Da die Strategien sich über Situationen hinweg unterscheiden können, stellen sie sogenannte time varying covariates dar. Diese müssen wir also auf Level 1 in unser Modell aufnehmen. Mal beispielhaft für den Fall mit einem Prädiktor:
Wir haben unser Modell also um den Term $\beta_{1i} \cdot x_{ti}$ erweitert und so einen Prädiktor auf Level 1 hinzugenommen (das Konzept lässt sich, analog zur Regression, um beliebig viele Prädiktoren erweitern). Wie in den Zeilen 2 und 3 der Gleichungen zu erkennen ist, nehmen wir hier zunächst an, dass es zufällige Effekte für die Intercepts gibt ($u_{0i}$), für die Regressionsgewichte nehmen wir aber nur einen globalen Effekt ($\gamma_{10}$) ohne personenspezifische Abweichungen an.
Konzeptuell lässt sich das Ganze so verbildlichen:
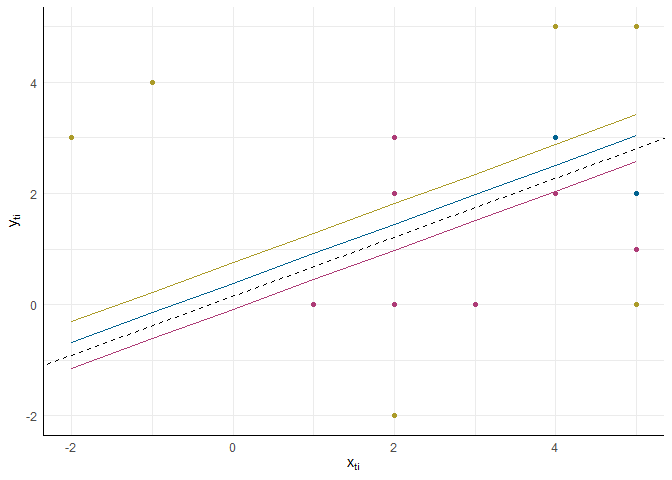
Hier haben wir drei Personen mit unterschiedlichen Beobachtungen auf $x_{ti}$ und $y_{ti}$. Die gestrichelte Linie beschreibt den globalen Effekt, den wir anhand der fixed effects beschreiben - diese Regressionsgerade hat also das Intercept $\gamma_{00}$ und die Steigung $\gamma_{10}$. Jeder der Linien ist personenspezifisch und daher um den Zufallseffekt im Intercept ($u_{0i}$) nach oben oder unten versetzt.
Im Modell von Liu et al. (2024, Table 6) werden hier zunächst die Effekte der Verhaltensweisen des Gegenübers als Prädiktoren aufgenommen. Diese sind dummy-kodiert, liegen also als 0 (wurde nicht genutzt) und 1 (wurde genutzt) vor. Wir können das Modell also wie folgt aufstellen:
# Random Intercept Modell
mod1 <- lmer(problem ~ 1 + reappraisal + solving + sharing + affection + invalidation + blaming + (1 | id), data = esm)
# Ergebniszusammenfassung
summary(mod1)
## Linear mixed model fit by REML. t-tests use Satterthwaite's method ['lmerModLmerTest']
## Formula: problem ~ 1 + reappraisal + solving + sharing + affection + invalidation +
## blaming + (1 | id)
## Data: esm
##
## REML criterion at convergence: 6559.1
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -4.6510 -0.5935 0.0270 0.5964 2.9172
##
## Random effects:
## Groups Name Variance Std.Dev.
## id (Intercept) 0.7442 0.8627
## Residual 2.9727 1.7242
## Number of obs: 1617, groups: id, 198
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) 0.6068 0.1016 395.7381 5.972 5.21e-09 ***
## reappraisal 1.0146 0.1111 1609.6440 9.134 < 2e-16 ***
## solving 0.8282 0.1011 1584.9433 8.195 5.11e-16 ***
## sharing 0.3876 0.1080 1609.1660 3.590 0.000341 ***
## affection 0.9573 0.1021 1606.2659 9.375 < 2e-16 ***
## invalidation -0.9646 0.1710 1584.2250 -5.640 2.01e-08 ***
## blaming -0.8392 0.1937 1565.3430 -4.333 1.56e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr) rpprsl solvng sharng affctn invldt
## reappraisal -0.251
## solving -0.295 -0.076
## sharing -0.235 -0.070 0.014
## affection -0.308 -0.044 0.047 -0.185
## invalidatin -0.216 0.091 0.028 0.105 0.053
## blaming -0.093 0.015 -0.047 0.004 0.029 -0.217
Wieder erhaltenn wir zwei random effects (Intercept und Residuum). Diese haben allerdings ihre Bedeutung gegenüber dem Nullmodell verändert, da das Intercept nun der Wert ist, der vorhergesagt wird, wenn keine der Verhaltensweisen an den Tag gelegt wurde. Das Residuum $r_{ti}$ ist hingegen die Abweichung von der Vorhersage, die wir aufgrund der gezeigten Verhaltensweisen des Gegenübers gemacht haben.
Hinsichtlich der fixed effects zeigen sich die erwarteten Ergebnisse: die generell als “positiv” klassifizierten Vehraltensweise (reappaisal, solving, sharing, affection) gehen mit einer wahrgenommenen Verbesserung der Problemeinschätzung einher, während die als “negativ” klassifizierten Verhaltensweisen (invalidation, blaming) mit einer Verschlechterung der Problemeinschätzung einhergehen. Die letzte Tabelle (Correlation of Fixed Effects) dient hauptsächlich der Modelldiagnostik, da sehr hohe Korrelationen zwischen den fixed effects auf Probleme in der Trennbarkeit von Prädiktoren oder Vermischung von Effekten hindeuten können.
Modellvergleiche
In der Regression war es üblich, die Relevanz von einer ganzen Menge von Prädiktoren mittels $\Delta R^2$ und dazugehörigem $F$-Test zu überprüfen. In gemischten Modellen ist dieses Vorgehen leider nicht mehr möglich, weil die Lokalisierung der Varianzen und deren Aufklärung nicht mehr ganz trivial ist. Stattdessen wird hier meist mit dem sogenannten Devianzentest gearbeitet. Dieser ist letztlich das Gleiche wie der Likelihood-Ratio-Test, den wir schon im Rahmen des Beitrags zur logistischen Regression besprochen haben. Auch hier gilt wieder das Prinzip, dass wir statt der Varianzen nun die Wahrscheinlichkeit der Daten gegeben des Modells miteinander vergleichen müssen. Probieren wir einfach mal aus, das dort vorgestellte Prinzip zum Vergleich von Nullmodell und Random-Intercept-Modell einzusetzen:
# Modellvergleich
anova(mod0, mod1)
## Error in anova.merMod(mod0, mod1): models were not all fitted to the same size of dataset
Der entstehende Fehler zeigt, dass die Datensätze sich in ihrer Größe unterscheiden. Das kommt daher, dass Beobachtungen immer dann aus Modellierung ausgeschlossen werden, wenn auf den Prädiktoren fehlende Werte vorliegen. Das ursprüngliche Nullmodell wurde auf insgesamt 1632 Beobachtungen angepasst (alle Beobachtungen, die Werte auf der id und problem-Variable hatten), während im Random-Intercept-Modell nur noch 1617 Beobachtungen genutzt werden konnten, weil in einigen Fällen auf mindestens einem der Prädiktoren ein fehlender Wert vorlag. Weil die Behandlung von Verfahren wie Multipler Imputation an dieser Stelle den Rahmen “ein wenig” sprengen würden, beschränken wir unsere Modelle statdessen auf alle vollständigen Beobachtungen. Dazu können wir beide Modelle einfach nochmal auf den Datensatz anwenden, der in mod1 genutzt wurde (dieser ist im Objekt als frame hinterlegt):
# Modelle auf vollständige Beobachtungen anwenden
mod0b <- update(mod0, data = mod1@frame)
mod1b <- update(mod1, data = mod1@frame)
# Modellvergleich
anova(mod0b, mod1b)
## refitting model(s) with ML (instead of REML)
## Data: mod1@frame
## Models:
## mod0b: problem ~ 1 + (1 | id)
## mod1b: problem ~ 1 + reappraisal + solving + sharing + affection + invalidation + blaming + (1 | id)
## npar AIC BIC logLik deviance Chisq Df Pr(>Chisq)
## mod0b 3 6904 6920.2 -3449 6898
## mod1b 9 6560 6608.4 -3271 6542 356.04 6 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Wie zu erwarten war, ist das Nullmodell deutlich schlechter als das Random-Intercept-Modell, sodass wir zunächst mit letzterem weiter arbeiten können.
Die erste Zeiles des Outputs weist uns direkt noch auf eine Besonderheit dieses Verfahrens hin. In der gemischten Modellierung wird der Modellvergleich dadurch erschwert, dass sich zwei unterschiedliche Formen der Modellschätzung etabliert haben: Restricted Maximum Likelihood (REML) und Full Maximum Likelihood (FML). Während das ML-Verfahren die Varianzen der random effects so schätzt, dass die Wahrscheinlichkeit der Daten insgesamt maximiert wird, schätzt das REML-Verfahren die Varianzen so, dass die Wahrscheinlichkeit der Daten bedingt auf die fixed effects maximiert wird. Generell wird dabei REML zugeschrieben, präzisere Schätzungen der Effekte zu ermöglichen, weswegen es auch in lme4 die Voreinstellung ist. Allerdings ist es mit diesem Ansatz nicht möglich Modelle zu vergleichen, welche sich in den fixed effects unterscheiden - dafür müssen wir FML heranziehen. Der Modellvergleich, den wir mit anova angefordert haben schätzt daher automatisch beide Modelle noch einmal mit FML, um den Vergleich durchführen zu können.
Über die inferenzstatistische Prüfung hinaus, interessiert uns auch häufig ein Effektschätzer dafür, wie gut unsere Prädiktoren insgesamt in der Vorhersage der Outcomes sind. Wie gesehen, haben wir leider unterschiedliche Quellen der Varianz, die wir im Modell berücksichtigen, sodass auch hier die Bestimmung des Pseudo-$R^2$ nicht super einfach ist. Zum Glück haben wir aber (was ein Zufall) das performance-Paket schon geladen, dass den praktischen r2-Befehl enthält:
# Bestimmung des Pseudo-R^2
r2(mod1b)
## # R2 for Mixed Models
##
## Conditional R2: 0.364
## Marginal R2: 0.205
Hier werden in Anlehnung an Nakagawa et al. (2017) zwei unterschiedliche Varianten des $R^2$ unterschieden. Das conditional $R^2$ beschreibt die Varianzaufklärung durch alle Effekte im Modell, währen das marginal $R^2$ nur die Varianzaufklärung durch die fixed effects berichtet. Das conditional $R^2$ ist also eine Aussage darüber, wie viel Residualvarianz noch in den Werten der einzelnen Situationen übrig ist, wenn wir auf die genutzten Strategien des Gegenübers (fixed effects) und die individuellen Zufallseffekte im Intercept (random effects) kontrollieren. Es ist also eine Güteschätzung für das gesamte Modell. Im marginal $R^2$ wird hingegen auch der Zufallseffekt der Intercepts als “nicht erklärt” eingestuft und nur die Varianzaufklärung durch die genutzten Strategien des Gegenübers betrachtet.
Level 2 Prädiktoren
Im Fokus des Papers von Liu et al. (2024) steht die MD Diagnose und ihre Auswirkungen auf IER. Die MD Diagnose ist eine personenbezogene Eigenschaft, die sich im Verlauf der 14-tägigen Erhebung vermutlich nicht ändert, sodass wir diese als Prädiktor auf Level 2 in unser Modell aufnehmen können. Liu et al. (2024, S. 66) beschreiben diesen Schritt wie folgt:
We then added the group variables at Level 2 to examine strategy-group interactions (Step 2).
Zu den Interaktionen kommen wir später noch, aber zunächst erweitern wir unser Modell um den neuen Prädiktor (wieder schematisch mit nur einem Prädiktor):
Um deutlich zu machen, welche Prädiktoren auf welcher Ebene angesiedelt sind, benennen wird die Prädiktoren üblicherweise unterschiedlich - hier nutzen wir $w_i$, wenn wir einen Prädiktor auf Level 2 meinen.
In diesem Schritt geht es uns also zunächst darum das Intercept vorherzusagen - wir nehmen also an, dass die Gruppenunterschiede sich gleichmäßig in einer anderen Einschätzung des Problems niederschlagen - zunächst kontrolliert auf die unterschiedlichen Strategien aber ohne Moderation (zu der kommen wir gleich). In der Umsetzung in R wird zwischen den Leveln der Prädiktoren nicht unterschieden, sondern die Verortung wird anhand der Daten festgelegt. Variablen, die innerhalb einer Person unterschiedliche Ausprägungen annehmen können, müssen per Definition situative Variablen sein. Variablen, die für jede Beobachtung (also Zeile im Datensatz) der gleichen Person auch den gleichen Wert annehmen, wrrden als personenspezifische Variablen angenommen. Daher erweitern wir unser Random-Intercept-Modell einfach um den neuen Prädiktor:
# Random Intercept Modell mit Level 2 Prädiktor
mod2 <- lmer(problem ~ 1 + reappraisal + solving + sharing + affection + invalidation + blaming +
group + (1 | id), data = esm)
# Ergebniszusammenfassung
summary(mod2)
## Linear mixed model fit by REML. t-tests use Satterthwaite's method ['lmerModLmerTest']
## Formula: problem ~ 1 + reappraisal + solving + sharing + affection + invalidation +
## blaming + group + (1 | id)
## Data: esm
##
## REML criterion at convergence: 6561.4
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -4.6580 -0.5884 0.0289 0.5936 2.9096
##
## Random effects:
## Groups Name Variance Std.Dev.
## id (Intercept) 0.7516 0.8669
## Residual 2.9729 1.7242
## Number of obs: 1617, groups: id, 198
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) 0.4782 0.1808 249.7763 2.645 0.00868 **
## reappraisal 1.0174 0.1112 1607.7146 9.151 < 2e-16 ***
## solving 0.8317 0.1012 1582.3088 8.221 4.15e-16 ***
## sharing 0.3898 0.1086 1603.2776 3.590 0.00034 ***
## affection 0.9582 0.1023 1603.5451 9.367 < 2e-16 ***
## invalidation -0.9620 0.1711 1582.1764 -5.621 2.24e-08 ***
## blaming -0.8294 0.1940 1559.8139 -4.275 2.03e-05 ***
## grouphealthy control 0.1713 0.2131 184.4525 0.804 0.42233
## groupremitted MDD 0.1554 0.2091 177.6160 0.743 0.45839
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr) rpprsl solvng sharng affctn invldt blamng grphlc
## reappraisal -0.165
## solving -0.196 -0.075
## sharing -0.145 -0.069 0.014
## affection -0.178 -0.044 0.047 -0.178
## invalidatin -0.138 0.092 0.029 0.103 0.052
## blaming -0.098 0.017 -0.045 0.005 0.030 -0.215
## grphlthycnt -0.749 0.028 0.033 0.058 0.028 0.009 0.052
## grprmttdMDD -0.738 0.023 0.032 -0.030 -0.019 0.027 0.048 0.619
Hier zeigt sich zunächst, dass die Strategien weiterhin bedeutsamen Einfluss auf die Problemeinschätzung haben, ein globaler Effekt der Gruppenzugehörigkeit aber nicht zu finden ist. Wir können natürlich per Modellvergleich auch noch einmal die Gruppenvariable als Ganzes testen:
# Modelle aktualisieren (gleicher Datensatz)
mod1b <- update(mod1, data = mod2@frame)
mod2b <- update(mod2, data = mod2@frame)
# Modellvergleich
anova(mod1b, mod2b)
## refitting model(s) with ML (instead of REML)
## Data: mod2@frame
## Models:
## mod1b: problem ~ 1 + reappraisal + solving + sharing + affection + invalidation + blaming + (1 | id)
## mod2b: problem ~ 1 + reappraisal + solving + sharing + affection + invalidation + blaming + group + (1 | id)
## npar AIC BIC logLik deviance Chisq Df Pr(>Chisq)
## mod1b 9 6560.0 6608.4 -3271.0 6542.0
## mod2b 11 6563.2 6622.5 -3270.6 6541.2 0.7588 2 0.6843
Und, wenn wir immer noch nicht von der Bedeutungslosigkeit der Gruppenzugehörigkeit in diesem Modell überzeugt sind, können wir noch einmal den Pseudo-$R^2$-Wert betrachten:
# Bestimmung des Pseudo-R^2
r2(mod2b)
## # R2 for Mixed Models
##
## Conditional R2: 0.365
## Marginal R2: 0.205
Gegenüber dem Random-Intercept-Modell hat sich hier lediglich das Conditional $R^2$ in der 3. Nachkommastelle verändert.
Kontexteffekte und Zentrierung
Das Vorgehen, zur Modellierung von situativen Effekten Level-1 Prädiktoren in Rohfassung in das Modell aufzunehmen ist wiederholt heftig kritisiert worden (sowohl für kontinuierliche als auch für kategoriale Level-1 Prädiktoren). Insbesondere Yaremych et al. (2021) liefern zum Grund dieser Kritik sehr detaillierte, statistische und mathematische Argumente. Inhaltlich zusammengefasst läuft das Problem darauf hinaus, dass diese Form der Modellierung zur Vermischung von Effekte innerhalb und zwischen Personen führt. Wenn die betrachteten Prädiktoren über die Situationen hinweg unterschiedlich sein können und gleichzeitig in ihren Mittelwerten über Personen hinweg variieren, kann im UN-Modell nicht zwischen diesen beiden Effektquellen getrennt werden, weil nur ein Regressionsgewicht geschätzt wird.
In Tabelle 6 von Liu et al. (2024) werden daher in einem UN(M)-Modell (uncentored with group-means) neben den Effekten der Verhaltensweisen des Gegenübers auch die “habituellen” Effekte dieser Verhaltensweisen berücksichtigt. Die Überlegung dahinter ist hier, dass Personen, die insgesamt häufiger z.B. von ihren Gegenüber Schuldzuweisung als Reaktion im IER erhalten, eventuell andere grundlegende Verhaltenstendenzen haben. Um diese globalen Effekte von den lokalen Effekten zu trennen, können die Einflüsse von situativen (also Level-1) Variablen in ihre Bestandteile zerlegt werden. Dabei machen wir uns die gleiche Annahme zunutze, die wir auch schon bei der abhängigen Variable als Argument benutzt haben: stabile Komponenten sollten sich über alle Wiederholungen der Messungen zeigen, situative Komponenten als Abweichung von dieser generellen Tendenz.
Als “stabile Komponente” können wir den Mittelwert aller Beobachtungen für eine Person nutzen, als “situative Komponenten” dann wiederum die Abweichungen der Variable von diesem Mittelwert in einer spezifischen Situation. Die Personenmittelwerte können wir einfach mit aggregate erzeugen:
# Personen-Mittelwerte berechnen (Aggregatvariablen)
w <- aggregate(esm[, c("reappraisal", "solving", "sharing", "affection", "invalidation", "blaming")], by = list(esm$id), mean, na.rm = TRUE)
# Spaltennamen anpassen
names(w) <- c("id", "mean_reappraisal", "mean_solving", "mean_sharing", "mean_affection", "mean_invalidation", "mean_blaming")
# Daten zusammenführen
esm <- merge(esm, w, by = "id")
Da unsere Prädiktoren ursprünglich dummy-kodierte Indikatoren waren, enthält dieser Personenmittelwert jetzt einfach den relativen Anteil der IER Situationen, in denen vom Gegenüber diese spezifische Verhaltensweise an den Tag gelegt wurde.
UN(M)-Modell
Im Modell in Tabelle 6, Panel 1 (Liu et al., 2024) werden diese Mittelwerte dann als Prädiktoren auf Level 2 aufgenommen (allerdings werden hier die MD-Gruppen nicht im Modell berücksichtigt, sodass auch wir diese wieder entfernen):
# Random Intercept Modell mit Kontext-Effekten
mod3 <- lmer(problem ~ 1 + reappraisal + solving + sharing + affection + invalidation + blaming +
mean_reappraisal + mean_solving + mean_sharing + mean_affection + mean_invalidation + mean_blaming +
(1 | id), data = esm)
# Ergebniszusammenfassung
summary(mod3)
## Linear mixed model fit by REML. t-tests use Satterthwaite's method ['lmerModLmerTest']
## Formula: problem ~ 1 + reappraisal + solving + sharing + affection + invalidation +
## blaming + mean_reappraisal + mean_solving + mean_sharing +
## mean_affection + mean_invalidation + mean_blaming + (1 | id)
## Data: esm
##
## REML criterion at convergence: 6549.4
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -4.6870 -0.5914 0.0285 0.5872 2.8966
##
## Random effects:
## Groups Name Variance Std.Dev.
## id (Intercept) 0.7345 0.857
## Residual 2.9701 1.723
## Number of obs: 1617, groups: id, 198
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) 8.051e-01 1.908e-01 1.900e+02 4.220 3.79e-05 ***
## reappraisal 1.017e+00 1.188e-01 1.427e+03 8.559 < 2e-16 ***
## solving 8.862e-01 1.057e-01 1.427e+03 8.383 < 2e-16 ***
## sharing 3.933e-01 1.144e-01 1.426e+03 3.437 0.000605 ***
## affection 9.633e-01 1.079e-01 1.426e+03 8.924 < 2e-16 ***
## invalidation -9.778e-01 1.787e-01 1.426e+03 -5.472 5.25e-08 ***
## blaming -7.357e-01 2.003e-01 1.426e+03 -3.673 0.000249 ***
## mean_reappraisal 5.452e-02 3.367e-01 2.776e+02 0.162 0.871485
## mean_solving -7.150e-01 3.648e-01 2.977e+02 -1.960 0.050965 .
## mean_sharing 1.288e-03 3.589e-01 2.395e+02 0.004 0.997139
## mean_affection 4.790e-02 3.475e-01 2.561e+02 0.138 0.890472
## mean_invalidation 8.079e-01 6.663e-01 2.746e+02 1.212 0.226413
## mean_blaming -1.820e+00 8.167e-01 2.423e+02 -2.228 0.026796 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation matrix not shown by default, as p = 13 > 12.
## Use print(x, correlation=TRUE) or
## vcov(x) if you need it
Auch hier sind wir wieder in der Lage, die Ergebnisse des Artikel exakt zu reproduzieren. Gegenüber dem vorherigen Modell ändern sich nicht nur die Werte der Regressionsgewichte, sondern auch deren Bedeutung. Die fixed effects der Level-1 Prädiktoren sind jetzt die reinen situativen Komponenten - also der Effekt, den das Zeigen einer Verhaltensweise in einer spezifischen Situation hat, wenn ich die stabilen Personenkomponenten auspartialisiere.
Die Personenkomponenten auf Level-2, die aus dieser Form der Modellierung resultieren werden häufig als Kontexteffekte bezeichnet. Um die Interpretation der Effekte zu verdeutlichen, ist es hilfreich sich auch noch eine weitere Parameterisierung dieser Effekt anzusehen.
CWC(M)-Modell
Im gerade beschriebenen, und bei Liu et al. (2024) genutzten UN(M)-Modell wurden auf Level-1 die dummy-kodierten Variablen als Prädiktoren beibhalten. Insbesondere in Fällen, in denen die Prädiktoren auf Level-1 kontinuierlich sind, hat sich aber ein anderes Vorgehen etabliert: die within-cluster-zentrierteten Werte aufzunehmen. Dafür werden die Personenmittelwerte, die wir gerade erzeugt haben noch von den ursprünglichen Werten abgezogen, sodass wir als neue Prädiktoren die situative Abweichung auf einem Prädiktor von der generellen Personentendenz nutzen:
# CWC Werte berechnen
esm$cwc_reappraisal <- esm$reappraisal - esm$mean_reappraisal
esm$cwc_solving <- esm$solving - esm$mean_solving
esm$cwc_sharing <- esm$sharing - esm$mean_sharing
esm$cwc_affection <- esm$affection - esm$mean_affection
esm$cwc_invalidation <- esm$invalidation - esm$mean_invalidation
esm$cwc_blaming <- esm$blaming - esm$mean_blaming
# Random Intercept Modell mit zentrierten Prädiktoren
mod4 <- lmer(problem ~ 1 + cwc_reappraisal + cwc_solving + cwc_sharing + cwc_affection + cwc_invalidation + cwc_blaming +
mean_reappraisal + mean_solving + mean_sharing + mean_affection + mean_invalidation + mean_blaming +
(1 | id), data = esm)
Interpretation der Modellansätze
Gucken wir uns kurz alle drei Ansätze gemeinsam an:
| UN Modell | UN(M) Modell | CWC(M) Modell | |
|---|---|---|---|
| intercept | 0.607 | 0.805 | 0.805 |
| L1_reappraisal | 1.015 | 1.017 | 1.017 |
| L1_solving | 0.828 | 0.886 | 0.886 |
| L1_sharing | 0.388 | 0.393 | 0.393 |
| L1_affection | 0.957 | 0.963 | 0.963 |
| L1_invalidation | -0.965 | -0.978 | -0.978 |
| L1_blaming | -0.839 | -0.736 | -0.736 |
| L2_reappraisal | NA | 0.055 | 1.072 |
| L2_solving | NA | -0.715 | 0.171 |
| L2_sharing | NA | 0.001 | 0.395 |
| L2_affection | NA | 0.048 | 1.011 |
| L2_invalidation | NA | 0.808 | -0.170 |
| L2_blaming | NA | -1.820 | -2.555 |
In dieser Tabelle sind die festen Effekte aus den drei bisherigen Modellen zur Untersuchung der Verhaltensweisen des Gegenübers zusammengetragen (UN Modell: mod1, UN(M) Modell: mod3, CWC(M)-Modell: mod4). Für das “einfache” UN Modell hatten wir festgehalten, dass z.B. der Effekt von blaming bedeutet, dass über alle Personen und Situationen hinweg, Schuldzuweisungen durch den Gegenüber mit einer Verschlechterung der Problemeinschätzung einhergehen. Leider ist dieser Effekt aber gemischt aus Effekten der Personen und Situationen, weswegen wir das UN(M) Modell aufgestellt haben. Dort ist der reine situative Effekt der Schuldzuweisung -0.736. Sowohl der Wert als auch die Interpretation ist im CWC(M) Modell identisch. Unterschiede ergeben sich erst auf Level-2. Im CWC(M) Modell ist der Effekt der habituellen Schuldzuweisung -2.555 - hierbei handelt es sich um den stabilen Personeneffekt. Wie vielleicht aus der Tabelle ersichtlich wird, ist der Effekt im UN(M) Modell dieser stabile Personeneffekt abzüglich der situativen Effekte von Level-1:
$\gamma_{06}^{\text{UN(M)}} = \gamma_{06}^{\text{CWC(M)}} - \gamma_{60} = -2.555 - -0.736 = -1.819$
Ein paar Gleichungen zur Verdeutlichung
Nehmen wir zwei Personen, die an den extremen liegen und vereinfachen wir das Modell auf den Fall, in dem wir nur Schuldzuweisungen betrachten. Person A erfährt in jeder IER Situation Schuldzuweisung ($w_A = 1$) und Person B niemals ($w_B = 0$). Wenn beide jetzt mit einer Situation konfrontiert werden, in der Schuldzuweisen stattfindet ($x_{ti} = 1$) ergibt sich im UM(M) Modell:
Im CWC(M) Modell ergibt sich hingegen:
Die vorhergesagten Werte sind (abgesehen vom Rundungsfehler) identisch, aber die Bedeutung der Werte unterscheidet sich. Für die Person A ist die Situation, dass Schuldzuweisung stattfindet “normal”: $x_{ti} = 0$, weil die Situation sicht nicht von der durchschnittlichen Situation unterscheidet. Für Person B hingegen, ist das Erleben der Schuldzuweisung etwas besonderes und weicht um eine Einheit von der durchschnittlichen Situation ab ($x_{ti} = 1$). Das wird darin abgebildet, dass hier die situative Komponente hinzugerechnet werden muss.
Etwas zusammenfassend ausgedrückt: im UN(M) Modell ist der Level-2 Effekt der erwartete Unterschied zwischen zwei Personen, die sich in der stabilen Tendenz um eine Unterscheiden, wenn wir sie in einer gleichen Situation beobachten. Im CWC(M) Modell ist der Level-2 Effekt der erwartete Unterschied zwischen zwei Personen, die sich in der stabilen Tendenz um eine Unterscheiden, wenn wir sie in einer für sie typischen Situation beobachten.
Random Slopes Modelle
Bisher hatten wir angenommen, dass die Auswirkungen der Verhaltensweisen des Gegenübers für alle Personen gleich sind. Liu et al. (2024, S. 64) haben allerdings als eine der zentralen Hypothesen genau darin Unterschiede postuliert:
We hypothesized that reappraisal, problem-solving, encouraging sharing, and affection would be more strongly associated with improved IER outcomes for the current-MDD group than for the control group, with the remitted-MDD group falling in between (Hypothesis 3a [H3a]). We hypothesized that invalidation and blaming would be more strongly associated with worsened problem and relationship outcomes for the current-MDD group than for the remitted-MDD and control groups, who were not expected to differ (Hypothesis 3b [H3b]).
Wenn eine Hypothese lautet, dass es Unterschiede zwischen Personen gibt, die sich anhand der MD Gruppe aufklären lassen, muss es zunächst irgendwelche Unterschiede geben. Im Random Slopes Modell werden zunächst unsystematische Unterschiede in den Effekten der Level-1 Prädiktoren zugelassen, welche wir dann zu einem späteren Zeitpunkt aufklären könnten. Um das ganze wieder in Form unserer vereinfachten Modellgleichung auszudrücken:
Hier haben wir das Random Intercept Modell (zunächst ohne L2-Prädiktoren) um die Zufallskomponente $u_{1i}$ erweitert. Diese erlaubt es nun, dass für jede Person $i$ der Zusammenhang zwischen $x_{ti}$ und $y_{ti}$ neben dem globalen Effekt $\gamma_{10}$ auch einen individuellen Effekt $u_{1i}$ enthält. Im Kontext der Studie heißt es also z.B., dass der Effekt der Schuldzuweisung auf die Problemeinschätzung für manche Personen stärker ist, als für andere.
Derzeit gibt es sehr viel Diskussion über die korrekte Vorgehensweise in der Aufnahme von Zufallseffekten. Barr et al., 2013 empfehlen, dass für die Modellierung von Zufallseffekten mit dem komplexest möglichen Modell angefangen werden, welches unter den theoretischen Annahmen sinnvoll ist. Das bedeutet in unserem Fall, dass wir - weil wir annehmen, dass es individuelle Effekte der Verhaltensweisen des Gegenübers geben kann - für alle Prädiktoren annehmen, dass sie random slopes haben.
Umgang mit Schätzproblemen
Wie Sie dem Titel dieses Abschnitts vielleicht entnehmen können, funktioniert das Random Slopes Modell nicht problemlos, wenn wir es auf unseren Fall anwenden. Weil die hier auftretenden Probleme insbesondere für Modelle mit komplexer Zufallsstruktur sehr häufig sind, habe ich hier das gesamte Vorgehen detailliert dargestellt. Wenn Sie einfach nur sehen wollen, wie das finale Modell aussieht und interpretiert wird, können Sie einfach zum fertigen Modell springen.
Wenn wir unsere Modell auftreten, springt uns direkt ein Warnhinweis ins Gesicht:
mod5 <- lmer(problem ~ 1 + reappraisal + solving + sharing + affection + invalidation + blaming +
mean_reappraisal + mean_solving + mean_sharing + mean_affection + mean_invalidation + mean_blaming +
(1 + reappraisal + solving + sharing + affection + invalidation + blaming | id), data = esm)
## Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, : Model failed to
## converge with max|grad| = 0.149434 (tol = 0.002, component 1)
Genau genommen bekommen wir zwei unterschiedliche Probleme. Das Zweite sagt, dass das Modell nicht konvergiert - der Schätzalgorithmus kommt also nicht zu einer Lösung, die den Anforderungen entspricht. Wir sollten uns zunächst damit befassen.
In der Hilfe von lme4 findet man unter ?convergence ein paar hilfreiche Aussagen zu diesen Problemen und potentiellen Auswegen:
- Check des Modells und der Daten. Generell können Fehler passieren, bevor wir den Aufwand betreiben, den gesamten Schätzprozess auseinander zu nehmen, sollten wir gucken, ob (a) die Daten die richtige Struktur haben und (b) das Modell nur Zufallseffekte für Level-1 Prädiktoren enthält.
- Reskalierung der Prädiktoren. Wenn Prädiktoren im Modell sind, die dramtisch unterschiedliche Skalierung verwenden (z.B. Fragebögen mit Werten von 1 bis 4 und Reaktionszeiten in ms), kann der numerische Unterschied zwischen z.B. Varianzschätzern zu Problemen führen. Dann macht es Sinn zu checken, dass alle Variablen ungefähr im gleichen Wertebereich liegen.
- Mit anderen Startwerten beginnen. Manchmal verläuft sich ein Algorithmus - wo anders anzufangen kann helfen.
- Das Modell mit anderen Schätzalgorithmen nochmal schätzen. Dafür bietet
lme4die immens praktischeallFit-Funktion - damit können wir das selbe Modell mit allen verfügbaren Schätzern ausprobieren. - Das Konvergenzkriterium herabsetzen. Letztlich könnte es auch einfach sein, dass wir zu streng darin waren, was denn wirklich “nötig” ist, damit wir das Modell als okay einordnen können.
- Das Modell vereinfachen. Manchmal ist das Modell für die Datenlage einfach zu komplex - bestimmte Effekte unterscheiden sich z.B. einfach nicht über Personen oder kodieren Beobachtungen, die so selten sind, dass kaum Varianz vorhanden ist.
Leider sind die Probleme 1 und 2 in unserem Fall nicht die Ursache. Sowohl die Daten sind mehrfach von unterschiedlichen Autor*innen gecheckt und die Prädiktoren sind alle in ihren Werten auf den Bereich 0 bis 1 beschränkt. Wenn Sie am Ausprobieren der technischen Schritte interessiert sind, können Sie den nächsten Abschnitt einfach aufklappen.
Technische Schritte zur Lösung der Schätzprobleme
Zunächst versuchen wir das Modell nochmal mit anderen Schätzwerte zu starten. Dafür können wir z.B. die ausgegebenen Werte des letzten Versuchs als Startwerte einsetzen:
# Letzte Schätzung extrahieren
vals <- getME(mod5, c("theta"))
# Werte als Startwerte einsetzen
mod5b <- update(mod5, start = vals)
## Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, : Model failed to
## converge with max|grad| = 0.0205038 (tol = 0.002, component 1)
Das behebt unser Problem leider nicht. Wir können auch andere Startwertkonstellationen ausprobieren, aber vielleicht gucken wir erst einmal, ob andere Schätzer das gleiche Problem haben. Dafür nutzen wir die bereits erwähnte allFit-Funktion:
allFit(mod5)
##
## bobyqa : boundary (singular) fit: see help('isSingular')
## Warning: Model failed to converge with 1 negative eigenvalue: -2.7e-01[OK]
## Nelder_Mead : Warning: unable to evaluate scaled gradientWarning: Model failed to converge: degenerate Hessian with 3 negative eigenvaluesWarning: Model failed to converge with 3 negative eigenvalues: -4.8e+00 -8.3e+00 -1.1e+01[OK]
## nlminbwrap : Warning: convergence code 1 from nlminbwrap: iteration limit reached without convergence (10)boundary (singular) fit: see help('isSingular')
## Warning: Model failed to converge with 1 negative eigenvalue: -4.1e+00[OK]
## optimx.L-BFGS-B : Warning: Parameters or bounds appear to have different scalings.
## This can cause poor performance in optimization.
## It is important for derivative free methods like BOBYQA, UOBYQA, NEWUOA.boundary (singular) fit: see help('isSingular')
## [OK]
## nloptwrap.NLOPT_LN_NELDERMEAD : Warning: Model failed to converge with max|grad| = 0.0831441 (tol = 0.002, component 1)[OK]
## nloptwrap.NLOPT_LN_BOBYQA : Warning: Model failed to converge with max|grad| = 0.016041 (tol = 0.002, component 1)[OK]
## original model:
## problem ~ 1 + reappraisal + solving + sharing + affection + invalidation + bl...
## data: esm
## optimizers (6): bobyqa, Nelder_Mead, nlminbwrap, optimx.L-BFGS-B, nloptwrap.NLOPT_LN_NELDERME...
## differences in negative log-likelihoods:
## max= 17.9 ; std dev= 7.3
Leider resultieren alle sechs Schätzer in einem Problem. Wenn hier ein Schätzer in der Lage gewesen wäre das Problem zu umgehen, hätten uns dessen Ergenisse ausgereicht. Es ist nicht notwendig, dass alle Schätzer ein zulässiges Ergebnis produzieren.
Zu guter Letzt können wir noch das Konvergenzkriterium herabsetzen, um so unsere Qualitätskriterien weniger strikt auszulegen:
# Modell mit herabgesetztem Konvergenzkriterium
mod5c <- update(mod5, control = lmerControl(optCtrl = list(ftol_abs = 1e3)))
## Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, : unable to evaluate
## scaled gradient
## Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, : Model failed to
## converge: degenerate Hessian with 1 negative eigenvalues
## Warning: Model failed to converge with 1 negative eigenvalue: -7.1e+01
Leider sind wir auch hier erfolglos und es scheint wirklich ein Problem unseres Modells zu sein.
Letztlich bleibt uns also leider nur Ansatz 6: wir müssen das Modell vereinfachen. Park et al. (2020) empfehlen bei solchen Problemen, die Korrelationen der Zufallseffekte auf 0 zu setzen, um so die potentiellen Problem besser identifizieren zu können.
Korrelationen zwischen Zufallseffekten
Wie in der Sitzung vor Ort besprochen, sind Zufallseffekte in gemischten Modellen üblicheweise korreliert. Rein inhaltlich würde das im Kontext der Studie bedeuten, dass z.B. Personen, die in Situationen, in denen keine der genannten Strategien vom Gegenüber an den Tag gelegt wird, besonders wenig Problemverbesserung wahrnehmen ($u_{0i} < 0$), auch Personen sind, die an negativem Feedback, wie z.B. Schuldzuweisungen besonders leiden ($u_{6i} < 0$). Diese Konstellatoon würde sich als $\mathbb{C}ov(u_{0i}, u_{6i}) > 0$ in den Modellergebnissen wiederfinden lassen.
Generell kann es aber jede Form des Zusammenhangs zwischen Zufallseffekten geben:
- $\mathbb{C}ov(u_{0i}, u_{6i}) > 0$ hatte ich als Beispiel gerade dargestellt
- $\mathbb{C}ov(u_{0i}, u_{6i}) = 0$ hieße, dass der Impact von Schuldzuweisungen nicht mit dem Niveau der Problemverbesserung in Situationen ohne konkretes IER Verhalten des Gegenüber in Verbindung steht
- $\mathbb{C}ov(u_{0i}, u_{6i}) < 0$, würde bedeuten, dass Personen die besonders viel Problemverbesserung ohne IER Strategie des Gegenübers wahrnehmen, diejenigen sind, die durch Schuldzuweisungen starken negativen Impact erfahren
In Fällen, in denen wir (anders als hier) auch als unabhängige Variablen Werte aus Fragebögen nutzen, haben wir aufgrund der Einschränkung des Wertebereichs häufig eine negative Korrelation zwischen Intercept und Slope. Das liegt einfach daran, dass Personen die mit hohen Werten starten nicht mehr so viel Platz nach oben haben (die Skala hat ein Maximum) und daher der Einfluss potentieller Prädiktoren nach unten verzerrt wird. Das gilt natürlich auch in die Gegenrichtung für negative Werte.
In unserem Fall hatten wir gerade festgehalten, dass wir keine vertrauenswürdigen Modellergebnisse bekommen, wenn wir annehmen, dass alle Zufallseffekte beliebig zusammenhängen dürfen. Die Ergebnisse können wir trotzdem inspizieren, um einen Eindruck davon zu bekommen, wo potentiell Probleme liegen könnten:
# Korrelationsmatrix der Zufallseffekte
VarCorr(mod5)
## Groups Name Std.Dev. Corr
## id (Intercept) 0.94901
## reappraisal 0.77593 -0.670
## solving 0.49481 0.027 0.569
## sharing 0.54975 -0.434 0.332 0.570
## affection 0.36660 -0.657 0.599 0.309 0.436
## invalidation 1.13032 -0.059 -0.485 -0.585 -0.140 0.350
## blaming 0.24750 0.508 -0.708 -0.545 -0.584 -0.109 0.762
## Residual 1.63134
(Diese Korrelationsmatrix ist auch in der summary enthalten.) Auf den ersten Blick scheint hier nichts eindeutig Bedenkliches vorzuliegen: alle Standardabweichungen sind deutliche größer als 0 (also gibt es individuelle Unterschiede in den Effekten) und keine der Korrelationen ist in der Nähe von 1 oder -1 (was hieße, dass sich die Effekte nicht trennen lassen). Wenn wir diese Korrelationen aber in Partialkorrelationen überführen, sehen wir, dass sich das gesamte System sehr nah an Singularität bewegt:
# Partialkorrelationen
attr(VarCorr(mod5)$id, 'correlation') |> corpcor::cor2pcor() |> round(3)
## [,1] [,2] [,3] [,4] [,5] [,6] [,7]
## [1,] 1.000 -0.460 0.938 -0.966 -0.693 0.674 -0.697
## [2,] -0.460 1.000 0.158 -0.367 0.310 -0.307 0.081
## [3,] 0.938 0.158 1.000 0.968 0.888 -0.884 0.873
## [4,] -0.966 -0.367 0.968 1.000 -0.758 0.769 -0.841
## [5,] -0.693 0.310 0.888 -0.758 1.000 0.991 -0.869
## [6,] 0.674 -0.307 -0.884 0.769 0.991 1.000 0.920
## [7,] -0.697 0.081 0.873 -0.841 -0.869 0.920 1.000
Was genau Singularität bedeutet und wo sie herkommt, hatten wir in Statistik I im Rahmen der Matrixalgebra genauer besprochen. Hier ist hauptsächlich relevant, dass es bedeutet, dass einige der Zufallseffekte quasi linear von Kombinationen anderer Zufallseffekte abhängen, was das Konzept des “Zufalls” in Zufallseffekte etwas in Frage zieht. Wie im letzten Abschnitt angerissen, wir bei persistenten Schätzproblemen empfohlen, die Korrelationen der Zufallseffekte zunächst auf 0 zu fixieren. Dazu können wir in lme4 die Kurzform || id benutzen, statt händisch einzelne Korrelationen unterdrücken zu müssen.
# Modell mit unkorrelierten Zufallseffekten
mod6 <- lmer(problem ~ 1 + reappraisal + solving + sharing + affection + invalidation + blaming +
mean_reappraisal + mean_solving + mean_sharing + mean_affection + mean_invalidation + mean_blaming +
(1 + reappraisal + solving + sharing + affection + invalidation + blaming || id), data = esm)
## boundary (singular) fit: see help('isSingular')
Wie wir sehen, behebt auch das unser Problem nicht. Allerdings können wir hier durch die Nutzung von allFit feststellen, dass es nur der voreingestellte Algorithmus ist, der Konvergenzprobleme verursacht. Wenn wir z.B. bobyqa nutzen konvergiert das Modell:
# bobyqa als Schätzer nutzen
mod6b <- update(mod6, control = lmerControl(optimizer = "bobyqa"))
## boundary (singular) fit: see help('isSingular')
Nun sind wir endlich an dem Punkt, dass wir uns um unser zweites Problem kümmern können: die singuläre Kovarianzmatrix der Zufallseffekte. Wenn wir uns die Ergebnisses des Modells angucken, finden wir direkt eindeutige Hinweise für mögliche Ursachen:
# Korrelationsmatrix der Zufallseffekte
VarCorr(mod6b)
## Groups Name Std.Dev.
## id (Intercept) 0.78422
## id.1 reappraisal 0.54615
## id.2 solving 0.45914
## id.3 sharing 0.47974
## id.4 affection 0.00000
## id.5 invalidation 1.13506
## id.6 blaming 0.00000
## Residual 1.65885
Wir sehen hier nur 0 bei den Standardabweichungen in den Slopes der affection und blaming. Entfernen wir also auch diese aus unserem Modell.
Finales Random Slopes Modell
Das finale Modell enthält jetzt nur noch die Zufallseffekte für das Intercept und vier der Prädiktoren. Zusammenhänge zwischen den Zufallseffekten hatten wir hier ausgeschlossen:
# Modellschätzung
mod7 <- lmer(problem ~ 1 + reappraisal + solving + sharing + affection + invalidation + blaming +
mean_reappraisal + mean_solving + mean_sharing + mean_affection + mean_invalidation + mean_blaming +
(1 + reappraisal + solving + sharing + invalidation || id), data = esm)
# Ergebniszusammenfassung
summary(mod7)
## Linear mixed model fit by REML. t-tests use Satterthwaite's method ['lmerModLmerTest']
## Formula: problem ~ 1 + reappraisal + solving + sharing + affection + invalidation +
## blaming + mean_reappraisal + mean_solving + mean_sharing +
## mean_affection + mean_invalidation + mean_blaming + (1 +
## reappraisal + solving + sharing + invalidation || id)
## Data: esm
##
## REML criterion at convergence: 6523
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -4.2041 -0.5549 0.0324 0.5792 2.9462
##
## Random effects:
## Groups Name Variance Std.Dev.
## id (Intercept) 0.6150 0.7842
## id.1 reappraisal 0.2983 0.5462
## id.2 solving 0.2108 0.4592
## id.3 sharing 0.2301 0.4797
## id.4 invalidation 1.2883 1.1350
## Residual 2.7518 1.6588
## Number of obs: 1617, groups: id, 198
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) 8.030e-01 1.876e-01 1.859e+02 4.280 2.99e-05 ***
## reappraisal 1.007e+00 1.304e-01 1.349e+02 7.728 2.24e-12 ***
## solving 9.232e-01 1.138e-01 1.354e+02 8.113 2.65e-13 ***
## sharing 4.110e-01 1.241e-01 1.533e+02 3.313 0.001151 **
## affection 9.622e-01 1.070e-01 1.407e+03 8.996 < 2e-16 ***
## invalidation -1.018e+00 2.261e-01 9.755e+01 -4.501 1.87e-05 ***
## blaming -6.849e-01 2.041e-01 1.289e+03 -3.355 0.000816 ***
## mean_reappraisal 8.185e-02 3.369e-01 2.518e+02 0.243 0.808235
## mean_solving -7.726e-01 3.669e-01 2.935e+02 -2.106 0.036096 *
## mean_sharing -3.302e-03 3.530e-01 2.320e+02 -0.009 0.992544
## mean_affection 1.309e-01 3.400e-01 2.498e+02 0.385 0.700618
## mean_invalidation 5.516e-01 6.762e-01 2.769e+02 0.816 0.415346
## mean_blaming -1.987e+00 8.025e-01 2.407e+02 -2.476 0.013983 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation matrix not shown by default, as p = 13 > 12.
## Use print(x, correlation=TRUE) or
## vcov(x) if you need it
Bezüglich der fixed effects egibt sich im Wesentlichen das gleiche Muster, dass wir schon im random intercept Modell gesehen hatten, nur dass die Gewichte auf Level-1 hier jetzt Aussagen über z.B. den durchschnittlichen Einfluss des reappraisal sind und die Effekte je nach Person, um diesen mittleren Effekte herum schwanken können.
Spezifische vorhergesagte Werte
Um den Effekt der random slopes zu verdeutlichen, können wir uns zwei Personen herausgreifen, die sich im Effekt der Lösungsvorschläge unterscheiden. Dafür bieten - wie schon beim random intercept Modell - die ranef einen Überblick über alle Zufallseffekte:
# Ausgabe der individuellen Zufallseffekte
# wegen head() nur die top 6 Zeilen
ranef(mod7)$id |> head()
## (Intercept) reappraisal solving sharing invalidation
## 2001 -0.07444811 0.0000000 0.1937274 0.1199613 0.000000
## 2009 -0.56470140 -0.2785829 -0.1968954 -0.2149273 0.000000
## 2010 1.12450916 0.0000000 0.0000000 0.0000000 1.394993
## 2016 -0.31310890 0.0000000 0.0000000 0.0000000 0.000000
## 2018 1.64828914 0.0000000 0.1248062 0.0000000 0.000000
## 2019 -0.45056091 -0.1360385 0.0000000 0.0000000 0.000000
Wie zu sehen ist, haben die beiden ersten Personen direkt gegenläufige Zufallseffekte. Gucken wir also, was passiert, wenn die beiden Personen jeweils mit einer IER Situation konfrontiert werden, in der nur solving vom Gegenüber gezeigt wird, und mit einer Situation, in der keine der Strategien gezeigt wird (ein dankbar einfacher Vergleichspunkt). Dafür können wir einen neuen Datensatz erstellen, in dem wir zwei hypothetische Situationen für diese beiden Personen erzeugen:
# Daten für die beiden Personen
new <- esm[esm$id %in% c(2001, 2009) & esm$index1 == 3, ]
new <- rbind(new, new)
rownames(new) <- c('2001:solving', '2009:solving', '2001:none', '2009:none')
Die hier ausgewählten beiden Zeilen enthalten praktischerweise schon alle Personenvariablen und wir müssen nur noch sicherstellen, dass die situativen Level-1 Prädiktoren die richtigen Werte annehmen.
# Künstliche Situationen erzeugen
new$reappraisal <- c(0, 0, 0, 0)
new$solving <- c(1, 1, 0, 0)
new$sharing <- c(0, 0, 0, 0)
new$affection <- c(0, 0, 0, 0)
new$invalidation <- c(0, 0, 0, 0)
new$blaming <- c(0, 0, 0, 0)
Jetzt können wir die vorhergesagten Werte für die beiden Personen in den beiden Situationen berechnen:
# Vorhersagen für die beiden Personen
predict(mod7, new) |> round(3)
## 2001:solving 2009:solving 2001:none 2009:none
## 1.358 0.683 0.241 -0.043
Die beiden Situationen der Person 2001 unterscheiden sich hier um den Effekt des Lösungsvorschlags, bestehend aus generellen Effekten ($\gamma_{10}$) und individuellen Effekten ($u_{1i}$):
Cross-Level-Interaktionen
Nachwievor ist die eigentlich Hypothese von Liu et al. (2024), dass sich die individuellen Effekte der Verhaltensweisen anhand der MD Gruppe unterscheiden sollten. In Formeln ausgedrückt, wird hier also behauptet, dass die random effects der slopes durch die Gruppe aufgeklärt werden können:
Neu dazu ist an dieser Stelle als der Term $\gamma_{11} \cdot w_i$ auf Level-2 gekommen. Hier wird also gesagt, dass wie Ausprägung des Slopes von einem Prädiktor abhängt. Wenn wir diese Gleichung dann in die Level-1 Gleichung einsetzen wird deutlich, warum dieser Effekt Cross-Level-Interaktion genannt wird: hier ergibt sich als neuer Term $\gamma_{11} \cdot w_i \cdot x_{ti}$.
In lme4 werden diese Interaktionen genauso aufgenommen, wie alle anderen Interaktionen. Ich formuliere an dieser Stelle die Interaktionen explizit mit : aus, auch wenn sich der Schreibaufwand mit der *-Notation erheblich verringern ließe:
# Modell mit allen Cross-Level Interaktionen
mod8 <- lmer(problem ~ 1 + reappraisal + solving + sharing + affection + invalidation + blaming +
mean_reappraisal + mean_solving + mean_sharing + mean_affection + mean_invalidation + mean_blaming +
group +
reappraisal:group + solving:group + sharing:group + affection:group + invalidation:group + blaming:group +
(1 + reappraisal + solving + sharing + invalidation || id), data = esm)
Die Ergebnisse des Modells könnten wir uns dann wie gewohnt mit summary ausgeben lassen. Allerdings macht es zunächst Sinn, auch die Interaktionen der Kontexteffekte mit in das Modell aufzunehmen, da für diese eigentlich in stärkerem Ausmaß als für die situativen Komponenten ein Unterschied aufgrund der Major Depression zu erwarten wäre:
# Modell mit allen Interaktionen
mod9 <- lmer(problem ~ 1 + reappraisal + solving + sharing + affection + invalidation + blaming +
mean_reappraisal + mean_solving + mean_sharing + mean_affection + mean_invalidation + mean_blaming +
reappraisal:group + solving:group + sharing:group + affection:group + invalidation:group + blaming:group +
group +
mean_reappraisal:group + mean_solving:group + mean_sharing:group + mean_affection:group + mean_invalidation:group + mean_blaming:group +
(1 + reappraisal + solving + sharing + invalidation || id), data = esm)
Bevor nun aber den erheblichen Aufwand betreiben die Ergebnisse eines Modells mit so vielen Effekten zu interpretieren, macht es Sinn per Modellvergleich festzustellen, ob diese Modellkomplexität überhaupt gerechtfertigt ist. Dafür können wir erneut den Devianzentest heranziehen:
# Modellvergleiche
anova(mod7, mod8, mod9)
## refitting model(s) with ML (instead of REML)
## Data: esm
## Models:
## mod7: problem ~ 1 + reappraisal + solving + sharing + affection + invalidation + blaming + mean_reappraisal + mean_solving + mean_sharing + mean_affection + mean_invalidation + mean_blaming + (1 + reappraisal + solving + sharing + invalidation || id)
## mod8: problem ~ 1 + reappraisal + solving + sharing + affection + invalidation + blaming + mean_reappraisal + mean_solving + mean_sharing + mean_affection + mean_invalidation + mean_blaming + group + reappraisal:group + solving:group + sharing:group + affection:group + invalidation:group + blaming:group + (1 + reappraisal + solving + sharing + invalidation || id)
## mod9: problem ~ 1 + reappraisal + solving + sharing + affection + invalidation + blaming + mean_reappraisal + mean_solving + mean_sharing + mean_affection + mean_invalidation + mean_blaming + reappraisal:group + solving:group + sharing:group + affection:group + invalidation:group + blaming:group + group + mean_reappraisal:group + mean_solving:group + mean_sharing:group + mean_affection:group + mean_invalidation:group + mean_blaming:group + (1 + reappraisal + solving + sharing + invalidation || id)
## npar AIC BIC logLik deviance Chisq Df Pr(>Chisq)
## mod7 19 6545.6 6648.0 -3253.8 6507.6
## mod8 33 6552.2 6730.1 -3243.1 6486.2 21.371 14 0.09249 .
## mod9 45 6561.7 6804.2 -3235.9 6471.7 14.500 12 0.26991
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Im Vergleich von mod7 zu mod8 wird der Einfluss der Gruppe auf das Intercept (zwei Gruppen, jeweils ein Effekt) und die Slopes (zwei Gruppen, jeweils sechs Effekte) getestet. Dabei fällt der Vergleich nicht statistisch bedeutsam aus, sodass wir hier davon ausgehen können, dass die MD keinen Einfluss auf die Problemwahrnehmung in IER hat. Der Vergleich von mod8 zu mod9 testet dann, ob die Interaktionen der Kontexteffekte mit der Gruppe (zwei Gruppen, jeweils sechs Effekte) einen signifikanten Einfluss auf die Problemwahrnehmung haben. Auch hier fällt der Test nicht signifikant aus, sodass wir davon ausgehen können, dass auch die habituellen IER Erfahrungen in ihrer Wirkung auf die Problemwahrnehmung nicht von der MD moderiert werden.
Auch im Pseudo-$R^2$ zeigen die Modelle nur geringfügige Unterschiede:
performance::r2(mod7)
## # R2 for Mixed Models
##
## Conditional R2: 0.377
## Marginal R2: 0.237
performance::r2(mod8)
## # R2 for Mixed Models
##
## Conditional R2: 0.384
## Marginal R2: 0.244
performance::r2(mod9)
## # R2 for Mixed Models
##
## Conditional R2: 0.392
## Marginal R2: 0.255
Liu et al. (2024, S. 68) berichten in ihrer Studie die Ergebnisse eines annähernd identischen Modells zu mod8 (wobei sie warmth noch als Kovariate aufnehmen). In beiden Modelle, sowohl mod8 als auch mod9, zeigt sich mit ihren Befunden konsistent, dass die situativen Effekte von reapparaisal (current MDD $\approx$ control $>$ remitted MDD) und affection (current MDD $>$ remitted MDD $\approx$ control) moderiert werden. Inhaltlich könnte man daraus schließen, dass diese beiden positiven Strategien des IER für Personen mit akuter Depression hilfreich sein können, um den Einschränkungen der traditionellen Emotionsregulation entgegenzuwirken.
An dieser Stelle ist vielleicht bereits aufgefallen, dass wir auch für die Verhaltensweisen Interaktionen aufgenommen haben, die in mod7 keinen random slope hatten. So etwas kann gemacht werden, wenn die Varianzen über alle Personen hinweg sehr klein sind, aber dennoch auf globale Effekte getestet werden soll, wobei einige Autor*innen wehement davon abraten (z.B. Bell et al., 2019). Auch ich würde dazu raten für diese Komponenten die Hypothese als falsch anzusehen, sobald sich herausstellt, dass es hinsichtlich dieser Level-1 Effekte keine relevanten random effects gibt, da dann keine Varianz existiert, welche durch unsere Prädiktoren aufgeklärt werden muss. Dennoch hat gerade aufgrund der Schätzprobleme, die auftreten wenn viele Zufallseffekte modelliert werden, ein inferenzstatistischer Test in den fixed effects etwas Beruhigendes (wobei diese Tests überproportional häufig signifikant werden).
Zusammenfassung
In diesem Beitrag haben wir in extremen Detail die Modellierung von ESM Daten mit gemischten Modellen gesehen. Dabei waren wir in der Lage die Ergebnisse von Liu et al. (2024) zu reproduzieren und konnten anhand der komplexeren Modelle auch einen Eindruck gewinnen, wie in Situationen vorgegangen werden sollte, in denen nicht alles reibungslos funktioniert.
Literatur
Barr, D. J., Levy, R., Scheepers, C., & Tily, H. J. (2013). Random effects structure for confirmatory hypothesis testing: Keep it maximal. Journal of Memory and Language, 68(3), 255–278. https://doi.org/10.1016/j.jml.2012.11.001
Bell, A., Fairbrother, M. & Jones, K. Fixed and random effects models: making an informed choice. Quality and Quantity, 53, 1051–1074 (2019). https://doi.org/10.1007/s11135-018-0802-x
Liu, D. Y., Strube, M. J., & Thompson, R. J. (2024). Do emotion regulation difficulties in depression extend to social context? Everyday interpersonal emotion regulation in current and remitted major depressive disorder. Journal of Psychopathology and Clinical Science, 133(1), 61–75. https://doi.org/10.1037/abn0000877
Nakagawa, S., Johnson, P. C. D., & Schielzeth, H. (2017). The coefficient of determination R2 and intra-class correlation coefficient from generalized linear mixed-effects models revisited and expanded. Journal of The Royal Society Interface, 14(134), 20170213. https://doi.org/10.1098/rsif.2017.0213
Park, J., Cardwell, R., & Yu, H.-T. (2020).Specifying the Random Effect Structure in Linear Mixed Effect Models for Analyzing Psycholinguistic Data. Methodology, 16(2), 92–111. https://doi.org/10.5964/meth.2809
Yaremych, H. E., Preacher, K. J., & Hedeker, D. (2021). Centering Categorical Predictors in Multilevel Models: Best Practices and Interpretation. Psychological Methods, 28(3), 613-630. https://doi.org/10.1037/met0000434
](/media/header/couple-bench.jpg)