](/media/header/prism_colors.jpg)
Einleitung
Vielleicht kam Ihnen aus der Welt der Verschwörungstheorien mal zu Ohren, dass die Anzahl der COVID-Erkrankungen mit der Anzahl der 5G-Tower zusammenhängt. Aber wussten Sie, dass auch der Konsum von Eiscreme und die Anzahl der Morde in New York, oder die Anzahl von Nicolas-Cage-Filmauftritten mit der Anzahl weiblicher Redakteure beim Harvard Law Review positiv korreliert sind? $^1$
Natürlich wissen Sie bereits, dass solch eine Korrelation kein Beweis dafür ist, dass 5G-Strahlung für COVID-Erkrankungen kausal verantwortlich ist, oder dass Eiskonsum zu einer erhöhten Mordrate führt. Auch bei der Regression wird zwar häufig vom Einfluss von Variablen aufeinander gesprochen – doch auch hierbei handelt es sich um eine Zusammenhangsanalyse, die oftmals gleichzeitig erhobene Konstrukte betrachtet (z.B. aus Fragebogenstudien) und mit der Korrelation eng verwandt ist. So würden wir, wenn wir berechnen würden, ob COVID-Fälle durch 5G-Tower vorhergesagt werden, zu genau dem gleichen Ergebnis kommen, wie wenn wir die Vorhersagerichtung austauschen würden und die Anzahl der 5G-Tower durch COVID-Fallzahlen vorhersagen ließen. Auch die Regression kann per se keine Aussagen über Kausalzusammenhänge machen!
Um sich Rückschlüssen über die wahren Wirkungsbeziehungen aber zumindest anzunähern, können wir den Einfluss von Drittvariablen auf korrelative Zusammenhänge näher betrachten. (So wird z.B. die Korrelation zwischen 5G-Towern mit den COVID-Erkrankungen durch die Ballungsgebiete erklärt, in denen die Leute enger beieinander leben.) In dieser Sitzung beschäftigen wir uns daher mit der Partial- und der Semipartialkorrelation, d.h. Methoden, mit denen der Einfluss einer oder mehrerer Drittvariablen kontrolliert werden kann, um hierdurch Scheinkorrelationen, redundante oder maskierte Zusammenhänge aufzudecken.
Anmerkungen:
$^1$ Falls Sie noch mehr solcher Scheinkorrelationen zu Gemüte führen wollen, gibt es einen ganzen Blog, der sich mit solchen spurious correlations befasst.
Vorbereitung des Datensatzes
Der Datensatz Depression, den wir zur Illustration des heutigen Themas heranziehen werden, enthält fiktive Daten bezüglich Depressivitätswerten und einigen anderen, damit in Beziehung stehenden Variablen. Zusätzlich sind die kategorialen Variablen Intervention und Geschlecht enthalten, die wir in dieser Sitzung aber nicht weiter betrachten werden.
| Variable | Kodierung |
|---|---|
Lebenszufriedenheit | 1 - 10 |
Episodenanzahl | 1 - 10 |
Depressivitaet | 1 - 10 |
Neurotizismus | 1 - 10 |
Diesen Satz laden wir uns erst einmal herunter und prüfen die Struktur des Datensatzes:
load(url("https://pandar.netlify.app/daten/Depression.rda"))
str(Depression)
## 'data.frame': 90 obs. of 6 variables:
## $ Lebenszufriedenheit: num 7 5 8 6 6 8 7 5 8 6 ...
## $ Episodenanzahl : num 4 5 7 4 9 7 6 6 8 7 ...
## $ Depressivitaet : num 7 8 6 5 8 8 7 6 8 6 ...
## $ Neurotizismus : num 5 3 6 5 5 6 6 5 6 7 ...
## $ Intervention : Factor w/ 3 levels "Kontrollgruppe",..: 1 1 1 1 1 1 1 1 1 1 ...
## $ Geschlecht : Factor w/ 2 levels "0","1": 1 2 1 2 2 2 2 1 2 1 ...
Da wir die Variablen Intervention und Geschlecht für diese Sitzung nicht brauchen, entfernen wir diese mit dem uns bereits bekannten subset()-Befehl:
dat <- subset(Depression, select = -c(Intervention, Geschlecht))
rm(Depression) # das nicht benötigte Objekt wird wieder gelöscht
Hier habe ich bei der Zuweisung in ein neues Objekt dat als kürzeren Namen für unser Dataframe gewählt, um etwas Platz im Skript zu sparen und das Auge zu schonen. So können wir uns besser auf das Wesentliche konzentrieren.
Vorher müssen wir allerdings noch die Kodierung der Variable Neurotizismus invertieren. Im ursprünglichen Datensatz wurde eine hohe Punktzahl als höhere emotionale Stablität (und damit geringerer Neurotizismus) kodiert, diese Kodierung wollen wir umkehren, damit eine höhere Punktzahl auch tatsächlich einen höheren Neurotizismus anzeigt:
# Neurotizismus invertieren
dat$Neurotizismus <- 11 - (dat$Neurotizismus)
Erinnerung: Korrelation
Wie Sie bereits aus Statistik 1 wissen, misst der Korrelationskoeffizient $r_{xy}$ die Stärke und Richtung einer linearen Beziehung zwischen zwei Variablen $X$ und $Y$:
Der Wert von $r_{xy}$ liegt dabei immer im Wertebereich zwischen +1 und -1. Man kann auch sagen, dass die Kovarianz “skaliert” wird, um diese besser interpretieren zu können, deshalb steht in obiger Formel auch, $\mathbb{C}ov[X,Y]$ (Kovarianz zwischen $X$ und $Y$) geteilt durch das Produkt aus der Wurzel der Varianzen $\mathbb{V}ar[X]$ und $\mathbb{V}ar[Y]$. Je höher der absolute Wert einer Korrelation zweier Variablen ist, desto mehr Varianz teilen die beiden Variablen miteinander.
Empirisches Beispiel
Schauen wir uns zwei Variablen aus unserem Datensatz ab, bei denen die Vermutung nahe liegt, dass es einen (umgekehrten) Zusammenhang geben könnte: Lebenszufriedenheit und Depressivität. Sind Personen, die angeben, zufriedener mit ihrem Leben zu sein, weniger depressiv? Diese vermutete Korrelation lässt sich grafisch in einem Streudiagramm darstellen, was Sie mit dem Wissen aus den Lektionen zum ggplot2-Paket wie folgt bewältigen können:
library(ggplot2) # notwendiges Paket für Grafiken laden
ggplot(dat, aes(x = Lebenszufriedenheit, y = Depressivitaet)) +
geom_point() +
theme_minimal() +
geom_smooth(method = "lm", se = FALSE)
## `geom_smooth()` using formula = 'y ~ x'
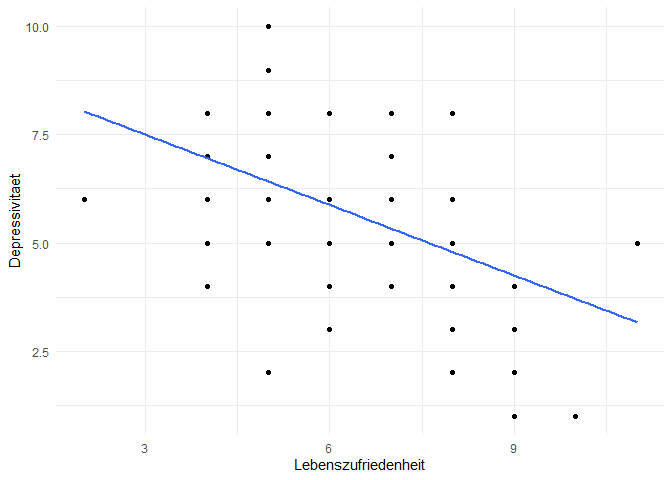
In dieser Abbildung mit einer dazugehörigen Regressionsgerade wird deutlich, dass hier deskriptiv ein negativer Zusammenhang vorliegt. Das heißt, eine höhere Lebenszufriedenheit geht mit einer geringeren Depressivität einher. Zu beachten ist hierbei natürlich, dass wir die x- und y-Achsen beliebig vertauschen könnten und aus diesem Befund daher keine Aussage über die Wirkungsrichtung ableitbar ist. Ob die Lebenszufriedenheit zu einer niedrigen Depressivität führt, oder eine niedrigere Depressivität nicht ursächlich für eine höhere Lebenszufriedenheit sein könnte, bleibt auf Basis dieser Daten komplett offen.
Mit cor.test() können wir diesen Zusammenhang auch inferenzstatistisch überprüfen:
cor.test(dat$Depressivitaet, dat$Lebenszufriedenheit)
##
## Pearson's product-moment correlation
##
## data: dat$Depressivitaet and dat$Lebenszufriedenheit
## t = -5.0256, df = 88, p-value = 2.614e-06
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## -0.6188046 -0.2938777
## sample estimates:
## cor
## -0.4722292
… und entnehmen dem Output entnehmen, dass die Korrelation $r =$ -0.47 mit $p$ < .001 statistisch signifikant von 0 verschieden ist. Quadrieren wir den Korrelationskoeffizienten, erhalten wir den Determinationskoeffizienten $R^2 =$ 0.22. Dieser gibt uns den Anteil der gemeinsamen Varianz zwischen den beiden Variablen an.
Die Beziehung zwischen der Stärke eines linearen Zusammenhangs und dem Anteil der gemeinsamen Varianz lässt sich durch Venn-Diagramme gut veranschaulichen:
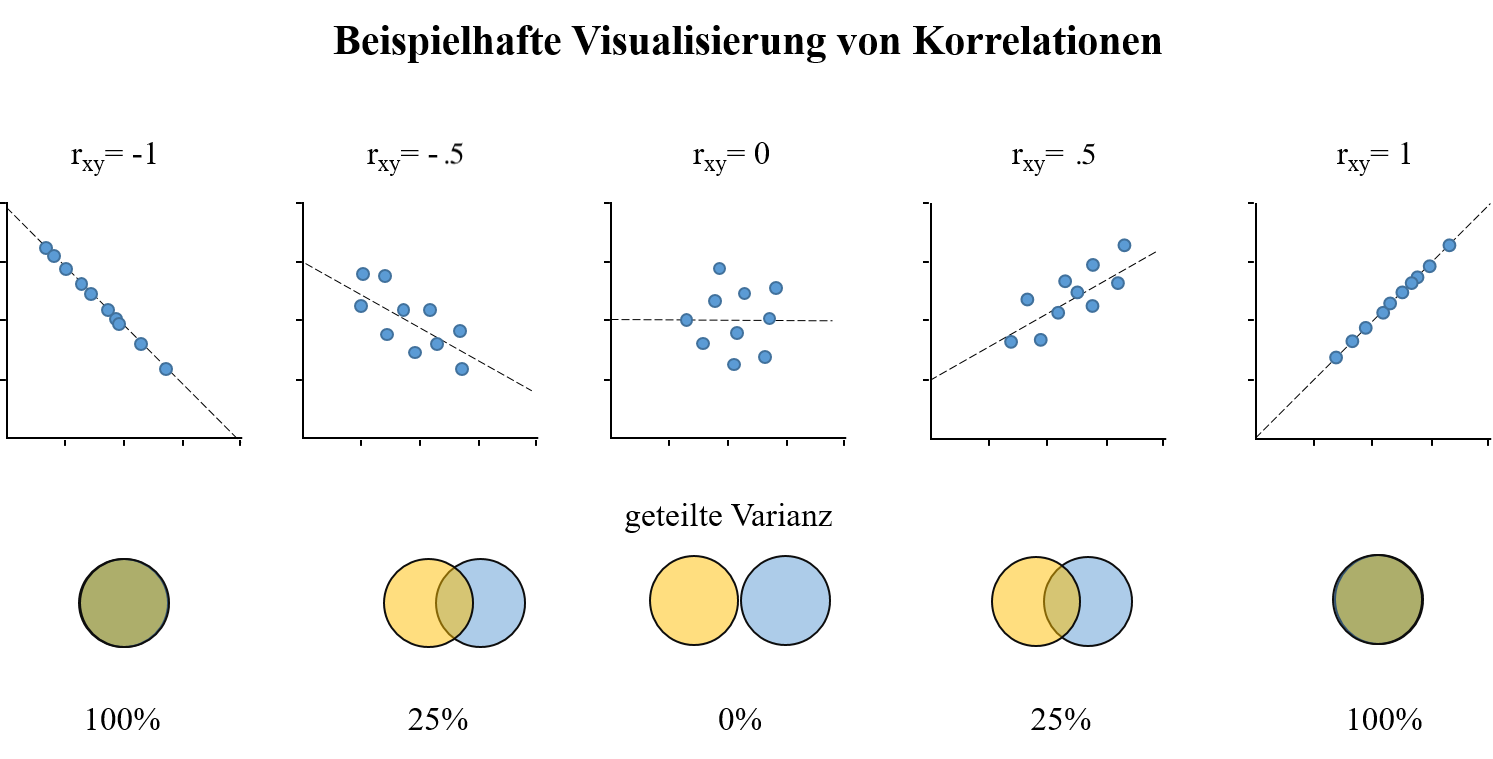
Die Überlappung der beiden Kreise stellt die geteilte Varianz, d.h. die Korrelation dar, während die sich nicht überlappenden Flächen die voneinander unabhängig variierenden Anteile der Variablen ausmachen.
Drittvariablen
Der Zusammenhang zwischen zwei Variablen $X$ und $Y$ kann aber auch durch eine Drittvariable $Z$ beeinflusst werden. In diesem Venn-Diagramm ist sie durch den roten Kreis verbildlicht:
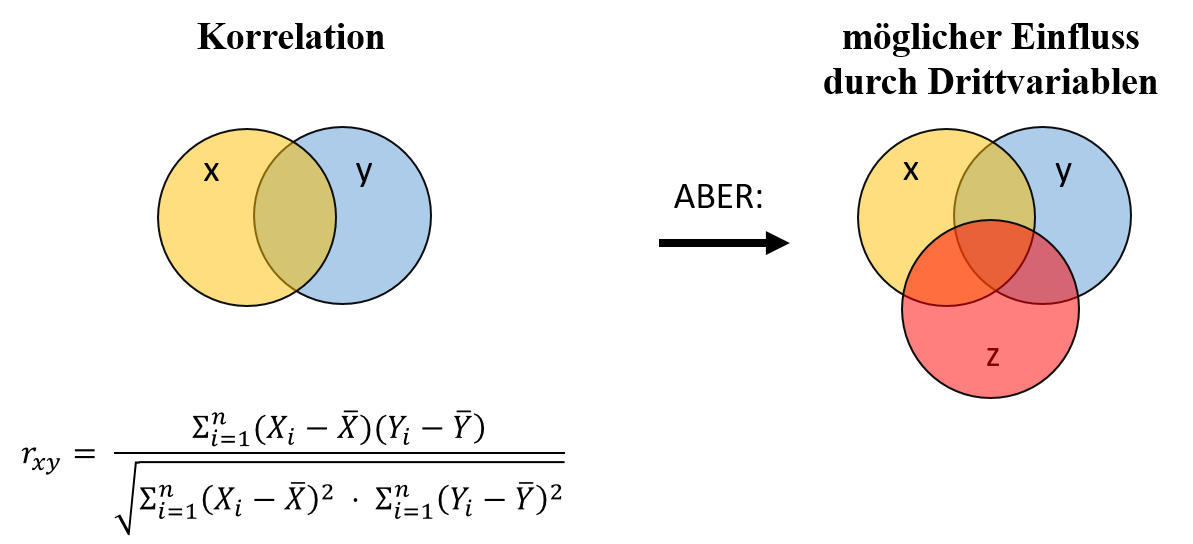
In unserem Datensatz wollen wir uns als eine solche Drittvariable Neurotizismus unter die Lupe nehmen. Während Lebenszufriedenheit und Depressivität in diesem Datensatz Zustände bezeichnen, die potenziell vorübergehend und zeitlich veränderlich sind (states). Im Gegensatz dazu ist Neurotizismus eine Persönlichkeitseigenschaft (trait), die eine stabile, langfristige Tendenz einer Person beschreibt, negative Emotionen wie Angst, Ärger und Traurigkeit zu erleben (vgl. Big-Five-Persönlichkeitsmodell nach Costa & McCrae, 1999).
Daher liegt es nahe, dass Neurotizismus im Zusammenhang mit Lebenszufriedenheit und Depressivität stehen könnte. Testen wir den vermuteten Zusammenhang in zwei einzelnen Korrelationstests:
# Korrelation der Drittvariablen mit den beiden ursprünglichen Variablen
cor.test(dat$Neurotizismus, dat$Lebenszufriedenheit)
##
## Pearson's product-moment correlation
##
## data: dat$Neurotizismus and dat$Lebenszufriedenheit
## t = -8.2276, df = 88, p-value = 1.587e-12
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## -0.7623706 -0.5238208
## sample estimates:
## cor
## -0.659383
cor.test(dat$Neurotizismus, dat$Depressivitaet)
##
## Pearson's product-moment correlation
##
## data: dat$Neurotizismus and dat$Depressivitaet
## t = 12.289, df = 88, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.7035951 0.8603383
## sample estimates:
## cor
## 0.7948675
In der Tat zeigen die Ergebnisse, dass der Neurotizismus sowohl mit der Lebenszufriedenheit (-0.66) als auch mit Depressivität (0.79) statistisch bedeutsam korreliert.
Ist der Zusammenhang zwischen Lebenszufriedenheit und Depressivität also allein auf den Neurotizismus zurückzuführen? Oder besteht noch ein Zusammenhang zwischen den beiden, wenn man den Einfluss der Neurotizismus kontrolliert? Um dies zu überprüfen, müssen wir auf Methoden zur Kontrolle von Drittvariablen und zur Aufdeckung von Scheinkorrelationen, redundanten oder maskierten Zusammenhängen zurückgreifen: Die Partial- und Semipartialkorrelation.
Partialkorrelation
Die Partialkorrelation ist die bivariate Korrelation zweier Variablen $X$ und $Y$, die bestehen würde, wenn zuvor der Einfluss einer weiteren Variable $Z$ statistisch kontrolliert (d.h. “auspartialisiert” oder “herausgerechnet”) wird:
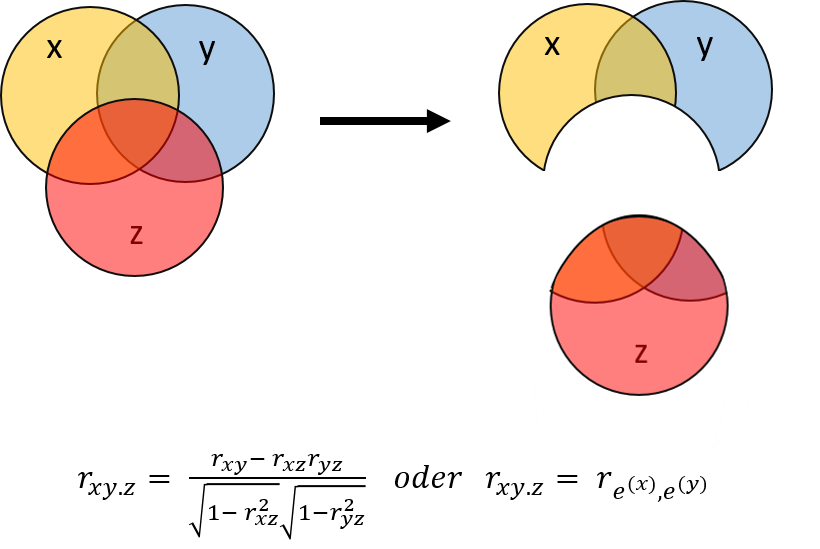
Denken wir nun an die Regression zurück, können wir die Partialkorrelation konzeptuell als etwas damit sehr verwandtes verstehen: Die Partialkorrelation $r_{xy.z}$ (dargestellt als Überlappung zwischen $X$ und $Y$ Abbildung, minus die Überlappung mit $Z$) kann auch als Korrelation der Regressionsresiduen von $X$ und von $Y$ verstanden werden, die nicht durch einen Prädiktor $Z$ erklärt werden. Ausführlichere Infos dazu gibt es in Appendix A.
An unserem empirischen Beispiel werden wir das praktisch veranschaulichen.
Beispiel: Zusammenhang von Neurotizismus mit Lebenszufriedenheit und Depressivität
Nun heißt es näher zu betrachten, ob Neurotizismus eine mögliche konfundierende Variable in der Beziehung zwischen Lebenszufriedenheit und Depressivität darstellt. Diese Vermutung können wir mit einer Partialkorrelation überprüfen, für die wir die Residuen heranziehen. Diese bekommen wir aus einer einfachen Regression.
Erstmal stellen wir zwei einfache Regressionsmodelle mit Neurotizismus als demjenigen Prädiktor auf, dessen Einfluss wir aus Depressivitaet und Lebenszufriedenheit isolieren möchten.
# Regression
reg_depr_neuro <- lm(Depressivitaet ~ Neurotizismus, data = dat)
reg_lz_neuro <- lm(Lebenszufriedenheit ~ Neurotizismus, data = dat)
Der Einfachheit halber legen wir die Residuen (also den von Neurotizismus unabhängigen Varianzteil) in einem neuen Objekt ab:
# Residuen in Objekt ablegen (Anteil von Depr., der nicht durch Neuro. erklärt wird)
res_depr_neuro <- residuals(reg_depr_neuro)
# Residuen in Objekt ablegen (Anteil von LZ, der nicht durch Neuro. erklärt wird)
res_lz_neuro <- residuals(reg_lz_neuro)
Partialkorrelation als Korrelation der Residuen
Damit können wir die Partialkorrelation nun bestimmen:
cor(res_depr_neuro, res_lz_neuro)
## [1] 0.1137543
Mit einem Wert von $r_{xy.z}$ = 0.1137543 ist diese Korrelation viel niedriger, als die urprüngliche Korrelation zwischen Depressivitaet und Lebenszufriedenheit ohne Berücksichtigung der Drittvariablen – der ursprüngliche Zusammenhang verschwindet also nahezu.
Beachten Sie, dass wir hier NICHT cor.test() verwenden, da die inferenzstatistische Absicherung die falschen Freiheitsgrade nutzen würde. Für interessierte Lesende findet sich in Appendix A eine genauere Erläuterung der Problematik.
Partialkorrelation mit Funktion
Natürlich müssen wir nicht jedes Mal die Residuen manuell berechnen, sondern können hierfür – nachdem Ihnen die Logik hinter der Partialkorrelation an diesem Beispiel deutlich werden konnte – auf eine Funktion zurückgreifen, die uns $r_{xy.z}$ direkt berechnet. Diese ist aber nicht in den Basis-Paketen erhalten, weshalb wir erstmal ppcor installieren und das Paket laden müssen.
# Paket für Partial- und Semipartialkorrelation
install.packages("ppcor")
library(ppcor)
Mit der Funktion pcor.test() lässt sich die Partialkorrelation direkt ermitteln:
# Partialkorrelation mit Funktion
pcor.test(x = dat$Depressivitaet, # Das Outcome
y = dat$Lebenszufriedenheit, # Die Prädiktorvariable
z = dat$Neurotizismus) # wird aus X und Y auspartialisiert
## estimate p.value statistic n gp Method
## 1 0.1137543 0.2884924 1.067961 90 1 pearson
Vorsicht: Hier herrscht Verwechslungsgefahr bei der Notation der Argumente! Während wir typischerweise bei der Regression mit $x$ den Prädiktor meinen, dessen Einfluss auf das Kriterium $y$ untersucht werden soll, haben die Argumente-Namen der pcor.test-Funktion in diesem Fall nichts damit zu tun. Mit x ist hier die primäre Variable gemeint, aus deren gemeinsamer Varianz mit y der Varianzanteil von z herauspartialisiert werden soll. Das entspricht eher der Notation in den Venn-Diagrammen in dieser Lektion. Bei den Semipartialkorrelationen weiter unten wird diese Reihenfolge noch relevant!
In diesem Fall beträgt die Partialkorrelation $r_{xy.z}$ also 0.11 und ist nicht signifikant von 0 verschieden ($p$ = 0.288).
Unter Kontrolle des Neurotizismus verschwindet der ursprüngliche Zusammenhang zwischen Depressivität und Lebenszufriedenheit. Es handelt sich also um eine Scheinkorrelation zwischen den beiden Variablen, die durch den Neurotizismus erklärt wird. Anders ausgedrückt: Wie ausgeprägt die Depressivität einer Person ist, hängt nicht direkt mit ihrer Lebenszufriedenheit zusammen, sondern beide hängen damit zusammen, wie neurotisch die Person ist.
Übertragen auf die Regression: Wenn wir in ein einfaches Regressionsmodell mit Prädiktor $x_1$ = Lebenszufriedenheit zusätzlich den Prädiktor $x_2$ = Neurotizismus aufnehmen, wird das Regressionsgewicht $b_1$ von Lebenszufriedenheit nicht signifikant ($p$ = 0.288).
# Einfache lineare Regression von Depressivität auf Neurotizismus
mod1 <- lm(Depressivitaet ~ Lebenszufriedenheit, data = dat)
summary(mod1)$coefficients |> round(3)
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 9.122 0.709 12.862 0
## Lebenszufriedenheit -0.542 0.108 -5.026 0
# Erweiterte Regression, die Episodenanzahl einschließt
mod2 <- lm(Depressivitaet ~ Lebenszufriedenheit + Neurotizismus, data = dat)
summary(mod2)$coefficients |> round(3)
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.008 0.950 1.061 0.292
## Lebenszufriedenheit 0.105 0.099 1.068 0.288
## Neurotizismus 0.881 0.089 9.950 0.000
Auswirkung des Einschlusses von Drittvariablen
Wenn wir eine Drittvariable berücksichtigen und sich daraufhin die ursprüngliche Korrelation verändert, kann es zwei Szenarien geben: Entweder der Betrag der Korrelation (d.h. die Effektgröße ohne das Vorzeichen) wird kleiner, oder er wird größer. Hier finden Sie eine Interpretationshilfe, was dies bedeutet:
- Scheinkorrelation: Die Partialkorrelation wird (betraglich) kleiner als die ursprüngliche Korrelation ($|r_{xy.z}| < |r_{xy}|$)
Wie in unserem Bespiel teilen alle drei Variablen miteinander Varianz. Partialisiert man nun eine Variable aus dem Zusammenhang der beiden anderen Variablen heraus, wird die geteilte Varianz weniger, womit die Korrelation betraglich sinkt (beachten Sie, dass es sich nur um die absolute Größe, d.h. den Betrag der Korrelation handelt, und nicht um die Vorzeichen!). Dieser Fall ist der am häufigsten eintretende, da in der Forschung oft Variablen auspartialisiert werden, weil es theoretische Annahme gibt, warum die Variablen Varianz teilen sollten, man aber eine isolierte Assoziation (Beziehung) zwischen $X$ auf $Y$ betrachten möchte. Der im Tutorial dargestellte Effekt ist die deutlichste Form dieser Klasse an Veränderung, bei der die Partialkorrelation dann nicht mehr statistisch signifikant wird.
- Suppressoreffekt: Partialkorrelation ist (betraglich) größer als die ursprüngliche Korrelation ($|r_{xy.z}| > |r_{xy}|$)
Es kann aber auch passieren, dass eine Drittvariable $Z$, die mit einer abhängigen Variable $X$ unkorreliert ist, dafür aber mit der unabhängigen Variable $Y$ korreliert ist. Wenn man den Einfluss der Drittvariable $Z$ mitberücksichtigt, wird die Partialkorrelation dadurch höher, nicht niedriger. In einem solchen Fall liegt meist ein Suppressoreffekt vor (ein Teil der Varianz in $X$ wird durch die Drittvariable unterdrückt bzw. supprimiert, der für den Zusammenhang mit $Y$ irrelevant ist). Der klassische Suppressoreffekt tritt dann auf, wenn $Z$ mit $X$ zu 0 korreliert (was nicht immer der Fall sein muss), mit $Y$ aber eine bedeutende Korrelation aufweist (vgl. untenstehende Abbildung). Dann wird der für $X$ irrelevante Varianzanteil in $Y$ durch den Supressor $Z$ gebunden, wodurch der relative Anteil an geteilter Varianz zwischen $X$ und $Y$ größer wird (Sonderformen eines Suppressoreffekts finden Interessierte in Eid & Gollwitzer, 2017; Kap. 18, 19).
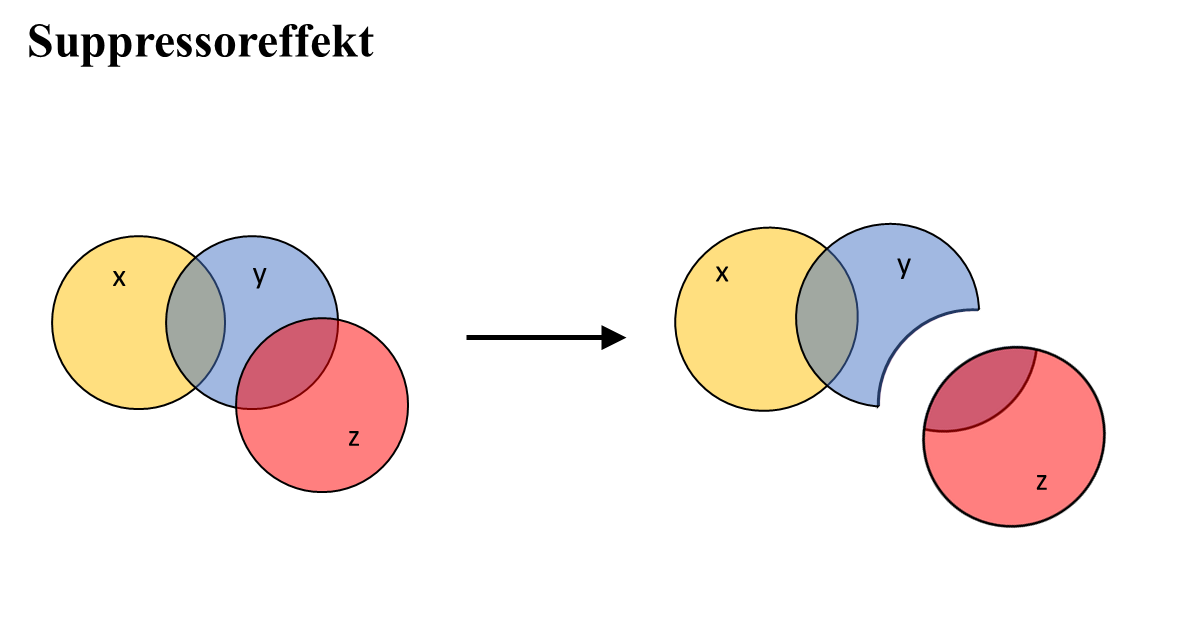
Ein Beispiel: Sie untersuchen den Zusammenhang zwischen $X$ = habitueller Stimmung (trait), $Y$ = momentaner Stimmung (state), und $Z$ = Stimmungsschwankungen (also wie stark die momentane Stimmung von ihrem durchschnittlichen Befinden abweicht).
Die habituelle Stimmung $X$ kann man aus der momentanen Stimmung $Y$ nur schlecht vorhersagen, ihr Zusammenhang ist also nicht sehr stark. Auch korreliert die habituelle Stimmung nicht mit der Stärke der Stimmungsschwankungen $Z$. Jedoch hängen die momentane Stimmung und das Ausmaß der Stimmungsschwankungen durchaus zusammen. In einer Partialkorrelation wird die Korrelation von $X$ (habitueller Stimmung) und $Y$ (momentaner Stimmung) noch größer, wenn für den Einfluss von $Z$ (Stimmungsschwankungen) kontrolliert wird. Daraus können Sie schließen, dass Stärke der Stimmungsschwankungen in diesem Fall als Suppressor agiert. Die inhaltliche Begründung wäre, dass die Stärke der Stimmungsschwankungen den Teil der Varianz mit $Y$ = momentaner Stimmung gemein hat und “bindet” bzw. supprimiert, der spezifisch für eine Situation ist. Wenn diese Varianz herauspartialisiert ist, kann der wahre Zusammenhang der nicht situationsbezogenen Variablenanteile stärker zum Tragen kommen - die Partialkorrelation wird größer. (Dieses empirische Beispiel ist bei Eid & Gollwitzer, 2018, im Kapitel 19.8 noch ausführlicher erklärt.)
Semipartialkorrelation
Es ist auch möglich, den Einfluss einer Drittvarible $Z$ nur einer der beiden Variablen (z.B. nur aus $Y$, aber nicht aus $X$ herauszurechnen), wenn inhaltliche Gründe dafür sprechen. Die Methode, mit der das bewerkstelligt werden kann, nennt sich Semipartialkorrelation. Die Semipartialkorrelation $r_{x(y.z)}$ entspricht der Korrelation zwischen $X$ und dem Varianzanteil von $Y$, der nicht durch $Z$ erklärt wird (Residuum). Im Gegensatz zur Partialkorrelation wird hierbei also die gesamte Varianz von $X$ in der Analyse belassen:
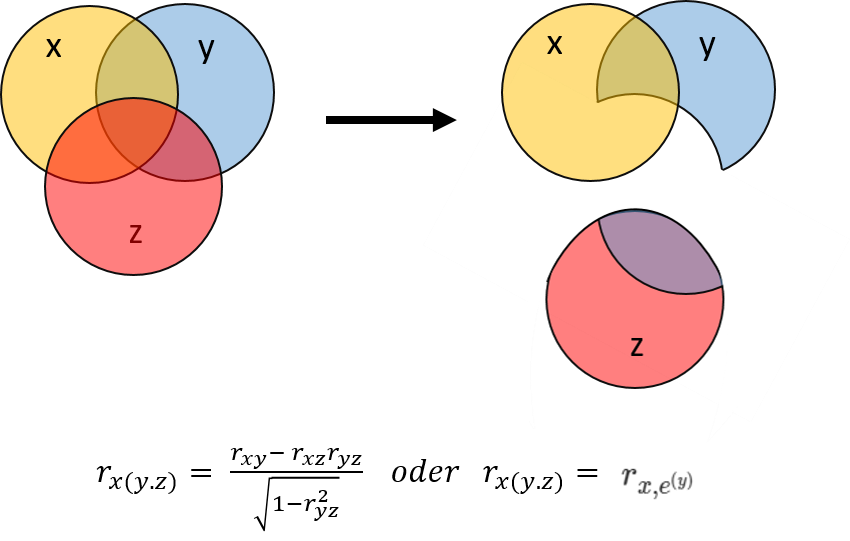
Wenn wir unser Beispiel wieder aufgreifen, entspricht das konzeptuell der Korrelation zwischen Depressivität (ihrer gesamten Varianz) und dem Residualateil von Lebenszufriedenheit, der von Neurotizismus unabhängig ist:
# Semipartialkorrelation als Korrelation zwischen Depressivität (X) und
# Lebenszufriedenheit (Y), bereinigt um den Einfluss von Neurotizismus (Z) auf
# Lebenszufriedenheit (Y)
cor(dat$Depressivitaet, res_lz_neuro)
## [1] 0.06902416
Auch hier verwenden wir absichtlich die Funktion cor() statt cor.test(), da die inferenzstatistische Absicherung nicht korrekt durchgeführt werden würde aufgrund der Freiheitsgrade.
Mit der Funktion spcor.test() aus dem zuvor installierten Paket ppcor lässt sich die Semipartialkorrelation direkt ermitteln und die inferenzstatistische Absicherung gelingt.
# Semipartialkorrelation mit Funktion
spcor.test(x = dat$Depressivitaet, # Outcome
y = dat$Lebenszufriedenheit, # Prädiktor
z = dat$Neurotizismus) # wird aus Y, aber nicht X auspartialisiert
## estimate p.value statistic n gp Method
## 1 0.06902416 0.5203964 0.6453536 90 1 pearson
Der Koeffizient der Semipartialkorrelation $r_{x(y.z)}$ beträgt 0.07 und ist nicht signifikant ($p$ = 0.52). Es zeigt sich also, dass der ursprüngliche Zusammenhang zwischen Depressivität und Lebenszufriedenheit ($r_{xz}$ = -0.47) verschwindet, wenn der Einfluss des Neurotizismus auf die Lebenszufriedenheit kontrolliert wird.
Wann brauche ich die Partial- und wann die Semipartialkorrelation?
Schließlich stellt sich natürlich die Frage, in welchem theoretischen Kontext man die Semipartialkorrelation gegenüber der Partialkorrelation überhaupt nutzen sollte.
Das kann sich in theoretischen Annahmen zur Wirkungsrichtung begründen. Bei der Partialkorrelation nehmen Sie an, dass die Drittvariable $Z$ mit beiden Variablen $X$ und $Y$ zusammenhängt. In unserem Beispiel stellen wir uns den Trait Neurotizismus als Ursache für die States Lebenszufriedenheit und Depressivität vor, daher wäre eine Partialkorrelation angebracht. Die Semipartialkorrelation ist dann das Mittel der Wahl, wenn die Drittvariable nur eine der beiden Variablen $X$ oder $Y$ theoretisch kausal bedingt und zwischen den anderen Variablen lediglich ein ungerichteter Zusammenhang angenommen wird. In unserem Beispiel würde dies bedeuten, dass wir beispielsweise lediglich annehmen, dass Neurotizismus die Depressivität. beeinflusst, nicht aber die Lebenszufriedenheit. Da solche Annahmen schwer empirisch zu stützen sind, greift man in der Praxis meist auf die Partialkorrelation zurück.
Trotzdem gibt es noch einen Bereich, in dem sich die Semipartialkorrelation als nützlich erweist: im Kontext der Regression.
Rolle der Semipartialkorrelation in der Regression
Relevant wird das Konzept der Semipartialkorrelation im Rahmen der multiplen Regression bei der Berechnung des Determinationskoeffizienten $R^2$.
Erinnerung: Einfache Regression
In Statistik 1 haben wir bereits erfahren, dass in der einfachen linearen Regression der standardisierte $\beta$-Koeffizient der Korrelation $r_{xy}$ zwischen Prädiktor $x$ und Kriterium $y$ entspricht:
# Paket für standardisierte Beta-Koeffizienten
library(lm.beta)
# Einfache lineare Regression von Depressivität auf Neurotizismus
mod1 <- lm(Depressivitaet ~ Neurotizismus, data = dat)
lm.beta(mod1)$standardized.coefficients
## (Intercept) Neurotizismus
## NA 0.7948675
# Korrelation entspricht dem Beta-Koeffizienten
cor(dat$Depressivitaet, dat$Neurotizismus)
## [1] 0.7948675
Entsprechend ist die quadrierte Korrelation $r^2$ = 0.79$^2$ = 0.63 identisch mit dem Determinationskoeffizienten $R^2$ des Modells.
Beispiel: Multiple Regression
Wir zeigen nun am Beispiel eines Modells mit zwei Prädiktoren – die in diesem Fall beide statistisch signifikanten Varianzanteil an der abhängigen Variable erklären – die Bedeutung der Semipartialkorrelation hierfür auf. Wir gehen hier wieder zur Notation über, in der $y$ die Outcome-Variable (das Kriterium) kennzeichnet und wir die Prädiktoren $x_1$ und $x_2$ nennen.
Bei multipler Regression ist der Determinationskoeffizient so definiert, dass für jeden weiteren Prädiktor das Quadrat einer Semipartialkorrelation aufaddiert wird, um den multiplen Determinationskoeffizienten zu bestimmen. Dabei wird der schon aufgenommene Prädiktor aus dem neuen herauspartialisiert und der Rest dann mit dem Kriterium korreliert (also die Semipartialkorrelation bestimmt):
$R^2 = r^2_{yx1} + r^2_{y(x2.x1)} + r^2_{y(x3.x2x1)}$
In unserem Fall haben wir lediglich zwei Prädiktoren, wobei wir als $x_2$ diesmal die Episodenanzahl wählen. Für diese lassen wir uns direkt die standardisierten $\beta$-Koeffizienten ausgeben:
# Ein Modell mit zwei Prädiktoren
mod2 <- lm(Depressivitaet ~ Neurotizismus + Episodenanzahl,
data = dat)
lm.beta(mod2) |> summary() # fügt std. Betas zum Output hinzu
##
## Call:
## lm(formula = Depressivitaet ~ Neurotizismus + Episodenanzahl,
## data = dat)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.02852 -0.51230 -0.08009 0.65804 1.74145
##
## Coefficients:
## Estimate Standardized Std. Error t value Pr(>|t|)
## (Intercept) -1.17653 NA 0.46337 -2.539 0.0129 *
## Neurotizismus 0.82155 0.79784 0.05088 16.147 < 2e-16 ***
## Episodenanzahl 0.51622 0.39471 0.06462 7.988 5.23e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.8243 on 87 degrees of freedom
## Multiple R-squared: 0.7876, Adjusted R-squared: 0.7827
## F-statistic: 161.3 on 2 and 87 DF, p-value: < 2.2e-16
Wir legen den Determinationskoeffizienzen in ein Objekt ab:
R2_mod2 <- summary(mod2)$r.squared
…und berechnen auch die Korrelation zwischen $y$ = Depression und $x_1$, sowie die Semipartialkorrelation zwischen $y$ und $x_2$ = Episodenanzahl, wenn der Einfluss von $x_1$ = Neurotizismus herausgerechnet wird. Zur leichteren Bearbeitung legen wir sie im Objekt corrs (Korrelationen) ab.
r_yx1 <- cor(dat$Depressivitaet, dat$Neurotizismus)
r_yx2.x1 <- spcor.test(x = dat$Depressivitaet, # Outcome
y = dat$Episodenanzahl, # hier rauspartialisieren
z = dat$Neurotizismus)$estimate
corrs <- data.frame(r_yx1, r_yx2.x1)
corrs
## r_yx1 r_yx2.x1
## 1 0.7948675 0.3947031
Wie in der obigen Formel abstrakt dargestellt, entspricht auch in unserem konkreten Fall $R^2$ der Summe der quadrierten Korrelationen:
sum(corrs^2) # Das entspricht dem Determinationskoeffizienten R^2
## [1] 0.7876049
R2_mod2
## [1] 0.7876049
Hierfür könnte man die Partialkorrelationen nicht verwenden – denn für jede Korrelation zwischen einem neuen hinzukommenden Prädiktor $x_m$ und müsste man die gesamte Varianz vom Outcome $y$ betrachten, und nur den Einfluss der bereits aufgenommenen Prädiktoren herausrechnen. Das ist genau das, was die Semipartialkorrelation leistet.
Zusammenfassung
Wir haben in diesem Tutorial die Partial- und Semipartialkorrelation als Erweiterungen der Korrelation kennengelernt und ihre Beziehung zur multiplen Regression beleuchtet. Die Zusammenhänge zwischen den drei Größen soll der folgende Plot nochmal zusammenfassen.
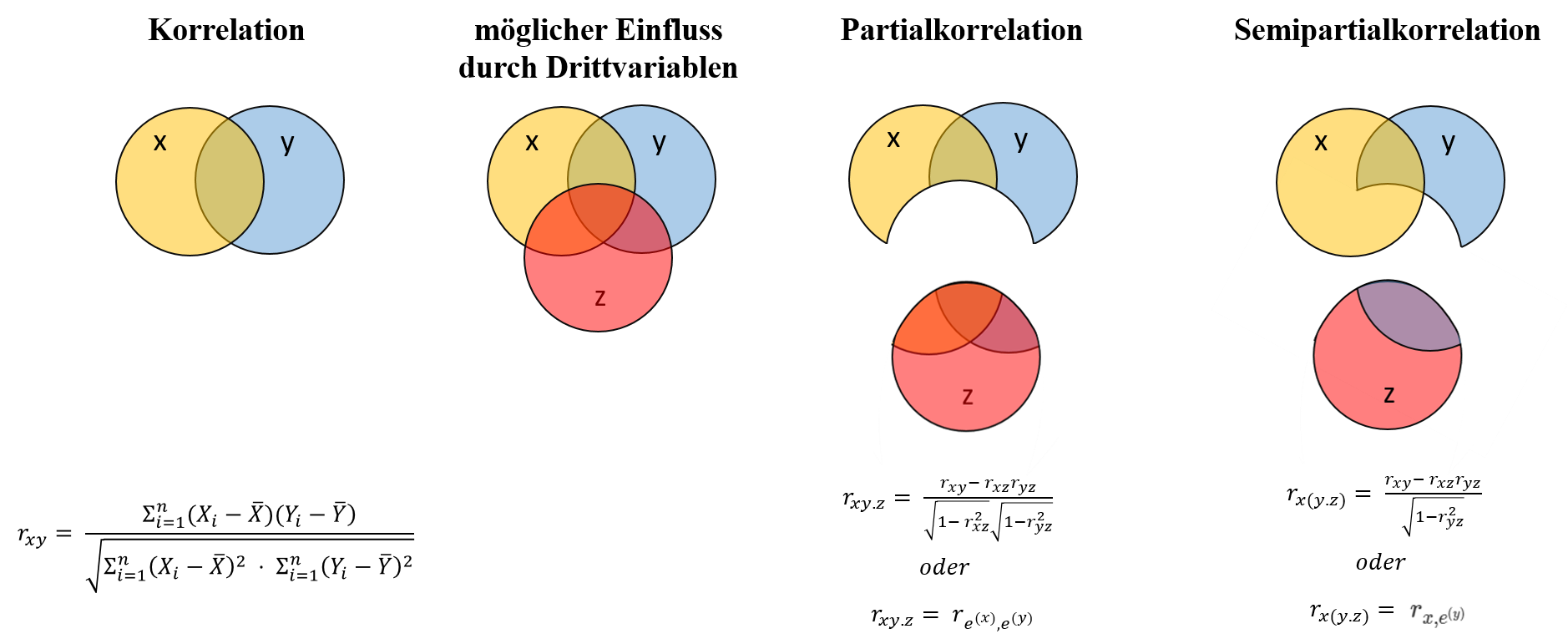
Ausblick: Noch mehr Partialkorrelationen!
Das kann man natürlich nicht nur für zwei oder drei, sondern potentiell eine sehr große Anzahl von Variablen machen. Wenn wir in die Funktion pcor mehrere Variablen übergeben, wird eine Matrix der Partialkorrelationen zurückgegeben. Hier ein Beispiel mit allen numerischen Variablen unseres Datensatzes. Die Funktion pcor() gibt uns nicht nur die Tabelle der Partialkorrelationskoeffizienten aus, sondern auch die zugehörigen $p$-Werte und die $t$-Statistik. An dieser Stelle extrahieren wir nur den Teil des Outputs, der die Partialkorrelationen enthält.
# Tabelle der Partialkorrelationen
pcor_table <- pcor(dat)
pcor_table$estimate |> round(3)
## Lebenszufriedenheit Episodenanzahl Depressivitaet Neurotizismus
## Lebenszufriedenheit 1.000 -0.173 0.199 -0.529
## Episodenanzahl -0.173 1.000 0.662 -0.565
## Depressivitaet 0.199 0.662 1.000 0.825
## Neurotizismus -0.529 -0.565 0.825 1.000
Man kann das ganze auch grafisch darstellen, um sich einen schnellen Überblick über ungerichtete Zusammenhänge zwischen einer größeren Anzahl von Variablen zu verschaffen. Dabei wird der Einfluss je aller anderen Variablen im Datensatz konstant gehalten (herauspartialisiert). Ein populäres Paket zur Visualisierung solcher ungerichteten Zusammenhänge ist das Paket qgraph. Für die numerischen Variablen aus unserem Depressionsdatensatz könnte das Ganze so aussehen:
library(qgraph)
# Partialkorrelationsnetzwerk grafisch darstellen:
Q <- qgraph(input = pcor_table$estimate,
layout = "spring", # grafische Anordnung der Variablen
edge.labels = TRUE, # Partialkorrelationen anzeigen
labels = substr(colnames(dat), 1, 5)) # die ersten 5 Zeichen der colnames
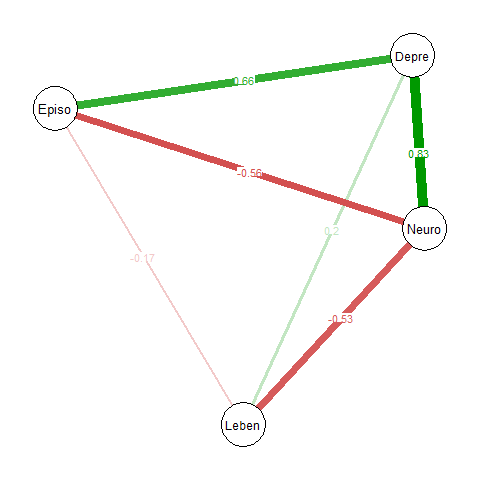
# Plot wird automatisch erzeugt, ohne dass wir Q ausführen müssen
Die Variablen werden automatisch durch die Einstellungen so angeordnet, dass Variablen, die stärker miteinander zusammenhängen, in der Abb. näher beieinander sind. Deskriptivstatistisch wird daran deutlich, dass z.B. der Zusammenhang zwischen Episodenlänge und Depressivität 0.66 beträgt, wenn der Einfluss von sowohl Neurotizismus als auch Lebenszufriedenheit herausgerechnet wird.
Ob die Zusammenhänge auch inferenzstatistisch abgesichert, d.h. auch in der Population von 0 verschieden sind, damit beschäftigen sich Forschende im Rahmen von Netzwerkanalysen. Diese Methode hat in der Persönlichkeits- und der klinischen Popularität in den letzten Jahren stark an Popularität gewonnen, um Zusammenhänge zwischen vielen simultan beobachteten, potenziell miteinander interagierenden Variablen zu untersuchen. Darüber können Sie in den pandaR-Lektionen zum KliPPs-Master noch mehr erfahren.
Appendix A
Inferenzstatistik der Partialkorrelation und weitere konzeptionelle Überlegungen
Bevor wir uns die Inferenzstatistik der Partialkorrelation genauer ansehen, wiederholen wir die Inferenzstatistik der Korrelation und schauen uns nochmal genau an, welche Eigenschaften eigentlich so ein Residuum hat.
Inferenzstatistik der Korrelation
Um eine Korrelation auf Signifikanz zu prüfen, untersuchen wir die Nullhypothese, dass die Korrelation $\rho$ in der Population tatsächlich 0 ist: $H_0:\rho=0$. Unter dieser Nullhypothese lässt sich eine Teststatistik $T$ für den empirischen Korrelationskoeffizient $r$ herleiten, welche $t(n-2)$ verteilt ist, also die der $t$-Verteilung, die wir aus Mittelwertsunterschieden bereits kennen, folgt (diese Formel gilt nur für die Pearson Produkt-Momentkorrelation):
\begin{align*} T=\frac{r\sqrt{n-2}}{\sqrt{1-r^2}}\sim t(n-2) \end{align*}
Liegt $T$ weit entfernt von der 0, so spricht dies gegen die $H_0$-Hypothese. Der zugehörige $t$ und $p$ Wert aus der cor.test Funktion werden genau mit dieser Formel, bzw. mit pt (für den zugehörigen $p$-Wert zu einem bestimmten $t$-Wert), bestimmt.
# Infos aus cor.test
cortest <- cor.test(dat$Depressivitaet, dat$Lebenszufriedenheit)
# correlation r
r_cortest <- cortest$estimate
# t-Wert
t_cortest <- cortest$statistic
# p-Wert
p_cortest <- cortest$p.value
# zu Fuß:
r <- cor(dat$Depressivitaet, dat$Lebenszufriedenheit)
n <- nrow(dat) # Anzahl Personen
t <- r*sqrt(n-2)/sqrt(1-r^2)
p <- 2*pt(q = abs(t), df = n-2, lower.tail = F) # ungerichtet (deswegen *2)
# Vergleiche
# t
t_cortest
## t
## -5.025552
t
## [1] -5.025552
# p
p_cortest
## [1] 2.614365e-06
p
## [1] 2.614365e-06
Super, die Formeln stimmen also. Widmen wir uns nun den Regressionsresiduen.
Eigenschaften der Regressionsresiduen
Wir wollen $Z$ aus $X$ und $Y$ herauspartialisieren. Wenn wir eine Regression rechnen und bspw. $Y$ durch $Z$ “vorhersagen”, dann schätzen wir ein Modell: $y=\beta_{y,0}+\beta_{y,1}z+\varepsilon_y$. Die Annahme an das Residuum lautet, dass es einen Mittelwert von 0 hat (auch Erwartungswert: $\mathbb{E}[\varepsilon_y]=0$) und dass es mit dem Prädiktor unkorreliert ist: $\mathbb{C}ov[z,\varepsilon_y]=0$. Wenn die Kovarianz mit $Z$ Null ist, so ist auch die Korrelation mit $Z$ Null. Gleichzeitig ist $\varepsilon_y$ aber hoch mit $Y$ korreliert. Es gilt $\mathbb{C}ov[y,\varepsilon_y]>0$. Damit haben wir quasi eine neue Variable $\varepsilon_y$ gefunden, die sehr viel mit $Y$ gemein hat, aber nichts mehr mit $Z$. Somit ist $\varepsilon_y$ also der Anteil von $Y$ der nichts mehr mit $Z$ zu tun hat. Hängt dieser noch mit dem ebenso bereinigten Anteil von $X$, $\varepsilon_x$ (resultierend aus $x=\beta_{x,0}+\beta_{x,1}z+\varepsilon_x$) zusammen, dann bedeutet dies, dass es Anteile von $X$ und $Y$ gibt, die mit einander linear Zusammenhang. Diese Beziehung ist dann nicht durch $Z$ erklärbar, da dieses unkorreliert zu den Residuen ist. Hier ein empirisches Beispiel:
# Regression
reg_depr_neuro <- lm(Depressivitaet ~ Neurotizismus, data = dat) # x ~ z
reg_lz_neuro <- lm(Lebenszufriedenheit ~ Neurotizismus, data = dat) # y ~ z
# Residuen in Objekt ablegen (Residuen x)
res_depr_neuro <- residuals(reg_depr_neuro) # eps_x
# Residuen in Objekt ablegen (Residuen y)
res_lz_neuro <- residuals(reg_lz_neuro) # eps_y
Prüfen wir doch mal ein paar Eigenschaften des Residuums:
# Mittelwert 0
mean(res_depr_neuro) # mean(eps_x)
## [1] -2.246858e-18
round(mean(res_depr_neuro), 14) # mean(eps_x) gerundet auf 14 Nachkommastellen
## [1] 0
Das Residuum hat wie im Erwartungswert festgehalten den Mittelwert von 0. Weiterhin zeigt es auch keinen Zusammenhang zum Prädiktor in der Regression, in der es aufgetreten ist:
# Korrelation/Kovarianze mit dem Prädiktor z
cov(dat$Neurotizismus, res_depr_neuro) # 0
## [1] 6.216704e-17
cor(dat$Neurotizismus, res_depr_neuro) # 0
## [1] 3.373551e-17
round(cor(dat$Neurotizismus, res_depr_neuro), 16) # 0 gerundet auf 16 Nachkommastellen
## [1] 0
Nun interessiert uns aber, wie stark dieses Residuum noch mit der abhängigen Variable ($X$ oder $Y$) zusammenhängt:
cor(dat$Depressivitaet, res_depr_neuro)
## [1] 0.6067831
Die Korrelation fällt relativ hoch aus: $r_{\varepsilon_y,y}=$ 0.607. Das ist doch super! Das heißt nämlich, dass $\varepsilon_y$ viel Information von $Y$ enthält, gleichzeitig aber nichts mehr mit $Z$ gemein hat!
Woher kommt die Formel der Partialkorrelation
Die Partialkorrelation hatten wir in diesem Beitrag über die Residuen einer Regression pro Variable definiert. Im vorherigen Abschnitt hatten wir die Eigenschaften dieser Residuen näher beleuchtet. Die Partialkorrelation war jetzt nichts weiter als die Korrelation der Residuen $\varepsilon_x$ mit $\varepsilon_y$ also dem Anteil von $X$ und $Y$, der nicht mit $Z$ korreliert war. Die Partialkorrelation lautet:
# Partialkorrelation
partial_cor <- cor(res_lz_neuro, res_depr_neuro)
partial_cor
## [1] 0.1137543
Wir kennen aber auch die Formel für die Partialkorrelation:
$$r_{xy.z}=\frac{r_{xy}-r_{xz}r_{yz}}{\sqrt{1-r_{xz}^2}\sqrt{1-r_{yz}^2}}$$
Wenn wir die Korrelationen in Objekten abspeichern, so lässt sich diese Formel sehr leicht umsetzen:
# Partialkorrelation via Formel
r_xy <- cor(dat$Lebenszufriedenheit, dat$Depressivitaet)
r_xz <- cor(dat$Lebenszufriedenheit, dat$Neurotizismus)
r_yz <- cor(dat$Depressivitaet, dat$Neurotizismus)
r_xy.z <- (r_xy - r_xz*r_yz)/(sqrt(1-r_xz^2)*sqrt(1-r_yz^2))
r_xy.z
## [1] 0.1137543
Offensichtlich kommen beide Befehle zum gleichen Ergebnis. Interessierten sei gesagt, dass der verwendete Code für die Berechnung r_xy.z das Gleiche ist wie:
r_xy.z <- (r_xy - r_xz*r_yz)/sqrt(1-r_xz^2)/sqrt(1-r_yz^2)
Hier besteht allerdings der Vorteil, dass man die Klammer im Nenner nicht vergessen kann.
Wir wollen uns nun der Frage widmen, wie diese Formel entsteht. Dazu müssen wir eine kleine Vorbereitung treffen: wir müssen den Depression Datensatz standardisieren. Danach ist der Mittelwert und die Varianz jeder Variable 0 (Mittelwert) und 1 (Varianz). Dies geht sehr leicht mit dem scale Befehl. Anschließend müssen wir alle Ananlysen nochmals wiederholen, aber keine Sorge, die Partialkorrelation bleibt identisch:
# Datensatz standardisieren:
dat_std <- data.frame(scale(dat))
# Regression
reg_depr_neuro <- lm(Depressivitaet ~ Neurotizismus, data = dat_std) # x ~ z
reg_lz_neuro <- lm(Lebenszufriedenheit ~ Neurotizismus, data = dat_std) # y ~ z
# Residuen in Objekt ablegen (Residuen x)
res_depr_neuro <- residuals(reg_depr_neuro) # eps_x
# Residuen in Objekt ablegen (Residuen y)
res_lz_neuro <- residuals(reg_lz_neuro) # eps_y
# Partialkorrelation
partial_cor <- cor(res_lz_neuro, res_depr_neuro)
partial_cor
## [1] 0.1137543
# Partialkorrelation via Formel
r_xy <- cor(dat_std$Lebenszufriedenheit, dat_std$Depressivitaet)
r_xz <- cor(dat_std$Lebenszufriedenheit, dat_std$Neurotizismus)
r_yz <- cor(dat_std$Depressivitaet, dat_std$Neurotizismus)
r_xy.z <- (r_xy - r_xz*r_yz)/(sqrt(1-r_xz^2)*sqrt(1-r_yz^2))
r_xy.z
## [1] 0.1137543
Sie sehen, alles bleibt identisch! Der Hauptunterschied ist nur, einige Korrelationen jetzt einfach Kovarianzen sind, da die Varianzen der Variablen = 1 sind:
cor(dat_std$Lebenszufriedenheit, dat_std$Depressivitaet)
## [1] -0.4722292
cov(dat_std$Lebenszufriedenheit, dat_std$Depressivitaet)
## [1] -0.4722292
Wir wissen, dass die Korrelation gerade die Kovarianz geteilt durch das Produkt der Standardabweichungen ist. Das bedeutet, dass in der Formel gelten muss:
\begin{align*} \mathbb{C}ov[\varepsilon_x, \varepsilon_y] &= r_{xy} - r_{xz}r_{yz}\ \mathbb{V}ar[\varepsilon_x] &= 1-r_{xz}^2\ \mathbb{V}ar[\varepsilon_y] &= 1-r_{yz}^2 \end{align*}
Die Wurzel aus den letzten beiden Ausdrücken ergibt dann die Standardabweichung (von $\varepsilon_x$ und $\varepsilon_y$). Prüfen wir das doch mal:
# Cov[eps_x, eps_y]
cov(res_lz_neuro, res_depr_neuro)
## [1] 0.05189286
r_xy - r_xz*r_yz
## [1] 0.05189286
# -> identisch!
# Var[eps_x]
var(res_lz_neuro)
## [1] 0.5652141
1-r_xz^2
## [1] 0.5652141
# -> identisch!
# Var[eps_y]
var(res_depr_neuro)
## [1] 0.3681857
1-r_yz^2
## [1] 0.3681857
# -> identisch!
Daraus können wir nun ableiten, dass die Partialkorrelationsformel sich einfach aus der Korrelation der Residuen $\varepsilon_x$ und $\varepsilon_y$ ableitet. Wir fanden es spannend dies einmal ausführlich nieder zu schreiben und wir hoffen, dass es eventuell beim Verständnis dieser doch etwas trockenen Materie geholfen hat. Weiterer Fun-Fact: $1-r_{xz}^2$ ist gerade der Anteil an Varianz von $X$, der nicht durch $Z$ erklärt werden kann - genau diesen haben wir auch für die Partialkorrelation benötigt. Das Gleiche gilt für $1-r_{yz}^2$ - nur eben für $Y$.
Inferenzstatistik der Partialkorrelation
Nun kommen wir endlich zur Inferenzstatistik der Partialkorrelation. Dabei geht es hauptsächlich um die Frage, warum wir nicht einfach cor.test() mit den Residuen nutzen können. Um eine Partialkorrelation auf Signifikanz zu prüfen, untersuchen wir die Nullhypothese, dass die Partialkorrelation $\rho_{xy.z}$ in der Population tatsächlich 0 ist: $H_0:\rho_{xy.z}=0$. Unter dieser Nullhypothese lässt sich eine Teststatistik $T$ für die empirischn Partialkorrelationskoeffizient $r_{xy.z}$ herleiten, welche $t(n-k-2)$ verteilt ist, wobei $k$ die Anzahl an Prädiktoren sind, die herauspartialisiert wurden (es wäre also auch vektorwertiges $Z$ zulässig!). $T$ folgt also wieder der $t$-Verteilung (diese Formel gilt nur Partialkorrelationen, die für die Pearson Produkt-Momentkorrelation bestimmt sind):
\begin{align*} T=\frac{r_{xy.z}\sqrt{n-k-2}}{\sqrt{1-r_{xy.z}^2}}\sim t(n-k-2) \end{align*}
Liegt $T$ weit entfernt von der 0, so spricht dies gegen die $H_0$-Hypothese. Der zugehörige $t$ und $p$ Wert aus dem ppcor Paket werden genau mit dieser Formel, bzw. mit pt (für den zugehörigen $p$-Wert zu einem bestimmten $t$-Wert), bestimmt.
Wir sehen also, dass die cor.test Funktion, wenn wir ihr die Residuen übergeben, gar nicht zum richtigen Ergebnis kommen kann,. Das liegt daran, dass die cor.test Funktion davon ausgeht, dass ganz normale Variablen korreliert werden sollen. Residuen sind aber dahingehend besonders, dass sie bereits verrechnet wurden. Wir haben ja bereits Regressionen mit $Z$ vorgenommen, um die entsprechenden Anteile von $Z$ herauszurechnen. Damit haben wir Informationen über die Daten benutzt. Nämlich diese, die die Korrelationen mit $X$ und $Y$ mit $Z$ betreffen. Diese genutzen Informationen müssen eingepreist werden, was durch das Anpassen der Freiheitsgrade in der $t$-Verteilung geschieht (wir nutzen hier df = n-1-2 und nicht df=n-2).
Weil es so viel Freude bereitet diese Inhalte tiefer zu verstehen, prüfen wir auch dies noch einmal:
# Infos aus pcor.test
pcortest <- pcor.test(dat$Depressivitaet, dat$Lebenszufriedenheit,
dat$Neurotizismus)
# correlation r
r_pcortest <- pcortest$estimate
# t-Wert
t_pcortest <- pcortest$statistic
# p-Wert
p_pcortest <- pcortest$p.value
# zu Fuß:
n <- nrow(dat) # Anzahl Personen
t <- r_xy.z*sqrt(n-1-2)/sqrt(1-r_xy.z^2)
p <- 2*pt(q = abs(t), df = n-1-2, lower.tail = F) # ungerichtet (deswegen *2)
# Vergleiche
# t
t_pcortest
## [1] 1.067961
t
## [1] 1.067961
# p
p_pcortest
## [1] 0.2884924
p
## [1] 0.2884924
Super, auch diesmal stimmen die Formeln. Im Laufe Ihres Studiums wird dieser Sachverhalt immer wieder aufgegriffen und auch noch näher erklärt. An dieser Stelle reicht es uns zu wissen, dass wir bei der Partialkorrelation andere $df$ verwenden müssen.
Tatiana Kvetnaya
Autorin
Marvin Schröder
Autor
Kai J. Nehler
Teammitglied
