Pfadanalysen und Strukturgleichungsmodelle
Analysen von komplexen gerichteten Beziehungen
In dieser Sitzung beschäftigen wir uns mit Pfadanalysen und Strukturgleichungsmodellen (engl. Structural Equation Modeling, SEM). Diese werden beispielsweise in Werner, Schermelleh-Engel, Gerhard und Gäde (2016, Kapitel 17 in Döring & Bortz, 2016) oder Eid, Gollwitzer und Schmitt (2017) in Kapitel 26 ausführlich beschrieben.
Pfadanalysen sind im Grunde genommen mehrere Regressionsanalysen, welche simultan geschätzt werden können. So werden auch mehrere Abhängigkeiten zwischen Variablen berücksichtigt. Strukturgleichungsmodelle kombinieren Pfadanalysen mit Messmodellen und berücksichtigen somit die Reliabilität der Messungen. Wir könnten also sagen: “SEM = CFA + Pfadanalyse”!
Mit SEM können ganz verschiedene Modelle spezifiziert werden, was im Grunde ein Wissenschaft für sich darstellt. Wir wollen uns die Grundlagen der SEM-Modellierung ansehen und einige wichtige Modelle kennenlernen!
In dieser Sitzung erweitern wir dafür unsere Kenntnisse mit dem R-Paket lavaan um gerichtete Abhängigkeiten. Möchten Sie die Grundlagen im Umgang damit wiederholen, so empfiehlt es sich, die erste Sitzung nochmals anzusehen (Einführungssitzung zu lavaan). Auch baut diese Sitzung auf der vergangenen Sitzung zur CFA auf.
Bevor wir mit den Analysen beginnen können, laden wir zunächst alle Pakete, welche wir im Folgenden benötigen werden.
library(lavaan)
library(semPlot) # grafische Darstellung von Pfadanalyse- und Strukturgleichungsmodellen
Datensatz
Der Datensatz StressAtWork, den wir im Folgenden untersuchen wollen, ist eine Zusammenstellung aus mehreren Studien der Arbeits- und Organisationspsychologie- Abteilung der Goethe-Universität, in welchen Call-Center-Mitarbeiter untersucht wurden. Wir können diesen wie gewohnt laden:
Sie können den im Folgenden verwendeten Datensatz “StressAtWork.rda” hier herunterladen.
Wir laden zunächst die Daten: entweder lokal von Ihrem Rechner:
load("C:/Users/Musterfrau/Desktop/StressAtWork.rda")
oder wir laden sie direkt über die Website:
load(url("https://pandar.netlify.app/daten/StressAtWork.rda"))
Verschaffen wir uns einen Überblick über die Datenlage:
head(StressAtWork)
## sex zd1 zd2 zd6 aop3 aop4 aop8 bf1 bf2 bf3 bf4 bf5 bf6 bf7 bf8 bf9 bf10 bf11 bf12 bf13 bf14 bf15
## 1 1 2 2 4 5 3 4 2 1 1 1 1 1 1 1 1 1 1 2 2 2 1
## 2 1 4 3 4 5 3 4 5 4 4 1 2 5 3 5 5 2 3 4 4 3 2
## 3 1 2 2 3 3 1 3 3 3 4 1 3 1 1 3 2 2 2 2 3 3 1
## 4 2 3 2 2 2 4 5 3 3 2 1 4 4 2 3 3 2 2 3 3 3 5
## 5 1 4 3 3 4 2 4 4 4 3 1 1 2 2 2 2 2 1 2 2 2 1
## 6 1 3 4 4 2 1 1 4 4 4 1 1 2 3 2 1 1 1 4 3 2 2
## bf16 bf17 bf18 bf19 bf20 bo1 bo6 bo12 bo19 bo7 bo8 bo21
## 1 1 1 1 2 2 2 1 1 1 4 5 7
## 2 3 2 1 4 2 3 1 2 2 2 2 2
## 3 2 1 2 4 1 4 3 1 2 3 3 4
## 4 3 3 1 3 3 4 2 2 1 6 6 4
## 5 3 3 2 3 4 3 1 1 2 5 4 6
## 6 3 1 3 3 1 2 3 1 2 5 3 6
names(StressAtWork)
## [1] "sex" "zd1" "zd2" "zd6" "aop3" "aop4" "aop8" "bf1" "bf2" "bf3" "bf4" "bf5" "bf6" "bf7"
## [15] "bf8" "bf9" "bf10" "bf11" "bf12" "bf13" "bf14" "bf15" "bf16" "bf17" "bf18" "bf19" "bf20" "bo1"
## [29] "bo6" "bo12" "bo19" "bo7" "bo8" "bo21"
dim(StressAtWork)
## [1] 305 34
Der Datensatz enthält das Geschlecht der Probanden (sex, 1=weiblich, 2=männlich), sowie ausgewählte Messungen der Variablen Zeitdruck (zd1, zd2 und zd6) und Arbeitsorganisationale Probleme (aop3, aop4 und aop8) aus dem Instrument zur stressbezogenen Tätigkeitsanalyse (ISTA) von Semmer, Zapf und Dunckel (1999), Psychosomatische Beschwerden (auch Befindlichkeit: bf1,…,bf20) aus der Psychosomatischen Beschwerdenliste von Mohr (1986), sowie Messungen zu Subskalen von Burnout: Emotionale Erschöpfung (bo1, bo6, b12 und b19) und Leistungserfüllung (bo7, bo8 und bo21) aus Maslachs Burnout-Inventar (Maslach & Jackson, 1986) in der deutschen Übersetzung von Büssing und Perrar (1992). Insgesamt wurden 305 Personen befragt.
Skalenbeschreibungen und Beispielitems
Unter Zeitdruck verstehen wir hier zusätzliche Zeiteinschränkungen, die dazu führen, dass mehr Energie nötig ist, um eine Handlung durchzuführen. Gleichzeitig kann dies auch dazu führen, dass eine Handlung nicht mehr oder nicht mehr rechtzeitig durchführbar ist. Ein Beispielitem ist: “Wie häufig passiert es, dass Sie schneller arbeiten, als sie es normalerweise tun, um die Arbeit zu schaffen?” Die Items wurden auf einer 5-Punkt-Likert Skala beantwortet (Semmer, et al., 1999).
Arbeitsorganisationale Probleme hindern bei der Durchführung einer Handlung durch zum Beispiel veraltete Informationen, schlechte Arbeitsgeräte oder organisationale Probleme, die zu einem Mehraufwand führen. Ein Beispielitem ist: “A kann die Arbeitsaufträge gut erledigen, wenn er/sie sich an die vom Betrieb vorgesehenen Wege hält. B kann die Arbeitsaufträge nur bewältigen, wenn er/sie von den vom Betrieb vorgesehenen Wegen abweicht. Welcher der beiden Arbeitsplätze ist Ihrem am ähnlichsten?” Die Items wurden auf einer 5-Punkt-Likert-Skala beantwortet (Semmer, et al., 1999).
Psychosomatische Beschwerden beschreiben körperliche Befindlichenkeiten, die mögliche Langzeitfolgen von Stress sind, wie etwa Schlaflosigkeit, Kopfschmerzen oder Nervosität. Im Gegensatz zu allen anderen Skalen, die hier verwendet werden, handelt es sich bei den psychosomatischen Beschwerden um einen Index, welchem ein formatives Messmodell (im Gegensatz zu reflexiven Messmodellen) zu Grunde liegt (siehe dazu Abschnitt reflexive vs. formative Messmodelle). Ein Beispielitem ist: “Ermüden Sie schnell?” Die Items wurden auf einer 5-Punkt-Likert-Skala beantwortet (Mohr, 1986).
Emotionale Erschöpfung ist hier das Gefühl, erschöpft, niedergeschlagen und frustriert durch die Arbeit zu sein und die Zusammenarbeit mit anderen als besonders anstrengend anzusehen. Ein Beispielitem ist: “Am Ende eines Arbeitstages fühle ich mich verbraucht.” Die Items wurden auf einer 7-Punkt-Likert-Skala beantwortet (Maslach & Jackson, 1986, in der deutschen Übersetzung von Büssing und Perrar, 1992).
Wir verstehen unter Leistungserfüllung energetische Gefühle, Dinge anzupacken und das Gefühl, die Möglichkeit zu haben, die eigenen Ambitionen zu erfüllen. Ein Beispielitem ist: “Ich fühle mich sehr tatkräftig.” Die Items wurden auf einer 7-Punkt-Likert-Skala beantwortet (Maslach & Jackson, 1986, in der deutschen Übersetzung von Büssing und Perrar, 1992).
Theoretische Grundlage
Pfadanalysen und Strukturgleichungsmodelle gehören, wie auch die CFA, zu den konfirmatorischen, also Theorie bestätigenden, Verfahren und sollen ganz im Popper’schen Sinn durch Vergleiche der Daten mit theoretischen Modellen wissenschaftliche Erkenntnis gewinnen. Wir haben in unseren Daten drei Arten von Variablen: Zeitdruck und Arbeitsorganisationale Probleme sind Stressoren und sollten also mit einer gewissen Wahrscheinlichkeit in einem Individuum zu einer Stressreaktion führen. Emotionale Erschöpfung ist eine Facette von Burnout und gehört somit zu den kurzfristigeren Stressfolgen. Psychosomatische Beschwerden treten unter anderem auf, wenn Stress über einen langen Zeitraum auf ein Individuum einwirkt. Somit können wir postulieren, dass Stress über emotionale Erschöpfung auf psychosomatische Beschwerden wirkt und somit nur einen indirekten Effekt auf die psychosomatischen Beschwerden hat (hierbei ist zu sagen, dass wir durch unsere Hypothesen kausale Beziehungen annehmen, die wir allerdings nicht durch SEM in diesem querschnittlichen Design prüfen können; dies ist ein gängies Problem in Querschnittsdaten):
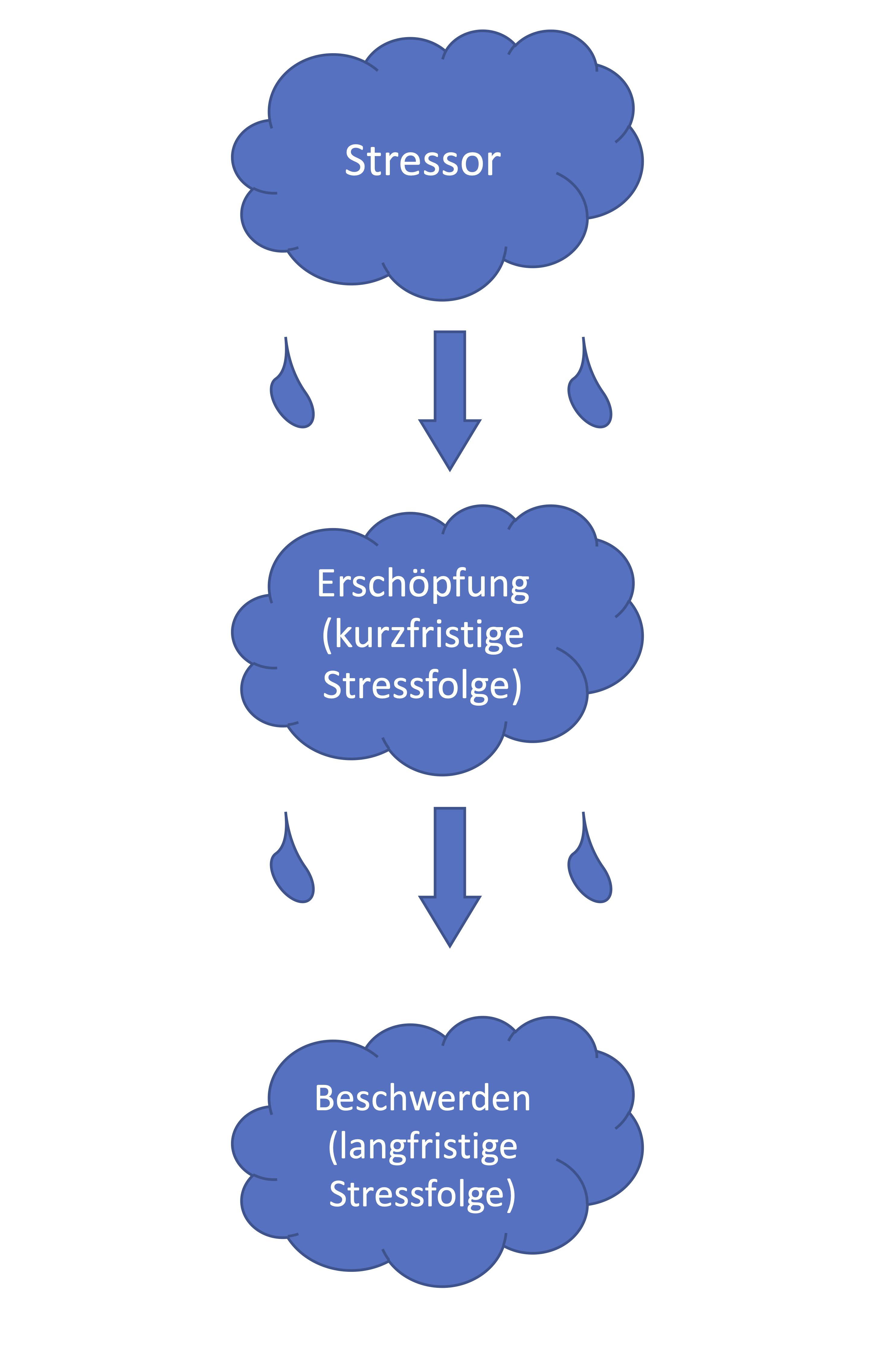
Das hier dargestellte schematische Modell postuliert also eine sogenannte vollständige Mediation (dazu mehr im nächsten Abschnitt zur Pfadanalyse) vom Stressor über die kurzfristige (Erschöpfung) auf die langfristigen (Beschwerden) Stressfolgen. Der Einfachheit halber wollen wir diese Hypothesen zunächst nur mit drei Variablen untersuchen: Zeitdruck, emotionale Erschöpfung und psychosomatische Beschwerden.
Pfadanalyse
Wir möchten die Hypothesen aus der letzten Sektion zunächst mit Skalenmittelwerten und einer Pfadanalyse untersuchen. Wir wollen außerdem den indirekten Effekt quantifizieren und inferenzstatistisch untersuchen. Dazu müssen wir pro Probanden einen Skalenmittelwert pro Variable berechnen. Dazu verwenden wir die bereits in der ersten Sitzung kennengelernte (bzw. aus dem letzten Semester bekannten) Funktion rowMeans und berechnen so den Mittelwert der psychosomatischen Beschwerden als BFs, den Zeitdruck als ZDs und die emotionale Erschöpfung als BOEEs; das kleine “s” hängen wir an die Skalennamen dran, um zu signialisieren, dass es sich hier um manifeste Skalenmittelwerte handelt:
StressAtWork$ZDs <- rowMeans(StressAtWork[,paste0("zd",c(1, 2, 6))])
StressAtWork$BOEEs <- rowMeans(StressAtWork[,paste0("bo",c(1, 6, 12, 19))])
StressAtWork$BFs <- rowMeans(StressAtWork[,paste0("bf",1:20)])
Hierbei hilft uns paste0 die Schreibweise abzukürzen: wir müssen nicht alle Itemnamen einzeln tippen, sondern die “Strings” werden automatisch erzeugt. Um dies genauer zu verstehen, könnten wir bspw. paste0("zd",c(1, 2, 6)) einmal ausführen. Dies kommt zum gleichen Ergebnis, wie wenn wir c("zd1", "zd2", "zd6") getippt hätten. Das Modell wird nun, ähnlich dem Regressionsmodell aus der ersten Sitzung, aufgestellt. In lavaan werden gerichtete Beziehungen zwischen Variablen mit ~ dargestellt, wobei links der Tilde die abhängige Variable (das Kriterium) und rechts der Tilde die unabhängige Variable (der Prädiktor) steht. Für unser angenommenes Modell gibt es folgende Beziehung: Zeitdruck wirkt auf emotionale Erschöpfung und auf psychosomatische Beschwerden. Emotionale Erschöpfung wirkt auf psychosomatische Beschwerden. In diesem Modell wird Zeitdruck die unabhängige Variable genannt, emotionale Erschöpfung ist der Mediator, der die Beziehung der unabhängigen auf die abhängige Variable psychosomatische Beschwerden mediiert. Hier hat Zeitdruck eine direkte Beziehung mit emotionaler Erschöpfung. Emotionale Erschöpfung hat eine direkte Beziehung mit psychosomatischen Beschwerden und Zeitdruck hat eine direkte und eine indirekte (über emotionale Erschöpfung) Beziehung mit psychosomatischen Beschwerden.
Es muss folglich zwei Gleichungen geben: in einer Gleichung ist BOEEs die abhängige Variable und wird durch ZDs vorhergesagt. In der zweiten Gleichung ist BFs die abhängige Variable und wird durch BOEEs und ZDs vorhergesagt. Nun hängt es außerdem von der Schätzfunktion ab, welche weiteren Beziehungen wir in unserem Modell spezifizieren müssen. Wir wollen die sem Funktion verwenden, um das Modell zu schätzen: sem ist, wie cfa (diese kennen Sie aus dem Themenblock CFA, um CFAs zu schätzen) auch eine “Convenience”-Funktion, die gewisse Voreinstellungen verwendet und diese an die lavaan-Funktion, die Sie in der ersten Sitzung kennengelernt hatten, übergibt. Sie hatten damals eine Regression mit lavaan geschätzt und mussten dabei bspw. mit Y ~ 1 + X die Regression anfordern, mit welcher durch X die abhängige Variable Y vorhergesagt wurde. Sie mussten hierbei explizit das Interzept (also den durch X bedingten Mittelwert von Y) sowie die Residualvarianz von Y anfordern via Y ~~ Y (für eine Wiederholung schauen Sie gerne in der Einführungssitzung vorbei). Wie auch die cfa-Funktion übernimmt die sem Funktion einige dieser Einstellungen für uns. So müssen wir bspw. Residualvarianzen nicht explizit anfragen. Die Mittelwertsstruktur wird in sem per Default nicht mitmodelliert. Wenn wir Mittelwerte betrachten wollen, können wir allerdings der sem-Funktion die Zusatzeinstellung meanstructure = TRUE übergeben. Die Default-Einstellungen für Messmodelle sind identisch mit jenen der Funktion cfa. Wir wiederholen diese, wenn es soweit ist. Somit landen wir bei dieser sehr effizienten Schreibweise für unser Modell:
model_paths <- '
BOEEs ~ ZDs
BFs ~ BOEEs + ZDs
'
Hätten wir dieses Modell mit lavaan (hier ist natürlich die Funktion ohne Convenience-Einstellungen und nicht das Paket gemeint) schätzen wollen, so hätten wir folgendes formulieren müssen (wir wollen die Mittelwertsstruktur auch hier ignorieren und lassen daher ~1 weg!):
model_paths_lavaan <- '
BOEEs ~ ZDs
BFs ~ BOEEs + ZDs
BOEEs ~~ BOEEs
BFs ~~ BFs
'
Wir können dieses Modell nun schätzen, indem wir die Funktion lavaan verwenden und ihr unser Modell sowie die Daten übergeben.
Mit summary erhalten wir detaillierte Informationen über Modellfit, Parameterschätzungen und deren Signifikanz. Mit rsq = T fordern wir dazu extra in der Summary das $R^2$ pro Variable sowie mit fit.measures = T die Fit-Indizes in ausführlicher Darstellung an.
fit_paths <- sem(model_paths, data = StressAtWork)
summary(fit_paths, rsq = T, fit.measures = T)
## lavaan 0.6.16 ended normally after 1 iteration
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 5
##
## Number of observations 305
##
## Model Test User Model:
##
## Test statistic 0.000
## Degrees of freedom 0
##
## Model Test Baseline Model:
##
## Test statistic 194.672
## Degrees of freedom 3
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 1.000
## Tucker-Lewis Index (TLI) 1.000
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -763.458
## Loglikelihood unrestricted model (H1) -763.458
##
## Akaike (AIC) 1536.916
## Bayesian (BIC) 1555.518
## Sample-size adjusted Bayesian (SABIC) 1539.660
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.000
## 90 Percent confidence interval - lower 0.000
## 90 Percent confidence interval - upper 0.000
## P-value H_0: RMSEA <= 0.050 NA
## P-value H_0: RMSEA >= 0.080 NA
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.000
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## BOEEs ~
## ZDs 0.481 0.066 7.271 0.000
## BFs ~
## BOEEs 0.329 0.028 11.682 0.000
## ZDs 0.073 0.035 2.081 0.037
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## .BOEEs 1.455 0.118 12.349 0.000
## .BFs 0.352 0.029 12.349 0.000
##
## R-Square:
## Estimate
## BOEEs 0.148
## BFs 0.380
Wie oben beschrieben kommt sem(model_paths, data = StressAtWork) und lavaan(model_paths_lavaan, data = StressAtWork) zum selben Ergebnis. Schauen Sie sich das doch einmal selbst an!
Nun zum Output der Summary: An
## [...]
## Model Test User Model:
##
## Test statistic 0.000
## Degrees of freedom 0
## [...]
erkennen wir, dass es sich hier um das saturierte Modell handelt (df = 0, $\chi^2=0$). Die Korrelationen zwischen den Skalenmittelwerten sind also nur retransformiert, um unser Modell abzubilden. Ein Modellfit-Test ist nicht möglich.
## [...]
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 1.000
## Tucker-Lewis Index (TLI) 1.000
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -763.458
## Loglikelihood unrestricted model (H1) -763.458
##
## Akaike (AIC) 1536.916
## Bayesian (BIC) 1555.518
## Sample-size adjusted Bayesian (SABIC) 1539.660
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.000
## 90 Percent confidence interval - lower 0.000
## 90 Percent confidence interval - upper 0.000
## P-value H_0: RMSEA <= 0.050 NA
## P-value H_0: RMSEA >= 0.080 NA
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.000
## [...]
Alle Fit-Indizes zeigen perfekten Fit an (CFI = 1, TLI = 1, RMSEA = 0, SRMR = 0). Das ist auch nicht verwunderlich, da es keine Diskrepanz (ausgedrückt durch den $\chi^2$-Wert) zwischen modellimplizierter und beobachteter Kovarianzmatrix der Daten (also keine Abweichung zwischen unserem Modell und den beobachteten Daten) gibt.
## [...]
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## BOEEs ~
## ZDs 0.481 0.066 7.271 0.000
## BFs ~
## BOEEs 0.329 0.028 11.682 0.000
## ZDs 0.073 0.035 2.081 0.037
## [...]
Im Gegensatz zur CFA wird uns nun ein Block in der Summary gezeigt, welcher die Regressionskoeffizienten unseres Modells enthält (ohne Interzept). Hier ist zu erkennen, dass alle Koeffizienten auf dem 5% Niveau signifikant von 0 verschieden sind. Es kann sich also maximal um eine partielle Mediation handeln, da die direkte Beziehung zwischen Zeitdruck und psychsomatischen Beschwerden laut dieser Signifikanzentscheidung mit einer Irrtumswahrscheinlichkeit von 5% auch in der Population besteht und somit der Effekt von Zeitdruck auf die Psychosomatischen Beschwerden nicht vollständig über die emotionale Erschöpfung mediiert wird.
Von einer vollständigen Mediation würden wir sprechen, wenn die direkte Beziehung zwischen Zeitdruck und psychosomatischen Beschwerden (also zwischen unabhängiger und abhängiger Variable) nicht bedeutsam von 0 verschieden ist und der indirekte Effekt von Zeitdruck über emotionale Erschöpfung auf psychsomatische Beschwerden signifikant von Null verschieden ist (dies war unsere Hypothese, die wir im vorherigen Abschnitt postuliert hatten). Für die Population würden wir also bei einer vollständigen Mediation davon ausgehen, dass die unabhängige Variable nur über den Mediator mit der abhängigen Variable zusammenhängt, also jegliche Veränderung in der unabhängigen Variable mit Veränderungen im Mediator zusammenhängt und durch diese Beziehung auch mit der abhängigen Variable kovariiert.
## [...]
## R-Square:
## Estimate
## BOEEs 0.148
## BFs 0.380
## [...]
Insgsamt ist die Vorhersage der emotionalen Erschöpfung und der psychosomatischen Beschwerden zwar statistisch signifikant, allerdings werden “nur” ca. 14.8% der Variation von BOEEs erklärt sowie ca. 38% der Variation von
BFs.
Im nächsten Abschnitt wollen wir unser Modell grafisch veranschaulichen. In der darauf folgenden Sektion wollen wir zusätzlich prüfen, ob der indirekte Effekt von Zeitdruck auf die psychosomatischen Beschwerden signfikant ist.
Grafische Veranschaulichung des Modells und der Ergebnisse
Das Paket semPlot bietet die Möglichkeit, Regressionen, CFAs, Pfadanalysen und Strukturgleichungsmodelle, die bspw. mit lavaan geschätzt wurden, grafisch zu veranschaulichen. Diese Grafiken sind denen, die wir in den inhaltlichen Sitzungen kennen gelernt haben, sehr ähnlich. semPaths (aus dem semPlot-Paket) ist die Funktion, welche wir hierzu nutzen wollen. Sie nimmt als Argument das geschätzte Objekt, welches in unserem Fall die Pfadanalyse enthält, entgegen; hier: fit_paths. Ohne weitere Zusatzeinstellungen sieht dieses so aus:
semPaths(fit_paths)
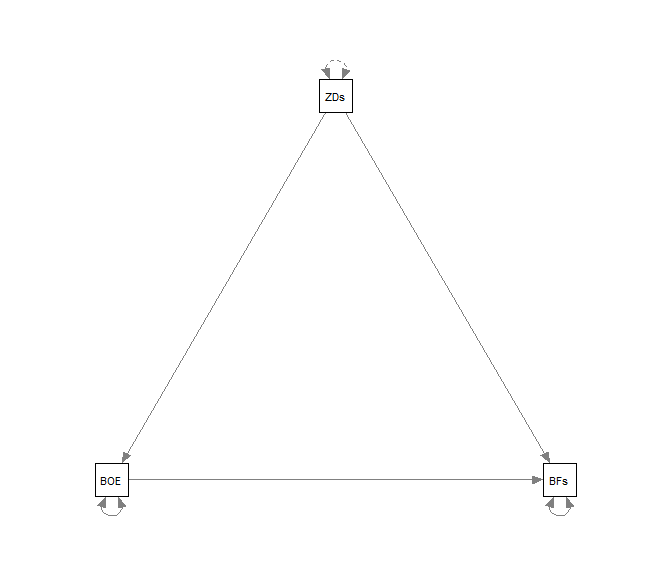
Der Default stellt also einfach nur das Modell grafisch dar, was sehr praktisch ist, um bspw. zu prüfen, ob alle wichtigen Beziehung im Modell enthalten sind. Gestrichelte Pfeile stehen hierbei für Restriktionen, hier wird also nichts geschätzt: in unserem Bespiel wird die Varianz von ZDs nicht geschätzt, da die Varianz der unabhängigen Variable nur implizit in die Regressionskoeffizenten einfließt, aber keinen (testbaren) Koeffizient des Modells darstellen. Würden wir wollen, dass die Varianz von ZDs geschätzt wird, so könnten wir prinzipiell ZDs ~~ ZDs in unser Modell mit aufnehmen.
Gerichtete Pfeile sind regressive Beziehungen (also Regressionsparameter, Pfadkoeffizienten oder Faktorladungen). Ungerichtete Pfeile stellen Kovarianzen oder Residualvarianzen dar. Hierbei wird immer dann von einer Kovarianz im Gegensatz zu einer Residualkovarianz gesprochen, wenn es sich um eine exogene (unabhängige) Variable handelt. Salopp gesprochen: hier kommen keine gerichteten Pfeile an! Ein weiteres wichtiges Argument, welches semPaths entgegennimmt, ist what. Hiermit wird festgelegt, was genau geplottet werden soll. Wählen wir what = "model", so wird das Modell ohne Parameterschätzungen und Einfärbungen grafisch dargestellt - dies ist der Default, welchen wir bereits oben gesehen haben. Wählen wir hingegen what = "est", so werden alle geschätzten Parameter in das Modell eingezeichnet; diese werden auch farblich hinsichtlich ihrere Ausprägung kodiert.
semPaths(fit_paths, what = "est")
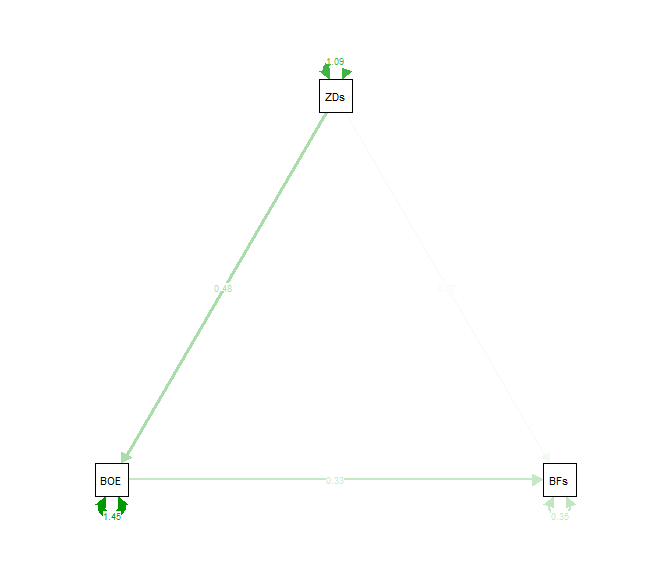
Probieren Sie doch selbst einmal aus, was die folgenden Zusatzeinstellungen bewirken. Dazu müssen Sie nur den Code kopieren und die Einstellungen verändern. Das Ziel einer solchen Grafik sollte sein, dass man die Gleichungen, die im Hintergrund stehen (wie in der Einführung in lavaan beschrieben), leicht zu verstehen sind und man alle Beziehungen zwischen den Variablen gut erkennen kann:
semPaths(object = fit_paths, what = "model", layout = "tree2", rotation = 2,
col = list(man = "skyblue"), edge.label.cex=1, sizeMan = 5)
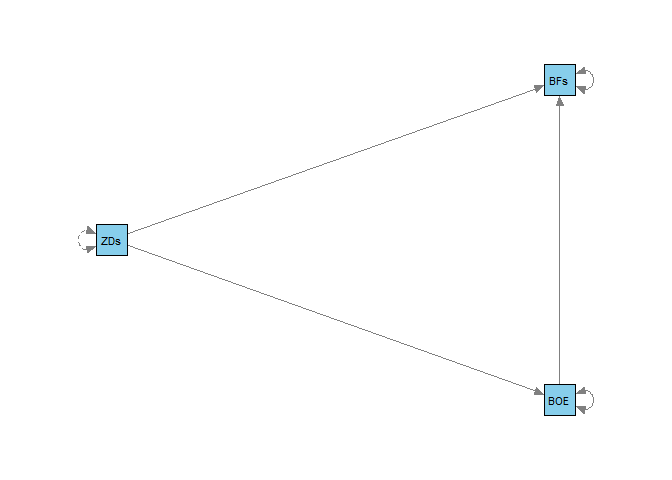
Sie können die Argumente der Funktion semPaths nachlesen, indem sie ??semPaths in einem neuen R-Studio Fenster ausführen und dann semPlot::semPaths in der Übersicht auswählen oder sie schauen sich die Dokumentation online hier an.
semPaths(object = fit_paths, what = "est", layout = "tree2", rotation = 2,
col = list(man = "skyblue"), edge.label.cex=1, sizeMan = 5)
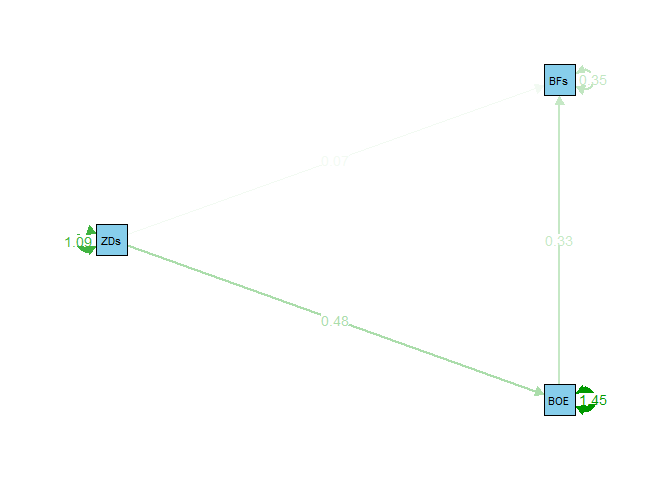
Wenn Sie eine solche Grafik in R-Studio erzeugen, gibt es viele Möglichkeiten, diese abzuspeichern. Bspw. können Sie mit dev.print(device = pdf, "MeinPlot.pdf") die Grafik als PDF abspeichern und ihr den Namen “MeinPlot.pdf” geben. Die Endung “.pdf” ist hierbei obligatorisch. Eine andere Möglichkeit ist in R-Studio im Grafikfenster auf “Export” zu klicken und dann den Anweisungen zu folgen. Natürlich wären auch andere Dateiformate, wie bspw. “.jpg” oder “.png” möglich!
Berechnen und Testen des indirekten Effektes von Zeitdruck über emotionale Erschöpfung auf psychosomatische Beschwerden
Der indirekte Effekt ist der Effekt, der von der unabhängigen Variable über den Mediator auf die abhängige Variable wirkt. Der Effekt der unabhängigen Variable auf den Mediator wird häufig mit a bezeichnet. Der Effekt des Mediators wird häufig b genannt. Der verbleibende direkte Effekt der unabhängigen auf die abhängige Variable wird, sie haben es sich womöglich schon gedacht, mit c bezeichnet. Nach diesem Schema wollen wir auch die Koeffizienten in unserem Modell benennen. Schauen wir uns dazu einmal die Gleichungen an (der Vollständigkeit halber führen wir auch die Interzepts $a_0$ und $c_0$ mit, $i$ symbolisiert hier den Index, z.B. für eine Person $i$):
$$BOEE_i = a_0 + aZD_i + \varepsilon_{BOEE,i},$$ $$BF_i = c_0 + bBOEE_i + cZD_i + \varepsilon_{BF,i}.$$ Nun haben wir allerdings eine Gleichung für $BOEE_i$, also können wir diese in die Gleichung von $BF_i$ einsetzen und erhalten den indirekten Effekt (IE) als Produkt der Parameter $IE:=ab$; der direkte Effekt (DE) verbleibt $DE:=c$:
\begin{align} BF_i &= c_0 + b(a_0 + aZD_i + \varepsilon_{BOEE,i}) + cZD_i + \varepsilon_{BF,i}\\[1.5ex] &= \underbrace{(c_0 + ba_0)}_{\text{Interzept}} + \underbrace{ab}_{_{\text{IE}}}ZD_i + \underbrace{c}_{_{\text{DE}}}ZD_i + \underbrace{(b \varepsilon_{BOEE,i}+ \varepsilon_{BF,i})}_\text{Residuum}. \end{align}Der totale Effekt von Zeitdruck auf die psychosomatischen Beschwerden ergibt sich als $TE:=IE + DE = ab+c$. Da wir bisher in lavaan die Mittelwertstruktur nicht mitmodelliert hatten, haben wir $a_0$ und $c_0$ auch noch nicht untersucht. Für weitere inhaltliche Informationen zu Pfadanalysen, direkten, indirekten und totalen Effekten lesen Sie gerne in Werner et al. (2016, pp. 952-) oder Eid et al. (2017, pp. 952-). Man bemerke den unfassbaren Zufall, dass beide Bücher an der gleichen Seitenzahl beginnend über Mediationen etc. sprechen!
In lavaan Koeffizienten zu benennen, ist ganz einfach. Sie haben es vielleicht schon im Appendix der letzten Sitzung zur CFA gesehen: der Variable wird der Koeffizientenname gefolgt von dem Multiplikationszeichen * vorangestellt. Also wird die Beziehung zwischen BOEEs und ZDs um das Präfix a* ergänzt zu: BOEEs ~ a*ZDs, usw.:
model_paths_abc <- '
BOEEs ~ a*ZDs
BFs ~ b*BOEEs + c*ZDs
'
Der Output bleibt nach Schätzen des Modells identisch, allerdings werden die Namen der Koeffizienten im Output mitgeführt. So lässt sich leicht prüfen, ob die Bennungen an den richtigen Stellen gelandet sind:
fit_paths_abc <- sem(model_paths_abc, data = StressAtWork)
summary(fit_paths_abc)
## [...]
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## BOEEs ~
## ZDs (a) 0.481 0.066 7.271 0.000
## BFs ~
## BOEEs (b) 0.329 0.028 11.682 0.000
## ZDs (c) 0.073 0.035 2.081 0.037
## [...]
Um nun den indirekten Effekt $ab$ und den totalen Effeket $ab + c$ mit aufzunehmen, können wir diese in das lavaan Modell inkludieren. Diese neu definierten Parameter stellen allerdings keine weiteren Modellparameter dar, es gehen also keine Freiheitsgrade verloren. Die lavaan-Syntax, die hinzukommt, ist :=; das mathematische “definiert als”-Zeichen. Links davon steht der Name, den wir dem neuen definierten Parameter geben wollen und rechts steht die Funktion der anderen Parameter aus unserem Modell. Beispielsweise können wir den indirekten Effekt wie folgt definieren: IE := a*b; das Produkt der beiden Pfadkoeffizienten, die wir bereits benannt haben.
model_paths_IE_TE <- '
BOEEs ~ a*ZDs
BFs ~ b*BOEEs + c*ZDs
# Neue Parameter
IE := a*b
TE := IE + c
'
Wenn wir nun das Modell erneut schätzen, erhalten wir einen neuen Teil im Output der Summary, welcher unsere definierten Parameter und deren Standardfehler, sowie die zugehörigen p-Werte enthält.
fit_paths_IE_TE <- sem(model_paths_IE_TE, data = StressAtWork)
summary(fit_paths_IE_TE)
## [...]
## Defined Parameters:
## Estimate Std.Err z-value P(>|z|)
## IE 0.158 0.026 6.173 0.000
## TE 0.232 0.039 5.916 0.000
## [...]
Achtung! Leider können wir den angezeigten Standardfehlern und dem zugehörigen p-Wert nicht unbedingt vertrauen, da einige Studien gezeigt haben, dass der indirekte Effekt asymptotisch nicht immer normalverteilt bzw. symmetrisch verteilt ist, weswegen ein einfaches Teilen des Estimates durch SE und der Vergleich mit der $z$-Verteilung (so wie wir dies eigentlich immer tun; also die einfache Parametersignifikanzentscheidung in komplexen Modellen) in diesem Fall nicht sinnvoll erscheint. Aus diesem Grund möchten wir dieser Problematik entgehen, indem wir die Bootstrap-Methode verwenden. Der Output sollte also nur für die Entnahme der Parameterwerte genutzt werden - nicht aber für die Signifikanzentscheidung!
Bootstrapping
Bootstrapping ist das wiederholte Ziehen mit Zurücklegen aus unserer Stichprobe, solange, bis wir eine neue Stichprobe erhalten, die genauso groß ist, wie die ursprünglich Beobachtete. In dieser neuen, gezogenen Stichprobe schätzen wir erneut unser Modell und notieren uns den indirekten Effekt. Dieses Vorgehen wiederholen wir sehr häufig (es hat sich irgendwie so ergeben, dass in der Statistik sehr häufig bei ungefähr und ziemlich genau 1000 liegt), sodass wir die Verteilung des indirekten Effektes und den wahren Standardfehler (also die Streuung des indirekten Effekts) annähern können. Dieses Vorgehen sollte, wenn unsere Stichprobe unabhängig gezogene Personen enthält und repräsentativ für die Gesamtpopulation ist, eine gute Schätzung der Verteilung des indirekten Effektes liefern, welcher Schlüsse auf die Gesamtpopulation zulässt. Wir können dann einfach den 2.5-ten und den 97.5-ten Prozentrang dieser Verteilung verwenden und erhalten ein 95%-Konfidenzintervall für den indirekten Effekt (dieses muss nicht immer symmetrisch sein, da der indirekte Effekt ja nicht unbedingt normalverteilt, bzw. symmetrisch verteilt ist!). Zum Glück müssen wir dies nicht per Hand programmieren, sondern können einfach unserere Parameterschätzung mit sem die Zusatzargumente se = "boot" und bootstrap = 1000 hinzufügen. Es empfiehlt sich, dieses Objekt anschließend anders zu nennen. Wir lassen unserer Phantasie freien Lauf und nennen die neue “gebootstrapte” Schätzung fit_paths_IE_TE_boot. Wenn wir dann auf das geschätzte (neue) Objekt die Funktion parameterEstimates mit der Zusatzeinstellung ci = TRUE anwenden, so werden uns alle Parameter inklusive Konfidenzintervall zurückgegeben. Da es sich hierbei um einen Zufallsprozess handelt, werden die Werte bei mehrmaligem Wiederholen (leicht) unterschiedlich sein. Möchten wir das Ergebnis replizierbar machen, so können wir set.seed() verwenden, wir müssen dieser Funktion lediglich eine beliebige natürliche Zahl übergeben (wie wäre es bspw. mit 1234? Wenn Sie die gleiche R-Version haben, sollte der folgende Code zum selben Ergebnis kommen!).
set.seed(1234)
fit_paths_IE_TE_boot <- sem(model_paths_IE_TE, data = StressAtWork, se = "boot", bootstrap = 1000)
parameterEstimates(fit_paths_IE_TE_boot, ci = TRUE)
## [...]
## lhs op rhs label est se z pvalue ci.lower ci.upper
## 7 IE := a*b IE 0.158 0.026 6.123 0 0.108 0.208
## 8 TE := IE+c TE 0.232 0.040 5.717 0 0.145 0.304
## [...]
Der Output zeigt die Konfidenzintervalle (sowie weitere Informationen) für alle Parameter in unserem Modell sowie für den indirekten und den totalen Effekt. Hierbei steht ci.lower für die untere Grenze und ci.upper für die obere Grenze des Konfidenzintervalls. Die Nummern 7 und 8 am Anfang der Zeilen zeigen an, dass hier insgesamt 8 Zeilen ausgegeben werden, wir uns aber nur die 7. und die 8. ansehen. Zeile 1 bis 6 (hier nicht dargestellt) zeigen den gleichen Output für alle weiteren Parameter im Modell (wir können help("parameterEstimates") für weitere Informationen in R-Studio ausführen, nachdem wir lavaan via library(lavaan) geladen haben). Das “gebootstrapte” Konfidenzintervall des indirekten Effekts erstreckt sich von 0.108 bis 0.208 und schließt die 0 somit nicht ein. Dies bedeutet, dass auf dem 5%-Signifikanzniveau der indirekte Effekt in der Population nicht 0 ist.
Dem Output zufolge scheint es also in der Population einen indirekten Effekt zu geben. Der totale Effekt ist auch signifikant. Die zugehörigen Grafiken unterscheiden sich kaum von denen, die wir uns zuvor angesehen hatten. Schauen wir uns die Modellstruktur an, so werden uns allerdings die Parameternamen mit eingezeichnet, was durchaus von Nutzen sein kann. Der indireke oder der totale Effekt sind keine Modellparameter, weswegen sie auch nicht in der Grafik dargestellt werden können.
semPaths(object = fit_paths_IE_TE, what = "model", layout = "tree2", rotation = 2,
col = list(man = "skyblue"), edge.label.cex=1)
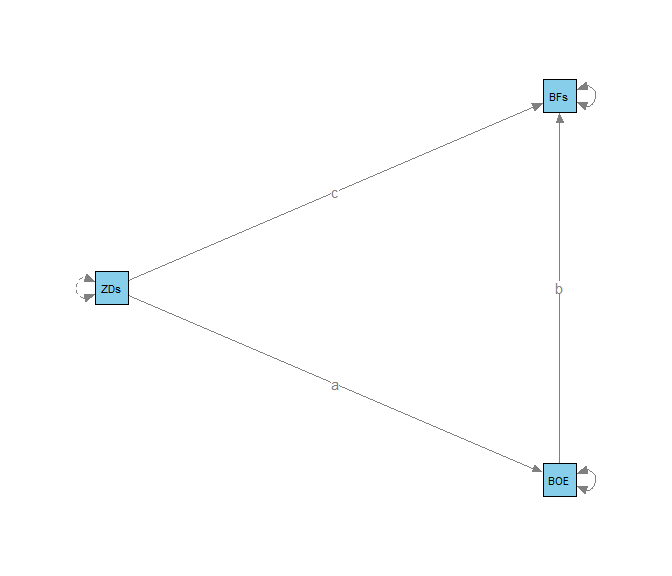
Die hier durchgeführten Analysen unterliegen leider einigen Einschränkungen. Bspw. wird beim Mitteln zu Skalenwerten davon ausgegangen, dass jede Messung (jede Variable pro Skala) gleichermaßen aus der dahinterliegenden latenten Variable besteht. Dies hatten wir in der letzten Sitzung im Anhang unter essentieller $\tau$-Äquivalenz kennengelernt (gleiche $\lambda$s in einem [CFA-] Messmodell). Essentielle $\tau$-Äquivalenz ist eine strenge Annahme, welche wir prüfen müssten, um den Analysen mit Skalenwerten komplett vertrauen zu können. Außerdem werden durch das Mitteln die Messfehler nicht vollständig modelliert, auch wenn die Analysen somit reliabler als Einzelitemanalysen (z.B. hätten wir auch jeweils ein Item pro Skala verwenden können) sind. Hierbei ist es nun so, dass Effekte stochastischer Regressoren konsistent unterschätzt werden, wenn diese messfehlerbehaftet sind. Wären die Variablen messfehlerfrei, würden die Effekte (die Regressionsparameter) größer ausfallen. Leider können wir nicht davon ausgehen, dass unsere beobachteten Variablen messfehlerfrei sind, wenn wir sie mit Fragebögen erheben! Aus diesem Grund ist in der multiplen Regression bspw. auch eine der Voraussetzungen die Messfehlerfreiheit der (stochastischen) Regressoren (siehe Eid, et al., 2017, Kapitel 19.13).
Wir können die Analysen auf die latente Ebene heben und Messmodelle für die latenten Variablen aufstellen, welche dann die unterschiedlichen Messgenauigkeiten pro Messung berücksichtigen und die Beziehung zwischen den latenten Variablen um die Ungenauigkeit der Einzelitems bereinigen.
Strukturgleichungsmodelle
Strukturgleichungsmodelle (SEM) kombinieren Pfadanalysen mit Messmodellen, also CFAs. Wir können mit SEM in unseren Analysen Messfehler berücksichtigen, aber dennoch gerichtete Beziehungen zwischen den latenten Variablen untersuchen. Bevor wir Messmodelle für unsere latenten Variablen aufstellen, müssen wir uns überlegen, ob dies denn für alle Variablen sinnvoll ist.
Reflexive vs. formative Messmodelle
Wenn es um Messmodelle geht, kann zwischen reflexiven und formativen Messmodellen unterschieden werden. Reflexive Messmodelle sind die Messmodelle, die wir in der letzten Sitzung zur CFA detailliert besprochen haben. Darin sind z.B. Eigenschaften von Personen latente Variablen, die sich nicht direkt beobachten lassen, sich aber in Verhalten und Aussagen niederschlagen. “Konservativismus” ist eine Einstellung von Personen (latente Variable), die sich z.B. darin äußert, dass Personen einer Aussage wie “Ein noch so geschulter und kritischer Verstand kann letzten Endes doch keine echte innere Befriedigung geben.” eher zustimmen (Item 36 der Machiavellismus-Konservatismus Skala; Cloetta, 2014). Die Annahme ist also, dass die latente Variable ursächlich für die Ausprägung bestimmter beobachtbarer (manifester) Variablen ist. Wie wir in der Sitzung zur CFA gesehen haben, sieht ein entsprechendes Pfaddiagramm so aus:
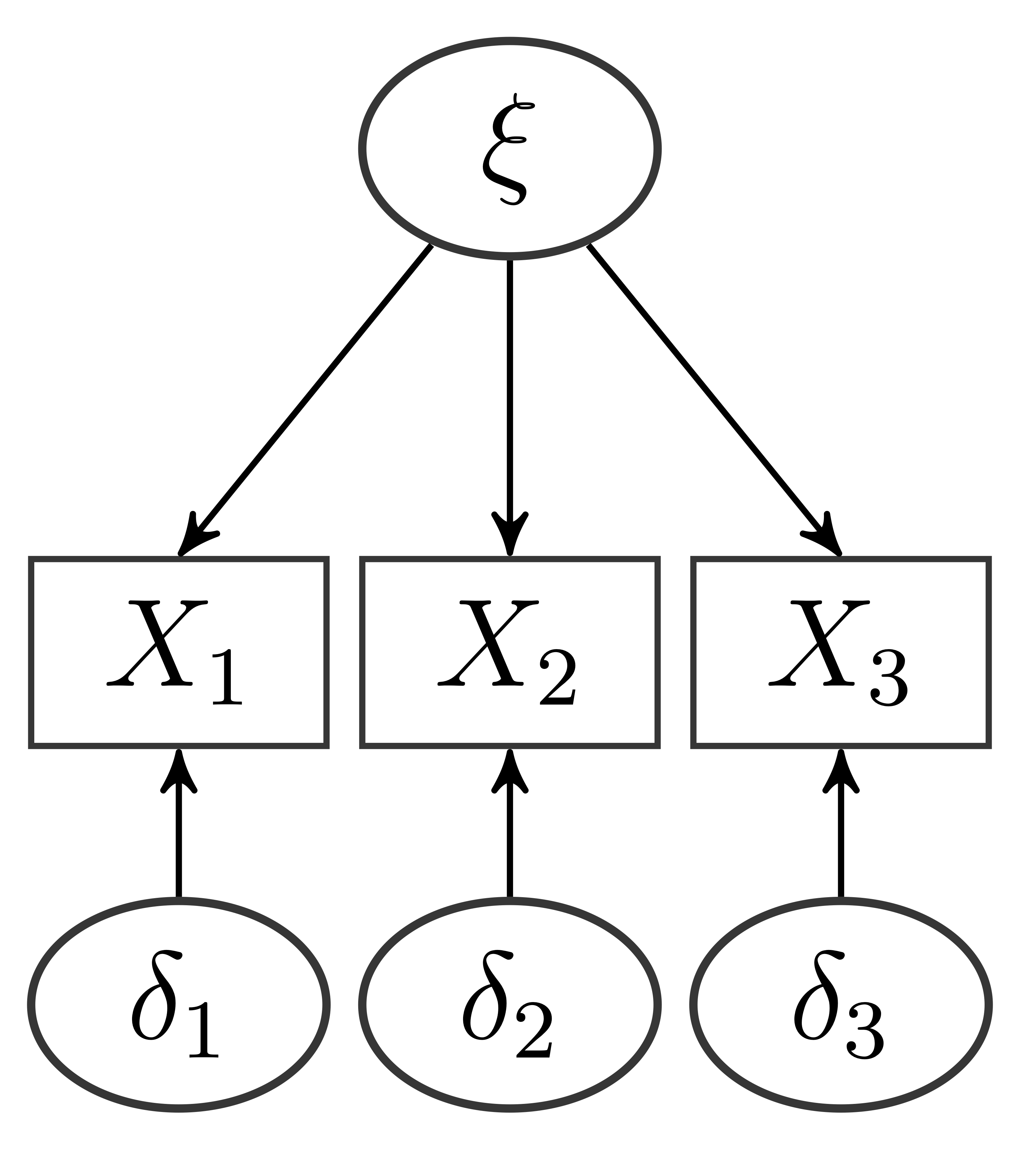
Die Variable $X_1$ ist also eine abhängige Variable, deren Ausprägung von der Ausprägung der latenten Variable $\xi$ und vom Messfehler $\delta_1$ abhängt: $X_1=\lambda_{1}\xi + \delta_1$. Deswegen gehen die Pfeile im Pfaddiagramm von den latenten Variablen (UV) zu den Items (AVs). Faktorladungen wurden in der Grafik nicht dargestellt, aber in der Formel der Vollständigkeit halber ergänzt.
Bei formativen Messmodellen ist es so, dass die latente Variable erst “geformt” wird. Sie ist eine Zusammensetzung aus den manifesten (beobachteten) Items, die als die (gewichtete) Summe (oder [gewichteter] Mittelwert) ihrer Items aufgefasst wird. Das zugehörige Pfaddiagramm sieht folgendermaßen aus:
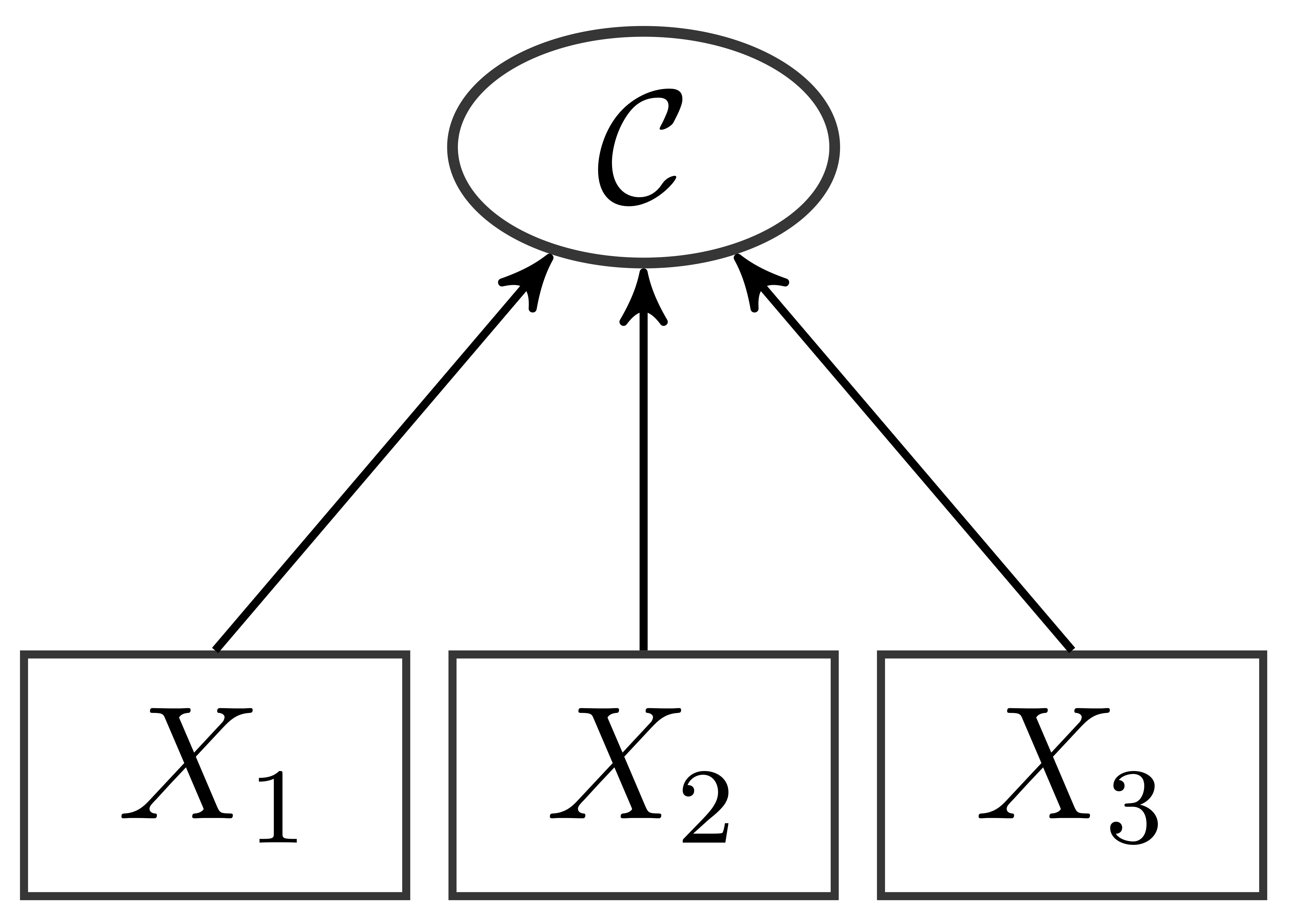
Es können keine Messfehler berücksichtigt werden und die “Kompositvariable” (deshalb auch die Benennung $\mathcal{C}$, engl. composite) ist eine Linearkombination der Items: $\mathcal{C}=X_1+X_2+X_3$ oder $\mathcal{C}=\lambda_1^\mathcal{C}X_1+\lambda_2^\mathcal{C}X_2+\lambda_3^\mathcal{C}X_3$ (also auch: $\mathcal{C}=\frac{X_1+X_2+X_3}{3}$)). Somit wirken sich Unterschiede zwischen Personen in bspw. $X_1$ (und gleichen $X_2$ und $X_3$) auf Unterschiede in $\mathcal{C}$ aus. Es lassen sich also Unterschiede in der latenten Variable auf unterschiedliche Kombinationen von Ausprägungen der Beobachtungen zurückführen. Gerade in den Wirtschaftswissenschaften und der Soziologie sind solche formativen Variablen sehr verbreitet. Ein bekanntes Beispiel ist der Human Development Index, der aus verschiedenen Komponenten wie Lebenserwartung, Schulbildung und Bruttoinlandsprodukt eine Kennzahl für den Entwicklungsstand eines Landes ermittelt. Ein psychologisches Beispiel für ein formatives Messmodell ist die Variable Umgebungsbelastung, welche auch mit dem ISTA erhoben werden kann (Semmer, et al., 1999). Mit dieser Variable sollen Umwelteinflüsse erfasst werden, die die Arbeit erschweren. Dies könnten z.B. schlechte Lichtverhältnisse oder Lärmbelästigung sein, welche durch längeres Auftreten Stress zur Folge haben können. Allerdings ist es in der Regel nicht so, dass an einem Arbeitsplatz immer dann Lärm auftritt, wenn auch die Lichtverhältnisse schlecht sind. Wenn jedoch beides auftritt, so ist die Umgebungsbelastung an diesem Arbeitsplatz besonders ausgeprägt. Demnach müssen beide Aspekte berücksichtigt werden, um eine gute Schätzung für die Umgebungsbelastung eines Arbeitsplatzes zu erhalten. Würden wir von einem reflexiven Messmodell ausgehen, würde eine hohe Ausprägung auf der latenten Variable Umgebungsbelastung auch zu einer erhöhten Antworttendenz auf beiden Items (Licht- und Lärmverhältnisse) führen.
Wem dieses Konzept bekannt vorkommt, hat sich wahrscheinlich an die Unterscheidung zwischen EFA und PCA zurückerinnert: Hier war es so, dass bei der PCA die Hauptkomponenten Linearkombinationen, also gewichtete Summen, der beobachteten Items waren, während bei EFA ein Messmodell mit dahinterliegenden latenten Variablen formuliert wurde und somit Messfehler modeliert werden konnten.
Bei Zeitdruck und emotionaler Erschöpfung handelt es sich um reflexive Messmodelle. Bei psychosomatischen Beschwerden werden unterschiedliche Beschwerden wie bspw. Kopfschmerzen und Rückenschmerzen abgefragt. Demnach handelt es sich bei dieser Variable eher um ein ein formatives Messmodell. Entsprechend könnten wir die Kompositformulierung in lavaan (<~) nutzen, um eine latente Kompositvariable zu erzeugen, oder wir behalten der Einfachheit halber unseren Skalenmittelwert BFs bei.
Das Modell
Das Modell in SEM unterscheidet sich im Vergleich zu CFAs: Es wird zwischen Messmodell und Strukturmodell unterschieden. Im Strukturmodell gibt es gerichtete Beziehungen, in welchen zwischen unabhängigen und abhängigen latenten Variablen unterschieden werden kann. Diese werden häufig auch exogene (unabhängige) und endogene (abhängige) latente Variablen genannt. Entsprechend gibt es zwei Arten von Messmodellen: ein exogenes und ein endogenes Messmodell. Diese Messmodelle sind quasi CFAs für die exogenen und die endogenen latenten Variablen; spezifizieren also die Beziehungen zwischen den latenten und den manifesten unabhängen bzw. abhängen Variablen. Wir wollen uns die Messmodelle sowie das Strukturmodell unserer Analyse ansehen:
Exogenes Messmodell $$\begin{pmatrix}ZD_1\\ZD_2\\ZD_6\end{pmatrix}=\begin{pmatrix}\tau_1^{x}\\\tau_2^{x}\\\tau_6^{x}\end{pmatrix}+\begin{pmatrix}\lambda_{11}^{x}=1\\\lambda_{21}^{x}\\\lambda_{31}^{x}\end{pmatrix}\xi_{\text{ZD}} + \begin{pmatrix}\delta_1\\\delta_2\\\delta_6\end{pmatrix}$$
Endogenes Messmodell $$\begin{pmatrix}BO_1\\BO_6\\BO_{12}\\BO_{19}\end{pmatrix}=\begin{pmatrix}\tau_1^{y}\\\tau_6^{y}\\\tau_{12}^{y}\\\tau_{19}^{y}\end{pmatrix}+\begin{pmatrix}\lambda_{11}^{y}=1\\\lambda_{21}^{y}\\\lambda_{31}^{y}\\\lambda_{41}^{y}\end{pmatrix}\eta_{\text{BOEE}} + \begin{pmatrix}\varepsilon_1\\\varepsilon_6\\\varepsilon_{12}\\\varepsilon_{19}\end{pmatrix}$$
Strukturmodell in Matrixnotation (wobei wir $BFs$ als latente Variable mitführen) $$\begin{pmatrix}\eta_\text{BOEE}\\BF_s\end{pmatrix}=\begin{pmatrix}\gamma_{11}\\\gamma_{21}\end{pmatrix}\xi_\text{ZD} + \begin{pmatrix}0&0\\\beta_{21}&0\end{pmatrix}\begin{pmatrix}\eta_\text{BOEE}\\BF_s\end{pmatrix} + \begin{pmatrix}\zeta_\text{BOEE}\\\zeta_{BF_s}\end{pmatrix}$$
Für die einzelnen abhängigen latenten Variablen erhalten wir also:
$$\eta_\text{BOEE}=\gamma_{11}\xi_\text{ZD} + \zeta_\text{BOEE}$$ und
$$BFs = \gamma_{21}\xi_\text{ZD} + \beta_{21}\eta_\text{BOEE} + \zeta_{BFs}.$$
Durch Einsetzen folgt: $$BFs = \gamma_{21}\xi_\text{ZD} + \beta_{21}\gamma_{11}\xi_\text{ZD}+ \beta_{21}\zeta_\text{BOEE} + \zeta_{BFs}.$$
Wenn wir nun genauer hinschauen, erkennen wir, dass $\gamma_{11}$ dem Pfad $a$, $\beta_{21}$ dem Pfad $b$ und $\gamma_{21}$ dem Pfad $c$ aus dem Mediationspfadmodell entspricht! Entsprechend quantifiziert $\beta_{21}\gamma_{11}$ den indirekten Effekt von $\xi_\text{ZD}$ über $\eta_\text{BOEE}$ auf $BFs$. Wir wollen das Modell model_paths_IE_TE, welches so aussah:
model_paths_IE_TE <- '
BOEEs ~ a*ZDs
BFs ~ b*BOEEs + c*ZDs
# Neue Parameter
IE := a*b
TE := IE + c
'
… so umstellen, dass es nicht mehr die Beziehung von manifesten Skalenwerten, sondern die Beziehungen zwischen latenten Variablen untersucht. Wir wenden dazu unser Wissen um die CFA aus der letzten Sitzung an und kombinieren dieses mit dem, was gerade in der Pfadaanalyse besprochen wurde. Wir nennen dazu die latente Variable für Zeitdruck am besten ZD (Items: zd1, zd2 und zd6) und die latente Variable emotionale Erschöpfung BOEE (Items: bo1, bo6, bo12 und bo19; Achtung: ohne “s” - diese Variablen gibt es nämlich im Datensatz - das waren die Skalenmittelwerte für Zeitdruck und emotionale Erschöpfung). Außerdem nehmen wir als Platzhalter der psychosomatischen Beschwerden die Variable BFs in das Modell auf. Zudem inkludieren wir die Berechnung des indirekten und des totalen Effekts mit den gleichen Bezeichnungen. Wir brauchen folglich 2 Messmodelle, eine Regression für die Beziehung zwischen ZD und BOEE, sowie eine Regression für die Beziehung zwischen ZD, BOEE und BFs. Zum Schluss brauchen wir noch die neu definierten Koeffizienten für den indirekten und den totalen Effekt (vgl. oben). Wir schätzen das Modell mit sem und schauen uns die Summary an! Im Modell ist es sehr sinnvoll, die Kommentarfunktion zu nutzen - das #. Alles was in der Zeile dahinter steht, wird von lavaan ignoriert.
model_sem_IE_TE <- '
# Messmodelle
ZD =~ zd1 + zd2 + zd6
BOEE =~ bo1 + bo6 + bo12 + bo19
# Strukturmodell
BOEE ~ a*ZD
BFs ~ b*BOEE + c*ZD
# Neue Parameter
IE := a*b
TE := IE + c
'
fit_sem_IE_TE <- sem(model_sem_IE_TE, StressAtWork)
Falls Sie diese Analysen an Ihrem Rechner nachprogrammieren, so sollten Sie folgenden Modellfit erhalten:
## [...]
## Model Test User Model:
##
## Test statistic 18.444
## Degrees of freedom 18
## P-value (Chi-square) 0.427
##
## Model Test Baseline Model:
##
## Test statistic 1297.870
## Degrees of freedom 28
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 1.000
## Tucker-Lewis Index (TLI) 0.999
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -3395.988
## Loglikelihood unrestricted model (H1) -3386.766
##
## Akaike (AIC) 6827.976
## Bayesian (BIC) 6894.942
## Sample-size adjusted Bayesian (SABIC) 6837.855
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.009
## 90 Percent confidence interval - lower 0.000
## 90 Percent confidence interval - upper 0.052
## P-value H_0: RMSEA <= 0.050 0.937
## P-value H_0: RMSEA >= 0.080 0.000
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.028
## [...]
Falls dem so ist - herzlichen Glückwunsch, Sie haben gerade ein vollständiges Strukturgleichungsmodell formuliert und geschätzt! Jetzt bleibt nur noch die leichteste Übung: Ergebnisse korrekt interpretieren.
Dem Modelfit ist zu entnehmen, dass wir, anders als im Beispiel der Pfadanalyse, nun die Passung zwischen Modell und Daten untersuchen können: der $\chi^2$-Wert liegt bei 18.444 bei $df=$ 18 mit zugehörigem $p$-Wert von 0.427. Demnach verwerfen unsere Daten das Modell nicht.
Die Fit-Indizes zeigen hier allesamt einen guten Fit des Modells an. Dies war Aufgrund des $\chi^2$-Wertes zu erwarten, da die Stichprobengröße ausreichend Power liefert (sodass das Modell sinnvoll geschätzt werden kann) und der $\chi^2$-Wert trotzdem nicht signifikant auf dem 5%-Niveau war. Es gibt also keinen Grund, an der $H_0$ (auf Modellpassung zwischen Daten und Modell) zu zweifeln. Denn nur in solchen Modellen, in denen tatsächlich die $H_1$-Hypothese gilt, wächst der $\chi^2$-Wert mit der Stichprobengröße (dies steht im Widerspruch zu einigen Textbüchern, welche propagieren, dass der $\chi^2$-Wert immer mit der Stichprobengröße wächst!). Es empfiehlt sich sehr, über die Beziehung zwischen Stichprobengröße, $\chi^2$-Wert und den Fit-Indizes noch einmal im entsprechenden Exkurs zum Modellfit nachzulesen!
Für die Messmodelle ergibt sich Folgendes:
## [...]
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## ZD =~
## zd1 1.000
## zd2 0.836 0.063 13.273 0.000
## zd6 0.823 0.061 13.568 0.000
## BOEE =~
## bo1 1.000
## bo6 0.915 0.054 17.068 0.000
## bo12 0.960 0.057 16.806 0.000
## bo19 1.051 0.060 17.574 0.000
## [...]
Diesen entnehmen wir, dass die Variablen auf der latenten Dimension ähnlich stark differenzieren (ähnlich große Faktorladungen). Wir sehen außerdem, dass die ersten Faktorladungen jeweils auf 1 gesetzt sind und hier entsprechend keine Signifikanzentscheidung vonnöten ist (wir haben den Wert hier “ohne Unsicherheit” aus Skalierungsgründen vorgegeben). Um die (Item-)Reliabilität beurteilen zu können, schauen wir uns die erklärten Varianzanateile an:
## [...]
## R-Square:
## Estimate
## zd1 0.786
## zd2 0.553
## zd6 0.581
## bo1 0.742
## bo6 0.658
## bo12 0.644
## bo19 0.683
## BFs 0.420
## BOEE 0.185
## [...]
Die beobachteten Variablen zeigen Reliabilitäten zwischen 0.553 und 0.786.
Nun wollen wir die Ergebnisse mit den Ergebnissen der Pfadanalyse vergleichen. Dazu schauen wir uns die gerichteten Beziehungen zwischen den latenten Variablen an:
## [...]
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## BOEE ~
## ZD (a) 0.500 0.075 6.717 0.000
## BFs ~
## BOEE (b) 0.365 0.035 10.536 0.000
## ZD (c) 0.055 0.039 1.432 0.152
## [...]
Hier werden uns erneut die Label “(a)”, “(b)” und “(c)” angezeigt. Der direkte Effekt (c) von Zeitdruck auf psychosomatische Beschwerden scheint, im Gegensatz zu den Ergebnissen der Pfadanalyse im Abschnitt zuvor, nicht signifikant von 0 verschieden zu sein. Die beiden anderen Pfade sind statistisch signifikant:
Auch für diese Analysen ist der $R^2$-Output interessant:
## [...]
## R-Square:
## Estimate
## zd1 0.786
## zd2 0.553
## zd6 0.581
## bo1 0.742
## bo6 0.658
## bo12 0.644
## bo19 0.683
## BFs 0.420
## BOEE 0.185
## [...]
Im Bezug auf die latenten Regressionen enthält der R-Square Output die Anteile erklärter Varianzen von BOEE und BFs. Demnach können 42.03% der Variation der psychosomatischen Beschwerden durch die emotionale Erschöpfung und Zeitdruck (obwohl die Beziehung nicht signifikant ist) erklärt werden. 18.52% der Variation der emotionalen Erschöpfung werden durch Zeitdruck erklärt. Somit kann etwas mehr Variation erklärt werden als im Pfadanalysefall (dort: 38.02% der Variation der psychosomatischen Beschwerden durch die emotionale Erschöpfung und Zeitdruck sowie 14.77% der Variation der emotionalen Erschöpfung durch Zeitdruck).
Berechnen und Testen des indirekten Effektes von Zeitdruck über emotionale Erschöpfung auf psychosomatische Beschwerden im SEM
Der indirekte und der totale Effekt liegen bei:
## [...]
## Defined Parameters:
## Estimate Std.Err z-value P(>|z|)
## IE 0.183 0.031 5.878 0.000
## TE 0.238 0.042 5.694 0.000
## [...]
Der indirekte Effekt aus dem Pfadanalysemodell lag bei 0.158 und der totale bei 0.232. Somit liegen auch diese beiden Werte (deskriptiv gesehen) etwas höher, wenn wir latente Modellierung nutzen im Vergleich zu ausschließlich Skalenmittelwerten! Um den indirekten Effekt auf Signifikanz zu prüfen, benutzten wir wieder die Bootstrap-Methode (set.seed soll die Analyse replizierbar machen; schauen Sie dazu noch einmal im Abschnitt zur Pfadanalyse nach):
set.seed(12345)
fit_sem_IE_TE_boot <- sem(model_sem_IE_TE, data = StressAtWork, se = "boot", bootstrap = 1000)
parameterEstimates(fit_sem_IE_TE_boot, ci = TRUE)
## lhs op rhs label est se z pvalue ci.lower ci.upper
## 21 IE := a*b IE 0.198 0.033 5.965 0 0.135 0.267
## 22 TE := IE+c TE 0.258 0.043 6.028 0 0.171 0.340
Die Nummern 21 und 22 am Anfang der Zeilen zeigen an, dass hier insgesamt 22 Zeilen ausgegeben werden, wir uns aber nur die 21. und die 22. ansehen. Auch hier ist zu sehen, dass der indirekte Effekt signifikant von 0 abweicht. Da der direkte Effekt von Zeitdruck auf die psychosomatischen Beschwerden nicht signifikant ist, handelt es sich in diesem Zusammenhang um eine vollständige Mediation. Die vollständige lineare Beziehung zwischen Zeitdruck und psychosomatischen Beschwerden “fließt” über die emotionale Erschöpfung. Die Frage ist nun, warum es hier zu Unterschieden zwischen der Pfadanalyse und SEM kommt. Naiverweise würden wir zunächst erwarten, dass alle Effekte eher signifikant werden, wenn für Messfehler kontrolliert wird. So hatten wir zuvor mit messfehlerbehaften Regressoren in einer Regressionsanalyse argumentiert. Demnach würden wir eher erwarten, dass der direkte Effekt mit SEM signifikant ist. Allerdings haben wir in der Pfadanalyse die Daten unter der Annahme der essentiellen $\tau$-Äquivalenz zusammengefasst: wir haben einfach Mittelwerte ohne bestimmte Gewichtung verwendet. Im SEM haben wir die Faktorladungen frei schätzen lassen - wir haben also statt eines gleichgewichteten formativen Konstrukts ein reflexives Konstrukt aus den Beziehungen in den Daten schätzen lassen. Zusammenfassend gehen wir also von einer vollständigen Mediation aus.
Grafische Repräsentation
Wir können diese Modelle auch wieder grafisch darstellen. Probieren Sie doch einmal aus, was in diesem Zusammenhang durch die folgendenen weiteren Einstellungen passiert:
semPaths(object = fit_sem_IE_TE, what = "model", layout = "tree2",
rotation = 2, curve = T, col = list(man = "skyblue", lat = "yellow"),
curvePivot = T, edge.label.cex=1.2, sizeMan = 5, sizeLat = 8)
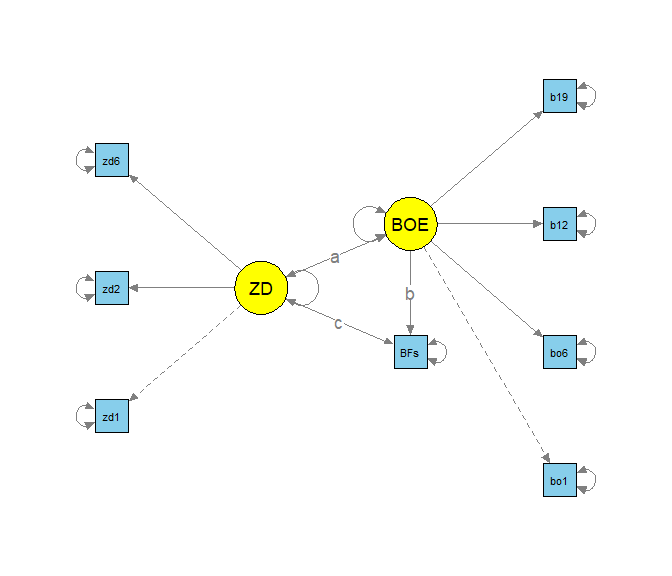
semPaths(object = fit_sem_IE_TE, what = "est", layout = "tree2",
rotation = 2, curve = T, col = list(man = "skyblue", lat = "yellow"),
curvePivot = T, edge.label.cex=1.2, sizeMan = 5, sizeLat = 8)
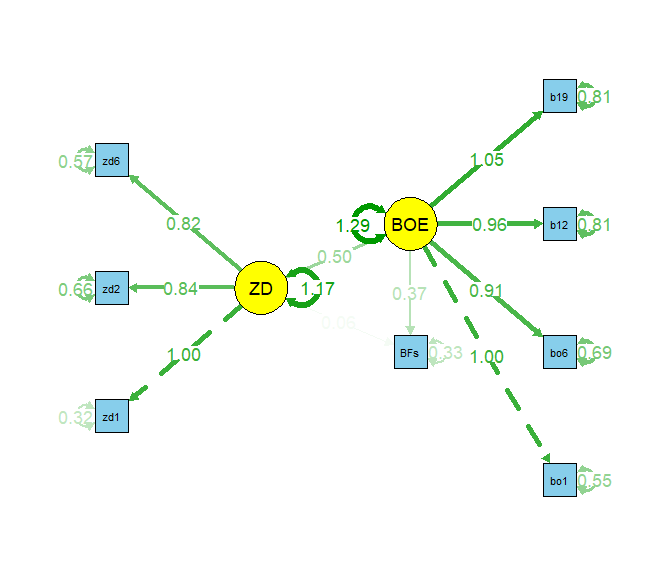
curve = T und curvePivot = T haben in diesem Modell keinen Effekt, da es hierbei um die Kovarianzen geht und werden nur der Vollständigkeit halber aufgeführt. Der Effekt dieser beiden Argumente kann im Exkurs zum Modellfit der ersten Grafik des $H_0$-Modells entnommen werden: diese Einstellungen bewirken die nicht vollständig runde Kurve der Fehlerkovarianz (durch curvePivot = T), welche vor allem dann die Übersichtlichkeit erhöht, wenn mehrere Kovarianzen vorhanden sind. Mit curve = F würden alle Fehlerkovarianzen und Kovarianzen (wenn vorhanden) als gerade Linien eingezeichnet werden.
BFs wird hier als Viereck dargestellt, da wir hier Werte gemittelt und diesen Skalenwert als direkt beobachtbare Variable in das Modell aufgenommen haben.
Konkurrierende Modelle können, wie auch in der Sitzung zur CFA, mit Hilfe des Likelihood-Ratio Tests ($\chi^2$-Differenzen-Test/ Likelihood-Ratio-Test, LRT) gegeneinander getestest werden mit der Funktion lavTestLRT.
Modellpassung
Die Modellpassung ist bei Modellvergleichen von großer Wichtigkeit. Es macht keinen Sinn, zwei überhaupt nicht zu den Daten passende Modelle miteinander zu vergleichen. Demnach sollten wir uns zunächst einigermaßen sicher sein, dass unser Modell sinnvoll zu den Daten passt. Da allerdings auch kleinste Abweichungen zwischen Daten und Modell zu signifikanten $\chi^2$-Werten führen, vor allem für große Stichproben, haben wir uns auch immer die Fit-Indizes angesehen, die entweder für die Stichprobengröße korrigieren, oder noch weitere Informationen heranziehen (z.B. das Modell mit dem schlechtesten Modell vergleichen). Dazu können Sie noch weiteres im Exkurs zum Modellfit erfahren.
Wann genau die Fit-Indizes für eine deutliche Abweichung zwischen Daten und Modell sprechen, hängt von vielen Dingen ab. Im Artikel von Schermelleh et al. (2003) wurden Cut-Kriterien für spezifische Modelle entwickelt ($CFI < .97$ und $RMSEA > .05$), welche nicht notwendigerweise auf alle anderen Modelle mit unterschiedlicher Komplexität, Stichprobengröße und Anzahl manifester Variablen, etc. übertragbar sind. Diesem Umstand geschuldet wurde das R-Paket ezCutoffs entwickelt, welches simulationsbasierte Cut-Kriterien speziell angepasst an das vorliegende Modell berechnet. Der ezCutoffs-Funktion müssten wir dazu einfach unser angenommenes Modell sowie die Daten übergeben. Schauen wir uns dem Output zu unserem model_sem_IE_TE Modell, in welchem die Mediation von Zeitdruck über emotionale Erschöpfung auf Burnout modelliert wurde, an:
library(ezCutoffs)
ezCutoffs(model = model_sem_IE_TE, data = StressAtWork)
## Data Generation
##
## |==================================================| 100% elapsed = 11s ~ 0s
##
## Model Fitting
##
## |==================================================| 100% elapsed = 8s ~ 0s
##
##
## Empirical fit Cutoff (alpha = 0.05)
## chisq 18.444008456 29.49324699
## cfi 0.999650351 0.97982435
## tli 0.999456102 0.96861566
## rmsea 0.008993101 0.04575465
## srmr 0.027500985 0.04021870
Emprircal fit ist hier gerade der Modelfit, den wir auch in unseren Daten beobachtet haben. Der $\chi^2$-Wert von 18.444 kommt uns auch sehr bekannt vor! In der Spalte Cutoff (alpha = 0.05) steht der zugehörige Cut-Off-Wert, ab welchem von keinem guten Fit mehr zu sprechen wäre. Hierbei ist zu beachten, dass für $TLI$ und $CFI$ kleine Werte (also kleiner als der Cut-Off-Wert) für einen schlechten Fit sprechen, während für $RMSEA$ und $SRMR$ große Werte (also größer als der Cut-Off-Wert) für einen schlechten Fit sprechen.
Wer davon noch nicht genug hat, ist herzlich eingeladen, sich im Appendix A mit dem Test auf essentielle $\tau$-Äquivalenz vertraut zu machen. Die Annahme der essentiellen $\tau$-Äquivalenz wurde in der Sitzung zur CFA bereits angesprochen und unterliegt implizit dem Zusammenfassen zu Skalenmittelwerten.
Appendix A
Essentielle $\tau$-Äquivalenz im SEM
Das Pfadanalysemodell auf Basis von Skalenmittelwerten hatte als Voraussetzung, dass alle Messungen der selben latenten Variable essentiell $\tau$-äquivalent sind, also alle $\lambda$s gleich sind pro latenter Variable. Dies können wir in unserem Modell prüfen, indem wir den Faktorladungen Namen geben, analog zur Benennung der gerichteten Beziehungen zwischen den latenten Variablen, die wir zur Berechnung des indirekten etc. Effekts gebraucht haben. Das letzte Modell sah so aus:
model_sem_IE_TE <- '
# Messmodelle
ZD =~ zd1 + zd2 + zd6
BOEE =~ bo1 + bo6 + bo12 + bo19
# Strukturmodell
BOEE ~ a*ZD
BFs ~ b*BOEE + c*ZD
# Neue Parameter
IE := a*b
TE := IE + c
'
Wenn wir weiterhin die Defaulteinstellungen der Funktion sem nutzen wollen (1. Faktorladung = 1, etc.), dann müssen wir bei der Benennung der Faktorladungen etwas aufpassen. Wenn nun alle Faktorladungen gleich sein sollen, so können wir einfach den Präfix 1* vor alle Faktorladungen schreiben. Dies kommt zum äquivalenten Ergebnis wie das Schreiben von bspw. l1* vor alle Messungen der selben latenten Variable (z.B. Zeitdruck): alle Faktorladungen würden auch so per Default auf 1 gesetzt und würden das Label l1 tragen. Das Vergeben von dem Label l1 ist der allgemeinere Ansatz, weswegen wir diesen hier verwenden wollen. Achtung, wenn wir hier die gleichen Labels über die latenten Variablen (auch l1) verwendet hätten, so wären die Faktorladungen gleich mit denen des Zeitdruck, was wir allerdings nicht wollen. Die essentielle $\tau$-Äquivalenzannahme gilt nur pro latenter Variable.
model_sem_IE_TE_tau <- '
# Messmodelle
ZD =~ l1*zd1 + l1*zd2 + l1*zd6
BOEE =~ l2*bo1 + l2*bo6 + l2*bo12 + l2*bo19
# Strukturmodell
BOEE ~ a*ZD
BFs ~ b*BOEE + c*ZD
# Neue Parameter
IE := a*b
TE := IE + c
'
fit_sem_IE_TE_tau <- sem(model_sem_IE_TE_tau, StressAtWork)
summary(fit_sem_IE_TE_tau, fit.measures = T, rsq = T)
Als Modellfit erhalten wir:
## [...]
## Model Test User Model:
##
## Test statistic 33.002
## Degrees of freedom 23
## P-value (Chi-square) 0.081
##
## Model Test Baseline Model:
##
## Test statistic 1297.870
## Degrees of freedom 28
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.992
## Tucker-Lewis Index (TLI) 0.990
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -3403.267
## Loglikelihood unrestricted model (H1) -3386.766
##
## Akaike (AIC) 6832.534
## Bayesian (BIC) 6880.898
## Sample-size adjusted Bayesian (SABIC) 6839.669
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.038
## 90 Percent confidence interval - lower 0.000
## 90 Percent confidence interval - upper 0.065
## P-value H_0: RMSEA <= 0.050 0.745
## P-value H_0: RMSEA >= 0.080 0.003
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.048
## [...]
Sowie folgende Ergebnisse für die Messmodelle:
## [...]
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## ZD =~
## zd1 (l1) 1.000
## zd2 (l1) 1.000
## zd6 (l1) 1.000
## BOEE =~
## bo1 (l2) 1.000
## bo6 (l2) 1.000
## bo12 (l2) 1.000
## bo19 (l2) 1.000
## [...]
Wir erkennen durch die gleiche Benennung, dass es sich hier um restringierte Koeffizienten handelt. Auch erkennen wir, dass die Faktorladungen von ZD und BOEE alle gleich heißen und auf 1 gesetzt wurden.
Dem Modellfit ist zu entnehmen, dass das Modell immer noch zu den Daten passt: der $\chi^2$-Wert liegt bei 33.002 bei $df=$ 23 mit zugehörigem $p$-Wert von 0.081. Demnach verwerfen unsere Daten das Modell nicht. Außerdem sind die $df$ genau um 5 größer als im unrestringierten Modell (ohne die Annahme der essentiellen $\tau$-Äquivalenz pro latenter Variable). Wir können diese Differenz leicht prüfen: es mussten 2 Faktorladungen weniger für ZD geschätzt werden und 3 weniger für BOEE - aus diesem Grund unterscheiden sich die $df$ gerade um 5! Da das Modell nicht durch die Daten verworfen wird, müssen wir uns auch nicht unbedingt die Fit-Indizes ansehen. Diese sind hier nämlich auch unauffällig. Ob sie überhaupt im Bezug zu diesem Modell interpretiert werden sollten, wird im Exkurs zum Modellfit näher beleuchtet.
Auch wenn die Daten unser Modell nicht verwerfen, können wir die beiden Modelle mit und ohne essentieller $\tau$-Äquivalenzannahme inferenzstatistisch miteinander vergleichen. Dazu verwenden wir wieder die Funktion lavTestLRT und führen also einen Likelihood-Ratio-Test ($\chi^2$-Differenzentest) durch.
lavTestLRT(fit_sem_IE_TE_tau, fit_sem_IE_TE)
##
## Chi-Squared Difference Test
##
## Df AIC BIC Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
## fit_sem_IE_TE 18 6828.0 6894.9 18.444
## fit_sem_IE_TE_tau 23 6832.5 6880.9 33.002 14.558 0.079168 5 0.01243 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Dem Modellvergleich ist zu entnehmen, dass das $\tau$-Äquivalenz-Modell signifikant schlechter zu den Daten passt. Der $p$-Wert liegt bei 5 und ist somit $<.05$. Auch die Differenz der $df$ lässt sich diesem Output entnehmen. Dies zeigt erneut, dass die Annahme der essentiellen $\tau$-Äquivalenz, auf welcher das Pfadanalysemodell untersucht wurde, auf dem 5% Signifikanzniveau nicht haltbar ist.
Auf die gleiche Art und Weise können wir auch Invarianz (zu Invarianz über Gruppen siehe Sitzung zur MSA) über die Zeit oder über Gruppen hinweg untersuchen. Über die Zeit würden wir zwei latente Variablen formulieren, welche einmal $t_1$ und einmal $t_2$ symbolisieren. Die Annahme, dass zu beiden Zeitpunkten die Messmodelle gleich sind, ist tatsächlich in vielen Situationen sinnvoll.
Literatur
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden (5. Auflage, 1. Auflage: 2010). Weinheim: Beltz.
Schermelleh-Engel, K., Moosbrugger, H., & Müller, H. (2003). Evaluation the fit of structural equation models: tests of significance and descriptive goodness-of-fit measures. Methods of Psychological Research Online, 8(2), 23-74.
Werner, C. S., Schermelleh-Engel, K., Gerhard, C., & Gäde, J. C. (2016). Strukturgleichungsmodelle. In N. Döring & J. Bortz, Forschungsmethoden und Evaluation (5., vollständig überarbeitete und erweiterte Auflage, pp. 945–975). Berlin: Springer.
Inhaltliche Literatur
Büssing, A., & Perrar, K.-M. (1992). Die Messung von Burnout. Untersuchung einer deutschen Fassung des Maslach Burnout Inventory (MBI-D) [The measurement of Burnout. The study of a German version of the Maslach Burnout Inventory (MBI-D)]. Diagnostica, 38, 328 – 353.
Cloetta, B. (2014). Machiavellismus-Konservatismus. Zusammenstellung sozialwissenschaftlicher Items und Skalen (ZIS). https://doi.org/10.6102/zis82
Maslach, C., & Jackson, S.E. (1986). Maslach Burnout Inventory (Vol. 2). Palo Alto, CA: Consulting Psychologists Press.
Mohr, G. (1986). Die Erfassung psychischer Befindensbeeinträchtigungen bei Arbeitern [Assessment of impaired psychological well-being in industrial workers]. Frankfurt am Main, Fermany: Lang.
Semmer, N. K., Zapf, D., & Dunckel, H. (1999). Instrument zur Stressbezogenen Tätigkeitsanalyse (ISTA) [Instrument for stress-oriented task analysis (ISTA)]. In H. Dunkel (Ed.), Handbuch psychologischer Arbeitsanalyseverfahren (pp. 179 – 204). Zürich, Switzerland: vdf Hochschulverlag an der ETH.
- Blau hinterlegte Autor:innenangaben führen Sie direkt zur universitätsinternen Ressource.
](/media/header/chocolate_construction.jpg)