Wiederholung von Grundlagen in R
Wiederholung von Grundlagen in R
Für die Inhalte, die wir in diesem Semester behandeln setzen wir - naheliegenderweise - da an, wo wir im letzten Semester aufgehört haben. Von besonderer Bedeutung, um direkt ins Semester starten zu können, ist es vor allem die R Grundlagen parat zu haben. Zum Einen gucken wir uns die wichtigsten Bestandteile hier an, zum Anderen können Sie aber auch Otter nutzen, um noch einmal aus einem anderen Blickwinkel die R Basics aufzuarbeiten. Neben diesen Grundlagen, betrachten wir hier auch ausgewählte Datenanalysen aus dem letzten Semester. Für interessierte Lesende gibt es im Anhang einführende Informationen dazu, wie man in R Dokumente mit Fließtext und Analyse in einer Datei - einem sogenannten R-Markdown - erstellen kann.
Wenn Sie sich nur bestimmte Abschnitte angucken wollen, um Ihre Unsicherheiten zu beseitigen, bevor wir in der kommenden Woche mit neuen Inhalten in R loslegen, können Sie die folgende Übersicht nutzen, um direkt zu den einzelnen Abschnitten zu springen:
Abschnitte in diesem Beitrag
- R Grundlagen (dieser Abschnitt…)
- Allgemeine Arbeitshinweise
R-Basics- Vektoren und Matrizen (könnte sogar etwas Neues enthalten!)
- Datenmanagement
- Statistik I
- Appendix A: Markdown (wie man Fließtext und
Rkombiniert) - Appendix B: ChatGPT (wie ChatGPT mit
Rhelfen kann)
Installation und Updates
Wir beginnen dieses Tutorial noch einmal mit der Installation von R und RStudio - das ist nicht nur nützlich, wenn Sie R in den Wochen seit dem ersten Semester deinstalliert haben sollten, sondern auch, um Ihre Version von R zu aktualisieren.
Für den Verlauf dieses Modul benötigen Sie die Statistiksoftware R und für eine bessere Bedienbarkeit die Benutzeroberfläche RStudio auf Ihrem Rechner. Sie haben beide Programme vermutlich schon runtergeladen und installiert, aber falls Sie zum Beispiel ein neues Gerät verwenden oder die Programme schon gelöscht haben, können Sie auf den folgenden Seiten einen kostenlosen Download durchführen.
Downloadlinks:
R für das Windows-Betriebssystem: Download von CRAN
R für das Mac-Betriebssystem: Download von CRAN
RStudio: Download von der posit Seite
Es ist sehr sinnvoll R aktuell zu halten, weil Pakete nur für die derzeitige R-Version weiterentwickelt werden und es so passieren kann, dass Ihre R-Version von bestimmten Pakete nicht mehr unterstützt wird. Die Aktuelle Version von R ist 4.3.0. Welche Version Sie zur Zeit nutzen, können Sie so herausfinden:
R.Version()$version.string
## [1] "R version 4.3.0 (2023-04-21 ucrt)"
Wie Sie sehen, ist die Version relativ neu. Wenn Sie eine andere Version nutzen, ist nun der perfekte Zeitpunkt für ein Update! Der typische Weg R auf Windows oder Mac zu aktualisieren ist es, die aktuelle Fassung herunterzuladen und ganz normal neu zu installieren. Die vorangegangene Version können Sie anschließend deinstallieren. Es ist möglich mehrere Versionen von R gleichzeitig installiert zu haben, um im Fall von größeren Updates Ergebnisse aus älteren Analyseskripten reproduzieren zu können.
Wenn die Versionsnummer sich nur in der dritten Zahl unterscheidet, werden die Pakete, die Sie aktuell installiert haben übernommen. Wenn die Version sich in einer der ersten beiden Zahlen unterscheidet, ist es meist sinnvoll, Pakete erneut zu installieren.
Neben R selbst, sollten Sie auch Ihre Pakete auf dem aktuellen Stand halten. Es ist sinnvoll alle zwei oder drei Wochen folgenden Befehl durchzuführen:
update.packages(ask = FALSE)
Damit werden alle Pakete aktualisiert, für die es neuere Versionen gibt. Wenn Sie das Argument ask = FALSE weglassen, werden Sie bei jedem Paket einzeln gefragt, ob Sie es updaten möchten. Sollte Ihre letzte Aktualisierung ein wenig her sein, könnte dieser Prozess einen Moment dauern.
Allgemeine Arbeitshinweise
Wir können Ihnen im Studium nur so viel beibringen, wie es unsere und Ihre Zeit zulässt. Diese Zeit schwankt von Person zu Person, wir können aber in jedem Fall mit Sicherheit behaupten, dass es nicht genug ist, um für jedes Problem, dem Sie im Laufe ihrer akademischen Karriere begegnen könnten, eine spezifische Lösung zu besprechen. Stattdessen versuchen wir (und Sie hoffentlich auch) Sie darauf vorzubereiten, diese Probleme selbst lösen zu können. Daher ist unser Ziel nicht nur, Ihnen alle für diesen Kurs relevanten Kompetenzen beizubringen, sondern Sie darüber hinaus zu kompetenten Problemlöser:innen in Statistik - unter Verwendung von R - zu machen. Nachfolgend wollen wir Ihnen daher einige Tipps & Ressourcen an die Hand geben, die wir Ihnen beim Erlernen, Vertiefen und Problemlösen empfehlen können.
ChatGPT und andere KI-Tools
Natürlich verschiebt sich der Umgang mit Programmiersprachen und die Herangehensweise an Datenaufbereitung und Auswertung im Moment. Insbesondere über ChatGPT in all seinen Formen, können Sie viele Bestandteile - mitunter ganze Auswertungsskripte - quasi automatisch generieren lassen. Allerdings ist der Code, den ChatGPT produziert meist nicht perfekt - produziert Fehler oder ist für dieses spezifische Beispiel nicht korrekt. Dennoch kann auf diese Weise sehr schnell das Skelett eines funktionierenden Codes erzeugt werden und auf den eigenen Anwendungsfall hin angepasst werden. Dies erfordert allerdings, dass Sie diese Diskrepanzen erkennen und Rückmeldungen korrekt interpretieren können. Im Appendix B ist eine kurze Interaktion mit ChatGPT dargestellt, in der für einen einfach Fall Code generiert wird und für einen anderen Fall Fehler im Code gefunden werden. Auch wird dort ein Weg beschrieben, wie sie die Kommunikation mit ChatGPT in die R-Konsole einbinden können.
Wenn Sie einen einen GitHub Account haben, können Sie GitHubs CoPilot nutzen, um direkt in RStudio Autoergänzungen und Syntax Vorschläge generieren zu lassen. Allerdings ist auch hier immense Vorsicht geboten, weil es dafür wichtig ist zu wissen, was Sie überhaupt erreichen wollen und ob der Code, der automatisch generiert wurde, Sie diesem Ziel näher bringt.
Offene Ressourcen
Für R gibt es eine Vielzahl von online Ressourcen, die Sie beim Lernen nutzen können und sollten. Zum Einen gibt es online sehr viele kostenlose Informationsangebote (z.B. die Introduction to R vom R Core Team, das R-Cookbook, das Buch R for Data Science, oder hier eine Einführung in R für Psychologie-Studierende, sowie teilweise kostenlosen Übungsplattformen (z.B. Datacamp, Codecademy usw.). Von der Goethe Uni direkt produziert wurde hierfür z.B. auch Otter, welches - anders als diese Seite - eine interaktive Oberfläche bietet (Sie den R-Code direkt auf der Seite ausführen können), aber nicht direkt auf die Inhalte des Psychologiestudiums angepasst ist. Für spezifische Aufgaben arbeiten wir (oder zumindest einige von uns) derzeit mit Hochdruck an neuen Aufgaben für tigeR - wenn Sie dafür gerne Zugangsdaten hätten, geben Sie uns Bescheid.
Dazu kommen die sehr aktiven Foren bzw. Communities, wie vor allem Stack Overflow für R-Programmierung und Cross Validated für allgemeine Statistikfragen. Lernen Sie, diese Ressourcen für sich zu nutzen!
Hilfe zur Selbsthilfe
Bei der Arbeit mit R sind Fehlermeldungen auch für langjährige Anwender:innen Alltag. Sie sollten also eine Frustrationstoleranz aufbauen und nicht erwarten, eine Aufgabe im ersten Anlauf perfekt und ohne Fehlermeldungen lösen zu können. Vielmehr sollten Sie lernen, Fehlermeldungen zu verstehen und daraus zu lernen. Versuchen Sie nachzuvollziehen, auf welches Element in Ihrem Code sich eine Fehlermeldung bezieht und was der Inhalt besagt.
Lernen Sie außerdem, mit der R-internen Hilfefunktion zu arbeiten. Jede Funktion in R hat eine Hilfeseite, auf der die Anwendung dieser Funktion erklärt wird. Die Struktur ist immer ähnlich und wir hatten sie hier im Detail beschrieben. Oft gibt es darüber hinaus online noch ausführlichere Informationen zur Anwendung. Beispielsweise gibt es hier eine ausführliche Anleitung zum Psych-Package, oder auch so genannte Cheatsheets, die eine Übersicht der wichtigsten Befehle zu bestimmten Themen erhalten (hier beispielsweise für Basics in R). Lernen Sie, sich selbstständig Informationen zu beschaffen, denn auch nach langjähriger Erfahrung mit R wird das immer wieder notwendig sein. Häufig bedeutet die Arbeit an einer komplexen, neuen Fragestellung, dass Sie eine Vielzahl verschiedener Ressourcen zu Rate ziehen müssen. Wir können Ihnen in der Veranstaltung nicht alle vorhandenen Möglichkeiten vermitteln (weil das R-Universum so umfangreich ist), aber wir können Ihnen hoffentlich das Handwerkszeug geben, sich selbst zu helfen!
Dokumentation
Dokumentieren Sie alle Schritte sorgfältig. Schreiben Sie dazu so viele Kommentare wie Sie für nötig halten (meistens mehr). In R werden Kommentare durch (beliebig viele) # begonnen und enden bei einem Zeilenumbruch. Mit Kommentaren kann Syntax auch in verschiedene Abschnitte gegliedert werden. Empfehlenswert ist es, solche Abschnittüberschriften mit #### zu beginnen und mit ---- zu beenden. RStudio erkennt solche Kommentare automatisch als Überschriften und stellt über den
 Button eine darauf basierende Gliederung zur Verfügung. Wenn Sie dazu tendieren, sehr viel Text zu schreiben, können Sie Ihren R-Code in RMarkdowns integrieren, wie wir im Anhang A dargestellt haben. Zunächst ist die Dokumentation ein zeitaufwendiger Schritt mehr, aber Future-You wird es Ihnen danken.
Button eine darauf basierende Gliederung zur Verfügung. Wenn Sie dazu tendieren, sehr viel Text zu schreiben, können Sie Ihren R-Code in RMarkdowns integrieren, wie wir im Anhang A dargestellt haben. Zunächst ist die Dokumentation ein zeitaufwendiger Schritt mehr, aber Future-You wird es Ihnen danken.

Strukturierung
Dinge gehen leichter von der Hand und sind im Nachhinein häufig leichter zu verstehen, wenn sie einer typischen Struktur folgen. Mein persönliches Template sieht dafür so aus:
#### Titel des Skripts ####
#### Datum der Erstellung ####
#### Vorbereitende Schritte ----
# Pakete laden
# Working directory setzen
#### Daten importieren ----
#### Daten aufbereiten ----
# Skalenwerte erstellen
# Fälle ausschließen
# Auf relevante Daten reduzieren
#### Deskriptivstatistik ----
# Demografische Variablen
# Outcomes und Kovariaten
#### Voraussetzungsprüfung ----
# Visuell
# Tests
#### Datenanalyse ----
#### Grafische Aufbereitung ----
Ihr Template kann anders aussehen. Wichtig ist nur, dass Sie eine Struktur erzeugen und die relevanten Abschnitt wieder finden können. Insbesondere ist es immens wichtig, dass alle Pakete an einem gemeinsamen und sinnvollerweise sehr frühen Ort geladen werden, damit alle, die das Skript nutzen sofort sehen können, welche Pakete sie installieren müssen. Außerdem sollte die Datenaufbereitung immer gemeinsam an einem Ort erfolgen und nicht - je nach Analyse - über das Skript verteilt sein. So kann garantiert werden, dass nachvollziehbar ist, welche Personen ausgeschlossen werden und welche Variablen erstellt werden müssen.
Ausprobieren
Scheuen Sie sich nicht, viel auszuprobieren. Oft gibt es viele Wege zum Ziel, und durch das Ausprobieren mehrerer Möglichkeiten lernen Sie umso mehr Vorgehensweisen kennen. Suchen Sie gerne nach alternativen Wegen, probieren Sie andere Funktionen aus, laden Packages herunter und probieren Sie, damit zu arbeiten! Haben Sie keine Angst, etwas falsch zu machen. Durch die Dokumentation (s.o.) können Sie jederzeit, wenn etwas schief gegangen ist, zum vorherigen Schritt zurückkehren, und es nochmal probieren (auch das ist Alltag für alle Anwender:innen!). Behalten Sie immer ein Kopie der Rohdaten, die Sie nicht verändert haben, so können Sie beim Ausprobieren nichts kaputt machen!
R-Basics
RStudio
Das traditionelle R ist im Rahmen seiner Nutzeroberfläche einer Konsole ähnlich und damit nicht sehr benutzerfreundlich. Durch die Erweiterung mit RStudio wird die Verwendung deutlich erleichtert, weshalb wir dieses auch herunterladen.
RStudio besteht aus vier Panels. Wenn wir RStudio zum ersten Mal öffnen sind jedoch nur drei sichtbar. Das vierte wird durch das Öffnen eines neuen Files sichtbar (oder auch durch Strg+Shift+n bzw. in OS X: Cmd+Shift+n).
Zunächst betrachten wir das Fenster unten links - die Konsole. In dieser kann Code ausgeführt werden. Beispielsweise können wir dort eine Addition eingeben und erhalten nach dem Drücken von Enter dann das Ergebnis der Operation.
2 + 1
## [1] 3
Auf diese Weise kann man zwar Aktionen ausführen, hat nach dem Schließen von RStudio aber keine Dokumentation, was man durchgeführt hat. Dafür ist das Script, also das eben neu geöffnete File, im linken oberen Fenster gedacht. Dort kann Code geschrieben und später auch gespeichert werden. Wenn wir unsere Addition nun dort notieren und anschließend Enter drücken passiert erstmal nichts. Damit etwas passiert, muss die Syntax mit Run Button
 oder mit Strg+Return (OS X: cmd+Return) ausgeführt werden. Das Ergebnis wird aber nicht im Script selbst, sondern in der Konsole angezeigt.
oder mit Strg+Return (OS X: cmd+Return) ausgeführt werden. Das Ergebnis wird aber nicht im Script selbst, sondern in der Konsole angezeigt.
Oben rechts wird per Voreinstellung das Environment angezeigt, das wir gleich noch füllen werden. Unten rechts gibt es verschiedene Tabs wie beispielsweise die Hilfe und die Anzeige von Plots.
Wenn Sie einmal etwas in der Konsole ausgeführt haben, anstatt es im Skript zu hinterlegen, können Sie anhand der History nachvollziehen, welche Schritte Sie durchlaufen haben. In dieser können Sie auch mehrere Zeilen bzw. Schritte markieren und diese über den
 Button in Ihre Syntax einfügen.
Button in Ihre Syntax einfügen.
Einfache Operationen
Um direkt die guten Vorsätze umzusetzen, die ich mir selbst oben geschrieben habe, versehen wir den kommenden Abschnitt erst einmal mit einer strukturierenden Überschrift und einem Kommentar:
1 + 2 # Addition
## [1] 3
In der Gliederung sollte in RStudio jetzt die Überschrift “Wiederholung in R” auftauchen.
Neben einfachen Taschenrechner-Funktionen mit numerischen Ergebnissen kann R auch logische Abfragen und Vergleiche durchführen. Hier folgt ein Beispiel für das Prüfen auf Gleichheit:
3 == 4 # Logische Abfrage auf Gleichheit
## [1] FALSE
Die Ergebnisse dieser Abfragen sind boolesch - also immer entweder wahr (TRUE) oder falsch (FALSE).
Hier finden Sie weiterführende Informationen und eine Übersicht zu Rechenoperationen und logischen Abfragen.
Funktionen und Argumente
Die Umsetzung der Addition anhand normaler Zeichen ist recht simpel. Das ist jedoch eher eine Ausnahme, weshalb es in R vorprogrammierte Funktionen gibt. Für unsere bisherige Operation könnte man beispielsweise folgende Funktion nutzen:
sum(1, 2) # Addition durch Funktion
## [1] 3
Hier wird die Funktion sum genutzt, um eine Summe der Argumente (1 und 2) zu bilden. An diesem Beispiel lässt sich bereits die generelle Struktur von Funktionen in R erkennen:
funktion(argument1, argument2, argument3, ...)
Wenn Argumente verschiedene Funktionen haben, sollten sie auch benannt werden. Ein einfaches Beispiel ist das Runden von Zahlen. Hier gibt es zusätzlich zu der Zahl auch die Menge an Nachkommastellen, die angegeben werden soll. Funktionen in R haben die Grundstruktur funktionsname(argument1 = ..., argument2 = ..., argument3 = ...). Die Argumente, die eine Funktion erwartet, können mit args() abgefragt werden.
args(round)
## function (x, digits = 0)
## NULL
Testen Sie diese Möglichkeit mit anderen Funktionen, die Sie aus dem letzten Semester kennen! Wenn es einen Default-Wert für ein Argument gibt, wird er hier hinter dem = angezeigt. Bei round sagt uns der Ausdruck digits = 0, dass per default auf 0 Nachkommastellen gerundet wird.
round(1.2859)
## [1] 1
Wenn wir diesen Default-Wert überschreiben, können wir stattdessen bspw. auf 2 Stellen runden.
round(1.2859, digits = 2)
## [1] 1.29
Argumente können durch die korrekte Reihenfolge oder durch explizite Benennung angesprochen werden. Wenn wir beispielsweise in der round Funktion die Reihenfolge der Argumente vertauschen, aber den Namen des Argumentes verwenden, funktioniert die Ausführung trotzdem.
round(digits = 2, x = 1.2859)
## [1] 1.29
In den allgemeinen Arbeitshinweisen haben wir bereits die interne Hilfe in R angesprochen. Anstatt nach der Funktion im Tab Help zu suchen, können Sie mit ? oder help() die Hilfe aufrufen, um sich detaillierte Informationen zu dieser Funktion ausgeben zu lassen. Nutzen Sie diese Möglichkeit immer, wenn Ihnen die Anwendung einer Funktion nicht klar ist.
Objekte und das Environment
Objekte dienen dazu, Ergebnisse abzulegen und diese in einer anderen Funktion zu verwenden. Die Zuweisung eines Ergebnisses zu einem Objekt erfolgt über den sog. Zuweisungspfeil <-.
my_num <- sum(3, 4, 1, 2) # Objekt zuweisen
Anders als zuvor wird in diesem Fall in der Konsole kein Ergebnis ausgedruckt, sondern lediglich der Befehl gespiegelt. Das Ergebnis der Summen-Funktion ist im Objekt my_num abgelegt. Dieses Objekt sollte nun auch im Panel oben rechts - spezifischer im Tab Environment - aufgetaucht sein. Nun können wir den Inhalt des Objektes an eine Funktionen weiterreichen - z.B. um die Quadratqurzel der Zahl zu bestimmen: sqrt.
sqrt(my_num) # Objekt in Funktion einbinden
## [1] 3.162278
Der Inhalt des Objektes wird so als Argument in die Funktion sqrt übergeben. Das ist letztlich das Gleiche wie
sqrt(sum(3, 4, 1, 2)) # Verschachtelte Funktionen
## [1] 3.162278
wo das Ergebnis nicht explizit in einem Objekt gespeichert wird, sondern direkt als Argument an eine Funktion weitergegeben wird. Dabei werden geschachtelte Funktionen von innen nach außen evaluiert. Die Aneinanderkettung von Objektzuweisungen und Schachtelungen ist unbegrenzt, sodass sehr komplexe Systeme entstehen können. Weil das aber sehr schnell anstrengend werden kann - und man dabei leicht den Überblick verliert, was eigentlich wann ausgeführt wird - gibt es noch eine weitere Variante, Funktionen aneinander zu reihen: die Pipe.
Bei der Pipe |> wird ein links stehendes Objekt oder Ergebnis genommen und als erstes Argument der rechts stehenden Funktion eingesetzt. Für unser Wurzelbeispiel also:
sum(3, 4, 1, 2) |> sqrt() # Nutzung Pipe
## [1] 3.162278
Das hat den immensen Vorteil, dass wir dadurch unseren Code wieder in der, im westlichen Kulturkreis üblichen Variante wie Text von links nach rechts lesen können. Dabei ist das was als erstes passiert links, das Ergebnis wird nach rechts weitergereicht und irgendetwas passiert damit. Ergebnisse, die man später noch braucht, sollten aber immer in einem Objekt abgelegt werden.
Vektoren und Matrizen
Vektoren
Vektoren sind ein spezieller Typ für Objekte, die in R durch den Befehl c() erstellt werden können:
zahlen <- c(8, 3, 4) #Vektorerstellung
Wird eine Rechenoperation auf einen Vektor angewandt, so wird die Operation elementeweise vorgenommen. Hier sehen Sie, dass jedes einzelne Element des Vektors zahlen mit 3 multipliziert wird.
zahlen * 3 # Multiplikation der Elemente des Vektors
## [1] 24 9 12
Vektoren können unterschiedlicher Art sein:
| Typ | Kurzform | Inhalt |
|---|---|---|
logical | logi | wahr (TRUE) oder falsch (FALSE) |
numeric | num | Beliebige Zahlen |
character | char | Kombinationen aus Zahlen und Buchstaben |
factor | fac | Faktor mit bestimmter Anzahl an Stufen |
Diese vier sind die häufigsten Arten von Vektoren, die Ihnen im Umgang mit psychologischen Daten begegnen werden. Allerdings sind sie weder alle Formen von Vektoren, noch wirklich unterschiedlich. Genau genommen ist das System etwas komplizierter, aber generell reichen für unsere Anwendung diese vier aus. Für einen vorhandenen Vektor kann die Klasse über die Funktion str() ermittelt werden.
str(zahlen)
## num [1:3] 8 3 4
Über die Funktion as.character() können die Elemente eines Vektors in Zeichen umgewandelt werden. Neben der Angabe chr sehen Sie auch, dass die Zahlen nun in Anführungszeichen dargestellt werden.
zeichen <- as.character(zahlen)
str(zeichen)
## chr [1:3] "8" "3" "4"
Wenn Sie nun beispielsweise eine mathematische Funktion auf diesen Vektor anwenden würden, erhalten Sie eine Fehlermeldung.
zeichen * 3
## Error in zeichen * 3: nicht-numerisches Argument für binären Operator
Nutzen Sie die Möglichkeit, die Klasse eines Objektes zu erfragen deshalb auch, wenn Sie eine Fehlermeldung erhalten, um zu prüfen, ob ein Vektor die richtige Klasse hat. Wenn Sie ein spezifische Klasse erwarten, können Sie z.B. mit dem Cousin von as. arbeiten: is.:
is.numeric(zeichen)
## [1] FALSE
Matrizen
Matrizen sind eine der vier Formen, in der in R mehrere Vektoren in einem gemeinsamen Objekt abgelegt werden können:
| Typ | Dimensionen | Inhalt |
|---|---|---|
matrix | 2 | Vektoren des gleichen Typs |
array | $n$ | Vektoren des gleichen Typs |
data.frame | 2 | Vektoren der gleichen Länge |
list | 1 | Beliebige Objekte |
Sie können mit dem matrix()-Befehl angelegt werden:
mat <- matrix(c(7, 3, 9, 1, 4, 6), ncol = 2) # Matrixerstellung
Schauen Sie sich die erstellte Matrix an, in dem sie mat ausführen. Prüfen sie mit dem Befehl str(), von welcher Art die erstellte Matrix ist.
mat
## [,1] [,2]
## [1,] 7 1
## [2,] 3 4
## [3,] 9 6
str(mat)
## num [1:3, 1:2] 7 3 9 1 4 6
Auf die Elemente innerhalb von Matrizen kann man über die sogenannte Indizierung zugreifen, indem man Zeile und Spalte nach der folgenden Form ansteuert: [Zeile, Spalte]. Das Element in der dritten Zeile und der ersten Spalte erreichen wir also über:
mat[3, 1]
## [1] 9
Die Dimensionen einer Matrix lassen sich bestimmen über:
nrow(mat)
## [1] 3
ncol(mat)
## [1] 2
dim(mat) # alternativer Befehl
## [1] 3 2
Matrixoperationen
Im letzten Semester hatten wir schon verschiedene Matrixoperationen besprochen. Alle diese Operationen sind auch in R implementiert und über einfache Befehle nutzbar.
Hier ein Überblick über die in der Vorlesung behandelten Matrixoperationen und ihre Umsetzung in R (m steht dabei immer für eine beliebige Matrix):
| Operation | Befehl | Anmerkungen |
|---|---|---|
| Diagonale | diag(m) | |
| Spur | sum(diag(m)) | alternativ: tr() im psych-Paket |
| Transposition | t(m) | |
| Symmetrie prüfen | isSymmetric(m) | |
| Einheitsmatrix | diag(1, i) | i: Anzahl der Zeilen/Spalten |
| Addition | m1 + m2 | |
| Subtraktion | m1 - m2 | |
| Multiplikation (Skalar) | m * x | x: Skalar |
| Multiplikation (Matrizen) | m1 %*% m2 | |
| Inverse | solve(m) | |
| Determinante | det(m) |
Datenmanagement
Einlesen von Datensätzen
In der praktischen Nutzung bekommt man es mit Datensätzen in den unterschieldlichsten Dateiformaten zu tun. R kann Daten aus sehr vielen Formaten einlesen (.csv, .sav, .txt, .dat, …). Teilweise müssen dafür spezielle Packages benutzt werden. Häufig empfiehlt sich (außerhalb der R-eigenen Formaten) die Nutzung von csv-Dateien. Hier finden Sie eine Zusammenfassung dazu. Wenn Daten bereits im R-eigenen .rda-Format vorliegen, können diese über den Befehl load() eingelesen werden.
Wir müssen R nur mitteilen, wo der Datensatz liegt et voilà, er wird uns zur Verfügung gestellt. Liegt der Datensatz bspw. auf dem Desktop, so müssen wir den Dateipfad dorthin legen und können dann den Datensatz laden (wir gehen hier davon aus, dass Ihr PC “Musterfrau” heißt):
load("C:/Users/Musterfrau/Desktop/mach.rda")
Bei Dateipfaden ist darauf zu achten, dass bei Linux oder Mac OS Rechnern immer Front-Slashes ("/") zum Anzeigen von Hierarchien zwischen Ordnern verwendet werden, während auf Windows Rechnern im System aber bei Dateipfaden mit Back-Slashes gearbeitet wird ("\"). R nutzt auf Windows Rechnern ebenfalls Front-Slashes ("/"). Das bedeutet, dass, wenn wir auf Windows Rechnern den Dateipfad aus dem Explorer kopieren, wir die Slashes “umdrehen” müssen.
Genauso sind Sie in der Lage, den Datensatz direkt aus dem Internet zu laden. Hierzu brauchen Sie nur die URL und müssen R sagen, dass es sich bei dieser um eine URL handelt, indem Sie die Funktion url auf den Link anwenden. Der funktionierende Befehl sieht so aus (wobei die URL in Anführungszeichen geschrieben werden muss):
load(url("https://pandar.netlify.app/daten/mach.rda"))
Durch die Betrachtung dieses Link erkennen wir, dass Webseiten im Grunde auch nur sehr anschaulich dargestellte Ordnerstrukturen sind. So liegt auf der Pandar-Seite, die auf netlify.app gehostet wird, ein Ordner namens daten, in welchem wiederum das mach.rda liegt.
Die hier verwendeten Daten stammen aus dem “Open-Source Psychometrics Project”, einer Online-Plattform, die eine Sammlung an Daten aus verschiedensten Persönlichkeitstests zur Verfügung stellt. Wir haben bereits eine kleine Aufbereitung der Daten durchgeführt, damit wir leichter in die Analysen starten können. Auf der genannten Seite kann man Fragebögen selbst ausfüllen, und so zum Datenpool beitragen. Der hier verwendete Datensatz enthält Items aus einem Machiavellismus-Fragebogen, den Sie bei Interesse hier selbst ausfüllen können.
Überblick im Datensatz
Wir können uns die ersten (6) Zeilen des Datensatzes mit der Funktion head ansehen. Dazu müssen wir diese Funktion auf den Datensatz (das Objekt) mach anwenden:
head(mach) # ersten 6 Zeilen
## TIPI1 TIPI2 TIPI3 TIPI4
## 1 6 5 6 1
## 2 2 5 6 2
## 3 1 7 6 7
## 4 6 5 5 7
## 5 2 5 5 6
## 6 2 4 6 2
## TIPI5 TIPI6 TIPI7 TIPI8
## 1 7 3 7 4
## 2 4 6 5 4
## 3 5 7 1 4
## 4 7 2 6 2
## 5 7 6 5 3
## 6 3 7 5 2
## TIPI9 TIPI10 education
## 1 7 1 2
## 2 6 5 2
## 3 1 4 1
## 4 2 3 4
## 5 4 5 2
## 6 7 1 1
## urban gender engnat age
## 1 3 1 1 26
## 2 2 1 1 18
## 3 1 2 1 15
## 4 3 2 2 31
## 5 2 1 2 20
## 6 1 1 2 17
## hand religion orientation
## 1 1 7 1
## 2 1 1 1
## 3 1 2 2
## 4 1 6 1
## 5 1 4 3
## 6 1 1 1
## race voted married
## 1 30 1 2
## 2 60 2 1
## 3 10 2 1
## 4 60 1 3
## 5 60 1 1
## 6 70 2 1
## familysize nit pit
## 1 5 4.00 2.666667
## 2 2 5.00 1.166667
## 3 2 5.00 1.000000
## 4 2 3.75 2.166667
## 5 2 4.75 1.666667
## 6 3 4.00 2.666667
## cvhn pvhn
## 1 3.833333 2.00
## 2 3.833333 2.75
## 3 4.000000 2.00
## 4 3.000000 1.50
## 5 2.666667 2.00
## 6 3.166667 2.25
Da es sich bei unserem Datensatz um ein Objekt vom Typ data.frame handelt, können wir die Variablennamen des Datensatzes außerdem mit der names-Funktion abfragen. Eine weitere interessante Funktion ist dim, die die Anzahl der Zeilen und Spalten ausgibt.
names(mach) # Namen der Variablen
## [1] "TIPI1"
## [2] "TIPI2"
## [3] "TIPI3"
## [4] "TIPI4"
## [5] "TIPI5"
## [6] "TIPI6"
## [7] "TIPI7"
## [8] "TIPI8"
## [9] "TIPI9"
## [10] "TIPI10"
## [11] "education"
## [12] "urban"
## [13] "gender"
## [14] "engnat"
## [15] "age"
## [16] "hand"
## [17] "religion"
## [18] "orientation"
## [19] "race"
## [20] "voted"
## [21] "married"
## [22] "familysize"
## [23] "nit"
## [24] "pit"
## [25] "cvhn"
## [26] "pvhn"
dim(mach) # Anzahl der Zeilen und Spalten
## [1] 65151 26
Die ersten Items beschäftigen sich mit den üblichen Persönlichkeitseigenschaften. Anschließend gibt es einige demografische Angaben wie Alter oder auch Geschlecht. Die letzten Variablen repräsentieren Eigenschaften des Machiavellismus. Die Bedeutung von einzelnen Variablen wird erläutert, wenn Sie diese einsetzen.
Was bisher geschah… (Statistik I)
Einfache Deskriptivstatistik
Um auf einzelne Variablen in einem Datensatz zuzugreifen, kann man das $-Zeichen nutzen, und dann Funktionen auf die angesprochene Variable anwenden. Der Mittelwert wird mit der Funktion mean berechnet. Eine Schätzung für die Populationsvarianz erhalten wir mit var. Wir wenden diese uns bekannten Funktionen auf die Variable cvhn an. Diese gibt an, ob eine Person eine zynische Sichtweise auf die menschliche Natur hat.
mean(mach$cvhn) # Mittelwert
## [1] 2.986698
var(mach$cvhn) # geschätzte Populationsvarianz
## [1] 0.6593046
Alternativ kann man analog zu oben auch die bereits besprochene Indizierung über eckige Klammern nutzen, um eine oder mehrere Variablen oder Beobachtungen auszuwählen. Unsere Variable ist dabei in Spalte 25 zu finden.
mach[, 25] # Alle Zeilen, Spalte 25
## 3.83333333333333
## 3.83333333333333
## 4
## 3
## 2.66666666666667
## 3.16666666666667
## 3.16666666666667
## 3.33333333333333
## 3.5
## 2.83333333333333
## ...
Um eine Anzahl an Beobachtungen für eine bestimmte Variable zu bestimmen, kann mit der table-Funktion gearbeitet werden. Überprüfen wir die Häufigkeiten für die Variable, ob die Muttersprache Englisch ist engnat.
table(mach$engnat)
##
## 1 2
## 41169 23982
str(mach$engnat)
## num [1:65151] 1 1 1 2 2 2 2 1 2 1 ...
Wir sehen, dass die Variable noch als numerisch hinterlegt ist. Wir wollen jedoch den Zahlen die Bedeutung zuordnen und so einen Faktor erstellen. Diesen werden wir später noch verwenden.
mach$engnat <- factor(mach$engnat, # Ausgangsvariable
levels = 1:2, # Faktorstufen
labels = c("Ja", "Nein")) # Bedeutung
str(mach$engnat) # Test der Umwandlung
## Factor w/ 2 levels "Ja","Nein": 1 1 1 2 2 2 2 1 2 1 ...
Packages
Sogenannte Pakete stellen zusätzliche Funktionen zur Verfügung, die in base R nicht verfügbar sind. Aktuell sind in dem offiziellen Repository für R über 15.000 ergänzende Pakete verfügbar. Sehen Sie sich hier die vollständige Liste an. Wenn Sie nach einem Paket für einen bestimmten Zweck suchen, ist es jedoch leichter, eine konventionelle Suchmaschine zu nutzen. Ein gutes Paket für die einfache Berechnung vieler deskriptiver Werte ist psych (mit der Funktion describe). Ohne Installation und Aktivierung ist diese nicht verfügbar.
describe(mach$cvhn)
## Error in describe(mach$cvhn): konnte Funktion "describe" nicht finden
Pakete müssen vor der ersten Nutzung zunächst einmal heruntergeladen werden. Für einige von Ihnen wird dieser Schritt nicht nötig sein, da Sie es bereits heruntergeladen haben.
install.packages("psych")
Danach muss man ein Package aus der library laden. Dies muss nach jedem Neustart von R erneut erfolgen, damit das Package genutzt werden kann.
library(psych)
## Warning: Paket 'psych' wurde
## unter R Version 4.3.2
## erstellt
##
## Attache Paket: 'psych'
## Die folgenden Objekte sind maskiert von 'package:ggplot2':
##
## %+%, alpha
describe(mach$cvhn)
## vars n mean sd
## X1 1 65151 2.99 0.81
## median trimmed mad min
## X1 3 2.99 0.99 1
## max range skew kurtosis
## X1 5 4 -0.09 -0.61
## se
## X1 0
Weil wir häufig dazu tendieren, aus sehr vielen unterschiedlichen Paketen Funktionen zu nutzen, kann es sehr schnell unübersichtlich werden. Daher ist es sinnvoll, wie oben bereits angesprochen, alle Pakete an einem Ort zu Beginn des Skripts alle gemeinsam zu laden.
Zusammenhang und lineare Regression
Die lineare Regression ist eine sehr einfache Analyse, um den Zusammenhang zwischen zwei Variablen zu untersuchen. Wir wollen die bereits betrachtete zynische Sichtweise auf die menschliche Natur cvhn als Kriterium nutzen. Prädiktor wird die positive Sichtweise auf die menschliche Natur pvhn. Man sollte von einem negativen Zusammenhang der Werte ausgehen.
Natürlich ist die Regressionsanalyse nicht ohne Voraussetzungen. Diese werden wir in den nächsten Wochen nochmal besprechen, an dieser Stelle also nicht betrachten. Eine simple Darstellung des Zusammenhangs kann man über die plot-Funktion abbilden. Schönere Grafiken erhält man mittels ggplot, was in der nächsten Sitzung unser Thema wird.
plot(mach$pvhn, mach$cvhn, xlab = "Positive Sichtweise", ylab = "Negative Sichtweise")
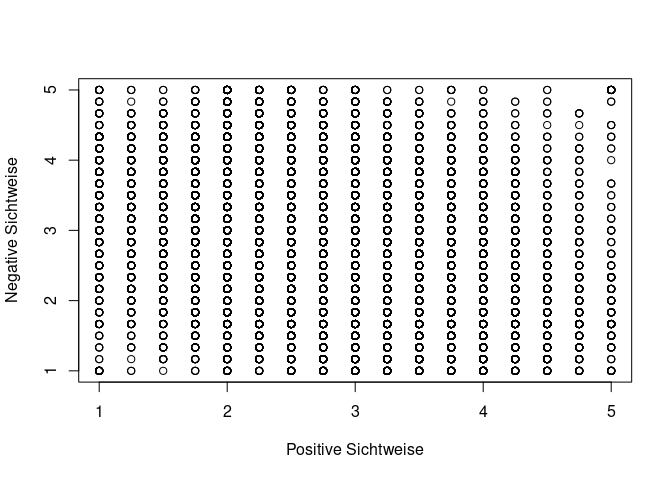
Gerade in diesem Plot sieht man, dass die Standardfunktionalität von R mit der Menge an Personen im Datensatz nicht zurechtkommt. Die Umsetzung der Parameterschätzung anhand der kleinsten Quadrate ist mit der Funktion lm möglich. Beachten Sie hierbei, dass angegeben wird, welche Variable durch welche Variable vorhergesagt wird. Das bedeutet, dass wir hier zuerst die zynische Sichtweise und dann das Alter nennen müssen.
lm(cvhn ~ pvhn, mach) # lineare Regression
##
## Call:
## lm(formula = cvhn ~ pvhn, data = mach)
##
## Coefficients:
## (Intercept) pvhn
## 4.2066 -0.4469
Das Steigungsgewicht ist wie erwartet negativ. Der hier gegebene Output enthält zwar die wichtigsten Informationen, doch wird eigentlich noch viel mehr innerhalb der Funktion berechnet. Dies ist ein gutes Beispiel dafür, dass es manchmal Sinn ergibt, auch die Ergebnisse der Analyse in ein Objekt abzulegen.
model <- lm(cvhn ~ pvhn, mach) # Objektzuweisung
Beispielsweise können wir wie bereits angedeutet die Funktion summary verwenden, um eine Zusammenfassung der Ergebnisse zu erhalten.
summary(model) # Ergebniszusammenfassung
##
## Call:
## lm(formula = cvhn ~ pvhn, data = mach)
##
## Residuals:
## Min 1Q Median
## -2.75965 -0.53245 0.02249
## 3Q Max
## 0.52249 3.02809
##
## Coefficients:
## Estimate
## (Intercept) 4.206587
## pvhn -0.446936
## Std. Error
## (Intercept) 0.011966
## pvhn 0.004249
## t value Pr(>|t|)
## (Intercept) 351.6 <2e-16
## pvhn -105.2 <2e-16
##
## (Intercept) ***
## pvhn ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01
## '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.7507 on 65149 degrees of freedom
## Multiple R-squared: 0.1451, Adjusted R-squared: 0.1451
## F-statistic: 1.106e+04 on 1 and 65149 DF, p-value: < 2.2e-16
Hier werden uns neben dem Steigungskoeffizienten und dem Achsenabschnitt auch noch beispielsweise deren Signifikanz und $R^2$ angezeigt. Beide werden hier als signifikant angegeben. Es handelt sich um einen mittleren Effekt.
Doch es gibt noch einige weitere Informationen, die von der Funktion lm abgelegt werden. Die Bezeichnung der Einträge in der Liste model kann über names abgefragt werden.
names(model) # andere Inhalte der Liste
## [1] "coefficients"
## [2] "residuals"
## [3] "effects"
## [4] "rank"
## [5] "fitted.values"
## [6] "assign"
## [7] "qr"
## [8] "df.residual"
## [9] "xlevels"
## [10] "call"
## [11] "terms"
## [12] "model"
Die weiteren Inhalte umfassen unter anderem die residuals, die für das Prüfen der Voraussetzungen wichtig wären, aber auch die vorhergesagten Werte (fitted.values).
Nachdem wir nun eine kurze Wiederholung zur Analyse zum Zusammenhang zwischen zwei Variablen betrachtet haben, geht es im folgenden Teil um den Unterschied zwischen Gruppen.
Der $t$-Test
Der $t$-Test stellt einen sehr einfachen Test auf einen Gruppenunterschied dar. Mithilfe dieses Tests soll untersucht werden, ob die Mittelwerte in zwei Gruppen gleich sind. Dazu brauchen wir drei wichtige Annahmen. Auch hier werden wir uns mit dem Prüfen der Voraussetzungen nicht nochmal genauer beschäftigen und gehen davon aus, dass diese gegeben sind. Sie können diese hier nochmal nachlesen.
In diesem Beispiel wollen wir uns damit beschäftigen, ob der zynische Blick auf die Menschheit in den Gruppen der native english speakers und non-native english speakers hinsichtlich des Mittelwerts gleich verteilt ist. Wir beschäftigen uns mit unabhängigen Stichproben. Für die Testung wird als Null-Hypothese die Gleichheit der Mittelwerte in den beiden Gruppen formuliert.
$$H_0: \mu_1=\mu_2$$ Diese Hypothese gilt nicht, wenn $\mu_1\neq\mu_2$. In diesem Fall gilt irgendeine Alternativhypothese ($H_1$) mit einer Mittelwertsdifferenz $d=\mu_1-\mu_2$, die nicht Null ist $(d\neq0)$.
Die Umsetzung in R ist dabei nicht schwer und funktioniert mittels t.test. Dabei müssen einige Argumente eingegeben werden. Zunächst geht es darum, unabhängige (engnat) und abhängie Variabe (cvhn) für den Test festzulegen. In data muss festgehalten werden, in welchem Datensatz diese Variablen zu finden sind. Das Argument paired hat ald Default FALSE, sodass standardmäßig unabhängige Stichproben angenommen werden. Wenn wir die Formelschreibweise benutzen, erlaubt uns R auch gar nicht, dieses Argument extra aufzuführen. Eine ungerichtete Hypothese ergibt für das Argument alternative den Input two.sided. Wir setzen die Varianzhomogenität var.equal auf TRUE, da wir wie beschrieben von der Erfüllung der Voraussetzungen ausgehen. Als Sicherheitsniveau (conf.level) legen wir 0.95 fest, was dann einem $\alpha$-Niveau von 0.05 entspricht.
t.test(cvhn ~ engnat, # abhängige Variable ~ unabhängige Variable
data = mach, # Datensatz
alternative = "two.sided", # zweiseitige Testung (Default)
var.equal = TRUE, # Homoskedastizität liegt vor (-> Levene-Test)
conf.level = .95) # alpha = .05 (Default)
##
## Two Sample t-test
##
## data: cvhn by engnat
## t = -46.855, df = 65149,
## p-value < 2.2e-16
## alternative hypothesis: true difference in means between group Ja and group Nein is not equal to 0
## 95 percent confidence interval:
## -0.3166909 -0.2912596
## sample estimates:
## mean in group Ja
## 2.874805
## mean in group Nein
## 3.178780
Der Output enthält folgende Informationen:
##
## Two Sample t-test
zeigt an, dass es sich um einen Zwei-Stichproben $t$-Test handelt.
## data: cvhn by engnat
## t = -46.855, df = 65149,
zeigt uns die Datengrundlage (X und Y), den $t$-Wert, die $df$ und den $p$-Wert.
$t$-Wert =-46.855 und $p$-Wert $p\approx$ 0, somit ist dieser Mittelwertsvergleich auf dem 5% Niveau signifikant ($p < .05$).
## p-value < 2.2e-16
## alternative hypothesis: true difference in means between group Ja and group Nein is not equal to 0
## 95 percent confidence interval:
## -0.3166909 -0.2912596
## sample estimates:
## mean in group Ja
## 2.874805
zeigt uns die Alternativhypothese ($H_1:d \neq 0$), das Konfidenzintervall der Mittelwertsdifferenz sowie die Mittelwerte in den beiden Gruppen. Dadurch können wir auch erkennen, dass die empirische Mittelwertsdifferenz bei liegt.
Wie bei der Regression können wir auch den Test als Objekt ablegen. Wenn wir names darauf anwenden, sehen wir wieder alle Namen, die wir hinter $ schreiben können.
ttest <- t.test(cvhn ~ engnat, # abhängige Variable ~ unabhängige Variable
data = mach, # Datensatz
alternative = "two.sided", # zweiseitige Testung (Default)
var.equal = TRUE, # Homoskedastizität liegt vor (-> Levene-Test)
conf.level = .95) # alpha = .05 (Default)
names(ttest) # alle möglichen Argumente, die wir diesem Objekt entlocken können
## [1] "statistic"
## [2] "parameter"
## [3] "p.value"
## [4] "conf.int"
## [5] "estimate"
## [6] "null.value"
## [7] "stderr"
## [8] "alternative"
## [9] "method"
## [10] "data.name"
ttest$statistic # (empirischer) t-Wert
## t
## -46.85501
ttest$p.value # zugehöriger p-Wert
## [1] 0
Da die Null-Hypothese verworfen wird, nehmen wir an, dass es in der Population einen Mittelwertsunterschied hinsichtlich des zynischen Blickes auf die Menschheit gibt.
Nun sind wir am Schluss des behandelten Codes in der Seminar-Sitzung angekommen. Die Grundlagen von R und einigen statistischen Verfahren sind nun aufgefrischt und wir können mit Mut ins zweite Semester starten!
Appendix
Appendix A
Dokumente erstellen mit R
Markdown-Dateien erstellen
Ein R-Markdown ist ein Dokument, welches im R-Editor erstellt wird, und sowohl Textbestandteile als auch R-Code enthalten kann. Dieses Dokument wird in R erstellt und bearbeitet, und kann danach z.B. als Word-, PDF- oder HTML-Datei ausgegeben werden. Ein Markdown besteht aus freien Textbereichen und aus sogenannten R-Chunks (Absätzen mit R-Code). In Textabsätzen können bestimmte Befehle genutzt werden, um die Formatierung des Textes (Überschriften, Fettdruck, etc.) anzupassen. Markdowns sind beispielsweise nützlich, um Berichte über Datenauswertungen zu schreiben, in denen Analysen und deren Beschreibung sowie Interpretation in einem Dokument gebündelt werden. Ergebnisse können direkt in den Text übernommen werden, was viel Arbeit und Fehler sparen kann.
Hier finden Sie eine sehr ausführliche Anleitung für die Arbeit mit Markdowns. Hier finden Sie ein sogenanntes Cheatsheet für R-Markdown, das viele wichtige Befehle kurz und knapp zusammenfasst.
Schritte zur Erstellung eines Markdowns
File -> New File -> R Markdown
Zielformat festlegen (Word, PDF, HTML…) und Titel geben
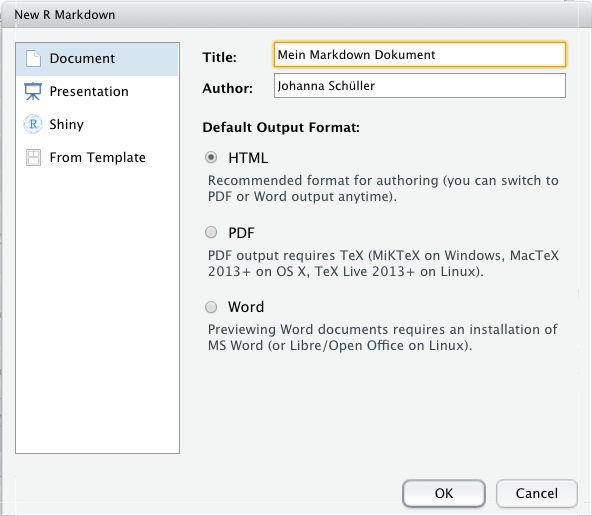
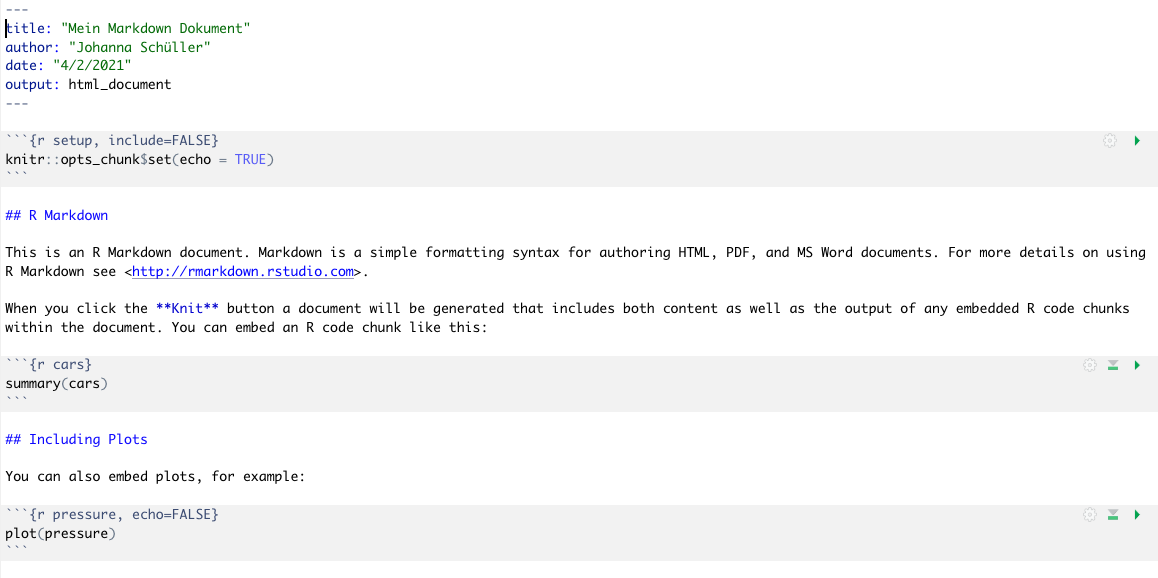
Das Skript, das dadurch erstellt wird ist eine Schablone mit Vorlagen für Freitext und R-Chunks und wichtigen Hinweisen für die Erstellung. Hier finden Sie viele Informationen, die Ihnen beim Bearbeiten Ihres Markdowns helfen. Diese Vorlage können Sie ganz einfach weiterbearbeiten, um Ihr eigenes Dokument zu erstellen.
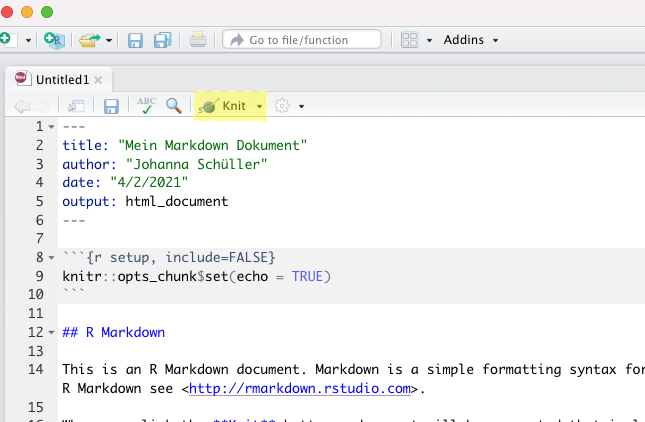
Indem Sie auf Knit (engl. “Stricken”) klicken, wird das Dokument in Zielformat erstellt. Ohne Änderungen an der Vorlage können Sie das Skript knitten, und sehen schon einmal, wie das finale Dokument aussehen wird. Wenn Sie Änderungen vornehmen, können Sie immer wieder überprüfen, wie sich das auf das erstellte Dokument auswirkt.
Papaja
Besonders hilfreich ist das Package papaja (Prepare Reproducible APA Journal Articles with R Markdown), mit dem RMarkdown-Dokumente automatisch in das APA-Format gebracht werden. Neben der korrekten Zitierweise können damit Tabellen und Abbildungen im passenden Format erstellt werden.
Wenn Sie das papaja-Package installiert haben, können Sie bei der Erstellung eines Markdowns mit den gleichen Schritten wie oben, unter Template den “APA article” auswählen, wodurch automatisch alle Einstellungen passend vorgenommen werden:
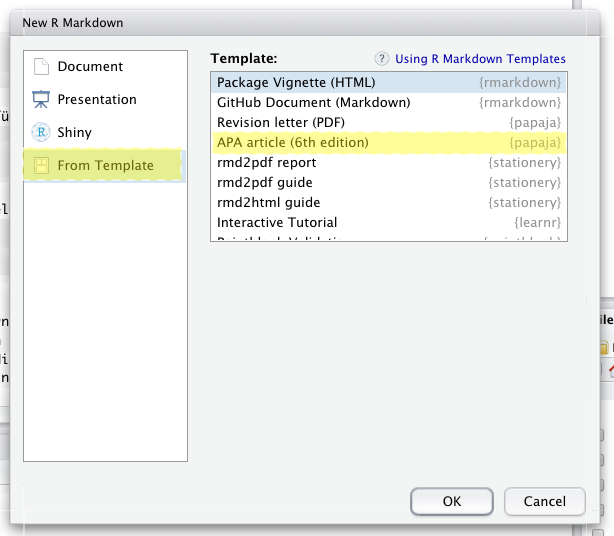
Das Manual für die Anwendung finden Sie online.
Appendix B
R-Code mit ChatGPT
t-Test mit ChatGPT
Wenn wir mit dem Datensatz mach prüfen wollen, ob Personen die nicht wählen (voted) insgesamt eine zynischere Betrachtung der Menschheit (cvhn) an den Tag legen, können wir ChatGPT darum bitten, den Code für uns zu generieren:
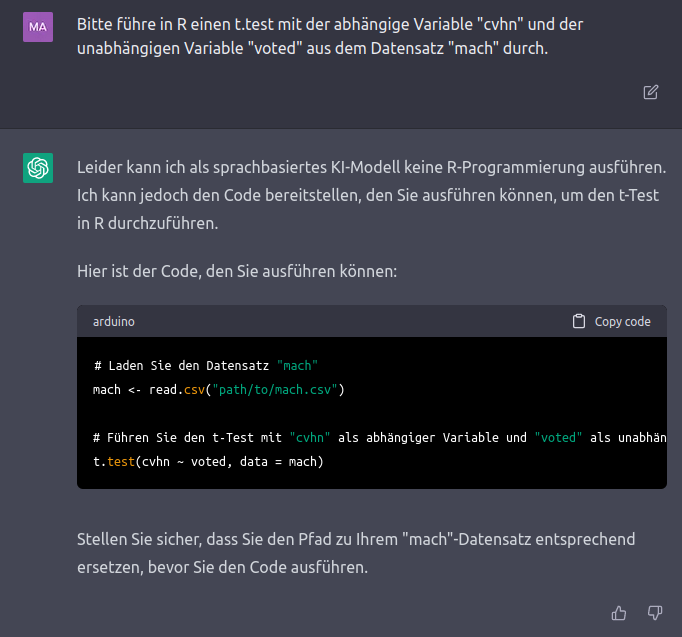
Diese Interaktion verdeutlicht bereits die oben genannten zwei wichtigen Aspekte, um ChatGPT sinnvoll für Hilfestellung mit R-Programmierung nutzen zu können:
- Sie müssen wissen, wie Sie diesen Code explizit auf Ihr Beispiel übertragen
- Sie müssen einschätzen können, ob das was hier passiert auch das ist, was Sie wollen.
Punkt 1 kann eventuell dadurch umgangen werden, dass Sie bessere Prompts schreiben als ich, aber mit ChatGPT 3.5, kann hier kein Code evaluiert werden - es wird also darauf hinauslaufen, dass Sie den Code bei sich durchführen und ihn dafür entsprechend anpassen. Wir können uns das verdeutlichen, indem wir ChatGPT um ein Beispiel mit simulierten Fragen bitten (weil es ja keinen Zugriff auf unsere Daten hat):
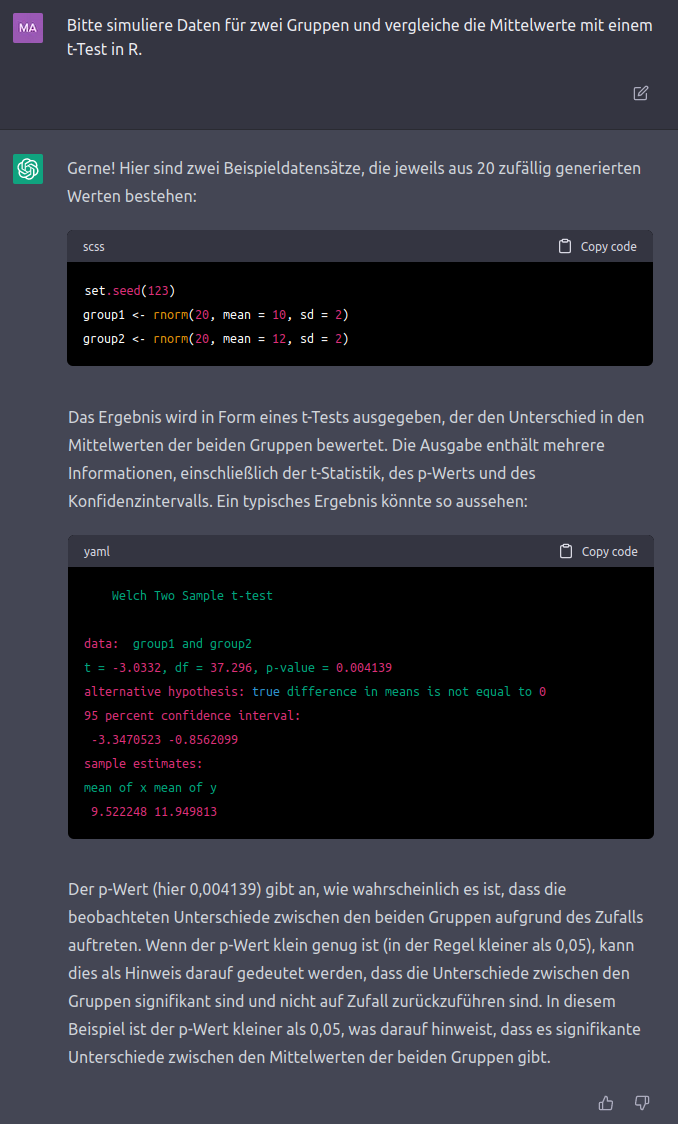
Die Antwort, die ChatGPT produziert ist beeindruckend detailliert (und größtenteils sogar richtig), aber Sie sollten hier Folgendes berücksichtigen:
set.seed(123)
group1 <- rnorm(20, mean = 10, sd = 2)
group2 <- rnorm(20, mean = 12, sd = 2)
t.test(group1, group2)
##
## Welch Two Sample t-test
##
## data: group1 and group2
## t = -2.823, df = 37.082,
## p-value = 0.007607
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -2.772764 -0.455712
## sample estimates:
## mean of x mean of y
## 10.28325 11.89749
Die Ergebnisse sind nicht die Gleichen, obwohl wir mit einem festen Seed gearbeitet haben. Wie wir in BSc2 mehrmals besprochen haben, ist set.seed aber explizit dafür da, dass bei jeder Durchführung des Zufallsexperiments auch exakt die gleichen Ergebnisse erzeugt werden. Das ist auch ChatGPT “bewusst”:
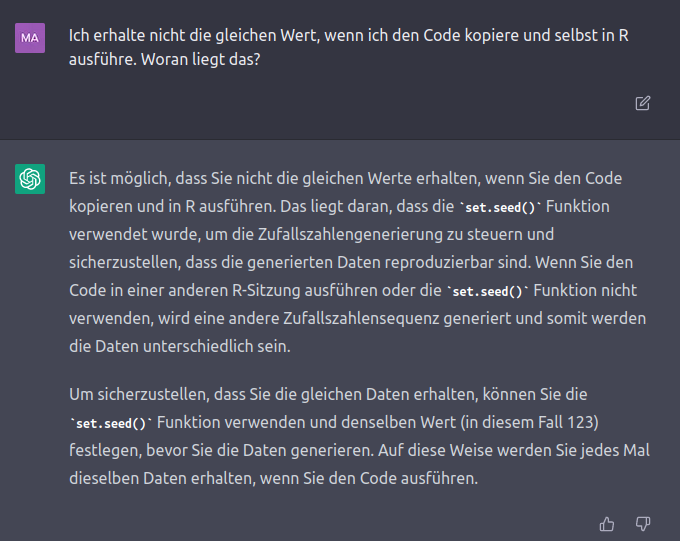
Was der KI hingegen an dieser Stelle nicht bewusst ist, ist dass Sie den Code nicht selbst ausgeführt hat, sondern es sich um eine (sehr komplexe) Zusammenstückelung von Informationen handelt, die online auffindbar sind. Sie können sich an dieser Stelle länger mit ChatGPT darüber streiten, wo dieser Unterschied herkommt, wenn Sie möchten (ich habe es probiert und irgendwann aufgegeben).
Den Aufmerksamen unter Ihnen ist auch direkt aufgefallen, was den 2. Punkt bekräftigt: ChatGPT hat ins in der ursprünglichen Anfrage nicht den R-Code für einen $t$-Test, sondern für einen Welch-Test präsentiert:
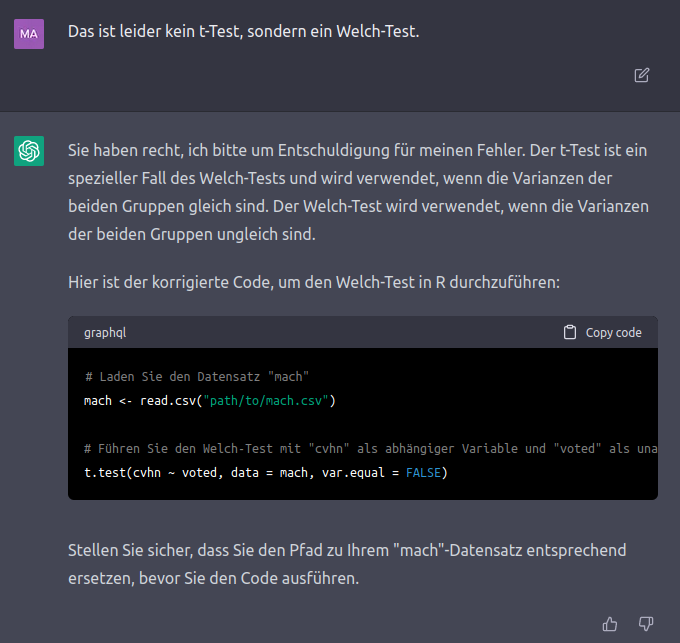
Dieser kurze Exkurs soll Ihnen zeigen, dass Sie ChatGPT durchaus sehr gut nutzen können, um R-Code erzeugen zu lassen (insbesondere, wenn es sich um komplexere Vorhaben handelt, als einfache $t$-Tests) - Sie sollten allerdings immer einschätzen können, ob der erzeugte Code sinnvoll ist und auch tatsächlich das macht, was Sie wollten.
Fehlerkorrektur mit ChatGPT
Neben der Möglichkeit mit ChatGPT neuen Code zu generieren, können Sie die Vorteile dieses Systems auch nutzen, um Fehler in Ihrem aktuellen Code zu identifizieren und zu beheben. Ein sehr vereinfachtes Beispiel:
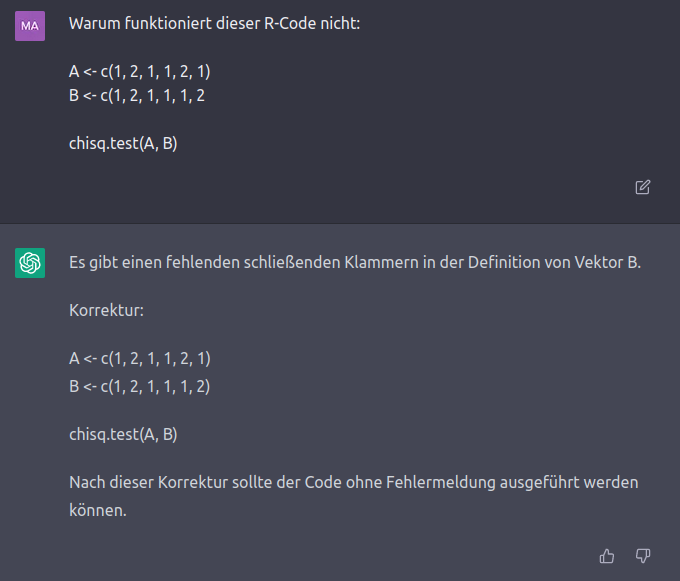
In diesem Beispiel sollten Sie bereits selbst den Fehler identifiziert haben, aber die KI ist auch bei komplexeren, längeren Skripten in der Lage, die Fehlerquellen relativ zuverlässig zu identifizieren. In Fällen, in denen das Problem nicht eindeutig klar aus dem Code hervorgeht, ohne ihn Zeile für Zeile zu evaluieren (wie wir oben gesehen haben, etwas das ChatGPT nicht kann), wird Ihnen eine Liste von möglichen Fehlerquellen gegeben, die Sie selbst inspizieren können.
Auch dabei das Skript Anderer (oder das eigene, schlecht kommentierte Skript) zu verstehen, kann ChatGPT behilflich sein. Nehmen Sie z.B. diese Funktion, die ich für BSc2 erstellt habe:
foo <- function(x) {
x <- na.omit(x)
sum((x - mean(x))^2)/length(x)
}
Sollte Ihnen nicht klar sein, was hier passiert, kann ChatGPT Abhilfe schaffen:
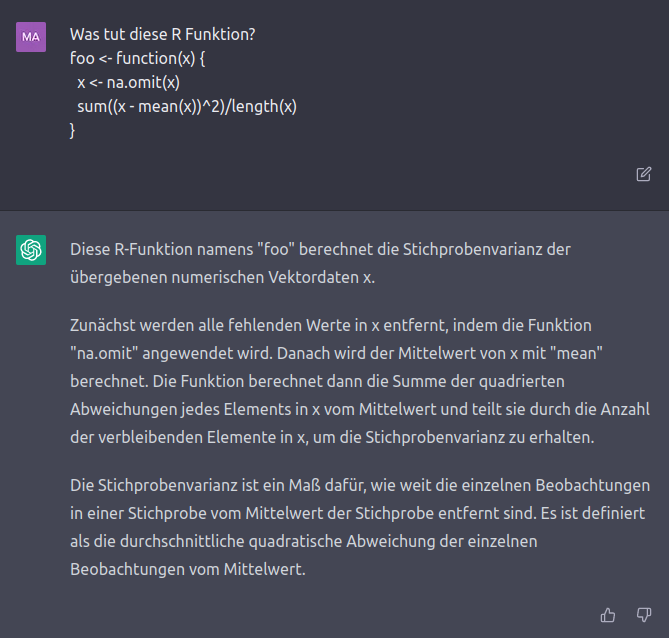
Darüber hinaus, könnten wir die KI an dieser Stelle auch bitten, solche selbstgeschriebenen Funktionen zu verbessern. Z.B. die Anzahl der Loops in unseren Skripten zu minimieren, damit die Auswertung schneller und effizienter läuft.
Generell sollten Sie ChatGPT als neues Werkzeug verstehen, welches Ihnen in vielen Belangen der R-Programmierung (und logischerweise auch darüber hinaus) behilflich sein kann. Wie bei jedem Werkzeug, sollte der Umgang aber gelernt und geübt sein, damit man für sich den meisten Nutzen daraus ziehen kann.
ChatGPT in R Konsole - Voraussetzungen
Inzwischen gibt es auch eine Möglichkeit, direkt in der R-Konsole mit ChatGPT zu interagieren. Dazu benötigen Sie allerdings einen ChatGPT Account, der mit API credentials ausgestattet ist. Das zugehörige Paket für die Funktionalität von ChatGPT in der R-Konsole heißt air. Dieses Paket muss wie üblich installiert werden, damit Sie auf die Funktionen zugreifen können. Mehr zu diesem Thema finden Sie hier in der Beschreibung des Pakets.
Literatur
Fox, J. & Weisberg, S. (2019). An {R} Companion to Applied Regression, Third Edition. Thousand Oaks CA: Sage. URL: https://socialsciences.mcmaster.ca/jfox/Books/Companion/
Revelle, W. (2020) psych: Procedures for Personality and Psychological Research, Northwestern University, Evanston, Illinois, USA, https://CRAN.R-project.org/package=psych Version = 2.0.9.
Robbins, S. B., Lauver, K., Le, H., Davis, D., Langley, R., & Carlstrom, A. (2004). Do psychosocial and study skill factors predict college outcomes? A meta-analysis. Psychological bulletin, 130(2), 261.
](/media/header/cat_with_glasses.jpg)